Article contents
Ripple modifications to alpha transport in tokamaks
Published online by Cambridge University Press: 02 November 2018
Abstract
Magnetic field ripple is inherent in tokamaks since the toroidal magnetic field is generated by a finite number of toroidal field coils. The field ripple results in departures from axisymmetry that cause radial transport losses of particles and heat. These ripple losses are a serious concern for alphas near their birth speed 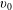 $v_{0}$ since alpha heating of the background plasma is required to make fusion reactors into economical power plants. Ripple in tokamaks gives rise to at least two alpha transport regimes of concern. As the slowing down time
$v_{0}$ since alpha heating of the background plasma is required to make fusion reactors into economical power plants. Ripple in tokamaks gives rise to at least two alpha transport regimes of concern. As the slowing down time 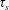 $\unicode[STIX]{x1D70F}_{s}$ is much larger than the time for an alpha just born to make a toroidal transit, a regime referred to as the
$\unicode[STIX]{x1D70F}_{s}$ is much larger than the time for an alpha just born to make a toroidal transit, a regime referred to as the 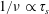 $1/\unicode[STIX]{x1D708}\propto \unicode[STIX]{x1D70F}_{s}$ regime can be encountered, with
$1/\unicode[STIX]{x1D708}\propto \unicode[STIX]{x1D70F}_{s}$ regime can be encountered, with  $\unicode[STIX]{x1D708}$ the appropriate alpha collision frequency. In this regime the radial transport losses increase as
$\unicode[STIX]{x1D708}$ the appropriate alpha collision frequency. In this regime the radial transport losses increase as 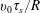 $v_{0}\unicode[STIX]{x1D70F}_{s}/R$, with
$v_{0}\unicode[STIX]{x1D70F}_{s}/R$, with 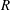 $R$ the major radius of the tokamak. The deleterious effect of ripple transport is mitigated by electric and magnetic drifts within the flux surface. When drift tangent to the flux surface becomes significant another ripple regime, referred to as the
$R$ the major radius of the tokamak. The deleterious effect of ripple transport is mitigated by electric and magnetic drifts within the flux surface. When drift tangent to the flux surface becomes significant another ripple regime, referred to as the 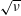 $\sqrt{\unicode[STIX]{x1D708}}$ regime, is encountered where a collisional boundary layer due to the drift plays a key role. We evaluate the alpha transport in both regimes, taking account of the alphas having a slowing down rather than a Maxwellian distribution function and their being collisionally scattered by a collision operator appropriate for alphas. Alpha ripple transport is found to be in the
$\sqrt{\unicode[STIX]{x1D708}}$ regime, is encountered where a collisional boundary layer due to the drift plays a key role. We evaluate the alpha transport in both regimes, taking account of the alphas having a slowing down rather than a Maxwellian distribution function and their being collisionally scattered by a collision operator appropriate for alphas. Alpha ripple transport is found to be in the 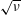 $\sqrt{\unicode[STIX]{x1D708}}$ regime where it will be a serious issue for typical tokamak reactors as it will be well above the axisymmetric neoclassical level and can be large enough to deplete the alpha slowing down distribution function unless toroidal rotation is strong.
$\sqrt{\unicode[STIX]{x1D708}}$ regime where it will be a serious issue for typical tokamak reactors as it will be well above the axisymmetric neoclassical level and can be large enough to deplete the alpha slowing down distribution function unless toroidal rotation is strong.
Keywords
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2018
References
A correction has been issued for this article:
- 9
- Cited by
Linked content
Please note a has been issued for this article.


