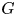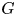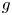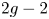1. Introduction
Tropical Geometry provides a framework to translate questions about an algebraic variety to questions about a polyhedral object associated to it called its tropicalization. In its most basic form, the framework is as follows.
Let $\mathbb {K}$![]() be a non-archimedean field, i.e. an algebraically closed field with a non-trivial non-archimedean valuation ${\rm val}$
be a non-archimedean field, i.e. an algebraically closed field with a non-trivial non-archimedean valuation ${\rm val}$![]() and complete with respect to it. Let $X$
and complete with respect to it. Let $X$![]() be a very affine variety over $\mathbb {K}$
be a very affine variety over $\mathbb {K}$![]() , i.e. a subvariety of the split torus $(\mathbb {K}^{\star })^n$
, i.e. a subvariety of the split torus $(\mathbb {K}^{\star })^n$![]() . The tropicalization map ${\rm trop}$
. The tropicalization map ${\rm trop}$![]() takes a point $(p_1,\ldots,p_n)$
takes a point $(p_1,\ldots,p_n)$![]() in $(\mathbb {K}^{\star })^n$
in $(\mathbb {K}^{\star })^n$![]() to its coordinatewise valuations $({\rm val}(p_1),\ldots,{\rm val}(p_n)) \in \mathbb {R}^n$
to its coordinatewise valuations $({\rm val}(p_1),\ldots,{\rm val}(p_n)) \in \mathbb {R}^n$![]() . The tropicalization of $X$
. The tropicalization of $X$![]() , denoted by ${\rm trop}(X)$
, denoted by ${\rm trop}(X)$![]() is then obtained by applying the map ${\rm trop}$
is then obtained by applying the map ${\rm trop}$![]() to every point in $X$
to every point in $X$![]() and taking the closure with respect to the Euclidean topology on $\mathbb {R}^n$
and taking the closure with respect to the Euclidean topology on $\mathbb {R}^n$![]() .
.
The notion of tropicalization can be extended in two ways: i. For very affine varieties over arbitrary algebraically ground fields equipped with the trivial valuation, the notion of tropicalization described above is not satisfactory. In this case, either an alternative description of tropicalization in terms of initial ideals [Reference Maclagan and Sturmfels23, Item (2),Theorem 3.2.3] or a base change to a field with a non-trivial valuation extending this trivial valuation is used [Reference Maclagan and Sturmfels23, Theorem 3.2.4] ii. the notion of tropicalization has been extended to arbitrary subvarieties of toric varieties (over algebraically closed, valued fields), referred to as the Kajiwara-Payne extended tropicalization [Reference Payne29], [Reference Maclagan and Sturmfels23, Chapter 6].
Tropical Graph Curves: The protagonists in this paper are tropical graph curves. Informally, a tropical graph curve $\mathbb {T}_G$![]() associated to a three-regular, connected, simple graph $G$
associated to a three-regular, connected, simple graph $G$![]() of genus $g$
of genus $g$![]() (also known as the first Betti number) is an arrangement of $2g-2$
(also known as the first Betti number) is an arrangement of $2g-2$![]() tropical lines in tropical projective space $\mathbb {TP}^{g-1}$
tropical lines in tropical projective space $\mathbb {TP}^{g-1}$![]() (equipped with the Euclidean topology) that contains $G$
(equipped with the Euclidean topology) that contains $G$![]() as a deformation retract. Tropical graph curves are tropical line arrangements in tropical projective space. Tropical hyperplane arrangements have recently received considerable attention in literature, see for example [Reference Ardila and Develin1, Reference Johnson and Kambites20]. On the other hand, tropical line arrangements have not received as much attention. We refer to [Reference Brandt, Jones, Lee and Ranganathan9, Theorem C] for a ‘universality’ property of tropical line arrangements in the plane. Our main result (see corollary 1.4) can be viewed as a construction of tropical line arrangements that are homeomorphic to a given simple, three-regular, three-connected planar graph.
as a deformation retract. Tropical graph curves are tropical line arrangements in tropical projective space. Tropical hyperplane arrangements have recently received considerable attention in literature, see for example [Reference Ardila and Develin1, Reference Johnson and Kambites20]. On the other hand, tropical line arrangements have not received as much attention. We refer to [Reference Brandt, Jones, Lee and Ranganathan9, Theorem C] for a ‘universality’ property of tropical line arrangements in the plane. Our main result (see corollary 1.4) can be viewed as a construction of tropical line arrangements that are homeomorphic to a given simple, three-regular, three-connected planar graph.
Our main motivation for studying tropical graph curves arises from the tropical lifting problem that we introduce in the following.
Tropical Lifting: The Bieri-Groves theorem [Reference Bieri and Groves6], [Reference Maclagan and Sturmfels23, Chapter 3, Section 3], a fundamental theorem in tropical geometry, states that ${\rm trop}(X)$![]() is a piecewise linear subset of $\mathbb {R}^n$
is a piecewise linear subset of $\mathbb {R}^n$![]() . Hence, ${\rm trop}(X)$
. Hence, ${\rm trop}(X)$![]() can be studied via polyhedral geometry. Furthermore, applications of tropical geometry crucially use this polyhedral structure. For most of these applications, an understanding of piecewise linear subsets of $\mathbb {R}^n$
can be studied via polyhedral geometry. Furthermore, applications of tropical geometry crucially use this polyhedral structure. For most of these applications, an understanding of piecewise linear subsets of $\mathbb {R}^n$![]() that arise as tropicalizations is essential, see [Reference Speyer31] for more details. This gives rise to the tropical lifting problem.
that arise as tropicalizations is essential, see [Reference Speyer31] for more details. This gives rise to the tropical lifting problem.
Problem 1.1 (Tropical Lifting Problem)
Let $\mathbb {K}$![]() be an algebraically closed, valued field. Characterize piecewise linear subsets of $\mathbb {R}^n$
be an algebraically closed, valued field. Characterize piecewise linear subsets of $\mathbb {R}^n$![]() (with finitely many pieces) that can be lifted, i.e. obtained as the tropicalization of a very affine variety over $\mathbb {K}$
(with finitely many pieces) that can be lifted, i.e. obtained as the tropicalization of a very affine variety over $\mathbb {K}$![]() or more generally, as the Kajiwara-Payne extended tropicalization of a subvariety of a toric variety over $\mathbb {K}$
or more generally, as the Kajiwara-Payne extended tropicalization of a subvariety of a toric variety over $\mathbb {K}$![]() .
.
The one-dimensional case, i.e. lifting piecewise linear subsets of $\mathbb {R}^n$![]() of dimension one is already highly non-trivial. Two necessary conditions are that every edge must have rational slope and that the set must satisfy the balancing condition (also known as the zero-tension condition): there is an assignment of a positive integer called multiplicity to each edge such that at every vertex, the sum of the outgoing slopes (where each outgoing slope is represented by a primitive point in $\mathbb {Z}^2$
of dimension one is already highly non-trivial. Two necessary conditions are that every edge must have rational slope and that the set must satisfy the balancing condition (also known as the zero-tension condition): there is an assignment of a positive integer called multiplicity to each edge such that at every vertex, the sum of the outgoing slopes (where each outgoing slope is represented by a primitive point in $\mathbb {Z}^2$![]() ) of the edges incident on it weighted by the corresponding multiplicity must be zero. A piecewise linear subset of $\mathbb {R}^n$
) of the edges incident on it weighted by the corresponding multiplicity must be zero. A piecewise linear subset of $\mathbb {R}^n$![]() satisfying these two necessary conditions is called a tropical curve [Reference Mikhalkin24, Section 2] and [Reference Maclagan and Sturmfels23, Section 1.3]. By the genus of a tropical curve, we mean its first Betti number when viewed as a metric graph (allowing infinite edge lengths), see [Reference Mikhalkin24, Definition 2.9].
satisfying these two necessary conditions is called a tropical curve [Reference Mikhalkin24, Section 2] and [Reference Maclagan and Sturmfels23, Section 1.3]. By the genus of a tropical curve, we mean its first Betti number when viewed as a metric graph (allowing infinite edge lengths), see [Reference Mikhalkin24, Definition 2.9].
The tropical lifting problem for tropical curves is wide open in general. The case of genus zero tropical curves is relatively well understood owing to the work of Mikhalkin [Reference Mikhalkin24, Corollary 3.16] for $n=2$![]() and to the works of Nishinou and Siebert [Reference Nishinou and Siebert26, Section 7] and Speyer [Reference Speyer31, Theorem 3.2] for arbitrary $n$
and to the works of Nishinou and Siebert [Reference Nishinou and Siebert26, Section 7] and Speyer [Reference Speyer31, Theorem 3.2] for arbitrary $n$![]() . Lifting genus one tropical curves was initiated by Speyer [Reference Speyer31, Theorem 3.2], also see Nishinou [Reference Nishinou27, Theorem 2], Tyomkin [Reference Tyomkin32], Ranganathan [Reference Ranganathan30, Theorems B and C] for further work. Katz [Reference Katz21, Theorem 1.1] introduced necessary conditions for lifting tropical curves of arbitrary genus that generalizes Speyer's condition and Nishinou's condition (both for genus one tropical curves and both called ‘well-spacedness’). Another flavour of the tropical lifting problem is to fix an ambient algebraic variety $\mathcal {S}$
. Lifting genus one tropical curves was initiated by Speyer [Reference Speyer31, Theorem 3.2], also see Nishinou [Reference Nishinou27, Theorem 2], Tyomkin [Reference Tyomkin32], Ranganathan [Reference Ranganathan30, Theorems B and C] for further work. Katz [Reference Katz21, Theorem 1.1] introduced necessary conditions for lifting tropical curves of arbitrary genus that generalizes Speyer's condition and Nishinou's condition (both for genus one tropical curves and both called ‘well-spacedness’). Another flavour of the tropical lifting problem is to fix an ambient algebraic variety $\mathcal {S}$![]() (for instance, an algebraic surface) and investigate lifting of tropical curves contained in the tropicalization of $\mathcal {S}$
(for instance, an algebraic surface) and investigate lifting of tropical curves contained in the tropicalization of $\mathcal {S}$![]() to algebraic curves contained in $\mathcal {S}$
to algebraic curves contained in $\mathcal {S}$![]() , we refer to [Reference Birkmeyer, Gathmann and Schmitz7, Reference Bogart and Katz8, Reference Brugallé and Shaw11] for more in this direction.
, we refer to [Reference Birkmeyer, Gathmann and Schmitz7, Reference Bogart and Katz8, Reference Brugallé and Shaw11] for more in this direction.
Since the tropical lifting problem is still wide open, studying weaker versions of the problem seems natural. One such weakening is the following: Classify metric graphs $\Gamma$![]() such that there is a tropical curve $T$
such that there is a tropical curve $T$![]() that contains $\Gamma$
that contains $\Gamma$![]() as a deformation retract and can be lifted to a smooth algebraic curve over $\mathbb {K}$
as a deformation retract and can be lifted to a smooth algebraic curve over $\mathbb {K}$![]() . Using the work of Baker, Payne and Rabinoff [Reference Baker, Payne and Rabinoff3, Theorem 1.1 and Theorem 5.20]Footnote 1, it follows that any metric graph $\Gamma$
. Using the work of Baker, Payne and Rabinoff [Reference Baker, Payne and Rabinoff3, Theorem 1.1 and Theorem 5.20]Footnote 1, it follows that any metric graph $\Gamma$![]() whose edge lengths are in the value group of $\mathbb {K}$
whose edge lengths are in the value group of $\mathbb {K}$![]() satisfies this property with the corresponding tropical curve $T$
satisfies this property with the corresponding tropical curve $T$![]() being contained in $\mathbb {R}^n$
being contained in $\mathbb {R}^n$![]() for a possibly “high” $n$
for a possibly “high” $n$![]() . Cheung, Fantini, Park and Ulirsch [Reference Cheung, Fantini, Park and Ulirsch13, Theorem 1.2] further refined this result by showing an effective upper bound on $n$
. Cheung, Fantini, Park and Ulirsch [Reference Cheung, Fantini, Park and Ulirsch13, Theorem 1.2] further refined this result by showing an effective upper bound on $n$![]() : the maximum of three and the valence of a vertex $v$
: the maximum of three and the valence of a vertex $v$![]() minus one over all vertices $v$
minus one over all vertices $v$![]() of $\Gamma$
of $\Gamma$![]() . In [Reference Cheung, Fantini, Park and Ulirsch13], the ground field $\mathbb {K}$
. In [Reference Cheung, Fantini, Park and Ulirsch13], the ground field $\mathbb {K}$![]() is the field of Puiseux series with coefficients in $\mathbb {C}$
is the field of Puiseux series with coefficients in $\mathbb {C}$![]() and hence, the edge lengths are required to be rational. Jell [Reference Jell19] introduced a strengthening of the notion of faithful tropicalization to so called fully faithful tropicalization and showed that every Mumford curve over $\mathbb {K}$
and hence, the edge lengths are required to be rational. Jell [Reference Jell19] introduced a strengthening of the notion of faithful tropicalization to so called fully faithful tropicalization and showed that every Mumford curve over $\mathbb {K}$![]() admits such a fully faithful tropicalization.
admits such a fully faithful tropicalization.
Tropical Lifting for Canonical Curves: From the viewpoint of applications of tropical geometry, lifting to specific classes of algebraic curves is important. One such class is that of smooth canonical curves: embeddings of a smooth, proper, non-hyperelliptic algebraic curve into projective space via the global sections of its canonical line bundle. Recall that for any integer $g \geq 3$![]() , a smooth curve in projective space $\mathbb {P}^{g-1}$
, a smooth curve in projective space $\mathbb {P}^{g-1}$![]() is a canonical curve of genus $g$
is a canonical curve of genus $g$![]() if and only if it is non-degenerate (not contained in any hyperplane) and has degree $2g-2$
if and only if it is non-degenerate (not contained in any hyperplane) and has degree $2g-2$![]() [Reference Eisenbud14, Theorem 9.3 and Section 9C, Exercise 5]. We refer to [Reference Eisenbud14, Chapter 9] for more information on canonical curves and to [Reference Geiger, Hashimoto, Sturmfels and Vlad16] for a recent combinatorial application thereof.
[Reference Eisenbud14, Theorem 9.3 and Section 9C, Exercise 5]. We refer to [Reference Eisenbud14, Chapter 9] for more information on canonical curves and to [Reference Geiger, Hashimoto, Sturmfels and Vlad16] for a recent combinatorial application thereof.
The lifting problem of metric graphs to smooth canonical curves takes the following form: Classify metric graphs $\Gamma$![]() such that there is a smooth canonical curve whose tropicalization deformation retracts to $\Gamma$
such that there is a smooth canonical curve whose tropicalization deformation retracts to $\Gamma$![]() . A classification is wide open: the techniques for arbitrary smooth curves are not directly applicable in this case, we refer to [Reference Brodsky, Joswig, Morrison and Sturmfels10] and [Reference Hahn, Markwig, Ren and Tyomkin18] for progress in the case of genus three metric graphs. A further weakening leads to a topological version of the problem where only the topological space underlying the metric graph is taken into account. Given an undirected, connected graph $G$
. A classification is wide open: the techniques for arbitrary smooth curves are not directly applicable in this case, we refer to [Reference Brodsky, Joswig, Morrison and Sturmfels10] and [Reference Hahn, Markwig, Ren and Tyomkin18] for progress in the case of genus three metric graphs. A further weakening leads to a topological version of the problem where only the topological space underlying the metric graph is taken into account. Given an undirected, connected graph $G$![]() (possibly with multiedges but with no loops), we denote the topological space underlying (any of) its geometric realizations (metric graphs whose underlying graph is $G$
(possibly with multiedges but with no loops), we denote the topological space underlying (any of) its geometric realizations (metric graphs whose underlying graph is $G$![]() ) by $G^{\rm top}$
) by $G^{\rm top}$![]() .
.
Problem 1.2 (Topological Tropical Lifting Problem for Smooth Canonical Curves)
Classify graphs $G$![]() such that there exists a smooth canonical curve whose tropicalization (in the extended sense) deformation retracts to $G^{\rm top}$
such that there exists a smooth canonical curve whose tropicalization (in the extended sense) deformation retracts to $G^{\rm top}$![]() .
.
Even in this topological version, a complete classification is wide open. We refer to [Reference Chan and Jiradilok12, Theorem 3.2] for the case when $G$![]() is the complete graph on four vertices. In the current article, we study the topological tropical lifting problem for certain non-smooth canonical curves, namely canonical embeddings of certain reducible nodal curves called graph curves. We refer to the work of Bayer and Eisenbud [Reference Bayer and Eisenbud4] for an introduction to this topic and to [Reference Geiger, Kuehn and Vlad17] for a recent combinatorial perspective.
is the complete graph on four vertices. In the current article, we study the topological tropical lifting problem for certain non-smooth canonical curves, namely canonical embeddings of certain reducible nodal curves called graph curves. We refer to the work of Bayer and Eisenbud [Reference Bayer and Eisenbud4] for an introduction to this topic and to [Reference Geiger, Kuehn and Vlad17] for a recent combinatorial perspective.
For a simpleFootnote 2 , three-regular, connected graph $G$![]() , the graph curve $X_G$
, the graph curve $X_G$![]() associated to it is the totally degenerate, nodal curve whose dual graph is $G$
associated to it is the totally degenerate, nodal curve whose dual graph is $G$![]() . By totally degenerate, we mean that each irreducible component is isomorphic to the projective line. The dual graph of a (reducible) curve is the graph whose vertices correspond to its irreducible components and there is an edge between two vertices if their corresponding components intersect. The three-regularity condition on the dual graph $G$
. By totally degenerate, we mean that each irreducible component is isomorphic to the projective line. The dual graph of a (reducible) curve is the graph whose vertices correspond to its irreducible components and there is an edge between two vertices if their corresponding components intersect. The three-regularity condition on the dual graph $G$![]() ensures that the graph curve $X_G$
ensures that the graph curve $X_G$![]() is independent of the choice of the nodes (thanks to the three transitivity of the action of the automorphism group of $\mathbb {P}^1$
is independent of the choice of the nodes (thanks to the three transitivity of the action of the automorphism group of $\mathbb {P}^1$![]() on $\mathbb {P}^1$
on $\mathbb {P}^1$![]() ). We address the topological tropical lifting problem for canonical embeddings of the graph curve $X_G$
). We address the topological tropical lifting problem for canonical embeddings of the graph curve $X_G$![]() where $G$
where $G$![]() is any three-regular, three-edge-connected planar graph. Before this, note that tropical projective space carries the Euclidean topology (see §§ 2.1 for more details) and hence, every extended tropicalization into it carries the induced topology. Our main theorem is the following:
is any three-regular, three-edge-connected planar graph. Before this, note that tropical projective space carries the Euclidean topology (see §§ 2.1 for more details) and hence, every extended tropicalization into it carries the induced topology. Our main theorem is the following:
Theorem 1.3 (Tropical Lifting for Canonically Embedded Planar Graph Curves)
Let $\kappa$![]() be an algebraically closed, valued field. For every three-regular, three-edge-connected planar graph $G$
be an algebraically closed, valued field. For every three-regular, three-edge-connected planar graph $G$![]() , there is a canonical embedding of the corresponding graph curve $X_G$
, there is a canonical embedding of the corresponding graph curve $X_G$![]() over $\kappa$
over $\kappa$![]() whose extended tropicalization (with respect to the given valuation on $\kappa$
whose extended tropicalization (with respect to the given valuation on $\kappa$![]() ) is homeomorphic to $G^{\rm top}$
) is homeomorphic to $G^{\rm top}$![]() .
.
To the best of our knowledge, the tropical lifting problem for singular algebraic curves has not been studied before and we emphasize that the graph curve $X_G$![]() in theorem 1.3 is canonically embedded. We say that a canonical embedding of $X_G$
in theorem 1.3 is canonically embedded. We say that a canonical embedding of $X_G$![]() admits a weakly faithful tropicalization or equivalently, that the tropicalization of this canonical embedding is weakly faithful if its tropicalization (in the extended sense and with respect to the given valuation on $\kappa$
admits a weakly faithful tropicalization or equivalently, that the tropicalization of this canonical embedding is weakly faithful if its tropicalization (in the extended sense and with respect to the given valuation on $\kappa$![]() ) contains $G^{\rm top}$
) contains $G^{\rm top}$![]() as a deformation retract. Furthermore, note that the Berkovich analytification $(X_G)_{\rm Berk}$
as a deformation retract. Furthermore, note that the Berkovich analytification $(X_G)_{\rm Berk}$![]() of $X_G$
of $X_G$![]() contains $G^{\rm top}$
contains $G^{\rm top}$![]() as a deformation retract. The space $(X_G)_{\rm Berk}$
as a deformation retract. The space $(X_G)_{\rm Berk}$![]() is constructed as follows: consider one copy of the Berkovich projective line $(\mathbb {P}^1_{\rm Berk})_u$
is constructed as follows: consider one copy of the Berkovich projective line $(\mathbb {P}^1_{\rm Berk})_u$![]() for each vertex $u$
for each vertex $u$![]() of $G$
of $G$![]() . For each edge $e=(u,v)$
. For each edge $e=(u,v)$![]() of $G$
of $G$![]() , note that there is a node $n_e$
, note that there is a node $n_e$![]() of $X_G$
of $X_G$![]() , and identify $(\mathbb {P}^1_{\rm Berk})_u$
, and identify $(\mathbb {P}^1_{\rm Berk})_u$![]() and $(\mathbb {P}^1_{\rm Berk})_v$
and $(\mathbb {P}^1_{\rm Berk})_v$![]() at the type I points corresponding to $n_e$
at the type I points corresponding to $n_e$![]() [Reference Berkovich5, Chapter 4] and [Reference Baker, Payne and Rabinoff2].
[Reference Berkovich5, Chapter 4] and [Reference Baker, Payne and Rabinoff2].
The extended tropicalization of the canonical embedding of $X_G$![]() promised by theorem 1.3 is an example of a tropical graph curve. As a corollary, we obtain the existence of tropical graph curves corresponding to three-regular, three-edge-connected planar graphs.
promised by theorem 1.3 is an example of a tropical graph curve. As a corollary, we obtain the existence of tropical graph curves corresponding to three-regular, three-edge-connected planar graphs.
Corollary 1.4 Any three-regular, three-edge-connected planar graph has a tropical graph curve associated to it.
For a three-regular graph, three-edge-connectivity is equivalent to three-vertex-connectivity [Reference Bayer and Eisenbud4, Lemma 2.6]. Hence, in this context we will use the term ‘three-connected’ for three-edge-connected. In the following, we outline the key steps in the proof of theorem 1.3.
1.1. Key ingredients of the proof of theorem 1.3
We explicitly construct a canonical embedding of $X_G$![]() and show that its extended tropicalization is weakly faithful. We refer to this embedding as the Schön embedding Footnote 3 of $X_G$
and show that its extended tropicalization is weakly faithful. We refer to this embedding as the Schön embedding Footnote 3 of $X_G$![]() , denoted by $X_G^{\rm sch}$
, denoted by $X_G^{\rm sch}$![]() . The Schön embedding can be described in geometric terms as follows. Since $G$
. The Schön embedding can be described in geometric terms as follows. Since $G$![]() is a three-vertex-connected planar graph, by Steinitz’ theorem ([Reference Ziegler34, Chapter 4]), it is the one-skeleton of a three-dimensional polytope $P$
is a three-vertex-connected planar graph, by Steinitz’ theorem ([Reference Ziegler34, Chapter 4]), it is the one-skeleton of a three-dimensional polytope $P$![]() . Furthermore, since $G$
. Furthermore, since $G$![]() is three-regular, the polar $P^{\vee }$
is three-regular, the polar $P^{\vee }$![]() of $P$
of $P$![]() is a simplicial polytope. Consider the Stanley–Reisner surface of the simplicial complex associated to $P^{\vee }$
is a simplicial polytope. Consider the Stanley–Reisner surface of the simplicial complex associated to $P^{\vee }$![]() . The Schön embedding is a hyperplane section of this surface. We refer to proposition 3.2 for more details. We also refer to Bayer and Eisenbud [Reference Bayer and Eisenbud4, Section 6] where general hyperplane sections of this Stanley–Reisner surface have been studied.
. The Schön embedding is a hyperplane section of this surface. We refer to proposition 3.2 for more details. We also refer to Bayer and Eisenbud [Reference Bayer and Eisenbud4, Section 6] where general hyperplane sections of this Stanley–Reisner surface have been studied.
We study the extended tropicalization of $X_G^{\rm sch}$![]() in terms of the primary decomposition of its defining radical ideal. The following explicit description of this primary decomposition plays an important role. The primary decomposition of the Schön embedding is constructed in terms of a planar embedding of $G$
in terms of the primary decomposition of its defining radical ideal. The following explicit description of this primary decomposition plays an important role. The primary decomposition of the Schön embedding is constructed in terms of a planar embedding of $G$![]() . The Euclidean closure of the unique unbounded component in the complement of $G$
. The Euclidean closure of the unique unbounded component in the complement of $G$![]() in $\mathbb {R}^2$
in $\mathbb {R}^2$![]() is called the exterior face. The Euclidean closures of the other components are called interior faces. By Euler's formula for planar graphs, there are precisely $g$
is called the exterior face. The Euclidean closures of the other components are called interior faces. By Euler's formula for planar graphs, there are precisely $g$![]() interior faces of a planar embedding of $G$
interior faces of a planar embedding of $G$![]() , where $g$
, where $g$![]() is the genus (also known as the first Betti number) of $G$
is the genus (also known as the first Betti number) of $G$![]() . We identify the homogenous coordinate ring of $\mathbb {P}_{\kappa }^{g-1}$
. We identify the homogenous coordinate ring of $\mathbb {P}_{\kappa }^{g-1}$![]() with $\kappa [x_F|$
with $\kappa [x_F|$![]() over all interior faces $F$
over all interior faces $F$![]() of $G$
of $G$![]() ] (equipped with its standard grading). Furthermore, any canonical embedding of a graph curve $X_G$
] (equipped with its standard grading). Furthermore, any canonical embedding of a graph curve $X_G$![]() of arithmetic genus $g$
of arithmetic genus $g$![]() (also, equal to the genus of $G$
(also, equal to the genus of $G$![]() ) is an arrangement of $2g-2$
) is an arrangement of $2g-2$![]() lines in $\mathbb {P}_{\kappa }^{g-1}$
lines in $\mathbb {P}_{\kappa }^{g-1}$![]() [Reference Bayer and Eisenbud4, Proposition 1.1 (and its proof)]. A three-regular graph of genus $g$
[Reference Bayer and Eisenbud4, Proposition 1.1 (and its proof)]. A three-regular graph of genus $g$![]() has $2g-2$
has $2g-2$![]() vertices and $3g-3$
vertices and $3g-3$![]() edges. The $2g-2$
edges. The $2g-2$![]() vertices are in bijection with the irreducible components of $X_G$
vertices are in bijection with the irreducible components of $X_G$![]() .
.
To each vertex $v$![]() of $G$
of $G$![]() , we associate a line in $\mathbb {P}_{\kappa }^{g-1}$
, we associate a line in $\mathbb {P}_{\kappa }^{g-1}$![]() defined by an ideal $L_v$
defined by an ideal $L_v$![]() corresponding to it. This line is the irreducible component of $X_G$
corresponding to it. This line is the irreducible component of $X_G$![]() corresponding to $v$
corresponding to $v$![]() . Note that $L_v$
. Note that $L_v$![]() is given by $g-2$
is given by $g-2$![]() linearly independent linear forms. We distinguish between two types of vertices, namely interior and the exterior vertices. An interior vertex is a vertex that is not incident on the exterior face. Otherwise, the vertex is called an exterior vertex. Note that an interior vertex has precisely three interior faces incident on it whereas an exterior vertex has precisely two interior faces incident on it.
linearly independent linear forms. We distinguish between two types of vertices, namely interior and the exterior vertices. An interior vertex is a vertex that is not incident on the exterior face. Otherwise, the vertex is called an exterior vertex. Note that an interior vertex has precisely three interior faces incident on it whereas an exterior vertex has precisely two interior faces incident on it.
For an interior vertex $v$![]() , the line $L_v$
, the line $L_v$![]() is cut out by the linear form $x_{F_i}+x_{F_j}+x_{F_k}$
is cut out by the linear form $x_{F_i}+x_{F_j}+x_{F_k}$![]() where $F_i,F_j,F_k$
where $F_i,F_j,F_k$![]() are the three interior faces that are incident on it and by the variables $x_F$
are the three interior faces that are incident on it and by the variables $x_F$![]() over all interior faces $F \notin \{ F_i,F_j,F_k\}$
over all interior faces $F \notin \{ F_i,F_j,F_k\}$![]() . Note that we have specified $g-2$
. Note that we have specified $g-2$![]() linearly independent linear forms. For an exterior vertex $v$
linearly independent linear forms. For an exterior vertex $v$![]() , the line $L_v$
, the line $L_v$![]() is generated by the variables $x_F$
is generated by the variables $x_F$![]() over all interior faces $F$
over all interior faces $F$![]() that are not incident on $v$
that are not incident on $v$![]() . Here again, we have specified $g-2$
. Here again, we have specified $g-2$![]() linearly independent linear forms.
linearly independent linear forms.
Example 1.5 Consider the one-skeleton of a cube (as shown in Fig. 1). Here $g=5$![]() and any canonical embedding of the associated graph curve is an arrangement of eight lines in $\mathbb {P}^4_{\kappa }$
and any canonical embedding of the associated graph curve is an arrangement of eight lines in $\mathbb {P}^4_{\kappa }$![]() . In this case, $v_1,v_2,v_3$
. In this case, $v_1,v_2,v_3$![]() and $v_4$
and $v_4$![]() are interior vertices and the others are exterior vertices. The eight lines are the following:
are interior vertices and the others are exterior vertices. The eight lines are the following:


Figure 1. A planar embedding of the cube.
We consider the extended tropicalization ${\rm tropproj}(X_G^{\rm sch})$![]() of the resulting arrangement of lines. This is an arrangement of $2g-2$
of the resulting arrangement of lines. This is an arrangement of $2g-2$![]() tropical lines $\{{\rm tropproj}(L_v)\}_v$
tropical lines $\{{\rm tropproj}(L_v)\}_v$![]() in $\mathbb {TP}^{g-1}$
in $\mathbb {TP}^{g-1}$![]() that we denote by $\mathcal {T}$
that we denote by $\mathcal {T}$![]() . We refer to figure 11 for examples. We identify $\mathbb {TP}^{g-1}$
. We refer to figure 11 for examples. We identify $\mathbb {TP}^{g-1}$![]() with a $(g-1)$
with a $(g-1)$![]() -simplex, see §§ 2.1 for more details. We construct a homeomorphism $\phi$
-simplex, see §§ 2.1 for more details. We construct a homeomorphism $\phi$![]() between $G^{\rm top}$
between $G^{\rm top}$![]() and $\mathcal {T}$
and $\mathcal {T}$![]() (§§ 4.1). In the following, we identify key properties of $\mathcal {T}$
(§§ 4.1). In the following, we identify key properties of $\mathcal {T}$![]() that go into the construction of $\phi$
that go into the construction of $\phi$![]() . The tropical lines ${\rm tropproj}(L_u)$
. The tropical lines ${\rm tropproj}(L_u)$![]() and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$![]() intersect if and only if $u$
intersect if and only if $u$![]() and $v$
and $v$![]() are adjacent in $G$
are adjacent in $G$![]() (Lemma 4.1). If $u$
(Lemma 4.1). If $u$![]() is an interior vertex, then ${\rm tropproj}(L_u)$
is an interior vertex, then ${\rm tropproj}(L_u)$![]() contains precisely one branch point and this is of valence three. If $u$
contains precisely one branch point and this is of valence three. If $u$![]() is an exterior vertex, then ${\rm tropproj}(L_u)$
is an exterior vertex, then ${\rm tropproj}(L_u)$![]() is an edge of $\mathbb {TP}^{g-1}$
is an edge of $\mathbb {TP}^{g-1}$![]() and hence, consists only of bivalent points. These properties lead to the following classification of the points of $\mathcal {T}$
and hence, consists only of bivalent points. These properties lead to the following classification of the points of $\mathcal {T}$![]() (Lemma 4.2) that we summarize in the following. The points of $\mathcal {T}$
(Lemma 4.2) that we summarize in the following. The points of $\mathcal {T}$![]() are either bivalent or trivalent. The trivalent points of $\mathcal {T}$
are either bivalent or trivalent. The trivalent points of $\mathcal {T}$![]() are exclusively of the following two types: i. Branch point $b_u$
are exclusively of the following two types: i. Branch point $b_u$![]() of ${\rm tropproj}(L_u)$
of ${\rm tropproj}(L_u)$![]() where $u$
where $u$![]() is an interior vertex. ii. The intersection point $\zeta _{(u,\iota (u))}$
is an interior vertex. ii. The intersection point $\zeta _{(u,\iota (u))}$![]() of ${\rm tropproj}(L_u)$
of ${\rm tropproj}(L_u)$![]() and ${\rm tropproj}(L_{\iota (u)})$
and ${\rm tropproj}(L_{\iota (u)})$![]() where $u$
where $u$![]() is an exterior vertex and $\iota (u)$
is an exterior vertex and $\iota (u)$![]() is the unique interior vertex adjacent to it (Item 4, proposition 2.4). With this information at hand, we define $\phi$
is the unique interior vertex adjacent to it (Item 4, proposition 2.4). With this information at hand, we define $\phi$![]() on the vertex set of $G^{\rm top}$
on the vertex set of $G^{\rm top}$![]() as follows:
as follows:

With some additional effort, this definition can be extended to $G^{\rm top}$![]() yielding the homeomorphism $\phi$
yielding the homeomorphism $\phi$![]() , we refer to §§ 4.1 for more details.
, we refer to §§ 4.1 for more details.
1.2 Connectivity between tropicalizations
Steinitz’ theorem ([Reference Ziegler34, Chapter 4], theorem 5.1) states that a graph is the one-skeleton of a three-polytope if and only if it is simple, planar and three-vertex-connected. A standard proof of this theorem shows a connectivity property of three-vertex-connected planar graphs with respect to an operation called the $\Delta Y$![]() -transformation. Motivated by this, we prove a connectivity result between the extended tropicalizations of Schön embeddings (§ 5). We define a tropical analogue of the notion of $\Delta Y$
-transformation. Motivated by this, we prove a connectivity result between the extended tropicalizations of Schön embeddings (§ 5). We define a tropical analogue of the notion of $\Delta Y$![]() (and $Y \Delta$
(and $Y \Delta$![]() ) transformations. A tropical $\Delta Y$
) transformations. A tropical $\Delta Y$![]() transformation is an operation that transforms a (certain type) of tropical line arrangement to another. We also use another operation called the contraction-elongation operation due to Pachner [Reference Pachner28] (although in the dual form) and define its tropical analogue. We show the following connectivity property.
transformation is an operation that transforms a (certain type) of tropical line arrangement to another. We also use another operation called the contraction-elongation operation due to Pachner [Reference Pachner28] (although in the dual form) and define its tropical analogue. We show the following connectivity property.
Theorem 1.6 Let $G_1$![]() and $G_2$
and $G_2$![]() be three-regular, three-connected planar graphs, and let $\mathcal {T}_{G_1}$
be three-regular, three-connected planar graphs, and let $\mathcal {T}_{G_1}$![]() and $\mathcal {T}_{G_2}$
and $\mathcal {T}_{G_2}$![]() be the extended tropicalizations of $X_{G_1}^{\rm sch}$
be the extended tropicalizations of $X_{G_1}^{\rm sch}$![]() and $X_{G_2}^{\rm sch}$
and $X_{G_2}^{\rm sch}$![]() , respectively. There exists a finite sequence consisting of tropical $\Delta Y$
, respectively. There exists a finite sequence consisting of tropical $\Delta Y$![]() , tropical $Y \Delta$
, tropical $Y \Delta$![]() and tropical contraction-elongation transformations that transforms $\mathcal {T}_{G_1}$
and tropical contraction-elongation transformations that transforms $\mathcal {T}_{G_1}$![]() to $\mathcal {T}_{G_2}$
to $\mathcal {T}_{G_2}$![]() .
.
One potential application of this connectivity result is in carrying out inductive arguments on the set $\{ \mathcal {T}_G\}_G$![]() .
.
A Future Direction: An approach to tropical lifting for (certain) smooth canonical curves by ‘deforming’ the Schön embedding of $X_G$![]() . It seems plausible that this deformation can be carried out via deformations of the associated Stanley–Reisner surface.
. It seems plausible that this deformation can be carried out via deformations of the associated Stanley–Reisner surface.
A Suggestion to the Reader: The construction of the Schön embedding and the connectivity result (theorem 1.6) nicely lend themselves to illustration. We recommend skimming over figures 4, 10 and 11 at this point.
2. Preliminaries
2.1. A brief interlude into tropical projective space
We start by briefly recalling tropical projective space, we refer to [Reference Maclagan and Sturmfels23, Chapter 6, Section 2] for a detailed discussion. Analogous to its classical counterpart, tropical projective space in $n$![]() -dimensions $\mathbb {TP}^n$
-dimensions $\mathbb {TP}^n$![]() can be constructed in different ways, we describe the one via compactification here. This mimics the construction of projective space as a torus compactification.
can be constructed in different ways, we describe the one via compactification here. This mimics the construction of projective space as a torus compactification.
Let $(1,\ldots,1)^{\perp }$![]() denote the hyperplane $\{ (y_0,\ldots,y_{n})|~\sum _{i=0}^{n}y_i=0\} \subseteq \mathbb {R}^{n+1}$
denote the hyperplane $\{ (y_0,\ldots,y_{n})|~\sum _{i=0}^{n}y_i=0\} \subseteq \mathbb {R}^{n+1}$![]() . We consider $(1,\ldots,1)^{\perp }$
. We consider $(1,\ldots,1)^{\perp }$![]() as a model for the tropical torus in $n$
as a model for the tropical torus in $n$![]() -dimensions. Each point in $(1,\ldots,1)^{\perp }$
-dimensions. Each point in $(1,\ldots,1)^{\perp }$![]() is a representative of an orbit of tropical multiplication of $\mathbb {R}$
is a representative of an orbit of tropical multiplication of $\mathbb {R}$![]() on $\mathbb {R}^{n+1}$
on $\mathbb {R}^{n+1}$![]() via $\lambda \odot (q_0,\ldots,q_n)=(\lambda +q_0,\ldots,\lambda +q_n)$
via $\lambda \odot (q_0,\ldots,q_n)=(\lambda +q_0,\ldots,\lambda +q_n)$![]() . We compactify it with the $(n+1)$
. We compactify it with the $(n+1)$![]() -coordinate hyperplanes. It is convenient to think of these hyperplanes $\mathcal {H}_0,\ldots,\mathcal {H}_{n}$
-coordinate hyperplanes. It is convenient to think of these hyperplanes $\mathcal {H}_0,\ldots,\mathcal {H}_{n}$![]() , say as living at ‘infinity’. In particular, $\mathcal {H}_i$
, say as living at ‘infinity’. In particular, $\mathcal {H}_i$![]() is the intersection of the affine copy of the hyperplane $(0,\ldots,0,\underbrace {1}_{i},0,\ldots,0)^{\perp }\cap (1,\ldots,1)^{\perp }$
is the intersection of the affine copy of the hyperplane $(0,\ldots,0,\underbrace {1}_{i},0,\ldots,0)^{\perp }\cap (1,\ldots,1)^{\perp }$![]() at ‘infinity’. Hence, $\mathbb {TP}^n$
at ‘infinity’. Hence, $\mathbb {TP}^n$![]() is homeomorphic to the $n$
is homeomorphic to the $n$![]() -simplex, also see [Reference Maclagan and Sturmfels23, Example 6.2.4 and remark 6.2.5]. For each $i$
-simplex, also see [Reference Maclagan and Sturmfels23, Example 6.2.4 and remark 6.2.5]. For each $i$![]() , the $i$
, the $i$![]() -dimensional faces of $\mathbb {TP}^n$
-dimensional faces of $\mathbb {TP}^n$![]() are in bijection with the $i$
are in bijection with the $i$![]() -dimensional orbits of the standard torus action on $\mathbb {P}^n$
-dimensional orbits of the standard torus action on $\mathbb {P}^n$![]() . This identification is particularly useful for visualization purposes. Note that $\mathbb {TP}^n$
. This identification is particularly useful for visualization purposes. Note that $\mathbb {TP}^n$![]() inherits a topology from the Euclidean topology on $\mathbb {R}^n$
inherits a topology from the Euclidean topology on $\mathbb {R}^n$![]() that we also refer to as the Euclidean topology on $\mathbb {TP}^n$
that we also refer to as the Euclidean topology on $\mathbb {TP}^n$![]() .
.
2.1.1. Tropicalizing into $\mathbb {TP}^n$ .
.
In the following, we briefly discuss tropicalization of a subvariety of projective space into tropical projective space to fit our needs in the future sections. We refer to [Reference Maclagan and Sturmfels23, Subsection 6.2] for a more thorough treatment of this topic.
Given a graded ideal $I$![]() of $\kappa [x_1,\ldots,x_{n+1}]$
of $\kappa [x_1,\ldots,x_{n+1}]$![]() where $\kappa$
where $\kappa$![]() is an algebraically closed and valued field, the extended (Kajiwara-Payne) tropicalization ${\rm tropproj}(I)$
is an algebraically closed and valued field, the extended (Kajiwara-Payne) tropicalization ${\rm tropproj}(I)$![]() of $I$
of $I$![]() (into $\mathbb {TP}^n$
(into $\mathbb {TP}^n$![]() ) is defined as the union of the tropicalizations of $I$
) is defined as the union of the tropicalizations of $I$![]() when restricted to each torus orbit of $\mathbb {P}^n$
when restricted to each torus orbit of $\mathbb {P}^n$![]() .
.
Note that each torus orbit of $\mathbb {P}^n$![]() corresponds to a (possibly) empty subset $\mathcal {V}$
corresponds to a (possibly) empty subset $\mathcal {V}$![]() of $[1,\ldots,n+1]$
of $[1,\ldots,n+1]$![]() . Its coordinate ring is identified with the Laurent polynomial ring $\kappa [x_j^{\pm 1}| j\notin \mathcal {V}]$
. Its coordinate ring is identified with the Laurent polynomial ring $\kappa [x_j^{\pm 1}| j\notin \mathcal {V}]$![]() . The restriction of $I=\langle g_1,\ldots,g_r \rangle$
. The restriction of $I=\langle g_1,\ldots,g_r \rangle$![]() to this torus orbit is the ideal $\tilde {I}=\langle \tilde {g_1},\ldots,\tilde {g_r} \rangle$
to this torus orbit is the ideal $\tilde {I}=\langle \tilde {g_1},\ldots,\tilde {g_r} \rangle$![]() of $\kappa [x_j^{\pm 1}| j\notin \mathcal {V}]$
of $\kappa [x_j^{\pm 1}| j\notin \mathcal {V}]$![]() where $\tilde {g_j}$
where $\tilde {g_j}$![]() is obtained from $g_j$
is obtained from $g_j$![]() by setting each variable $x_j$
by setting each variable $x_j$![]() where $j \in \mathcal {V}$
where $j \in \mathcal {V}$![]() to zero.
to zero.
Recall that a generating set $B$![]() of $I$
of $I$![]() is called a tropical basis for $I$
is called a tropical basis for $I$![]() if $\cap _{f \in B}{\rm trop}(f)={\rm trop}(I)$
if $\cap _{f \in B}{\rm trop}(f)={\rm trop}(I)$![]() [Reference Maclagan and Sturmfels23, Definition 2.6.3]. A homogenous generating set $B$
[Reference Maclagan and Sturmfels23, Definition 2.6.3]. A homogenous generating set $B$![]() of $I$
of $I$![]() is called an extended tropical basis for $I$
is called an extended tropical basis for $I$![]() if $\cap _{f\in B}{\rm tropproj}(f)={\rm tropproj}(I)$
if $\cap _{f\in B}{\rm tropproj}(f)={\rm tropproj}(I)$![]() .
.
2.1.2. Linear subspaces of tropical projective space.
We primarily encounter tropicalizations of linear subspaces of projective space, in particular lines.
Definition 2.1 [Reference Maclagan and Sturmfels23, Definition 4.2.1]
A $k$![]() -dimensional tropicalized linear subspace in $\mathbb {TP}^n$
-dimensional tropicalized linear subspace in $\mathbb {TP}^n$![]() is defined as the extended tropicalization ${\rm tropproj}(I)$
is defined as the extended tropicalization ${\rm tropproj}(I)$![]() of the defining ideal $I$
of the defining ideal $I$![]() of a $k$
of a $k$![]() -dimensional linear subspace of $\mathbb {P}^{n}$
-dimensional linear subspace of $\mathbb {P}^{n}$![]() .
.
In order to tropicalize an ideal into $\mathbb {TP}^n$![]() , knowing an extended tropical basis apriori is particularly useful. The linear subspaces we encounter in this paper are all defined by a set of linear forms with mutually disjoint support. For instance, the ideal $L_{v_2}=\langle x_{F_1}+x_{F_3}+x_{F_4}, x_{F_2}, x_{F_5} \rangle$
, knowing an extended tropical basis apriori is particularly useful. The linear subspaces we encounter in this paper are all defined by a set of linear forms with mutually disjoint support. For instance, the ideal $L_{v_2}=\langle x_{F_1}+x_{F_3}+x_{F_4}, x_{F_2}, x_{F_5} \rangle$![]() from the introduction. Such a linear subspace has a particularly simple extended tropical basis.
from the introduction. Such a linear subspace has a particularly simple extended tropical basis.
Lemma 2.2 Suppose that the ideal $I$![]() is generated by non-zero linear forms $\ell _1,\ldots,\ell _r$
is generated by non-zero linear forms $\ell _1,\ldots,\ell _r$![]() such that their supports are mutually disjoint. The set $\{\ell _1,\ldots,\ell _r\}$
such that their supports are mutually disjoint. The set $\{\ell _1,\ldots,\ell _r\}$![]() is an extended tropical basis for $I$
is an extended tropical basis for $I$![]() .
.
Proof. Recall that a circuit of $I$![]() is a linear form whose support is inclusion-minimal. By [Reference Maclagan and Sturmfels23, Lemma 4.3.16], the circuits of $I$
is a linear form whose support is inclusion-minimal. By [Reference Maclagan and Sturmfels23, Lemma 4.3.16], the circuits of $I$![]() form a tropical basis for it. The main idea behind the proof is to apply this lemma to every torus orbit of $\mathbb {P}^n$
form a tropical basis for it. The main idea behind the proof is to apply this lemma to every torus orbit of $\mathbb {P}^n$![]() .
.
For any torus orbit of $\mathbb {P}^n$![]() , let $\tilde {\ell }_j$
, let $\tilde {\ell }_j$![]() and $\tilde {I}$
and $\tilde {I}$![]() be the restrictions of $\ell _j$
be the restrictions of $\ell _j$![]() and $I$
and $I$![]() , respectively to this torus orbit. Since the supports of $\ell _1,\ldots,\ell _r$
, respectively to this torus orbit. Since the supports of $\ell _1,\ldots,\ell _r$![]() are mutually disjoint, they are precisely the set of circuits of $I$
are mutually disjoint, they are precisely the set of circuits of $I$![]() . More generally, the set of non-zero elements of $\{\tilde {\ell }_1,\ldots,\tilde {\ell }_r \}$
. More generally, the set of non-zero elements of $\{\tilde {\ell }_1,\ldots,\tilde {\ell }_r \}$![]() are precisely the set of circuits of $\tilde {I}$
are precisely the set of circuits of $\tilde {I}$![]() and by [Reference Maclagan and Sturmfels23, Lemma 4.3.16], we know that this set is a tropical basis for $\tilde {I}$
and by [Reference Maclagan and Sturmfels23, Lemma 4.3.16], we know that this set is a tropical basis for $\tilde {I}$![]() . Hence, $\{\ell _1,\ldots,\ell _r\}$
. Hence, $\{\ell _1,\ldots,\ell _r\}$![]() is an extended tropical basis for $I$
is an extended tropical basis for $I$![]() .
.
2.2. Remarks on planar embeddings
In the following, we make precise the sense in which we use the term ‘planar embedding’ throughout the article and record facts about them that we use frequently. Before this, we note that each edge of $G$![]() corresponds to an open interval in $G^{\rm top}$
corresponds to an open interval in $G^{\rm top}$![]() .
.
Definition 2.3 A planar embedding of a simple graph $G$![]() is a continuous, injective function $\tau :G^{\rm top} \rightarrow \mathbb {R}^2$
is a continuous, injective function $\tau :G^{\rm top} \rightarrow \mathbb {R}^2$![]() such that the following properties are satisfied:
such that the following properties are satisfied:
1. The function $\tau$
 takes each edge $e$
takes each edge $e$ of $G^{\rm top}$
of $G^{\rm top}$ to an open interval.
to an open interval.2. The set $\mathbb {R}^2 \setminus ({\rm Im}(\tau ))$
 , where ${\rm Im}(\tau )$
, where ${\rm Im}(\tau )$ is the image of $\tau$
is the image of $\tau$ , consists of finitely many connected components. All connected components, except precisely one, are bounded. The (Euclidean) closure of each bounded connected component is a convex polygon. The unbounded component is the complement of a convex polygon.
, consists of finitely many connected components. All connected components, except precisely one, are bounded. The (Euclidean) closure of each bounded connected component is a convex polygon. The unbounded component is the complement of a convex polygon.
Recall from the introduction that the Euclidean closures of the bounded components are called the interior faces of the planar embedding and the Euclidean closure of the unbounded component is called the exterior face of the planar embedding. By Steinitz’ theorem ([Reference Ziegler34, Chapter 4]), every three-vertex-connected planar graph $G$![]() is a one-skeleton of a three-dimensional polytope and an embedding of $G$
is a one-skeleton of a three-dimensional polytope and an embedding of $G$![]() can be obtained via a stereographic projection of this polytope into $\mathbb {R}^2$
can be obtained via a stereographic projection of this polytope into $\mathbb {R}^2$![]() . We also refer to the related notion of convex embeddings of planar graphs [Reference Lovász and Vesztergombi22, Chapter 4]. In the following, we record properties of $\tau$
. We also refer to the related notion of convex embeddings of planar graphs [Reference Lovász and Vesztergombi22, Chapter 4]. In the following, we record properties of $\tau$![]() that will be useful in the forthcoming sections.
that will be useful in the forthcoming sections.
Proposition 2.4 Let $G$![]() be a planar graph embedded by $\tau$
be a planar graph embedded by $\tau$![]() . The following properties hold:
. The following properties hold:
1. Three distinct vertices that are pairwise adjacent do not share two distinct interior faces. Three distinct vertices can share at most one face (interior or exterior).
2. Every edge is shared by precisely two faces (one of which might be the exterior face). If a pair of distinct vertices are not both exterior vertices and are adjacent, then they share precisely two interior faces. If both are exterior vertices and are adjacent, then they share precisely one interior face of $G$
 . If $G$
. If $G$ is three-regular and if a pair of distinct vertices are not adjacent, then they share at most one interior face of $G$
is three-regular and if a pair of distinct vertices are not adjacent, then they share at most one interior face of $G$ . Furthermore, with the same hypothesis on $G$
. Furthermore, with the same hypothesis on $G$ , if both these vertices are exterior vertices that are not adjacent, then they do not share an interior face.
, if both these vertices are exterior vertices that are not adjacent, then they do not share an interior face.3. If $G$
 is a three-regular, three-connected graph, then every interior face can share at most one edge with the exterior face.
is a three-regular, three-connected graph, then every interior face can share at most one edge with the exterior face.4. If $G$
 is three-regular, every exterior vertex has a unique interior vertex adjacent to it.
is three-regular, every exterior vertex has a unique interior vertex adjacent to it.
The proof of proposition 2.4 mainly uses the convexity property of the faces (Item 2, definition 2.3).
3. The Schön embedding of $X_G$
We begin by recalling the Schön embedding of a graph curve $X_G$![]() where $G$
where $G$![]() is a three-regular, three-connected planar graph. Let $G$
is a three-regular, three-connected planar graph. Let $G$![]() be a three-regular, three-connected planar graph. We label the interior faces of the planar embedding by variables: let $x_F$
be a three-regular, three-connected planar graph. We label the interior faces of the planar embedding by variables: let $x_F$![]() be the variable corresponding to the face $F$
be the variable corresponding to the face $F$![]() . Let $R$
. Let $R$![]() be the graded polynomial ring with coefficients in $\kappa$
be the graded polynomial ring with coefficients in $\kappa$![]() (the ground field) and variables $x_F$
(the ground field) and variables $x_F$![]() where $F$
where $F$![]() ranges over all the interior faces of the planar embedding of $G$
ranges over all the interior faces of the planar embedding of $G$![]() . We identify $\mathbb {P}^{g-1}$
. We identify $\mathbb {P}^{g-1}$![]() with ${\rm Proj}(R)$
with ${\rm Proj}(R)$![]() .
.
To each vertex $v$![]() of $G$
of $G$![]() , we associate an ideal $L_v$
, we associate an ideal $L_v$![]() defined by a collection of linear forms as follows. Let $\Sigma _v$
defined by a collection of linear forms as follows. Let $\Sigma _v$![]() be the ideal generated by the variables $x_F$
be the ideal generated by the variables $x_F$![]() over all interior faces $F$
over all interior faces $F$![]() that are not incident on $v$
that are not incident on $v$![]() .
.
1. If $v$
 is an interior vertex, then $L_v:=\Sigma _v+ \langle x_{F_i}+x_{F_j}+x_{F_k} \rangle$
is an interior vertex, then $L_v:=\Sigma _v+ \langle x_{F_i}+x_{F_j}+x_{F_k} \rangle$ where $x_{F_i},x_{F_j}$
where $x_{F_i},x_{F_j}$ and $x_{F_k}$
and $x_{F_k}$ are the variables corresponding to the three interior faces that are incident on $v$
are the variables corresponding to the three interior faces that are incident on $v$ .
.2. If $v$
 is an exterior vertex, then $L_v:=\Sigma _v$
is an exterior vertex, then $L_v:=\Sigma _v$ .
.
In both the cases above, $L_v$![]() defines a line in $\mathbb {P}^{g-1}$
defines a line in $\mathbb {P}^{g-1}$![]() . We refer to the algebraic curve in $\mathbb {P}^{g-1}$
. We refer to the algebraic curve in $\mathbb {P}^{g-1}$![]() corresponding to the line arrangement defined by $L_v$
corresponding to the line arrangement defined by $L_v$![]() as $v$
as $v$![]() varies over all the vertices of $G$
varies over all the vertices of $G$![]() as the Schön embedding of the graph curve $X_G$
as the Schön embedding of the graph curve $X_G$![]() . As we shall see in proposition 3.4, this is a canonical embedding of $X_G$
. As we shall see in proposition 3.4, this is a canonical embedding of $X_G$![]() .
.
Proposition 3.1 The dual graph of the Schön embedding of $X_G$![]() is $G$
is $G$![]() . Furthermore, the Schön embedding is non-degenerate, i.e. it is not contained in any hyperplane of $\mathbb {P}^{g-1}$
. Furthermore, the Schön embedding is non-degenerate, i.e. it is not contained in any hyperplane of $\mathbb {P}^{g-1}$![]() .
.
Proof. The first part of the proposition follows by noting that if vertices $u \neq v$![]() are adjacent, then, by Item 2, proposition 2.4, they share precisely two distinct faces $F_i$
are adjacent, then, by Item 2, proposition 2.4, they share precisely two distinct faces $F_i$![]() and $F_j$
and $F_j$![]() (one of which is the exterior face precisely when both $u$
(one of which is the exterior face precisely when both $u$![]() and $v$
and $v$![]() are exterior vertices). Furthermore, if at least one of $u$
are exterior vertices). Furthermore, if at least one of $u$![]() or $v$
or $v$![]() is an interior vertex, then $L_u+L_v=\langle x_{F_i}+x_{F_j},~x_F|$
is an interior vertex, then $L_u+L_v=\langle x_{F_i}+x_{F_j},~x_F|$![]() $F$
$F$![]() is not incident on either $u$
is not incident on either $u$![]() or $v$
or $v$![]() $\rangle$
$\rangle$![]() and otherwise, $L_u+L_v=\langle x_F|$
and otherwise, $L_u+L_v=\langle x_F|$![]() $F$
$F$![]() is not incident on either $u$
is not incident on either $u$![]() or $v$
or $v$![]() $\rangle$
$\rangle$![]() . In both cases, $L_u+L_v$
. In both cases, $L_u+L_v$![]() defines a point in $\mathbb {P}^{g-1}$
defines a point in $\mathbb {P}^{g-1}$![]() . Conversely, if vertices $u \neq v$
. Conversely, if vertices $u \neq v$![]() are not adjacent, then by Item 2, proposition 2.4, $L_u+L_v$
are not adjacent, then by Item 2, proposition 2.4, $L_u+L_v$![]() is the irrelevant ideal. Hence, the dual graph of the Schön embedding is $G$
is the irrelevant ideal. Hence, the dual graph of the Schön embedding is $G$![]() .
.
For the second part, suppose for the sake of contradiction that a hyperplane defined by the linear form $\sum _{F}a_Fx_F$![]() contains the Schön embedding. Hence, $\sum _{F}a_Fx_F \in L_v$
contains the Schön embedding. Hence, $\sum _{F}a_Fx_F \in L_v$![]() for all vertices $v$
for all vertices $v$![]() . For each interior vertex $v$
. For each interior vertex $v$![]() , the condition that $\sum _{F}a_Fx_F \in L_v$
, the condition that $\sum _{F}a_Fx_F \in L_v$![]() implies that the coefficients $a_{F_i}=a_{F_j}=a_{F_k}$
implies that the coefficients $a_{F_i}=a_{F_j}=a_{F_k}$![]() for the three interior faces $F_i,F_j$
for the three interior faces $F_i,F_j$![]() and $F_k$
and $F_k$![]() that are incident on $v$
that are incident on $v$![]() . By Steinitz’ theorem, $G$
. By Steinitz’ theorem, $G$![]() is the one-skeleton of a three-dimensional polytope $P$
is the one-skeleton of a three-dimensional polytope $P$![]() . Note that the polar polytope $P^{\vee }$
. Note that the polar polytope $P^{\vee }$![]() of $P$
of $P$![]() is also a three-dimensional polytope. Its vertices are in bijection with the faces of $G$
is also a three-dimensional polytope. Its vertices are in bijection with the faces of $G$![]() (including the exterior one). By Steinitz’ theorem, the one-skeleton of $P^{\vee }$
(including the exterior one). By Steinitz’ theorem, the one-skeleton of $P^{\vee }$![]() is three-vertex-connected. Hence, the graph obtained from the one-skeleton of $P^{\vee }$
is three-vertex-connected. Hence, the graph obtained from the one-skeleton of $P^{\vee }$![]() by deleting the vertex corresponding to the exterior face of $G$
by deleting the vertex corresponding to the exterior face of $G$![]() is connected and this implies that all the coefficients $a_F$
is connected and this implies that all the coefficients $a_F$![]() are equal. Hence, the hyperplane must be defined by $\sum _{F}x_F$
are equal. Hence, the hyperplane must be defined by $\sum _{F}x_F$![]() . However, this hyperplane does not contain the line corresponding to $L_v$
. However, this hyperplane does not contain the line corresponding to $L_v$![]() for any exterior vertex $v$
for any exterior vertex $v$![]() .
.
In the following, we describe the Schön embedding in terms of certain Stanley–Reisner ideals. Recall that the Stanley–Reisner ideal of a simplicial complex $\Delta$![]() with vertex set $\{1,\ldots,n\}$
with vertex set $\{1,\ldots,n\}$![]() is a monomial ideal $I_{\Delta }$
is a monomial ideal $I_{\Delta }$![]() in $\kappa [x_1,\ldots,x_n]$
in $\kappa [x_1,\ldots,x_n]$![]() , [Reference Francisco, Mermin and Schweig15]. It is generated by products of variables $\prod _{i \in \bar {F}} x_i$
, [Reference Francisco, Mermin and Schweig15]. It is generated by products of variables $\prod _{i \in \bar {F}} x_i$![]() where $\bar {F} \subseteq \{1,\ldots,n\}$
where $\bar {F} \subseteq \{1,\ldots,n\}$![]() is a non-face of $\Delta$
is a non-face of $\Delta$![]() . We refer to its associated projective variety as the Stanley–Reisner variety of $\Delta$
. We refer to its associated projective variety as the Stanley–Reisner variety of $\Delta$![]() .
.
Recall that for a polytope $Q$![]() , its dual simplicial complex is the simplicial complex whose vertex set is the set of facets of $Q$
, its dual simplicial complex is the simplicial complex whose vertex set is the set of facets of $Q$![]() and the simplices are the subsets consisting of facets of $Q$
and the simplices are the subsets consisting of facets of $Q$![]() whose intersection is non-empty. Let $M$
whose intersection is non-empty. Let $M$![]() be the dual simplicial complex of the three-dimensional polytope $P$
be the dual simplicial complex of the three-dimensional polytope $P$![]() associated to $G$
associated to $G$![]() . Let $\mathcal {F}$
. Let $\mathcal {F}$![]() be the set of faces (both interior and exterior) of the planar embedding of $G$
be the set of faces (both interior and exterior) of the planar embedding of $G$![]() . Note that the vertices of $M$
. Note that the vertices of $M$![]() are in bijection with the facets of $P$
are in bijection with the facets of $P$![]() and the facets of $P$
and the facets of $P$![]() are in turn in bijection with the elements of $\mathcal {F}$
are in turn in bijection with the elements of $\mathcal {F}$![]() . Hence, we consider the graded polynomial ring $\tilde {R}$
. Hence, we consider the graded polynomial ring $\tilde {R}$![]() with coefficients in $\kappa$
with coefficients in $\kappa$![]() , with variables $x_F$
, with variables $x_F$![]() where $F$
where $F$![]() varies over $\mathcal {F}$
varies over $\mathcal {F}$![]() . We identify $\mathbb {P}^{g}$
. We identify $\mathbb {P}^{g}$![]() with ${\rm Proj}(\tilde {R})$
with ${\rm Proj}(\tilde {R})$![]() . Since $M$
. Since $M$![]() is a two-dimensional simplicial complex, the quotient ring $\tilde {R}/I_{M}$
is a two-dimensional simplicial complex, the quotient ring $\tilde {R}/I_{M}$![]() of its Stanley–Reisner ideal has Krull dimension three [Reference Miller and Sturmfels25, Corollary 1.15], [Reference Francisco, Mermin and Schweig15, Theorem 6.15]. Hence, it defines a surface $S_M$
of its Stanley–Reisner ideal has Krull dimension three [Reference Miller and Sturmfels25, Corollary 1.15], [Reference Francisco, Mermin and Schweig15, Theorem 6.15]. Hence, it defines a surface $S_M$![]() in $\mathbb {P}^g$
in $\mathbb {P}^g$![]() referred to as the Stanley–Reisner surface of $M$
referred to as the Stanley–Reisner surface of $M$![]() . Furthermore, we identify ${\rm Proj}(R)$
. Furthermore, we identify ${\rm Proj}(R)$![]() with the hyperplane $\sum _{F \in \mathcal {F}} x_F$
with the hyperplane $\sum _{F \in \mathcal {F}} x_F$![]() of $\mathbb {P}^g$
of $\mathbb {P}^g$![]() .
.
In the following proposition, we show that the Schön embedding is the intersection of the Stanley–Reisner surface of $M$![]() with the hyperplane $\sum _{F \in \mathcal {F}} x_F$
with the hyperplane $\sum _{F \in \mathcal {F}} x_F$![]() . Two key facts to keep in mind are that the number of vertices of $G$
. Two key facts to keep in mind are that the number of vertices of $G$![]() is precisely $2g-2$
is precisely $2g-2$![]() where $g$
where $g$![]() is the genus of $G$
is the genus of $G$![]() and a fact from Stanley–Reisner theory that the irreducible components of $S_M$
and a fact from Stanley–Reisner theory that the irreducible components of $S_M$![]() are in bijection with the vertices of $G$
are in bijection with the vertices of $G$![]() . For a homogenous ideal $I$
. For a homogenous ideal $I$![]() , let $V(I)$
, let $V(I)$![]() be the projective variety defined by it.
be the projective variety defined by it.
Proposition 3.2 (Schön Embedding in terms of the Stanley–Reisner Surface)
Let $I_{\rm sch}$![]() be the ideal of $R$
be the ideal of $R$![]() generated by polynomials obtained by replacing the variable $x_E$
generated by polynomials obtained by replacing the variable $x_E$![]() , corresponding to the exterior face, in each monomial minimal generator of $I_M$
, corresponding to the exterior face, in each monomial minimal generator of $I_M$![]() by $-\sum _{F \neq E} x_F$
by $-\sum _{F \neq E} x_F$![]() . The projective variety $V(I_{\rm sch})$
. The projective variety $V(I_{\rm sch})$![]() is the Schön embedding of $X_G$
is the Schön embedding of $X_G$![]() .
.
Proof. The Stanley–Reisner ideal $I_M$![]() is a radical ideal and hence, its primary decomposition is the intersection of its associated primes. By [Reference Francisco, Mermin and Schweig15, Proposition 4.11], it has the primary decomposition $\cap _{v \in V(G)}\mathcal {P}_v$
is a radical ideal and hence, its primary decomposition is the intersection of its associated primes. By [Reference Francisco, Mermin and Schweig15, Proposition 4.11], it has the primary decomposition $\cap _{v \in V(G)}\mathcal {P}_v$![]() where $V(G)$
where $V(G)$![]() is the set of vertices of $G$
is the set of vertices of $G$![]() and $\mathcal {P}_v$
and $\mathcal {P}_v$![]() is the ideal generated by the variables $x_F$
is the ideal generated by the variables $x_F$![]() where $F\in \mathcal {F}$
where $F\in \mathcal {F}$![]() is not incident on $v$
is not incident on $v$![]() (note the difference with $\Sigma _v$
(note the difference with $\Sigma _v$![]() ). Hence, the associated Stanley–Reisner surface $S_M$
). Hence, the associated Stanley–Reisner surface $S_M$![]() is an arrangement of $2g-2$
is an arrangement of $2g-2$![]() two-dimensional planes in $\mathbb {P}^g$
two-dimensional planes in $\mathbb {P}^g$![]() . Note that, for each $v$
. Note that, for each $v$![]() , the intersection of $V(\mathcal {P}_v)$
, the intersection of $V(\mathcal {P}_v)$![]() with the hyperplane $\sum _{F \in \mathcal {F}} x_F$
with the hyperplane $\sum _{F \in \mathcal {F}} x_F$![]() is precisely $L_v$
is precisely $L_v$![]() , via the identification of ${\rm Proj}(R)$
, via the identification of ${\rm Proj}(R)$![]() with the hyperplane $\sum _{F \in \mathcal {F}} x_F$
with the hyperplane $\sum _{F \in \mathcal {F}} x_F$![]() . Hence, $V(I_M+\langle \sum _{F \in \mathcal {F}} x_F \rangle )=V(I_{\rm sch})$
. Hence, $V(I_M+\langle \sum _{F \in \mathcal {F}} x_F \rangle )=V(I_{\rm sch})$![]() is the Schön embedding of $X_G$
is the Schön embedding of $X_G$![]() .
.
Remark 3.3 To the best of our knowledge, it is not known whether $I_{\rm sch}$![]() is a radical ideal, i.e. if $I_{\rm sch}=\cap _{v \in V(G)}L_v$
is a radical ideal, i.e. if $I_{\rm sch}=\cap _{v \in V(G)}L_v$![]() or not.
or not.
Note that by [Reference Bayer and Eisenbud4, Corollary 2.2], the canonical bundle of $X_G$![]() is very ample. Next, we deduce using proposition 3.2 that the Schön embedding of $X_G$
is very ample. Next, we deduce using proposition 3.2 that the Schön embedding of $X_G$![]() is a canonical embedding.
is a canonical embedding.
Proposition 3.4 The Schön embedding is a canonical embedding of $X_G$![]() , i.e. an embedding by the complete linear series associated to the canonical bundle of $X_G$
, i.e. an embedding by the complete linear series associated to the canonical bundle of $X_G$![]() .
.
Proof. By proposition 3.1, the dual graph of the Schön embedding is isomorphic to $G$![]() . The rest of the proof is based on the proof of [Reference Bayer and Eisenbud4, Corollary 6.2] where an analogous statement for a general hyperplane section of $S_M$
. The rest of the proof is based on the proof of [Reference Bayer and Eisenbud4, Corollary 6.2] where an analogous statement for a general hyperplane section of $S_M$![]() is shown. Since the boundary of the polar polytope of $P$
is shown. Since the boundary of the polar polytope of $P$![]() is a geometric realization of $M$
is a geometric realization of $M$![]() , the simplicial complex $M$
, the simplicial complex $M$![]() is homeomorphic to a $2$
is homeomorphic to a $2$![]() -sphere. Hence, by [Reference Bayer and Eisenbud4, Theorem 6.1] the Stanley–Reisner surface of $M$
-sphere. Hence, by [Reference Bayer and Eisenbud4, Theorem 6.1] the Stanley–Reisner surface of $M$![]() has a trivial canonical bundle. By the adjunction formula [Reference Vakil33, Proposition 30.4.8], we know that $\omega _{G} \cong (\omega _S \otimes _{\mathcal {O}_S} \mathcal {O}_S(X_G))|_{X_G}= (\omega _S \otimes _{\mathcal {O}_S} \mathcal {O}_S(1))|_{X_G}$
has a trivial canonical bundle. By the adjunction formula [Reference Vakil33, Proposition 30.4.8], we know that $\omega _{G} \cong (\omega _S \otimes _{\mathcal {O}_S} \mathcal {O}_S(X_G))|_{X_G}= (\omega _S \otimes _{\mathcal {O}_S} \mathcal {O}_S(1))|_{X_G}$![]() where $\omega _G$
where $\omega _G$![]() and $\omega _S$
and $\omega _S$![]() are the canonical bundles of $X_G$
are the canonical bundles of $X_G$![]() and $S_M$
and $S_M$![]() respectively. Hence, we conclude that $\omega _G \cong \mathcal {O}_S(1)|_{X_G}$
respectively. Hence, we conclude that $\omega _G \cong \mathcal {O}_S(1)|_{X_G}$![]() and hence, the Schön embedding is an embedding by a linear series of $\omega _G$
and hence, the Schön embedding is an embedding by a linear series of $\omega _G$![]() . Finally, we note that by proposition 3.1, the Schön embedding is non-degenerate and that $h^0(X_G,\omega _G)=g$
. Finally, we note that by proposition 3.1, the Schön embedding is non-degenerate and that $h^0(X_G,\omega _G)=g$![]() [Reference Bayer and Eisenbud4, Proposition 1.1] to conclude that the Schön embedding is an embedding by the complete linear series of $\omega _G$
[Reference Bayer and Eisenbud4, Proposition 1.1] to conclude that the Schön embedding is an embedding by the complete linear series of $\omega _G$![]() .
.
As corollary, we obtain the following.
Corollary 3.5 The Schön embedding of $X_G$![]() is independent of the choice of planar embedding of $G$
is independent of the choice of planar embedding of $G$![]() .
.
The following proposition determines an extended tropical basis for the Schön embedding and will not be used subsequently. We include it for possible future applications.
Proposition 3.6 (Tropical Basis of the Schön Embedding)
The minimal generating set $\mathcal {G}$![]() of $I_{\rm sch}$
of $I_{\rm sch}$![]() that is presented in proposition 3.2 is an extended tropical basis.
that is presented in proposition 3.2 is an extended tropical basis.
Proof. Let $\mathcal {G}=\{g_1,\ldots,g_r\}$![]() . Suppose for the sake of contradiction that $\mathcal {G}$
. Suppose for the sake of contradiction that $\mathcal {G}$![]() is not an extended tropical basis, then there is a point $p \in \cap _{j=1}^{r} {\rm tropproj}(g_j)$
is not an extended tropical basis, then there is a point $p \in \cap _{j=1}^{r} {\rm tropproj}(g_j)$![]() that is not contained in the extended tropicalization of $I_{\rm sch}$
that is not contained in the extended tropicalization of $I_{\rm sch}$![]() . Since the elements in $\mathcal {G}$
. Since the elements in $\mathcal {G}$![]() are all products of linear forms, this implies that there is a choice of linear forms $\ell _1,\ldots,\ell _r$
are all products of linear forms, this implies that there is a choice of linear forms $\ell _1,\ldots,\ell _r$![]() such that $\ell _j | g_j$
such that $\ell _j | g_j$![]() for each $j$
for each $j$![]() from one to $r$
from one to $r$![]() and such that $p \in \cap _{j=1}^{r} {\rm tropproj}(\ell _j)$
and such that $p \in \cap _{j=1}^{r} {\rm tropproj}(\ell _j)$![]() .
.
Consider the ideal generated by the linear forms $\ell _1,\ldots,\ell _r$![]() . This ideal contains $I_{\rm sch}$
. This ideal contains $I_{\rm sch}$![]() . Since it is generated by linear forms, its zero locus, being non-empty, is either a point or an irreducible component of the Schön embedding. Furthermore, any $\ell _j$
. Since it is generated by linear forms, its zero locus, being non-empty, is either a point or an irreducible component of the Schön embedding. Furthermore, any $\ell _j$![]() is either a variable or of the form $\sum _{F \in \mathcal {F}, F \neq E}x_F$
is either a variable or of the form $\sum _{F \in \mathcal {F}, F \neq E}x_F$![]() where $E$
where $E$![]() is the exterior face. We claim that $\ell _1,\ldots,\ell _r$
is the exterior face. We claim that $\ell _1,\ldots,\ell _r$![]() is an extended tropical basis. If $\ell _1,\ldots,\ell _r$
is an extended tropical basis. If $\ell _1,\ldots,\ell _r$![]() are all variables, then this is immediate (also, see lemma 2.2). Otherwise, we may assume that $\ell _r=\sum _{F \in \mathcal {F}, F \neq E}x_F$
are all variables, then this is immediate (also, see lemma 2.2). Otherwise, we may assume that $\ell _r=\sum _{F \in \mathcal {F}, F \neq E}x_F$![]() and $\ell _1,\ldots,\ell _{r-1}$
and $\ell _1,\ldots,\ell _{r-1}$![]() are all variables. Let $\ell '_r=\sum _{F \in \mathcal {F}, F \neq E,x_F \notin \{\ell _1,\ldots,\ell _{r-1}\}}x_F$
are all variables. Let $\ell '_r=\sum _{F \in \mathcal {F}, F \neq E,x_F \notin \{\ell _1,\ldots,\ell _{r-1}\}}x_F$![]() . By the definition of extended tropicalization, we have $\cap _{j=1}^{r} {\rm tropproj}(\ell _j)= \cap _{j=1}^{r-1} {\rm tropproj}(\ell _j) \cap {\rm tropproj}(\ell '_r)$
. By the definition of extended tropicalization, we have $\cap _{j=1}^{r} {\rm tropproj}(\ell _j)= \cap _{j=1}^{r-1} {\rm tropproj}(\ell _j) \cap {\rm tropproj}(\ell '_r)$![]() . By lemma 2.2, the set $\{\ell _1,\ldots,\ell _{r-1},\ell '_r\}$
. By lemma 2.2, the set $\{\ell _1,\ldots,\ell _{r-1},\ell '_r\}$![]() is an extended tropical basis for $\langle \ell _1,\ldots,\ell _r \rangle$
is an extended tropical basis for $\langle \ell _1,\ldots,\ell _r \rangle$![]() and hence, so is $\{\ell _1,\ldots,\ell _r\}$
and hence, so is $\{\ell _1,\ldots,\ell _r\}$![]() . This implies that $p$
. This implies that $p$![]() is contained in the extended tropicalization of $\langle \ell _1,\ldots,\ell _r \rangle$
is contained in the extended tropicalization of $\langle \ell _1,\ldots,\ell _r \rangle$![]() and hence, in the extended tropicalization of the Schön embedding. This is a contradiction.
and hence, in the extended tropicalization of the Schön embedding. This is a contradiction.
Example 3.7 Let $\mathcal {C}$![]() be the one-skeleton of the three-dimensional cube, as shown in figure 1. The minimal generating set of the Schön embedding of $X_{\mathcal {C}}$
be the one-skeleton of the three-dimensional cube, as shown in figure 1. The minimal generating set of the Schön embedding of $X_{\mathcal {C}}$![]() described in proposition 3.2 is the following.
described in proposition 3.2 is the following.
Hence, the Schön embedding is a complete intersection cut-out by three (degenerate) quadrics in $\mathbb {P}^4$![]() and according to proposition 3.6, these quadrics also form an extended tropical basis. However, canonical embeddings of graph curves are not, in general, complete intersections.
and according to proposition 3.6, these quadrics also form an extended tropical basis. However, canonical embeddings of graph curves are not, in general, complete intersections.
4. Tropicalization of the Schön embedding
In the following, we study the extended tropicalization of the Schön embedding of $X_G$![]() when $G$
when $G$![]() is a three-regular, three-connected planar graph. Recall that this extended tropicalization is contained in $\mathbb {TP}^{g-1}$
is a three-regular, three-connected planar graph. Recall that this extended tropicalization is contained in $\mathbb {TP}^{g-1}$![]() and that $\mathbb {TP}^{g-1}$
and that $\mathbb {TP}^{g-1}$![]() is homeomorphic to the $(g-1)$
is homeomorphic to the $(g-1)$![]() -simplex. As in the previous section, we identify $\mathbb {P}^{g-1}$
-simplex. As in the previous section, we identify $\mathbb {P}^{g-1}$![]() with ${\rm Proj}(R)$
with ${\rm Proj}(R)$![]() where $R=\kappa [x_F|~$
where $R=\kappa [x_F|~$![]() $F$
$F$![]() ranges over the interior faces of the planar embedding of $G]$
ranges over the interior faces of the planar embedding of $G]$![]() equipped with the standard grading. Note that each facet of $\mathbb {TP}^{g-1}$
equipped with the standard grading. Note that each facet of $\mathbb {TP}^{g-1}$![]() corresponds to a coordinate hyperplane $x_F$
corresponds to a coordinate hyperplane $x_F$![]() where $F$
where $F$![]() is an interior face of the planar embedding of $G$
is an interior face of the planar embedding of $G$![]() . We label each facet of $\mathbb {TP}^{g-1}$
. We label each facet of $\mathbb {TP}^{g-1}$![]() with the corresponding interior face $F$
with the corresponding interior face $F$![]() . More generally, we label each $i$
. More generally, we label each $i$![]() -dimensional face of $\mathbb {TP}^{g-1}$
-dimensional face of $\mathbb {TP}^{g-1}$![]() for $i \in [0,\ldots,g-2]$
for $i \in [0,\ldots,g-2]$![]() with the union of the labels of each facet containing it. Note that for faces $\mathfrak {f}$
with the union of the labels of each facet containing it. Note that for faces $\mathfrak {f}$![]() and $\mathfrak {g}$
and $\mathfrak {g}$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() , we have $\mathfrak {f} \subseteq \mathfrak {g}$
, we have $\mathfrak {f} \subseteq \mathfrak {g}$![]() if and only if the label of $\mathfrak {f}$
if and only if the label of $\mathfrak {f}$![]() contains the label of $\mathfrak {g}$
contains the label of $\mathfrak {g}$![]() . For an algebraically closed field $\mathbb {K}$
. For an algebraically closed field $\mathbb {K}$![]() with a non-trivial valuation, the homogenous coordinates on $\mathbb {P}_{\mathbb {K}}^{g-1}$
with a non-trivial valuation, the homogenous coordinates on $\mathbb {P}_{\mathbb {K}}^{g-1}$![]() , via the extended tropicalization map, induce coordinates on $\mathbb {TP}^{g-1}$
, via the extended tropicalization map, induce coordinates on $\mathbb {TP}^{g-1}$![]() . We refer to [Reference Maclagan and Sturmfels23, Section 6.2] for more details. In the following, we specify points in $\mathbb {TP}^{g-1}$
. We refer to [Reference Maclagan and Sturmfels23, Section 6.2] for more details. In the following, we specify points in $\mathbb {TP}^{g-1}$![]() by corresponding points in $\mathbb {P}_{\mathbb {K}}^{g-1}$
by corresponding points in $\mathbb {P}_{\mathbb {K}}^{g-1}$![]() .
.
For an edge $\xi$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() whose label is $\{F|~F \notin \{F_s,F_t\} \}$
whose label is $\{F|~F \notin \{F_s,F_t\} \}$![]() , we associate a point $m_{\xi } \in \xi$
, we associate a point $m_{\xi } \in \xi$![]() as follows: it is the tropicalization of the point in $\mathbb {P}_{\mathbb {K}}^{g-1}$
as follows: it is the tropicalization of the point in $\mathbb {P}_{\mathbb {K}}^{g-1}$![]() with coordinates $(p_F)_F$
with coordinates $(p_F)_F$![]() such that $p_{F_s},~p_{F_t}$
such that $p_{F_s},~p_{F_t}$![]() are both not zero, ${\rm val}(p_{F_s})={\rm val}(p_{F_t})$
are both not zero, ${\rm val}(p_{F_s})={\rm val}(p_{F_t})$![]() and $p_F=0$
and $p_F=0$![]() for any interior face $F$
for any interior face $F$![]() that is neither $F_s$
that is neither $F_s$![]() nor $F_t$
nor $F_t$![]() .
.
Tropicalization of the Irreducible Components: Recall that each irreducible component of the Schön embedding is a line defined by the ideal $L_v$![]() . If $v$
. If $v$![]() is an interior vertex incident on faces $F_i,~F_j$
is an interior vertex incident on faces $F_i,~F_j$![]() and $F_k$
and $F_k$![]() then $L_v=\langle x_{F_i}+x_{F_j}+x_{F_k},x_F|~F$
then $L_v=\langle x_{F_i}+x_{F_j}+x_{F_k},x_F|~F$![]() is an interior face of $G$
is an interior face of $G$![]() not incident on $v \rangle$
not incident on $v \rangle$![]() . The extended tropicalization ${\rm tropproj}(L_v)$
. The extended tropicalization ${\rm tropproj}(L_v)$![]() of $L_v$
of $L_v$![]() is contained in the two-dimensional face $D_v$
is contained in the two-dimensional face $D_v$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() labelled by $\{F|~F$
labelled by $\{F|~F$![]() is an interior face of $G$
is an interior face of $G$![]() not incident on $v\}$
not incident on $v\}$![]() . Furthermore, ${\rm tropproj}(L_v)$
. Furthermore, ${\rm tropproj}(L_v)$![]() contains precisely one branch point (of valence three). The three branches are labelled by $\{F_i,F_j\},~\{F_i,F_k\}$
contains precisely one branch point (of valence three). The three branches are labelled by $\{F_i,F_j\},~\{F_i,F_k\}$![]() and $\{F_j,F_k\}$
and $\{F_j,F_k\}$![]() according to the two coordinates that are minimum at each point of that branch, i.e. the sum of the pairs of the corresponding variables that is the initial form along that branch [Reference Maclagan and Sturmfels23, Definition 3.1.1, Theorem 3.1.3]. Each such pair of faces shares a unique edge of $G$
according to the two coordinates that are minimum at each point of that branch, i.e. the sum of the pairs of the corresponding variables that is the initial form along that branch [Reference Maclagan and Sturmfels23, Definition 3.1.1, Theorem 3.1.3]. Each such pair of faces shares a unique edge of $G$![]() and hence, a branch is also labelled by that edge. The branch with the label $\{F_s,F_t\}$
and hence, a branch is also labelled by that edge. The branch with the label $\{F_s,F_t\}$![]() intersects the edge $\xi$
intersects the edge $\xi$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() with the label $\{F|~F$
with the label $\{F|~F$![]() is an interior face that is neither $F_s$
is an interior face that is neither $F_s$![]() nor $F_t \}$
nor $F_t \}$![]() at precisely one point. This point of intersection $\zeta _e$
at precisely one point. This point of intersection $\zeta _e$![]() , corresponding to the edge $e$
, corresponding to the edge $e$![]() of $G$
of $G$![]() , is $m_{\xi }$
, is $m_{\xi }$![]() . Hence, the point of intersection lies in the relative interior of this edge $\xi$
. Hence, the point of intersection lies in the relative interior of this edge $\xi$![]() . We refer to figure 2 for an illustration of ${\rm tropproj}(L_v)$
. We refer to figure 2 for an illustration of ${\rm tropproj}(L_v)$![]() .
.

Figure 2. The extended tropicalization of $L_v$![]() where $v$
where $v$![]() is an interior vertex is shown in thick lines and the two-dimensional $D_v$
is an interior vertex is shown in thick lines and the two-dimensional $D_v$![]() is shown in thin lines. The branch point is depicted by the square dot and the intersection points of ${\rm tropproj}(L_v)$
is shown in thin lines. The branch point is depicted by the square dot and the intersection points of ${\rm tropproj}(L_v)$![]() with the boundary of $D_v$
with the boundary of $D_v$![]() are depicted by the hollow circular dots.
are depicted by the hollow circular dots.
Next, we turn to ${\rm tropproj}(L_v)$![]() where $v$
where $v$![]() is an exterior vertex. In this case, $L_v=\langle x_F|~F$
is an exterior vertex. In this case, $L_v=\langle x_F|~F$![]() is an interior face of $G$
is an interior face of $G$![]() not incident on $v\rangle$
not incident on $v\rangle$![]() and hence, ${\rm tropproj}(L_v)$
and hence, ${\rm tropproj}(L_v)$![]() is equal to the edge $\xi _v$
is equal to the edge $\xi _v$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() with the label $\{F|~F$
with the label $\{F|~F$![]() is an interior face of $G$
is an interior face of $G$![]() not incident on $v\}$
not incident on $v\}$![]() .
.
In the following lemma, we determine the points of intersection between the tropical lines ${\rm tropproj}(L_u)$![]() and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$![]() where $u,~v$
where $u,~v$![]() are distinct vertices of $G$
are distinct vertices of $G$![]() .
.
Lemma 4.1 Let $u$![]() and $v$
and $v$![]() be distinct vertices of $G$
be distinct vertices of $G$![]() . The intersection ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$
. The intersection ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$![]() is non-empty if and only if $u$
is non-empty if and only if $u$![]() and $v$
and $v$![]() are adjacent in $G$
are adjacent in $G$![]() . If ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$
. If ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$![]() is non-empty, then it is a point and this intersection point is as follows:
is non-empty, then it is a point and this intersection point is as follows:
• If $u$
 and $v$
and $v$ are not both exterior vertices, then ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$
are not both exterior vertices, then ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$ is contained in the relative interior of the edge of $\mathbb {TP}^{g-1}$
is contained in the relative interior of the edge of $\mathbb {TP}^{g-1}$ that is labelled by $\{F|~F$
that is labelled by $\{F|~F$ is an interior face that does not contain both $u$
is an interior face that does not contain both $u$ and $v\}$
and $v\}$ .
.• If both $u$
 and $v$
and $v$ are exterior vertices, then ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$
are exterior vertices, then ${\rm tropproj}(L_u) \cap {\rm tropproj}(L_v)$ is the vertex of $\mathbb {TP}^{g-1}$
is the vertex of $\mathbb {TP}^{g-1}$ that is labelled by $\{F|~F$
that is labelled by $\{F|~F$ is an interior face that does not contain both $u$
is an interior face that does not contain both $u$ and $v\}$
and $v\}$ .
.
Proof. In the following, we implicitly invoke Item 2, proposition 2.4. Suppose that $u$![]() and $v$
and $v$![]() are adjacent and let $e=(u,v)$
are adjacent and let $e=(u,v)$![]() . We distinguish the following cases:
. We distinguish the following cases:
• If both $u$
 and $v$
and $v$ are interior vertices, then the two-dimensional faces $D_u$
are interior vertices, then the two-dimensional faces $D_u$ and $D_v$
and $D_v$ of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$ , that contain ${\rm tropproj}(L_u)$
, that contain ${\rm tropproj}(L_u)$ and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ respectively, share an edge $\mu _{u,v}$
respectively, share an edge $\mu _{u,v}$ that is labelled by the set of interior faces that do not contain both $u$
that is labelled by the set of interior faces that do not contain both $u$ and $v$
and $v$ . Both ${\rm tropproj}(L_u)$
. Both ${\rm tropproj}(L_u)$ and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ intersect $\mu _{u,v}$
intersect $\mu _{u,v}$ at its relative interior, more precisely at the point $\zeta _e$
at its relative interior, more precisely at the point $\zeta _e$ (recall from the text preceding this lemma). This is their only point of intersection. We refer to A, figure 3 for a depiction.
(recall from the text preceding this lemma). This is their only point of intersection. We refer to A, figure 3 for a depiction.• If one of the two vertices, say $u$
 is an interior vertex and the vertex $v$
is an interior vertex and the vertex $v$ is an exterior vertex, then recall that ${\rm tropproj}(L_u)$
is an exterior vertex, then recall that ${\rm tropproj}(L_u)$ is contained in $D_u$
is contained in $D_u$ and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ is equal to the edge $\xi _v$
is equal to the edge $\xi _v$ of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$ . The label of $D_u$
. The label of $D_u$ is contained in the label of $\xi _v$
is contained in the label of $\xi _v$ . Hence, $\xi _v$
. Hence, $\xi _v$ is an edge of $D_u$
is an edge of $D_u$ and ${\rm tropproj}(L_u)$
and ${\rm tropproj}(L_u)$ intersects ${\rm tropproj}(L_v)$
intersects ${\rm tropproj}(L_v)$ precisely at the point $\zeta _e$
precisely at the point $\zeta _e$ . Item B, figure 3 illustrates this case.
. Item B, figure 3 illustrates this case.• If both $u$
 and $v$
and $v$ are exterior vertices, then ${\rm tropproj}(L_u)$
are exterior vertices, then ${\rm tropproj}(L_u)$ and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ are the edges $\xi _u$
are the edges $\xi _u$ and $\xi _v$
and $\xi _v$ , respectively. We refer to B, figure 3 for an illustration. The vertices $u$
, respectively. We refer to B, figure 3 for an illustration. The vertices $u$ and $v$
and $v$ share precisely one interior face $F_{u,v}$
share precisely one interior face $F_{u,v}$ . The edges $\xi _u$
. The edges $\xi _u$ and $\xi _v$
and $\xi _v$ share a vertex whose label is the set of all interior faces apart from $F_{u,v}$
share a vertex whose label is the set of all interior faces apart from $F_{u,v}$ . This is the only intersection point of ${\rm tropproj}(L_u)$
. This is the only intersection point of ${\rm tropproj}(L_u)$ and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ . We refer to C, figure 3 for an illustration.
. We refer to C, figure 3 for an illustration.
If $u$![]() and $v$
and $v$![]() are not adjacent, then by Item 2, proposition 2.4, they share at most one interior face. The following cases arise:
are not adjacent, then by Item 2, proposition 2.4, they share at most one interior face. The following cases arise:
• If $u$
 and $v$
and $v$ are both interior vertices, then based on whether $u$
are both interior vertices, then based on whether $u$ and $v$
and $v$ share an interior face or not, the two-dimensional faces $D_u$
share an interior face or not, the two-dimensional faces $D_u$ and $D_v$
and $D_v$ either share precisely one vertex or are disjoint. Since ${\rm tropproj}(L_u)$
either share precisely one vertex or are disjoint. Since ${\rm tropproj}(L_u)$ intersects each edge of $D_u$
intersects each edge of $D_u$ in the relative interior of that edge, we conclude that ${\rm tropproj}(L_u)$
in the relative interior of that edge, we conclude that ${\rm tropproj}(L_u)$ and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ are disjoint.
are disjoint.• If $u$
 is an interior vertex and $v$
is an interior vertex and $v$ is an exterior vertex, then $\xi _v$
is an exterior vertex, then $\xi _v$ is not an edge of $D_u$
is not an edge of $D_u$ . More precisely, based on whether $u$
. More precisely, based on whether $u$ and $v$
and $v$ share an interior face or not, $D_u$
share an interior face or not, $D_u$ and $\xi _v$
and $\xi _v$ either intersect at a vertex or are disjoint. As in the previous case, we conclude that ${\rm tropproj}(L_u)$
either intersect at a vertex or are disjoint. As in the previous case, we conclude that ${\rm tropproj}(L_u)$ and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ are disjoint.
are disjoint.• If $u$
 and $v$
and $v$ are both exterior vertices, then they do not share an interior face of $G$
are both exterior vertices, then they do not share an interior face of $G$ . Hence, $\xi _u={\rm tropproj}(L_u)$
. Hence, $\xi _u={\rm tropproj}(L_u)$ and $\xi _v={\rm tropproj}(L_v)$
and $\xi _v={\rm tropproj}(L_v)$ are disjoint.
are disjoint.
This concludes the proof.

Figure 3. Intersection of $t_u={\rm tropproj}(L_u)$![]() and $t_v={\rm tropproj}(L_v)$
and $t_v={\rm tropproj}(L_v)$![]() : Figures A, B and C illustrate the cases where (A) $u$
: Figures A, B and C illustrate the cases where (A) $u$![]() and $v$
and $v$![]() are both interior vertices, (B) $u$
are both interior vertices, (B) $u$![]() is an interior vertex and $v$
is an interior vertex and $v$![]() is an exterior vertex and (C) $u$
is an exterior vertex and (C) $u$![]() and $v$
and $v$![]() are both exterior vertices, respectively.
are both exterior vertices, respectively.
Next, we use lemma 4.1 to classify the trivalent points of the extended tropicalization $\mathcal {T}$![]() of the Schön embedding of $X_G$
of the Schön embedding of $X_G$![]() . Before this, we note that in any planar embedding of a three-regular graph, every exterior vertex has precisely one interior vertex adjacent to it. The following lemma will play a key role in constructing a homeomorphism between $G^{\rm top}$
. Before this, we note that in any planar embedding of a three-regular graph, every exterior vertex has precisely one interior vertex adjacent to it. The following lemma will play a key role in constructing a homeomorphism between $G^{\rm top}$![]() and the extended tropicalization of the Schön embedding of $X_G$
and the extended tropicalization of the Schön embedding of $X_G$![]() .
.
Lemma 4.2 The points of $\mathcal {T}$![]() are either bivalent or trivalent. The trivalent points of $\mathcal {T}$
are either bivalent or trivalent. The trivalent points of $\mathcal {T}$![]() are of the following two distinct types:
are of the following two distinct types:
• A branch point of ${\rm tropproj}(L_u)$
 where $u$
where $u$ is an interior vertex.
is an interior vertex.• An intersection point of ${\rm tropproj}(L_u)$
 and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$ where $u$
where $u$ is an exterior vertex and $v$
is an exterior vertex and $v$ is the unique interior vertex adjacent to $u$
is the unique interior vertex adjacent to $u$ .
.
Proof. We start by noting that points in each tropical line are either bivalent or trivalent as points in that line. If $u$![]() is an interior vertex, then the tropical line ${\rm tropproj}(L_u)$
is an interior vertex, then the tropical line ${\rm tropproj}(L_u)$![]() contains a branch point and this is its only trivalent point. Otherwise, ${\rm tropproj}(L_u)$
contains a branch point and this is its only trivalent point. Otherwise, ${\rm tropproj}(L_u)$![]() does not contain a trivalent point. Furthermore, by Lemma 4.1, ${\rm tropproj}(L_u)$
does not contain a trivalent point. Furthermore, by Lemma 4.1, ${\rm tropproj}(L_u)$![]() (when $u$
(when $u$![]() is an interior vertex) does not intersect any other tropical line at its branch point. Hence, each such branch point remains a trivalent point as a point in $\mathcal {T}=\cup _u {\rm tropproj}(L_u)$
is an interior vertex) does not intersect any other tropical line at its branch point. Hence, each such branch point remains a trivalent point as a point in $\mathcal {T}=\cup _u {\rm tropproj}(L_u)$![]() . Any other trivalent point of $\mathcal {T}$
. Any other trivalent point of $\mathcal {T}$![]() must be an intersection point of two distinct tropical lines. Suppose that $u$
must be an intersection point of two distinct tropical lines. Suppose that $u$![]() is an interior vertex and $v$
is an interior vertex and $v$![]() is an exterior vertex, and that they are adjacent. Let $e=(u,v)$
is an exterior vertex, and that they are adjacent. Let $e=(u,v)$![]() . By Lemma 4.1, the intersection point $\zeta _e$
. By Lemma 4.1, the intersection point $\zeta _e$![]() of ${\rm tropproj}(L_u)$
of ${\rm tropproj}(L_u)$![]() and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$![]() is a trivalent point of ${\rm tropproj}(L_u) \cup {\rm tropproj}(L_v)$
is a trivalent point of ${\rm tropproj}(L_u) \cup {\rm tropproj}(L_v)$![]() , see B, figure 3. In the following, we show that $\zeta _e$
, see B, figure 3. In the following, we show that $\zeta _e$![]() is not contained in ${\rm tropproj}(L_w)$
is not contained in ${\rm tropproj}(L_w)$![]() for $w \notin \{u,v\}$
for $w \notin \{u,v\}$![]() . Suppose the contrary, by lemma 4.1, we deduce that $w$
. Suppose the contrary, by lemma 4.1, we deduce that $w$![]() is adjacent to both $u$
is adjacent to both $u$![]() and $v$
and $v$![]() , and $w$
, and $w$![]() is contained in the two interior faces that are shared by $u$
is contained in the two interior faces that are shared by $u$![]() and $v$
and $v$![]() . By Item 1, proposition 2.4, this is a contradiction. Hence, $\zeta _e$
. By Item 1, proposition 2.4, this is a contradiction. Hence, $\zeta _e$![]() is a trivalent point of $\mathcal {T}$
is a trivalent point of $\mathcal {T}$![]() .
.
Next, we show that any other point in $\mathcal {T}$![]() that is an intersection point of tropical lines is bivalent. Consider the intersection point $\zeta _e$
that is an intersection point of tropical lines is bivalent. Consider the intersection point $\zeta _e$![]() of ${\rm tropproj}(L_u)$
of ${\rm tropproj}(L_u)$![]() and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$![]() where $u$
where $u$![]() and $v$
and $v$![]() are both interior vertices, see A, figure 3. The point $\zeta _e$
are both interior vertices, see A, figure 3. The point $\zeta _e$![]() is a bivalent point of ${\rm tropproj}(L_u) \cup {\rm tropproj}(L_v)$
is a bivalent point of ${\rm tropproj}(L_u) \cup {\rm tropproj}(L_v)$![]() . Suppose that, for the sake of contradiction, $\zeta _e$
. Suppose that, for the sake of contradiction, $\zeta _e$![]() is a point of higher valence in $\mathcal {T}$
is a point of higher valence in $\mathcal {T}$![]() . This implies that there is a vertex $w$
. This implies that there is a vertex $w$![]() apart from $u$
apart from $u$![]() and $v$
and $v$![]() such that ${\rm tropproj}(L_w)$
such that ${\rm tropproj}(L_w)$![]() contains $\zeta _e$
contains $\zeta _e$![]() . By lemma 4.1, we deduce that the vertices $u,~v$
. By lemma 4.1, we deduce that the vertices $u,~v$![]() and $w$
and $w$![]() share two distinct interior faces and this is a contradiction by Item 1, proposition 2.4. Consider the case where $u$
share two distinct interior faces and this is a contradiction by Item 1, proposition 2.4. Consider the case where $u$![]() and $v$
and $v$![]() are both exterior vertices that are adjacent. We note that the intersection point $\zeta _e$
are both exterior vertices that are adjacent. We note that the intersection point $\zeta _e$![]() of ${\rm tropproj}(L_u)$
of ${\rm tropproj}(L_u)$![]() and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$![]() , as shown in C, figure 3, is a bivalent point of ${\rm tropproj}(L_u) \cup {\rm tropproj}(L_v)$
, as shown in C, figure 3, is a bivalent point of ${\rm tropproj}(L_u) \cup {\rm tropproj}(L_v)$![]() . We show that it cannot be contained in any other tropical line ${\rm tropproj}(L_w)$
. We show that it cannot be contained in any other tropical line ${\rm tropproj}(L_w)$![]() . Suppose the contrary, by Lemma 4.1, $w$
. Suppose the contrary, by Lemma 4.1, $w$![]() is adjacent to both $u$
is adjacent to both $u$![]() and $v$
and $v$![]() , and must be an exterior vertex (since $\zeta _e$
, and must be an exterior vertex (since $\zeta _e$![]() is a vertex of $\mathbb {TP}^{g-1}$
is a vertex of $\mathbb {TP}^{g-1}$![]() and ${\rm tropproj}(L_q)$
and ${\rm tropproj}(L_q)$![]() contains a vertex of $\mathbb {TP}^{g-1}$
contains a vertex of $\mathbb {TP}^{g-1}$![]() precisely when $q$
precisely when $q$![]() is an exterior vertex). Furthermore, Lemma 4.1 also implies that $u,~v$
is an exterior vertex). Furthermore, Lemma 4.1 also implies that $u,~v$![]() and $w$
and $w$![]() share an interior face. Since the vertices $u,~v$
share an interior face. Since the vertices $u,~v$![]() and $w$
and $w$![]() must be in general position, their convex hull is a triangle $\delta$
must be in general position, their convex hull is a triangle $\delta$![]() and this triangle must be their common interior face. The graph $G$
and this triangle must be their common interior face. The graph $G$![]() is three-regular. Hence, $u$
is three-regular. Hence, $u$![]() has another vertex that we denote by $u_n$
has another vertex that we denote by $u_n$![]() apart from $v$
apart from $v$![]() and $w$
and $w$![]() that is adjacent to it. This vertex $u_n$
that is adjacent to it. This vertex $u_n$![]() must also be incident on the exterior face (since $u_n$
must also be incident on the exterior face (since $u_n$![]() shares two faces with $u$
shares two faces with $u$![]() and is not incident on the triangle $\delta$
and is not incident on the triangle $\delta$![]() ) implying that $u$
) implying that $u$![]() has three distinct exterior vertices adjacent to it. Since $u$
has three distinct exterior vertices adjacent to it. Since $u$![]() is an exterior vertex, this is a contradiction.
is an exterior vertex, this is a contradiction.
4.1 Proof of theorem 1.3
We construct a homeomorphism $\phi$![]() between $G^{\rm top}$
between $G^{\rm top}$![]() and the extended tropicalization $\mathcal {T}$
and the extended tropicalization $\mathcal {T}$![]() of the Schön embedding of $X_G$
of the Schön embedding of $X_G$![]() when $G$
when $G$![]() is a three-regular, three-connected planar graph. Our strategy is to first construct a bijection between the set of trivalent points of $G^{\rm top}$
is a three-regular, three-connected planar graph. Our strategy is to first construct a bijection between the set of trivalent points of $G^{\rm top}$![]() , i.e. the set of vertices $V(G)$
, i.e. the set of vertices $V(G)$![]() of $G$
of $G$![]() , and the set of trivalent points of $\mathcal {T}$
, and the set of trivalent points of $\mathcal {T}$![]() . For this, we use the description of the trivalent points of $\mathcal {T}$
. For this, we use the description of the trivalent points of $\mathcal {T}$![]() provided by lemma 4.2. We define $\phi |V(G)$
provided by lemma 4.2. We define $\phi |V(G)$![]() as follows. For an interior vertex $u$
as follows. For an interior vertex $u$![]() , we denote the branch point of ${\rm tropproj}(L_u)$
, we denote the branch point of ${\rm tropproj}(L_u)$![]() by $b_u$
by $b_u$![]() . For an exterior vertex $u$
. For an exterior vertex $u$![]() , let $\iota (u)$
, let $\iota (u)$![]() denote the unique interior vertex adjacent to it. Recall that for an edge $e=(u,v)$
denote the unique interior vertex adjacent to it. Recall that for an edge $e=(u,v)$![]() of $G$
of $G$![]() , we denote by $\zeta _e$
, we denote by $\zeta _e$![]() the (unique) intersection point of ${\rm tropproj}(L_u)$
the (unique) intersection point of ${\rm tropproj}(L_u)$![]() and ${\rm tropproj}(L_v)$
and ${\rm tropproj}(L_v)$![]() . For a vertex $u$
. For a vertex $u$![]() of $G$
of $G$![]() ,
,

By lemma 4.2, $\phi |V(G)$![]() is a bijection between $V(G)$
is a bijection between $V(G)$![]() and the set of trivalent points of $\mathcal {T}$
and the set of trivalent points of $\mathcal {T}$![]() . We extend $\phi$
. We extend $\phi$![]() to $G^{\rm top}$
to $G^{\rm top}$![]() via the following observations. Note that, by definition, $G^{\rm top} \setminus V(G)$
via the following observations. Note that, by definition, $G^{\rm top} \setminus V(G)$![]() is a disjoint union of open intervals that is in bijection with the edges of $G$
is a disjoint union of open intervals that is in bijection with the edges of $G$![]() . Consider the set $\mathcal {B}$
. Consider the set $\mathcal {B}$![]() of bivalent points of $\mathcal {T}$
of bivalent points of $\mathcal {T}$![]() . By the Bieri-Groves theorem [Reference Bieri and Groves6], [Reference Maclagan and Sturmfels23, Theorem 3.3.5], $\mathcal {B}$
. By the Bieri-Groves theorem [Reference Bieri and Groves6], [Reference Maclagan and Sturmfels23, Theorem 3.3.5], $\mathcal {B}$![]() is also a disjoint union of finitely many open intervals.
is also a disjoint union of finitely many open intervals.
Lemma 4.2 yields the following description of these open intervals. Recall, from the paragraph ‘tropicalization of Irreducible Components’, that each branch of ${\rm tropproj}(L_u)$![]() , where $u$
, where $u$![]() is an interior vertex, is labelled by an edge $e$
is an interior vertex, is labelled by an edge $e$![]() that is incident on $u$
that is incident on $u$![]() . Consider the set of bivalent points of $\mathcal {T}$
. Consider the set of bivalent points of $\mathcal {T}$![]() that are contained in a branch of ${\rm tropproj}(L_u)$
that are contained in a branch of ${\rm tropproj}(L_u)$![]() where $u$
where $u$![]() is an interior vertex. We denote this set by $\chi _{u,e}$
is an interior vertex. We denote this set by $\chi _{u,e}$![]() . Consider an exterior vertex $u$
. Consider an exterior vertex $u$![]() , the set ${\rm tropproj}(L_u) \setminus \{\zeta _{(u,\iota (u))}\}$
, the set ${\rm tropproj}(L_u) \setminus \{\zeta _{(u,\iota (u))}\}$![]() consists of two connected components. Each connected component is a half-open interval and based on the intersection point that it contains, it corresponds to an edge $e$
consists of two connected components. Each connected component is a half-open interval and based on the intersection point that it contains, it corresponds to an edge $e$![]() of the form $(u,v)$
of the form $(u,v)$![]() where $v$
where $v$![]() is an exterior vertex. We denote this component by $\chi _{u,e}$
is an exterior vertex. We denote this component by $\chi _{u,e}$![]() . There are three types of open intervals, they are as follows.
. There are three types of open intervals, they are as follows.
1. If $e=(u,v)$
 where $u$
where $u$ and $v$
and $v$ are both interior vertices, then the set $\chi _{u,e} \cup \chi _{v,e}$
are both interior vertices, then the set $\chi _{u,e} \cup \chi _{v,e}$ is an open interval.
is an open interval.2. If $e=(u,v)$
 such that $u$
such that $u$ is an interior vertex and $v$
is an interior vertex and $v$ is an exterior vertex, then $\chi _{u,e}$
is an exterior vertex, then $\chi _{u,e}$ is an open interval.
is an open interval.3. If $e=(u,v)$
 where $u$
where $u$ and $v$
and $v$ are both exterior vertices, then the set $\chi _{u,e} \cup \chi _{v,e}$
are both exterior vertices, then the set $\chi _{u,e} \cup \chi _{v,e}$ is an open interval.
is an open interval.
We denote each of these three types of open intervals by $\chi _e$![]() where $e$
where $e$![]() is the corresponding edge. We extend $\phi$
is the corresponding edge. We extend $\phi$![]() to $G^{\rm top}$
to $G^{\rm top}$![]() as follows. Suppose that $\mathcal {I}_e$
as follows. Suppose that $\mathcal {I}_e$![]() is the open line segment in $G^{\rm top}$
is the open line segment in $G^{\rm top}$![]() corresponding to the edge $e$
corresponding to the edge $e$![]() . We define $\phi |{\mathcal {I}_e}$
. We define $\phi |{\mathcal {I}_e}$![]() to be any homeomorphism between $\mathcal {I}_e$
to be any homeomorphism between $\mathcal {I}_e$![]() and $\chi _e$
and $\chi _e$![]() that when extended to $\bar {\mathcal {I}_e}$
that when extended to $\bar {\mathcal {I}_e}$![]() by taking $u$
by taking $u$![]() to $\phi (u)$
to $\phi (u)$![]() and $v$
and $v$![]() to $\phi (v)$
to $\phi (v)$![]() induces a homeomorphism between $\bar {\mathcal {I}_e}$
induces a homeomorphism between $\bar {\mathcal {I}_e}$![]() and $\bar {\chi _e}$
and $\bar {\chi _e}$![]() . This completes the definition of $\phi$
. This completes the definition of $\phi$![]() .
.
Finally, we note that $\phi$![]() is a homeomorphism between $G^{\rm top}$
is a homeomorphism between $G^{\rm top}$![]() and $\mathcal {T}$
and $\mathcal {T}$![]() . We start by noting that, by construction, $\phi$
. We start by noting that, by construction, $\phi$![]() is a bijection. Let $N(u)$
is a bijection. Let $N(u)$![]() be the open neighbourhood $(\cup _{e|u \in e} \mathcal {I}_e) \cup \{u\}$
be the open neighbourhood $(\cup _{e|u \in e} \mathcal {I}_e) \cup \{u\}$![]() of the vertex $u \in G^{\rm top}$
of the vertex $u \in G^{\rm top}$![]() . Similarly, let $N(\phi (u))$
. Similarly, let $N(\phi (u))$![]() be the open neighbourhood $(\cup _{e|u \in e} \chi _e) \cup \{\phi (u)\}$
be the open neighbourhood $(\cup _{e|u \in e} \chi _e) \cup \{\phi (u)\}$![]() of the trivalent point $\phi (u) \in \mathcal {T}$
of the trivalent point $\phi (u) \in \mathcal {T}$![]() . Note that, by construction, the endpoints of $\bar {\chi _e}$
. Note that, by construction, the endpoints of $\bar {\chi _e}$![]() are precisely $\phi (u)$
are precisely $\phi (u)$![]() and $\phi (v)$
and $\phi (v)$![]() for each $e=(u,v)$
for each $e=(u,v)$![]() . Hence, we deduce that $\phi$
. Hence, we deduce that $\phi$![]() induces a homeomorphism between $N(u)$
induces a homeomorphism between $N(u)$![]() and $N(\phi (u))$
and $N(\phi (u))$![]() for every vertex $u$
for every vertex $u$![]() of $G$
of $G$![]() . This shows that $\phi$
. This shows that $\phi$![]() is a bijective local homeomorphism and is hence, also a homeomorphism.
is a bijective local homeomorphism and is hence, also a homeomorphism.
We refer to figure 4 for the case when $G$![]() is the envelope graph. The graph $G$
is the envelope graph. The graph $G$![]() is shown on the left and the extended tropicalization of the Schön embedding of $X_G$
is shown on the left and the extended tropicalization of the Schön embedding of $X_G$![]() is shown in thick lines on the right. Note that this tropicalization is contained in $\mathbb {TP}^3$
is shown in thick lines on the right. Note that this tropicalization is contained in $\mathbb {TP}^3$![]() which is identified with a three-dimensional simplex. It is contained in two facets of this simplex and these two facets are the visible facets in the figure. The image $\phi (i)$
which is identified with a three-dimensional simplex. It is contained in two facets of this simplex and these two facets are the visible facets in the figure. The image $\phi (i)$![]() of $\phi$
of $\phi$![]() on $i$
on $i$![]() is denoted by $\phi _i$
is denoted by $\phi _i$![]() . The open interval $\chi _{(i,j)}$
. The open interval $\chi _{(i,j)}$![]() is denoted by $\chi _{i,j}$
is denoted by $\chi _{i,j}$![]() and is the open interval corresponding to the segment with endpoints $\phi _i$
and is the open interval corresponding to the segment with endpoints $\phi _i$![]() and $\phi _j$
and $\phi _j$![]() that appears just below the symbol $\chi _{i,j}$
that appears just below the symbol $\chi _{i,j}$![]() in the figure.
in the figure.

Figure 4. An illustration of the homeomorphism $\phi$![]() in the case when $G$
in the case when $G$![]() is the envelope graph.
is the envelope graph.
5. Connectivity between tropicalizations of the Schön embedding
In this subsection, we show theorem 1.6 that states that the set of extended tropicalizations of Schön embeddings of $X_G$![]() (as $G$
(as $G$![]() varies over simple, three-regular, three-connected graphs) is connected via certain ‘local’ operations. Recall from the introduction that these local operations are tropical analogues of $\Delta Y$
varies over simple, three-regular, three-connected graphs) is connected via certain ‘local’ operations. Recall from the introduction that these local operations are tropical analogues of $\Delta Y$![]() , $Y \Delta$
, $Y \Delta$![]() and contraction-elongation transformations, and are motivated by Steinitz’ theorem. We start by recalling Steinitz’ theorem [Reference Ziegler34, Chapter 4] and a part of this standard proof.
and contraction-elongation transformations, and are motivated by Steinitz’ theorem. We start by recalling Steinitz’ theorem [Reference Ziegler34, Chapter 4] and a part of this standard proof.
Theorem 5.1 (Steinitz’ theorem)
A graph is the one-skeleton of a three-dimensional polytope if and only if it is simple, planar and three-vertex-connected.
A key ingredient in the proof is the notion of a $\Delta Y$![]() transformation, i.e. replace a $\Delta$
transformation, i.e. replace a $\Delta$![]() -subgraph (a triangular face) by a $Y$
-subgraph (a triangular face) by a $Y$![]() -subgraph. More formally, a $\Delta Y$
-subgraph. More formally, a $\Delta Y$![]() transformation replaces a triangle that bounds a face by a three-star that connects the same set of vertices. This operation is reversed for a $Y \Delta$
transformation replaces a triangle that bounds a face by a three-star that connects the same set of vertices. This operation is reversed for a $Y \Delta$![]() transformation. Figure 5 illustrates the transformations in the case of three-regular graphs, the situation that is relevant for us.
transformation. Figure 5 illustrates the transformations in the case of three-regular graphs, the situation that is relevant for us.

Figure 5. $Y \Delta$![]() and $\Delta Y$
and $\Delta Y$![]() transformations.
transformations.
A simple $Y \Delta$![]() transformation is a $Y \Delta$
transformation is a $Y \Delta$![]() transformation followed by edge contractions to eliminate valence two vertices and replacing each set of resulting parallel edges by corresponding single edges. A key step in the proof is to show that every three-vertex-connected planar graph can be obtained from $K_4$
transformation followed by edge contractions to eliminate valence two vertices and replacing each set of resulting parallel edges by corresponding single edges. A key step in the proof is to show that every three-vertex-connected planar graph can be obtained from $K_4$![]() by a sequence of simple $Y \Delta$
by a sequence of simple $Y \Delta$![]() transformations.
transformations.
We take cue from this part of the proof. Since we are concerned with three-regular planar graphs rather than arbitrary planar graphs, we employ a sequence of ‘local operations’ that transform a three-regular, three-connected planar graph to $K_4$![]() that keep the properties three-regular and three-connected invariant. We perform the following two operations:
that keep the properties three-regular and three-connected invariant. We perform the following two operations:
1. $\Delta Y$
 (and $Y \Delta$
(and $Y \Delta$ ) transformations.
) transformations.2. Pachner's contraction-elongation transformations, as shown in figure 6. We say that the operation is performed along the edge $e_1$
 .
.

Figure 6. Contraction-elongation transformation.
Pachner [Reference Pachner28] shows that for any simplicial two-sphere there is a sequence of moves consisting of the so-called $0$![]() -move, that is dual to the $\Delta Y$
-move, that is dual to the $\Delta Y$![]() transformation, and the $2$
transformation, and the $2$![]() -move, that is dual to the contraction-elongation operation, that transforms it to a tetrahedron. In the light of Steinitz’ theorem, the dual version of this statement is that for any three-regular, three-connected planar graph, there is a sequence of $\Delta Y$
-move, that is dual to the contraction-elongation operation, that transforms it to a tetrahedron. In the light of Steinitz’ theorem, the dual version of this statement is that for any three-regular, three-connected planar graph, there is a sequence of $\Delta Y$![]() and contraction-elongation transformations that transforms it to $K_4$
and contraction-elongation transformations that transforms it to $K_4$![]() while maintaining the three-regularity and the three-connectivity properties. Nevertheless, we include a proof of this property in Appendix A for easy reference and since the original paper of Pachner is written in German.
while maintaining the three-regularity and the three-connectivity properties. Nevertheless, we include a proof of this property in Appendix A for easy reference and since the original paper of Pachner is written in German.
In the following, we define tropical analogues of the notion of $Y \Delta$![]() and contraction-elongation transformations. We define these operations on any tropical line arrangement in tropical projective space $\mathbb {TP}^n$
and contraction-elongation transformations. We define these operations on any tropical line arrangement in tropical projective space $\mathbb {TP}^n$![]() given some additional data. Our primary example in the current article of such a tropical line arrangement is the extended tropicalization $\mathcal {T}$
given some additional data. Our primary example in the current article of such a tropical line arrangement is the extended tropicalization $\mathcal {T}$![]() of the Schön embedding of $X_G$
of the Schön embedding of $X_G$![]() where $G$
where $G$![]() is a three-regular, three-connected planar graph. However, these operations can be carried out in greater generality and can be a topic of future investigation.
is a three-regular, three-connected planar graph. However, these operations can be carried out in greater generality and can be a topic of future investigation.
Given a finite set $[0,\ldots,n]$![]() , consider tropical projective space $\mathbb {TP}^n$
, consider tropical projective space $\mathbb {TP}^n$![]() (identified with the $n$
(identified with the $n$![]() -simplex) each of whose facets are labelled by a distinct element in $[0,\ldots,n]$
-simplex) each of whose facets are labelled by a distinct element in $[0,\ldots,n]$![]() . Suppose we fix the following additional data: for each edge $\xi$
. Suppose we fix the following additional data: for each edge $\xi$![]() of $\mathbb {TP}^n$
of $\mathbb {TP}^n$![]() , we fix a unique point $\rho _{\xi }$
, we fix a unique point $\rho _{\xi }$![]() in the relative interior of $\xi$
in the relative interior of $\xi$![]() that we refer to as the marked point of $\xi$
that we refer to as the marked point of $\xi$![]() . For each two-dimensional face $D$
. For each two-dimensional face $D$![]() of $\mathbb {TP}^n$
of $\mathbb {TP}^n$![]() , there is a unique branched tropical lineFootnote 4 $\mathcal {TL}_D$
, there is a unique branched tropical lineFootnote 4 $\mathcal {TL}_D$![]() contained in $D$
contained in $D$![]() that passes through $\rho _{\xi }$
that passes through $\rho _{\xi }$![]() for each edge $\xi$
for each edge $\xi$![]() that is contained in $D$
that is contained in $D$![]() . This tropical line is the collection of three rays, corresponding to the three marked points, emanating from the origin in the interior of $D$
. This tropical line is the collection of three rays, corresponding to the three marked points, emanating from the origin in the interior of $D$![]() (note that the interior of $D$
(note that the interior of $D$![]() is identified with $\mathbb {R}^2$
is identified with $\mathbb {R}^2$![]() via the extended tropicalization map). We refer to $\mathcal {TL}_D$
via the extended tropicalization map). We refer to $\mathcal {TL}_D$![]() as the standard tropical line associated to $D$
as the standard tropical line associated to $D$![]() .
.
In the following, we identify $\mathbb {TP}^{g-1}$![]() with a facet of $\mathbb {TP}^g$
with a facet of $\mathbb {TP}^g$![]() . Note that given a two-dimensional face $D$
. Note that given a two-dimensional face $D$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() , there is a unique three-dimensional face $\beta _D$
, there is a unique three-dimensional face $\beta _D$![]() of $\mathbb {TP}^g$
of $\mathbb {TP}^g$![]() that contains $D$
that contains $D$![]() and the unique vertex $\nu$
and the unique vertex $\nu$![]() of $\mathbb {TP}^{g}$
of $\mathbb {TP}^{g}$![]() that is not contained in $\mathbb {TP}^{g-1}$
that is not contained in $\mathbb {TP}^{g-1}$![]() .
.
Definition 5.2 (Tropical $Y \Delta$![]() Transformation at a Two-Dimensional Face)
Transformation at a Two-Dimensional Face)
A tropical $Y \Delta$![]() transformation of a tropical line arrangement $\mathcal {T} \subset \mathbb {TP}^{g-1}$
transformation of a tropical line arrangement $\mathcal {T} \subset \mathbb {TP}^{g-1}$![]() at a two-dimensional face $D$
at a two-dimensional face $D$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() such that $\mathcal {T}$
such that $\mathcal {T}$![]() contains the standard line of $D$
contains the standard line of $D$![]() is the tropical line arrangement $\hat {\mathcal {T}}:=(\mathcal {T} \setminus \mathcal {TL}_D) \cup \mathcal {TL}_{D^{(1)}} \cup \mathcal {TL}_{D^{(2)}} \cup \mathcal {TL}_{D^{(3)}}$
is the tropical line arrangement $\hat {\mathcal {T}}:=(\mathcal {T} \setminus \mathcal {TL}_D) \cup \mathcal {TL}_{D^{(1)}} \cup \mathcal {TL}_{D^{(2)}} \cup \mathcal {TL}_{D^{(3)}}$![]() where $D^{(1)},~D^{(2)}$
where $D^{(1)},~D^{(2)}$![]() and $D^{(3)}$
and $D^{(3)}$![]() are the two-dimensional faces of $\beta _D$
are the two-dimensional faces of $\beta _D$![]() apart from $D$
apart from $D$![]() .
.
We refer to figure 7 for an illustration of a tropical $Y \Delta$![]() transformation at the face $\{2,3,4\}$
transformation at the face $\{2,3,4\}$![]() . The tropical line $a$
. The tropical line $a$![]() is the standard tropical line of $\{2,3,4\}$
is the standard tropical line of $\{2,3,4\}$![]() and the tropical lines $b,~c$
and the tropical lines $b,~c$![]() and $d$
and $d$![]() are the standard tropical lines of $\{1,2,4\},~\{1,2,3\}$
are the standard tropical lines of $\{1,2,4\},~\{1,2,3\}$![]() and $\{1,3,4\}$
and $\{1,3,4\}$![]() respectively.
respectively.

Figure 7. A tropical $Y \Delta$![]() transformation at a two-dimensional face.
transformation at a two-dimensional face.
Given an edge $\xi$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() , there is a unique two-dimensional face $D_{\xi }$
, there is a unique two-dimensional face $D_{\xi }$![]() of $\mathbb {TP}^g$
of $\mathbb {TP}^g$![]() that contains $\xi$
that contains $\xi$![]() and the vertex $\nu$
and the vertex $\nu$![]() of $\mathbb {TP}^{g}$
of $\mathbb {TP}^{g}$![]() not in $\mathbb {TP}^{g-1}$
not in $\mathbb {TP}^{g-1}$![]() .
.
Definition 5.3 (Tropical $Y \Delta$![]() Transformation at an Edge)
Transformation at an Edge)
A tropical $Y \Delta$![]() transformation of $\mathcal {T}$
transformation of $\mathcal {T}$![]() at an edge $\xi$
at an edge $\xi$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() that is also contained in $\mathcal {T}$
that is also contained in $\mathcal {T}$![]() is the tropical line arrangement $\hat {\mathcal {T}}=(\mathcal {T} \setminus \xi ) \cup \mathcal {TL}(D_{\xi }) \cup \xi ^{(1)} \cup \xi ^{(2)}$
is the tropical line arrangement $\hat {\mathcal {T}}=(\mathcal {T} \setminus \xi ) \cup \mathcal {TL}(D_{\xi }) \cup \xi ^{(1)} \cup \xi ^{(2)}$![]() where $\xi ^{(1)}$
where $\xi ^{(1)}$![]() and $\xi ^{(2)}$
and $\xi ^{(2)}$![]() are the two edges of $D_{\xi }$
are the two edges of $D_{\xi }$![]() apart from $\xi$
apart from $\xi$![]() .
.
Figure 8 illustrates a tropical $Y \Delta$![]() transformation at the edge $\xi$
transformation at the edge $\xi$![]() , the tropical line $a$
, the tropical line $a$![]() is the standard tropical line of $D_{\xi }$
is the standard tropical line of $D_{\xi }$![]() .
.

Figure 8. A tropical $Y \Delta$![]() transformation at an edge.
transformation at an edge.
For any pair of two-dimensional faces $(D_1,D_2)$![]() of $\mathcal {TP}^{g-1}$
of $\mathcal {TP}^{g-1}$![]() that shares a common edge, let $\beta _{D_1,D_2}$
that shares a common edge, let $\beta _{D_1,D_2}$![]() be the unique three-dimensional face of $\mathcal {TP}^{g-1}$
be the unique three-dimensional face of $\mathcal {TP}^{g-1}$![]() that contains both $D_1$
that contains both $D_1$![]() and $D_2$
and $D_2$![]() .
.
Definition 5.4 (Tropical Contraction-Elongation Transformation)
A tropical contraction-elongation transformation of a tropical line arrangement $\mathcal {T}$![]() at a pair of two-dimensional faces $(D_1,D_2)$
at a pair of two-dimensional faces $(D_1,D_2)$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() that shares a common edge and such that $\mathcal {T}$
that shares a common edge and such that $\mathcal {T}$![]() contains both $\mathcal {TL}_{D_1}$
contains both $\mathcal {TL}_{D_1}$![]() and $\mathcal {TL}_{D_2}$
and $\mathcal {TL}_{D_2}$![]() is defined as the tropical line arrangement $\mathcal {T} \setminus (\mathcal {TL}_{D_1} \cup \mathcal {TL}_{D_2}) \cup \mathcal {TL}_{\bar {D_1}} \cup \mathcal {TL}_{\bar {D_2}}$
is defined as the tropical line arrangement $\mathcal {T} \setminus (\mathcal {TL}_{D_1} \cup \mathcal {TL}_{D_2}) \cup \mathcal {TL}_{\bar {D_1}} \cup \mathcal {TL}_{\bar {D_2}}$![]() where $\bar {D_1}$
where $\bar {D_1}$![]() and $\bar {D_2}$
and $\bar {D_2}$![]() are the two-dimensional faces of $\beta _{D_1,D_2}$
are the two-dimensional faces of $\beta _{D_1,D_2}$![]() apart from $D_1$
apart from $D_1$![]() and $D_2$
and $D_2$![]() .
.
We refer to figure 9 for an example. The tropical lines $a$![]() and $b$
and $b$![]() are the standard tropical lines of the faces $\{1,2,4\}$
are the standard tropical lines of the faces $\{1,2,4\}$![]() and $\{1,3,4\}$
and $\{1,3,4\}$![]() respectively and the tropical lines $c$
respectively and the tropical lines $c$![]() and $d$
and $d$![]() are the standard tropical lines of $\{1,2,3\}$
are the standard tropical lines of $\{1,2,3\}$![]() and $\{2,3,4\}$
and $\{2,3,4\}$![]() respectively.
respectively.

Figure 9. A tropical contraction-elongation transformation.
In the following, we relate the $Y \Delta$![]() transformation and the contraction-elongation transformation to their tropical analogues. The set up is as in § 4. For each edge $\xi$
transformation and the contraction-elongation transformation to their tropical analogues. The set up is as in § 4. For each edge $\xi$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() , we set $\rho _\xi :=m_\xi$
, we set $\rho _\xi :=m_\xi$![]() (recall its definition from § 4: suppose that $F_s$
(recall its definition from § 4: suppose that $F_s$![]() and $F_t$
and $F_t$![]() are the two interior faces that do not contain $\xi$
are the two interior faces that do not contain $\xi$![]() , the point $m_\xi$
, the point $m_\xi$![]() is the tropicalization of the point in $\mathbb {P}_{\mathbb {K}}^{g-1}$
is the tropicalization of the point in $\mathbb {P}_{\mathbb {K}}^{g-1}$![]() with coordinates $(p_F)_F$
with coordinates $(p_F)_F$![]() such that $p_{F_s},~p_{F_t}$
such that $p_{F_s},~p_{F_t}$![]() are both not zero, ${\rm val}(p_{F_s})={\rm val}(p_{F_t})$
are both not zero, ${\rm val}(p_{F_s})={\rm val}(p_{F_t})$![]() and $p_F=0$
and $p_F=0$![]() for any interior face $F$
for any interior face $F$![]() that is neither $F_s$
that is neither $F_s$![]() nor $F_t$
nor $F_t$![]() ).
).
With this choice of marked points, the standard tropical line of each two-dimensional face $D$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() is the extended tropicalization of the line defined by $\langle x_{F_i}+x_{F_j}+x_{F_k},~x_F|~F \notin \{F_i,F_j,F_k\} \rangle$
is the extended tropicalization of the line defined by $\langle x_{F_i}+x_{F_j}+x_{F_k},~x_F|~F \notin \{F_i,F_j,F_k\} \rangle$![]() where $F_i,F_j$
where $F_i,F_j$![]() and $F_k$
and $F_k$![]() are the three facets of $\mathbb {TP}^{g-1}$
are the three facets of $\mathbb {TP}^{g-1}$![]() not containing $D$
not containing $D$![]() . In the following, we denote the extended tropicalization of the Schön embedding of $X_{G}$
. In the following, we denote the extended tropicalization of the Schön embedding of $X_{G}$![]() by $\mathcal {T}_G$
by $\mathcal {T}_G$![]() . Recall, from § 4, that corresponding to each interior vertex $u$
. Recall, from § 4, that corresponding to each interior vertex $u$![]() of $G$
of $G$![]() , there is a unique two-dimensional face $D_u$
, there is a unique two-dimensional face $D_u$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() that contains ${\rm tropproj}(L_u)$
that contains ${\rm tropproj}(L_u)$![]() .
.
Proposition 5.5 Suppose that the graph $G_2$![]() is the result of a $Y \Delta$
is the result of a $Y \Delta$![]() transformation of $G_1$
transformation of $G_1$![]() at an interior vertex $u$
at an interior vertex $u$![]() . The extended tropicalization $\mathcal {T}_{G_2}$
. The extended tropicalization $\mathcal {T}_{G_2}$![]() is the result of a tropical $Y \Delta$
is the result of a tropical $Y \Delta$![]() transformation of $\mathcal {T}_{G_1}$
transformation of $\mathcal {T}_{G_1}$![]() at $D_u$
at $D_u$![]() with respect to the marked points $\{m_{\xi }\}_{\xi }$
with respect to the marked points $\{m_{\xi }\}_{\xi }$![]() .
.
Proof. Note that $\mathcal {T}_{G_2}=\mathcal {T}_{G_1} \setminus \{ {\rm tropproj}(L_{u})\} \cup {\rm tropproj}(L_{u^{(1)}}) \cup {\rm tropproj}(L_{u^{(2)}}) \cup {\rm tropproj}(L_{u^{(3)}})$![]() where $u^{(1)},u^{(2)}$
where $u^{(1)},u^{(2)}$![]() and $u^{(3)}$
and $u^{(3)}$![]() are the three vertices of $\Delta$
are the three vertices of $\Delta$![]() , the new face that is created by the transformation. Consider the three-dimensional subsimplex $\beta$
, the new face that is created by the transformation. Consider the three-dimensional subsimplex $\beta$![]() of $\mathbb {TP}^g$
of $\mathbb {TP}^g$![]() whose label is the complement of the set $\{F_i,F_j,F_k,\Delta \}$
whose label is the complement of the set $\{F_i,F_j,F_k,\Delta \}$![]() where $F_i,F_j$
where $F_i,F_j$![]() and $F_k$
and $F_k$![]() are the three interior faces of $G_1$
are the three interior faces of $G_1$![]() that contain $u$
that contain $u$![]() . The two-dimensional face $D_u$
. The two-dimensional face $D_u$![]() is a face of $\beta$
is a face of $\beta$![]() . The proof follows from the observation that the other three two-dimensional faces of $\beta$
. The proof follows from the observation that the other three two-dimensional faces of $\beta$![]() are precisely $D_{u^{(i)}}$
are precisely $D_{u^{(i)}}$![]() for each $i$
for each $i$![]() from one to three.
from one to three.
Recall that for an exterior vertex $u$![]() of $G$
of $G$![]() , the tropical line ${\rm tropproj}(L_u)$
, the tropical line ${\rm tropproj}(L_u)$![]() coincides with an edge of $\mathbb {TP}^{g-1}$
coincides with an edge of $\mathbb {TP}^{g-1}$![]() .
.
Proposition 5.6 Suppose that the graph $G_2$![]() is the result of a $Y \Delta$
is the result of a $Y \Delta$![]() transformation of $G_1$
transformation of $G_1$![]() at an exterior vertex $u$
at an exterior vertex $u$![]() . The extended tropicalization $\mathcal {T}_{G_2}$
. The extended tropicalization $\mathcal {T}_{G_2}$![]() is the result of a tropical $Y \Delta$
is the result of a tropical $Y \Delta$![]() transformation of $\mathcal {T}_{G_1}$
transformation of $\mathcal {T}_{G_1}$![]() at the edge ${\rm tropproj}(L_u)$
at the edge ${\rm tropproj}(L_u)$![]() with respect to the marked points $\{m_{\xi }\}_{\xi }$
with respect to the marked points $\{m_{\xi }\}_{\xi }$![]() .
.
The proof of proposition 5.6 is analogous to the proof of proposition 5.5.
Proposition 5.7 Suppose that the graph $G_2$![]() is the result of a contraction-elongation transformation of $G_1$
is the result of a contraction-elongation transformation of $G_1$![]() along the edge $e=(u,v)$
along the edge $e=(u,v)$![]() (both $u$
(both $u$![]() and $v$
and $v$![]() are interior vertices). The extended tropicalization $\mathcal {T}_{G_2}$
are interior vertices). The extended tropicalization $\mathcal {T}_{G_2}$![]() is the result of a tropical contraction-elongation transformation of $\mathcal {T}_{G_1}$
is the result of a tropical contraction-elongation transformation of $\mathcal {T}_{G_1}$![]() at the pair $(D_u,D_v)$
at the pair $(D_u,D_v)$![]() with respect to the marked points $\{m_{\xi }\}_{\xi }$
with respect to the marked points $\{m_{\xi }\}_{\xi }$![]() .
.
The proof follows a strategy akin to that of proposition 5.5.
Proof. Suppose that $F_i,~F_k$![]() are the two faces incident on $e$
are the two faces incident on $e$![]() and that $F_j$
and that $F_j$![]() ($F_l$
($F_l$![]() , respectively) is the other face incident on $u$
, respectively) is the other face incident on $u$![]() ($v$
($v$![]() , respectively). Consider the three-dimensional subsimplex $\beta$
, respectively). Consider the three-dimensional subsimplex $\beta$![]() of $\mathbb {TP}^{g-1}$
of $\mathbb {TP}^{g-1}$![]() that is labelled by the complement of the set $\{F_i,F_j,F_k,F_l\}$
that is labelled by the complement of the set $\{F_i,F_j,F_k,F_l\}$![]() . Suppose that $D_i,D_j,D_k$
. Suppose that $D_i,D_j,D_k$![]() and $D_l$
and $D_l$![]() are the four two-dimensional faces of $\beta$
are the four two-dimensional faces of $\beta$![]() defined by the property that the label of $D_r$
defined by the property that the label of $D_r$![]() additionally contains $F_r$
additionally contains $F_r$![]() for $r \in \{i,j,k,l\}$
for $r \in \{i,j,k,l\}$![]() . The proof follows from the observation that ${\mathcal {T}}_{G_2}=\mathcal {T}_{G_1}\setminus ({\mathcal {TL}}(D_j) \cup {\mathcal {TL}}(D_l) ) \cup (\mathcal {TL}(D_i) \cup \mathcal {TL}(D_k))$
. The proof follows from the observation that ${\mathcal {T}}_{G_2}=\mathcal {T}_{G_1}\setminus ({\mathcal {TL}}(D_j) \cup {\mathcal {TL}}(D_l) ) \cup (\mathcal {TL}(D_i) \cup \mathcal {TL}(D_k))$![]() .
.
Definition 5.8 Tropical line arrangements $\mathcal {T}_1$![]() and $\mathcal {T}_2$
and $\mathcal {T}_2$![]() in tropical projective space are said to be related by a tropical $\Delta Y$
in tropical projective space are said to be related by a tropical $\Delta Y$![]() transformation if one of them, $\mathcal {T}_2$
transformation if one of them, $\mathcal {T}_2$![]() say, is a tropical $Y \Delta$
say, is a tropical $Y \Delta$![]() transform of the other. We say that $\mathcal {T}_1$
transform of the other. We say that $\mathcal {T}_1$![]() is a tropical $\Delta Y$
is a tropical $\Delta Y$![]() transform of $\mathcal {T}_2$
transform of $\mathcal {T}_2$![]() .
.
As a corollary to propositions 5.5 and 5.6, we obtain:
Corollary 5.9 Suppose that the graph $G_1$![]() is the result of a $\Delta Y$
is the result of a $\Delta Y$![]() transformation on $G_2$
transformation on $G_2$![]() . The extended tropicalization $\mathcal {T}_{G_1}$
. The extended tropicalization $\mathcal {T}_{G_1}$![]() is a tropical $\Delta Y$
is a tropical $\Delta Y$![]() transform of $\mathcal {T}_{G_2}$
transform of $\mathcal {T}_{G_2}$![]() with respect to the marked points $\{m_{\xi }\}_{\xi }$
with respect to the marked points $\{m_{\xi }\}_{\xi }$![]() .
.
As a corollary to Pachner's result (lemma A.2) and the correspondence between $\Delta Y$![]() , $Y \Delta$
, $Y \Delta$![]() , contraction-elongation transformations and their respective tropical analogues, we obtain theorem 1.6.
, contraction-elongation transformations and their respective tropical analogues, we obtain theorem 1.6.
Example 5.10 Consider the one-skeleton of the three-dimensional cube. A sequence of transformations following lemma A.2 to transform it into $K_4$![]() is shown in figure 10. This sequence is the one-skeleton of the following polytopes:
is shown in figure 10. This sequence is the one-skeleton of the following polytopes:
cube $\rightarrow$
 triangular prism sliced at a vertex $\rightarrow$
triangular prism sliced at a vertex $\rightarrow$ triangular prism $\rightarrow$
triangular prism $\rightarrow$ tetrahedron.
tetrahedron.

Figure 10. A sequence of $Y \Delta$![]() and contraction-elongation transformations.
and contraction-elongation transformations.
The tropical counterpart of the sequence is shown in figure 11.

Figure 11. The corresponding tropical operations.
Acknowledgements
We thank Bo Lin, Ralph Morrison and Bernd Sturmfels very much, this work has significantly benefitted from the several discussions we had with them. We have benefitted very much from our discussions with Lorenzo Fantini, particularly in relation to Berkovich spaces. We thank Omid Amini, Erwan Brugallé, Alex Fink, Dhruv Ranganathan and Martin Ulirsch for the helpful discussions. We thank the anonymous referee for the generous suggestions.
Part of this work was carried out while the author was affiliated to UC, Berkeley, QMUL London and while visiting the IHES and ICTP. He was supported by the Feoder-Lynen Fellowship of the Humboldt Foundation. He thanks the generous support and the warm hospitality of these institutions. The author was supported by a MATRICS grant of the Department of Science and Technology (DST), India.
Appendix A. $\Delta Y$ and contraction-elongation transformations
and contraction-elongation transformations
Recall that an exterior vertex of a planar embedding is a vertex that is not incident on the exterior face. The following characteriztion of three-regular, three-connected planar graphs turns out be useful.
Lemma A.1 Let $G$![]() be a simple, three-regular, two-edge-connected planar graph. The graph $G$
be a simple, three-regular, two-edge-connected planar graph. The graph $G$![]() is three-edge-connected if and only if for any planar embedding of $G$
is three-edge-connected if and only if for any planar embedding of $G$![]() , no two non-adjacent exterior vertices share an interior face.
, no two non-adjacent exterior vertices share an interior face.
Proof. $\Rightarrow$![]() Suppose that there is a planar graph $G$
Suppose that there is a planar graph $G$![]() with a planar embedding such that there exist two non-adjacent exterior vertices $u$
with a planar embedding such that there exist two non-adjacent exterior vertices $u$![]() and $v$
and $v$![]() that share an interior face $F$
that share an interior face $F$![]() . Since $G$
. Since $G$![]() is three-regular, for each of these vertices there is a unique edge incident on it that is shared by both the interior face $F$
is three-regular, for each of these vertices there is a unique edge incident on it that is shared by both the interior face $F$![]() and the exterior face. Suppose that $e_1$
and the exterior face. Suppose that $e_1$![]() and $e_2$
and $e_2$![]() are such edges incident on $u$
are such edges incident on $u$![]() and $v$
and $v$![]() , respectively. We claim that deleting edges $e_1$
, respectively. We claim that deleting edges $e_1$![]() and $e_2$
and $e_2$![]() will disconnect the graph. To see this, consider an arc $\mathcal {A}_1$
will disconnect the graph. To see this, consider an arc $\mathcal {A}_1$![]() contained (in the interior of) the exterior face such that the closure of $\mathcal {A}_1$
contained (in the interior of) the exterior face such that the closure of $\mathcal {A}_1$![]() (with respect to this face) contains one interior point $p_1$
(with respect to this face) contains one interior point $p_1$![]() , say in $e_1$
, say in $e_1$![]() and one interior point $p_2$
and one interior point $p_2$![]() , say in $e_2$
, say in $e_2$![]() as its two end points. Consider another arc $\mathcal {A}_2$
as its two end points. Consider another arc $\mathcal {A}_2$![]() contained in the interior of $F$
contained in the interior of $F$![]() such that the closure of $\mathcal {A}_2$
such that the closure of $\mathcal {A}_2$![]() with respect to $F$
with respect to $F$![]() is $\mathcal {A}_2 \cup \{p_1,p_2\}$
is $\mathcal {A}_2 \cup \{p_1,p_2\}$![]() . The interior and exterior regions of the closed curve $\mathcal {A}_1 \cup \mathcal {A}_2 \cup \{p_1,p_2\}$
. The interior and exterior regions of the closed curve $\mathcal {A}_1 \cup \mathcal {A}_2 \cup \{p_1,p_2\}$![]() both intersect $G$
both intersect $G$![]() non-trivially, and $\mathcal {A}_1 \cup \mathcal {A}_2$
non-trivially, and $\mathcal {A}_1 \cup \mathcal {A}_2$![]() does not intersect $G \setminus \{e_1,e_2\}$
does not intersect $G \setminus \{e_1,e_2\}$![]() . We conclude that $G \setminus \{e_1,e_2\}$
. We conclude that $G \setminus \{e_1,e_2\}$![]() is disconnected. Hence, $G$
is disconnected. Hence, $G$![]() is not three-edge-connected.
is not three-edge-connected.
($\Leftarrow$![]() ) Conversely, suppose that $G$
) Conversely, suppose that $G$![]() is not a three-edge-connected graph. Suppose that deleting edges $e_1$
is not a three-edge-connected graph. Suppose that deleting edges $e_1$![]() and $e_2$
and $e_2$![]() disconnects $G$
disconnects $G$![]() . The edges $e_1$
. The edges $e_1$![]() and $e_2$
and $e_2$![]() cannot share a vertex $v$
cannot share a vertex $v$![]() since this implies that the other edge incident on $v$
since this implies that the other edge incident on $v$![]() is a bridge. Hence, in any planar embedding of $G$
is a bridge. Hence, in any planar embedding of $G$![]() , the edges $e_1$
, the edges $e_1$![]() and $e_2$
and $e_2$![]() bind an interior face $F$
bind an interior face $F$![]() of $G$
of $G$![]() , and are both contained in the exterior face, see figure A12. The vertices $v_1$
, and are both contained in the exterior face, see figure A12. The vertices $v_1$![]() and $u_2$
and $u_2$![]() are not adjacent, are both exterior vertices and share an interior face.
are not adjacent, are both exterior vertices and share an interior face.
Lemma A.2 Every simple, three-regular, three-connected planar graph $G$![]() can be transformed to $K_4$
can be transformed to $K_4$![]() by a sequence of $\Delta Y$
by a sequence of $\Delta Y$![]() and contraction-elongation transformations such that the graph at each step remains a simple, three-regular, three-connected planar graph.
and contraction-elongation transformations such that the graph at each step remains a simple, three-regular, three-connected planar graph.
Proof. The minimum genus of $G$![]() is three and in this case, it is a $K_4$
is three and in this case, it is a $K_4$![]() . Hence, there is nothing to prove. Otherwise, the genus of $G$
. Hence, there is nothing to prove. Otherwise, the genus of $G$![]() is at least four. We consider a planar embedding of $G$
is at least four. We consider a planar embedding of $G$![]() and perform the following operations on it.
and perform the following operations on it.
1. Suppose that $G$
 has a triangular face in this embedding then perform a $\Delta Y$
has a triangular face in this embedding then perform a $\Delta Y$ transformation on it.
transformation on it.2. Nevertheless, $G$
 has an interior face. Consider an interior face $F$
has an interior face. Consider an interior face $F$ of the minimum length, $k$
of the minimum length, $k$ say. By Item 3, proposition 2.4, it has at least $k-1$
say. By Item 3, proposition 2.4, it has at least $k-1$ interior edges (edges not contained in the exterior face). Perform a sequence of contraction-elongation transformations on any $k-3$
interior edges (edges not contained in the exterior face). Perform a sequence of contraction-elongation transformations on any $k-3$ interior edges. This results in (at least) one triangular face.
interior edges. This results in (at least) one triangular face.3. Perform a $\Delta Y$
 transformation on one of these triangular faces.
transformation on one of these triangular faces.

Figure A.12. Two exterior vertices sharing an interior face.

Figure A.13. Forbidden subgraph.
We first show that every graph produced by this procedure is simple, three-regular and three-connected. Any contraction-elongation transformation along an interior edge does not create a bridge. Suppose it does then this implies that the bridge is the edge $e_2$![]() , see figure 6. Since if any other edge is a bridge, then the corresponding edge in the original graph must be a bridge. But if $e_2$
, see figure 6. Since if any other edge is a bridge, then the corresponding edge in the original graph must be a bridge. But if $e_2$![]() is a bridge, then the original graph can be disconnected by deleting two edges. For instance, deleting the edges $(u_1,v_1)$
is a bridge, then the original graph can be disconnected by deleting two edges. For instance, deleting the edges $(u_1,v_1)$![]() and $(u_3,v_2)$
and $(u_3,v_2)$![]() will disconnect the original graph. Furthermore, this procedure does not alter the exterior face and the set of faces incident on each exterior vertex remains unaltered. Hence, no two non-adjacent exterior vertices can share an interior face after the operation. Furthermore, the resulting graph remains simple and three-regular. Hence, by lemma A.1, it remains three-connected. Next, we show that the graph resulting from a $\Delta Y$
will disconnect the original graph. Furthermore, this procedure does not alter the exterior face and the set of faces incident on each exterior vertex remains unaltered. Hence, no two non-adjacent exterior vertices can share an interior face after the operation. Furthermore, the resulting graph remains simple and three-regular. Hence, by lemma A.1, it remains three-connected. Next, we show that the graph resulting from a $\Delta Y$![]() transformation remains simple, three-regular and three-connected. For a multiple edge to occur from a $\Delta Y$
transformation remains simple, three-regular and three-connected. For a multiple edge to occur from a $\Delta Y$![]() transformation, some two vertices of the $\Delta$
transformation, some two vertices of the $\Delta$![]() must share a neighbour as shown in figure A13. But this contradicts the three-connectivity of the graph on which the operation is performed, since deleting the edges $e_1$
must share a neighbour as shown in figure A13. But this contradicts the three-connectivity of the graph on which the operation is performed, since deleting the edges $e_1$![]() and $e_2$
and $e_2$![]() would disconnect the graph. Hence, the graph remains simple. It remains three-regular by construction and by the proof of Steinitz’ theorem [Reference Ziegler34, Chapter 4, lemmas 4.2, 4.2*], the graph remains three-connected. Hence, after each application of either Step 1 or Step 3 the resulting graph $G'$
would disconnect the graph. Hence, the graph remains simple. It remains three-regular by construction and by the proof of Steinitz’ theorem [Reference Ziegler34, Chapter 4, lemmas 4.2, 4.2*], the graph remains three-connected. Hence, after each application of either Step 1 or Step 3 the resulting graph $G'$![]() is a simple, three-regular, three-connected graph and its genus $g(G')=g(G)-1$
is a simple, three-regular, three-connected graph and its genus $g(G')=g(G)-1$![]() . We repeat the three operations until the genus of the resulting graph is three, this graph must be a $K_4$
. We repeat the three operations until the genus of the resulting graph is three, this graph must be a $K_4$![]() since it is the only simple, three-regular graph of genus three.
since it is the only simple, three-regular graph of genus three.