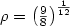A reversible automaton is a finite automaton in which eachletter induces a partial one-to-one map from the set of states intoitself. We solve the following problem proposed by Pin. Given an alphabet A, does there exist a sequence of languages K n on A which can be accepted by a reversible automaton, and such that the number of states of the minimal automaton of K n is in O(n), while the minimal number of states of a reversible automaton accepting K n is in O(ρ n ) for some ρ > 1? We give such an example with $\rho=\left(\frac{9}{8}\right)^{\frac{1}{12}}$ .

Considering each occurrence of a word w in a recurrentinfinite word, we define the setof return words of w to be the set of all distinct words beginningwith an occurrence of wand ending exactly just before the next occurrence of w in the infiniteword. We give a simpler proof of therecent result (of the second author) that an infinite word is Sturmianif and only if each of its factors has exactly two return words in it.Then, considering episturmian infinite words, which are a naturalgeneralization of Sturmian words,we study the position of the occurrences of any factorin such infinite wordsand we determinate the return words. At last, we apply these results inorder to get a kind of balance property ofepisturmian words and to calculate the recurrence function of thesewords.

We show that one-way Π2-alternating Turing machines cannotaccept unary nonregular languages in o(log n) space. This holdsfor an accept mode of space complexity measure, defined asthe worst cost of any accepting computation. This lower boundshould be compared with the corresponding bound for one-wayΣ2-alternating machines, that are able to accept unarynonregular languages in space O(log log n). Thus, Σ2-alternation is more powerful than Π2-alternationfor space bounded one-way machines with unary inputs.

Fine and Wilf's theorem has recently been extended to words having threeperiods. Following the method of the authors we extend it to anarbitrary number of periods and deduce from that a characterization ofgeneralized Arnoux-Rauzy sequences or episturmian infinite words.

Foundations of the notion of quantum Turing machines areinvestigated. According to Deutsch's formulation, the time evolution of a quantum Turing machine is to be determined by the localtransition function. In this paper, the local transition functions are characterized for fully general quantum Turing machines, including multi-tape quantum Turing machines, extending the results due to Bernstein and Vazirani.

The aim of this paper is to evaluate the growth orderof the complexity function (in rectangles)for two-dimensional sequencesgenerated by a linear cellular automatonwith coefficients in $\mathbb{Z}/l \mathbb{Z}$ , and polynomial initial condition.We prove that the complexity functionis quadratic when l is a prime and that it increases with respect to the number of distinct prime factors of l.