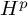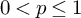TRILINEAR FOURIER MULTIPLIERS ON HARDY SPACES

Abstract

In this paper, we obtain the $H^{p_1}\times H^{p_2}\times H^{p_3}\to H^p$ boundedness for trilinear Fourier multiplier operators, which is a trilinear analogue of the multiplier theorem of Calderón and Torchinsky [4]. Our result improves the trilinear estimate in [22] by additionally assuming an appropriate vanishing moment condition, which is natural in the boundedness into the Hardy space $H^p$ for $0<p\le 1$.

1 Introduction

For a function $\sigma $ on ${{\mathbb R}^n}$ , let $T_\sigma $ be the corresponding Fourier multiplier operator given by

$$ \begin{align*}T_\sigma f(x) := \int_{\mathbb{R}^n} \sigma(\xi) \widehat{f}(\xi) e^{2\pi i\langle x,\xi\rangle} \;d\xi \end{align*} $$

for a Schwartz function f on ${{\mathbb R}^n}$ , where $\widehat {f}(\xi ):=\int _{{{\mathbb R}^n}}f(x)e^{2\pi i\langle x,\xi \rangle }dx$ is the Fourier transform of f. The function $\sigma $ is called an $L^p$ multiplier if $T_\sigma $ is bounded on $L^p({{\mathbb R}^n})$ for $1<p<\infty $ . For several decades, figuring out a sharp condition for $\sigma $ to be an $L^p$ multiplier has been one of the most interesting problems in harmonic analysis. Although there is no complete answer to this question, we have some satisfactory results. In 1956, Mihlin [23] proved that $\sigma $ is an $L^p$ multiplier provided that

(1.1) $$ \begin{align} |\partial^\alpha \sigma (\xi)| \lesssim |\xi|^{-|\alpha|},\quad \xi \not=0 \qquad \text{ for any multi-indices }~ |\alpha|\le [n/2]+1. \end{align} $$

This result was refined by Hörmander [21] who replaced (1.1) by the weaker condition

$$ \begin{align*} \sup_{k\in{\mathbb{Z}}}\big\Vert \sigma(2^k\cdot)\widehat{\psi} \big\Vert_{L_s^2({{\mathbb R}^n})}<\infty \qquad \text{ for }~ s>n/2, \end{align*} $$

where $L_s^2({{\mathbb R}^n})$ denotes the fractional Sobolev space on ${{\mathbb R}^n}$ and $\psi $ is a Schwartz function on ${{\mathbb R}^n}$ generating Littlewood–Paley functions, which will be officially defined in Section 2.1. We also remark that $s>n/2$ is the best possible regularity condition for the $L^p$ boundedness of $T_{\sigma }$ .

Now, we define the (real) Hardy space. Let $\phi $ be a smooth function on ${{\mathbb R}^n}$ that is supported in $\{x\in {{\mathbb R}^n}: |x|\le 1\}$ , and we define $\phi _l:=2^{ln}\phi (2^l\cdot )$ . Then the Hardy space $H^p({{\mathbb R}^n})$ , $0<p\le \infty $ , consists of tempered distributions f on ${{\mathbb R}^n}$ such that

(1.2) $$ \begin{align} \Vert f\Vert_{H^p({{\mathbb R}^n})}:= \Big\Vert \sup_{l\in{\mathbb{Z}}} \big| \phi_l\ast f\big| \Big\Vert_{L^p({{\mathbb R}^n})} \end{align} $$

is finite. The space provides an extension to $0<p\le 1$ in the scale of classical $L^p$ spaces for $1<p\le \infty $ , which is more natural and useful in many respects than the corresponding $L^p$ extension. Indeed, $L^p({{\mathbb R}^n})=H^p({{\mathbb R}^n})$ for $1<p\le \infty $ and several essential operators, such as singular integrals of Calderón–Zygmund type, that are well-behaved on $L^p({{\mathbb R}^n})$ only for $1<p\le \infty $ are also well-behaved on $H^p({{\mathbb R}^n})$ for $0<p\le 1$ . Now, let $\mathscr {S}({{\mathbb R}^n})$ denote the Schwartz space on ${{\mathbb R}^n}$ and $\mathscr {S}_0({{\mathbb R}^n})$ be its subspace consisting of f satisfying

$$ \begin{align*}\int_{{{\mathbb R}^n}}x^{\alpha}f(x) \; dx=0 \quad \text{ for all multi-indices}~\alpha.\end{align*} $$

Then it turns out that

(1.3) $$ \begin{align} \mathscr{S}_0({{\mathbb R}^n}) ~ \text{ is dense in }~ H^p({{\mathbb R}^n})~\text{ for all }~0<p<\infty. \end{align} $$

We remark that $\mathscr {S}({{\mathbb R}^n})$ is also dense in $H^p({{\mathbb R}^n})=L^p({{\mathbb R}^n})$ for $1<p<\infty $ , but not for $0<p\le 1$ . See [31, Chapter III, §5.2] for more details. Moreover, as mentioned in [31, Chapter III, §5.4], if $f\in L^1({{\mathbb R}^n})\cap H^p({{\mathbb R}^n})$ for $0<p\le 1$ , then

(1.4) $$ \begin{align} \int_{{{\mathbb R}^n}}x^{\alpha}f(x) \; dx=0 \quad \text{ for all multi-indices }~|\alpha|\le \frac{n}{p}-n. \end{align} $$

We refer to [2, 3, 7, 31, 33] for more details.

In 1977, Calderón and Torchinsky [4] provided a natural extension of the result of Hörmander to the Hardy space $H^p({{\mathbb R}^n})$ for $0<p\le 1$ . For the purpose of investigating $H^p$ estimates for $0<p\le 1$ , the operator $T_{\sigma }$ is assumed to initially act on $\mathscr {S}_0({{\mathbb R}^n})$ and then to admit an $H^p$ -bounded extension for $0<p< \infty $ via density, in view of (1.3). Then Calderón and Torchinsky proved

Theorem A [4].

Let $0<p\le 1$ . Suppose that $s>n/p-n/2$ . Then we have

$$ \begin{align*} \big\Vert T_{\sigma}f\big\Vert_{H^p({{\mathbb R}^n})}\lesssim \sup_{k\in {\mathbb{Z}}}\big\Vert \sigma(2^k\cdot)\widehat{\psi}\big\Vert_{L_s^2({{\mathbb R}^n})}\Vert f\Vert_{H^p({{\mathbb R}^n})} \end{align*} $$

for all $f\in \mathscr {S}_0({{\mathbb R}^n})$ .

For more information about the theory of Fourier multipliers, we also refer the reader to [1, 13, 19, 20, 25, 28, 29, 30] and the references therein.

We now turn our attention to multilinear extensions of the above multiplier results. Let m be a positive integer greater or equal to $2$ . For a bounded function $\sigma $ on $({{\mathbb R}^n})^m$ , let $T_\sigma $ now denote an m-linear Fourier multiplier operator given by

$$ \begin{align*} T_\sigma\big(f_1, \cdots, f_m\big)(x) := \int_{({{\mathbb R}^n})^m} \sigma(\vec{\boldsymbol{\xi}}\,)\Big( \prod_{j=1}^m \widehat{f_j}(\xi_j)\Big) \; e^{2\pi i\langle x,\xi_1+\dots+\xi_m\rangle}\, d\vec{\boldsymbol{\xi}},\quad \vec{\boldsymbol{\xi}} :=(\xi_1, \cdots, \xi_m) \end{align*} $$

for $f_1,\dots ,f_m\in \mathscr {S}_0({{\mathbb R}^n})$ . The first important result concerning multilinear multipliers was obtained by Coifman and Meyer [5] who proved that if N is sufficiently large and

(1.5) $$ \begin{align} \big| \partial_{\xi_1}^{\alpha_m}\cdots \partial_{\xi_m}^{\alpha_m}\sigma(\xi_1,\dots,\xi_m)\big|\lesssim_{\alpha_1,\dots,\alpha_m} \big| (\xi_1,\dots,\xi_m)\big|^{-(|\alpha_1|+\dots+|\alpha_m|)}, \quad (\xi_1,\dots,\xi_m)\not= \vec{\boldsymbol{0}} \end{align} $$

for all $|\alpha _1|+\cdots + |\alpha _m|\le N$ , then $T_{\sigma }$ is bounded from $L^{p_1}({{\mathbb R}^n})\times \cdots \times L^{p_m}({{\mathbb R}^n})$ into $L^p({{\mathbb R}^n})$ for $1<p_1,\dots ,p_m<\infty $ and $1\le p<\infty $ . This result is a multilinear analogue of Mihlin’s result in which Equation (1.1) is required, but the optimal regularity condition, such as $|\alpha |\le [n/2]+1$ in Equation (1.1), is not considered in the result of Coifman and Meyer. Afterwards, Tomita [32] provided a sharp estimate for multilinear multiplier $T_{\sigma }$ , as a multilinear counterpart of Hörmander’s result. Let $\Psi ^{(m)}$ be a Schwartz function on $({{\mathbb R}^n})^m$ having the properties that

$$ \begin{align*} \mbox{supp}(\widehat{\Psi^{(m)}})\subset \big\{\vec{\boldsymbol{\xi}}:=(\xi_1,\dots,\xi_m)\in ({{\mathbb R}^n})^m: 1/2\leq |\vec{\boldsymbol{\xi}}|\leq 2 \big\}, \quad \sum_{j\in\mathbb{Z}}{\widehat{\Psi^{(m)}}}(2^{-j}\vec{\boldsymbol{\xi}})=1,~\vec{\boldsymbol{\xi}}\not= \vec{\boldsymbol{0}}. \end{align*} $$

For $s\geq 0$ , we define the Sobolev norm

(1.6) $$ \begin{align} \Vert F\Vert_{L_s^2(({{\mathbb R}^n})^m)}:=\Big( \int_{({{\mathbb R}^n})^m}{\big(1+4\pi^2|\vec{\boldsymbol{\xi}}|^2 \big)^s\big|\widehat{F}(\vec{\boldsymbol{\xi}})\big|^2}\;d\vec{\boldsymbol{\xi}}\Big)^{1/2}. \end{align} $$

Theorem B [32].

Let $1<p,p_1,\dots ,p_m<\infty $ with $1/p=1/p_1+\cdots +1/p_m$ . Suppose that

$$ \begin{align*} \sup_{k \in \mathbb{Z}} \big\|\sigma(2^k \vec{\cdot}\;) \widehat{\Psi^{(m)}}\; \big\|_{L^2_s(({{\mathbb R}^n})^m)}<\infty \end{align*} $$

for $s>mn/2$ . Then we have

(1.7) $$ \begin{align} \big\Vert T_{\sigma}\big(f_1,\dots,f_m \big)\big\Vert_{L^p} \lesssim \sup_{k \in \mathbb{Z}} \big\|\sigma(2^k \vec{\cdot}\;) \widehat{\Psi^{(m)}}\; \big\|_{L^2_s(({{\mathbb R}^n})^m)}\prod_{j=1}^{m}\Vert f_j\Vert_{L^{p_j}({{\mathbb R}^n})} \end{align} $$

for $f_1,\dots ,f_m \in \mathscr {S}_0({{\mathbb R}^n})$ .

The standard Sobolev space $L_s^2(({{\mathbb R}^n})^m)$ in Equation (1.7) is replaced by a product-type Sobolev space in many recent papers.

Theorem C [14, 15, 18, 24].

Let $0<p_1,\dots ,p_m\leq \infty $ and $0<p<\infty $ with $1/p=1/p_1+\dots +1/p_m$ . Suppose that

(1.8) $$ \begin{align} s_1,\dots,s_m>\frac{n}{2},\qquad \sum_{j\in J}\Big(\frac{s_j}{n}-\frac{1}{p_j} \Big)>-\frac{1}{2} \end{align} $$

for any nonempty subsets J of $ \{1,\dots ,m\}$ , and

(1.9) $$ \begin{align} \sup_{k\in{\mathbb{Z}}}\big\Vert \sigma(2^k\vec{\cdot}\;)\widehat{\Psi^{(m)}}\big\Vert_{L_{(s_1,\dots,s_m)}^2(({{\mathbb R}^n})^m)}<\infty. \end{align} $$

Then we have

(1.10) $$ \begin{align} \big\Vert T_{\sigma}\big(f_1,\dots,f_n \big) \big\Vert_{L^p({{\mathbb R}^n})} \lesssim \sup_{k\in{\mathbb{Z}}}\big\Vert \sigma(2^k\vec{\cdot}\;)\widehat{\Psi^{(m)}}\big\Vert_{L_{(s_1,\dots,s_m)}^2(({{\mathbb R}^n})^m)} \prod_{j=1}^{m}{\Vert f_j\Vert_{H^{p_j}({{\mathbb R}^n})}} \end{align} $$

for $f_1,\dots ,f_m\in \mathscr {S}_0({{\mathbb R}^n})$ .

Here, the space $L_{(s_1,\dots ,s_m)}^{2}(({{\mathbb R}^n})^m)$ indicates the product type Sobolev space on $({{\mathbb R}^n})^m$ , in which the norm is defined by replacing the term $(1+4\pi ^2 |\vec {\boldsymbol {\xi }}|^2)^s$ in Equation (1.6) by $\prod _{j=1}^{m}\big ( 1+4\pi ^2|\xi _j|^2\big )^{s_j}$ . It is known in [27] that the condition (1.8) is sharp in the sense that if the condition does not hold, then there exists $\sigma $ such that the corresponding operator $T_{\sigma }$ does not satisfy Equation (1.10). We also refer the reader to [6, 11] for weighted estimates for multilinear Fourier multipliers.

As an extension of Theorem A to the whole range $0<p_1,\dots ,p_m\le \infty $ , in the recent paper of the authors, Lee, Heo, Hong, Park and Yang [22], we provide a multilinear multiplier theorem with standard Sobolev space conditions.

Theorem D [22].

Let $0<p_1, \cdots , p_m \le \infty $ and $0<p<\infty $ with $1/p=1/p_1+\cdots +1/p_m$ . Suppose that

(1.11) $$ \begin{align} s> \frac{mn}{2}\quad \text{and}\quad \frac{1}{p}-\frac{1}{2} < \frac{s}{n}+\sum_{j \in J} \Big( \frac{1}{p_j}-\frac{1}{2}\Big) \end{align} $$

for any subsets J of $\{1,\dots ,m\}$ , and

(1.12) $$ \begin{align} \sup_{k \in \mathbb{Z}} \big\|\sigma(2^k \;\vec{\cdot}\;) \widehat{\Psi^{(m)}} \big\|_{L^2_s(({{\mathbb R}^n})^m)}<\infty. \end{align} $$

Then we have

(1.13) $$ \begin{align} \big\| {T}_{\sigma}(f_1,\dots,f_m)\|_{ L^p({{\mathbb R}^n})} \lesssim \sup_{k \in \mathbb{Z}} \big\|\sigma(2^k \;\vec{\cdot}\;) \widehat{\Psi^{(m)}} \big\|_{L^2_s(({{\mathbb R}^n})^m)} \, \prod_{j=1}^m \|f_j\|_{H^{p_j}({{\mathbb R}^n})} \end{align} $$

for $f_1,\dots ,f_m\in \mathscr {S}_0({{\mathbb R}^n})$ .

The optimality of the condition (1.11) was achieved by Grafakos, He and Hónzik [12] who proved that if Equation (1.13) holds, then we must necessarily have $s\ge mn/2$ and $1/p-1/2\le s/n+\sum _{j\in J}\big (1/p-1/2\big )$ for all subsets J of $\{1,\dots ,m\}$ .

We remark that in the bilinear case $m=2$ , Theorem D follows from Theorem C as Equation (1.11) implies the existence of $s_1$ and $s_2$ , with $s_1+s_2=s$ , satisfying Equation (1.8). This is well described in the first proof of Theorem D in [22]. However, when $m\ge 3$ , this inclusion is not evident even if similar types of regularity conditions are required in both theorems.

Unlike the estimate in Theorem A, the multilinear extensions in Theorems C and D consider the Lebesgue space $L^p$ as a target space when $p\le 1$ (recall that $L^p=H^p$ for $1<p<\infty $ ).

If a function $\sigma $ on $({{\mathbb R}^n})^m$ satisfies Equation (1.9) for $s_1,\dots ,s_m>n/2$ or (1.12) for $s>mn/2$ , then Theorems C and D imply that $T_{\sigma }(f_1,\dots ,f_m)\in L^1$ for all $f_1,\dots ,f_m\in \mathscr {S}_0({{\mathbb R}^n})$ . Therefore, in order for $T_{\sigma }(f_1,\dots ,f_m)$ to belong to $H^p({{\mathbb R}^n})$ for $0<p\le 1$ , it should be necessary that

(1.14) $$ \begin{align} \int_{{{\mathbb R}^n}}x^{\alpha}T_{\sigma}\big(f_1,\dots,f_m \big)\; dx =0 \quad \text{ for } ~ |\alpha|\le \frac{n}{p}-n, \end{align} $$

in view of Equation (1.4). However, this property is generally not guaranteed, even if all the functions $f_1,\dots ,f_m$ satisfy the moment conditions, in the multilinear setting, while, in the linear case,

$$ \begin{align*}\int_{{{\mathbb R}^n}}x^{\alpha}f(x)\; dx=0, ~ |\alpha|\le N \quad \text{ implies }\quad \int_{{{\mathbb R}^n}}x^{\alpha}T_{\sigma}f(x)\; dx=0, ~ |\alpha|\le N\end{align*} $$

for $N\ge 0$ . Recently, by imposing additional cancellation conditions corresponding to (1.14), Grafakos, Nakamura, Nguyen and Sawano [16, 17] obtain a mapping property into Hardy spaces for $T_{\sigma }$ .

Theorem E [16, 17].

Let $0<p_1, \cdots , p_m \le \infty $ and $0<p\le 1$ with $1/p=1/p_1+\cdots +1/p_m$ . Let N be sufficiently large and $\sigma $ satisfy Equation (1.5) for all multi-indices $|\alpha _1|+\dots +|\alpha _m|\le N$ . Suppose that

$$ \begin{align*}\int_{{{\mathbb R}^n}}x^{\alpha}T_{\sigma}\big(a_1,\dots,a_m\big)(x)\; dx=0\end{align*} $$

for all multi-indices $|\alpha |\le \frac {n}{p}-n$ , where $a_j$ ’s are $(p_j,\infty )$ -atoms. Then we have

(1.15) $$ \begin{align} \big\| {T}_{\sigma}(f_1,\dots,f_m)\big\|_{ H^p({{\mathbb R}^n})} \lesssim_{\sigma,N} \prod_{j=1}^m \|f_j\|_{H^{p_j}({{\mathbb R}^n})} \end{align} $$

for $f_1,\dots ,f_m\in \mathscr {S}_0({{\mathbb R}^n})$ .

Here, the $(p,\infty )$ -atom is similar, but more generalized concept than $H^{p}$ -atoms defined in Section 2, and we adopt the convention that $(\infty ,\infty )$ -atom a simply means $a\in L^{\infty }({{\mathbb R}^n})$ with no cancellation condition. See [16, 17] for the definition and properties of the $(p,\infty )$ -atom.

We remark that Theorem E successfully shows the boundedness into $H^p({{\mathbb R}^n})$ , but the optimal regularity conditions considered in Theorems C and D are not pursued at all as it requires sufficiently large N.

The aim of this paper is to establish the boundedness into $H^p$ for trilinear multiplier operators, analogous to Equation (1.15), with the same regularity conditions as in Theorem D, which is significantly more difficult in general. Unfortunately, we do not obtain the desired results for general m-linear operators for $m\ge 4$ and we will discuss some obstacles for this generalization in the appendix.

To state our main result, let us write $\Psi :=\Psi ^{(3)}$ and in what follows, we will use the notation

$$ \begin{align*}\mathcal{L}_s^2[\sigma]:=\sup_{k\in{\mathbb{Z}}}\big\Vert \sigma( 2^k{\vec{\cdot}\;}) \widehat{\Psi}\big\Vert_{L^2_s(({{\mathbb R}^n})^3)}\end{align*} $$

for a function $\sigma $ on $({{\mathbb R}^n})^3$ . Let $0<p\le 1$ , and we will consider trilinear multipliers $\sigma $ satisfying

(1.16) $$ \begin{align} \int_{{{\mathbb R}^n}} x^{\alpha}T_{\sigma}\big(f_1,f_2,f_3 \big)(x) \; dx =0 \quad \text{ for all multi-indices }~ |\alpha|\le \frac{n}{p}-n \end{align} $$

for all $f_1,f_2,f_3\in \mathscr {S}_0({{\mathbb R}^n})$ . Then the main result is as follows:

Theorem 1. Let $0<p_1,p_2,p_3<\infty $ and $0<p\le 1$ with $1/p=1/p_1+1/p_2+1/p_3$ . Suppose that

(1.17) $$ \begin{align} s>\frac{3n}{2} \quad \text{ and }\quad \frac{1}{p}-\frac{1}{2}<\frac{s}{n}+\sum_{j\in J}\Big(\frac{1}{p_j}-\frac{1}{2} \Big), \end{align} $$

where J is an arbitrary subset of $\{1,2,3\}$ . Let $\sigma $ be a function on $({{\mathbb R}^n})^3$ satisfying $\mathcal {L}_s^2[\sigma ]<\infty $ and the vanishing moment condition (1.16). Then we have

(1.18) $$ \begin{align} \big\Vert T_{\sigma}(f_1,f_2,f_3)\big\Vert_{H^{p}({{\mathbb R}^n})}\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^{p_1}({{\mathbb R}^n})}\Vert f_2\Vert_{H^{p_2}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{p_3}({{\mathbb R}^n})} \end{align} $$

for $f_1,f_2,f_3\in \mathscr {S}_0({{\mathbb R}^n})$ .

We remark that $(1/p_1,1/p_2,1/p_3)$ in Theorem 1 is contained in one of the following sets:

$$ \begin{align*} \mathscr{R}_0&:= \big\{ ( t_1,t_2,t_3) : 0< t_1,t_2,t_3 < 1,~ 0<t_{1}+t_2, t_2+t_3,t_3+t_1 <3/2,\, 1\le t_1+t_2+t_3< 2 \big\},\\ \mathscr{R}_{{\mathrm{i}}} &:= \big\{ ( t_1,t_2,t_3) : 0 < t_j < {1}/{2},~1\le t_{{\mathrm{i}}} <\infty , \,\, j\not= {\mathrm{i}} \big\}, \quad {\mathrm{i}}=1,2,3,\\ \mathscr{R}_4 &:=\big\{ ( t_1,t_2,t_3) : 0< t_3 < {1}/{2},~ 1/2 \le t_{1}, t_2 <\infty, ~ 3/2\le t_1+t_2 \big\}, \\ \mathscr{R}_5&:= \big\{ ( t_1,t_2,t_3) : 0< t_1 <{1}/{2},~ 1/2 \le t_{2}, t_3 <\infty, ~ 3/2\le t_2+t_3 \big\},\\ \mathscr{R}_6&:= \big\{ ( t_1,t_2,t_3) : 0< t_2 < {1}/{2},~ 1/2 \le t_{1}, t_3 <\infty, ~ 3/2\le t_1+t_3 \big\},\\ \mathscr{R}_7&:= \big\{ ( t_1,t_2,t_3) : 1/2\le t_1,t_2,t_3<\infty,~ 2\le t_1+t_2+t_3<\infty \big\}. \end{align*} $$

See Figure 1 for the regions $\mathscr {R}_{{\mathrm {i}}}$ . Then the condition (1.17) becomes

(1.19) $$ \begin{align} s>\begin{cases} 3n/2, & (1/p_1,1/p_2,1/p_3)\in \mathscr{R}_{0},\\ n/p_{{\mathrm{i}}}+n/2, & (1/p_1,1/p_2,1/p_3)\in \mathscr{R}_{{\mathrm{i}}}, ~{\mathrm{i}}=1,2,3\\ n/p_1+n/p_2, & (1/p_1,1/p_2,1/p_3)\in \mathscr{R}_{4},\\ n/p_2+n/p_3, & (1/p_1,1/p_2,1/p_3)\in \mathscr{R}_{5},\\ n/p_3+n/p_1, & (1/p_1,1/p_2,1/p_3)\in \mathscr{R}_{6},\\ n/p_1+n/p_2+n/p_3-n/2, & (1/p_1,1/p_2,1/p_3)\in \mathscr{R}_7. \end{cases} \end{align} $$

Figure 1 The regions $\mathscr {R}_{{\mathrm {i}}}$ , $0\le {\mathrm {i}}\le 7$ .

In the proof of Theorem 1, we will mainly focus on the case $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_{{\mathrm {i}}}$ , ${\mathrm {i}}=1,2,3$ , in which $s>n/p_{{\mathrm {i}}}+n/2$ is required. Then the remaining cases follow from interpolation methods. More precisely, via interpolation,

$$ \begin{align*} \text{the estimates (1.18) in } \mathscr{R}_1 \text{ and } \mathscr{R}_2 ~\Rightarrow~ \text{ the estimate (1.18) in } \mathscr{R}_4, \end{align*} $$

$$ \begin{align*} \text{the estimates (1.18) in } \mathscr{R}_2 \text{ and } \mathscr{R}_3 ~\Rightarrow~ \text{ the estimate (1.18) in } \mathscr{R}_5, \end{align*} $$

$$ \begin{align*} \text{the estimates (1.18) in } \mathscr{R}_3 \text{ and } \mathscr{R}_1 ~\Rightarrow~ \text{ the estimate (1.18) in } \mathscr{R}_6, \end{align*} $$

$$ \begin{align*} \text{the estimates (1.18) in } \mathscr{R}_1, \mathscr{R}_2, \text{ and } \mathscr{R}_3 ~\Rightarrow~ \text{ the estimate (1.18) in } \mathscr{R}_0, \end{align*} $$

$$ \begin{align*} \text{the estimates (1.18) in } \mathscr{R}_1, \mathscr{R}_2, \text{ and } \mathscr{R}_3 ~\Rightarrow~ \text{ the estimate (1.18) in } \mathscr{R}_7, \end{align*} $$

where the case $1/p_1+1/p_2+1/p_3=1$ for $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_0$ will be treated separately. Here, a complex interpolation method will be applied, but the regularity condition on s will be fixed. Moreover, the index p will be also fixed so that the vanishing moment condition (1.16) will not be damaged in the process of the interpolation. For example, when $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_4$ , we set $s>n/p_1+n/p_2$ and fix the index p with $1/p=1/p_1+1/p_2+1/p_3$ . We also fix $\sigma $ satisfying the vanishing moment condition (1.16). Now, we choose $(1/p_1^0,1/p_2^0,1/p_3)\in R_1$ and $(1/p_1^1,1/p_2^1,1/p_3)\in \mathscr {R}_2$ so that

$$ \begin{align*}s>n/p_1^0+n/2,\quad s>n/p_2^1+n/2,\end{align*} $$

$$ \begin{align*}1/p=1/p_1^0+1/p_2^0+1/p_3=1/p_1^1+1/p_2^1+1/p_3.\end{align*} $$

Then the two estimates

$$ \begin{align*}\Vert T_{\sigma}\Vert_{H^{p_1^0}\times H^{p_2^0}\times H^{p_3}\to H^p},\Vert T_{\sigma}\Vert_{H^{p_1^1}\times H^{p_2^1}\times H^{p_3}\to H^p}\lesssim \mathcal{L}_s^2[\sigma]\end{align*} $$

imply

$$ \begin{align*}\Vert T_{\sigma}\Vert_{H^{p_1}\times H^{p_2}\times H^{p_3}\to H^p}\lesssim \mathcal{L}_s^2[\sigma].\end{align*} $$

The detailed arguments concerning the interpolation (for all the cases) will be provided in Section 3.

The estimates for $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_{{\mathrm {i}}}$ , ${\mathrm {i}}=1,2,3$ , will be restated in Proposition 3.1 below, and they will be proved throughout three sections (Sections 5–7). Since one of $p_j$ ’s is less or equal to $1$ , we benefit from the atomic decomposition for the Hardy space. Moreover, for other indices greater than 2, we employ the techniques of (variant) $\varphi $ -transform, introduced by Frazier and Jawerth [8, 9, 10] and Park [26], which will be presented in Section 2. Then $T_{\sigma }(f_1,f_2,f_3)$ can be decomposed in the form

$$ \begin{align*}T_{\sigma}(f_1,f_2,f_3)=\sum_{\kappa\in \mathrm{K}}T^{\kappa}(f_1,f_2,f_3)\end{align*} $$

where $\mathrm {K}$ is a finite set, and then we will actually prove that each $T^{\kappa }(f_1,f_2,f_3)$ satisfies the estimate

(1.20) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\big| \phi_l\ast \big(T^{\kappa}(f_1,f_2,f_3)\big)(x)\big| \lesssim \mathcal{L}_s^2[\sigma]u_1(x)u_2(x)u_3(x), \end{align} $$

where $\Vert u_{{\mathrm {i}}}\Vert _{L^{p_{{\mathrm {i}}}}({{\mathbb R}^n})}\lesssim \Vert f_{{\mathrm {i}}}\Vert _{H^{p_{{\mathrm {i}}}}({{\mathbb R}^n})}$ for ${\mathrm {i}}=1,2,3$ . Since the above estimate separates the left-hand side into three functions of x, we may apply Hölder’s inequality with exponents $1/p=1/p_1+1/p_2+1/p_3$ to obtain, in view of Equation (1.2),

$$ \begin{align*} \big\Vert T^{\kappa}(f_1,f_2,f_3)\big\Vert_{H^p({{\mathbb R}^n})}&=\Big\Vert \sup_{l\in{\mathbb{Z}}}\big|\phi_l\ast \big( T^{\kappa}(f_1,f_2,f_3)\big) \big|\Big\Vert_{L^p({{\mathbb R}^n})}\\ &\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^{p_1}({{\mathbb R}^n})}\Vert f_2\Vert_{H^{p_2}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{p_3}({{\mathbb R}^n})}. \end{align*} $$

Such pointwise estimates (1.20) will be described in several lemmas in Sections 6 and 7, and the proofs will be given in Section 9 separately, which is one of the keys in this paper.

Notation

For a cube Q in ${{\mathbb R}^n}$ let ${\mathbf {x}}_Q$ be the lower left corner of Q and $\ell (Q)$ be the side-length of Q. We denote by $Q^*$ , $Q^{**}$ and $Q^{***}$ the concentric dilates of Q with $\ell (Q^*)=10\sqrt {n}\ell (Q)$ , $\ell (Q^{**})=\big (10\sqrt {n} \big )^2\ell (Q)$ and $\ell (Q^{***})=\big (10\sqrt {n} \big )^3\ell (Q)$ . Let $\mathcal {D}$ stand for the family of all dyadic cubes in ${{\mathbb R}^n}$ and $\mathcal {D}_j$ be the subset of $\mathcal {D}$ consisting of dyadic cubes of side-length $2^{-j}$ . For each ${\mathbf {x}}\in {{\mathbb R}^n}$ and $l\in {\mathbb {Z}}$ , let $B_{{\mathbf {x}}}^l:=B({\mathbf {x}},100n2^{-l})$ be the ball of radius $100n2^{-l}$ and center ${\mathbf {x}}$ . We use the notation $\langle \cdot \rangle $ to denote both the inner product of functions and $\langle y\rangle := (1+4\pi ^2|y|^2)^{1/2}$ for $y\in \mathbb {R}^M$ , $M\in {\mathbb {N}}$ . That is, $\langle f, g \rangle =\int _{{{\mathbb R}^n}} f(x) \overline {g(x)}\,dx$ for two functions f and g, and $\langle x_1\rangle :=(1+4\pi ^2|x_1|^2)^{1/2}$ , $\langle (x_1,x_2)\rangle :=\big (1+4\pi ^2(|x_1|^2+|x_2|^2)\big )^{1/2}$ for $x_1,x_2\in {{\mathbb R}^n}$ .

2 Preliminaries

2.1 Hardy spaces

Let $\theta $ be a Schwartz function on ${{\mathbb R}^n}$ such that $\mbox {supp}(\widehat {\theta })\subset \{\xi \in {{\mathbb R}^n}: |\xi |\le 2\}$ and $\widehat {\theta }(\xi )=1$ for $|\xi |\le 1$ . Let $\psi :=\theta -2^{-n}\theta (2^{-1}\cdot )$ , and for each $j\in {\mathbb {Z}}$ we define $\theta _j:=2^{jn}\theta (2^j\cdot )$ and $\psi _j:=2^{jn}\psi (2^j\cdot )$ . Then $\{\psi _j\}_{j\in {\mathbb {Z}}}$ forms a Littlewood–Paley partition of unity, satisfying

$$ \begin{align*}\mbox{supp}(\widehat{\psi_j})\subset \big\{\xi\in{{\mathbb R}^n}: 2^{j-1}\le |\xi|\le 2^{j+1}\big\} \quad\text{ and }\quad \sum_{j\in{\mathbb{Z}}}\widehat{\psi_j}(\xi)=1, ~\xi\not= 0.\end{align*} $$

We define the convolution operators ${\Gamma }_j$ and ${\Lambda }_j$ by

$$ \begin{align*}{\Gamma}_jf:=\theta_j\ast f, \qquad {\Lambda}_jf:=\psi_j\ast f.\end{align*} $$

The Hardy space $H^p({{\mathbb R}^n})$ can be characterized with the (quasi-)norm equivalences

(2.1) $$ \begin{align} \Vert f\Vert_{H^p({{\mathbb R}^n})}\sim\big\Vert \big\{ {\Gamma}_jf \big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^p(\ell^{\infty})}, \qquad 0<p\le \infty \end{align} $$

and

(2.2) $$ \begin{align} \Vert f\Vert_{H^p({{\mathbb R}^n})}\sim \big\Vert \big\{{\Lambda}_jf\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^p(\ell^{2})}, \qquad 0<p<\infty, \end{align} $$

which is the Littlewood–Paley theory for Hardy spaces. In addition, when $p\le 1$ , every $f\in H^p({{\mathbb R}^n})$ can be decomposed as

(2.3) $$ \begin{align} f=\sum_{k=1}^{\infty}\lambda_k a_k \quad \text{ in the sense of tempered distributions}, \end{align} $$

where $a_k$ ’s are $H^p$ -atoms having the properties that $\mbox {supp}(a_k)\subset Q_k$ , $\Vert a_k\Vert _{L^{\infty }({{\mathbb R}^n})}\le |Q_k|^{-1/p}$ for some cube $Q_k$ , $\int x^{\gamma }a_k(x)dx=0$ for all multi-indices $|\gamma |\le M$ , and $\big ( \sum _{k=1}^{\infty }|\lambda _k|^p\big )^{1/p}\lesssim \Vert f\Vert _{H^p({{\mathbb R}^n})},$ where M is a fixed integer satisfying $M\ge [n/p-n]_+$ , which may be actually arbitrarily large. Furthermore, each $H^p$ -atom $a_k$ satisfies

$$ \begin{align*} \Vert a_k\Vert_{H^1({{\mathbb R}^n})}\lesssim |Q_k|^{-1/p+1}. \end{align*} $$

2.2 Maximal inequalities

Let $\mathcal {M}$ denote the Hardy–Littlewood maximal operator, defined by

$$ \begin{align*}\mathcal{M}f(x):=\sup_{Q:x\in Q}\frac{1}{|Q|}\int_Q{|f(y)|}dy\end{align*} $$

for a locally integrable function f on ${{\mathbb R}^n}$ , where the supremum ranges over all cubes Q containing x. For given $0<r<\infty $ , we define $\mathcal {M}_rf:=\big ( \mathcal {M}\big (|f|^r\big )\big )^{1/r}$ . Then it is well-known that

(2.4) $$ \begin{align} \big\Vert \big\{ \mathcal{M}_rf_k \big\}_{k\in{\mathbb{Z}}}\big\Vert_{L^p(\ell^q)}\lesssim \Vert \{f_k\}_{k\in{\mathbb{Z}}}\Vert_{L^p(\ell^q)} \end{align} $$

whenever $r<p< \infty $ and $r<q\le \infty $ . We note that for $1\le r<\infty $

(2.5) $$ \begin{align} \bigg\Vert \frac{f(x-\cdot)}{\langle 2^j\cdot\rangle^t}\bigg\Vert_{L^r({{\mathbb R}^n})}\lesssim 2^{-{jn}/{r}}\mathcal{M}_rf(x)\qquad \text{ if }~t>n/r. \end{align} $$

For ${\boldsymbol {m}} \in {{\mathbb Z}^n}$ and any dyadic cubes $Q\in \mathcal {D}$ , we use the notation

$$ \begin{align*}Q({\boldsymbol{m}}):=Q+ \ell(Q)\,{\boldsymbol{m}}.\end{align*} $$

Then we define the dyadic shifted maximal operator $\mathcal {M}_{dyad}^{ {\boldsymbol {m}}}$ by

$$\begin{align*}\mathcal{M}_{dyad}^{ {\boldsymbol{m}}}f(x):=\sup_{Q\in\mathcal{D}: x\in Q} \frac{1}{|Q|} \int_{{Q({\boldsymbol{m}}})} |f(y)|\, dy,\end{align*}$$

where the supremum is taken over all dyadic cubes Q containing x. It is clear that $\mathcal {M}_{dyad}^{\mathbf {0}}f(x)\le \mathcal {M}f(x)$ and accordingly, $\mathcal {M}_{dyad}^{\mathbf {0}}$ is bounded on $L^p$ for $p>1$ . In general, the following maximal inequality holds: For $1<p<\infty $ and ${\boldsymbol {m}}\in {{\mathbb Z}^n}$ we have

(2.6) $$ \begin{align} \big\|\mathcal{M}_{dyad}^{{\boldsymbol{m}}}f\big\|_{L^p({{\mathbb R}^n})} \lesssim \big(\log{(10+|{\boldsymbol{m}}|)}\big)^{n/p}\, \|f\|_{L^p({{\mathbb R}^n})}. \end{align} $$

The inequality (2.6) follows from the repeated use of the inequality in one-dimensional setting that appears in [31, Chapter II, §5.10], and we omit the detailed proof here. Refer to [22, Appendix] for the argument.

2.3 Variants of $\varphi $ -transform

For a sequence of complex numbers ${\boldsymbol {b}}:=\{b_Q\}_{Q\in \mathcal {D}}$ , we define

$$ \begin{align*}\Vert {\boldsymbol{b}}\Vert_{\dot{f}^{p,q}}:=\big\Vert g^q({\boldsymbol{b}})\big\Vert_{L^p({{\mathbb R}^n})}\end{align*} $$

for $0<p<\infty $ , where

$$ \begin{align*}g^q({\boldsymbol{b}})(x):=\big\Vert \big\{ |b_Q||Q|^{-{1}/{2}}\chi_Q(x)\big\}_{Q\in\mathcal{D}}\big\Vert_{\ell^q}, \qquad 0<q\le\infty.\end{align*} $$

Let $\widetilde {\psi _j}:=\psi _{j-1}+\psi _j+\psi _{j+1}$ for $j\in {\mathbb {Z}}$ . Observe that $\widetilde {\psi _j}$ enjoys the properties that $\mbox {supp}(\widehat {\widetilde {\psi }})\subset \{\xi \in {{\mathbb R}^n}: 2^{j-2}\le |\xi |\le 2^{j+2}\}$ and $\psi _j=\psi _j\ast \widetilde {\psi _j}$ . Then we have the representation

(2.7) $$ \begin{align} {\Lambda}_jf(x)=\sum_{Q\in\mathcal{D}_j}b_Q\psi^{Q}(x), \end{align} $$

where $\psi ^Q(x):=|Q|^{{1}/{2}}\psi _j(x-{\mathbf {x}}_Q)$ , $\widetilde {\psi }^Q(x):=|Q|^{{1}/{2}}\widetilde {\psi _j}(x-{\mathbf {x}}_Q)$ for each $Q\in \mathcal {D}_j$ , and $b_Q=\langle f,\widetilde {\psi }^Q\rangle $ . This implies that

$$ \begin{align*}f=\sum_{j\in{\mathbb{Z}}}{\Lambda}_jf=\sum_{j\in{\mathbb{Z}}}\sum_{Q\in\mathcal{D}_j}b_Q\psi^Q \quad \text{ in }~\mathcal{S}'/\mathcal{P},\end{align*} $$

where $\mathcal {S}'/\mathcal {P}$ stands for a tempered distribution modulo polynomials. Moreover, in this case, we have

(2.8) $$ \begin{align} \Vert {\boldsymbol{b}}\Vert_{\dot{f}^{p,q}}\sim \big\Vert \{{\Lambda}_jf\}_{j\in{\mathbb{Z}}}\big\Vert_{L^p(\ell^q)}. \end{align} $$

Therefore, the Hardy space $H^p({{\mathbb R}^n})$ can be characterized by the discrete function space $\dot {f}^{p,2}$ , in view of the equivalence in Equation (2.2). We refer to [8, 9, 10] for more details.

It is also known in [26] that ${\Gamma }_jf$ has a representation analogous to (2.7) with an equivalence similar to (2.8), while $f\not = \sum _{j\in {\mathbb {Z}}}{\Gamma }_jf$ generally. Let $\widetilde {\theta }:=2^n\theta (2\cdot )$ and $\widetilde {\theta _j}:=2^{jn}\widetilde {\theta }(2^j\cdot )=\theta _{j+1}$ so that $\theta _j=\theta _j\ast \widetilde {\theta _{j}}$ . Let $\theta ^Q(x):=|Q|^{{1}/{2}}\theta _j(x-{\mathbf {x}}_Q)$ , $\widetilde {\theta }^Q(x):=|Q|^{{1}/{2}}\widetilde {\theta _{j}}(x-{\mathbf {x}}_Q)$ , and $b_Q=\langle f,\widetilde {\theta }^Q\rangle $ for each $Q\in \mathcal {D}_j$ . Then we have

(2.9) $$ \begin{align} {\Gamma}_jf(x)=\sum_{Q\in\mathcal{D}_j}b_Q\theta^Q(x) \end{align} $$

and for $0<p<\infty $ and $0<q\le \infty $

(2.10) $$ \begin{align} \big\Vert \{{\Gamma}_jf\}_{j\in{\mathbb{Z}}}\big\Vert_{L^p(\ell^q)}\sim \Vert {\boldsymbol{b}}\Vert_{\dot{f}^{p,q}}. \end{align} $$

We refer to [26, Lemma 3.1] for more details.

3 Proof of Theorem 1: reduction and interpolation

The proof of Theorem 1 can be obtained by interpolating the estimates in the following propositions.

Proposition 3.1. Let $0<p_1,p_2,p_3< \infty $ and $0<p< 1$ with $1/p=1/p_1+1/p_2+1/p_3$ . Suppose that $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_{1}\cup \mathscr {R}_2\cup \mathscr {R}_3$ and

$$ \begin{align*} s>\frac{n}{\min\{p_1,p_2,p_3\}}+\frac{n}{2}. \end{align*} $$

Let $\sigma $ be a function on $({{\mathbb R}^n})^3$ satisfying $\mathcal {L}_s^2[\sigma ]<\infty $ and the vanishing moment condition (1.16). Then we have

$$ \begin{align*} \big\Vert T_{\sigma}(f_1,f_2,f_3)\big\Vert_{H^{p}({{\mathbb R}^n})}\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^{p_1}({{\mathbb R}^n})}\Vert f_2\Vert_{H^{p_2}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{p_3}({{\mathbb R}^n})} \end{align*} $$

for $f_1,f_2,f_3\in \mathscr {S}_0({{\mathbb R}^n})$ .

Proposition 3.2. Let $0<p\le 1$ . Suppose that one of $p_1,p_2,p_3$ is equal to p and the other two are infinity. Suppose that $s>n/p+n/2$ . Let $\sigma $ be a function on $({{\mathbb R}^n})^3$ satisfying $\mathcal {L}_s^2[\sigma ]<\infty $ and the vanishing moment condition (1.16). Then we have

$$ \begin{align*} \big\Vert T_{\sigma}(f_1,f_2,f_3)\big\Vert_{H^{p}({{\mathbb R}^n})}\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^{p_1}({{\mathbb R}^n})}\Vert f_2\Vert_{H^{p_2}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{p_3}({{\mathbb R}^n})} \end{align*} $$

for $f_1,f_2,f_3\in \mathscr {S}_0({{\mathbb R}^n})$ .

We present the proof of Proposition 3.1 in Sections 5, 6 and 7 and that of Proposition 3.2 in Section 8. For now, we proceed with the following interpolation argument, simply assuming the above propositions hold.

Lemma 3.1. Let $0<p_1^0, p_2^0, p_3^0\le \infty $ , $0<p_1^1, p_2^1, p_3^1\le \infty $ and $0<p^0,p^1<\infty $ . Suppose that

$$ \begin{align*}\big\Vert T_{\sigma} \big\Vert_{H^{p_1^l}\times H^{p_2^l}\times H^{p_3^l}\to H^{p^l}}\lesssim \mathcal{A}, \qquad l=0,1.\end{align*} $$

Then for any $0<\theta <1$ , $0<p_1,p_2,p_3\le \infty $ and $0<p<\infty $ satisfying

$$ \begin{align*}1/p_j=(1-\theta)/p_j^0+\theta/p_j^1 \qquad \text{for }~ j=1,2,3,\end{align*} $$

$$ \begin{align*}1/p=(1-\theta)/p^0+\theta/p^1,\end{align*} $$

we have

$$ \begin{align*}\Vert T_{\sigma}\Vert_{H^{p_1}\times H^{p_2}\times H^{p_3}\to H^p}\lesssim \mathcal{A}.\end{align*} $$

The proof of the lemma is essentially same as that of [22, Lemma 2.4], so it is omitted here.

3.1 Proof of Equation (1.18) when $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_4\cup \mathscr {R}_5\cup \mathscr {R}_6$

We need to work only with $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_4$ since the other cases are just symmetric versions. In this case, $2<p_3<\infty $ and as mentioned in Equation (1.19), the condition (1.17) is equivalent to

$$ \begin{align*}s>n/p_1+n/p_2.\end{align*} $$

Now, choose $\widetilde {p_1},\widetilde {p_2}<1$ such that

$$ \begin{align*}1/p_1+1/p_2=1/\widetilde{p_1}+1/2=1/2+1/\widetilde{p_2}\end{align*} $$

and thus

$$ \begin{align*}s>n/\widetilde{p_1}+n/2, \quad s>n/2+n/\widetilde{p_2}.\end{align*} $$

Let $\epsilon _1, \epsilon _2>0$ be numbers with

$$ \begin{align*}s>n/(\widetilde{p_1}-\epsilon_1)+n/2, \quad s>n/2+n/(\widetilde{p_2}-\epsilon_2)\end{align*} $$

and select $q_1,q_2>2$ such that

$$ \begin{align*}1/p=1/(\widetilde{p_1}-\epsilon_1)+1/q_1+1/p_3=1/q_2+1/(\widetilde{p_2}-\epsilon_2)+1/p_3.\end{align*} $$

Then we observe that

$$ \begin{align*}(1-\theta)\Big(\frac{1}{\widetilde{p_1}-\epsilon_1},\frac{1}{q_1},\frac{1}{p_3} \Big)+\theta \Big( \frac{1}{q_2},\frac{1}{\widetilde{p_2}-\epsilon_2},\frac{1}{p_3}\Big)=\Big(\frac{1}{p_1},\frac{1}{p_2},\frac{1}{p_3}\Big)\end{align*} $$

for some $0<\theta <1$ . Let $C_1:=(1/(\widetilde {p_1}-\epsilon _1),1/q_1,1/p_3)$ and $C_2:=(1/q_2,1/(\widetilde {p_2}-\epsilon _2),1/p_3)$ . It is obvious that $C_1\in \mathscr {R}_1$ , $C_2\in \mathscr {R}_2$ , and thus it follows from Proposition 3.1 that

$$ \begin{align*} \Vert T_{\sigma}\Vert_{H^{\widetilde{p_1}-\epsilon_1}\times H^{q_1}\times H^{p_3}\to H^p}\lesssim \mathcal{L}_s^2[\sigma] \quad &\text{ at }~ C_1=(1/(\widetilde{p_1}-\epsilon_1),1/q_1,1/p_3)\in \mathscr{R}_1, \\ \Vert T_{\sigma}\Vert_{H^{q_2}\times H^{\widetilde{p_2}-\epsilon_2}\times H^{p_3}\to H^p}\lesssim \mathcal{L}_s^2[\sigma] \quad &\text{ at }~ C_2=(1/q_2,1/(\widetilde{p_2}-\epsilon_2),1/p_3)\in \mathscr{R}_2. \end{align*} $$

Finally, the assertion (1.18) for $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_4$ is derived by means of interpolation in Lemma 3.1. See Figure 2 for the interpolation.

Figure 2 $(1-\theta )\big (\frac {1}{\widetilde {p_1}-\epsilon _1},\frac {1}{q_1},\frac {1}{p_3} \big )+\theta \big ( \frac {1}{q_2},\frac {1}{\widetilde {p_2}-\epsilon _2},\frac {1}{p_3}\big )=(\frac {1}{p_1},\frac {1}{p_2},\frac {1}{p_3})\in \mathscr {R}_4$ .

3.2 Proof of Equation (1.18) when $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_0$

We first fix $1/2<p<1$ such that $1/p_1+1/p_2+1/p_3=1/p$ and assume that, in view of Equation (1.19),

$$ \begin{align*}s>3n/2=n/1+n/2.\end{align*} $$

Then we choose $2<p_0<\infty $ such that $1+1/2+1/p_0=1/p$ . Then it is clear that $(1/p_1,1/p_2,1/p_3)$ is located inside the hexagon with the vertices $(1,1/p_0,1/2)$ , $(1,1/2,1/p_0)$ , $(1/2,1,1/p_0)$ , $(1/p_0,1,1/2)$ , $(1/p_0,1/2,1)$ and $(1/2,1/p_0,1)$ . Now, we choose a sufficiently small $\epsilon>0$ and $2<\widetilde {p_0}<\infty $ such that

$$ \begin{align*}\frac{1}{2+\epsilon}+\frac{1}{\widetilde{p_0}}=\frac{1}{2}+\frac{1}{p_0},\end{align*} $$

and the point $(1/p_1,1/p_2,1/p_3)$ is still inside the smaller hexagon with $D_1:=(1,1/\widetilde {p_0},1/(2+\epsilon ))$ , $D_2:=(1,1/(2+\epsilon ),1/\widetilde {p_0})$ , $D_3:=(1/(2+\epsilon ),1,1/\widetilde {p_0})$ , $D_4:=(1/\widetilde {p_0},1,1/ (2+\epsilon ))$ , $D_5:=(1/\widetilde {p_0},1/(2+\epsilon ),1)$ , and $D_6:=(1/(2+\epsilon ),1/\widetilde {p_0},1)$ . Now, Proposition 3.1 deduces that

$$ \begin{align*}\big\Vert T_{\sigma}\big\Vert_{H^{q_1}\times H^{q_2}\times H^{q_3}\to H^p}\lesssim \mathcal{L}_s^2[\sigma]\end{align*} $$

for $(1/q_1,1/q_2,1/q_3)\in \{D_1,D_2,D_3,D_4,D_5,D_6 \}$ , as $D_1,D_2\in \mathscr {R}_1$ , $D_3,D_4\in \mathscr {R}_2$ and $D_5,D_6\in \mathscr {R}_3$ . This implies, via interpolation in Lemma 3.1,

$$ \begin{align*}\big\Vert T_{\sigma}(f_1,f_2,f_3)\big\Vert_{H^p({{\mathbb R}^n})}\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^{p_1}({{\mathbb R}^n})}\Vert f_2\Vert_{H^{p_2}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{p_3}({{\mathbb R}^n})}.\end{align*} $$

See Figure 3 for the interpolation.

Figure 3 $\big (\frac {1}{p_1},\frac {1}{p_2},\frac {1}{p_3}\big )\in \mathscr {R}_0$ .

For the case $p=1$ , we interpolate the estimates in Proposition 3.2. To be specific, for any given $0<p_1,p_2,p_3<\infty $ with $1/p_1+1/p_2+1/p_3=1$ , the estimate (1.18) with $p=1$ follows from interpolating

$$ \begin{align*} \big\Vert T_{\sigma}(f_1,f_2,f_3)\big\Vert_{H^1({{\mathbb R}^n})}&\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^1({{\mathbb R}^n})}\Vert f_2\Vert_{H^{\infty}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{\infty}({{\mathbb R}^n})},\\ \big\Vert T_{\sigma}(f_1,f_2,f_3)\big\Vert_{H^1({{\mathbb R}^n})}&\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^{\infty}({{\mathbb R}^n})}\Vert f_2\Vert_{H^{1}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{\infty}({{\mathbb R}^n})},\\ \big\Vert T_{\sigma}(f_1,f_2,f_3)\big\Vert_{H^1({{\mathbb R}^n})}&\lesssim \mathcal{L}_s^2[\sigma]\Vert f_1\Vert_{H^{\infty}({{\mathbb R}^n})}\Vert f_2\Vert_{H^{\infty}({{\mathbb R}^n})}\Vert f_3\Vert_{H^{1}({{\mathbb R}^n})}. \end{align*} $$

3.3 Proof of Equation (1.18) when $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_7$

Let $0<p\le 1/2$ be such that $1/p=1/p_1+1/p_2+1/p_3$ , and assume that

$$ \begin{align*}s>n/p-n/2.\end{align*} $$

We choose $0<p_0\le 1$ , satisfying $1/p_0+1=1/p$ , so that

$$ \begin{align*}s>n/p_0+n/2.\end{align*} $$

Then there exist $\epsilon>0$ and $2<q<\infty $ so that $s>n/(p_0-\epsilon )+n/2$ and $1/p=1/(p_0-\epsilon )+2/q$ . Let $E_1:=\big (1/(p_0-\epsilon ),1/q,1/q\big )$ , $E_2:=\big (1/q,1/(p_0-\epsilon ),1/q\big )$ , and $E_3:=\big (1/q,1/q,1/(p_0-\epsilon )\big )$ . Then it is immediately verified that $E_1\in \mathscr {R}_1$ , $E_2\in \mathscr {R}_2$ , $E_3\in \mathscr {R}_3$ , and

$$ \begin{align*}\theta_1\Big(\frac{1}{(p_0-\epsilon)},\frac{1}{q},\frac{1}{q}\Big)+\theta_2\Big(\frac{1}{q},\frac{1}{(p_0-\epsilon)},\frac{1}{q}\Big)+\theta_3\Big(\frac{1}{q},\frac{1}{q},\frac{1}{(p_0-\epsilon)}\Big)=\Big(\frac{1}{p_1},\frac{1}{p_2},\frac{1}{p_3}\Big)\end{align*} $$

for some $0<\theta _1,\theta _2,\theta _3<1$ with $\theta _1+\theta _2+\theta _3=1$ . Therefore, Proposition 3.1 yields that

$$ \begin{align*} \Vert T_{\sigma}\Vert_{H^{p_0-\epsilon}\times H^{q}\times H^{q}\to H^p}\lesssim \mathcal{L}_s^2[\sigma] \quad &\text{ at }~ E_1=\big(1/(p_0-\epsilon),1/q,1/q\big)\in \mathscr{R}_1, \\ \Vert T_{\sigma}\Vert_{H^{q}\times H^{p_0-\epsilon}\times H^{q}\to H^p}\lesssim \mathcal{L}_s^2[\sigma] \quad &\text{ at }~ E_2=\big(1/q,1/(p_0-\epsilon),1/q\big)\in \mathscr{R}_2, \\ \Vert T_{\sigma}\Vert_{H^{q}\times H^{q}\times H^{p_0-\epsilon}\to H^p}\lesssim \mathcal{L}_s^2[\sigma] \quad &\text{ at }~ E_3=\big(1/q,1/q,1/(p_0-\epsilon)\big)\in \mathscr{R}_3, \end{align*} $$

and using the interpolation method in Lemma 3.1, we conclude the estimate (1.18) holds for $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_7$ . See Figure 4 for the interpolation.

Figure 4 $\theta _1\big (\frac {1}{p_0-\epsilon },\frac {1}{q},\frac {1}{q}\big )+\theta _2\big (\frac {1}{q},\frac {1}{p_0-\epsilon },\frac {1}{q}\big )+\theta _3\big (\frac {1}{q},\frac {1}{q},\frac {1}{p_0-\epsilon }\big )=\big (\frac {1}{p_1},\frac {1}{p_2},\frac {1}{p_3}\big )\in \mathscr {R}_7$ .

4 Auxiliary lemmas

This section is devoted to providing several technical results which will be repeatedly used in the proof of Propositions 3.1 and 3.2.

Lemma 4.1. Let $N\in \mathbb {N}$ and $a\in \mathbb {R}^n$ . Suppose that a Schwartz function f, defined on ${{\mathbb R}^n}$ , satisfies

(4.1) $$ \begin{align} \int_{\mathbb{R}^n}{x^{\alpha}f(x)}dx=0 \quad \text{for all multi-indices}~ \alpha ~ \text{ with }~|\alpha|\leq N. \end{align} $$

Then for any $0\leq \epsilon \leq 1$ , there exists a constant $C_{\epsilon }>0$ such that

$$ \begin{align*} \big\Vert \phi_l \ast f\big\Vert_{L^{\infty}(\mathbb{R}^n)}\le C_{\epsilon} 2^{l(N+n+\epsilon)}\int_{\mathbb{R}^n}{|y-a|^{N+\epsilon}|f(y)|}\; dy. \end{align*} $$

Proof. Using the Taylor theorem for $\phi _l$ , we write

$$ \begin{align*} \phi_l(x-y)&=\sum_{|\alpha|\le N-1}\frac{\partial^{\alpha}\phi_l(x-a)}{\alpha !}(a-y)^{\alpha}\\ &\qquad +N\sum_{|\alpha|=N}\frac{1}{\alpha !}\Big(\int_0^1{(1-t)^{N-1}\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big)}dt \Big) (a-y)^{\alpha}. \end{align*} $$

Then it follows from the condition (4.1) that

$$ \begin{align*} \big| \phi_l\ast f(x)\big|&\lesssim_{N} \sum_{|\alpha|=N}\Big| \int_{\mathbb{R}^n}{\Big( \int_0^1 (1-t)^{N-1}\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big) dt\Big) (a-y)^{\alpha}f(y)}\; dy\Big|\\ &\lesssim_{N} \sum_{|\alpha|=N}\Big| \int_{\mathbb{R}^n}{\Big[ \int_0^1 (1-t)^{N-1}\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big) \; dt}\\ &\qquad\qquad\qquad\qquad {-\int_0^1 (1-t)^{N-1}\partial^{\alpha}\phi_l(x-a) dt \Big] (a-y)^{\alpha}f(y)}\; dy\Big|\\ &\lesssim \sum_{|\alpha|=N}\int_{\mathbb{R}^n}\Big(\int_0^1\big|\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big)-\partial^{\alpha}\phi_l(x-a) \big|dt\Big) |y-a|^N |f(y)| \; dy. \end{align*} $$

For $|\alpha |=N$ , we note that

(4.2) $$ \begin{align} \big|\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big)-\partial^{\alpha}\phi_l(x-a) \big|\lesssim 2^{l(N+n+1)}|y-a| \end{align} $$

and

(4.3) $$ \begin{align} &\big|\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big)-\partial^{\alpha}\phi_l(x-a) \big|\nonumber\\ & \quad \le \big|\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big)\big|+\big|\partial^{\alpha}\phi_l(x-a)\big|\lesssim 2^{l(N+n)}. \end{align} $$

Then by averaging both Equation (4.2) and Equation (4.3), we obtain that

$$ \begin{align*} \big|\partial^{\alpha}\phi_l\big(x-a+t(a-y)\big)-\partial^{\alpha}\phi_l(x-a) \big|\lesssim_{\epsilon} 2^{l(N+n+\epsilon)}|y-a|^{\epsilon}, \qquad 0\le \epsilon\le 1, \end{align*} $$

which completes the proof.

Now, we recall that $\widetilde {\psi _j}=\psi _{j-1}+\psi _j+\psi _{j+1}$ and $\widetilde {\theta _j}=2^{n}\theta _j(2\cdot )$ , and then define $\widetilde {{\Lambda }_j}g:=\widetilde {\psi _j}\ast g$ and $\widetilde {{\Gamma }_j}g:=\widetilde {\theta _j}\ast g$ .

Lemma 4.2. Let $2\le q<\infty $ , $s>{n}/{q}$ , and $L>n,s$ . Let $\varphi $ be a function on ${{\mathbb R}^n}$ satisfying

$$ \begin{align*}|\varphi(x)|\lesssim_M\frac{1}{(1+|x|)^M} \qquad \text{ for all}~ M>0.\end{align*} $$

For $j\in \mathbb {Z}$ and for each $Q\in \mathcal {D}_j$ , let

$$ \begin{align*}\varphi^Q(x):=2^{{jn}/{2}}\varphi\big(2^j(x-{\mathbf{x}}_Q)\big),\end{align*} $$

and for a Schwartz function g on ${{\mathbb R}^n}$ let

$$ \begin{align*}\mathscr{B}_Q(g):=\Big\langle \big| \widetilde{{\Lambda}_j}g\big|,\frac{2^{{jn}/{2}}}{\langle 2^j(\cdot-{\mathbf{x}}_Q)\rangle^L}\Big\rangle \quad \text{ or }\quad \Big\langle \big| \widetilde{{\Gamma}_j}g\big|,\frac{2^{{jn}/{2}}}{\langle 2^j(\cdot-{\mathbf{x}}_Q)\rangle^L}\Big\rangle.\end{align*} $$

Then we have

$$ \begin{align*} &\bigg\Vert \sum_{Q\in\mathcal{D}_j} |\mathscr{B}_Q(g)|\frac{\chi_{Q^c}(x)}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{s}}\big| \varphi^Q(z)\big|\bigg\Vert_{L^q(z)}\\ & \quad \lesssim_L 2^{-{jn}/{q}}\bigg(\sum_{Q\in\mathcal{D}_j}\Big(|\mathscr{B}_Q(g)| |Q|^{-1/2}\frac{\chi_{Q^c}(x)}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{s}} \Big)^q \bigg)^{{1}/{q}}. \end{align*} $$

Proof. For $2\le q<\infty $ , we have

$$ \begin{align*} &\Big(\sum_{Q\in\mathcal{D}_j} |\mathscr{B}_Q(g)|\frac{\chi_{Q^c}(x)}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{s}}\big| \varphi^Q(z)\big|\Big)^q\\ & \quad \lesssim \Big(\sum_{Q\in\mathcal{D}_j} |\mathscr{B}_Q(g)|^{{q}/{2}}\frac{\chi_{Q^c}(x)}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{{qs}/{2}}}\big| \varphi^Q(z)\big|\Big)^2\Big(\sum_{Q\in\mathcal{D}_j}\big|\varphi^Q(z) \big| \Big)^{q-2}, \end{align*} $$

where Hölder’s inequality is applied if $2<q<\infty $ . Clearly,

$$ \begin{align*} \Big(\sum_{Q\in\mathcal{D}_j}\big|\varphi^Q(z) \big| \Big)^{q-2}&\lesssim_M 2^{{jn(q-2)}/{2} }\Big(\sum_{Q\in\mathcal{D}_j}\frac{1}{\langle 2^j(z-{\mathbf{x}}_Q)\rangle^M} \Big)^{q-2}\\ &=2^{{jn(q-2)}/{2} }\Big(\sum_{{\boldsymbol{m}} \in \mathbb{Z}^n}\frac{1}{\langle 2^jz-{\boldsymbol{m}}\rangle^M} \Big)^{q-2}\lesssim_M 2^{{jn(q-2)}/{2}} \end{align*} $$

for sufficiently large $M>n$ . Therefore, the left-hand side of the claimed estimate is less than a constant times

(4.4) $$ \begin{align} 2^{jn({1}/{2}-{1}/{q})}\Big\Vert \sum_{Q\in\mathcal{D}_j} |\mathscr{B}_P(g)|^{{q}/{2}}\frac{\chi_{Q^c}(x)}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{{qs}/{2}}}\big| \varphi^Q(z)\big| \Big\Vert_{L^2(z)}^{{2}/{q}}. \end{align} $$

The $L^2$ norm is dominated by

$$ \begin{align*} & \Big( \sum_{Q\in\mathcal{D}_j}|\mathscr{B}_Q(g)|^{{q}/{2}}\frac{\chi_{Q^c(x)}}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{{qs}/{2}}} \sum_{R\in\mathcal{D}_j}|\mathscr{B}_R(g)|^{{q}/{2}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{{qs}/{2}}}\big\langle |\varphi^Q|,|\varphi^R|\big\rangle\Big)^{{1}/{2}}.\end{align*} $$

Note that

$$ \begin{align*}\big\langle |\varphi^Q|,|\varphi^R|\big\rangle\lesssim_{q,L} \frac{1}{\langle 2^j({\mathbf{x}}_Q-{\mathbf{x}}_R)\rangle^{{3Lq}/{2}}}\end{align*} $$

and thus the preceding term is controlled by a constant multiple of

$$ \begin{align*}\Big(\sum_{Q\in\mathcal{D}_j}\big|\mathscr{B}_Q(g)\big|^q\frac{\chi_{Q^c}(x)}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{qs}}\sum_{R\in\mathcal{D}_j}\frac{1}{\langle 2^j({\mathbf{x}}_Q-{\mathbf{x}}_R)\rangle^{{Lq}/{2}}}\Big)^{{1}/{2}}.\end{align*} $$

Here, we used the facts that

$$ \begin{align*}\frac{\big|\mathscr{B}_R(g)\big|}{(1+2^j|{\mathbf{x}}_Q-{\mathbf{x}}_R|)^{L}}\le \big|\mathscr{B}_Q(g)\big|\end{align*} $$

and

$$ \begin{align*}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{{qs}/{2}}\langle 2^j({\mathbf{x}}_Q-{\mathbf{x}}_R)\rangle^{{Lq}/{2}}}\le \frac{1}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{{qs}/{2}}}.\end{align*} $$

Since the sum over $R\in \mathcal {D}_j$ converges, we deduce

$$ \begin{align*} (4.4) &\lesssim 2^{-{jn}/{q}} \bigg(\sum_{Q\in\mathcal{D}_j} \Big( \big|\mathscr{B}_Q(g)\big||Q|^{-{1}/{2}}\frac{\chi_{Q^c}(x)}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{s}}\Big)^q \bigg)^{{1}/{q}} \end{align*} $$

and thus the desired result follows.

Lemma 4.3. Let $2\le p,q< \infty $ , $s>{n}/\min {\{p,q\}}$ and $L>n,s$ . For $j\in {\mathbb {Z}}$ and $Q\in \mathcal {D}_j$ , let

$$ \begin{align*}\mathscr{B}_Q(g):= \Big\langle \big| \widetilde{{\Lambda}_j}g\big|,\frac{2^{{jn}/{2}}}{\langle 2^j(\cdot-{\mathbf{x}}_Q)\rangle^L}\Big\rangle,\end{align*} $$

where g is a Schwartz function on ${{\mathbb R}^n}$ . Then we have

(4.5) $$ \begin{align} &\bigg\Vert \bigg( \sum_{j\in{\mathbb{Z}}}\sum_{Q\in\mathcal{D}_j}\Big( \big|\mathscr{B}_Q(g)\big||Q|^{-{1}/{2}}\frac{\chi_{Q^c}(\cdot)}{\langle 2^j(\cdot-{\mathbf{x}}_Q)\rangle^s}\Big)^q \bigg)^{{1}/{q}} \bigg\Vert_{L^p({{\mathbb R}^n})}\lesssim \Vert g\Vert_{L^p({{\mathbb R}^n})}. \end{align} $$

Proof. It is easy to verify that for $Q\in \mathcal {D}_j$

$$ \begin{align*}\frac{1}{\langle 2^j|x-{\mathbf{x}}_Q|\rangle^{s}}\chi_{Q^c}(x)\lesssim \mathcal{M}_{\frac{n}{s}}\chi_Q(x)\end{align*} $$

and thus the left-hand side of Equation (4.5) is less than a constant multiple of

$$ \begin{align*} &\bigg\Vert \bigg( \sum_{Q\in\mathcal{D}} \Big( \big|\mathscr{B}_Q(g) \big| |Q|^{-{1}/{2}} \mathcal{M}_{\frac{n}{s}}\chi_Q(\cdot)\Big)^q\bigg)^{{1}/{q}}\bigg\Vert_{L^p({{\mathbb R}^n})}\\ & \quad \lesssim \bigg\Vert \bigg( \sum_{Q\in\mathcal{D}} \Big( \big|\mathscr{B}_Q(g) \big| |Q|^{-{1}/{2}} \chi_Q(\cdot)\Big)^q\bigg)^{{1}/{q}}\bigg\Vert_{L^p({{\mathbb R}^n})} \end{align*} $$

by virtue of the maximal inequality (2.4) with $s>{n}/\min {\{p,q \}}$ . We see that

$$ \begin{align*} & \bigg( \sum_{Q\in\mathcal{D}} \Big( \big|\mathscr{B}_Q(g) \big| |Q|^{-{1}/{2}} \chi_Q(x)\Big)^q\bigg)^{{1}/{q}} \le \bigg( \sum_{Q\in\mathcal{D}} \Big( \big|\mathscr{B}_Q(g) \big| |Q|^{-{1}/{2}} \chi_Q(x)\Big)^2\bigg)^{{1}/{2}}\\ &\quad =\bigg( \sum_{j\in{\mathbb{Z}}}\sum_{Q\in\mathcal{D}_j}\chi_Q(x)\Big(\int_{{{\mathbb R}^n}}\big| \widetilde{{\Lambda}_j}g(y)\big|\frac{2^{jn}}{\langle 2^j(y-{\mathbf{x}}_Q)\rangle^L} \; dy \Big)^2\bigg)^{{1}/{2}}\\ &\quad \lesssim\bigg( \sum_{j\in{\mathbb{Z}}}\Big(\int_{{{\mathbb R}^n}}\big| \widetilde{{\Lambda}_j}g(y)\big|\frac{2^{jn}}{\langle 2^j(y-x)\rangle^L} \;dy \Big)^2\bigg)^{{1}/{2}}\lesssim \big\Vert \big\{ \mathcal{M}{\Lambda}_jg(x)\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2} \end{align*} $$

since $\ell ^2\hookrightarrow \ell ^q$ , $L>n$ and $\langle 2^j(y-{\mathbf {x}}_Q)\rangle \gtrsim \langle 2^j(y-x)\rangle $ for $Q\in \mathcal {D}_j$ and $x\in Q$ . Using Equation (2.4) again, the left-hand side of Equation (4.5) is less than a constant times

$$ \begin{align*} \big\Vert \big\{ {\Lambda}_jg\big\}_{j\in{\mathbb{Z}}} \big\Vert_{L^{p}(\ell^2)}\sim \Vert g\Vert_{L^{p}({{\mathbb R}^n})}.\\[-41pt] \end{align*} $$

Lemma 4.4. Let $1 \le q < \infty $ , $s>{n}/{q}$ and $L>n,s$ . For $j\in {\mathbb {Z}}$ and $Q\in \mathcal {D}_j$ , let

$$ \begin{align*}\mathscr{B}_Q(g):= \Big\langle \big| \widetilde{{\Gamma}_j}g\big|,\frac{2^{\frac{jn}{2}}}{\langle 2^j(\cdot-c_Q)\rangle^L}\Big\rangle,\end{align*} $$

where g is a Schwartz function on ${{\mathbb R}^n}$ . Then for $1<p\le \infty $ with $q\le p$ we have

(4.6) $$ \begin{align} &\bigg\Vert \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{Q\in\mathcal{D}_j}\Big( \big|\mathscr{B}_Q(g)\big||Q|^{-{1}/{2}}\frac{1}{\langle 2^j(\cdot-c_Q)\rangle^s}\Big)^q \bigg)^{{1}/{q}} \bigg\Vert_{L^p({{\mathbb R}^n})}\lesssim \Vert g\Vert_{L^p({{\mathbb R}^n})}. \end{align} $$

Proof. For any $j\in {\mathbb {Z}}$ and $Q\in \mathcal {D}_j$ , there exists a unique lattice ${\boldsymbol {m}}_Q\in {{\mathbb Z}^n}$ such that ${\mathbf {x}}_Q=2^{-j}{\boldsymbol {m}}_Q$ . For any $j\in {\mathbb {Z}}$ and $x\in {{\mathbb R}^n}$ , let $Q_{j,x}$ be a unique dyadic cube in $\mathcal {D}_j$ containing x. Then we have the representations ${\mathbf {x}}_{Q_{j,x}}=2^{-j}{\boldsymbol {m}}_{Q_{j,x}}$ for ${\boldsymbol {m}}_{Q_{j,x}}\in {{\mathbb Z}^n}$ and

$$ \begin{align*}x=2^{-j}({\boldsymbol{m}}_{Q_{j,x}}+u_x) \qquad \text{ for some }~ ~u_x\in [0,1)^n.\end{align*} $$

Now, for $Q\in \mathcal {D}_j$ , we write

$$ \begin{align*} |\mathscr{B}_Q(g)| |Q|^{-{1}/{2}}&\lesssim_L\int_{{{\mathbb R}^n}} \big| \mathcal{M}g(y)\big| \frac{2^{jn}}{\langle 2^j(y-{\mathbf{c}}_Q)\rangle^L} dy\lesssim \int_{{{\mathbb R}^n}} \big| \mathcal{M}g(y)\big| \frac{2^{jn}}{\langle 2^j(y-{\mathbf{x}}_Q)\rangle^L} \; dy\\[3pt]&=\int_{{{\mathbb R}^n}} \big| \mathcal{M}g(y)\big| \frac{2^{jn}}{\big\langle 2^j(y-x)+{\boldsymbol{m}}_{Q_{j,x}}-{\boldsymbol{m}}_Q+u_x \big\rangle^L} \; dy\\[3pt]&\lesssim_L\int_{{{\mathbb R}^n}} \big| \mathcal{M}g(y)\big| \frac{2^{jn}}{\big\langle 2^j(y-x)+{\boldsymbol{m}}_{Q_{j,x}}-{\boldsymbol{m}}_Q \big\rangle^L} \; dy\\[3pt]&\lesssim \mathcal{M}_{dyad}^{{\boldsymbol{m}}_{Q_{j,x}}-{\boldsymbol{m}}_Q}\mathcal{M}g(x), \end{align*} $$

where the penultimate inequality follows from the fact that $u_x\in [0,1)^n$ . This deduces

$$ \begin{align*} &\sup_{j\in{\mathbb{Z}}}\bigg( \sum_{Q\in\mathcal{D}_j}\Big( \big|\mathscr{B}_Q(g)\big||Q|^{-{1}/{2}}\frac{1}{\langle 2^j(x-c_Q)\rangle^s}\Big)^q \bigg)^{{1}/{q}}\\ &\lesssim \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{{\boldsymbol{m}}\in{{\mathbb Z}^n}}\Big( \mathcal{M}_{dyad}^{{\boldsymbol{m}}_{Q_{j,x}}-{\boldsymbol{m}}}\mathcal{M}g(x)\frac{1}{\langle {\boldsymbol{m}}_{Q_{j,x}}-{\boldsymbol{m}}\rangle^s} \Big)^q \bigg)^{{1}/{q}}\\ &=\bigg( \sum_{{\boldsymbol{m}}\in{{\mathbb Z}^n}}\Big( \mathcal{M}_{dyad}^{{\boldsymbol{m}}}\mathcal{M}g(x)\frac{1}{\langle {\boldsymbol{m}}\rangle^s} \Big)^q \bigg)^{{1}/{q}}. \end{align*} $$

Therefore, the left-hand side of Equation (4.6) is less than a constant times

$$ \begin{align*} \Big( \sum_{{\boldsymbol{m}}\in{{\mathbb Z}^n}} \langle {\boldsymbol{m}}\rangle^{-sq}\big\Vert \mathcal{M}_{dyad}^{{\boldsymbol{m}}}\mathcal{M}g \big\Vert_{L^p({{\mathbb R}^n})}^q \Big)^{{1}/{q}}&\lesssim \Vert \mathcal{M}g\Vert_{L^p({{\mathbb R}^n})}\Big( \sum_{{\boldsymbol{m}}\in{{\mathbb Z}^n}}\langle {\boldsymbol{m}}\rangle^{-sq}\big(\log \big(10+|{\boldsymbol{m}}| \big) \big)^{{qn}/{p}}\Big)^{{1}/{q}}\\ &\lesssim \Vert g\Vert_{L^p({{\mathbb R}^n})} \end{align*} $$

as $sq>n$ , where we applied Minkowski’s inequality if $p> q$ and the maximal inequality (2.6). This completes the proof.

Lemma 4.5. Let a be an $H^p$ -atom associated with Q, satisfying

(4.7) $$ \begin{align} \int_{{{\mathbb R}^n}}x^{\gamma }a(x) \; dx=0 \quad \text{ for all multi-indices }~ |\gamma |\le M, \end{align} $$

and fix $L_0>0$ . Then we have

(4.8) $$ \begin{align} \big| {\Lambda}_j a (x) \big| \lesssim_{L_0} l(Q)^{-{n}/{p}} \min\big\{ 1, \big( 2^jl(Q) \big)^{M+n+1} \big\} \bigg( \chi_{Q^{*}}(x) + \chi_{(Q^{*})^c}(x)\frac{1}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{L_0}} \bigg), \end{align} $$

and

(4.9) $$ \begin{align} \big| {\Gamma}_j a (x) \big| \lesssim_{L_0} l(Q)^{-{n}/{p}} \min\big\{ 1, \big( 2^jl(Q) \big)^{M+n+1} \big\} \bigg( \chi_{Q^{*}}(x) + \chi_{(Q^{*})^c}(x)\frac{1}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{L_0}} \bigg). \end{align} $$

Moreover, for $1\leq r \leq \infty $ ,

(4.10) $$ \begin{align} \| {\Lambda}_j a \|_{L^r({{\mathbb R}^n})}, \| {\Gamma}_j a \|_{L^r({{\mathbb R}^n})} \lesssim l(Q)^{-{n}/{p} + {n}/{r}} \min\{ 1, (2^jl(Q))^{M+n - {n}/{r}+1} \}. \end{align} $$

Proof. We will prove only the estimates for ${\Lambda }_ja$ , and the exactly same argument is applicable to ${\Gamma }_ja$ as well. Let us first assume $2^j\ell (Q)\ge 1$ . Then we have

$$ \begin{align*} \big| {\Lambda}_j a(x)\big|&\le \ell(Q)^{-{n}/{p}}\Big( \chi_{Q^*}(x)\Vert \psi_j\Vert_{L^1({{\mathbb R}^n})}+\chi_{(Q^*)^c}(x)\int_{y\in Q}\big|\psi_j(x-y)\big| \; dy \Big)\\ &\lesssim_{L_0} \ell(Q)^{-{n}/{p}}\Big( \chi_{Q^*}(x)+\chi_{(Q^*)^c}(x)\int_{y\in Q}\frac{2^{jn}}{\langle 2^j(x-y)\rangle^{n+1}}\frac{1}{\langle 2^j(x-y)\rangle^{L_0}} \; dy \Big)\\ &\lesssim \ell(Q)^{-{n}/{p}}\Big( \chi_{Q^*}(x)+\chi_{(Q^*)^c}(x)\frac{1}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{L_0}} \Big) \end{align*} $$

since $|x-y|\gtrsim |x-{\mathbf {x}}_Q| $ for $x\in (Q^*)^c$ and $y\in Q$ .

Now, suppose that $2^j\ell (Q)<1$ . By using the vanishing moment condition (4.7), we obtain

$$ \begin{align*}\big| {\Lambda}_j a(x)\big|\le 2^{j(M+n+1)}\int_Q \int_0^1 \frac{1}{\langle 2^j(x-ty-(1-t){\mathbf{x}}_Q)\rangle^{L_0}}|y-{\mathbf{x}}_Q|^{M+1}|a(y)| \; dt dy.\end{align*} $$

If $x\in Q^*$ , then it is clear that

$$ \begin{align*}\big| {\Lambda}_j a(x)\big|\lesssim \big( 2^j\ell(Q)\big)^{M+n+1} \ell(Q)^{-{n}/{p}}.\end{align*} $$

If $x\in (Q^*)^c$ , then we have

$$ \begin{align*}\langle 2^j(x-ty-(1-t){\mathbf{x}}_Q)\rangle^{-1}\lesssim \langle 2^j(x-{\mathbf{x}}_Q)\rangle^{-1},\end{align*} $$

which implies

$$ \begin{align*}\big| {\Lambda}_j a(x)\big|\lesssim_{L_0} \frac{1}{\langle 2^j(x-{\mathbf{x}}_Q)\rangle^{L_0}}\big( 2^j\ell(Q)\big)^{M+n+1} \ell(Q)^{-{n}/{p}}.\end{align*} $$

This proves Equation (4.8).

Moreover, using the estimate (4.8), we have

$$ \begin{align*} \big\Vert {\Lambda}_ja\big\Vert_{L^r({{\mathbb R}^n})}&\le \big\Vert {\Lambda}_ja\big\Vert_{L^r(Q^*)}+\big\Vert {\Lambda}_ja\big\Vert_{L^r((Q^*)^c)}\\ &\lesssim \ell(Q)^{-{n}/{p}}\min\big\{ 1, \big( 2^jl(Q) \big)^{M+n+1} \big\}\Big(|Q|^{{1}/{r}}+\Big\Vert \frac{1}{\langle 2^j(\cdot-{\mathbf{x}}_Q)\rangle^{{n+1}}}\Big\Vert_{L^r({{\mathbb R}^n})} \Big)\\ &\lesssim \ell(Q)^{-{n}/{p}+{n}/{r}}\min\big\{ 1, \big( 2^jl(Q) \big)^{M+n+1} \big\}\Big( 1+\big( 2^j\ell(Q)\big)^{-{n}/{r}}\Big)\\ &\le \ell(Q)^{-{n}/{p}+{n}/{r}}\min\big\{ 1, \big( 2^jl(Q) \big)^{M+n-{n}/{r}+1} \big\}. \end{align*} $$

This concludes the proof of Equation (4.10).

5 Proof of Proposition 3.1: Reduction

5.1 Reduction via paraproduct

Without loss of generality, we may assume

$$ \begin{align*}\Vert f_1\Vert_{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert_{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert_{H^{p_3}({{\mathbb R}^n})}=1 \quad \text{and}\quad \mathcal{L}_s^2[\sigma]=1.\end{align*} $$

We first note that $T_{\sigma }(f_1,f_2,f_3)$ can be written as

$$ \begin{align*} T_{\sigma}(f_1,f_2,f_3)=\sum_{j_1,j_2,j_3\in{\mathbb{Z}}}T_{\sigma}\big({\Lambda}_{j_1}f_1,{\Lambda}_{j_2}f_2,{\Lambda}_{j_3}f_3\big). \end{align*} $$

We shall work with only the case $j_1\ge j_2\ge j_3$ as other cases follow from a symmetric argument. When $j_1\ge j_2\ge j_3$ , it is easy to verify that

$$ \begin{align*}T_{\sigma}\big({\Lambda}_{j_1}f_1,{\Lambda}_{j_2}f_2,{\Lambda}_{j_3}f_3\big)=T_{\sigma_{j_1}}\big({\Lambda}_{j_1}f_1,{\Lambda}_{j_2}f_2,{\Lambda}_{j_3}f_3\big)\end{align*} $$

where $\sigma _j(\vec {\boldsymbol {\xi }}):=\sigma (\vec {\boldsymbol {\xi }}) \widehat {\Theta }(\vec {\boldsymbol {\xi }}/2^j)$ and $\widehat {\Theta }(\vec {\boldsymbol {\xi }}):=\sum _{l=-2}^2\widehat {\Psi }(2^{l}\vec {\boldsymbol {\xi }})$ so that $\widehat {\Theta }(\vec {\boldsymbol {\xi }})=1$ for $2^{-2}\le |\vec {\boldsymbol {\xi }}|\le 2^{2}$ and $\mbox {supp}(\widehat {\Theta })\subset \{\vec {\boldsymbol {\xi }}\in ({{\mathbb R}^n})^3:2^{-3}\le |\vec {\boldsymbol {\xi }}|\le 2^3\}$ . Then we observe that

(5.1) $$ \begin{align} \sup_{k\in{\mathbb{Z}}}\big\Vert \sigma_k(2^k{\vec{\cdot}\;})\big\Vert_{L_s^2(({{\mathbb R}^n})^3)}\lesssim \mathcal{L}_{s}^{2}[\sigma]=1 \end{align} $$

by virtue of the triangle inequality. Moreover, using the fact that $ {\Gamma }_jf=\sum _{k\le j}{\Lambda }_kf, $ we write

$$ \begin{align*} &\sum_{j_1\in{\mathbb{Z}}}\;\sum_{j_2,j_3\in{\mathbb{Z}}: j_3\le j_2\le j_1}T_{\sigma_{j_1}}\big({\Lambda}_{j_1}f_1,{\Lambda}_{j_2}f_2,{\Lambda}_{j_3}f_3\big)\\& \quad =\sum_{j\in{\mathbb{Z}}}T_{\sigma_{j}}\big({\Lambda}_{j}f_1,{\Gamma}_{j-10}f_2,{\Gamma}_{j-10}f_3\big)+\sum_{k=0}^{9}\sum_{j\in{\mathbb{Z}}}T_{\sigma_{j}}\big({\Lambda}_{j}f_1,{\Lambda}_{j-k}f_2,{\Gamma}_{j-k}f_3\big)\\& \quad =:T_{\sigma}^{(1)}(f_1,f_2,f_3)+\sum_{k=0}^{9}T_{\sigma}^{(2),k}(f_1,f_2,f_3), \end{align*} $$

and especially, let $T_{\sigma }^{(2)}:=T_{\sigma }^{(2),0}$ . Then it is enough to prove that

(5.2) $$ \begin{align} \big\Vert T_{\sigma}^{(\mu)}(f_1,f_2,f_3)\big\Vert_{H^p({{\mathbb R}^n})}\lesssim 1, \qquad \mu=1,2 \end{align} $$

since the operator $T_{\sigma }^{(2),k}$ , $1\le k\le 9$ , can be handled in the same way as $T_{\sigma }^{(2)}$ .

It should be remarked that the vanishing moment condition (1.16) now implies

(5.3) $$ \begin{align} \int_{{{\mathbb R}^n}}x^{\alpha}T_{\sigma_j}\big( f_1,f_2,f_3\big)(x) \; dx=0 \quad \text{ for all multi-indices ~}|\alpha|\le \frac{n}{p}-n. \end{align} $$

5.2 Proof of (5.2) for $\mu =1$

In this case, we may simply follow the arguments used in the proof of Theorems B and D. The proof is based on the fact that if $\widehat {g_k}$ is supported in $\{\xi \in {{\mathbb R}^n}: C_0^{-1} 2^{k}\le |\xi |\le C_02^{k}\}$ for $C_0>1$ , then

(5.4) $$ \begin{align} \bigg\Vert \Big\{ {\Lambda}_j \Big(\sum_{k\in{\mathbb{Z}}}{g_k}\Big)\Big\}_{j\in\mathbb{Z}}\bigg\Vert_{L^p(\ell^q)}\lesssim_{C_0} \big\Vert \big\{ g_j\big\}_{j\in\mathbb{Z}}\big\Vert_{L^p(\ell^q)}. \end{align} $$

The proof of Equation (5.4) is elementary and standard, simply using the estimate

$$ \begin{align*}\bigg| {\Lambda}_j \Big(\sum_{k\in{\mathbb{Z}}}{g_k}\Big)(x)\bigg|=\bigg| {\Lambda}_j\Big(\sum_{k=j-h}^{j+h}{g_k}\Big)(x)\bigg|\lesssim_{r,h}\mathcal{M}_rg_j(x)\end{align*} $$

for all $0<r<\infty $ and for some $h\in {\mathbb {N}}$ , depending on $C_0$ , and the maximal inequality (2.4). We refer to [34, Theorem 3.6] for details.

By using the equivalence in Equation (2.2),

$$ \begin{align*} \big\Vert T_{\sigma}^{(1)}(f_1,f_2,f_3)\big\Vert_{H^p({{\mathbb R}^n})}\sim \bigg\Vert \bigg\{ {\Lambda}_j \Big(\sum_{k\in{\mathbb{Z}}}{ T_{\sigma_k}\big({\Lambda}_kf_1,{\Gamma}_{k-10}f_2,{\Gamma}_{k-10}f_3 \big)}\Big)\bigg\}_{j\in\mathbb{Z}}\bigg\Vert_{L^p(\ell^2)}. \end{align*} $$

We see that the Fourier transform of $T_{\sigma _k}\big ({\Lambda }_kf_1,{\Gamma }_{k-10}f_2,{\Gamma }_{k-10}f_3 \big )$ is supported in $\big \{\xi \in {{\mathbb R}^n} : 2^{k-2}\leq |\xi |\leq 2^{k+2} \big \}$ and thus the estimate (5.4) yields that

$$ \begin{align*} \big\Vert T_{\sigma}^{(1)}(f_1,f_2,f_3)\big\Vert_{H^p({{\mathbb R}^n})}\lesssim \Big\Vert \Big( \sum_{j\in{\mathbb{Z}}}\big| T_{\sigma_j}\big({\Lambda}_jf_1,{\Gamma}_{j-10}f_2,{\Gamma}_{j-10}f_3 \big) \big|^2\Big)^{1/2}\Big\Vert_{L^p({{\mathbb R}^n})}. \end{align*} $$

Then it is already proved in [14, (3.14)] that the preceding expression is dominated by the right-hand side of Equation (5.2) for $s>n/\min {\{p_1,p_2,p_3\}}+n/2$ , where we remark that $\min {\{p_1,p_2,p_3\}}\le 1$ . This proves Equation (5.2) for $\mu =1$ .

5.3 Proof of Equation (5.2) for $\mu =2$

Recall that

(5.5) $$ \begin{align} T_{\sigma}^{(2)}(f_1,f_2,f_3)=\sum_{j\in{\mathbb{Z}}}T_{\sigma_j}\big({\Lambda}_jf_1,{\Lambda}_jf_2,{\Gamma}_jf_3\big) \end{align} $$

and observe that

$$ \begin{align*}T_{\sigma_j}\big({\Lambda}_jf_1,{\Lambda}_jf_2,{\Gamma}_jf_3\big)(x)=\sigma_j^{\vee}\ast_{3n}\big({\Lambda}_jf_1\otimes {\Lambda}_jf_2\otimes {\Gamma}_jf_3 \big)(x,x,x),\end{align*} $$

where $\ast _{3n}$ means the convolution on $\mathbb {R}^{3n}$ .

It suffices to consider the case when $(1/p_1,1/p_2,1/p_3)$ belongs to $\mathscr {R}_1$ or $\mathscr {R}_3$ , as the remaining case is symmetrical to the case $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_1$ , in view of Equation (5.5). We will mainly focus on the case $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_1$ , while simply providing a short description for the case $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_3$ in the remark below as almost same arguments will be applied in that case.

Therefore, we now assume $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and in turn, suppose that $s>n/p_1+n/2$ . By using the atomic decomposition in Equation (2.3), the function $f_1\in H^{p_1}({{\mathbb R}^n})$ can be written as $f_1=\sum _{k=1}^{\infty }\lambda _k a_k$ , where $a_k$ ’s are $H^{p_1}$ -atoms associated with cubes $Q_k$ , and

(5.6) $$ \begin{align} \Big(\sum_{k=1}^{\infty}|\lambda_k|^{p_1}\Big)^{1/{p_1}}\lesssim 1. \end{align} $$

As mentioned before, we may assume that M is sufficiently large and $\int {x^{\gamma }a_k(x)}dx=0$ holds for all multi-indices $|\gamma |\le M$ .

By the definition in Equation (1.2), we have

$$ \begin{align*} \big\Vert T_{\sigma}^{(2)}(f_1,f_2,f_3)\big\Vert_{H^p({{\mathbb R}^n})}\sim \bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty}\lambda _k\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})} \end{align*} $$

and thus we need to prove that

(5.7) $$ \begin{align} \bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty}\lambda _k\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})}\lesssim 1. \end{align} $$

The left-hand side is less than the sum of

$$ \begin{align*}\mathcal{I}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\Big| \sum_{k=0}^{\infty}\lambda _k \chi_{Q_k^{***}} \phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})}\end{align*} $$

and

$$ \begin{align*}\mathcal{J}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\Big| \sum_{k=0}^{\infty}\lambda _k \chi_{(Q_k^{***})^c}\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})},\end{align*} $$

recalling that $Q_k^{***}$ is the dilate of $Q_k$ by a factor $(10\sqrt {n})^3$ . The two terms $\mathcal {I}$ and $\mathcal {J}$ will be treated separately in the next two sections.

Remark. When $(1/p_1,1/p_2,1/p_3)\in \mathscr {R}_3$ (that is, $0<p_3\le 1, ~2<p_1,p_2< \infty $ ), we need to prove

$$ \begin{align*}\bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty}\lambda _k\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_jf_1,{\Lambda}_jf_2,{\Gamma}_j\widetilde{a_k}) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})}\lesssim 1,\end{align*} $$

where $\widetilde {a_k}$ is the $H^{p_3}$ -atom associated with $f_3$ . This is actually, via symmetry, equivalent to the estimate that for $0<p_1\le 1$ and $2<p_2,p_3< \infty $ ,

(5.8) $$ \begin{align} \bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty}\lambda _k\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Gamma}_ja_k,{\Lambda}_jf_2,{\Lambda}_jf_3) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})}\lesssim 1, \end{align} $$

where $a_k$ is the $H^{p_1}$ -atom for $f_1$ . The proof of Equation (5.8) is almost same as that of Equation (5.7) which will be discussed in Sections 6 and 7. So this will not be pursued in this paper, just saying that Equation (4.9) will be needed rather than Equation (4.8), and the estimate $\big \Vert \big \{ {\Gamma }_ja_k\big \}_{j\in {\mathbb {Z}}}\big \Vert _{L^r(\ell ^{\infty })}\sim \Vert a_k\Vert _{H^r({{\mathbb R}^n})}$ will be required in place of the equivalence $\big \Vert \big \{ {\Lambda }_ja_k\big \}_{j\in {\mathbb {Z}}}\big \Vert _{L^r(\ell ^{2})}\sim \Vert a_k\Vert _{H^r({{\mathbb R}^n})}$ .

6 Proof of Proposition 3.1: estimate for $\mathcal {I}$

For the estimation of $\mathcal {I}$ , we need the following lemma whose proof will be given in Section 9.

Lemma 6.1. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*}\Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3,\end{align*} $$

and for $x\in {{\mathbb R}^n}$

(6.1) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\Big|\sum_{k=0}^{\infty}\lambda _k\chi_{Q_k^{***}}(x)\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

This lemma, together with Hölder’s inequality, clearly shows that

$$ \begin{align*}\mathcal{I}\lesssim \Vert u_1\Vert_{L^{p_1}({{\mathbb R}^n})}\Vert u_2\Vert_{L^{p_2}({{\mathbb R}^n})}\Vert u_3\Vert_{L^{p_3}({{\mathbb R}^n})}\lesssim 1.\end{align*} $$

7 Proof of Proposition 3.1: estimate for $\mathcal {J}$

Recall that for each $Q_k$ and $l\in {\mathbb {Z}}$ , $B_{{\mathbf {x}}_{Q_k}}^l=B({\mathbf {x}}_{Q_k},100n2^{-l})$ stands for the ball of radius $100n2^{-l}$ and center ${\mathbf {x}}_{Q_k}$ . Simply writing $B_k^l:=B_{{\mathbf {x}}_{Q_k}}^l$ , we bound $\mathcal {J}$ by the sum of

$$ \begin{align*}\mathcal{J}_1:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\Big| \sum_{k=0}^{\infty}\lambda _k \chi_{(Q_k^{***})^c}\chi_{(B_{k}^l)^c}\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})}\end{align*} $$

and

$$ \begin{align*}\mathcal{J}_2:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\Big| \sum_{k=0}^{\infty}\lambda _k \chi_{(Q_k^{***})^c}\chi_{B_k^l}\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big) \Big|\bigg\Vert_{L^p({{\mathbb R}^n})}\end{align*} $$

and treat them separately.

7.1 Estimate for $\mathcal {J}_1$

Using the representations in Equations (2.7) and (2.9), we write

$$ \begin{align*}{\Lambda}_jf_2(x):=\sum_{P\in\mathcal{D}_j}b_P^2\psi^P(x),\qquad {\Gamma}_jf_3(x):=\sum_{R\in\mathcal{D}_j}b_R^3\theta^R(x),\end{align*} $$

where we recall $\psi ^P(x)=|P|^{{1}/{2}}\psi _j(x-{\mathbf {x}}_P)$ and $\theta ^R(x)=|R|^{{1}/{2}}\theta _j(x-{\mathbf {x}}_R)$ for $P,R\in \mathcal {D}_j$ . Then it follows from Equations (2.8), (2.10), (2.1) and (2.2) that

(7.1) $$ \begin{align} \big\Vert \{b_P^2\}_{P\in\mathcal{D}}\big\Vert_{\dot{f}^{p_2,2}}\sim \big\Vert \big\{{\Lambda}_jf_2\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^{p_2}(\ell^2)}\sim \Vert f_2\Vert_{H^{p_2}({{\mathbb R}^n})}= 1 \end{align} $$

and

(7.2) $$ \begin{align} \big\Vert \{b_R^3\}_{R\in\mathcal{D}}\big\Vert_{\dot{f}^{p_3,\infty}}\sim \big\Vert \big\{{\Gamma}_jf_3\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^{p_3}(\ell^{\infty})}\sim \Vert f_3\Vert_{H^{p_3}({{\mathbb R}^n})}=1. \end{align} $$

We write

$$ \begin{align*} \phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big)(x)= \sum_{\nu=1}^{4} \phi_l\ast \big( \mathcal{U}_{\nu}(x,\cdot)\big)(x), \end{align*} $$

where

(7.3) $$ \begin{align} \Omega_{\nu}(P,R):=\begin{cases} P\cap R & \nu=1\\ P^c\cap R & \nu=2\\ P\cap R^c & \nu=3\\ P^c \cap R^c & \nu=4 \end{cases} \end{align} $$

and

(7.4) $$ \begin{align} \mathcal{U}_{\nu}(x,y):= \sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{\Omega_{\nu}(P,R)}(x), \quad \nu=1,2,3,4. \end{align} $$

Then we have

$$ \begin{align*}\mathcal{J}_1 \lesssim_p \mathcal{J}_{1}^1+\mathcal{J}_{1}^2+\mathcal{J}_{1}^3+\mathcal{J}_{1}^4,\end{align*} $$

where

$$ \begin{align*} \mathcal{J}_{1}^{\nu}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x) \phi_l\ast\big( \mathcal{U}_{\nu}(x,\cdot)\big)(x)\Big|\bigg\Vert_{L^p(x)},\qquad \nu=1,2,3,4. \end{align*} $$

Now, we will show that

(7.5) $$ \begin{align} \mathcal{J}_1^{\nu}\lesssim 1, \qquad \nu=1,2,3,4. \end{align} $$

7.1.1 Proof of Equation (7.5) for $\nu =1$

We further decompose $\mathcal {U}_1(x,y)$ as

$$ \begin{align*}\mathcal{U}_1(x,y)=\mathcal{U}_1^{\mathrm{in}}(x,y)+\mathcal{U}_1^{\mathrm{out}}(x,y),\end{align*} $$

where

(7.6) $$ \begin{align} \begin{aligned} \mathcal{U}_1^{\mathrm{in}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{Q_k^*}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R}(x),\\ \mathcal{U}_1^{\mathrm{out}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{(Q_k^*)^c}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R}(x), \end{aligned} \end{align} $$

and accordingly, we define

$$ \begin{align*} \mathcal{J}_1^{1,\mathrm{in}/\mathrm{out}}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x) \phi_l\ast\big( \mathcal{U}_{1}^{\mathrm{in}/\mathrm{out}}(x,\cdot)\big)(x)\Big|\bigg\Vert_{L^p(x)}. \end{align*} $$

Then we claim the following lemma.

Lemma 7.1. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_1^{\mathrm {in}/\mathrm {out}}$ be defined as in Equation (7.6). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1^{\mathrm {in}}$ , $u_1^{\mathrm {out}}$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*}\big\Vert u_1^{\mathrm{in}/\mathrm{out}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim 1, \qquad \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=2,3,\end{align*} $$

and for $x\in {{\mathbb R}^n}$

(7.7) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x) \phi_l\ast\big( \mathcal{U}_{1}^{\mathrm{in}/\mathrm{out}}(x,\cdot)\big)(x)\Big| \lesssim u_1^{\mathrm{in}/\mathrm{out}}(x) u_2(x) u_3(x). \end{align} $$

The proof of Lemma 7.1 will be given in Section 9. Taking the lemma for granted and using Hölder’s inequality, we can easily show that

$$ \begin{align*}\mathcal{J}_1^1\lesssim_p \mathcal{J}_1^{1,\mathrm{in}}+\mathcal{J}_1^{1,\mathrm{out}}\lesssim 1.\end{align*} $$

7.1.2 Proof of Equation (7.5) for $\nu =2$

For $P\in \mathcal {D}$ and $l\in {\mathbb {Z}}$ let $B_P^l:=B_{{\mathbf {x}}_P}^l=B({\mathbf {x}}_P,100n2^{-l})$ . By introducing

(7.8) $$ \begin{align} \begin{aligned} \mathcal{U}_2^{1,\mathrm{in}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{Q_k^*}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P^c\cap (B_P^l)^c\cap R}(x),\\ \mathcal{U}_2^{1,\mathrm{out}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{(Q_k^*)^c}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P^c\cap (B_P^l)^c\cap R}(x),\\ \mathcal{U}_2^{2,\mathrm{in}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{Q_k^*}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P^c\cap B_P^l\cap R}(x),\\ \mathcal{U}_2^{2,\mathrm{out}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{(Q_k^*)^c}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P^c\cap B_P^l\cap R}(x), \end{aligned} \end{align} $$

we write $\mathcal {U}_2=\mathcal {U}_2^{1,\mathrm {in}}+\mathcal {U}_2^{1,\mathrm {out}}+\mathcal {U}_2^{2,\mathrm {in}}+\mathcal {U}_2^{2,\mathrm {out}}$ and consequently,

$$ \begin{align*}\mathcal{J}_1^2 \lesssim_p \mathcal{J}_1^{2,1,\mathrm{in}}+\mathcal{J}_1^{2,1,\mathrm{out}}+\mathcal{J}_1^{2,2,\mathrm{in}}+\mathcal{J}_1^{2,2,\mathrm{out}},\end{align*} $$

where

$$ \begin{align*} \mathcal{J}_{1}^{2,\eta,\mathrm{in}/\mathrm{out}}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\; \Big|\sum_{k=0}^{\infty}\lambda _k \chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x)\; \phi_l\ast\big( \mathcal{U}_{2}^{\eta,\mathrm{in}/\mathrm{out}}(x,\cdot)\big)(x) \Big| \bigg\Vert_{L^p(x)},\quad \eta=1,2. \end{align*} $$

Then we apply the following lemma that will be proved in Section 9.

Lemma 7.2. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_2^{\eta ,\mathrm {in}/\mathrm {out}}$ be defined as in Equation (7.8). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1^{\mathrm {in}}$ , $u_1^{\mathrm {out}}$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*}\big\Vert u_1^{\mathrm{in}/\mathrm{out}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim 1, \qquad \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=2,3,\end{align*} $$

and for each $\eta =1,2$

(7.9) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x) \phi_l\ast\big( \mathcal{U}_{2}^{\eta,\mathrm{in}/\mathrm{out}}(x,\cdot)\big)(x)\Big| \lesssim u_1^{\mathrm{in}/\mathrm{out}}(x) u_2(x) u_3(x). \end{align} $$

Then Lemma 7.2 and Hölder’s inequality yield that $\mathcal {J}_1^2$ is controlled by the sum of four terms in the form

$$ \begin{align*} \big\Vert u_1^{\mathrm{in}/\mathrm{out}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\Vert u_2\Vert_{L^{p_2}({{\mathbb R}^n})} \Vert u_3\Vert_{L^{p_3}({{\mathbb R}^n})}, \end{align*} $$

which is obviously less than a constant. This proves Equation (7.5) for $\nu =2$ .

7.1.3 Proof of Equation (7.5) for $\nu =3$

This case is essentially symmetrical to the case $\nu =2$ . For $R\in \mathcal {D}$ and $l\in {\mathbb {Z}}$ , let $B_R^l:=B_{{\mathbf {x}}_R}^l=B({\mathbf {x}}_R,100n2^{-l})$ . Let

(7.10) $$ \begin{align} \begin{aligned} \mathcal{U}_3^{1,\mathrm{in}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{Q_k^*}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R^c\cap (B_R^l)^c}(x),\\ \mathcal{U}_3^{1,\mathrm{out}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{(Q_k^*)^c}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R^c\cap (B_R^l)^c}(x),\\ \mathcal{U}_3^{2,\mathrm{in}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{Q_k^*}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R^c\cap B_R^l}(x),\\ \mathcal{U}_3^{2,\mathrm{out}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{(Q_k^*)^c}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R^c\cap B_R^l}(x), \end{aligned} \end{align} $$

and then we write

$$ \begin{align*}\mathcal{J}_1^3\lesssim_p \mathcal{J}_1^{3,1,\mathrm{in}}+\mathcal{J}_1^{3,1,\mathrm{out}}+\mathcal{J}_1^{3,2,\mathrm{in}}+\mathcal{J}_1^{3,2,\mathrm{out}},\end{align*} $$

where

$$ \begin{align*} \mathcal{J}_{1}^{3,\eta,\mathrm{in}/\mathrm{out}}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty} \lambda _k \chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x)\; \phi_l\ast\big( \mathcal{U}_{3}^{\eta,\mathrm{in}/\mathrm{out}}(x,\cdot)\big)(x) \Big|\bigg\Vert_{L^p(x)}, \quad \eta=1,2. \end{align*} $$

Now, Equation (7.5) for $\nu =3$ follows from the lemma below.

Lemma 7.3. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_3^{\eta ,\mathrm {in}/\mathrm {out}}$ be defined as in Equation (7.10). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1^{\mathrm {in}}$ , $u_1^{\mathrm {out}}$ , $u_2$ , and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*}\big\Vert u_1^{\mathrm{in}/\mathrm{out}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim 1, \qquad \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=2,3,\end{align*} $$

and for each $\eta =1,2$

$$ \begin{align*} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x) \phi_l\ast\big( \mathcal{U}_{3}^{\eta,\mathrm{in}/\mathrm{out}}(x,\cdot)\big)(x)\Big| \lesssim u_1^{\mathrm{in}/\mathrm{out}}(x) u_2(x) u_3(x). \end{align*} $$

The proof of the lemma will be provided in Section 9.

7.1.4 Proof of Equation (7.5) for $\nu =4$

In this case, we divide $\mathcal {U}_4$ into eight types depending on whether x belongs to each of $B_P^l$ and $B_R^l$ and whether ${\Lambda }_ja_k$ is supported in $Q_k^*$ . Indeed, let

(7.11) $$ \begin{align} \Xi_{\eta}(P,R,l):=\begin{cases} P^c\cap R^c\cap (B_P^l)^c\cap (B_R^l)^c, & \eta=1\\ P^c\cap R^c\cap (B_P^l)^c\cap B_R^l, & \eta=2\\ P^c\cap R^c\cap B_P^l\cap (B_R^l)^c, & \eta=3\\ P^c\cap R^c\cap B_P^l\cap B_R^l, & \eta=4, \end{cases} \end{align} $$

and we define

(7.12) $$ \begin{align} \begin{aligned} \mathcal{U}_4^{\eta,\mathrm{in}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{Q_k^*}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{\Xi_{\eta}}(x),\\ \mathcal{U}_4^{\eta,\mathrm{out}}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big(\chi_{(Q_k^*)^c}{\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{\Xi_{\eta}}(x) \end{aligned} \end{align} $$

for $\eta =1,2,3,4$ .

Then we use the following lemma to obtain the desired result.

Lemma 7.4. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_4^{\eta ,\mathrm {in}/\mathrm {out}}$ be defined as in Equation (7.12). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1^{\mathrm {in}}$ , $u_1^{\mathrm {out}}$ , $u_2$ , and $u_3$ on ${{\mathbb R}^n}$ such that

(7.13) $$ \begin{align} \big\Vert u_1^{\mathrm{in}/\mathrm{out}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim 1, \qquad \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=2,3, \end{align} $$

and for each $\eta =1,2,3,4,$

(7.14) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x) \phi_l\ast\big( \mathcal{U}_{4}^{\eta,\mathrm{in}/\mathrm{out}}(x,\cdot)\big)(x)\Big| \lesssim u_1^{\mathrm{in}/\mathrm{out}}(x) u_2(x) u_3(x). \end{align} $$

We will prove the lemma in Section 9.

7.2 Estimate for $\mathcal {J}_2$

Let $x\in (Q_k^{***})^c\cap B_{k,l}$ . For $\nu =1,2,3,4$ , let $\Omega _{\nu }(P,R)$ be defined as in Equation (7.3). Then as in the proof of the estimate for $\mathcal {J}_1$ , we consider the four cases: $x \in \Omega _{1}(P,R)$ , $x \in \Omega _{2}(P,R)$ , $x \in \Omega _{3}(P,R)$ and $x \in \Omega _{4}(P,R)$ . That is, for each $\nu =1,2,3,4$ , let $\mathcal {U}_{\nu }$ be defined as in Equation (7.4) and

$$ \begin{align*}\mathcal{J}_2^{\nu}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty} \lambda _k \chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast \big(\mathcal{U}_{\nu}(x,\cdot) \big)(x)\Big| \bigg\Vert_{L^p(x)}.\end{align*} $$

Then it suffices to show that for each $\nu =1,2,3,4$ ,

(7.15) $$ \begin{align} \mathcal{J}_2^{\nu}\lesssim 1. \end{align} $$

7.2.1 Proof of Equation (7.15) for $\nu =1$

In this case, the proof can be simply reduced to the following lemma, which will be proved in Section 9.

Lemma 7.5. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_1$ be defined as in Equation (7.4). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*}\Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3, \end{align*} $$

and for $x\in {{\mathbb R}^n}$

(7.16) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast\big( \mathcal{U}_{1}(x,\cdot)\big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

Then it follows from Hölder’s inequality that

$$ \begin{align*}\mathcal{J}_2^1\lesssim \Vert u_1\Vert_{L^{p_1}({{\mathbb R}^n})}\Vert u_2\Vert_{L^{p_2}({{\mathbb R}^n})}\Vert u_3\Vert_{L^{p_3}({{\mathbb R}^n})}\lesssim 1.\end{align*} $$

7.2.2 Proof of Equation (7.15) for $\nu =2$

For $P\in \mathcal {D}$ and $l\in {\mathbb {Z}}$ , let $B_P^l:=B_{{\mathbf {x}}_P}^l$ be the ball of center ${\mathbf {x}}_P$ and radius $100n2^{-l}$ as before. We define

(7.17) $$ \begin{align} \begin{aligned} \mathcal{U}_2^{1}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P^c\cap (B_{P}^l)^c\cap R}(x),\\ \mathcal{U}_2^{2}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P^c\cap B_P^l\cap R}(x) \end{aligned} \end{align} $$

and write

$$ \begin{align*}\mathcal{J}_2^2\lesssim\mathcal{J}_2^{2,1}+\mathcal{J}_2^{2,2}\end{align*} $$

where

$$ \begin{align*}\mathcal{J}_2^{2,\eta}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty} \lambda _k \chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast \big(\mathcal{U}_{2}^{\eta}(x,\cdot) \big)(x)\Big|\; \bigg\Vert_{L^p(x)}, \quad \eta=1,2.\end{align*} $$

Then we need the following lemmas.

Lemma 7.6. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ and let $\mathcal {U}_2^{1}$ be defined as in (7.17). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*} \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3, \end{align*} $$

and

(7.18) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast\big( \mathcal{U}_{2}^{1}(x,\cdot)\big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

Lemma 7.7. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_2^{2}$ be defined as in Equation (7.17). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*} \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3, \end{align*} $$

and

$$ \begin{align*} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast\big( \mathcal{U}_{2}^{2}(x,\cdot)\big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align*} $$

The above lemmas will be proved in Section 9. Using Lemmas 7.6 and 7.7, we obtain

$$ \begin{align*} \mathcal{J}_2^{2,\eta}\lesssim \Vert u_1\Vert_{L^{p_1}({{\mathbb R}^n})}\Vert u_2\Vert_{L^{p_2}({{\mathbb R}^n})}\Vert u_3\Vert_{L^{p_3}({{\mathbb R}^n})}\lesssim 1,\qquad \eta=1,2, \end{align*} $$

which finishes the proof of Equation (7.15) for $\nu =2$ .

7.2.3 Proof of Equation (7.15) for $\nu =3$

We use the notation $B_R^l:=B_{{\mathbf {x}}_R}^l$ for $R\in \mathcal {D}$ and $l\in {\mathbb {Z}}$ as before and write

$$ \begin{align*}\mathcal{J}_2^3\lesssim \mathcal{J}_2^{3,1}+\mathcal{J}_2^{3,2},\end{align*} $$

where

(7.19) $$ \begin{align} \begin{aligned} \mathcal{U}_3^{1}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R^c\cap (B_R^l)^c}(x),\\ \mathcal{U}_3^{2}(x,y)&:=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{P\cap R^c\cap B_R^l}(x), \end{aligned} \end{align} $$

and

$$ \begin{align*}\mathcal{J}_2^{3,\eta}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty} \lambda _k \chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast \big(\mathcal{U}_{3}^{\eta}(x,\cdot) \big)(x)\Big| \bigg\Vert_{L^p(x)}, \quad \eta=1,2.\end{align*} $$

As in the proof of the case $\nu =2$ , it suffices to prove the following two lemmas.

Lemma 7.8. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_3^{1}$ be defined as in Equation (7.19). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

(7.20) $$ \begin{align} \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3, \end{align} $$

and

(7.21) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast\big( \mathcal{U}_{3}^{1}(x,\cdot)\big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

Lemma 7.9. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_3^{2}$ be defined as in Equation (7.19). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

(7.22) $$ \begin{align} \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3, \end{align} $$

and

(7.23) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast\big( \mathcal{U}_{3}^{2}(x,\cdot)\big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

The proof of Lemmas 7.8 and 7.9 will be provided in Section 9.

7.2.4 Proof of Equation (7.15) for $\nu =4$

Let $B_P^l:=B_{{\mathbf {x}}^P}^l$ and $B_R^l:=B_{{\mathbf {x}}_R}^l$ for $P,R\in \mathcal {D}$ and $l\in {\mathbb {Z}}$ , and let $\Xi _{\eta }(P,R,l)$ be defined as in Equation (7.11). Now, we write

$$ \begin{align*}\mathcal{U}_4=\mathcal{U}_4^{1}+\mathcal{U}_4^{2}+\mathcal{U}_4^{3}+\mathcal{U}_4^{4},\end{align*} $$

where

(7.24) $$ \begin{align} \mathcal{U}_4^{\eta}(x,y):=\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} b_P^2 b_R^3 T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \chi_{\Xi_{\eta}(P,R,l)}(x), \quad \eta=1,2,3,4. \end{align} $$

Accordingly, we define

$$ \begin{align*}\mathcal{J}_2^{4,\eta}:=\bigg\Vert \sup_{l\in{\mathbb{Z}}} \Big| \sum_{k=0}^{\infty}\lambda _k \chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast \big(\mathcal{U}_{4}^{\eta}(x,\cdot) \big)(x)\Big|\; \bigg\Vert_{L^p(x)}, \quad \eta=1,2,3,4.\end{align*} $$

Then we obtain the desired result from the following lemmas.

Lemma 7.10. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_4^{\eta }$ , $\eta =1,2,3$ , be defined as in Equation (7.24). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*} \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3, \end{align*} $$

and for each $\eta =1,2,3$

(7.25) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast\big( \mathcal{U}_{4}^{\eta}(x,\cdot)\big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

Lemma 7.11. Let $0<p_1\le 1$ and $2<p_2,p_3<\infty $ , and let $\mathcal {U}_4^{4}$ be defined as in Equation (7.24). Suppose that $\Vert f_1\Vert _{H^{p_1}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{p_2}({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{p_3}({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p_1+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

(7.26) $$ \begin{align} \Vert u_{{\mathrm{i}}}\Vert_{L^{p_{{\mathrm{i}}}}({{\mathbb R}^n})}\lesssim 1 \quad \text{ for }~ {\mathrm{i}}=1,2,3, \end{align} $$

and

(7.27) $$ \begin{align} \sup_{l\in{\mathbb{Z}}}\; \Big| \sum_{k=0}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x) \phi_l\ast\big( \mathcal{U}_{4}^{4}(x,\cdot)\big)(x)\Big| \lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

The proof of the lemmas will be given in Section 9.

8 Proof of Proposition 3.2

We need to deal only with, via symmetry, the case when $0<p_1=p\le 1$ and $p_2=p_3=\infty $ . As before, we assume that $\| f_1 \|_{H^p({{\mathbb R}^n})} = \|f_2 \|_{L^\infty ({{\mathbb R}^n})} = \| f_3 \|_{L^\infty ({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p+n/2$ . In this case, we do not decompose the frequencies of $f_2, f_3$ and only make use of the atomic decomposition on $f_1$ . Let $a_k$ ’s be $H^p$ -atoms associated with $Q_k$ so that $f_1=\sum _{k=1}^{\infty }\lambda _k a_k$ and $\big (\sum _{k=1}^{\infty }|\lambda _k|^p\big )^{1/p}\lesssim 1$ . Then we will prove that

(8.1) $$ \begin{align} \bigg\| \sup_{l\in\mathbb{Z}} \Big|\sum_{k=1}^{\infty} \lambda_k \chi_{Q_k^{***}}\;\phi_l \ast T_{\sigma}(a_k, f_2, f_3)\Big| \bigg\|_{L^p({{\mathbb R}^n})} \lesssim 1 \end{align} $$

and

(8.2) $$ \begin{align} \bigg\| \sup_{l\in\mathbb{Z}} \Big|\sum_{k=1}^{\infty} \lambda_k \chi_{(Q_k^{***})^c}\;\phi_l \ast T_{\sigma}(a_k, f_2, f_3)\Big| \bigg\|_{L^p({{\mathbb R}^n})} \lesssim 1. \end{align} $$

8.1 Proof of Equation (8.1)

Since

$$ \begin{align*}\big| \phi_l\ast T_{\sigma}(a_k,f_2,f_3)(x)\big|\lesssim \mathcal{M}T_{\sigma}(a_k,f_2,f_3)(x),\end{align*} $$

the left-hand side of Equation (8.1) is controlled by

$$ \begin{align*} \Big(\sum_{k=1}^{\infty}|\lambda _k|^p\big\Vert \mathcal{M}T_{\sigma}(a_k,f_2,f_3) \big\Vert_{L^p(Q^{***})}^p \Big)^{1/p}. \end{align*} $$

Using Hölder’s inequality, the $L^2$ boundedness of $\mathcal {M}$ and Theorem D, we have

$$ \begin{align*} \big\Vert \mathcal{M}T_{\sigma}(a_k,f_2,f_3) \big\Vert_{L^p(Q^{***})}\lesssim |Q_k|^{1/p-1/2}\big\Vert T_{\sigma}(a_k,f_2,f_3)\big\Vert_{L^2({{\mathbb R}^n})}\lesssim |Q_k|^{1/p-1/2}\Vert a_k\Vert_{L^2({{\mathbb R}^n})}\lesssim 1 \end{align*} $$

and thus Equation (8.1) follows from $\big (\sum _{k=1}^{\infty }|\lambda _k|^p\big )^{1/p}\lesssim 1$ .

8.2 Proof of Equation (8.2)

Let $B_k^l=B({\mathbf {x}}_{Q_k},100 n2^{-l})$ as before. We now decompose the left-hand side of Equation (8.2) as the sum of

$$ \begin{align*}\mathcal{V}_1:= \bigg\| \sup_{l\in\mathbb{Z}} \Big|\sum_{k=1}^{\infty} \lambda_k \chi_{(Q_k^{***})^c}\chi_{(B_k^l)^c}\;\phi_l \ast T_{\sigma}(a_k,f_2,f_3)\Big| \bigg\|_{L^p({{\mathbb R}^n})},\end{align*} $$

$$ \begin{align*}\mathcal{V}_2:= \bigg\| \sup_{l\in\mathbb{Z}} \Big|\sum_{k=1}^{\infty} \lambda_k \chi_{(Q_k^{***})^c}\chi_{B_k^l}\;\phi_l \ast T_{\sigma}(a_k,f_2,f_3)\Big)\Big| \bigg\|_{L^p({{\mathbb R}^n})},\end{align*} $$

and thus we need to show that

$$ \begin{align*} \mathcal{V}_{1},\mathcal{V}_2\lesssim 1. \end{align*} $$

Actually, the proof of these estimates will be complete once we have verified the following lemmas.

Lemma 8.1. Let $0<p\le 1$ . Suppose that $\Vert f_1\Vert _{H^{p}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{\infty }({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{\infty }({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*} \Vert u_{1}\Vert_{L^{p}({{\mathbb R}^n})}\lesssim 1, \qquad \Vert u_{{\mathrm{i}}}\Vert_{L^{\infty}({{\mathbb R}^n})}\lesssim 1\quad \text{ for }~ {\mathrm{i}}=2,3, \end{align*} $$

and

(8.3) $$ \begin{align} \sup_{l\in\mathbb{Z}} \Big|\sum_{k=1}^{\infty} \lambda_k \chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x)\;\phi_l \ast T_{\sigma}\big(a_k,f_2,f_3\big)(x)\Big|\lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

Lemma 8.2. Let $0<p\le 1$ . Suppose that $\Vert f_1\Vert _{H^{p}({{\mathbb R}^n})}=\Vert f_2\Vert _{H^{\infty }({{\mathbb R}^n})}=\Vert f_3\Vert _{H^{\infty }({{\mathbb R}^n})}=1$ and $\mathcal {L}_s^2[\sigma ]=1$ for $s>n/p+n/2$ . Then there exist nonnegative functions $u_1$ , $u_2$ and $u_3$ on ${{\mathbb R}^n}$ such that

$$ \begin{align*} \Vert u_{1}\Vert_{L^{p}({{\mathbb R}^n})}\lesssim 1, \qquad \Vert u_{{\mathrm{i}}}\Vert_{L^{\infty}({{\mathbb R}^n})}\lesssim 1\quad \text{ for }~ {\mathrm{i}}=2,3, \end{align*} $$

and

(8.4) $$ \begin{align} \sup_{l\in\mathbb{Z}} \Big|\sum_{k=1}^{\infty} \lambda_k \chi_{(Q_k^{***})^c}(x)\chi_{B_k^l}(x)\;\phi_l \ast T_{\sigma}\big(a_k,f_2,f_3\big)(x)\Big|\lesssim u_1(x) u_2(x) u_3(x). \end{align} $$

The proof of the two lemmas will be given in Section 9.

9 Proof of the key lemmas

9.1 Proof of Lemma 6.1

Let $1<r<2$ such that $s>{3n}/{r}>{3n}/{2}$ , and we claim the pointwise estimate

(9.1) $$ \begin{align} \big|T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3)(y)\big|\lesssim \mathcal{M}_r{\Lambda}_ja_k(y)\mathcal{M}_r{\Lambda}_jf_2(y)\mathcal{M}_r{\Gamma}_jf_3(y). \end{align} $$

Indeed, choosing t so that ${3n}/{r}<3t<s$ , we apply Hölder’s inequality to bound the left-hand side of Equation (9.1) by

$$ \begin{align*} &\int_{({{\mathbb R}^n})^3} \langle 2^j\vec{\boldsymbol{z}}\rangle^{3t} \big| \sigma_j^{\vee}(\vec{\boldsymbol{z}})\big| \frac{|{\Lambda}_ja_k(y-z_1)|}{\langle 2^jz_1\rangle^t} \frac{|{\Lambda}_jf_2(y-z_2)|}{\langle 2^jz_2\rangle^t} \frac{|{\Gamma}_jf_3(y-z_3)|}{\langle 2^jz_3\rangle^t} \; d\vec{\boldsymbol{z}}\\& \quad \le \big\Vert \langle 2^j{\vec{\cdot}\;}\rangle^{3t} \sigma_j^{\vee}\big\Vert_{L^{r'}(({{\mathbb R}^n})^3)} \bigg\Vert \frac{{\Lambda}_ja_k(y-\cdot)}{\langle 2^j\cdot \rangle^t}\bigg\Vert_{L^{r}({{\mathbb R}^n})} \bigg\Vert \frac{{\Lambda}_jf_2(y-\cdot)}{\langle 2^j\cdot \rangle^t}\bigg\Vert_{L^{r}({{\mathbb R}^n})}\bigg\Vert \frac{{\Gamma}_jf_3(y-\cdot)}{\langle 2^j\cdot \rangle^t}\bigg\Vert_{L^{r}({{\mathbb R}^n})}. \end{align*} $$

We observe that

$$ \begin{align*}\big\Vert \langle 2^j{\vec{\cdot}\;}\rangle^{3t} \sigma_j^{\vee}\big\Vert_{L^{r'}(({{\mathbb R}^n})^3)}\lesssim 2^{{3jn}/{r}}\Vert \sigma(2^j{\vec{\cdot}\;}) \Vert_{L^r_{3t}(({{\mathbb R}^n})^3)}\lesssim 2^{{3jn}/{r}}\Vert \sigma(2^j{\vec{\cdot}\;})\Vert_{L^2_s(({{\mathbb R}^n})^3)}\lesssim 2^{{3jn}/{r}}\end{align*} $$

using the Hausdorff–Young inequality, Equation (5.1) and the inclusion

$$ \begin{align*}L_{s_0}^{t_0}(A)\hookrightarrow L_{s_1}^{t_1}(A)\quad \text{ for } ~s_0\ge s_1,~ t_0\ge t_1,\end{align*} $$

where A is a ball of a constant radius, whose proof is contained in [19, (1.8)]. Applying Equation (2.5) to the remaining three $L^r$ norms, we finally obtain Equation (9.1).

Now, we choose $\widetilde {r}$ and q such that $2<\widetilde {r}<p_2,p_3$ and ${1}/{q}+{2}/{\widetilde {r}}=1$ . Finally, using the estimate (9.1) and Hölder’s inequality, we have

$$ \begin{align*} &\Big|\sum_{k=0}^{\infty}\lambda _k\chi_{Q_k^{***}}(x)\phi_l\ast \Big( \sum_{j\in{\mathbb{Z}}} T_{\sigma_j}({\Lambda}_ja_k,{\Lambda}_jf_2,{\Gamma}_jf_3) \Big)(x)\Big|\\&\quad \lesssim \sum_{k=0}^{\infty}\lambda _k\chi_{Q_k^{***}}(x) 2^{ln}\int_{|x-y|\le 2^{-l} } \big\Vert \big\{ \mathcal{M}_r{\Lambda}_ja_k(y)\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2}\big\Vert \big\{ \mathcal{M}_r{\Lambda}_jf_2(y)\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2} \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \times \big\Vert \big\{ \mathcal{M}_r{\Gamma}_jf_3(y)\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^{\infty}}\; dy\\&\quad \lesssim u_1(x) u_2(x)u_3(x), \end{align*} $$

where we choose

$$ \begin{align*} u_1(x)&:= \sum_{k=0}^{\infty}\lambda _k\chi_{Q_k^{***}}(x) \mathcal{M}_{q}\big( \big\Vert \big\{ \mathcal{M}_r{\Lambda}_ja_k\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2}\big)(x),\\ u_2(x)&:=\mathcal{M}_{\widetilde{r}}\big( \big\Vert \big\{ \mathcal{M}_r{\Lambda}_jf_2\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2}\big)(x),\\ u_3(x)&:=\mathcal{M}_{\widetilde{r}}\big( \big\Vert \big\{ \mathcal{M}_r{\Gamma}_jf_3\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^{\infty}}\big)(x) \end{align*} $$

and this proves (6.1). Moreover,

$$ \begin{align*} \Vert u_1\Vert_{L^{p_1}({{\mathbb R}^n})} \le \Big( \sum_{k=0}^{\infty}|\lambda _k|^{p_1}\Big\Vert \mathcal{M}_{q}\big( \big\Vert \big\{ \mathcal{M}_r{\Lambda}_ja_k\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2}\big) \Big\Vert_{L^{p_1}(Q_k^{***})}^{p_1} \Big)^{{1}/{p_1}}\lesssim 1, \end{align*} $$

where the last inequality follows from Equation (5.6) and the estimate

$$ \begin{align*} &\Big\Vert \mathcal{M}_{q}\big( \big\Vert \big\{ \mathcal{M}_r{\Lambda}_ja_k\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2}\big) \Big\Vert_{L^{p_1}(Q_k^{***})}\lesssim |Q_k|^{{1}/{p_1}-{1}/{r_0}}\Big\Vert \mathcal{M}_{q}\big( \big\Vert \big\{ \mathcal{M}_r{\Lambda}_ja_k\big\}_{j\in{\mathbb{Z}}}\big\Vert_{\ell^2}\big) \Big\Vert_{L^{r_0}({{\mathbb R}^n})}\\&\quad \qquad \qquad \qquad \qquad \lesssim |Q_k|^{{1}/{p_1}-{1}/{r_0}}\big\Vert \big\{ {\Lambda}_j a_k\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^{r_0}(\ell^2)}\sim |Q_k|^{{1}/{p_1}-{1}/{r_0}}\Vert a_k\Vert_{L^{r_0}({{\mathbb R}^n})}\lesssim 1 \end{align*} $$

for $q<r_0<\infty $ . Here, we applied Hölder’s inequality, the maximal inequality (2.4), the equivalence in (2.2) and properties of the $H^{p_1}$ -atom $a_k$ . It is also easy to verify

$$ \begin{align*}\Vert u_2\Vert_{L^{p_2}({{\mathbb R}^n})}\lesssim \big\Vert \big\{ {\Lambda}_jf_2\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^{p_2}(\ell^2)}\sim 1\end{align*} $$

and

$$ \begin{align*}\Vert u_3\Vert_{L^{p_3}({{\mathbb R}^n})}\lesssim \big\Vert \big\{ {\Gamma}_jf_3\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^{p_3}(\ell^{\infty})}\sim 1\end{align*} $$

using Equations (2.4), (2.1) and (2.2).

9.2 Proof of Lemma 7.1

Since

$$ \begin{align*}s>{n}/{p_1}+{n}/{2}=\big({n}/{p_1}-{n}/{2}\big)+{n}/{2}+{n}/{2},\end{align*} $$

we can choose $s_1,s_2,s_3$ such that $s_1>{n}/{p_1}-{n}/{2}$ , $s_2,s_3>{n}/{2}$ , and $s=s_1+s_2+s_3$ .

Using the estimates

$$ \begin{align*}\big\Vert \psi^P \big\Vert_{L^{\infty}({{\mathbb R}^n})}\le |P|^{-{1}/{2}}\quad \text{ and }\quad \big\Vert \theta^R \big\Vert_{L^{\infty}({{\mathbb R}^n})}\le |R|^{-{1}/{2}},\end{align*} $$

we have

(9.2) $$ \begin{align} \big|\mathcal{U}_1^{\mathrm{in}}(x,y)\big|&\lesssim\sum_{j\in{\mathbb{Z}}} \Big(\sum_{P\in\mathcal{D}_j}|b_P^2||P|^{-{1}/{2}}\chi_P(x) \Big)\Big(\sum_{R\in\mathcal{D}_j}|b_R^3| |R|^{-{1}/{2}}\chi_R(x) \Big) \nonumber \\&\quad \times \int_{({{\mathbb R}^n})^3} \big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\big| {\Lambda}_ja_k(z_1)\big|\chi_{Q_k^*}(z_1) \; d\vec{\boldsymbol{z}} \nonumber \\&\le g^2\big(\{b_P^2\}_{P\in\mathcal{D}} \big)(x) g^{\infty}\big( \{b_R^3\}_{R\in\mathcal{D}}\big)(x)\nonumber\\&\quad \times \bigg( \sum_{j\in{\mathbb{Z}}}\Big(\int_{({{\mathbb R}^n})^3} \big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\big| {\Lambda}_ja_k(z_1)\big| \chi_{Q_k^*}(z_1) \; d\vec{\boldsymbol{z}} \Big)^2 \bigg)^{{1}/{2}} . \end{align} $$

We observe that for $|x-y|\le 2^{-l}$ , $x\in (Q_k^{***})^c\cap (B_k^l)^c$ and $z_1\in Q_k^*$ ,

(9.3) $$ \begin{align} |x-{\mathbf{x}}_{Q_k}|\lesssim |y-z_1| \end{align} $$

and thus, by using Lemma 4.5,

$$ \begin{align*} &\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}\int_{({{\mathbb R}^n})^3} \big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\big| {\Lambda}_ja_k(z_1)\big| \chi_{Q_k^*}(z_1) \; d\vec{\boldsymbol{z}} \\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min \big\{1,\big(2^j\ell(Q_k)\big)^M \big\} \int_{({{\mathbb R}^n})^3} \langle 2^j(y-z_1)\rangle^{s_1}\big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\chi_{Q_k^*}(z_1) \; d\vec{\boldsymbol{z}} \\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min \big\{1,\big(2^j\ell(Q_k)\big)^M \big\} \big\Vert \langle 2^j\cdot \rangle^{-s_2}\big\Vert_{L^2({{\mathbb R}^n})}\big\Vert \langle 2^j\cdot \rangle^{-s_3}\big\Vert_{L^2({{\mathbb R}^n})} 2^{jn} I_{k,j,s}^{\mathrm{in}}(y) \\&\quad \sim \ell(Q_k)^{-{n}/{p_1}}\min \big\{1,\big(2^j\ell(Q_k)\big)^M \big\} I_{k,j,s}^{\mathrm{in}}(y) \end{align*} $$

for sufficiently large M, where

(9.4) $$ \begin{align} I_{k,j,s}^{\mathrm{in}}(y):= 2^{-jn}\int_{Q_k^*}\Big\Vert \langle 2^j(y-z_1),2^jz_2,2^jz_3\rangle^s\big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\Big\Vert_{L^2(z_2,z_3)} \; dz_1. \end{align} $$

This proves that

(9.5) $$ \begin{align} &\int_{({{\mathbb R}^n})^3} \big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\big| {\Lambda}_ja_k(z_1)\big| \chi_{Q_k^*}(z_1) \; d\vec{\boldsymbol{z}} \nonumber\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min \big\{1,\big(2^j\ell(Q_k)\big)^M \big\} \langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-s_1} I_{k,j,s}^{\mathrm{in}}(y), \end{align} $$

and therefore, we obtain

(9.6) $$ \begin{align} \big| \mathcal{U}_1^{\mathrm{in}}(x,y)\big|&\lesssim g^2\big(\{b_P^2\}_{P\in\mathcal{D}} \big)(x) g^{\infty}\big( \{b_R^3\}_{R\in\mathcal{D}}\big)(x) \ell(Q_k)^{-{n}/{p_1}} | x-{\mathbf{x}}_{Q_k}|^{-s_1}\\&\quad \times \bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j} \min \big\{1,\big(2^j\ell(Q_k)\big)^{M} \big\} I_{k,j,s}^{\mathrm{in}}(y)\Big)^2 \bigg)^{1/2}\nonumber. \end{align} $$

Similar to Equation (9.2), we write

$$ \begin{align*} \big|\mathcal{U}_1^{\mathrm{out}}(x,y)\big|&\lesssim g^2\big(\{b_P^2\}_{P\in\mathcal{D}} \big)(x) g^{\infty}\big( \{b_R^3\}_{R\in\mathcal{D}}\big)(x) \\&\quad \times \bigg( \sum_{j\in{\mathbb{Z}}}\Big(\int_{({{\mathbb R}^n})^3} \big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\big| {\Lambda}_ja_k(z_1)\big| \chi_{(Q_k^*)^c}(z_1) d\vec{\boldsymbol{z}} \Big)^2 \bigg)^{{1}/{2}}. \end{align*} $$

Instead of Equation (9.3), we make use of the estimate

(9.7) $$ \begin{align} \langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle \lesssim \langle 2^j(y-{\mathbf{x}}_{Q_k})\rangle\le \langle 2^j(y-z_1)\rangle \langle 2^j(z_1-{\mathbf{x}}_{Q_k})\rangle \end{align} $$

for $|x-y|\le 2^{-l}$ and $x\in (Q_k^{***})^c\cap (B_k^l)^c$ . Then, using the argument that led to Equation (9.5), we have

(9.8) $$ \begin{align} &\int_{({{\mathbb R}^n})^3} \big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\big| {\Lambda}_ja_k(z_1)\big| \chi_{(Q_k^*)^c}(z_1) \; d\vec{\boldsymbol{z}} \nonumber\\ &\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min\big\{ 1,\big( 2^j\ell(Q_k)\big)^M\big\} \langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-s_1}I_{k,j,s}^{\mathrm{out}}(y), \end{align} $$

where M, $L_0$ are sufficiently large numbers and

(9.9) $$ \begin{align} I_{k,j,s}^{\mathrm{out}}(y)&:=2^{-jn}\int_{(Q_k^*)^c} \frac{(2^j\ell(Q_k))^n}{\langle 2^j(z_1-{\mathbf{x}}_{Q_k})\rangle^{L_0-s_1}} \\ &\quad \times \Big\Vert \langle 2^j(y-z_1),2^jz_2,2^jz_3\rangle^s\big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big|\Big\Vert_{L^2(z_2,z_3)} \; dz_1.\nonumber \end{align} $$

Now, we deduce

(9.10) $$ \begin{align} \big| \mathcal{U}_1^{\mathrm{out}}(x,y)\big|&\lesssim g^2\big(\{b_P^2\}_{P\in\mathcal{D}} \big)(x) g^{\infty}\big( \{b_R^3\}_{R\in\mathcal{D}}\big)(x) \ell(Q_k)^{-{n}/{p_1}}| x-{\mathbf{x}}_{Q_k}|^{-s_1}\\ &\quad \times \bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j} \min \big\{1,\big(2^j\ell(Q_k)\big)^{M} \big\} I_{k,j,s}^{\mathrm{out}}(y)\Big)^2 \bigg)^{{1}/{2}}.\nonumber \end{align} $$

According to Equations (9.6) and (9.10), the estimate (7.7) follows from taking

$$ \begin{align*} u_1^{\mathrm{in}/\mathrm{out}}(x)&:=\sum_{k=0}^{\infty}|\lambda _k|\ell(Q_k)^{-{n}/{p_1}}\chi_{(Q_k^{***})^c}(x)| x-{\mathbf{x}}_{Q_k}|^{-s_1}\\ &\quad \times\mathcal{M}\bigg[\bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j}\min{\{1,(2^j\ell(Q_k))^M\}}I_{k,j,s}^{\mathrm{in}/\mathrm{out}}(\cdot) \Big)^2 \bigg)^{{1}/{2}}\bigg](x),\nonumber\\ u_2(x)&:=g^2\big(\{b_P^2\}_{P\in\mathcal{D}} \big)(x) ,\nonumber\\ u_3(x)&:=g^{\infty}\big( \{b_R^3\}_{R\in\mathcal{D}}\big)(x).\nonumber \end{align*} $$

It is clear that

(9.11) $$ \begin{align} \Vert u_2\Vert_{L^{p_2}({{\mathbb R}^n})}&=\big\Vert \{b_P^2\}_{P\in\mathcal{D}}\big\Vert_{\dot{f}^{p_2,2}}\sim 1 \end{align} $$

(9.12) $$ \begin{align} \Vert u_3\Vert_{L^{p_3}({{\mathbb R}^n})}&=\big\Vert \{b_R^3\}_{R\in\mathcal{D}}\big\Vert_{\dot{f}^{p_3,\infty}}\sim 1 \end{align} $$

in view of Equations (7.1) and (7.2). To estimate $u_1^{\mathrm {in}}$ and $u_1^{\mathrm {out}}$ , we note that

(9.13) $$ \begin{align} \big\Vert I_{k,j,s_1}^{\mathrm{in}}\big\Vert_{L^2({{\mathbb R}^n})}&\le 2^{-jn}\int_{Q_k}\bigg( \int_{{{\mathbb R}^n}}\Big\Vert \langle 2^jy,2^jz_2,2^jz_3\rangle^s \big| \sigma_j^{\vee}(y,z_2,z_3)\big|\Big\Vert_{L^2(z_2,z_3)}^2 \; dy\bigg)^{{1}/{2}} \; dz_1\nonumber\\0 &=2^{-jn}\ell(Q_k)^n\big\Vert \langle 2^j{\vec{\cdot}\;}\rangle^s\sigma_j^{\vee}\big\Vert_{L^2(({{\mathbb R}^n})^3)}\le 2^{{jn}/{2}}\ell(Q_k)^n, \end{align} $$

where we applied Minkowski’s inequality and a change of variables, and similarly,

(9.14) $$ \begin{align} \big\Vert I_{k,j,s}^{\mathrm{out}}\big\Vert_{L^2({{\mathbb R}^n})}&\lesssim 2^{-jn}\int_{(Q_k^*)^c} \frac{(2^j\ell(Q_k))^n}{\langle 2^j(z_1-{\mathbf{x}}_{Q_k})\rangle^{L_0-s_1}} \; dz_1 \big\Vert \langle 2^j{\vec{\cdot}\;}\rangle^s\sigma_j^{\vee} \big\Vert_{L^2(({{\mathbb R}^n})^3)}\nonumber\\ &\lesssim 2^{{jn}/{2}}\ell(Q_k)^n\big( 2^j\ell(Q_k)\big)^{-(L_0-s_1-n)} \end{align} $$

for $L_0>s+n$ . Now, we have

$$ \begin{align*} \big\Vert u_1^{\mathrm{in}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}^{p_1}&\le \sum_{k=0}^{\infty}|\lambda _k|^{p_1}\ell(Q_k)^{-n}\int_{(Q_k^{***})^c} | x-{\mathbf{x}}_{Q_k}|^{-s_1p_1}\\ &\quad \times \bigg( \mathcal{M}\bigg[\bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j}\min{\big\{1,\big(2^j\ell(Q_k)\big)^M\big\}}I_{k,j,s_1}^{\mathrm{in}}(\cdot) \Big)^2 \bigg)^{1/2}\bigg](x) \bigg)^{p_1}\, dx \end{align*} $$

and the integral is dominated by

$$ \begin{align*} &\big\Vert |\cdot-{\mathbf{x}}_{Q_k}|^{-{s_1p_1}}\big\Vert_{L^{({2}/{p_1})'}((Q_k^{***})^c)}\\ &\quad \times \bigg\Vert \bigg( \mathcal{M}\bigg[\bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j}\min{\big\{1,\big(2^j\ell(Q_k)\big)^M\big\}}I_{k,j,s_1}^{\mathrm{in}}(\cdot) \Big)^2 \bigg)^{1/2}\bigg] \bigg)^{p_1} \bigg\Vert_{L^{{2}/{p_1}}({{\mathbb R}^n})}. \end{align*} $$

The first term is no more than a constant times $\ell (Q_k)^{-p_1(s_1-({n}/{p_1}-{n}/{2}))}$ , and the second one is bounded by

$$ \begin{align*} &\bigg( \sum_{j\in{\mathbb{Z}}} \Big(2^{-s_1j}\min \big\{1,\big( 2^j\ell(Q_k)\big)^N \big\}\big\Vert I_{k,j,s_1}^{\mathrm{in}}\big\Vert_{L^2({{\mathbb R}^n})} \Big)^2\bigg)^{{p_1}/{2}}\\ &\quad \lesssim \ell(Q_k)^{p_1n}\bigg(\sum_{j\in{\mathbb{Z}}}\Big( 2^{-s_1j} \min \big\{1,\big( 2^j\ell(Q_k)\big)^M \big\} 2^{{jn}/{2}} \Big)^2 \bigg)^{{p_1}/{2}}\lesssim \ell(Q_k)^{s_1p_1+{p_1n}/{2}}, \end{align*} $$

due to Equation (9.13). This proves

(9.15) $$ \begin{align} \big\Vert u_1^{\mathrm{in}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim \Big( \sum_{k=0}^{\infty}|\lambda _k|^{p_1}\Big)^{{1}/{p_1}}\lesssim 1. \end{align} $$

In a similar way, together with Equation (9.14), we can also prove

(9.16) $$ \begin{align} \big\Vert u_1^{\mathrm{out}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim \Big( \sum_{k=0}^{\infty}|\lambda _k|^{p_1}\Big)^{{1}/{p_1}}\lesssim 1, \end{align} $$

choosing $M>L_0-{3n}/{2}$ .

9.3 Proof of Lemma 7.2

As in the proof of Lemma 7.1, we pick $s_1,s_2,s_3$ satisfying $s_1>{n}/{p_1}-{n}/{2}$ , $s_2,s_3>{n}/{2}$ , and $s=s_1+s_2+s_3>n/p_1+n/2$ .

We first consider the case $\eta =1$ . For $x\in P^c\cap (B_P^l)^c$ and $|x-y|\le 2^{-l}$ , we have

(9.17) $$ \begin{align} \langle 2^j(x-{\mathbf{x}}_{P})\rangle\lesssim \langle 2^j(y-{\mathbf{x}}_P)\rangle \le \langle 2^j(y-z_2)\rangle \langle 2^j(z_2-{\mathbf{x}}_P)\rangle. \end{align} $$

By using

$$ \begin{align*}\big\Vert \theta^R\big\Vert_{L^{\infty}({{\mathbb R}^n})}\le |R|^{-{1}/{2}},\end{align*} $$

we have

(9.18) $$ \begin{align} \big| \mathcal{U}_2^{1,\mathrm{in}}(x,y)\big| &\lesssim \sum_{j\in{\mathbb{Z}}}\Big( \sum_{R\in\mathcal{D}_j}|b_R^3||R|^{-{1}/{2}}\chi_R(x)\Big)\int_{({{\mathbb R}^n})^3} \big|\sigma_j^{\vee}(y-z_1,y-z_2,z_3) \big|\\&\quad \times \big| {\Lambda}_ja_k(z_1)\big|\chi_{Q_k^*}(z_1)\Big(\sum_{P\in\mathcal{D}_j} |b_P^2|\chi_{P^c}(x)\chi_{(B_P^l)^c}(x)\big| \psi^P(z_2)\big| \Big) \; d\vec{\boldsymbol{z}}.\nonumber \end{align} $$

Using Equations (9.3) and (9.17) and Lemma 4.5, the integral in the preceding expression is bounded by

$$ \begin{align*} & \ell(Q_k)^{-{n}/{p_1}}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}\langle2^j(x-c_{Q_k})\rangle^{-s_1}\int_{({{\mathbb R}^n})^3} \langle 2^j(y-z_1)\rangle^{s_1}\langle 2^j(y-z_2)\rangle^{s_2} \\& \qquad \times \big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3)\big|\chi_{Q_k^*}(z_1)\bigg(\sum_{P\in\mathcal{D}_j}|b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\big| \widetilde{\psi^P}(z_2)\big| \bigg) \; d\vec{\boldsymbol{z}}\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\} \langle2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-s_1}I_{k,j,s}^{\mathrm{in}}(y) \\&\qquad \times 2^{{jn}/{2}}\bigg\Vert \sum_{P\in\mathcal{D}_j}|b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\big| \widetilde{\psi^P}(\cdot)\big|\bigg\Vert_{L^2({{\mathbb R}^n})} \end{align*} $$

for sufficiently large $M>0$ , where $\widetilde {\psi ^P}(z_2):=\langle 2^j(z_2-{\mathbf {x}}_P)\rangle ^{s_2}\psi ^P(z_2)$ for $P\in \mathcal {D}_j$ and $I_{k,j,s}^{\mathrm {in}}$ is defined as in Equation (9.4). Note that

(9.19) $$ \begin{align} |b_P^2|\lesssim \mathscr{B}_P^2(f_2):=\Big\langle \big| \widetilde{{\Lambda}_j}f_2\big|,\frac{2^{{jn}/{2}}}{\langle 2^j(\cdot-{\mathbf{x}}_P)\rangle^L}\Big\rangle \quad \text{ for }~L>n,s, \end{align} $$

and thus it follows from Lemma 4.2 that the $L^2$ norm in the last displayed expression is dominated by

$$ \begin{align*}2^{-{jn}/{2}}\bigg( \sum_{P\in\mathcal{D}_j} \Big( | \mathscr{B}_P^2(f_2)| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2\bigg)^{{1}/{2}}.\end{align*} $$

This yields that

(9.20) $$ \begin{align} \big| \mathcal{U}_2^{1,\mathrm{in}}(x,y) \big|&\lesssim \ell(Q_k)^{-{n}/{p_1}}|x-c_{Q_k}|^{-s_1}\Big( \sum_{j\in{\mathbb{Z}}} \big(2^{-js_1}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}I_{k,j,s}^{\mathrm{in}}(y) \big)^2\Big)^{{1}/{2}} \nonumber\\&\quad \times \bigg( \sum_{P\in\mathcal{D}} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}}g^{\infty}\big(\{b_R^3\}_{R\in\mathcal{D}}\big)(x). \end{align} $$

Similarly, using Equations (9.7) and (9.17), Lemma 4.5 and Lemma 4.2, we have

(9.21) $$ \begin{align} \big| \mathcal{U}_2^{1,\mathrm{out}}(x,y) \big|&\lesssim \sum_{j\in{\mathbb{Z}}}\Big(\sum_{R\in\mathcal{D}_j} |b_R^3| |R|^{-{1}/{2}}\chi_R(x) \Big) \int_{({{\mathbb R}^n})^3} \big|\sigma_j^{\vee}(y-z_1,y-z_2,z_3) \big|\nonumber\\&\qquad \times \big| {\Lambda}_ja_k(z_1)\big|\chi_{(Q_k^*)^c}(z_1)\Big(\sum_{P\in\mathcal{D}_j} |b_P^2|\chi_{P^c}(x)\chi_{(B_P^l)^c}(x)\big| \psi^P(z_2)\big| \Big) \; d\vec{\boldsymbol{z}} \nonumber\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}|x-{\mathbf{x}}_{Q_k}|^{-s_1}\Big( \sum_{j\in{\mathbb{Z}}} \big(2^{-js_1}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}I_{k,j,s}^{\mathrm{out}}(y) \big)^2\Big)^{{1}/{2}} \nonumber\\&\qquad \times \bigg( \sum_{P\in\mathcal{D}} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}}g^{\infty}\big(\{b_R^3\}_{R\in\mathcal{D}}\big)(x), \end{align} $$

where $I_{k,j,s}^{\mathrm {out}}$ is defined as in Equation (9.9).

When $\eta =2$ , we use the inequality

(9.22) $$ \begin{align} \langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-1}\le \langle 2^j (x-{\mathbf{x}}_{P})\rangle^{-1} \end{align} $$

for $x\in (B_k^l)^c \cap B_{P}^l$ . Then, similar to Equation (9.18), we have

$$ \begin{align*} \big| \mathcal{U}_2^{2,\mathrm{in}}(x,y) \big|&\lesssim \sum_{j\in{\mathbb{Z}}}\Big( \sum_{R\in\mathcal{D}_j}|b_R^3||R|^{-{1}/{2}}\chi_R(x)\Big)\int_{({{\mathbb R}^n})^3} \big|\sigma_j^{\vee}(y-z_1,y-z_2,z_3) \big|\\[3pt]&\quad \times \big| {\Lambda}_ja_k(z_1)\big|\chi_{Q_k^*}(z_1)\Big(\sum_{P\in\mathcal{D}_j} |b_P^2|\chi_{P^c}(x)\chi_{B_P^l}(x)\big| \psi^P(z_2)\big| \Big) \; d\vec{\boldsymbol{z}}\nonumber, \end{align*} $$

and the integral is dominated by a constant times

$$ \begin{align*} &\ell(Q_k)^{-{n}/{p_1}}\min \{1,\big( 2^j\ell(Q_k)\big)^M\}\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-(s_1+s_2)}\int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_1)\rangle^{s_1+s_2}\\[3pt]&\qquad \times \big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3)\big|\chi_{Q_k^*}(z_1)\Big( \sum_{P\in\mathcal{D}_j}|b_P^2|\chi_{P^c}(x)\chi_{B_P^l}(x)\big| {\psi^P}(z_2)\big|\Big)\;d\vec{\boldsymbol{z}}\\[3pt]&\quad \le \ell(Q_k)^{-{n}/{p_1}}\min \{1,\big( 2^j\ell(Q_k)\big)^M\}\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-s_1}\int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_1)\rangle^{s_1+s_2}\\[3pt]&\qquad\times \big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3)\big|\chi_{Q_k^*}(z_1)\Big( \sum_{P\in\mathcal{D}_j}|b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\big| {\psi^P}(z_2)\big|\Big)\;d\vec{\boldsymbol{z}}\\[3pt]&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\} \langle2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-s_1}I_{k,j,s}^{\mathrm{in}}(y)\\[3pt]&\qquad \times \bigg( \sum_{P\in\mathcal{D}} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}} \end{align*} $$

due to Equations (9.3) and (9.22), Lemma 4.5 and Lemma 4.2, where $I_{k,j,s}^{\mathrm {in}}$ and $\mathscr {B}_P^2(f_2)$ are defined as in Equations (9.4) and (9.19). Therefore,

(9.23) $$ \begin{align} \big| \mathcal{U}_2^{2,\mathrm{in}}(x,y)\big|&\lesssim \ell(Q_k)^{-{n}/{p_1}}|x-{\mathbf{x}}_{Q_k}|^{-s_1}\Big( \sum_{j\in{\mathbb{Z}}} \big(2^{-js_1}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}I_{k,j,s}^{\mathrm{in}}(y) \big)^2\Big)^{{1}/{2}}\nonumber\\&\quad \times \bigg( \sum_{P\in\mathcal{D}} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}} g^{\infty}\big(\{b_R^3\}_{R\in\mathcal{D}}\big)(x). \end{align} $$

Similarly, we can also prove that

(9.24) $$ \begin{align} \big| \mathcal{U}_2^{2,\mathrm{out}}(x,y)\big|&\lesssim \ell(Q_k)^{-{n}/{p_1}}|x-{\mathbf{x}}_{Q_k}|^{-s_1}\Big( \sum_{j\in{\mathbb{Z}}} \big(2^{-js_1}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}I_{k,j,s}^{\mathrm{out}}(y) \big)^2\Big)^{{1}/{2}}\nonumber\\&\quad \times \bigg( \sum_{P\in\mathcal{D}} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}} g^{\infty}\big(\{b_R^3\}_{R\in\mathcal{D}}\big)(x). \end{align} $$

Combining Equations (9.20), (9.21), (9.23) and (9.24), the estimate (7.9) holds with

$$ \begin{align*} u_1^{\mathrm{in}/\mathrm{out}}(x)&:=\sum_{k=0}^{\infty}|\lambda _k|\ell(Q_k)^{-{n}/{p_1}}\chi_{(Q_k^{***})^c}(x)| x-{\mathbf{x}}_{Q_k}|^{-s_1}\\&\quad \times\mathcal{M}\bigg[\bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j}\min{\{1,(2^j\ell(Q_k))^M\}}I_{k,j,s}^{\mathrm{in}/\mathrm{out}}(\cdot) \Big)^2 \bigg)^{{1}/{2}}\bigg](x),\\u_2(x)&:= \bigg(\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}},\\u_3(x)&:=g^{\infty}\big( \{b_R^3\}_{R\in\mathcal{D}}\big)(x). \end{align*} $$

Clearly, as in Equations (9.15), (9.16) and (9.12),

$$ \begin{align*} \big\Vert u_1^{\mathrm{in}/\mathrm{out}}\big\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim 1, \qquad \Vert u_3\Vert_{L^{p_3}({{\mathbb R}^n})}\lesssim 1 \end{align*} $$

and Lemma 4.3 proves that

$$ \begin{align*} \Vert u_2\Vert_{L^{p_2}({{\mathbb R}^n})}\lesssim 1. \end{align*} $$

9.4 Proof of Lemma 7.3

The proof is almost same as that of Lemma 7.2. By letting $M>0$ be sufficiently large and exchanging the role of terms associated with $f_2$ and $f_3$ in the estimate (9.18), we may obtain

(9.25) $$ \begin{align} \big| \mathcal{U}_3^{1,\mathrm{in}}(x,y)\big|&\lesssim \sum_{j\in{\mathbb{Z}}}\Big( \sum_{P\in\mathcal{D}_j}|b_P^2||P|^{-{1}/{2}}\chi_P(x)\Big)\int_{({{\mathbb R}^n})^3} \big|\sigma_j^{\vee}(y-z_1,z_2,y-z_3) \big|\nonumber\\&\qquad \times \big| {\Lambda}_ja_k(z_1)\big|\chi_{Q_k^*}(z_1)\Big(\sum_{R\in\mathcal{D}_j} |b_R^3|\chi_{R^c}(x)\chi_{(B_R^l)^c}(x)\big| \theta^R(z_3)\big| \Big) \; d\vec{\boldsymbol{z}}\nonumber\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}|x-{\mathbf{x}}_{Q_k}|^{-s_1}\bigg( \sum_{j\in{\mathbb{Z}}} \Big( 2^{-js_1}\min{\big\{ 1,\big( 2^j\ell(Q_k)\big)^M\big\}} I_{k,j,s}^{\mathrm{in}}(y)\Big)^2 \bigg)^{{1}/{2}}\nonumber\\&\qquad \times g^2\big(\{b_P^2 \}_{P\in\mathcal{D}} \big)(x)\sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j} \Big(\big| \mathscr{B}_R^3(f_3) \big| |R|^{-{1}/{2}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle ^{s_3}} \Big)^2 \bigg)^{{1}/{2}}, \end{align} $$

where $I_{k,j,s}^{\mathrm {in}}$ is defined as in Equation (9.4), $\widetilde {\theta ^R}(z_3):=\langle 2^j(z_3-{\mathbf {x}}_R)\rangle ^{s_3}\theta ^R(z_3)$ for $R\in \mathcal {D}_j$ and

(9.26) $$ \begin{align} \mathscr{B}_R^3(f_3):=\Big\langle \big| \widetilde{{\Gamma}_j}f_3\big|,\frac{2^{{jn}/{2}}}{\langle 2^j(\cdot-{\mathbf{x}}_R)\rangle^L}\Big\rangle \quad \text{ for }~L>s,n. \end{align} $$

Similarly,

(9.27) $$ \begin{align} \big| \mathcal{U}_3^{1,\mathrm{out}}(x,y) \big|&\lesssim \ell(Q_k)^{-{n}/{p_1}} |x-{\mathbf{x}}_{Q_k}|^{-s_1} \bigg( \sum_{j\in{\mathbb{Z}}} \Big(2^{-js_1} \min{\big\{ 1,\big( 2^j\ell(Q_k)\big)^M\big\}} I_{k,j,s}^{\mathrm{out}}(y)\Big)^2 \bigg)^{{1}/{2}}\nonumber\\&\quad \times g^2\big(\{b_P^2 \}_{P\in\mathcal{D}} \big)(x)\sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j} \Big(\big| \mathscr{B}_R^3(f_3) \big| |R|^{-{1}/{2}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle ^{s_3}} \Big)^2 \bigg)^{{1}/{2}}, \end{align} $$

where $I_{k,j,s}^{\mathrm {out}}$ is defined as in Equation (9.9).

For the case $\eta =2$ , we use the fact that for $x\in (B_k^l)^c\cap B_R^l$ ,

$$ \begin{align*}\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{-1}\le \langle 2^j(x-{\mathbf{x}}_R)\rangle^{-1},\end{align*} $$

instead of Equation (9.22). Then we have

$$ \begin{align*} \big| \mathcal{U}_3^{2,\mathrm{in}}(x,y)\big| &\lesssim \ell(Q_k)^{-{n}/{p_1}}|x-{\mathbf{x}}_{Q_k}|^{-s_1}\Big( \sum_{j\in{\mathbb{Z}}} \big(2^{-js_1}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}I_{k,j,s}^{\mathrm{in}}(y) \big)^2\Big)^{{1}/{2}}\\&\quad \times g^{2}\big(\{b_P^2\}_{P\in\mathcal{D}}\big)(x) \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j} \Big(\big| \mathscr{B}_R^3(f_3) \big| |R|^{-{1}/{2}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle ^{s_3}} \Big)^2 \bigg)^{{1}/{2}} \end{align*} $$

and

$$ \begin{align*} \big| \mathcal{U}_3^{2,\mathrm{out}}(x,y) \big|&\lesssim \ell(Q_k)^{-{n}/{p_1}}\bigg( \sum_{j\in{\mathbb{Z}}} \Big( \min{\big\{ 1,\big( 2^j\ell(Q_k)\big)^M\big\}} \langle 2^j(x-{\mathbf{x}}_Q)\rangle^{-s_1}I_{k,j,s}^{\mathrm{out}}(y)\Big)^2 \bigg)^{{1}/{2}}\\&\quad \times g^2\big(\{b_P^2 \}_{P\in\mathcal{D}} \big)\sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j} \Big(\big| \mathscr{B}_R^3(f_3) \big| |R|^{-{1}/{2}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle ^{s_3}} \Big)^2 \bigg)^{{1}/{2}} \end{align*} $$

which are analogous to Equations (9.25) and (9.27).

Then Lemma 7.3 follows from Equations (9.15), (9.16) and (9.11) and Lemma 4.4 by choosing

$$ \begin{align*} u_1^{\mathrm{in}/\mathrm{out}}(x)&:= \sum_{k=0}^{\infty}|\lambda _k|\ell(Q_k)^{-{n}/{p_1}}\chi_{(Q_k^{***})^c}(x)| x-{\mathbf{x}}_{Q_k}|^{-s_1}\\&\quad \times\mathcal{M}\bigg[\bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j}\min{\{1,(2^j\ell(Q_k))^M\}}I_{k,j,s}^{\mathrm{in}/\mathrm{out}}(\cdot) \Big)^2 \bigg)^{{1}/{2}}\bigg](x) \\u_2(x)&:= g^2\big(\{b_P^2 \}_{P\in\mathcal{D}} \big)(x) \\u_3(x)&:= \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j} \Big(\big| \mathscr{B}_R^3(f_3) \big| |R|^{-{1}/{2}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle ^{s_3}} \Big)^2 \bigg)^{{1}/{2}}. \end{align*} $$

9.5 Proof of Lemma 7.4

Let $I_{k,j,s}^{\mathrm {in}}$ , $I_{k,j,s}^{\mathrm {out}}$ , $\mathscr {B}_P^2(f_2)$ and $\mathscr {B}_R^3(f_3)$ be defined as before. Let $M>0$ be a sufficiently large number. We claim the pointwise estimates that for each $\eta =1,2,3,4$ ,

$$ \begin{align*} \big| \mathcal{U}_4^{\eta,\mathrm{in}/\mathrm{out}}(x,y)\big|&\lesssim \ell(Q_k)^{-{n}/{p_1}}|x-x_{Q_k}|^{-s_1}\bigg( \sum_{j\in{\mathbb{Z}}}\Big( 2^{-js_1}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\}I_{k,j,s}^{\mathrm{in}/\mathrm{out}}(y) \Big)^2\bigg)^{{1}/{2}}\\&\quad \times \bigg( \sum_{P\in\mathcal{D}} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P_c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}} \Big)^2\bigg)^{{1}/{2}} \\&\quad \times \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{P\in\mathcal{D}_j}\Big( \big| \mathscr{B}_R^3(f_3)\big| |R|^{-{1}/{2}} \frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}} \Big)^2\bigg)^{{1}/{2}}. \end{align*} $$

The proof of the above claim is a repetition of the arguments used in the proof of Lemmas 7.2 and 7.3, so we omit the details. We now take

$$ \begin{align*} u_1^{\mathrm{in}/\mathrm{out}}(x)&:= \sum_{k=0}^{\infty}|\lambda _k|\ell(Q_k)^{-{n}/{p_1}}\chi_{(Q_k^{***})^c}(x)| x-{\mathbf{x}}_{Q_k}|^{-s_1}\\&\quad \times\mathcal{M}\bigg[\bigg(\sum_{j\in{\mathbb{Z}}}\Big(2^{-s_1j}\min{\{1,(2^j\ell(Q_k))^M\}}I_{k,j,s}^{\mathrm{in}/\mathrm{out}}(\cdot) \Big)^2 \bigg)^{{1}/{2}}\bigg](x) \\u_2(x)&:= \bigg(\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j} \Big( \big| \mathscr{B}_P^2(f_2)\big| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}} \\u_3(x)&:= \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j} \Big(\big| \mathscr{B}_R^3(f_3) \big| |R|^{-{1}/{2}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_R)\rangle ^{s_3}} \Big)^2 \bigg)^{{1}/{2}}. \end{align*} $$

Then it is obvious that Equations (7.13) and (7.14) hold.

9.6 Proof of Lemma 7.5

We choose $0<\epsilon <1$ such that

(9.28) $$ \begin{align} N_{p_1}:=\big[{n}/{p_1}-n\big]\le {n}/{p_1}-n<\big[ {n}/{p_1}-n\big]+\epsilon<s-{3n}/{2}. \end{align} $$

We note that

$$ \begin{align*} 2^l\lesssim |x-{\mathbf{x}}_{Q_k}|^{-1} \quad \text{ for }~ x\in B_k^l. \end{align*} $$

By using Lemma 4.1 with the vanishing moment condition (5.3), we have

$$ \begin{align*} \big| \phi_l\ast \big( \mathcal{U}_{1}(x,\cdot)\big)(x)\big| & \lesssim \sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j}|b_P^2| |b_R^3|\chi_{P\cap R}(x) 2^{l(n+N_{p_1}+\epsilon)}\nonumber\\&\qquad\times \int_{{{\mathbb R}^n}}|y-{\mathbf{x}}_{Q_k}|^{N_{p_1}+\epsilon}\big|T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R\big)(y) \big| \; dy\nonumber\\&\quad \lesssim \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{n+N_{p_1}+\epsilon}}\sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j}|b_P^2| |b_R^3|\chi_{P\cap R}(x)\\&\qquad \times \Big(\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{in}}(Q_k,P,R)+\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{out}}(Q_k,P,R) \Big)\nonumber, \end{align*} $$

where

$$ \begin{align*}\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{in}}(Q_k,P,R):=\int_{Q_k^{**}} |y-{\mathbf{x}}_{Q_k}|^{N_{p_1}+\epsilon}\big| T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(y)\big| \; dy,\end{align*} $$

and

$$ \begin{align*}\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{out}}(Q_k,P,R):=\int_{(Q_k^{**})^c} |y-{\mathbf{x}}_{Q_k}|^{N_{p_1}+\epsilon}\big| T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(y)\big| \; dy.\end{align*} $$

Now, the left-hand side of Equation (7.16) is dominated by $\mathscr {J}^{in}(x)+\mathscr {J}^{out}(x)$

$$ \begin{align*} \mathscr{J}^{\mathrm{in}/\mathrm{out}}(x)&:=\sum_{k=0}^{\infty}|\lambda _k|\chi_{(Q_{k}^{***})^c}(x)\frac{1}{|x-{\mathbf{x}}_{Q_k}|^{n+N_{p_1}+\epsilon}}\\&\quad \times \sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j}|b_P^2| |b_R^3| \chi_{P\cap R}(x)\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{in}/ \mathrm{out}}(Q_k,P,R). \end{align*} $$

To estimate $\mathscr {J}^{\mathrm {in}}$ , we first see that

$$ \begin{align*} &\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{in}}(Q_k,P,R)\\&\quad \lesssim \ell(Q_k)^{N_{p_1}+\epsilon}|P|^{-{1}/{2}}|R|^{-{1}/{2}}\int_{y\in Q_k^{**}}\int_{({{\mathbb R}^n})^3}\big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big| \big|{\Lambda}_ja_k(z_1) \big| \; d\vec{\boldsymbol{z}} dy\\&\quad \lesssim \ell(Q_k)^{N_{p_1}+\epsilon}|P|^{-{1}/{2}}|R|^{-{1}/{2}}\Vert {\Lambda}_ja_k\Vert_{L^{1}({{\mathbb R}^n})}, \end{align*} $$

using the Cauchy–Schwarz inequality with $s>{3n}/{2}$ , and thus

(9.29) $$ \begin{align} &\sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} |b_P^2| |b_R^3| \chi_{P\cap R}(x)\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{in}}(Q_k,P,R)\nonumber\\&\quad \lesssim \ell(Q_k)^{N_{p_1}+\epsilon}\big\Vert \big\{ {\Lambda}_ja_k\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^1(\ell^2)}g^2\big(\big\{ b_P^2\big\}_{P\in\mathcal{D}} \big)(x)g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x)\nonumber\\&\quad \lesssim |Q_k|^{-1/p_1} \ell(Q_k)^{n+N_{p_1}+\epsilon}g^2\big(\big\{ b_P^2\big\}_{P\in\mathcal{D}} \big)(x)g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x) \end{align} $$

by using the fact that

$$ \begin{align*} \big\Vert \big\{ {\Lambda}_ja_k\big\}_{j\in{\mathbb{Z}}}\big\Vert_{L^1(\ell^2)}\sim \Vert a_k\Vert_{H^1({{\mathbb R}^n})}\lesssim \ell(Q_k)^{-{n}/{p_1}+n}. \end{align*} $$

For the other term $\mathscr {J}^{out}$ , we choose $s_1$ such that

(9.30) $$ \begin{align} N_{p_1}+{n}/{2}+\epsilon<s_1<s-n, \end{align} $$

which is possible due to Equation (9.28), and $s_2,s_3>{n}/{2}$ such that

(9.31) $$ \begin{align} s_1+n<s_1+s_2+s_3=s. \end{align} $$

We observe that, for $y\in (Q_k^{**})^c$ ,

$$ \begin{align*} &\langle 2^j(y-{\mathbf{x}}_{Q_k})\rangle^{s_1}\big| {\Lambda}_ja_k(z_1)\big|\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min{\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\}}\langle 2^j(y-{\mathbf{x}}_{Q_k})\rangle^{s_1} \\&\qquad \times \Big(\chi_{Q_k^*}(z_1)+\chi_{(Q_k^*)^c}(z_1)\frac{(2^j\ell(Q_k))^n}{\langle 2^j(z_1-{\mathbf{x}}_{Q_k})\rangle^{L_0}} \Big)\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min{\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\}} \langle 2^j(y-z_1)\rangle^{s_1}\\&\qquad \times \Big(\chi_{Q_k^*}(z_1)+\chi_{(Q_k^*)^c}(z_1)\frac{(2^j\ell(Q_k))^n}{\langle 2^j(z_1-{\mathbf{x}}_{Q_k})\rangle^{L_0-s_1}} \Big), \end{align*} $$

where Lemma 4.5 is applied in the first inequality. Here, M and $L_0$ are sufficiently large numbers such that $L_0-s_1>n$ and $M-L_0+3n/2>0$ . By letting

(9.32) $$ \begin{align} A_{j,Q_k}(z_1):=\chi_{Q_k^*}(z_1)+\chi_{(Q_k^*)^c}(z_1)\frac{(2^j\ell(Q_k))^n}{\langle 2^j(z_1-{\mathbf{x}}_{Q_k})\rangle^{L_0-s_1}}, \end{align} $$

we have

(9.33) $$ \begin{align} &\big| T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(y)\big|\chi_{(Q_k^{**})^c}(y)\nonumber\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}}\min \big\{ 1,\big( 2^j\ell(Q_k)\big)^M\big\}\frac{1}{\langle 2^j(y-{\mathbf{x}}_{Q_k})\rangle^{s_1}}|P|^{-{1}/{2}} |R|^{-{1}/{2}}\\&\qquad \times \int_{({{\mathbb R}^n})^3} \langle 2^j(y-z_1)\rangle^{s_1}\big| \sigma_j^{\vee}(y-z_1,z_2,z_3)\big| A_{j,Q_k}(z_1)\; d\vec{\boldsymbol{z}} \nonumber \end{align} $$

and the integral is, via the Cauchy-Schwarz inequality, less than

$$ \begin{align*}2^{-jn}\int_{{{\mathbb R}^n}} |A_{j,Q_k}(z_1)| \big\Vert \langle 2^j(y-z_1,z_2,z_3)\rangle^{s}\sigma_j^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2,z_3)} \; dz_1. \end{align*} $$

This deduces that

$$ \begin{align*} &\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{out}}(Q_k,P,R)\\&\quad \lesssim \ell(Q_k)^{-n/{p_1}}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\} |P|^{-{1}/{2}}|R|^{-{1}/{2}}2^{-js_1}2^{-jn} \int_{{{\mathbb R}^n}} \big|A_{j,Q_k}(z_1)\big|\\&\qquad \times \Big(\int_{(Q_k^{**})^c} \frac{1}{|y-{\mathbf{x}}_{Q_k}|^{s_1-(N_{p_1}+\epsilon)}} \big\Vert \langle 2^j(y-z_1,z_2,z_3)\rangle^{s}\sigma_j^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2,z_3)} \, dy\Big) \; dz_1\\&\quad\lesssim \ell(Q_k)^{-n/{p_1}}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\} |P|^{-{1}/{2}}|R|^{-{1}/{2}}2^{-js_1}2^{-jn} \Vert A_{j,Q_k}\Vert_{L^1({{\mathbb R}^n})}\\&\qquad \times \bigg\Vert \frac{1}{|\cdot-{\mathbf{x}}_{Q_k}|^{s_1-(N_{p_1}+\epsilon)}}\bigg\Vert_{L^2((Q_k^{**})^c)}\big\Vert \langle 2^j{\vec{\cdot}\;}\rangle^s\sigma_j^{\vee}\big\Vert_{L^2(({{\mathbb R}^n})^3)}\\&\quad \lesssim \ell(Q_k)^{-n/p_1+n+N_{p_1}+\epsilon} \big( 2^j\ell(Q_k)\big)^{-(s_1-{n}/{2})} \min\big\{1,\big( 2^j\ell(Q_k)\big)^{M-L_0+s_1+n} \big\} |P|^{-{1}/{2}}|R|^{-{1}/{2}} \end{align*} $$

since

$$ \begin{align*}\Vert A_{j,Q_k}\Vert_{L^1({{\mathbb R}^n})}\lesssim \ell(Q_k)^n\Big(1+(2^j\ell(Q_k))^{-(L_0-s_1-n)} \Big) \quad \text{ for }~ L_0-s_1>n.\end{align*} $$

Therefore, by using the Cauchy–Schwarz inequality

(9.34) $$ \begin{align} &\sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j} |b_P^2| |b_R^3| \chi_{P\cap R}(x)\mathscr{K}_{N_{p_1}+\epsilon}^{j,\mathrm{out}}(Q_k,P,R)\nonumber\\&\quad \lesssim |Q_k|^{-{1}/{p_1}}\ell(Q_k)^{n+N_{p_1}+\epsilon}g^2\big(\big\{ b_P^2\big\}_{P\in\mathcal{D}} \big)(x)g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x)\nonumber\\&\qquad \times \bigg( \sum_{j\in{\mathbb{Z}}}\Big(\big( 2^j\ell(Q_k)\big)^{-(s_1-{n}/{2})} \min\big\{1,\big( 2^j\ell(Q_k)\big)^{M-L_0+s_1+n} \big\} \Big)^2\bigg)^{{1}/{2}} \nonumber\\&\quad\lesssim |Q_k|^{-{1}/{p_1}}\ell(Q_k)^{n+N_{p_1}+\epsilon}g^2\big(\big\{ b_P^2\big\}_{P\in\mathcal{D}} \big)(x)g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x), \end{align} $$

where the last inequality holds due to $s_1>{n}/{2}$ and $M-L_0+{3n}/{2}>0$ .

In conclusion, the estimate (7.16) can be derived from Equations (9.29) and (9.34), using the choices of

$$ \begin{align*} u_1(x)&:= \sum_{k=0}^{\infty}|\lambda _k| |Q_k|^{-{1}/{p_1}} \chi_{(Q^{**})^c} \frac{\ell(Q_k)^{n+N_{p_1}+\epsilon}}{|x-{\mathbf{x}}_{Q_k}|^{n+N_{p_1}+\epsilon}} , \\ u_2(x)&:= g^2\big(\big\{ b_P^2\big\}_{P\in\mathcal{D}} \big)(x), \\ u_3(x)&:= g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x). \end{align*} $$

It is obvious from Equations (7.1) and (7.2) that $\Vert u_2\Vert _{L^{p_2}({{\mathbb R}^n})}, \Vert u_3\Vert _{L^{p_3}({{\mathbb R}^n})}\lesssim 1$ . Furthermore,

(9.35) $$ \begin{align} \Vert u_1\Vert_{L^{p_1}({{\mathbb R}^n})}&\lesssim \bigg(\sum_{k=0}^{\infty}|\lambda _k|^{p_1}|Q_k|^{-1}\int_{(Q_k^{***})^c}\frac{\ell(Q_k)^{(n+N_{p_1}+\epsilon)p_1}}{|x-{\mathbf{x}}_{Q_k}|^{(n+N_{p_1}+\epsilon)p_1}} dx \bigg)^{{1}/{p_1}}\nonumber\\ &\lesssim \Big( \sum_{k=0}^{\infty}|\lambda _k|^{p_1}\Big)^{{1}/{p_1}}\lesssim 1. \end{align} $$

This completes the proof.

9.7 Proof of Lemma 7.6

Choose $s_1$ , $s_2$ , and $s_3$ such that $s_1>{n}/{p_1}-{n}/{2}$ , $s_2>{n}/{2}$ , $s_3>{n}/{2}$ and $s=s_1+s_2+s_3$ . For $x\in B_k^l\cap (B_P^l)^c$ and $|x-y|\le 2^{-l}$ , we have

(9.36) $$ \begin{align} |x-{\mathbf{x}}_{Q_k}|\le |x-{\mathbf{x}}_{P}|\lesssim |y-{\mathbf{x}}_P|. \end{align} $$

This implies

$$ \begin{align*} &\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}\big| \phi_l\ast T_{\sigma_j}\big({\Lambda}_ja_k,\psi^P,\theta^R \big)(x)\big|\\&\quad\lesssim |R|^{-{1}/{2}} 2^{ln}\int_{|x-y|\le 2^{-l}} \int_{({{\mathbb R}^n})^3}\langle 2^j(y-{\mathbf{x}}_P)\rangle^{s_1+s_2}\\&\qquad \times\big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3)\big| \big| {\Lambda}_ja_k(z_1)\big| \big| {\psi^P}(z_2)\big|\;d\vec{\boldsymbol{z}}\; dy\\&\quad \le |R|^{-{1}/{2}} 2^{ln}\int_{|x-y|\le 2^{-l}}\int_{({{\mathbb R}^n})^3} \langle 2^j(y-z_2)\rangle^{s_1+s_2} \\&\qquad\times \big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3)\big| \big| {\Lambda}_ja_k(z_1)\big| \big|\widetilde{\psi^P}(z_2) \big|\;d\vec{\boldsymbol{z}}\; dy, \end{align*} $$

where

$$ \begin{align*}\widetilde{\psi^P}(z_2) :=\langle 2^j(z_2-{\mathbf{x}}_P)\rangle^{s_1+s_2}\psi^P(z_2).\end{align*} $$

By using the Cauchy–Schwarz inequality and Lemma 4.2, we obtain

(9.37) $$ \begin{align} &\big| \phi_l\ast \big( \mathcal{U}_2^1(x,\cdot)\big)(x)\big| \nonumber\\[3pt]&\quad \lesssim \sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j}\sum_{R\in\mathcal{D}_j}|b_P^2| |b_R^3|\chi_{P^c}(x)\chi_R(x)\frac{1}{\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}} \frac{1}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}} |R|^{-{1}/{2}}\nonumber\\[3pt]&\qquad \times 2^{ln}\int_{|x-y|\le 2^{-l}} \int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_2)\rangle^{s_1+s_2}\big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3) \big| \big| {\Lambda}_ja_k(z_1)\big| \; d\vec{\boldsymbol{z}} dy\nonumber\\[3pt]&\quad \lesssim g^{\infty}\big( \big\{ b_R^3\big\}_{R\in\mathcal{D}}\big)(x) \sum_{j\in{\mathbb{Z}}}\frac{1}{\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}} 2^{ln}\int_{|x-y|\le 2^{-l}} \int_{({{\mathbb R}^n})^3} \langle 2^j(y-z_2)\rangle^{s_1+s_2} \nonumber\\[3pt]&\qquad \times \big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3)\big| \big| {\Lambda}_ja_k(z_1)\big|\Big(\sum_{P\in\mathcal{D}_j}|b_P^2|\frac{\chi_{(P)^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}} \big|\widetilde{\psi^P}(z_3) \big| \Big) \; d\vec{\boldsymbol{z}} dy\nonumber\\[3pt]&\quad \lesssim g^{\infty}\big( \big\{ b_R^3\big\}_{R\in\mathcal{D}}\big)(x) \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{s_1}}\Big( \sum_{j\in{\mathbb{Z}}} \big(2^{-js_1}\mathcal{M}J_{k,j,s}^1(x) \big)^2\Big)^{{1}/{2}} \nonumber\\[3pt]&\qquad \times\Big( \sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j} \Big( \big|\mathscr{B}_P^2(f_2)\big||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \Big)^{{1}/{2}}, \end{align} $$

where $\mathscr {B}_P^2(f_2)$ is defined as in Equation (9.19) for some $L>n,s_2$ , and

(9.38) $$ \begin{align} J_{k,j,s}^1(y):= 2^{-jn}\int_{{{\mathbb R}^n}} \big| {\Lambda}_ja_k(z_1)\big|\Big\Vert \langle 2^j(y-z_1,z_2,z_3)\rangle^s\sigma_j^{\vee}(y-z_1,z_2,z_3) \Big\Vert_{L^2(z_2,z_3)} dz_1. \end{align} $$

Now, we choose

$$ \begin{align*} u_1(x)&:=\sum_{k=0}^{\infty}|\lambda _k|\chi_{(Q_k^{***})^c}(x)\frac{1}{|x-{\mathbf{x}}_{Q_k}|^{s_1}}\Big( \sum_{j\in{\mathbb{Z}}}\big(2^{-js_1}\mathcal{M}J_{k,j,s}^1(x) \big)^2\Big)^{{1}/{2}},\\ u_2(x)&:=\bigg( \sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j} \Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}},\\ u_3(x)&:=g^{\infty}\big( \big\{ b_R^3\big\}_{R\in\mathcal{D}}\big)(x). \end{align*} $$

Clearly, Equation (7.18) holds and $\Vert u_2\Vert _{L^{p_2}({{\mathbb R}^n})}, \Vert u_3\Vert _{L^{p_3}({{\mathbb R}^n})} \lesssim 1$ due to Lemma 4.3 and Equation (7.2). In addition,

$$ \begin{align*} \Vert u_1\Vert_{L^{p_1}({{\mathbb R}^n})}^{p_1}\lesssim \sum_{k=0}^{\infty} |\lambda _k|^{p_1}\int_{(Q_k^{***})^c} |x-{\mathbf{x}}_{Q_k}|^{-s_1p_1}\Big(\sum_{j\in{\mathbb{Z}}}\big(2^{-s_1j}\mathcal{M}J_{k,j,s}^1(x) \big)^2 \Big)^{{p_1}/{2}} dx \end{align*} $$

and the integral is controlled by

$$ \begin{align*} &\big\Vert |\cdot-{\mathbf{x}}_{Q_k}|^{-s_1p_1}\big\Vert_{L^{({2}/{p_1})'}((Q_k^{***})^c)}\bigg\Vert \Big( \sum_{j\in{\mathbb{Z}}}\big(2^{-s_1j}\mathcal{M}J_{k,j,s}^1(x) \big)^2 \Big)^{{p_1}/{2}}\bigg\Vert_{L^{{2}/{p_1}}({{\mathbb R}^n})}\\&\quad \lesssim \ell(Q_k)^{-p_1(s_1-({n}/{p_1}-{n}/{2}))} \Big( \sum_{j\in{\mathbb{Z}}}2^{-2js_1}\big\Vert J_{k,j,s}^1 \big\Vert_{L^2({{\mathbb R}^n})}^2\Big)^{{p_1}/{2}} \end{align*} $$

by using Hölder’s inequality and the $L^2$ boundedness of $\mathcal {M}$ . It follows from Minkowski’s inequality and Lemma 4.5 that

$$ \begin{align*} \big\Vert J_{k,j,s}^{1}\big\Vert_{L^2({{\mathbb R}^n})}&\lesssim 2^{-jn}\big\Vert {\Lambda}_ja_k\big\Vert_{L^1({{\mathbb R}^n})}\Big\Vert \langle 2^j{\vec{\cdot}\;}\rangle^s\big| \sigma_j^{\vee}\big|\Big\Vert_{L^2(({{\mathbb R}^n})^3)}\\ &\lesssim \ell(Q_k)^{-{n}/{p_1}+n}2^{{jn}/{2}}\min\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}, \end{align*} $$

and this finally yields that

(9.39) $$ \begin{align} \Vert u_1\Vert_{L^{p_1}({{\mathbb R}^n})}\lesssim \Big( \sum_{k=0}^{\infty}|\lambda _k|^{p_1}\Big)^{{1}/{p_1}}\lesssim 1. \end{align} $$

9.8 Proof of Lemma 7.7

For $x\in B_k^l\cap B_P^l$ ,

(9.40) $$ \begin{align} 2^l\lesssim |x-{\mathbf{x}}_{Q_k}|^{-1}, |x-{\mathbf{x}}_P|^{-1}. \end{align} $$

Since $s>{n}/{p_1}+{n}/{2}$ , there exist $0<\epsilon _0,\epsilon _1<1$ such that

$$ \begin{align*}{n}/{p_1}+{n}/{p_2}<\big[ {n}/{p_1}+{n}/{p_2}\big]+\epsilon_0 \quad \text{ and }\quad \big[ {n}/{p_1}+{n}/{p_2}\big]+\epsilon_0+\epsilon_1 <s-\big({n}/{2} -{n}/{p_2}\big). \end{align*} $$

Choose $t_1$ and $t_2$ satisfying $t_1>{n}/{p_1}$ , $t_2>{n}/{p_2}$ and $t_1+t_2=\big [ {n}/{p_1}+{n}/{p_2}\big ]+\epsilon _0$ , and let $N_0:=\big [ {n}/{p_1}+{n}/{p_2}\big ]-n $ . Then Lemma 4.1, together with the vanishing moment condition (5.3), and the estimate (9.40) yield that

$$ \begin{align*} &\big| \phi_l\ast T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(x)\big|\\[3pt]&\quad \lesssim 2^{l(N_0+n+\epsilon_0)}\int_{{{\mathbb R}^n}}|y-{\mathbf{x}}_P |^{N_0+\epsilon_0} \big| T_{\sigma_j} \big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(y)\big| \; dy\\[3pt]&\quad \lesssim |R|^{-{1}/{2}}\frac{1}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}2^{-j(t_1-n)}\int_{{{\mathbb R}^n}} \int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_2)\rangle^{N_0+\epsilon_0}\\[3pt]&\qquad \times \big| \sigma_j^{\vee}(y-z_1,y-z_2,z_3)\big| \big| {\Lambda}_ja_k(z_1)\big| \frac{| \widetilde{\psi^P}(z_2)|}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}} \; d\vec{\boldsymbol{z}} dy, \end{align*} $$

where

$$ \begin{align*}\widetilde{\psi^P}(z_2):= \langle z_2-{\mathbf{x}}_P\rangle^{N_0+\epsilon_0}\psi^P(z_2).\end{align*} $$

This deduces

(9.41) $$ \begin{align} &\big| \phi_l\ast \big( \mathcal{U}_2^2(x,\cdot)\big)(x)\big| \nonumber\\[3pt]&\quad \lesssim g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x)\frac{1}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}\sum_{j\in{\mathbb{Z}}}2^{-j(t_1-n)}\int_{{{\mathbb R}^n}} \int_{({{\mathbb R}^n})^3} \langle 2^j(y-z_2)\rangle^{N_0+\epsilon_0} \nonumber\\[3pt]&\qquad \times \big| \sigma_j(y-z_1,y-z_2,z_3)\big| \big| {\Lambda}_ja_k(z_1)\big| \Big( \sum_{P\in\mathcal{D}_j} |b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\big| \widetilde{\psi^P}(z_2)\big| \Big) \; d\vec{\boldsymbol{z}} dy. \end{align} $$

Using Hölder’s inequality with $\frac {1}{2}+\frac {1}{(1/p_2'-1/2)^{-1}}+\frac {1}{p_2}=1$ and Lemma 4.2, we see that

$$ \begin{align*} &\int_{{{\mathbb R}^n}} \langle 2^j(y-z_2)\rangle^{N_0+\epsilon_0} \big| \sigma_j(y-z_1,y-z_2,z_3)\big| \Big( \sum_{P\in\mathcal{D}_j} |b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\big| \widetilde{\psi^P}(z_2)\big| \Big) \; dz_2\\[3pt]&\quad \le \big\Vert \langle 2^jz_2\rangle^{s-n-\epsilon_1}\sigma_j^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2)}\big\Vert \langle 2^j\cdot \rangle^{-(s-t_1-t_2-\epsilon_1)}\big\Vert_{L^{({1}/{p_2'}-{1}/{2})^{-1}}({{\mathbb R}^n})}\\[3pt]&\qquad \times \Big\Vert \sum_{P\in\mathcal{D}_j} |b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\big| \widetilde{\psi^P}(z_2)\big| \Big\Vert_{L^{p_2}({{\mathbb R}^n})}\\[3pt]&\quad \lesssim 2^{-\frac{jn}{2}}\big\Vert \langle 2^jz_2\rangle^{s-n-\epsilon_1}\sigma_j^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2)}\\[3pt]&\qquad \times \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}} \end{align*} $$

because $s-n-\epsilon _1=s-t_1-t_2-\epsilon _1+N_0+\epsilon _0$ , $s-t_1-t_2-\epsilon _1>n(1/p_2'-1/2)$ . This shows that the integral in the right-hand side of Equation (9.41) is dominated by a constant times

$$ \begin{align*} &\Vert {\Lambda}_ja_k\Vert_{L^1({{\mathbb R}^n})} \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}} \\&\qquad \times 2^{-{jn}/{2}}\int_{({{\mathbb R}^n})^2} \big\Vert \langle 2^jz_2\rangle^{s-n-\epsilon_1}\sigma_j^{\vee}(y,z_2,z_3)\big\Vert_{L^2(z_2)} \;dy\; dz_3\\&\quad \lesssim \ell(Q_k)^{-{n}/{p_1}+n}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\} \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}, \end{align*} $$

where $\mathscr {B}_P^2(f_2)$ is defined as in Equation (9.19) and M is sufficiently large. Consequently,

(9.42) $$ \begin{align} &\big| \phi_l\ast \big( \mathcal{U}_2^2(x,\cdot)\big)(x)\big| \nonumber\\&\quad \lesssim g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x) \;\sup_{j\in{\mathbb{Z}}} \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}\nonumber\\&\qquad \times \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}\ell(Q_k)^{-{n}/{p_1}+n}\sum_{j\in{\mathbb{Z}}} 2^{-j(t_1-n)} \min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\}\nonumber\\&\quad \lesssim |Q_k|^{-1/p_1} \frac{\ell(Q_k)^{t_1}}{|x-{\mathbf{x}}_{Q_k}|^{t_1}} \bigg( \sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}\\&\qquad\times g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x).\nonumber \end{align} $$

Now, we are done with

$$ \begin{align*} u_1(x)&:= \sum_{k=0}^{\infty}|\lambda _k| |Q_k|^{-{1}/{p_1}}\frac{\ell(Q_k)^{t_1}}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}\chi_{(Q_k^{***})^c}(x)\\u_2(x)&:= \bigg(\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}\\u_3(x)&:= g^{\infty}\big(\big\{ b_R^3\big\}_{R\in\mathcal{D}} \big)(x) \end{align*} $$

as $\Vert u_{{\mathrm {i}}}\Vert _{L^{p_{{\mathrm {i}}}}({{\mathbb R}^n})}\lesssim 1$ , ${\mathrm {i}}=1,2,3$ , follow from Lemma 4.3, Equation (7.2) and the argument that led to (9.35) with $t_1>n/p_1$ .

9.9 Proof of Lemma 7.8

Let $s_1$ , $s_2$ and $s_3$ satisfy $s_1>{n}/{p_1}-{n}/{2}$ , $s_2>{n}/{2}$ , $s_3>{n}/{2}$ and $s=s_1+s_2+s_3$ . By mimicking the argument that led to Equation (9.37) with

$$ \begin{align*}|x-{\mathbf{x}}_{Q_k}|\le |x-{\mathbf{x}}_R|\lesssim |y-{\mathbf{x}}_R|\end{align*} $$

for $x\in B_k^l\cap (B_R^l)^c$ and $|x-y|\le 2^{-l}$ , instead of Equation (9.36), we can prove

$$ \begin{align*} \big| \phi_l\ast \big(\mathcal{U}_{3}^{1}(x,\cdot)\big)(x) \big|&\lesssim \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{s_1}}\Big( \sum_{j\in{\mathbb{Z}}} \big(2^{-js_1}\mathcal{M}J_{k,j,s}^1(x) \big)^2\Big)^{{1}/{2}} \; g^2\big(\big\{ b_P^2\big\}_{P\in\mathcal{D}} \big)(x)\\&\quad \times \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j} \Big( \big|\mathscr{B}_R^3(f_3)\big||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}}\Big)^2\bigg)^{{1}/{2}}, \end{align*} $$

where $J_{k,j,s}^1$ and $\mathscr {B}_R^3(f_3)$ are defined as in Equations (9.38) and (9.26) for some $L>n,s_3$ .

Now, let

$$ \begin{align*} u_1(x)&:= \sum_{k=0}^{\infty}|\lambda _k|\chi_{(Q_k^{***})^c}(x)\frac{1}{|x-{\mathbf{x}}_{Q_k}|^{s_1}}\Big( \sum_{j\in{\mathbb{Z}}}\big(2^{-js_1}\mathcal{M}J_{k,j,s}^1(x) \big)^2\Big)^{{1}/{2}} \\ u_2(x)&:=g^2\big( \big\{ b_P^2\big\}_{P\in\mathcal{D}}\big)(x)\\ u_3(x)&:= \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)| |R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}}\Big)^2\bigg)^{{1}/{2}}. \end{align*} $$

Then the estimate (7.21) is clear and it follows from Equations (9.39) and (7.1) and Lemma 4.4 that Equation (7.20) holds.

9.10 Proof of Lemma 7.9

Let $0<\epsilon _0,\epsilon _1<1$ satisfy

$$ \begin{align*}{n}/{p_1}+{n}/{p_3}<\big[ {n}/{p_1}+{n}/{p_3}\big]+\epsilon_0 \quad \text{ and }\quad \big[ {n}/{p_1}+{n}/{p_3}\big]+\epsilon_0+\epsilon_1<s-\big( {n}/{2}-{n}/{p_3}\big),\end{align*} $$

and select $t_1,t_3$ so that $t_1>{n}/{p_1}$ , $t_3>{n}/{p_3}$ and $t_1+t_3=\big [{n}/{p_1}+{n}/{p_3} \big ]+\epsilon _0$ . Let $N_0:= \big [ {n}/{p_1}+{n}/{p_3}\big ]-n$ and $B_R^3(f_3)$ be defined as in Equation (9.26). Then, as the counterpart of Equation (9.42), we can get

$$ \begin{align*} \big| \phi_l\ast \big(\mathcal{U}_{3}^{2}(x,\cdot)\big)(x)\big|&\lesssim |Q_k|^{-1/p_1} \frac{\ell(Q_k)^{t_1}}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}g^{2}\big( \big\{b_P^2 \big\}_{P\in\mathcal{D}}\big)(x)\\ &\qquad \qquad \times \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3}\bigg)^{{1}/{p_3}}, \end{align*} $$

where the embedding $\ell ^2\hookrightarrow \ell ^{\infty }$ is applied. By taking

$$ \begin{align*} u_1(x)&:= \sum_{k=0}^{\infty}|\lambda _k| |Q_k|^{-{1}/{p_1}}\frac{\ell(Q_k)^{t_1}}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}\chi_{(Q_k^{***})^c}(x) \\ u_2(x)&:= g^2\big( \big\{ b_P^2\big\}_{P\in\mathcal{D}}\big)(x), \\ u_3(x)&:= \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3}\bigg)^{{1}/{p_3}}, \end{align*} $$

we obtain the inequality (7.22) and Equation (7.23).

9.11 Proof of Lemma 7.10

The proof is almost same as that of Lemmas 7.6 and 7.8. Let $s_1$ , $s_2$ and $s_3$ be numbers such that $s_1>{n}/{p_1}-{n}/{2}$ , $s_2>{n}/{2}$ , $s_3>{n}/{2}$ and $s=s_1+s_2+s_3$ . We claim that for $\eta =1,2,3$ ,

(9.43) $$ \begin{align} \big| \phi_l\ast \big( \mathcal{U}_4^{\eta}(x,\cdot)\big)(x)\big| &\lesssim \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{s_1}} \Big( \sum_{j\in{\mathbb{Z}}}\big( 2^{-js_1}\mathcal{M}J_{k,j,s}^1(x)\big)^2\Big)^{{1}/{2}}\\&\quad \times\bigg( \sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j} \Big(|\mathscr{B}_P^2(f_2)| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}}\nonumber\\&\quad \times \sup_{j\in{\mathbb{Z}}}\bigg(\sum_{R\in\mathcal{D}_j} \Big( |\mathscr{B}_R^3(f_3)| |R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}}\Big)^2\bigg)^{{1}/{2}}\nonumber, \end{align} $$

where $J_{k,j,s}^1$ , $\mathscr {B}_P^2(f_2)$ and $\mathscr {B}_R^3(f_3)$ are defined as in Equations (9.38), (9.19) and (9.26), respectively. Then we have Equation (7.25) with the choice

$$ \begin{align*} u_1(x)&:= \sum_{k=0}^{\infty}|\lambda _k|\chi_{(Q_k^{***})^c}(x)\frac{1}{|x-{\mathbf{x}}_{Q_k}|^{s_1}}\Big( \sum_{j\in{\mathbb{Z}}}\big(2^{-js_1}\mathcal{M}J_{k,j,s}^1(x) \big)^2\Big)^{{1}/{2}}, \\ u_2(x)&:= \bigg( \sum_{j\in{\mathbb{Z}}}\sum_{P\in\mathcal{D}_j} \Big(|\mathscr{B}_P^2(f_2)| |P|^{-{1}/{2}} \frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}}\Big)^2 \bigg)^{{1}/{2}}, \\ u_3(x)&:= \sup_{j\in{\mathbb{Z}}}\bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)| |R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}}\Big)^2\bigg)^{{1}/{2}}. \end{align*} $$

The estimates for $u_1,u_2,u_3$ follow from Equation (9.39), Lemma 4.3 and Lemma 4.4.

Now, we return to the proof of Equation (9.43). For $x\in B_k^l\cap (B_P^l)^c\cap (B_R^l)^c$ and $|x-y|\le 2^{-l}$ , we have

(9.44) $$ \begin{align} |x-{\mathbf{x}}_{Q_k}|\le |x-{\mathbf{x}}_P|\lesssim |y-{\mathbf{x}}_P| \quad \text{and} \quad |x-{\mathbf{x}}_R|\lesssim |y-{\mathbf{x}}_R|. \end{align} $$

Then we have

$$ \begin{align*} &\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}\big| \phi_l\ast T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(x)\big|\\&\quad\lesssim 2^{ln}\int_{|x-y|\le 2^{-l}} \int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_2)\rangle^{s_1+s_2}\langle 2^j(y-z_3)\rangle^{s_3}\big|\sigma_j^{\vee}(y-z_1,y-z_2,y-z_3) \big| \\&\qquad\times |{\Lambda}_ja_k(z_1)|\big|\widetilde{\psi^P}(z_2)\big| \big|\widetilde{\theta^R}(z_3)\big| \; d\vec{\boldsymbol{z}} dy, \end{align*} $$

where

$$ \begin{align*} \widetilde{\psi^P}(z_2)&:=\langle 2^j(z_2-{\mathbf{x}}_P)\rangle^{s_1+s_2}\psi^P(z_2),\\ \widetilde{\theta^R}(z_3)&:=\langle 2^j(z_3-{\mathbf{x}}_R)\rangle^{s_3}\theta^R(z_3). \end{align*} $$

Now, using the method similar to that used in the proof of Equation (9.37), we obtain Equation (9.43) for $\eta =1$ .

For the case $\eta =2$ , we use the fact, instead of Equation (9.44), that for $x\in B_k^l\cap (B_P^l)^c\cap B_R^l$ and $|x-y|\le 2^{-l}$ ,

$$ \begin{align*}|x-{\mathbf{x}}_{Q_k}|, |x-{\mathbf{x}}_R|\le |x-{\mathbf{x}}_P|\lesssim |y-{\mathbf{x}}_P|.\end{align*} $$

This shows that

$$ \begin{align*} &\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}\big| \phi_l\ast T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(x)\big|\\&\quad \lesssim 2^{ln}\int_{|x-y|\le 2^{-l}} \int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_2)\rangle^{s}\big|\sigma_j^{\vee}(y-z_1,y-z_2,y-z_3) \big| \\&\qquad\times |{\Lambda}_ja_k(z_1)|\big|{\widetilde{\psi^P}}(z_2)\big| \big|{\theta^R}(z_3)\big| \; d\vec{\boldsymbol{z}} dy, \end{align*} $$

where

$$ \begin{align*}\widetilde{\psi^P}(z_2):=\langle 2^j(z_2-{\mathbf{x}}_P)\rangle^{s}\psi^P(z_2),\end{align*} $$

and then Equation (9.43) for $\eta =2$ follows.

Similarly, we can prove that for $x\in B_k^l\cap B_P^l\cap (B_R^l)^c$ and $|x-y|\le 2^{-l}$ ,

$$ \begin{align*} &\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}\langle 2^j(x-{\mathbf{x}}_P)\rangle^{s_2}\langle 2^j(x-{\mathbf{x}}_R)\rangle^{s_3}\big| \phi_l\ast T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(x)\big|\\&\quad \lesssim 2^{ln}\int_{|x-y|\le 2^{-l}} \int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_3)\rangle^{s}\big|\sigma_j^{\vee}(y-z_1,y-z_2,y-z_3) \big| \\&\qquad\times |{\Lambda}_ja_k(z_1)|\big|{\psi^P}(z_2)\big| \big|\widetilde{\theta^R}(z_3)\big| \; d\vec{\boldsymbol{z}} dy, \end{align*} $$

where

$$ \begin{align*}\widetilde{\theta^R}(z_3):=\langle 2^j(z_3-{\mathbf{x}}_R)\rangle^{s}\theta^R(z_3).\end{align*} $$

This proves (9.43) for $\eta =3$ .

9.12 Proof of Lemma 7.11

We first note that

(9.45) $$ \begin{align} 2^l\lesssim |x-{\mathbf{x}}_{Q_k}|^{-1}, |x-{\mathbf{x}}_P|^{-1}, |x-{\mathbf{x}}_R|^{-1} \end{align} $$

for $x\in B_k^l\cap B_P^l\cap B_R^l$ . Since ${n}/{p}<s-\big ({n}/{2}-{n}/{p_2}-{n}/{p_3} \big )$ , there exist $0<\epsilon _0,\epsilon _1<1$ such that

$$ \begin{align*}{n}/{p}<\big[ {n}/{p}\big]+\epsilon_0 \quad \text{ and }\quad \big[ {n}/{p}\big]+\epsilon_0+\epsilon_1<s-\big({n}/{2} -{n}/{p_2}-{n}/{p_3}\big).\end{align*} $$

Choose $t_1$ , $t_2$ , and $t_3$ satisfying $t_1>{n}/{p_1}$ , $t_2>{n}/{p_2}$ , $t_3>{n}/{p_3}$ , and $t_1+t_2+t_3=\big [ {n}/{p}\big ]+\epsilon _0$ and let $N_0:=\big [ {n}/{p}\big ]-n $ . Then it follows from Lemma 4.1 and the estimate (9.45) that

$$ \begin{align*} &\big| \phi_l\ast T_{\sigma_j}\big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(x)\big|\\&\quad \lesssim 2^{l(N_0+n+\epsilon_0)}\int_{{{\mathbb R}^n}}|y-{\mathbf{x}}_P |^{N_0+\epsilon_0} \big| T_{\sigma_j} \big( {\Lambda}_ja_k,\psi^P,\theta^R\big)(y)\big| \; dy\\&\quad \lesssim \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}2^{-j(t_1-n)}\int_{{{\mathbb R}^n}} \int_{({{\mathbb R}^n})^3}\langle 2^j(y-z_2)\rangle^{N_0+\epsilon_0}\big| \sigma_j^{\vee}(y-z_1,y-z_2,y-z_3)\big| \\[3pt]&\qquad \times \big| {\Lambda}_ja_k(z_1)\big| \frac{| \widetilde{\psi^P}(z_2)|}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\frac{|\theta^R(z_3)|}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}} \; d\vec{\boldsymbol{z}} dy, \end{align*} $$

where

$$ \begin{align*}\widetilde{\psi^P}(z_2):= \langle z_2-{\mathbf{x}}_P\rangle^{N_0+\epsilon_0}\psi^P(z_2).\end{align*} $$

This deduces that

(9.46) $$ \begin{align} &\big| \phi_l\ast \big( \mathcal{U}_4^4(x,\cdot)\big)(x)\big| \nonumber\\[3pt]&\quad \lesssim \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}\sum_{j\in{\mathbb{Z}}}2^{-j(t_1-n)}\int_{{{\mathbb R}^n}} \int_{({{\mathbb R}^n})^3} \langle 2^j(y-z_2)\rangle^{N_0+\epsilon_0} \big| \sigma_j(y-z_1,y-z_2,z_3)\big| \big| {\Lambda}_ja_k(z_1)\big|\nonumber\\[3pt]&\qquad \times \bigg( \sum_{P\in\mathcal{D}_j} |b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\big| \widetilde{\psi^P}(z_2)\big| \bigg) \bigg( \sum_{R\in\mathcal{D}_j} |b_R^3|\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\big| {\theta^R}(z_3)\big| \bigg) \; d\vec{\boldsymbol{z}} dy. \end{align} $$

Since $s-\big [{n}/{p} \big ]+{n}/{2}-\epsilon _0-\epsilon _1>\big ({n}/{2}-{n}/{p_2} \big )+\big ({n}/{2}-{n}/{p_3}\big )$ , there exist $\mu _2$ and $\mu _3$ such that $\mu _2>{n}/{2}-{n}/{p_2}$ , $\mu _3>{n}/{2}-{n}/{p_3}$ , and $\mu _1+\mu _2=s-\big [ {n}/{p}\big ]+{n}/{2}-\epsilon _0-\epsilon _1$ . Using Hölder’s inequality with

$$ \begin{align*}\frac{1}{2}+\frac{1}{(1/p_2'-1/2)^{-1}}+\frac{1}{p_2}=\frac{1}{2}+\frac{1}{(1/p_3'-1/2)^{-1}}+\frac{1}{p_3}=1,\end{align*} $$

we have

$$ \begin{align*} &\int_{({{\mathbb R}^n})^2} \langle 2^j(y-z_2)\rangle^{N_0+\epsilon_0} \big| \sigma_j(y-z_1,y-z_2,y-z_3)\big| \\[3pt]&\qquad \times \bigg( \sum_{P\in\mathcal{D}_j} |b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\big| \widetilde{\psi^P}(z_2)\big| \bigg) \bigg( \sum_{R\in\mathcal{D}_j} |b_R^3|\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\big| {\theta^R}(z_3)\big| \bigg) \; dz_2 dz_3\\[3pt]&\quad \le \big\Vert \langle 2^jz_2\rangle^{N_0+\epsilon_0+\mu_2}\langle 2^jz_3\rangle^{\mu_3}\sigma_j^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2,z_3)}\big\Vert \langle 2^j\cdot \rangle^{-\mu_2}\big\Vert_{L^{({1}/{p_2'}-{1}/{2})^{-1}}({{\mathbb R}^n})}\\[3pt]&\qquad \times \big\Vert \langle 2^j\cdot \rangle^{-\mu_3}\big\Vert_{L^{({1}/{p_3'}-{1}/{2})^{-1}}({{\mathbb R}^n})}\bigg\Vert \sum_{P\in\mathcal{D}_j} |b_P^2|\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\big| \widetilde{\psi^P}(z_2)\big| \bigg\Vert_{L^{p_2}(z_2)}\\[3pt]&\qquad \times \bigg\Vert \sum_{R\in\mathcal{D}_j} |b_R^3|\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\big| {\theta^R}(z_3)\big| \bigg\Vert_{L^{p_2}(z_3)}, \end{align*} $$

and then Lemma 4.2 yields that the preceding expression is less than a constant times

$$ \begin{align*} & 2^{-jn}\big\Vert \langle 2^j(z_2,z_3)\rangle^{N_0+\epsilon_0+\mu_1+\mu_2}\sigma_j^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2,z_3)}\\&\quad \times \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}\\&\quad \times \bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3} \bigg)^{{1}/{p_3}} \end{align*} $$

because $\mu _2>n(1/p_2'-1/2)$ and $\mu _3>n(1/p_3'-1/2)$ , where $\mathscr {B}_P^2(f_2)$ and $\mathscr {B}_R(f_3)$ are defined as in Equations (9.19) and (9.26).

Now, the integral in the right-hand side of Equation (9.46) is dominated by a constant times

$$ \begin{align*} &2^{-{jn}}\Vert {\Lambda}_ja_k\Vert_{L^1({{\mathbb R}^n})} \int_{{{\mathbb R}^n} } \big\Vert \langle 2^j(z_2,z_3)\rangle^{s-{n}/{2}-\epsilon_1}\sigma_j^{\vee}(y,z_2,z_3)\big\Vert_{L^2(z_2,z_3)} dy \\&\quad \times \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}} \\&\quad \times\bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3} \bigg)^{{1}/{p_3}}, \\ \end{align*} $$

and this is no more than

$$ \begin{align*} & \ell(Q_k)^{-n/p_1+n}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\} \\&\quad \times \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}\\&\quad \times \bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3} \bigg)^{{1}/{p_3}}, \end{align*} $$

where $N_0+\epsilon _0+\mu _2+\mu _3=s-\frac {n}{2}-\epsilon _1$ . Hence, it follows that

$$ \begin{align*} &\big| \phi_l\ast \big( \mathcal{U}_4^4(x,\cdot)\big)(x)\big|\\ & \lesssim \frac{1}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}\ell(Q_k)^{-{n}/{p_1}+n}\sum_{j\in{\mathbb{Z}}} 2^{-j(t_1-n)} \min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\}\\ &\qquad \times \sup_{j\in{\mathbb{Z}}} \bigg( \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}} \\ &\qquad \times \sup_{j\in{\mathbb{Z}}} \bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3} \bigg)^{{1}/{p_3}}\\ &\lesssim |Q_k|^{-1/p_1} \frac{\ell(Q_k)^{t_1}}{|x-{\mathbf{x}}_{Q_k}|^{t_1}} \bigg( \sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}\\ &\qquad \qquad \qquad \qquad \qquad \times \sup_{j\in{\mathbb{Z}}} \bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3} \bigg)^{{1}/{p_3}}. \end{align*} $$

Now, let

$$ \begin{align*} u_1(x)&:= \sum_{k=0}^{\infty}|\lambda _k| |Q_k|^{-{1}/{p_1}}\frac{\ell(Q_k)^{t_1}}{|x-{\mathbf{x}}_{Q_k}|^{t_1}}\chi_{(Q_k^{***})^c}(x), \\ u_2(x)&:= \bigg(\sum_{j\in{\mathbb{Z}}} \sum_{P\in\mathcal{D}_j}\Big( |\mathscr{B}_P^2(f_2)||P|^{-{1}/{2}}\frac{\chi_{P^c}(x)}{\langle 2^j(x-{\mathbf{x}}_P)\rangle^{t_2}}\Big)^{p_2} \bigg)^{{1}/{p_2}}, \\ u_3(x)&:= \sup_{j\in{\mathbb{Z}}} \bigg( \sum_{R\in\mathcal{D}_j}\Big( |\mathscr{B}_R^3(f_3)||R|^{-{1}/{2}}\frac{\chi_{R^c}(x)}{\langle 2^j(x-{\mathbf{x}}_R)\rangle^{t_3}}\Big)^{p_3} \bigg)^{{1}/{p_3}}. \end{align*} $$

Then it is easy to prove Equations (7.26) and (7.27).

9.13 Proof of Lemma 8.1

Using the fact that $\sum _{j\in {\mathbb {Z}}}\widehat {\Psi }(2^{-j}\vec {\boldsymbol {\xi }})=1$ for $\vec {\boldsymbol {\xi }}\not =\vec {\boldsymbol {0}}$ , we can write

(9.47) $$ \begin{align} T_{\sigma}(a_k,f_2,f_3)=\sum_{j\in{\mathbb{Z}}}T_{\widetilde{\sigma_j}}(a_k,f_2,f_3), \end{align} $$

where $\widetilde {\sigma _j}(\vec {\boldsymbol {\xi }}):=\sigma (\vec {\boldsymbol {\xi }})\widehat {\Psi }(2^{-j}\vec {\boldsymbol {\xi }})$ so that

$$ \begin{align*}\sup_{k\in{\mathbb{Z}}}\big\Vert \widetilde{\sigma_k}(2^k{\vec{\cdot}\;})\big\Vert_{L^2_s(({{\mathbb R}^n})^3)}=\mathcal{L}_s^2[\sigma]=1.\end{align*} $$

Moreover, due to the support of $\widetilde {\sigma _j}$ ,

(9.48) $$ \begin{align} T_{\widetilde{\sigma_j}}(a_k,f_2,f_3)=T_{\widetilde{\sigma_j}}({\Gamma}_{j+1}a_k,f_2,f_3). \end{align} $$

Now, the left-hand side of Equation (8.3) is less than

$$ \begin{align*}\sup_{l\in{\mathbb{Z}}} \Big|\sum_{k=1}^{\infty}\lambda _k\chi_{(Q_k^{***})^c}(x)\chi_{(B_k^l)^c}(x)\phi_l\ast \Big(\sum_{j\in{\mathbb{Z}}}T_{\widetilde{\sigma_j}}\big( {\Gamma}_{j+1}a_k,f_2,f_3\big)(x) \Big)(x) \Big|.\end{align*} $$

Let $s_1,s_2,s_3$ be numbers such that $s_1>n/p-n/2$ , $s_2,s_3>n/2$ , and $s=s_1+s_2+s_3$ . For $x\in (Q^{***})^c\cap (B_k^l)^c$ and $|x-y| \le 2^{-l}$ ,

$$ \begin{align*} |x - {\mathbf{x}}_{Q_k}| \lesssim | y - {\mathbf{x}}_{Q_k}|. \end{align*} $$

In the same argument as in the proof of Equations (9.5) and (9.8), with Equation (4.8) replaced by Equation (4.9), we can get

$$ \begin{align*} &\langle 2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1}\big| T_{\widetilde{\sigma_j}}\big({\Gamma}_{j+1}a_k,f_2,f_3\big)(y) \big|\\ & \lesssim\Vert f_2\Vert_{L^{\infty}({{\mathbb R}^n})}\Vert f_3\Vert_{L^{\infty}({{\mathbb R}^n})} \langle2^j(x-{\mathbf{x}}_{Q_k})\rangle^{s_1} \int_{({{\mathbb R}^n})^3}\big|\widetilde{\sigma_j}^{\vee}(y-z_1,z_2,z_3)\big| |{\Gamma}_{j+1}a_k(z_1)| \; d\vec{\boldsymbol{z}} \\ &\lesssim \ell(Q_k)^{-n/p}\min{\big\{1,\big(2^j\ell(Q_k) \big)^M \big\}}I_{k,j,s}(y), \end{align*} $$

where $I_{k,j,s}^{in}$ and $I_{k,j,s}^{out}$ are defined as in Equaitons (9.4) and (9.9), respectively, and

$$ \begin{align*}I_{k,j,s}(y):=I_{k,j,s}^{in}(y)+I_{k,j,s}^{out}(y).\end{align*} $$

This yields that

$$ \begin{align*} &\Big| \phi_l\ast \Big(\sum_{j\in{\mathbb{Z}}}T_{\widetilde{\sigma_j}}\big({\Gamma}_{j+1}a_k,f_2,f_3\big) \Big)(x)\Big|\\ &\lesssim \ell(Q_k)^{-n/p}|x-{\mathbf{x}}_{Q_k}|^{-s_1}\mathcal{M}\Big( \sum_{j\in{\mathbb{Z}}}2^{-s_1 j}\min{\big\{1,\big( 2^j\ell(Q_k)\big)^M\big\}}I_{k,j,s}(\cdot) \Big)(x) \end{align*} $$

and thus Equation (8.3) follows from choosing $u_2(x)=u_3(x):=1$ and

$$ \begin{align*} u_1(x)&:=\sum_{k=1}^{\infty}|\lambda _k|\chi_{(Q_k^{***})^c}(x)\ell(Q_k)^{-n/p}|x-{\mathbf{x}}_{Q_k}|^{-s_1}\\ &\qquad \qquad \times \mathcal{M}\Big( \sum_{j\in{\mathbb{Z}}}2^{-s_1 j}\min{\big\{1,\big( 2^j\ell(Q_k)\big)^M\big\}}I_{k,j,s}(\cdot) \Big)(x). \end{align*} $$

Now, it is straightforward that $\Vert u_1\Vert _{L^p({{\mathbb R}^n})}$ is less than

$$ \begin{align*} \bigg(\sum_{k=1}^{\infty}|\lambda _k|^p\ell(Q_k)^{-n}\bigg\Vert |\cdot-{\mathbf{x}}_{Q_k}|^{-s_1} \mathcal{M}\Big( \sum_{j\in{\mathbb{Z}}}2^{-s_1 j}\min{\big\{1,\big( 2^j\ell(Q_k)\big)^M\big\}}I_{k,j,s}(\cdot) \Big) \bigg\Vert_{L^p((Q_k^{***})^c)}^p \bigg)^{1/p}, \end{align*} $$

and the $L^p$ -norm in the preceding expression is less than

$$ \begin{align*} &\big\Vert |\cdot-{\mathbf{x}}_{Q_k}|^{-{s_1}}\big\Vert_{L^{p({2}/{p})'}((Q_k^{***})^c)} \bigg\Vert \mathcal{M}\Big(\sum_{j\in{\mathbb{Z}}}2^{-s_1j}\min{\big\{1,\big(2^j\ell(Q_k)\big)^M\big\}}I_{k,j,s_1}(\cdot) \Big) \bigg\Vert_{L^{{2}}({{\mathbb R}^n})}\\ &\lesssim \ell(Q_k)^{-(s_1-(n/p-n/2))}\sum_{j\in{\mathbb{Z}}}2^{-s_1 j}\min\big\{1,\big(2^j\ell(Q_k) \big)^M\big\}\Vert I_{k,j,s}\Vert_{L^2({{\mathbb R}^n})}\\ &\lesssim \ell(Q_k)^{-(s_1-(n/p-n/2))}\ell(Q_k)^n\sum_{j\in{\mathbb{Z}}}2^{-(s_1-n/2) j} \min\big\{1,\big(2^j\ell(Q_k) \big)^M\big\}\lesssim \ell(Q_k)^{n/p}, \end{align*} $$

where Equations (9.13) and (9.14) are applied in the penultimate inequality for sufficiently large M. This concludes that

$$ \begin{align*}\Vert u_1\Vert_{L^p({{\mathbb R}^n})}\lesssim \Big( \sum_{k=1}^{\infty}|\lambda _k|^p\Big)^{1/p}\lesssim 1.\end{align*} $$

9.14 Proof of Lemma 8.2

Select $0<\epsilon <1$ such that

$$ \begin{align*}N_p:=[n/p-n]\le n/p-n<[n/p-n]+\epsilon<s-3n/2.\end{align*} $$

Then Lemma 4.1 yields that

$$ \begin{align*} \big| \phi_l \ast T_{\sigma}\big(a_k, f_2, f_3\big)(x) \big| &\lesssim 2^{l(N_p+n+\epsilon)} \int_{{{\mathbb R}^n}} |y - {\mathbf{x}}_{Q_k}|^{N_p + \epsilon} \big|T_{\sigma}(a_k, f_2, f_3)(y) \big| \;dy\\ &\lesssim \frac{1}{ |x - {\mathbf{x}}_{Q_k}|^{N_p+n+\epsilon} } \int_{\mathbb{R}^n}| y - {\mathbf{x}}_{Q_k} |^{N_p+\epsilon } \big|T_{\sigma}(a_k, f_2, f_3)(y) \big| \; dy\\ &\le \frac{1}{ |x - {\mathbf{x}}_{Q_k}|^{N_p+n+\epsilon} } \big( \mathcal{K}_{N_p+\epsilon}^{in}(a_k,f_2,f_3)+ \mathcal{K}_{N_p+\epsilon}^{in}(a_k,f_2,f_3)\big), \end{align*} $$

where we applied $2^l\lesssim |x-{\mathbf {x}}_{Q_k}|$ for $x\in B_k^l$ in the penultimate inequality and

$$ \begin{align*}\mathcal{K}_{N_p+\epsilon}^{\mathrm{in}}(a_k,f_2,f_3):=\int_{Q_k^{**}}| y - {\mathbf{x}}_{Q_k} |^{N_p+\epsilon } \big|T_{\sigma}(a_k, f_2, f_3)(y) \big| \; dy,\end{align*} $$

$$ \begin{align*}\mathcal{K}_{N_p+\epsilon}^{\mathrm{out}}(a_k,f_2,f_3):=\int_{(Q_k^{**})^c}| y - {\mathbf{x}}_{Q_k} |^{N_p+\epsilon } \big|T_{\sigma}(a_k, f_2, f_3)(y) \big| \; dy.\end{align*} $$

Now, we claim that

(9.49) $$ \begin{align} \mathcal{K}_{N_p+\epsilon}^{\mathrm{in}/\mathrm{out}}(a_k,f_2,f_3)\lesssim \ell(Q_k)^{N_p-n/p+n+\epsilon}. \end{align} $$

Once Equation (9.49) holds, we obtain

$$ \begin{align*}\big| \phi_l \ast T_{\sigma}\big(a_k, f_2, f_3\big)(x) \big| \lesssim |Q_k|^{-1/p}\frac{\ell(Q_k)^{N_p+n+\epsilon}}{|x-{\mathbf{x}}_{Q_k}|^{N_p+n+\epsilon}},\end{align*} $$

which implies (8.4) with $u_2(x)=u_3(x):=1$ and

$$ \begin{align*}u_1(x):=\sum_{k=1}^{\infty}|\lambda _k||Q_k|^{-1/p}\frac{\ell(Q_k)^{N_p+n+\epsilon}}{|x-{\mathbf{x}}_{Q_k}|^{N_p+n+\epsilon}}\chi_{(Q_k^{***})^c}(x).\end{align*} $$

Moreover,

$$ \begin{align*} \Vert u_1\Vert_{L^p({{\mathbb R}^n})}&\le \Big( \sum_{k=1}^{\infty}|\lambda _k|^p|Q_k|^{-1}\ell(Q_k)^{p(N_p+n+\epsilon)}\big\Vert |\cdot-{\mathbf{x}}_{Q_k}|^{-(N_p+n+\epsilon)}\big\Vert_{L^p((Q_k^{***})^c)}^p \Big)^{1/p}\\ &\lesssim \Big(\sum_{k=1}^{\infty}|\lambda _k|^p \Big)^{1/p}\lesssim 1 \end{align*} $$

because $N_p+n+\epsilon>n/p$ .

Therefore, it remains to show Equation (9.49). Indeed, it follows from Theorem D that

$$ \begin{align*} \mathcal{K}_{N_p+\epsilon}^{\mathrm{in}}(a_k,f_2,f_3)&\lesssim \ell(Q_k)^{N_p+\epsilon}\big\Vert T_{\sigma}(a_k,f_2,f_3)\big\Vert_{L^1({{\mathbb R}^n})}\\ &\lesssim \ell(Q_k)^{N_p+\epsilon}\Vert a_k\Vert_{L^1({{\mathbb R}^n})}\lesssim \ell(Q_k)^{N_p-n/p+n+\epsilon}. \end{align*} $$

For the other term, we use both Equations (9.47) and (9.48) to write

$$ \begin{align*}\mathcal{K}_{\hspace{1pt}N_p+\epsilon}^{\hspace{1pt}\mathrm{out}}(a_k,f_2,f_3)\lesssim \sum_{j\in{\mathbb{Z}}}2^{-j(N_p+\epsilon)}\int_{(Q_k^{**})^c}{ \langle 2^j(y-{\mathbf{x}}_{Q_k})\rangle^{N_p+\epsilon}\big| T_{\widetilde{\sigma_j}}\big({\Gamma}_{j+1}a_k,f_2,f_3\big)(y)\big|} \; dy.\end{align*} $$

Let $s_1,s_2,s_3$ be numbers satisfying

$$ \begin{align*}N_p+n/2+\epsilon<s_1<s-n,\quad s_2,s_3>n/2,\quad s_1+n<s_1+s_2+s_3=s,\end{align*} $$

similar to Equations (9.30) and (9.31). Then, using the argument in Equation (9.33), we have

$$ \begin{align*} &\big| T_{\widetilde{\sigma_j}}\big({\Gamma}_{j+1}a_k,f_2,f_3 \big)(y)\big|\chi_{(Q_k^{**})^c}(y)\lesssim \ell(Q_k)^{-n/p}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M \big\}\frac{1}{\langle 2^j(y-{\mathbf{x}}_{Q_k})\rangle^{s_1}}\\ &\qquad \qquad \qquad \times 2^{-jn}\int_{{{\mathbb R}^n}} |A_{j,Q_k}(z_1)|\big\Vert \langle 2^j(y-z_1,z_2,z_3)\rangle^{s}\widetilde{\sigma_j}^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2,z_3)} dz_1, \end{align*} $$

where $A_{j,Q_k}$ is defined as in Equation (9.32). This finally yields that

$$ \begin{align*} &\mathcal{K}_{N_p+\epsilon}^{\mathrm{out}}(a_k,f_2,f_3)\lesssim \ell(Q_k)^{-n/p}\sum_{j\in{\mathbb{Z}}}2^{-j(N_p+n+\epsilon)}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M\big\} \int_{{{\mathbb R}^n}}|A_{j,Q_k}(z_1)| \\ &\qquad \times \Big(\int_{(Q_k^{**})^c} \frac{1}{\langle 2^j(y-{\mathbf{x}}_{Q_k})\rangle^{s_1-(N_p+\epsilon)}} \big\Vert \langle 2^j(y-z_1,z_2,z_3)\rangle^{s}\widetilde{\sigma_j}^{\vee}(y-z_1,z_2,z_3)\big\Vert_{L^2(z_2,z_3)} dy \Big) \; dz_1\\ &\lesssim \ell(Q_k)^{-n/p}\sum_{j\in{\mathbb{Z}}}2^{-j(s_1+n)}\min\big\{1,\big( 2^j\ell(Q_k)\big)^M\big\}\Vert A_{j,Q_k}\Vert_{L^1({{\mathbb R}^n})}\\ &\qquad \qquad \qquad \qquad \times \big\Vert \langle 2^j{\vec{\cdot}\;} \rangle^s\widetilde{\sigma_j}^{\vee}\big\Vert_{L^2(({{\mathbb R}^n})^3)} \big\Vert |\cdot-{\mathbf{x}}_{Q_k}|^{-(s_1-(N_p+\epsilon))}\big\Vert_{L^2({{\mathbb R}^n})}\\ &\lesssim \ell(Q_k)^{-n/p+n}\ell(Q_k)^{-(s_1-(N_p+n/2+\epsilon))}\sum_{j\in{\mathbb{Z}}}2^{-j(s_1-n/2)}\min \big\{1,\big( 2^j\ell(Q_k)\big)^{M-(L_0-s_1-n)} \big\}\\ &\lesssim \ell(Q_k)^{N_p-n/p+n+\epsilon} \end{align*} $$

for M and $L_0$ satisfying $M>L_0-s_1-n$ , which completes the proof of Equation (9.49).