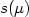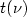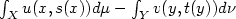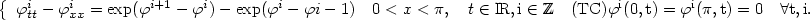Research Article
Carleman estimates for the non-stationary Lamé systemand theapplication to an inverse problem
-
- Published online by Cambridge University Press:
- 15 December 2004, pp. 1-56
-
- Article
- Export citation
An optimal matching problem
-
- Published online by Cambridge University Press:
- 15 December 2004, pp. 57-71
-
- Article
- Export citation
On periodic motions of a two dimensional Toda type chain
-
- Published online by Cambridge University Press:
- 15 December 2004, pp. 72-87
-
- Article
- Export citation
Optimal networks for mass transportation problems
-
- Published online by Cambridge University Press:
- 15 December 2004, pp. 88-101
-
- Article
- Export citation
On the optimal control of coefficients in elliptic problems. Application to the optimization of the head slider
-
- Published online by Cambridge University Press:
- 15 December 2004, pp. 102-121
-
- Article
- Export citation
A differential inclusion: the case of an isotropic set
-
- Published online by Cambridge University Press:
- 15 December 2004, pp. 122-138
-
- Article
- Export citation
Spatial heterogeneity in 3D-2D dimensional reduction
-
- Published online by Cambridge University Press:
- 15 December 2004, pp. 139-160
-
- Article
- Export citation