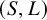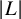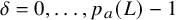1 Introduction
Let S be a smooth, projective complex surface and L a line bundle on S. Let
![]() $p_a(L)=\frac {1}{2}L \cdot (L+K_S)+1$
denote the arithmetic (or sectional) genus of L. For any integer
$p_a(L)=\frac {1}{2}L \cdot (L+K_S)+1$
denote the arithmetic (or sectional) genus of L. For any integer
![]() $\delta $
satisfying
$\delta $
satisfying
![]() $0 \leq \delta \leq p_a(L)$
, we denote by
$0 \leq \delta \leq p_a(L)$
, we denote by
![]() $V_{|L|,\delta }(S)$
the Severi variety parametrising irreducible
$V_{|L|,\delta }(S)$
the Severi variety parametrising irreducible
![]() $\delta $
-nodal curves in
$\delta $
-nodal curves in
![]() $|L|$
. A heuristic count shows that the expected dimension of
$|L|$
. A heuristic count shows that the expected dimension of
![]() $V_{|L|,\delta }(S)$
is
$V_{|L|,\delta }(S)$
is
![]() $\dim (|L|)-\delta $
. Severi varieties were introduced by Severi in [Reference Severi30, Anhang F], where he proved that all Severi varieties of irreducible
$\dim (|L|)-\delta $
. Severi varieties were introduced by Severi in [Reference Severi30, Anhang F], where he proved that all Severi varieties of irreducible
![]() $\delta $
-nodal curves of degree d in
$\delta $
-nodal curves of degree d in
![]() ${\mathbb {P}}^2$
are nonempty and smooth of the expected dimension. Severi also claimed irreducibility of such varieties, but his proof contains a gap. The irreducibility was proved by Harris in [Reference Harris21].
${\mathbb {P}}^2$
are nonempty and smooth of the expected dimension. Severi also claimed irreducibility of such varieties, but his proof contains a gap. The irreducibility was proved by Harris in [Reference Harris21].
Severi varieties on other surfaces have received much attention in recent years, especially in connection with enumerative formulas computing their degrees (see [Reference Beauville1, Reference Bryan, Oberdieck, Pandharipande and Yin2, Reference Caporaso and Harris3, Reference Debarre14, Reference Göttsche19, Reference Klemm, Maulik, Pandharipande and Scheidegger22, Reference Lange and Sernesi26, Reference Tzeng36, Reference Yau and Zaslow37]). Nonemptiness, smoothness, dimension, and irreducibility for Severi varieties have been widely investigated on various rational surfaces (see, e.g., [Reference Greuel, Lossen and Shustin20, Reference Tannenbaum31, Reference Testa33, Reference Testa34, Reference Tyomkin35]), as well as K3 and abelian surfaces (see, e.g., [Reference Chen5, Reference Knutsen and Lelli-Chiesa24, Reference Knutsen, Lelli-Chiesa and Mongardi25, Reference Lange and Sernesi26, Reference Mori and Mukai27, Reference Tannenbaum32, Reference Zahariuc39]). Extremely little is known on other surfaces. In particular, Severi varieties may have unexpected behaviour: Examples are given in [Reference Chiantini and Ciliberto7] of surfaces of general type with reducible Severi varieties, and also with components of dimension different from the expected one.
In this paper, we consider the case of Enriques surfaces. If S is an Enriques surface, it is known (cf. [Reference Ciliberto, Dedieu, Galati and Knutsen9, Proposition 1]) that
![]() $V_{|L|,\delta }(S)$
, if nonempty, is smooth and every irreducible component has dimension either
$V_{|L|,\delta }(S)$
, if nonempty, is smooth and every irreducible component has dimension either
![]() $p_a(L)-\delta -1$
or
$p_a(L)-\delta -1$
or
![]() $p_a(L)-\delta $
. Moreover, if S is general in moduli, the latter case can only occur if L is
$p_a(L)-\delta $
. Moreover, if S is general in moduli, the latter case can only occur if L is
![]() $2$
-divisible in
$2$
-divisible in
![]() $\operatorname {Pic} (S)$
. Any component of dimension
$\operatorname {Pic} (S)$
. Any component of dimension
![]() $p_a(L)-\delta -1$
is called regular, and these components can only be nonempty for
$p_a(L)-\delta -1$
is called regular, and these components can only be nonempty for
![]() $\delta \leq p_a(L)-1$
, that is, they parametrize nodal curves of genus at least one. The nonemptiness problem has remained open until now.
$\delta \leq p_a(L)-1$
, that is, they parametrize nodal curves of genus at least one. The nonemptiness problem has remained open until now.
For any integer
![]() $g \geq 2$
, let
$g \geq 2$
, let
![]() ${\mathcal E}_{g}$
denote the moduli space of complex polarised Enriques surfaces
${\mathcal E}_{g}$
denote the moduli space of complex polarised Enriques surfaces
![]() $(S,L)$
of (sectional) genus g, that is, S is an Enriques surface and L is an ample line bundle on S, such that
$(S,L)$
of (sectional) genus g, that is, S is an Enriques surface and L is an ample line bundle on S, such that
![]() $L^2=2g-2$
. Thus, g is the arithmetic genus of all curves in the linear system
$L^2=2g-2$
. Thus, g is the arithmetic genus of all curves in the linear system
![]() $|L|$
. The spaces
$|L|$
. The spaces
![]() ${\mathcal E}_g$
have many irreducible components. A way to determine this has recently been given in [Reference Knutsen23], after partial results were obtained in [Reference Ciliberto, Dedieu, Galati and Knutsen10] (cf. Theorem 5.7 below).
${\mathcal E}_g$
have many irreducible components. A way to determine this has recently been given in [Reference Knutsen23], after partial results were obtained in [Reference Ciliberto, Dedieu, Galati and Knutsen10] (cf. Theorem 5.7 below).
Denote by
![]() ${\mathcal E}_g[2]$
the locus in
${\mathcal E}_g[2]$
the locus in
![]() ${\mathcal E}_{g}$
parametrising pairs
${\mathcal E}_{g}$
parametrising pairs
![]() $(S,L)$
, such that L is
$(S,L)$
, such that L is
![]() $2$
-divisible in
$2$
-divisible in
![]() $\operatorname {Num}(S)$
. The main result of this paper settles the existence of regular components of all Severi varieties on general polarised Enriques surfaces outside
$\operatorname {Num}(S)$
. The main result of this paper settles the existence of regular components of all Severi varieties on general polarised Enriques surfaces outside
![]() ${\mathcal E}_g[2]$
:
${\mathcal E}_g[2]$
:
Theorem 1.1. Let
![]() $(S,L)$
be a general element of any irreducible component of
$(S,L)$
be a general element of any irreducible component of
![]() ${\mathcal E}_{g} \setminus {\mathcal E}_g[2]$
. Then
${\mathcal E}_{g} \setminus {\mathcal E}_g[2]$
. Then
![]() $V_{|L|,\delta }(S)$
is nonempty and has a regular component, of dimension
$V_{|L|,\delta }(S)$
is nonempty and has a regular component, of dimension
![]() $g-1-\delta $
, for all
$g-1-\delta $
, for all
![]() $0 \leq \delta <g$
.
$0 \leq \delta <g$
.
By [Reference Ciliberto, Dedieu, Galati and Knutsen9, Corollary 1], the theorem follows as soon as one proves the case of maximal
![]() $\delta $
, that is,
$\delta $
, that is,
![]() $\delta =g-1$
, in which case, the parametrised curves are elliptic.
$\delta =g-1$
, in which case, the parametrised curves are elliptic.
We note that Theorem 1.1 implies a conjecture due to Pandharipande and Schmitt regarding smooth curves of genus
![]() $g\geq 2$
on Enriques surfaces (see [Reference Pandharipande and Schmitt28, Conjecture 5.1]). Our result implies this conjecture for curves whose classes are not 2-divisible (see [Reference Pandharipande and Schmitt28, Proposition 2.2 and text after Conjecture 5.1]).
$g\geq 2$
on Enriques surfaces (see [Reference Pandharipande and Schmitt28, Conjecture 5.1]). Our result implies this conjecture for curves whose classes are not 2-divisible (see [Reference Pandharipande and Schmitt28, Proposition 2.2 and text after Conjecture 5.1]).
We shall prove Theorem 1.1 by degenerating a general Enriques surface to the union of two surfaces R and P, birational to the symmetric square of a general elliptic curve and the projective plane, respectively, and glued along a smooth elliptic curve T numerically anticanonical on each surface. We need the assumption that L is not
![]() $2$
-divisible to ensure that the degenerations of the curves we are interested in do not contain the curve
$2$
-divisible to ensure that the degenerations of the curves we are interested in do not contain the curve
![]() $T = R \cap S$
(see Lemma 3.6), which is well known to be a major issue in the general context of degenerations.
$T = R \cap S$
(see Lemma 3.6), which is well known to be a major issue in the general context of degenerations.
We introduce the degenerations we need in Section 2. On such a semistable limit, we identify suitable curves that deform to elliptic nodal curves on the general Enriques surface and with the prescribed linear equivalence class that are rigid, that is, they do not move in a positive dimensional family. As remarked above, this suffices to prove the theorem. The aforementioned suitable curves consist, apart from some
![]() $(-1)$
-curves as components, of an irreducible nodal elliptic curve
$(-1)$
-curves as components, of an irreducible nodal elliptic curve
![]() $C_R$
on R and an irreducible nodal rational curve
$C_R$
on R and an irreducible nodal rational curve
![]() $C_P$
on P intersecting at one single point on T, where both
$C_P$
on P intersecting at one single point on T, where both
![]() $C_R$
and
$C_R$
and
![]() $C_P$
are smooth and have a contact of high order. Such curves are members of so-called logarithmic Severi varieties on the surfaces on which they lie. We develop all necessary tools and results on such varieties on the two types of surfaces in question in Section 3.
$C_P$
are smooth and have a contact of high order. Such curves are members of so-called logarithmic Severi varieties on the surfaces on which they lie. We develop all necessary tools and results on such varieties on the two types of surfaces in question in Section 3.
The analysis of the conditions under which the limit curves actually deform to rigid nodal elliptic curves on the general Enriques surface is performed in the crucial Section 4. This includes the most delicate part of our proof (Propositions 4.2 and 4.3), which consists in showing that the abovementioned curves
![]() $C_R$
and
$C_R$
and
![]() $C_P$
can be put together nicely. We end up eventually with numerical conditions to be verified by the line bundles determined on each component of the limit surfaces. An important ingredient next is the description of all components of moduli spaces of polarised Enriques surfaces in terms of decompositions of the polarising line bundles into effective isotropic divisors as developed recently in [Reference Ciliberto, Dedieu, Galati and Knutsen10, Reference Knutsen23], which we review in Section 5. The corresponding identification of suitable isotropic Cartier divisors on the limit surfaces is done in Section 6. Finally, Section 7 is devoted to exhibiting, for each component of the moduli spaces of polarised Enriques surfaces, a suitable isotropic decomposition of the limit polarising line bundle, such that its restriction on each component verifies the conditions necessary to deform the curves mentioned above.
$C_P$
can be put together nicely. We end up eventually with numerical conditions to be verified by the line bundles determined on each component of the limit surfaces. An important ingredient next is the description of all components of moduli spaces of polarised Enriques surfaces in terms of decompositions of the polarising line bundles into effective isotropic divisors as developed recently in [Reference Ciliberto, Dedieu, Galati and Knutsen10, Reference Knutsen23], which we review in Section 5. The corresponding identification of suitable isotropic Cartier divisors on the limit surfaces is done in Section 6. Finally, Section 7 is devoted to exhibiting, for each component of the moduli spaces of polarised Enriques surfaces, a suitable isotropic decomposition of the limit polarising line bundle, such that its restriction on each component verifies the conditions necessary to deform the curves mentioned above.
2 Flat limits of Enriques surfaces
In this section, we will introduce the semistable degenerations of general Enriques surfaces that we will use in our proof of Theorem 1.1.
Let E be a smooth elliptic curve. Denote by
![]() $\oplus $
(and
$\oplus $
(and
![]() $\ominus $
) the group operation on E and by
$\ominus $
) the group operation on E and by
![]() $e_0$
the neutral element. Let
$e_0$
the neutral element. Let
![]() $R:=\operatorname {Sym}^2(E)$
and
$R:=\operatorname {Sym}^2(E)$
and
![]() $\pi : R \to E$
be the (Albanese) projection map sending
$\pi : R \to E$
be the (Albanese) projection map sending
![]() $x+y$
to
$x+y$
to
![]() $x\oplus y$
. We denote the fibre of
$x\oplus y$
. We denote the fibre of
![]() $\pi $
over a point
$\pi $
over a point
![]() $e \in E$
by
$e \in E$
by
which is the
![]() ${\mathbb {P}}^1$
defined by the linear system
${\mathbb {P}}^1$
defined by the linear system
![]() $|e+e_0|$
(here, and throughout the paper,
$|e+e_0|$
(here, and throughout the paper,
![]() $\sim $
denotes linear equivalence of divisors). We denote the algebraic equivalence class of the fibres by
$\sim $
denotes linear equivalence of divisors). We denote the algebraic equivalence class of the fibres by
![]() $\mathfrak {f}$
. Symmetric products of elliptic curves have been studied in detail in [Reference Catanese and Ciliberto4], to which we will frequently refer in this paragraph.
$\mathfrak {f}$
. Symmetric products of elliptic curves have been studied in detail in [Reference Catanese and Ciliberto4], to which we will frequently refer in this paragraph.
For each
![]() $e \in E$
, we define the curve
$e \in E$
, we define the curve
![]() $\mathfrak {s}_e$
(called
$\mathfrak {s}_e$
(called
![]() $D_e$
in [Reference Catanese and Ciliberto4]) as the image of the section
$D_e$
in [Reference Catanese and Ciliberto4]) as the image of the section
![]() $E \to R$
mapping x to
$E \to R$
mapping x to
![]() $e+ (x \ominus e)$
. We let
$e+ (x \ominus e)$
. We let
![]() $\mathfrak {s}$
denote the algebraic equivalence class of these sections, which are the ones with minimal self-intersection, namely,
$\mathfrak {s}$
denote the algebraic equivalence class of these sections, which are the ones with minimal self-intersection, namely,
![]() $1$
(cf. [Reference Catanese and Ciliberto4]). We note that
$1$
(cf. [Reference Catanese and Ciliberto4]). We note that
![]() $\operatorname {Sym}^2(E)$
is the
$\operatorname {Sym}^2(E)$
is the
![]() $\mathbb P^1$
-bundle on E with invariant
$\mathbb P^1$
-bundle on E with invariant
![]() $-1$
. We observe for later use that for
$-1$
. We observe for later use that for
![]() $x \neq y$
, we have
$x \neq y$
, we have
We also note that
Let
![]() $\eta $
be any of the three nonzero
$\eta $
be any of the three nonzero
![]() $2$
-torsion points of E. The map
$2$
-torsion points of E. The map
![]() $E \to R$
defined by
$E \to R$
defined by
![]() $e\mapsto e + (e \oplus \eta )$
realises E as an unramified double cover of its image curve
$e\mapsto e + (e \oplus \eta )$
realises E as an unramified double cover of its image curve
![]() $T:= \{ e+ (e\oplus \eta ) \; | \; e \in E\}$
, which is a smooth elliptic curve. We have
$T:= \{ e+ (e\oplus \eta ) \; | \; e \in E\}$
, which is a smooth elliptic curve. We have
by [Reference Catanese and Ciliberto4, (2.10)]. In particular,
![]() $T \not \sim -K_R \; \; \mbox {and} \; \; 2T \sim -2K_R$
.
$T \not \sim -K_R \; \; \mbox {and} \; \; 2T \sim -2K_R$
.
Embed T as a cubic in
![]() $P:={\mathbb {P}}^2$
. Consider nine (possibly coinciding) points
$P:={\mathbb {P}}^2$
. Consider nine (possibly coinciding) points
![]() $y_1,\ldots ,y_9 \in T$
. Divide the nine points into two subsets, say of i and
$y_1,\ldots ,y_9 \in T$
. Divide the nine points into two subsets, say of i and
![]() $9-i$
points, with
$9-i$
points, with
![]() $0 \leq i \leq 9$
. Let
$0 \leq i \leq 9$
. Let
![]() $\widetilde {R} \to R$
and
$\widetilde {R} \to R$
and
![]() $\widetilde {P} \to P$
, respectively, denote the blowups at the schemes on T determined by these two subsets of i and
$\widetilde {P} \to P$
, respectively, denote the blowups at the schemes on T determined by these two subsets of i and
![]() $9-i$
points, respectively. Denote by
$9-i$
points, respectively. Denote by
![]() ${\mathfrak {e}}_R$
and
${\mathfrak {e}}_R$
and
![]() ${\mathfrak {e}}_P$
the total exceptional divisors on
${\mathfrak {e}}_P$
the total exceptional divisors on
![]() $\widetilde {R}$
and
$\widetilde {R}$
and
![]() $\widetilde {P}$
, respectively, and denote the strict transforms of
$\widetilde {P}$
, respectively, and denote the strict transforms of
![]() $T,\mathfrak {s},\mathfrak {f}$
with the same symbols. We have
$T,\mathfrak {s},\mathfrak {f}$
with the same symbols. We have
where
![]() $\ell $
is the pullback on
$\ell $
is the pullback on
![]() $\widetilde {P}$
of a general line in P. Define
$\widetilde {P}$
of a general line in P. Define
![]() $X=\widetilde {R} \cup _T \widetilde {P}$
as the surface obtained by gluing
$X=\widetilde {R} \cup _T \widetilde {P}$
as the surface obtained by gluing
![]() $\widetilde {R}$
and
$\widetilde {R}$
and
![]() $\widetilde {P}$
along T. Denote by
$\widetilde {P}$
along T. Denote by
![]() ${\mathcal D}_{[i]}$
the family of such surfaces. It is easy to see that
${\mathcal D}_{[i]}$
the family of such surfaces. It is easy to see that
![]() ${\mathcal D}_{[i]}$
is irreducible of dimension
${\mathcal D}_{[i]}$
is irreducible of dimension
![]() $10$
(when one also allows E to vary in moduli). We define
$10$
(when one also allows E to vary in moduli). We define
![]() ${\mathcal D}:=\cup _{i=0}^9 {\mathcal D}_{[i]}$
.
${\mathcal D}:=\cup _{i=0}^9 {\mathcal D}_{[i]}$
.
Let X be a member of
![]() ${\mathcal D}$
. The first cotangent sheaf
${\mathcal D}$
. The first cotangent sheaf
![]() $T^1_{X}:=\operatorname { \mathfrak {e}\mathfrak {x}\mathfrak {t} }^1_{{\mathcal {O}}_X}(\Omega _{X},{\mathcal {O}}_{X})$
of X (cf. [Reference Sernesi29, Corollary 1.1.11] or [Reference Friedman16, Section 2]) satisfies
$T^1_{X}:=\operatorname { \mathfrak {e}\mathfrak {x}\mathfrak {t} }^1_{{\mathcal {O}}_X}(\Omega _{X},{\mathcal {O}}_{X})$
of X (cf. [Reference Sernesi29, Corollary 1.1.11] or [Reference Friedman16, Section 2]) satisfies
by [Reference Friedman16, Proposition 2.3], which is trivial if and only if the nine points satisfy the condition
Thus, X is semistable if and only if (5) holds (cf. [Reference Friedman16, Definition (1.13)] and [Reference Friedman17, (0.4)]). We will denote by
![]() ${\mathcal D}^*_{[i]}$
the subfamily of
${\mathcal D}^*_{[i]}$
the subfamily of
![]() ${\mathcal D}_{[i]}$
consisting of semistable surfaces. It is easy to see that
${\mathcal D}_{[i]}$
consisting of semistable surfaces. It is easy to see that
![]() ${\mathcal D}^*_{[i]}$
is irreducible of dimension
${\mathcal D}^*_{[i]}$
is irreducible of dimension
![]() $9$
. We define
$9$
. We define
![]() ${\mathcal D}^*:=\cup _{i=0}^9 {\mathcal D}^*_{[i]}$
.
${\mathcal D}^*:=\cup _{i=0}^9 {\mathcal D}^*_{[i]}$
.
We recall that a Cartier divisor, or a line bundle,
![]() ${\mathcal {L}}$
in
${\mathcal {L}}$
in
![]() $\operatorname {Pic} (X)$
, is a pair
$\operatorname {Pic} (X)$
, is a pair
![]() $(L',L")$
, such that
$(L',L")$
, such that
![]() $[L'] \in \operatorname {Pic} (\widetilde {R})$
,
$[L'] \in \operatorname {Pic} (\widetilde {R})$
,
![]() $[L"] \in \operatorname {Pic}( \widetilde {P})$
and
$[L"] \in \operatorname {Pic}( \widetilde {P})$
and
![]() $L'|_T \simeq L"|_T$
. Since T is numerically equivalent to the anticanonical divisor on both
$L'|_T \simeq L"|_T$
. Since T is numerically equivalent to the anticanonical divisor on both
![]() $\widetilde {R}$
and
$\widetilde {R}$
and
![]() $\widetilde {P}$
, we have
$\widetilde {P}$
, we have
The canonical divisor
![]() $K_{X}$
is represented by
$K_{X}$
is represented by
In particular, by (2)–(4), we have
By [Reference Knutsen23, Lemma 3.5], the Cartier divisor
![]() $K_X$
is the only nonzero torsion element of
$K_X$
is the only nonzero torsion element of
![]() $\operatorname {Pic} (X)$
(the proof is for
$\operatorname {Pic} (X)$
(the proof is for
![]() $i=2$
but carries over to the general case).
$i=2$
but carries over to the general case).
Remark 2.1. There are exactly two elements of
![]() $\operatorname {Pic}^0(\widetilde R)\simeq E$
that restrict trivially on T, namely,
$\operatorname {Pic}^0(\widetilde R)\simeq E$
that restrict trivially on T, namely,
![]() $\mathcal O_{\widetilde R}$
and
$\mathcal O_{\widetilde R}$
and
![]() $\mathcal O_{\widetilde R}(\mathfrak {f}_{\eta }-\mathfrak {f}_{e_0})$
(see [Reference Knutsen23, Lemma 3.3]). Accordingly, for any
$\mathcal O_{\widetilde R}(\mathfrak {f}_{\eta }-\mathfrak {f}_{e_0})$
(see [Reference Knutsen23, Lemma 3.3]). Accordingly, for any
![]() $[L'] \in \operatorname {Pic} (\widetilde {R})$
and
$[L'] \in \operatorname {Pic} (\widetilde {R})$
and
![]() $[L"] \in \operatorname {Pic}(\widetilde {P})$
, such that
$[L"] \in \operatorname {Pic}(\widetilde {P})$
, such that
![]() $L'\cdot T=L"\cdot T$
, there are two line bundles
$L'\cdot T=L"\cdot T$
, there are two line bundles
![]() $\overline L'$
on
$\overline L'$
on
![]() $\widetilde {R}$
numerically equivalent to
$\widetilde {R}$
numerically equivalent to
![]() $L'$
such that
$L'$
such that
![]() $(\overline L', L")$
is a line bundle on X. By (6), their difference is
$(\overline L', L")$
is a line bundle on X. By (6), their difference is
![]() $K_X$
. These line bundles are numerically equivalent, and we will denote by
$K_X$
. These line bundles are numerically equivalent, and we will denote by
![]() $[L',L"]$
their numerical equivalence class.
$[L',L"]$
their numerical equivalence class.
By (5), if X is semistable, it also carries the Cartier divisor
![]() $\xi $
represented by the pair
$\xi $
represented by the pair
in
![]() $\operatorname {Pic} (\widetilde {R}) \times \operatorname {Pic} (\widetilde {P})$
(see [Reference Friedman17, (3.3)]).
$\operatorname {Pic} (\widetilde {R}) \times \operatorname {Pic} (\widetilde {P})$
(see [Reference Friedman17, (3.3)]).
The central result for our purposes is:
Theorem 2.2. Let
![]() $y_1,\ldots ,y_9 \in T$
be general, such that
$y_1,\ldots ,y_9 \in T$
be general, such that
![]() $X=\widetilde {R} \cup _T \widetilde {P}$
is a member of
$X=\widetilde {R} \cup _T \widetilde {P}$
is a member of
![]() ${\mathcal D}^*$
.
${\mathcal D}^*$
.
There is a flat family
![]() $\pi :\mathfrak {X} \to {\mathbb D}$
over the unit disc, such that
$\pi :\mathfrak {X} \to {\mathbb D}$
over the unit disc, such that
![]() $\mathfrak {X}$
is smooth and, setting
$\mathfrak {X}$
is smooth and, setting
![]() $S_t:=\pi ^{-1}(t)$
, we have that
$S_t:=\pi ^{-1}(t)$
, we have that
-
•
 $S_0=X$
, and
$S_0=X$
, and -
•
 $S_t$
is a smooth general Enriques surface for
$S_t$
is a smooth general Enriques surface for
 $t\neq 0$
.
$t\neq 0$
.
Furthermore, denoting by
![]() $\iota _t: S_t \subset \mathfrak {X}$
the inclusion, there is a short exact sequence
$\iota _t: S_t \subset \mathfrak {X}$
the inclusion, there is a short exact sequence
Proof. This follows from [Reference Knutsen23, Proposition 3.7, Theorem 3.10 and Corollary 3.11] in the case where X lies in
![]() ${\mathcal D}_{[2]}^*$
. Once we have the statement in this case, we can prove it in the other cases by making a birational transformation of
${\mathcal D}_{[2]}^*$
. Once we have the statement in this case, we can prove it in the other cases by making a birational transformation of
![]() $\mathfrak {X}$
to flop any of the exceptional curves between
$\mathfrak {X}$
to flop any of the exceptional curves between
![]() $\widetilde {P}$
and
$\widetilde {P}$
and
![]() $\widetilde {R}$
(see, for example [Reference Ciliberto and Miranda12, Section 4.1], where the flop is called a 1-throw).
$\widetilde {R}$
(see, for example [Reference Ciliberto and Miranda12, Section 4.1], where the flop is called a 1-throw).
3 Logarithmic Severi varieties
Theorem 1.1 will be proved by degenerating a general Enriques surface to a surface
![]() $\widetilde R\cup _T \widetilde {P}$
in
$\widetilde R\cup _T \widetilde {P}$
in
![]() ${\mathcal D}^*$
. It will be essential to construct curves on
${\mathcal D}^*$
. It will be essential to construct curves on
![]() $\widetilde R\cup _T \widetilde {P}$
that will deform to nodal irreducible elliptic curves on the general Enriques surface. As we will see in Section 4, the good limit curves on
$\widetilde R\cup _T \widetilde {P}$
that will deform to nodal irreducible elliptic curves on the general Enriques surface. As we will see in Section 4, the good limit curves on
![]() $\widetilde R$
and
$\widetilde R$
and
![]() $ \widetilde {P}$
are nodal curves with high order tangency with T at the same point on each component. These are members of so-called logarithmic Severi varieties, parametrising nodal curves with given tangency conditions to a fixed curve. This will be the topic of this section. We start with some general definitions and results:
$ \widetilde {P}$
are nodal curves with high order tangency with T at the same point on each component. These are members of so-called logarithmic Severi varieties, parametrising nodal curves with given tangency conditions to a fixed curve. This will be the topic of this section. We start with some general definitions and results:
Definition 3.1. Let S be a smooth projective surface,
![]() $T \subset S$
a smooth, irreducible curve and L a line bundle or a divisor class on S. Let g be an integer satisfying
$T \subset S$
a smooth, irreducible curve and L a line bundle or a divisor class on S. Let g be an integer satisfying
![]() $0 \leq g \leq p_a(L)$
.
$0 \leq g \leq p_a(L)$
.
For any effective divisor
![]() ${\mathfrak {d}}=m_1p_1+\cdots +m_lp_l$
on T, where the
${\mathfrak {d}}=m_1p_1+\cdots +m_lp_l$
on T, where the
![]() $p_i$
are pairwise distinct, we denote by
$p_i$
are pairwise distinct, we denote by
![]() $V_{g,{\mathfrak {d}}}(S,T, L)$
the locus of curves in S, such that
$V_{g,{\mathfrak {d}}}(S,T, L)$
the locus of curves in S, such that
-
• C is irreducible of geometric genus g and algebraically equivalent to L,
-
• denoting by
 $\nu :\widetilde {C} \to S$
the normalisation of C composed with the inclusion
$\nu :\widetilde {C} \to S$
the normalisation of C composed with the inclusion
 $C \subset S$
, there exists
$C \subset S$
, there exists
 $q_i \in \nu ^{-1}(p_i)$
, such that
$q_i \in \nu ^{-1}(p_i)$
, such that
 $\nu ^*T$
contains
$\nu ^*T$
contains
 $m_iq_i$
, for all
$m_iq_i$
, for all
 $i \in \{1,\ldots ,l\}$
.
$i \in \{1,\ldots ,l\}$
.
For any integer m satisfying
![]() $0<m \leq L \cdot T$
, we let
$0<m \leq L \cdot T$
, we let
![]() $V_{g,m}(S,T, L)$
denote the locus of curves contained in some
$V_{g,m}(S,T, L)$
denote the locus of curves contained in some
![]() $V_{g,mp}(S,T, L)$
for some (nonfixed)
$V_{g,mp}(S,T, L)$
for some (nonfixed)
![]() $p \in T$
.
$p \in T$
.
We denote by
![]() $V_{g,m}^*(S,T, L)$
the open sublocus of
$V_{g,m}^*(S,T, L)$
the open sublocus of
![]() $V_{g,m}(S,T, L)$
parametrising curves that are smooth at the intersection points with T and otherwise nodal.
$V_{g,m}(S,T, L)$
parametrising curves that are smooth at the intersection points with T and otherwise nodal.
In the sequel,
![]() $\equiv $
will denote numerical equivalence of divisors. We will need:
$\equiv $
will denote numerical equivalence of divisors. We will need:
Proposition 3.2. Let
![]() $S,T,L,{\mathfrak {d}},g$
and m be as in Definition 3.1. Assume that
$S,T,L,{\mathfrak {d}},g$
and m be as in Definition 3.1. Assume that
![]() $T \equiv -K_S$
.
$T \equiv -K_S$
.
-
(i) If
 $L \cdot T> \sum _{i=1}^l m_i$
, then all irreducible components of
$L \cdot T> \sum _{i=1}^l m_i$
, then all irreducible components of
 $V_{g,{\mathfrak {d}}}(S,T, L)$
have dimension
$V_{g,{\mathfrak {d}}}(S,T, L)$
have dimension
 $g-1+L \cdot T - \sum _{i=1}^l m_i$
.
$g-1+L \cdot T - \sum _{i=1}^l m_i$
. -
(ii) All irreducible components of
 $V_{g,m}(S,T, L)$
have dimension
$V_{g,m}(S,T, L)$
have dimension
 $g+L \cdot T-m$
.
$g+L \cdot T-m$
. -
(iii) If
 $m \leq L \cdot T-2$
, then the general member
$m \leq L \cdot T-2$
, then the general member
 $[C]$
in any component of
$[C]$
in any component of
 $V_{g,m}(S,T, L)$
is smooth at its intersection points with T; moreover, if we fix
$V_{g,m}(S,T, L)$
is smooth at its intersection points with T; moreover, if we fix
 $G\subset S$
any curve not having T as an irreducible component, and
$G\subset S$
any curve not having T as an irreducible component, and
 $\Gamma \subset S$
any finite set, then for general
$\Gamma \subset S$
any finite set, then for general
 $[C]$
, the curve C is transverse to G and does not intersect
$[C]$
, the curve C is transverse to G and does not intersect
 $\Gamma $
.
$\Gamma $
. -
(iv) If
 $m \leq L \cdot T-3$
, then the general member in any component of
$m \leq L \cdot T-3$
, then the general member in any component of
 $V_{g,m}(S,T, L)$
is nodal.
$V_{g,m}(S,T, L)$
is nodal.
Proof. The result follows from [Reference Caporaso and Harris3, Section 2], as outlined in [Reference Dedieu15, Theorem (1.4)].
3.1 Families of blownup surfaces
We will also need to work in families in the following way. For
![]() $S=R$
or P containing T as above and for any nonnegative integer n, we consider the family
$S=R$
or P containing T as above and for any nonnegative integer n, we consider the family
![]() $\mathcal {S}^{\langle n\rangle } \to T^n$
with fibre
$\mathcal {S}^{\langle n\rangle } \to T^n$
with fibre
![]() $\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
over
$\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
over
![]() $(y_1,\ldots ,y_n) \in T^n$
, the blowup of S at
$(y_1,\ldots ,y_n) \in T^n$
, the blowup of S at
![]() $y_1,\ldots ,y_n$
(when the points are coinciding, this has to be interpreted as blowing up curvilinear schemes on T). To be precise, the fibres are marked, in the sense that their (total) exceptional divisors are labelled with
$y_1,\ldots ,y_n$
(when the points are coinciding, this has to be interpreted as blowing up curvilinear schemes on T). To be precise, the fibres are marked, in the sense that their (total) exceptional divisors are labelled with
![]() $1,\ldots ,n$
. Whenever we have a line bundle on a single surface
$1,\ldots ,n$
. Whenever we have a line bundle on a single surface
![]() $\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
, we can write it in terms of the generators of
$\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
, we can write it in terms of the generators of
![]() $\operatorname {Pic} (S)$
and of the exceptional divisors over each
$\operatorname {Pic} (S)$
and of the exceptional divisors over each
![]() $y_i$
, and thus we can extend it to a relative line bundle on the whole family
$y_i$
, and thus we can extend it to a relative line bundle on the whole family
![]() $\mathcal {S}^{\langle n\rangle }$
in the obvious way. We will therefore mostly not distinguish notationally between a relative line bundle L and its restriction to any surface in the family.
$\mathcal {S}^{\langle n\rangle }$
in the obvious way. We will therefore mostly not distinguish notationally between a relative line bundle L and its restriction to any surface in the family.
Similarly, there is for all
![]() $i=1,\ldots ,n$
a relative (total) exceptional divisor
$i=1,\ldots ,n$
a relative (total) exceptional divisor
![]() ${\mathfrak {e}}_i$
on
${\mathfrak {e}}_i$
on
![]() $\mathcal {S}^{\langle n\rangle }$
, whose fibre over a point
$\mathcal {S}^{\langle n\rangle }$
, whose fibre over a point
![]() $(y_1,\ldots ,y_n) \in T^n$
is the exceptional divisor on
$(y_1,\ldots ,y_n) \in T^n$
is the exceptional divisor on
![]() $\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
over the point
$\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
over the point
![]() $y_i$
, which we by abuse of notation still denote by
$y_i$
, which we by abuse of notation still denote by
![]() ${\mathfrak {e}}_i$
.
${\mathfrak {e}}_i$
.
Definition 3.3. Let L be a relative line bundle on
![]() $\mathcal {S}^{\langle n\rangle }$
. The value of L on the ith exceptional divisor is the number
$\mathcal {S}^{\langle n\rangle }$
. The value of L on the ith exceptional divisor is the number
![]() $L \cdot {\mathfrak {e}}_i$
on any fibre
$L \cdot {\mathfrak {e}}_i$
on any fibre
![]() $\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
. We say that L is positive on the ith exceptional divisor if
$\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
. We say that L is positive on the ith exceptional divisor if
![]() $L \cdot {\mathfrak {e}}_i>0$
.
$L \cdot {\mathfrak {e}}_i>0$
.
We shall consider the relative Hilbert scheme
whose fibres are the Hilbert schemes of curves on
![]() $\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
algebraically (or equivalently numerically) equivalent to L. We have a (possibly empty) scheme
$\operatorname {Bl}_{y_1,\ldots ,y_n}(S)$
algebraically (or equivalently numerically) equivalent to L. We have a (possibly empty) scheme
whose fibres are
![]() $V_{g,m}(\operatorname {Bl}_{y_1,\ldots ,y_n}(S),T,L) \subset {\mathcal {H}}^{\langle n\rangle }_{S,L}$
(here, as usual, we denote by T, its strict transform on the blowup). Taking the closure in
$V_{g,m}(\operatorname {Bl}_{y_1,\ldots ,y_n}(S),T,L) \subset {\mathcal {H}}^{\langle n\rangle }_{S,L}$
(here, as usual, we denote by T, its strict transform on the blowup). Taking the closure in
![]() ${\mathcal {H}}^{\langle n\rangle }_{S,L}$
, we obtain a (possibly empty) scheme with a morphism
${\mathcal {H}}^{\langle n\rangle }_{S,L}$
, we obtain a (possibly empty) scheme with a morphism
whose fibres we denote by
Note that for any
![]() $(y_1,\ldots ,y_n) \in T^n$
, one has
$(y_1,\ldots ,y_n) \in T^n$
, one has
3.2 Logarithmic Severi varieties on blowups of the symmetric square of an elliptic curve
Let
![]() $T \subset R=\operatorname {Sym}^2(E)$
, as defined in Section 2. Let
$T \subset R=\operatorname {Sym}^2(E)$
, as defined in Section 2. Let
![]() $y_1,\ldots ,y_n \in T$
, and let
$y_1,\ldots ,y_n \in T$
, and let
![]() $\widetilde R:=\operatorname {Bl}_{y_1,\ldots ,y_n}(R)$
denote the blowup of R at
$\widetilde R:=\operatorname {Bl}_{y_1,\ldots ,y_n}(R)$
denote the blowup of R at
![]() $y_1,\ldots ,y_n$
, with (total) exceptional divisors
$y_1,\ldots ,y_n$
, with (total) exceptional divisors
![]() ${\mathfrak {e}}_i$
over
${\mathfrak {e}}_i$
over
![]() $y_i$
. We denote the strict transforms of
$y_i$
. We denote the strict transforms of
![]() $\mathfrak {s}$
,
$\mathfrak {s}$
,
![]() $\mathfrak {f}$
and T on
$\mathfrak {f}$
and T on
![]() $\widetilde R$
by the same names. We also still denote by
$\widetilde R$
by the same names. We also still denote by
![]() $\pi :\widetilde {R} \to E$
the composition of the blowup
$\pi :\widetilde {R} \to E$
the composition of the blowup
![]() $\widetilde {R} \to R$
with the Albanese morphism
$\widetilde {R} \to R$
with the Albanese morphism
![]() $R \to E$
(cf. beginning of Section 2). By (2)-(3), we have
$R \to E$
(cf. beginning of Section 2). By (2)-(3), we have
Definition 3.4. A line bundle or Cartier divisor L on
![]() $\widetilde {R}$
is odd if
$\widetilde {R}$
is odd if
![]() $L \cdot \mathfrak {f}$
is odd.
$L \cdot \mathfrak {f}$
is odd.
Notation 3.5. We denote by
![]() $ \operatorname {Sym}^n(T)_m \subset \operatorname {Sym}^n(T)$
the subscheme consisting of divisors with a point of multiplicity
$ \operatorname {Sym}^n(T)_m \subset \operatorname {Sym}^n(T)$
the subscheme consisting of divisors with a point of multiplicity
![]() $\geq m$
.
$\geq m$
.
Lemma 3.6. Let L be an odd line bundle or Cartier divisor on
![]() $\widetilde {R}$
. Let m be any integer satisfying
$\widetilde {R}$
. Let m be any integer satisfying
![]() $1 \leq m \leq L \cdot T$
. Then the following hold:
$1 \leq m \leq L \cdot T$
. Then the following hold:
-
(i) No curve C in
 $\overline {V}_{1,m}(\widetilde {R},T ,L)$
contains T.
$\overline {V}_{1,m}(\widetilde {R},T ,L)$
contains T. -
(ii) For any component
 $V \subset \overline {V}_{1,m}(\widetilde {R},T, L)$
, the restriction map is well-defined, finite and surjective. In particular,
$V \subset \overline {V}_{1,m}(\widetilde {R},T, L)$
, the restriction map is well-defined, finite and surjective. In particular, $$ \begin{align*} V & \longrightarrow \operatorname{Sym}^{L \cdot T}(T)_m \\ C &\mapsto C \cap T \end{align*} $$
$$ \begin{align*} V & \longrightarrow \operatorname{Sym}^{L \cdot T}(T)_m \\ C &\mapsto C \cap T \end{align*} $$
 $$ \begin{align*} \dim(V)=L\cdot T-m+1. \end{align*} $$
$$ \begin{align*} \dim(V)=L\cdot T-m+1. \end{align*} $$
-
(iii) For a general curve C in any component of
 $V^*_{1,m}(\widetilde {R},T ,L)$
, let N be the reduced subscheme of
$V^*_{1,m}(\widetilde {R},T ,L)$
, let N be the reduced subscheme of
 $\widetilde R$
supported at the nodes of C, and Z any subscheme of
$\widetilde R$
supported at the nodes of C, and Z any subscheme of
 $C \cap T$
of degree
$C \cap T$
of degree
 $C \cdot T-1$
. Then the linear system
$C \cdot T-1$
. Then the linear system
 $|{\mathcal {O}}_{\widetilde {R}}(C) \otimes {\mathcal J}_{N \cup Z}|$
consists only of C.
$|{\mathcal {O}}_{\widetilde {R}}(C) \otimes {\mathcal J}_{N \cup Z}|$
consists only of C.
Proof. Assume that we have
![]() $C=hT+C'$
in
$C=hT+C'$
in
![]() $\overline {V}_{1,m}(\widetilde {R},T, L)$
for some
$\overline {V}_{1,m}(\widetilde {R},T, L)$
for some
![]() $h>0$
, with
$h>0$
, with
![]() $C'$
not containing T. We have
$C'$
not containing T. We have
![]() $L \cdot \mathfrak {f}=C \cdot \mathfrak {f}=2h+C' \cdot \mathfrak {f}$
, whence
$L \cdot \mathfrak {f}=C \cdot \mathfrak {f}=2h+C' \cdot \mathfrak {f}$
, whence
![]() $C' \cdot \mathfrak {f}>0$
since L is assumed to be odd. Hence,
$C' \cdot \mathfrak {f}>0$
since L is assumed to be odd. Hence,
![]() $C'$
has at least one component dominating E via
$C'$
has at least one component dominating E via
![]() $\pi : \widetilde {R} \to E$
, and therefore C cannot be a limit of an elliptic curve. Thus, (i) follows.
$\pi : \widetilde {R} \to E$
, and therefore C cannot be a limit of an elliptic curve. Thus, (i) follows.
It also follows that the restriction map in (ii) is everywhere defined. The fibre over a
![]() $Z \in \operatorname {Sym}^{L \cdot T}(T)$
consists of all curves C in V, such that
$Z \in \operatorname {Sym}^{L \cdot T}(T)$
consists of all curves C in V, such that
![]() $C \cap T=Z$
. This must be finite, for otherwise, we would find a member of the fibre passing through an additional general point
$C \cap T=Z$
. This must be finite, for otherwise, we would find a member of the fibre passing through an additional general point
![]() $p \in T$
, a contradiction (using again that no curve in V contains T). Hence, the restriction morphism in (ii) is finite. We have
$p \in T$
, a contradiction (using again that no curve in V contains T). Hence, the restriction morphism in (ii) is finite. We have
![]() $\dim (V)\geq L \cdot T+1-m$
by Proposition 3.2(ii) and semicontinuity, which equals
$\dim (V)\geq L \cdot T+1-m$
by Proposition 3.2(ii) and semicontinuity, which equals
![]() $\dim \left (\operatorname {Sym}^{L \cdot T}(T)_m\right )$
. The morphism is therefore surjective, and equality holds for the dimension. This proves (ii).
$\dim \left (\operatorname {Sym}^{L \cdot T}(T)_m\right )$
. The morphism is therefore surjective, and equality holds for the dimension. This proves (ii).
Let now C be a curve in
![]() $V^*_{1,m}(\widetilde {R},T ,L)$
and Z be any subscheme of
$V^*_{1,m}(\widetilde {R},T ,L)$
and Z be any subscheme of
![]() $C \cap T$
of degree
$C \cap T$
of degree
![]() $C \cdot T-1$
. Let
$C \cdot T-1$
. Let
![]() $\widehat {R} \to \widetilde {R}$
denote the blowup of
$\widehat {R} \to \widetilde {R}$
denote the blowup of
![]() $\widetilde {R}$
along Z, considered as a curvilinear subscheme of T, and let
$\widetilde {R}$
along Z, considered as a curvilinear subscheme of T, and let
![]() $\widehat {C}$
and
$\widehat {C}$
and
![]() $\widehat {T}$
denote the strict transforms of C and T, respectively, and
$\widehat {T}$
denote the strict transforms of C and T, respectively, and
![]() $\widehat {L}:={\mathcal {O}}_{\widehat {R}}(\widehat {C})$
. Then
$\widehat {L}:={\mathcal {O}}_{\widehat {R}}(\widehat {C})$
. Then
![]() $\widehat {C}$
is a member of
$\widehat {C}$
is a member of
![]() $V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
. To prove (iii), we may reduce to proving that if X is a general member of a component of
$V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
. To prove (iii), we may reduce to proving that if X is a general member of a component of
![]() $V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
, and N is the subscheme of its nodes, then the linear system
$V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
, and N is the subscheme of its nodes, then the linear system
![]() $|{\mathcal {O}}_{\widehat {R}}(X) \otimes {\mathcal J}_N|$
consists only of X.
$|{\mathcal {O}}_{\widehat {R}}(X) \otimes {\mathcal J}_N|$
consists only of X.
Let
![]() $\delta =p_a(C)-1$
. The variety
$\delta =p_a(C)-1$
. The variety
![]() $V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
is the open subset of the Severi variety of
$V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
is the open subset of the Severi variety of
![]() $\delta $
-nodal curves, algebraically equivalent to
$\delta $
-nodal curves, algebraically equivalent to
![]() $\widehat {L}$
consisting of curves with nodes off
$\widehat {L}$
consisting of curves with nodes off
![]() $\widehat {T}$
. All of its components have dimension
$\widehat {T}$
. All of its components have dimension
![]() $\widehat {L} \cdot \widehat {T}=1$
by (ii) (or Proposition 3.2(ii)), and it is smooth by standard arguments (see, e.g. [Reference Ciliberto, Dedieu, Galati and Knutsen11, Proposition 2.2]). Let W be any component of
$\widehat {L} \cdot \widehat {T}=1$
by (ii) (or Proposition 3.2(ii)), and it is smooth by standard arguments (see, e.g. [Reference Ciliberto, Dedieu, Galati and Knutsen11, Proposition 2.2]). Let W be any component of
![]() $V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
. Then W is fibred over
$V^*_{1,1}(\widehat {R},\widehat {T},\widehat {L})$
. Then W is fibred over
![]() $\operatorname {Pic}^0(E) \simeq E$
in subvarieties
$\operatorname {Pic}^0(E) \simeq E$
in subvarieties
![]() $W_{\widehat {L}'}$
parametrising
$W_{\widehat {L}'}$
parametrising
![]() $\delta $
-nodal curves in
$\delta $
-nodal curves in
![]() $|\widehat {L}'|$
, where
$|\widehat {L}'|$
, where
![]() $\widehat {L}'$
is any line bundle numerically equivalent to
$\widehat {L}'$
is any line bundle numerically equivalent to
![]() $\widehat {L}$
. By (ii), the linear equivalence classes of the curves in W vary. Thus,
$\widehat {L}$
. By (ii), the linear equivalence classes of the curves in W vary. Thus,
![]() $W_{\widehat {L}'}$
is nonempty for general
$W_{\widehat {L}'}$
is nonempty for general
![]() $\widehat {L}'$
, whence smooth and zero-dimensional. The tangent space to
$\widehat {L}'$
, whence smooth and zero-dimensional. The tangent space to
![]() $W_{\widehat {L}'}$
at any point
$W_{\widehat {L}'}$
at any point
![]() $[X]$
is isomorphic to
$[X]$
is isomorphic to
![]() $H^0(\widehat {L}' \otimes {\mathcal J}_N)/{\mathbb C}$
, where N is the scheme of nodes of X (see, e.g. [Reference Chiantini and Sernesi8, Section 1]). In particular, for a general X in W, we have
$H^0(\widehat {L}' \otimes {\mathcal J}_N)/{\mathbb C}$
, where N is the scheme of nodes of X (see, e.g. [Reference Chiantini and Sernesi8, Section 1]). In particular, for a general X in W, we have
whence
![]() $|{\mathcal {O}}_{\widehat {R}}(X) \otimes {\mathcal J}_N|$
consists only of X, as desired. This proves (iii).
$|{\mathcal {O}}_{\widehat {R}}(X) \otimes {\mathcal J}_N|$
consists only of X, as desired. This proves (iii).
In view of part (iii) of the previous result, we introduce the following:
Notation 3.7. We let
![]() $V^{**}_{1,m}(\widetilde R,T, L)$
denote the open subvariety of
$V^{**}_{1,m}(\widetilde R,T, L)$
denote the open subvariety of
![]() $V^{*}_{1,m}(\widetilde R,T, L)$
parametrising curves C, such that, for N, its scheme of nodes and for every subscheme Z of
$V^{*}_{1,m}(\widetilde R,T, L)$
parametrising curves C, such that, for N, its scheme of nodes and for every subscheme Z of
![]() $C \cap T$
of degree
$C \cap T$
of degree
![]() $C \cdot T-1$
, the linear system
$C \cdot T-1$
, the linear system
![]() $|{\mathcal {O}}_{\widetilde {R}}(C) \otimes {\mathcal J}_{N \cup Z}|$
consists only of C.
$|{\mathcal {O}}_{\widetilde {R}}(C) \otimes {\mathcal J}_{N \cup Z}|$
consists only of C.
The main existence result of this subsection is Proposition 3.9 right below. To state it, we need a definition:
Definition 3.8. A line bundle or Cartier divisor L on
![]() $\widetilde R$
is said to verify condition
$\widetilde R$
is said to verify condition
![]() $(\star )$
if it is of the form
$(\star )$
if it is of the form
![]() $L\equiv \alpha \mathfrak {s}+\beta \mathfrak {f}-\sum _{i=1}^n \gamma _i {\mathfrak {e}}_{i}$
, such that:
$L\equiv \alpha \mathfrak {s}+\beta \mathfrak {f}-\sum _{i=1}^n \gamma _i {\mathfrak {e}}_{i}$
, such that:
-
(i)
 $\alpha \geq 1$
and
$\alpha \geq 1$
and
 $\beta \geq 0$
;
$\beta \geq 0$
; -
(ii)
 $\alpha \geq \gamma _i$
for
$\alpha \geq \gamma _i$
for
 $i=1,\ldots , n$
;
$i=1,\ldots , n$
; -
(iii)
 $\alpha +\beta \geq \sum _{i=1}^n\gamma _i$
;
$\alpha +\beta \geq \sum _{i=1}^n\gamma _i$
; -
(iv)
 $\alpha +2\beta \geq \sum _{i=1}^n\gamma _i+4$
(equivalently,
$\alpha +2\beta \geq \sum _{i=1}^n\gamma _i+4$
(equivalently,
 $-L\cdot K_{\widetilde R}\geq 4$
).
$-L\cdot K_{\widetilde R}\geq 4$
).
Proposition 3.9. Let E and
![]() $y_1,\ldots ,y_n \in T$
be general. Assume that L is a line bundle on
$y_1,\ldots ,y_n \in T$
be general. Assume that L is a line bundle on
![]() $\widetilde R$
that is odd (cf. Definition 3.4) and satisfies condition
$\widetilde R$
that is odd (cf. Definition 3.4) and satisfies condition
![]() $(\star )$
(cf. Definition 3.8). Then, if
$(\star )$
(cf. Definition 3.8). Then, if
![]() $ 0< m \leq L \cdot T-3$
, the variety
$ 0< m \leq L \cdot T-3$
, the variety
![]() $V^{**}_{1,m}(\widetilde R,T, L)$
(cf. Definitions 3.1 and 3.7) has pure dimension
$V^{**}_{1,m}(\widetilde R,T, L)$
(cf. Definitions 3.1 and 3.7) has pure dimension
![]() $L\cdot T-m+1$
. Moreover, for all curves
$L\cdot T-m+1$
. Moreover, for all curves
![]() $G \subset \widetilde R$
not having T as an irreducible component, the general member of
$G \subset \widetilde R$
not having T as an irreducible component, the general member of
![]() $V^{**}_{1,m}(\widetilde R,T, L)$
intersects G transversely.
$V^{**}_{1,m}(\widetilde R,T, L)$
intersects G transversely.
Proof. By Proposition 3.2(ii)–(iv) and Lemma 3.6(iii), we only need to prove nonemptiness of
![]() $V_{1,m}(\widetilde R,T,L)$
. Following an idea in the proof of [Reference Chen, Gounelas and Liedtke6, Theorem 3.10], we will prove this by induction on m. The base case
$V_{1,m}(\widetilde R,T,L)$
. Following an idea in the proof of [Reference Chen, Gounelas and Liedtke6, Theorem 3.10], we will prove this by induction on m. The base case
![]() $m=1$
follows from [Reference Ciliberto, Dedieu, Galati and Knutsen11, Proposition 2.3], which requires all of (i)–(iv) from condition
$m=1$
follows from [Reference Ciliberto, Dedieu, Galati and Knutsen11, Proposition 2.3], which requires all of (i)–(iv) from condition
![]() $(\star )$
.
$(\star )$
.
Assume that we have proved nonemptiness of
![]() $V_{1,m}(\widetilde R,T,L)$
for some
$V_{1,m}(\widetilde R,T,L)$
for some
![]() $1 \leq m \leq L \cdot T-4$
. By Lemma 3.6(ii), its general member C satisfies
$1 \leq m \leq L \cdot T-4$
. By Lemma 3.6(ii), its general member C satisfies
where
![]() $p_0,\ldots ,p_{l+1}$
are pairwise distinct, general points on T. Set
$p_0,\ldots ,p_{l+1}$
are pairwise distinct, general points on T. Set
![]() ${\mathfrak {d}}=mp_0+p_1+\cdots +p_{l}$
. Then
${\mathfrak {d}}=mp_0+p_1+\cdots +p_{l}$
. Then
![]() $V_{1,{\mathfrak {d}}}(\widetilde R,T, L) \neq \emptyset $
and all its components are one-dimensional, by Proposition 3.2(i). The general member in any component intersects T in
$V_{1,{\mathfrak {d}}}(\widetilde R,T, L) \neq \emptyset $
and all its components are one-dimensional, by Proposition 3.2(i). The general member in any component intersects T in
![]() $mp_0+p_1+\cdots +p_{l}+q$
, where the point q varies in the family, by Proposition 3.2(iii). Pick a component
$mp_0+p_1+\cdots +p_{l}+q$
, where the point q varies in the family, by Proposition 3.2(iii). Pick a component
![]() $\overline {V}$
of its closure inside the component of the Hilbert scheme of
$\overline {V}$
of its closure inside the component of the Hilbert scheme of
![]() $\widetilde R$
containing
$\widetilde R$
containing
![]() $|L|$
. After a finite base change, we find a smooth projective curve B, a surjective morphism
$|L|$
. After a finite base change, we find a smooth projective curve B, a surjective morphism
![]() $B \to \overline {V}$
and a family
$B \to \overline {V}$
and a family

of stable maps of genus one, such that, setting
![]() ${\mathcal C}_b:=g^*b$
for any
${\mathcal C}_b:=g^*b$
for any
![]() $b \in B$
, the curve
$b \in B$
, the curve
![]() $f_*{\mathcal C}_b$
is a member of
$f_*{\mathcal C}_b$
is a member of
![]() $\overline {V}$
, and such that
$\overline {V}$
, and such that
where
-
(I)
 $P_i$
and Q are sections of g, for
$P_i$
and Q are sections of g, for
 $i \in \{0,\ldots ,l\}$
,
$i \in \{0,\ldots ,l\}$
, -
(II)
 $f(P_i)=p_i$
, for
$f(P_i)=p_i$
, for
 $i \in \{0,\ldots ,l\}$
,
$i \in \{0,\ldots ,l\}$
, -
(III)
 $f(Q)=T$
,
$f(Q)=T$
, -
(IV)
 $g_*W=0$
,
$g_*W=0$
, -
(V)
 $f_*W=0$
;
$f_*W=0$
;
the latter property follows from the fact that no member of the family contains T, by Lemma 3.6(i). Property (III) implies that
![]() $f^{-1}(T)$
is connected as follows. Consider the Stein factorization
$f^{-1}(T)$
is connected as follows. Consider the Stein factorization
![]() $\mathcal {C} \xrightarrow {f'} R' \xrightarrow h \tilde R$
of f. Then
$\mathcal {C} \xrightarrow {f'} R' \xrightarrow h \tilde R$
of f. Then
![]() $h^{-1}(T)$
is of pure dimension
$h^{-1}(T)$
is of pure dimension
![]() $1$
. Since all irreducible components of
$1$
. Since all irreducible components of
![]() $f^*T$
except Q are contracted by f, it follows that
$f^*T$
except Q are contracted by f, it follows that
![]() $h^{-1}(T) = f'(Q)$
, in particular, it is irreducible. Eventually, since
$h^{-1}(T) = f'(Q)$
, in particular, it is irreducible. Eventually, since
![]() $f'$
has connected fibres,
$f'$
has connected fibres,
![]() $f^{-1}(T) = (f')^{-1} (h^{-1}(T))$
is connected.
$f^{-1}(T) = (f')^{-1} (h^{-1}(T))$
is connected.
In particular,
![]() $P_0$
and Q are connected by an effective (possibly zero) divisor
$P_0$
and Q are connected by an effective (possibly zero) divisor
![]() $W' \subset f^{-1}(p_0) \cap {\mathcal C}_{b_0} \subset W$
for some
$W' \subset f^{-1}(p_0) \cap {\mathcal C}_{b_0} \subset W$
for some
![]() $b_0 \in B$
. Thus,
$b_0 \in B$
. Thus,
By the generality of the points
![]() $p_0,\ldots ,p_l$
, they cannot be contained in any
$p_0,\ldots ,p_l$
, they cannot be contained in any
![]() $(-1)$
-curve on
$(-1)$
-curve on
![]() $\widetilde R$
, nor can any two of them lie in a fibre of
$\widetilde R$
, nor can any two of them lie in a fibre of
![]() $\pi :\widetilde R \to E$
. Consequently,
$\pi :\widetilde R \to E$
. Consequently,
![]() $ f_* {\mathcal C}_{b_0}$
cannot contain any rational component. Moreover,
$ f_* {\mathcal C}_{b_0}$
cannot contain any rational component. Moreover,
![]() $f_* {\mathcal C}_{b_0}$
must be a reduced curve by (9). Therefore,
$f_* {\mathcal C}_{b_0}$
must be a reduced curve by (9). Therefore,
![]() $f_* {\mathcal C}_{b_0}=C$
is an irreducible curve of geometric genus one, hence,
$f_* {\mathcal C}_{b_0}=C$
is an irreducible curve of geometric genus one, hence,
![]() ${\mathcal C}_{b_0}$
consists of one smooth elliptic curve
${\mathcal C}_{b_0}$
consists of one smooth elliptic curve
![]() $\widetilde {C}$
, such that
$\widetilde {C}$
, such that
![]() $f(\widetilde {C})=C$
and otherwise chains of rational curves contracted by f and attached to
$f(\widetilde {C})=C$
and otherwise chains of rational curves contracted by f and attached to
![]() $\widetilde {C}$
at one single point each. Therefore,
$\widetilde {C}$
at one single point each. Therefore,
![]() $f^{-1}(p_0) \cap \widetilde {C}$
is a single (smooth) point of
$f^{-1}(p_0) \cap \widetilde {C}$
is a single (smooth) point of
![]() $\widetilde {C}$
, hence,
$\widetilde {C}$
, hence,
![]() $[C] \in V_{1,(m+1)p_0+p_1+\cdots +p_{l}}(\widetilde R,T, L)$
by (9), which implies
$[C] \in V_{1,(m+1)p_0+p_1+\cdots +p_{l}}(\widetilde R,T, L)$
by (9), which implies
![]() $[C] \in V_{1,m+1}(\widetilde R,T,L)$
.
$[C] \in V_{1,m+1}(\widetilde R,T,L)$
.
3.3 Logarithmic Severi varieties on blownup planes
Fix a smooth cubic curve
![]() $T \subset P={\mathbb {P}}^2$
. Let
$T \subset P={\mathbb {P}}^2$
. Let
![]() $y_1,\ldots ,y_n \in T$
, for
$y_1,\ldots ,y_n \in T$
, for
![]() $n\geq 0$
, and consider the blowup
$n\geq 0$
, and consider the blowup
![]() $\widetilde P:=\operatorname {Bl}_{y_1,\ldots ,y_n}(P) \to P$
at
$\widetilde P:=\operatorname {Bl}_{y_1,\ldots ,y_n}(P) \to P$
at
![]() $y_1,\ldots ,y_n$
. We denote the strict transforms of the general line on P by
$y_1,\ldots ,y_n$
. We denote the strict transforms of the general line on P by
![]() $\ell $
and by
$\ell $
and by
![]() ${\mathfrak {e}}_i$
the (total) exceptional divisor over
${\mathfrak {e}}_i$
the (total) exceptional divisor over
![]() $y_i$
. We denote still by T the strict transform of T. Note that
$y_i$
. We denote still by T the strict transform of T. Note that
![]() $T \sim -K_{\widetilde P} \sim 3\ell -{\mathfrak {e}}_1-\cdots -{\mathfrak {e}}_n$
.
$T \sim -K_{\widetilde P} \sim 3\ell -{\mathfrak {e}}_1-\cdots -{\mathfrak {e}}_n$
.
The next result parallels Lemma 3.6.
Lemma 3.10. Let L be a line bundle or Cartier divisor on
![]() $\widetilde {P}$
. Let m be any integer satisfying
$\widetilde {P}$
. Let m be any integer satisfying
![]() $1 \leq m \leq L \cdot T$
. Then the following hold:
$1 \leq m \leq L \cdot T$
. Then the following hold:
-
(i) No curve C in
 $\overline {V}_{0,m}(\widetilde {P},T, L)$
contains T.
$\overline {V}_{0,m}(\widetilde {P},T, L)$
contains T. -
(ii) For any component
 $V \subset \overline {V}_{0,m}(\widetilde {P},T, L)$
, the restriction map is well-defined and finite, with image
$V \subset \overline {V}_{0,m}(\widetilde {P},T, L)$
, the restriction map is well-defined and finite, with image $$ \begin{align*} V & \longrightarrow \operatorname{Sym}^{L \cdot T}(T)_m \\ C &\mapsto C \cap T \end{align*} $$
$$ \begin{align*} V & \longrightarrow \operatorname{Sym}^{L \cdot T}(T)_m \\ C &\mapsto C \cap T \end{align*} $$
 $|L \otimes {\mathcal {O}}_T| \cap \operatorname {Sym}^{L \cdot T}(T)_m$
, which has codimension one. In particular,
$|L \otimes {\mathcal {O}}_T| \cap \operatorname {Sym}^{L \cdot T}(T)_m$
, which has codimension one. In particular,  $$ \begin{align*}\dim(V)=L\cdot T-m. \end{align*} $$
$$ \begin{align*}\dim(V)=L\cdot T-m. \end{align*} $$
Proof. Since the members of
![]() $\overline {V}_{0,m}(\widetilde {P},T,L)$
are limits of rational curves, none of them can contain T as a component, which proves (i). As in the proof of Lemma 3.6(ii), the restriction map is everywhere defined and finite. Its image lies in
$\overline {V}_{0,m}(\widetilde {P},T,L)$
are limits of rational curves, none of them can contain T as a component, which proves (i). As in the proof of Lemma 3.6(ii), the restriction map is everywhere defined and finite. Its image lies in
![]() $|L|_T|\cap \operatorname {Sym}^{L \cdot T}(T)_m$
. Since, by Proposition 3.2(ii) and semicontinuity,
$|L|_T|\cap \operatorname {Sym}^{L \cdot T}(T)_m$
. Since, by Proposition 3.2(ii) and semicontinuity,
![]() $\dim (V)\geq L \cdot T-m$
, which equals
$\dim (V)\geq L \cdot T-m$
, which equals
![]() $\dim \left (|L|_T| \cap \operatorname {Sym}^{L \cdot T}(T)_m\right )$
, the latter is in fact the image. This proves (ii).
$\dim \left (|L|_T| \cap \operatorname {Sym}^{L \cdot T}(T)_m\right )$
, the latter is in fact the image. This proves (ii).
The next result is about the relative version
![]() $\nu ^{\langle n\rangle }_{g,m}: \overline {{\mathcal V}^{\langle n\rangle }_{g,m}\left (P,T, L\right )} \longrightarrow T^n$
of the logarithmic Severi variety
$\nu ^{\langle n\rangle }_{g,m}: \overline {{\mathcal V}^{\langle n\rangle }_{g,m}\left (P,T, L\right )} \longrightarrow T^n$
of the logarithmic Severi variety
![]() $\overline {V}_{0,m}(\widetilde {P},T, L)$
considered in Lemma 3.10 above (see Section 3.1).
$\overline {V}_{0,m}(\widetilde {P},T, L)$
considered in Lemma 3.10 above (see Section 3.1).
Lemma 3.11. (i) Assume that
![]() $n>0$
and L is a relative line bundle that is positive on the i-th exceptional divisor. Fix a point
$n>0$
and L is a relative line bundle that is positive on the i-th exceptional divisor. Fix a point
![]() $(y_1,\ldots ,y_{i-1},y_{i+1}, \ldots ,y_n) \in T^{n-1}$
. Let
$(y_1,\ldots ,y_{i-1},y_{i+1}, \ldots ,y_n) \in T^{n-1}$
. Let
![]() ${\mathcal V}$
be any component of
${\mathcal V}$
be any component of
Then the restriction map
is finite and surjective.
(ii) Assume, furthermore, that
![]() $n \geq 2$
and L is positive, with two different values, on the i-th and j-th exceptional divisor,
$n \geq 2$
and L is positive, with two different values, on the i-th and j-th exceptional divisor,
![]() $i < j$
. Fix any linear series
$i < j$
. Fix any linear series
![]() $\mathfrak {g}$
of type
$\mathfrak {g}$
of type
![]() $g^1_2$
on T and any point
$g^1_2$
on T and any point
![]() $(y_1,\ldots ,y_{i-1},y_{i+1}, \ldots ,y_{j-1},y_{j+1}, \ldots , y_n) \in T^{n-2}$
. Let
$(y_1,\ldots ,y_{i-1},y_{i+1}, \ldots ,y_{j-1},y_{j+1}, \ldots , y_n) \in T^{n-2}$
. Let
![]() ${\mathcal V}$
be any component of the subset
${\mathcal V}$
be any component of the subset
Then the restriction map
is finite and surjective.
Proof. Assume
![]() $L \cdot {\mathfrak {e}}_i>0$
for some i. Varying p, we obtain a one-dimensional nontrivial family of surfaces
$L \cdot {\mathfrak {e}}_i>0$
for some i. Varying p, we obtain a one-dimensional nontrivial family of surfaces
![]() $\operatorname {Bl}_{y_1,\ldots ,y_{i-1},p,y_{i+1}, \ldots ,y_n}(P)$
and a one-dimensional nonconstant family of line bundles whose restrictions to T yield a one-dimensional nonconstant family of line bundles. This together with Lemma 3.10(ii) yields (i).
$\operatorname {Bl}_{y_1,\ldots ,y_{i-1},p,y_{i+1}, \ldots ,y_n}(P)$
and a one-dimensional nonconstant family of line bundles whose restrictions to T yield a one-dimensional nonconstant family of line bundles. This together with Lemma 3.10(ii) yields (i).
Finally, assume
![]() $L \cdot {\mathfrak {e}}_i=a_i>0$
and
$L \cdot {\mathfrak {e}}_i=a_i>0$
and
![]() $L \cdot {\mathfrak {e}}_j=a_j>0$
, with
$L \cdot {\mathfrak {e}}_j=a_j>0$
, with
![]() $a_i \neq a_j$
. Varying
$a_i \neq a_j$
. Varying
![]() $p+q \in \mathfrak {g}$
, we get a one-dimensional nontrivial family of surfaces
$p+q \in \mathfrak {g}$
, we get a one-dimensional nontrivial family of surfaces
![]() $\operatorname {Bl}_{y_1,\ldots ,y_{i-1},p,y_{i+1}, \ldots ,y_{j-1},q,y_{j+1}, \ldots ,y_n}(P)$
as above and a one-dimensional family of line bundles, all of the form
$\operatorname {Bl}_{y_1,\ldots ,y_{i-1},p,y_{i+1}, \ldots ,y_{j-1},q,y_{j+1}, \ldots ,y_n}(P)$
as above and a one-dimensional family of line bundles, all of the form
![]() $L'-a_i{\mathfrak {e}}_i-a_j{\mathfrak {e}}_j$
, with
$L'-a_i{\mathfrak {e}}_i-a_j{\mathfrak {e}}_j$
, with
![]() $L'$
fixed (on
$L'$
fixed (on
![]() $\operatorname {Bl}_{y_1,\ldots ,y_{i-1},y_{i+1}, \ldots ,y_{j-1},y_{j+1}, \ldots ,y_n}(P)$
) and
$\operatorname {Bl}_{y_1,\ldots ,y_{i-1},y_{i+1}, \ldots ,y_{j-1},y_{j+1}, \ldots ,y_n}(P)$
) and
![]() ${\mathfrak {e}}_i$
and
${\mathfrak {e}}_i$
and
![]() ${\mathfrak {e}}_j$
varying with p and q. To prove (ii), we will prove that the family of restrictions
${\mathfrak {e}}_j$
varying with p and q. To prove (ii), we will prove that the family of restrictions
to T is nonconstant. Assume that
This yields
![]() $(a_i-a_j) p \sim (a_i-a_j) p'$
and
$(a_i-a_j) p \sim (a_i-a_j) p'$
and
![]() $(a_i-a_j) q \sim (a_i-a_j) q'$
. For fixed
$(a_i-a_j) q \sim (a_i-a_j) q'$
. For fixed
![]() $x \in T$
, there are only finitely many points
$x \in T$
, there are only finitely many points
![]() $y \in T$
, such that
$y \in T$
, such that
![]() $(a_i-a_j) x \sim (a_i-a_j) y$
. For general
$(a_i-a_j) x \sim (a_i-a_j) y$
. For general
![]() $p+q, p'+q' \in \mathfrak {g}$
, condition (10) is therefore not fulfilled. This finishes the proof of (ii).
$p+q, p'+q' \in \mathfrak {g}$
, condition (10) is therefore not fulfilled. This finishes the proof of (ii).
The main existence result of this subsection is the following:
Proposition 3.12. Let
![]() $y_1, \ldots , y_n \in T$
be general,
$y_1, \ldots , y_n \in T$
be general,
![]() $n \leq 8$
and L be big and nef on
$n \leq 8$
and L be big and nef on
![]() $\widetilde {P}$
. If
$\widetilde {P}$
. If
![]() $ 0< m \leq L \cdot T-3$
, the variety
$ 0< m \leq L \cdot T-3$
, the variety
![]() $V^*_{0,m}(\widetilde {P},T,L)$
is nonempty of dimension
$V^*_{0,m}(\widetilde {P},T,L)$
is nonempty of dimension
![]() $T\cdot L-m$
. Moreover, its general member intersects any fixed curve on
$T\cdot L-m$
. Moreover, its general member intersects any fixed curve on
![]() $\widetilde {P}$
different from T transversely.
$\widetilde {P}$
different from T transversely.
Proof. This is an application of [Reference Chen, Gounelas and Liedtke6, Corollary 3.11]; there are some conditions to check, so we give a proof for completeness.
The statements about dimension and transversal intersection follow from Proposition 3.2(ii) and (iii), respectively, once nonemptiness is proved. By Proposition 3.2(iii)–(iv), we have that
![]() $V^*_{0,m}(\widetilde {P},L) \neq \emptyset $
as soon as
$V^*_{0,m}(\widetilde {P},L) \neq \emptyset $
as soon as
![]() $V_{0,m}(\widetilde {P},T,L) \neq \emptyset $
, because of the condition
$V_{0,m}(\widetilde {P},T,L) \neq \emptyset $
, because of the condition
![]() $m \leq L \cdot T-3$
. We therefore have left to prove nonemptiness of
$m \leq L \cdot T-3$
. We therefore have left to prove nonemptiness of
![]() $V_{0,m}(\widetilde {P},T,L)$
. We will prove this by induction on m, as in the proof of Proposition 3.9, again following an idea in the proof of [Reference Chen, Gounelas and Liedtke6, Theorem 3.10].
$V_{0,m}(\widetilde {P},T,L)$
. We will prove this by induction on m, as in the proof of Proposition 3.9, again following an idea in the proof of [Reference Chen, Gounelas and Liedtke6, Theorem 3.10].
Since
![]() $y_1\ldots ,y_n \in T$
are general and
$y_1\ldots ,y_n \in T$
are general and
![]() $n \leq 8$
, we may take
$n \leq 8$
, we may take
![]() $y_1,\ldots ,y_n$
to be general points of
$y_1,\ldots ,y_n$
to be general points of
![]() ${\mathbb {P}}^2$
and T a general plane cubic containing them. Hence,
${\mathbb {P}}^2$
and T a general plane cubic containing them. Hence,
![]() $\widetilde {P}$
is a Del Pezzo surface, so that T is ample on it. It is then well-known, by [Reference Greuel, Lossen and Shustin20, Theorems 3–4], that
$\widetilde {P}$
is a Del Pezzo surface, so that T is ample on it. It is then well-known, by [Reference Greuel, Lossen and Shustin20, Theorems 3–4], that
![]() $V_{0,1}(\widetilde {P},T,L) \neq \emptyset $
.
$V_{0,1}(\widetilde {P},T,L) \neq \emptyset $
.
Assume now that we have proved nonemptiness of
![]() $V_{0,m}(\widetilde {P},T,L)$
for some
$V_{0,m}(\widetilde {P},T,L)$
for some
![]() $1 \leq m \leq L \cdot T-4$
. By Lemma 3.10(ii), its general member C satisfies
$1 \leq m \leq L \cdot T-4$
. By Lemma 3.10(ii), its general member C satisfies
where
![]() $p_0,\ldots ,p_{l+2}$
are distinct, and we may take
$p_0,\ldots ,p_{l+2}$
are distinct, and we may take
![]() $p_0,\ldots ,p_{l+1}$
general on T.
$p_0,\ldots ,p_{l+1}$
general on T.
For later purposes, we observe that, since there are only finitely many divisor classes D, such that
![]() $C-D>0$
(by which we mean that
$C-D>0$
(by which we mean that
![]() $C-D$
is effective and nonzero), hence,
$C-D$
is effective and nonzero), hence,
![]() $C\cdot T>D\cdot T$
, and for each such class, the image of the restriction morphism
$C\cdot T>D\cdot T$
, and for each such class, the image of the restriction morphism
![]() $|D| \to \operatorname {Sym}^{D \cdot T} (T)$
has codimension one, the generality of the points implies that
$|D| \to \operatorname {Sym}^{D \cdot T} (T)$
has codimension one, the generality of the points implies that
 $$ \begin{align}\begin{aligned} &\mbox{there is no effective divisor $D\neq T$ such that}\\&C-D>0 \; \; \mbox{and} \; \; D \cap T \subset \{p_0,p_1,\ldots,p_l\}.\end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} &\mbox{there is no effective divisor $D\neq T$ such that}\\&C-D>0 \; \; \mbox{and} \; \; D \cap T \subset \{p_0,p_1,\ldots,p_l\}.\end{aligned} \end{align} $$
Set
![]() ${\mathfrak {d}}=mp_0+p_1+\cdots +p_{l}$
. Then
${\mathfrak {d}}=mp_0+p_1+\cdots +p_{l}$
. Then
![]() $V_{0,{\mathfrak {d}}}(\widetilde {P},T, L) \neq \emptyset $
, and all its components are one-dimensional, by Proposition 3.2(i). The general member in any component intersects T in
$V_{0,{\mathfrak {d}}}(\widetilde {P},T, L) \neq \emptyset $
, and all its components are one-dimensional, by Proposition 3.2(i). The general member in any component intersects T in
![]() $mp_0+p_1+\cdots +p_{l}+q_1+q_2$
, where the points
$mp_0+p_1+\cdots +p_{l}+q_1+q_2$
, where the points
![]() $q_1,q_2$
vary in the family, by Proposition 3.2(iii). Pick a component
$q_1,q_2$
vary in the family, by Proposition 3.2(iii). Pick a component
![]() $\overline {V}$
of its closure inside the component of the Hilbert scheme of
$\overline {V}$
of its closure inside the component of the Hilbert scheme of
![]() $\widetilde {P}$
containing
$\widetilde {P}$
containing
![]() $|L|$
. After a finite base change, we find a smooth projective curve B, a surjection
$|L|$
. After a finite base change, we find a smooth projective curve B, a surjection
![]() $B \to \overline {V}$
and a family
$B \to \overline {V}$
and a family

of stable maps of genus zero, such that, setting
![]() ${\mathcal C}_b:=g^*b$
for any
${\mathcal C}_b:=g^*b$
for any
![]() $b \in B$
, the curve
$b \in B$
, the curve
![]() $f_*{\mathcal C}_b$
is a member of
$f_*{\mathcal C}_b$
is a member of
![]() $\overline {V}$
, and such that
$\overline {V}$
, and such that
where
-
(I)
 $P_i$
and
$P_i$
and
 $Q_j$
are sections of g, for
$Q_j$
are sections of g, for
 $i \in \{0,\ldots ,l\}$
,
$i \in \{0,\ldots ,l\}$
,
 $j \in \{1,2\}$
,
$j \in \{1,2\}$
, -
(II)
 $f(P_i)=p_i$
, for
$f(P_i)=p_i$
, for
 $i \in \{0,\ldots ,l\}$
,
$i \in \{0,\ldots ,l\}$
, -
(III)
 $f(Q_j)=T$
, for
$f(Q_j)=T$
, for
 $j \in \{1,2\}$
,
$j \in \{1,2\}$
, -
(IV)
 $g_*W=0$
,
$g_*W=0$
, -
(V)
 $f_*W=0$
;
$f_*W=0$
;
the latter property follows from the fact that no member of
![]() $\overline {V}$
contains T, by Lemma 3.10(i). Since T is ample,
$\overline {V}$
contains T, by Lemma 3.10(i). Since T is ample,
![]() $f^*T$
is big and nef, hence, its support
$f^*T$
is big and nef, hence, its support
![]() $f^{-1}(T)$
is connected as a consequence of Kawamata–Viehweg vanishing. Therefore,
$f^{-1}(T)$
is connected as a consequence of Kawamata–Viehweg vanishing. Therefore,
![]() $P_0$
and
$P_0$
and
![]() $Q_2$
are connected by a chain
$Q_2$
are connected by a chain
![]() $W' \subset W$
, such that
$W' \subset W$
, such that
![]() $W' \subset {\mathcal C}_{b_0}$
for some
$W' \subset {\mathcal C}_{b_0}$
for some
![]() $b_0 \in B$
, and
$b_0 \in B$
, and
![]() $f(W')=p_0$
. Thus,
$f(W')=p_0$
. Thus,
Since T is ample, all components of
![]() $f_* {\mathcal C}_{b_0}$
intersect T. By (11) and (12),
$f_* {\mathcal C}_{b_0}$
intersect T. By (11) and (12),
![]() $f_* {\mathcal C}_{b_0}$
must be reduced and irreducible, say
$f_* {\mathcal C}_{b_0}$
must be reduced and irreducible, say
![]() $ f_* {\mathcal C}_{b_0}=C$
, an irreducible rational curve. Since
$ f_* {\mathcal C}_{b_0}=C$
, an irreducible rational curve. Since
![]() ${\mathcal C}_{b_0}$
has arithmetic genus
${\mathcal C}_{b_0}$
has arithmetic genus
![]() $0$
, it consists of a tree of smooth rational curves, with one component
$0$
, it consists of a tree of smooth rational curves, with one component
![]() $\widetilde {C}$
, such that
$\widetilde {C}$
, such that
![]() $f(\widetilde {C})=C$
, and the other components contracted by f. Therefore,
$f(\widetilde {C})=C$
, and the other components contracted by f. Therefore,
![]() $f^{-1}(p_0) \cap \widetilde {C}=(W'+P_0) \cap \widetilde {C}$
is a single (smooth) point of
$f^{-1}(p_0) \cap \widetilde {C}=(W'+P_0) \cap \widetilde {C}$
is a single (smooth) point of
![]() $\widetilde {C}$
. It follows that
$\widetilde {C}$
. It follows that
![]() $[C] \in V_{0,(m+1)p_0+p_1+\cdots +p_{l}}(\widetilde {P},T, L)$
, which implies
$[C] \in V_{0,(m+1)p_0+p_1+\cdots +p_{l}}(\widetilde {P},T, L)$
, which implies
![]() $[C] \in V_{0,m+1}(\widetilde {P},T,L)$
.
$[C] \in V_{0,m+1}(\widetilde {P},T,L)$
.
4 Deforming to rigid elliptic curves
As mentioned in the Introduction, to prove Theorem 1.1, it will suffice by [Reference Ciliberto, Dedieu, Galati and Knutsen9, Corollary 1] to prove that
![]() $V_{|L|,g-1}(S)$
has a
$V_{|L|,g-1}(S)$
has a
![]() $0$
-dimensional component. We will call any element of such a
$0$
-dimensional component. We will call any element of such a
![]() $0$
-dimensional component a rigid nodal elliptic curve. We will prove the existence of such a curve on a general
$0$
-dimensional component a rigid nodal elliptic curve. We will prove the existence of such a curve on a general
![]() $(S,L)$
in any component of
$(S,L)$
in any component of
![]() ${\mathcal E}_g \setminus {\mathcal E}_g[2]$
by degeneration, using Theorem 2.2, constructing suitable curves on limit surfaces in
${\mathcal E}_g \setminus {\mathcal E}_g[2]$
by degeneration, using Theorem 2.2, constructing suitable curves on limit surfaces in
![]() $\mathcal D^*$
that will deform to rigid curves in
$\mathcal D^*$
that will deform to rigid curves in
![]() $V_{|L|,g-1}(S)$
. In this section, we will identify numerical conditions on limit line bundles under which deformations to such curves can be achieved. The general strategy of proof is given in the following:
$V_{|L|,g-1}(S)$
. In this section, we will identify numerical conditions on limit line bundles under which deformations to such curves can be achieved. The general strategy of proof is given in the following:
Proposition 4.1. Let
![]() $X=\widetilde {R} \cup _T \widetilde {P}$
be a general member of a component of
$X=\widetilde {R} \cup _T \widetilde {P}$
be a general member of a component of
![]() ${\mathcal D}^*$
and
${\mathcal D}^*$
and
![]() $Y=C \cup _T D$
a curve on X, with
$Y=C \cup _T D$
a curve on X, with
![]() $C \subset \widetilde {R}$
and
$C \subset \widetilde {R}$
and
![]() $D \subset \widetilde {P}$
, having the following properties: there are distinct points
$D \subset \widetilde {P}$
, having the following properties: there are distinct points
![]() $x,p_1,\ldots ,p_k,q_1,\ldots ,q_l$
on T, for nonnegative integers
$x,p_1,\ldots ,p_k,q_1,\ldots ,q_l$
on T, for nonnegative integers
![]() $k,l$
and a positive integer m, such that
$k,l$
and a positive integer m, such that
-
•
 $C=C_0+C_1+ \cdots + C_l$
is nodal, with
$C=C_0+C_1+ \cdots + C_l$
is nodal, with
 $[C_0] \in V^{**}_{1,m}(\widetilde {R},T, C_0)$
and
$[C_0] \in V^{**}_{1,m}(\widetilde {R},T, C_0)$
and
 $C_i$
a
$C_i$
a
 $(-1)$
-curve,
$(-1)$
-curve,
 $i \in \{1,\ldots ,l\}$
,
$i \in \{1,\ldots ,l\}$
, -
•
 $C_0 \cap T=mx+p_1+\cdots + p_k$
,
$C_0 \cap T=mx+p_1+\cdots + p_k$
, -
•
 $C_0$
is odd,
$C_0$
is odd, -
•
 $C_i \cap T=\{q_i\}$
,
$C_i \cap T=\{q_i\}$
,
 $i \in \{1,\ldots ,l\}$
,
$i \in \{1,\ldots ,l\}$
,
and
-
•
 $D=D_0+D_1+ \cdots + D_k$
is nodal, with
$D=D_0+D_1+ \cdots + D_k$
is nodal, with
 $[D_0] \in V^{*}_{0,m}(\widetilde {P},T, D_0)$
and
$[D_0] \in V^{*}_{0,m}(\widetilde {P},T, D_0)$
and
 $D_i$
a
$D_i$
a
 $(-1)$
-curve,
$(-1)$
-curve,
 $i \in \{1,\ldots ,k\}$
,
$i \in \{1,\ldots ,k\}$
, -
•
 $D_0 \cap T=mx+q_1+\cdots + q_l$
,
$D_0 \cap T=mx+q_1+\cdots + q_l$
, -
•
 $D_i \cap T=\{p_i\}$
,
$D_i \cap T=\{p_i\}$
,
 $i \in \{1,\ldots ,k\}$
.
$i \in \{1,\ldots ,k\}$
.
Then Y deforms to an irreducible rigid nodal elliptic curve on the general deformation S of X.
Proof. Here is a picture of what Y looks like:
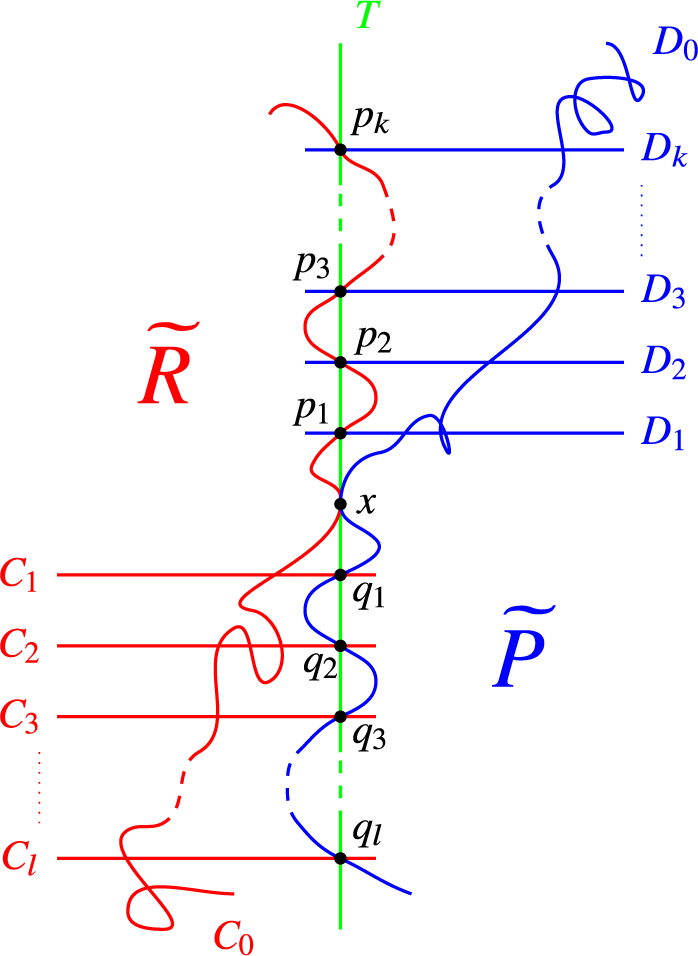
We note that Y is Cartier, has an m-tacnode at x and is otherwise nodal. Moreover, an easy computation as in [Reference Knutsen23, p. 119] shows that
We define
-
•
 $N_{C_0}$
the scheme of nodes of
$N_{C_0}$
the scheme of nodes of
 $C_0$
and
$C_0$
and
 $\gamma _0$
its degree,
$\gamma _0$
its degree, -
•
 $N_{C}$
the scheme of intersection points between components of C and
$N_{C}$
the scheme of intersection points between components of C and
 $\gamma $
its degree,
$\gamma $
its degree, -
•
 $N_{D_0}$
the scheme of nodes of
$N_{D_0}$
the scheme of nodes of
 $D_0$
and
$D_0$
and
 $\delta _0$
its degree,
$\delta _0$
its degree, -
•
 $N_{D}$
the scheme of intersection points between components of D and
$N_{D}$
the scheme of intersection points between components of D and
 $\delta $
its degree.
$\delta $
its degree.
Then
![]() $N_{C_0} \cup N_C \cup N_{D_0}\cup N_D$
is the set of nodes of Y off T. Since
$N_{C_0} \cup N_C \cup N_{D_0}\cup N_D$
is the set of nodes of Y off T. Since
and, similarly,
we compute
 $$ \begin{align} p_a(Y)& = \frac{1}{2}Y^2+1=\frac{1}{2}\left(C^2+D^2\right)+1=\frac{1}{2}\left(C_0^2-l+2\gamma+D_0^2-k+2\delta\right)+1\\& = \frac{1}{2}\left(C_0^2-m-k\right) +\frac{1}{2}\left(D_0^2-m-l\right) +m+\gamma+\delta+1 \nonumber \\& = \gamma_0+(\delta_0-1)+m+\gamma+\delta+1 = \gamma_0+\gamma+\delta_0+\delta+m.\nonumber \end{align} $$
$$ \begin{align} p_a(Y)& = \frac{1}{2}Y^2+1=\frac{1}{2}\left(C^2+D^2\right)+1=\frac{1}{2}\left(C_0^2-l+2\gamma+D_0^2-k+2\delta\right)+1\\& = \frac{1}{2}\left(C_0^2-m-k\right) +\frac{1}{2}\left(D_0^2-m-l\right) +m+\gamma+\delta+1 \nonumber \\& = \gamma_0+(\delta_0-1)+m+\gamma+\delta+1 = \gamma_0+\gamma+\delta_0+\delta+m.\nonumber \end{align} $$
Let
![]() $\mathfrak {X} \to {\mathbb D}$
be the deformation of X to a general smooth Enriques surface
$\mathfrak {X} \to {\mathbb D}$
be the deformation of X to a general smooth Enriques surface
![]() $S_t$
in Theorem 2.2. Then Y deforms to a Cartier divisor
$S_t$
in Theorem 2.2. Then Y deforms to a Cartier divisor
![]() $Y_t$
on
$Y_t$
on
![]() $S_t$
by the same theorem. By (13), we have
$S_t$
by the same theorem. By (13), we have
![]() $\dim (|Y|)=\dim (|Y_t|)$
. Let
$\dim (|Y|)=\dim (|Y_t|)$
. Let
![]() $\mathfrak {D}$
be the sublinear system of
$\mathfrak {D}$
be the sublinear system of
![]() $|Y|$
of curves with an
$|Y|$
of curves with an
![]() $(m-1)$
-tacnode at x and passing through
$(m-1)$
-tacnode at x and passing through
![]() $N_{C_0} \cup N_C \cup N_{D_0}\cup N_D$
. We claim that
$N_{C_0} \cup N_C \cup N_{D_0}\cup N_D$
. We claim that
GrantingFootnote
1
this for the moment, (13)-(15) yields that the codimension of
![]() $\mathfrak {D}$
is
$\mathfrak {D}$
is
![]() $m-1+\gamma _0+\gamma +\delta _0+\delta $
. Thus, the hypotheses of [Reference Galati and Knutsen18, Theorem 3.3, Corollary 3.12 and proof of Theorem 1.1] are fulfilled,Footnote
2
and we conclude that, under the deformation of X to
$m-1+\gamma _0+\gamma +\delta _0+\delta $
. Thus, the hypotheses of [Reference Galati and Knutsen18, Theorem 3.3, Corollary 3.12 and proof of Theorem 1.1] are fulfilled,Footnote
2
and we conclude that, under the deformation of X to
![]() $S_t$
, we may deform Y in such a way that the m-tacnode of Y at x deforms to
$S_t$
, we may deform Y in such a way that the m-tacnode of Y at x deforms to
![]() $m-1$
nodes and the
$m-1$
nodes and the
![]() $\gamma _0+\gamma +\delta _0+\delta $
nodes of Y in the smooth locus of X are preserved, whereas the nodes of` Y on T automatically smooth. Thus, Y deforms to a nodal curve
$\gamma _0+\gamma +\delta _0+\delta $
nodes of Y in the smooth locus of X are preserved, whereas the nodes of` Y on T automatically smooth. Thus, Y deforms to a nodal curve
![]() $Y_t \subset S_t$
with a total of
$Y_t \subset S_t$
with a total of
nodes (using (14)). Since one easily sees that no subcurve of Y is Cartier,
![]() $Y_t$
is irreducible, whence
$Y_t$
is irreducible, whence
![]() $Y_t$
is nodal and elliptic, as desired. It is rigid, as Y is rigid on X.
$Y_t$
is nodal and elliptic, as desired. It is rigid, as Y is rigid on X.
We have left to prove (15). To this end, let
![]() $A \cup _T B \in |Y|$
be a curve with an
$A \cup _T B \in |Y|$
be a curve with an
![]() $(m-1)$
-tacnode at x and passing through
$(m-1)$
-tacnode at x and passing through
![]() $N_{C_0} \cup N_C \cup N_{D_0}\cup N_D$
, where
$N_{C_0} \cup N_C \cup N_{D_0}\cup N_D$
, where
![]() $A \subset \widetilde {R}$
and
$A \subset \widetilde {R}$
and
![]() $B \subset \widetilde {P}$
. Then both A and B must intersect T in a scheme containing
$B \subset \widetilde {P}$
. Then both A and B must intersect T in a scheme containing
![]() $(m-1)x$
and, moreover,
$(m-1)x$
and, moreover,
![]() $N_{C_0} \cup N_C \subset A$
and
$N_{C_0} \cup N_C \subset A$
and
![]() $N_{D_0} \cup N_D \subset B$
.
$N_{D_0} \cup N_D \subset B$
.
The fact that
![]() $N_D \subset B$
implies that B must contain all
$N_D \subset B$
implies that B must contain all
![]() $(-1)$
-curves
$(-1)$
-curves
![]() $D_1,\ldots ,D_k$
. Hence,
$D_1,\ldots ,D_k$
. Hence,
![]() $B =B_0+D_1+\cdots + D_k$
, with
$B =B_0+D_1+\cdots + D_k$
, with
![]() $B_0 \sim D_0$
. Similarly, the fact that
$B_0 \sim D_0$
. Similarly, the fact that
![]() $N_C \subset A$
implies that A must contain all
$N_C \subset A$
implies that A must contain all
![]() $(-1)$
-curves
$(-1)$
-curves
![]() $C_1,\ldots ,C_k$
. Hence,
$C_1,\ldots ,C_k$
. Hence,
![]() $A =A_0+C_1+\cdots +C_k$
, with
$A =A_0+C_1+\cdots +C_k$
, with
![]() $A_0 \sim C_0$
. Since
$A_0 \sim C_0$
. Since
![]() $A \cup _T B$
is Cartier,
$A \cup _T B$
is Cartier,
![]() $A_0$
must pass through
$A_0$
must pass through
![]() $p_1,\ldots ,p_k$
and
$p_1,\ldots ,p_k$
and
![]() $B_0$
must pass through
$B_0$
must pass through
![]() $q_1,\ldots ,q_l$
. Thus
$q_1,\ldots ,q_l$
. Thus
Hence,
![]() $A_0 \in |{\mathcal {O}}_{\widetilde {R}}(C_0) \otimes {\mathcal J}_{N_{C_0} \cup Z_C}|$
. Since
$A_0 \in |{\mathcal {O}}_{\widetilde {R}}(C_0) \otimes {\mathcal J}_{N_{C_0} \cup Z_C}|$
. Since
![]() $\deg (Z_C)=C_0 \cdot T-1$
and
$\deg (Z_C)=C_0 \cdot T-1$
and
![]() $[C_0] \in V^{**}_{1,m}(\widetilde {R},T, C_0)$
, this implies
$[C_0] \in V^{**}_{1,m}(\widetilde {R},T, C_0)$
, this implies
![]() $A_0=C_0$
(recall Definition 3.7), whence
$A_0=C_0$
(recall Definition 3.7), whence
![]() $A=C$
.
$A=C$
.
Similarly,
![]() $B_0 \in |{\mathcal {O}}_{\widetilde {P}}(D_0) \otimes {\mathcal J}_{N_{D_0} \cup Z_D}|$
, whence, if
$B_0 \in |{\mathcal {O}}_{\widetilde {P}}(D_0) \otimes {\mathcal J}_{N_{D_0} \cup Z_D}|$
, whence, if
![]() $B_0 \neq D_0$
, we would get
$B_0 \neq D_0$
, we would get
 $$ \begin{align*} D_0^2 & = B_0 \cdot D_0 \geq \deg (Z_D) +2\deg(N_{D_0}) = (D_0 \cdot T-1)+ 2p_a(D_0)\\ & = -D_0 \cdot K_{\widetilde{P}}-1+D_0^2+D_0 \cdot K_{\widetilde{P}}+2>D_0^2, \end{align*} $$
$$ \begin{align*} D_0^2 & = B_0 \cdot D_0 \geq \deg (Z_D) +2\deg(N_{D_0}) = (D_0 \cdot T-1)+ 2p_a(D_0)\\ & = -D_0 \cdot K_{\widetilde{P}}-1+D_0^2+D_0 \cdot K_{\widetilde{P}}+2>D_0^2, \end{align*} $$
a contradiction. Thus,
![]() $B_0=D_0$
, whence
$B_0=D_0$
, whence
![]() $B=D$
. This proves (15).
$B=D$
. This proves (15).
The next two results form the basis for our proof of Theorem 1.1. We henceforth assume that E is a general elliptic curve.
Proposition 4.2. Let
![]() $R'$
(respectively,
$R'$
(respectively,
![]() $P'$
) be a blowup of R (respectively, P) at
$P'$
) be a blowup of R (respectively, P) at
![]() $s \geq 0$
(respectively,
$s \geq 0$
(respectively,
![]() $t \geq 1$
) general points of T. Assume
$t \geq 1$
) general points of T. Assume
![]() $L'$
(respectively,
$L'$
(respectively,
![]() $L"$
) is a line bundle (or Cartier divisor) on
$L"$
) is a line bundle (or Cartier divisor) on
![]() $R'$
(respectively,
$R'$
(respectively,
![]() $P'$
) and k is an integer, such that the following conditions are satisfied:
$P'$
) and k is an integer, such that the following conditions are satisfied:
-
(i)
 $s+t-5\leq k \leq \min \{3,s,t-1\}$
,
$s+t-5\leq k \leq \min \{3,s,t-1\}$
, -
(ii)
 $L'\cdot T=L"\cdot T$
,
$L'\cdot T=L"\cdot T$
, -
(iii)
 $L' \equiv L^{\prime }_0+C_1+ \cdots +C_k$
, where the
$L' \equiv L^{\prime }_0+C_1+ \cdots +C_k$
, where the
 $C_i$
are disjoint
$C_i$
are disjoint
 $(-1)$
-curves and
$(-1)$
-curves and
 $L^{\prime }_0$
satisfies condition
$L^{\prime }_0$
satisfies condition
 $(\star )$
and is odd,
$(\star )$
and is odd, -
(iv)
 $L" \sim L^{\prime \prime }_0+D_1+ \cdots +D_k$
, where the
$L" \sim L^{\prime \prime }_0+D_1+ \cdots +D_k$
, where the
 $D_i$
are disjoint
$D_i$
are disjoint
 $(-1)$
-curves and
$(-1)$
-curves and
 $L^{\prime \prime }_0$
is big and nef,
$L^{\prime \prime }_0$
is big and nef, -
(v) there are
 $t-k$
additional
$t-k$
additional
 $(-1)$
-curves on
$(-1)$
-curves on
 $P'$
, mutually disjoint and disjoint from
$P'$
, mutually disjoint and disjoint from
 $D_1,\ldots ,D_k$
, such that
$D_1,\ldots ,D_k$
, such that
 $L"$
is positive on at least one of them.
$L"$
is positive on at least one of them.
Then there are blowups
![]() $\widetilde R\to R'$
and
$\widetilde R\to R'$
and
![]() $\widetilde P\to P'$
at distinct points of T, such that
$\widetilde P\to P'$
at distinct points of T, such that
![]() $\widetilde R\cup _T\widetilde P$
is general in a component of
$\widetilde R\cup _T\widetilde P$
is general in a component of
![]() $\mathcal D^*$
and, denoting by
$\mathcal D^*$
and, denoting by
![]() $\widetilde L'$
and
$\widetilde L'$
and
![]() $\widetilde L"$
the pullbacks of
$\widetilde L"$
the pullbacks of
![]() $L'$
and
$L'$
and
![]() $L"$
to
$L"$
to
![]() $\widetilde R$
and
$\widetilde R$
and
![]() $\widetilde P$
, respectively, there is a line bundle
$\widetilde P$
, respectively, there is a line bundle
![]() $\widetilde L\in [\widetilde L',\widetilde L"]$
(cf. Remark 2.1), such that
$\widetilde L\in [\widetilde L',\widetilde L"]$
(cf. Remark 2.1), such that
![]() $(\widetilde R \cup _T \widetilde P, \widetilde L)$
deforms to a smooth polarised Enriques surface
$(\widetilde R \cup _T \widetilde P, \widetilde L)$
deforms to a smooth polarised Enriques surface
![]() $(S,L)$
with S containing an irreducible, rigid nodal elliptic curve in
$(S,L)$
with S containing an irreducible, rigid nodal elliptic curve in
![]() $|L|$
.
$|L|$
.
Proof. Set
![]() $m:=L_0'\cdot T-3=L^{\prime \prime }_0\cdot T-3$
(equality follows from assumptions (ii)–(iv)). By condition (iv) in
$m:=L_0'\cdot T-3=L^{\prime \prime }_0\cdot T-3$
(equality follows from assumptions (ii)–(iv)). By condition (iv) in
![]() $(\star )$
, we have
$(\star )$
, we have
![]() $m>0$
. The line bundle
$m>0$
. The line bundle
![]() $L^{\prime }_0$
satisfies the conditions of Proposition 3.9. Hence,
$L^{\prime }_0$
satisfies the conditions of Proposition 3.9. Hence,
![]() $V^{**}_{1,m}(R',T, L^{\prime }_0) \neq \emptyset $
and its general member intersects
$V^{**}_{1,m}(R',T, L^{\prime }_0) \neq \emptyset $
and its general member intersects
![]() $C_1,\ldots ,C_k$
transversely. Let
$C_1,\ldots ,C_k$
transversely. Let
![]() $C_0$
be such a general member; we have
$C_0$
be such a general member; we have
![]() $L' \equiv C_0+C_1+ \cdots +C_k$
by assumption (iii).
$L' \equiv C_0+C_1+ \cdots +C_k$
by assumption (iii).
The surface
![]() $R'$
is a blowup of R at s general points
$R'$
is a blowup of R at s general points
![]() $y_1,\ldots , y_s$
of T, where
$y_1,\ldots , y_s$
of T, where
![]() $k\leq s\leq 4$
by assumption (i). Denoting the exceptional divisor over
$k\leq s\leq 4$
by assumption (i). Denoting the exceptional divisor over
![]() $y_i$
by
$y_i$
by
![]() ${\mathfrak {e}}_i$
, the surface
${\mathfrak {e}}_i$
, the surface
![]() $R'$
contains precisely s additional
$R'$
contains precisely s additional
![]() $(-1)$
-curves
$(-1)$
-curves
![]() ${\mathfrak {e}}^{\prime }_i$
,
${\mathfrak {e}}^{\prime }_i$
,
![]() $i=1,\ldots ,s$
, such that
$i=1,\ldots ,s$
, such that
![]() ${\mathfrak {e}}_i \cdot {\mathfrak {e}}^{\prime }_i=1$
and each
${\mathfrak {e}}_i \cdot {\mathfrak {e}}^{\prime }_i=1$
and each
![]() ${\mathfrak {e}}_i + {\mathfrak {e}}^{\prime }_i$
is a fibre of the projection
${\mathfrak {e}}_i + {\mathfrak {e}}^{\prime }_i$
is a fibre of the projection
![]() $R'\to E$
. Set
$R'\to E$
. Set
![]() $y^{\prime }_i:={\mathfrak {e}}^{\prime }_i \cap T$
. Since
$y^{\prime }_i:={\mathfrak {e}}^{\prime }_i \cap T$
. Since
![]() $C_1, \ldots , C_k$
are disjoint
$C_1, \ldots , C_k$
are disjoint
![]() $(-1)$
-curves by assumption (iii), we have, after renumbering, that
$(-1)$
-curves by assumption (iii), we have, after renumbering, that
![]() $C_i={\mathfrak {e}}_i$
or
$C_i={\mathfrak {e}}_i$
or
![]() ${\mathfrak {e}}^{\prime }_i$
. We will in the following, for simplicity, assume that
${\mathfrak {e}}^{\prime }_i$
. We will in the following, for simplicity, assume that
![]() $C_i={\mathfrak {e}}_i$
; the other cases can be treated in the same way by substituting
$C_i={\mathfrak {e}}_i$
; the other cases can be treated in the same way by substituting
![]() $y_i$
with
$y_i$
with
![]() $y^{\prime }_i$
at the appropriate places. Thus, we have
$y^{\prime }_i$
at the appropriate places. Thus, we have
 $$ \begin{align*} C_0 \cap T & = mp+p_1+p_2+p_3, \; \; \mbox{for} \; \; p,p_1,p_2,p_3 \in T, \\ C_i \cap T & = y_i, \; \; i \in \{1,\ldots,k\}. \end{align*} $$
$$ \begin{align*} C_0 \cap T & = mp+p_1+p_2+p_3, \; \; \mbox{for} \; \; p,p_1,p_2,p_3 \in T, \\ C_i \cap T & = y_i, \; \; i \in \{1,\ldots,k\}. \end{align*} $$
By Lemma 3.6(ii), the points
![]() $p,p_1,p_2,p_3$
are general on T (even for fixed
$p,p_1,p_2,p_3$
are general on T (even for fixed
![]() $y_1,\ldots ,y_k$
). The points
$y_1,\ldots ,y_k$
). The points
![]() $y_1,\ldots ,y_k$
are general on T by the assumption that
$y_1,\ldots ,y_k$
are general on T by the assumption that
![]() $R'$
is a blowup of R at general points on T.
$R'$
is a blowup of R at general points on T.
The surface
![]() $P'$
is a blowup of
$P'$
is a blowup of
![]() ${\mathbb {P}}^2$
at t general points on T, where
${\mathbb {P}}^2$
at t general points on T, where
![]() $k<t\leq 5$
by assumption (i). The line bundle
$k<t\leq 5$
by assumption (i). The line bundle
![]() $L^{\prime \prime }_0$
is big and nef by assumption (iv), whence, by Proposition 3.12, we have
$L^{\prime \prime }_0$
is big and nef by assumption (iv), whence, by Proposition 3.12, we have
![]() $V^*_{0,m}(P',T,L^{\prime \prime }_0) \neq \emptyset $
and its general member intersects
$V^*_{0,m}(P',T,L^{\prime \prime }_0) \neq \emptyset $
and its general member intersects
![]() $D_1,\ldots ,D_k$
transversely. Let
$D_1,\ldots ,D_k$
transversely. Let
![]() $D_0$
be such a general member; we have
$D_0$
be such a general member; we have
![]() $L" \sim D_0+D_1+ \cdots +D_k$
by assumption (iv).
$L" \sim D_0+D_1+ \cdots +D_k$
by assumption (iv).
By assumption (iv)–(v),
![]() $D_1,\ldots ,D_k$
are disjoint
$D_1,\ldots ,D_k$
are disjoint
![]() $(-1)$
-curves belonging to a set of t disjoint
$(-1)$
-curves belonging to a set of t disjoint
![]() $(-1)$
-curves, which we may therefore take as an exceptional set for a blowdown
$(-1)$
-curves, which we may therefore take as an exceptional set for a blowdown
![]() $P' \to {\mathbb {P}}^2$
centred at points that we denote by
$P' \to {\mathbb {P}}^2$
centred at points that we denote by
![]() $x_1,\ldots , x_t \in T$
. Furthermore, there is an exceptional curve, different from
$x_1,\ldots , x_t \in T$
. Furthermore, there is an exceptional curve, different from
![]() $D_1,\ldots ,D_k$
, call it
$D_1,\ldots ,D_k$
, call it
![]() $D_{k+1}$
, such that
$D_{k+1}$
, such that
![]() $D_{k+1} \cdot L^{\prime \prime }_0>0$
. We have
$D_{k+1} \cdot L^{\prime \prime }_0>0$
. We have
 $$ \begin{align*} D_0 \cap T & = mq+q_1+q_2+q_3, \; \; \mbox{for} \; \; q,q_1,q_2,q_3 \in T, \\ D_i \cap T & = x_i, \; \; i \in \{1,\ldots,k\}. \end{align*} $$
$$ \begin{align*} D_0 \cap T & = mq+q_1+q_2+q_3, \; \; \mbox{for} \; \; q,q_1,q_2,q_3 \in T, \\ D_i \cap T & = x_i, \; \; i \in \{1,\ldots,k\}. \end{align*} $$
Since
![]() $D_{k+1} \cdot L^{\prime \prime }_0>0$
, we can apply Lemma 3.11(i), which ensures that, even for fixed
$D_{k+1} \cdot L^{\prime \prime }_0>0$
, we can apply Lemma 3.11(i), which ensures that, even for fixed
![]() $x_1,\ldots , x_k$
, by moving
$x_1,\ldots , x_k$
, by moving
![]() $x_{k+1}$
, the intersection
$x_{k+1}$
, the intersection
![]() $D_0 \cap T$
is a general element in
$D_0 \cap T$
is a general element in
![]() $\operatorname {Sym}^{L^{\prime \prime }_0\cdot T}(T)_m$
. Hence, the points
$\operatorname {Sym}^{L^{\prime \prime }_0\cdot T}(T)_m$
. Hence, the points
![]() $q,q_1,q_2,q_3$
are general on T. The points
$q,q_1,q_2,q_3$
are general on T. The points
![]() $x_1,\ldots ,x_k$
are general on T by the assumption that
$x_1,\ldots ,x_k$
are general on T by the assumption that
![]() $P'$
is a blowup of P at general points on T.
$P'$
is a blowup of P at general points on T.
Since the points
![]() $p,p_1,p_2,p_3,y_1,\ldots ,y_k$
are general on T, and likewise the points
$p,p_1,p_2,p_3,y_1,\ldots ,y_k$
are general on T, and likewise the points
![]() $q,q_1,q_2,q_3,x_1,\ldots ,x_k$
, we may assume that our choices of
$q,q_1,q_2,q_3,x_1,\ldots ,x_k$
, we may assume that our choices of
![]() $C_0$
and
$C_0$
and
![]() $D_0$
come with the identifications
$D_0$
come with the identifications
 $$ \begin{align*} & p = q \\ x_i=p_i, \; \; y_i=q_i \; \; \mbox{for} \; \; 1 &\leq i \leq k \quad (\text{recall that } k\leq 3), & \\ p_i=q_i \; \; \mbox{for} \; \; k+1 \leq i \leq 3 \quad &(\text{if } k= 3, \text{ this condition is empty}), \end{align*} $$
$$ \begin{align*} & p = q \\ x_i=p_i, \; \; y_i=q_i \; \; \mbox{for} \; \; 1 &\leq i \leq k \quad (\text{recall that } k\leq 3), & \\ p_i=q_i \; \; \mbox{for} \; \; k+1 \leq i \leq 3 \quad &(\text{if } k= 3, \text{ this condition is empty}), \end{align*} $$
so that we can glue
![]() $R'$
and
$R'$
and
![]() $P'$
along T in such a way that
$P'$
along T in such a way that
![]() $(C_0+C_1+ \cdots +C_k,D_0+D_1+ \cdots +D_k)$
is Cartier on
$(C_0+C_1+ \cdots +C_k,D_0+D_1+ \cdots +D_k)$
is Cartier on
![]() $R' \cup _T P'$
. The following picture shows the case
$R' \cup _T P'$
. The following picture shows the case
![]() $k=2$
:
$k=2$
:
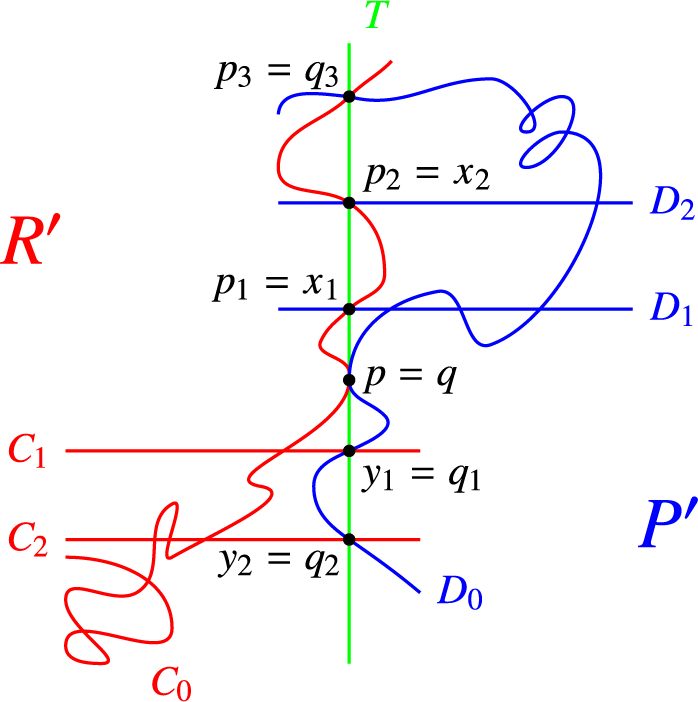
By assumption (i), we have that
![]() $s+t \leq k+5 \leq 8$
. The set of points
$s+t \leq k+5 \leq 8$
. The set of points
is therefore a set of
![]() $s+t+3-k \leq 8$
general points on T. Pick now points
$s+t+3-k \leq 8$
general points on T. Pick now points
![]() $w_1,\ldots , w_{k+6-s-t}$
on T, general under the condition that
$w_1,\ldots , w_{k+6-s-t}$
on T, general under the condition that
Note that, in this way, we get a general divisor of
![]() $|{\mathcal N}_{T/R} \otimes {\mathcal N}_{T/P}|$
. Then blowup either
$|{\mathcal N}_{T/R} \otimes {\mathcal N}_{T/P}|$
. Then blowup either
![]() $R'$
or
$R'$
or
![]() $P'$
at the points
$P'$
at the points
to obtain
![]() $\widetilde {R} \cup _T \widetilde {P}$
, which is a general member of a component of
$\widetilde {R} \cup _T \widetilde {P}$
, which is a general member of a component of
![]() ${\mathcal D}^*$
, containing the inverse image Y of the curve
${\mathcal D}^*$
, containing the inverse image Y of the curve
![]() $(C_0+C_1+ \cdots +C_k) \cup _T (D_0+D_1+ \cdots +D_k)$
, which satisfies the conditions of Proposition 4.1. The result therefore follows by Proposition 4.1 (the following picture shows the inverse image of the curve in the previous image in the case
$(C_0+C_1+ \cdots +C_k) \cup _T (D_0+D_1+ \cdots +D_k)$
, which satisfies the conditions of Proposition 4.1. The result therefore follows by Proposition 4.1 (the following picture shows the inverse image of the curve in the previous image in the case
![]() $k=2$
: an additional
$k=2$
: an additional
![]() $(-1)$
-curve appears over
$(-1)$
-curve appears over
![]() $p_3=q_3$
).
$p_3=q_3$
).

Proposition 4.3. Let
![]() $\widetilde {R}$
(respectively,
$\widetilde {R}$
(respectively,
![]() $\widetilde {P}$
) be a blowup of R (respectively, P) at
$\widetilde {P}$
) be a blowup of R (respectively, P) at
![]() $4$
(respectively,
$4$
(respectively,
![]() $5$
) general points of T. Assume
$5$
) general points of T. Assume
![]() $L'$
(respectively,
$L'$
(respectively,
![]() $L"$
) is a line bundle (or Cartier divisor) on
$L"$
) is a line bundle (or Cartier divisor) on
![]() $\widetilde {R}$
(respectively,
$\widetilde {R}$
(respectively,
![]() $\widetilde {P}$
), such that the following conditions are satisfied:
$\widetilde {P}$
), such that the following conditions are satisfied:
-
(i)
 $L' \cdot T=L" \cdot T $
,
$L' \cdot T=L" \cdot T $
, -
(ii)
 $L' \equiv L^{\prime }_0+C_1+ C_2 +C_3$
, where the
$L' \equiv L^{\prime }_0+C_1+ C_2 +C_3$
, where the
 $C_i$
are disjoint
$C_i$
are disjoint
 $(-1)$
-curves and
$(-1)$
-curves and
 $L^{\prime }_0$
satisfies condition
$L^{\prime }_0$
satisfies condition
 $(\star )$
and is odd,
$(\star )$
and is odd, -
(iii)
 $L" \sim L^{\prime \prime }_0+D_1+ D_2 +D_3$
, where the
$L" \sim L^{\prime \prime }_0+D_1+ D_2 +D_3$
, where the
 $D_i$
are disjoint
$D_i$
are disjoint
 $(-1)$
-curves and
$(-1)$
-curves and
 $L^{\prime \prime }_0$
is big and nef,
$L^{\prime \prime }_0$
is big and nef, -
(iv) there are two additional
 $(-1)$
-curves
$(-1)$
-curves
 $D_4,D_5$
on
$D_4,D_5$
on
 $\widetilde {P}$
, mutually disjoint and disjoint from
$\widetilde {P}$
, mutually disjoint and disjoint from
 $D_1,D_2,D_3$
, satisfying
$D_1,D_2,D_3$
, satisfying
 $L"\cdot D_4 \neq L" \cdot D_5$
.
$L"\cdot D_4 \neq L" \cdot D_5$
.
Then there exist
![]() $\overline {R}$
(respectively,
$\overline {R}$
(respectively,
![]() $\overline {P}$
) a blowup of R (respectively, P) at
$\overline {P}$
) a blowup of R (respectively, P) at
![]() $4$
(respectively,
$4$
(respectively,
![]() $5$
) points of T and a line bundle
$5$
) points of T and a line bundle
![]() $\overline L'$
on
$\overline L'$
on
![]() $\overline R$
(respectively,
$\overline R$
(respectively,
![]() $\overline L"$
on
$\overline L"$
on
![]() $\overline P$
), such that:
$\overline P$
), such that:
-
(a) the pair
 $(\overline R,\overline L')$
(respectively,
$(\overline R,\overline L')$
(respectively,
 $(\overline P,\overline L")$
) is a deformation of
$(\overline P,\overline L")$
) is a deformation of
 $(\widetilde R, L')$
(respectively,
$(\widetilde R, L')$
(respectively,
 $(\widetilde P, L")$
),
$(\widetilde P, L")$
), -
(b) the surface
 $\overline R\cup _T\overline P$
is a general member of
$\overline R\cup _T\overline P$
is a general member of
 $\mathcal D^*_{[4]}$
and
$\mathcal D^*_{[4]}$
and
 $(\overline L', \overline L")$
is a line bundle on it,
$(\overline L', \overline L")$
is a line bundle on it, -
(c)
 $(\overline R\cup _T\overline P, (\overline L', \overline L"))$
deforms to a smooth polarised Enriques surface
$(\overline R\cup _T\overline P, (\overline L', \overline L"))$
deforms to a smooth polarised Enriques surface
 $(S,L)$
, such that
$(S,L)$
, such that
 $|L|$
contains an irreducible, rigid nodal elliptic curve.
$|L|$
contains an irreducible, rigid nodal elliptic curve.
Proof. We argue as in the beginning of the previous proof with
![]() $k=3$
,
$k=3$
,
![]() $s=4$
and
$s=4$
and
![]() $t=5$
, noting that
$t=5$
, noting that
![]() $L"$
is positive on at least one of the two curves
$L"$
is positive on at least one of the two curves
![]() $D_4,D_5$
. We find, as before, a Cartier divisor in a surface
$D_4,D_5$
. We find, as before, a Cartier divisor in a surface
for general
![]() $y_i \in T$
,
$y_i \in T$
,
![]() $i \in \{1,\ldots ,9\}$
, such that, denoting by
$i \in \{1,\ldots ,9\}$
, such that, denoting by
![]() ${\mathfrak {e}}_i$
the exceptional divisor over
${\mathfrak {e}}_i$
the exceptional divisor over
![]() $y_i$
, one has
$y_i$
, one has
with
![]() $C\equiv L'$
and
$C\equiv L'$
and
![]() $D\sim L"$
both nodal,
$D\sim L"$
both nodal,
![]() $C_0\in V^{**}_{1,m}(\widetilde R, T, L^{\prime }_0)$
,
$C_0\in V^{**}_{1,m}(\widetilde R, T, L^{\prime }_0)$
,
![]() $D_0\in V^*_{0,m}(\widetilde P, T, L^{\prime \prime }_0)$
, and we set
$D_0\in V^*_{0,m}(\widetilde P, T, L^{\prime \prime }_0)$
, and we set
![]() $C_i={\mathfrak {e}}_i$
for
$C_i={\mathfrak {e}}_i$
for
![]() $i \in \{1,2,3\}$
and
$i \in \{1,2,3\}$
and
![]() $D_i={\mathfrak {e}}_{i+4}$
for
$D_i={\mathfrak {e}}_{i+4}$
for
![]() $i \in \{1,2,3,4,5\}$
. Moreover, setting
$i \in \{1,2,3,4,5\}$
. Moreover, setting
![]() $m:=C_0 \cdot T-3=D_0 \cdot T-3$
, there is a point
$m:=C_0 \cdot T-3=D_0 \cdot T-3$
, there is a point
![]() $x\in T$
, such that
$x\in T$
, such that
As in the previous proof, the points
![]() $x,y_i$
are general on T.
$x,y_i$
are general on T.
The problem now is that we cannot a priori guarantee that
![]() $\sum _{i=1}^9y_i \in |{\mathcal N}_{T/{R}} \otimes {\mathcal N}_{T/{P}}|$
to ensure that X is a member of
$\sum _{i=1}^9y_i \in |{\mathcal N}_{T/{R}} \otimes {\mathcal N}_{T/{P}}|$
to ensure that X is a member of
![]() ${\mathcal D}^*$
and therefore conclude, as in the previous proof; we only know that X is a member of
${\mathcal D}^*$
and therefore conclude, as in the previous proof; we only know that X is a member of
![]() ${\mathcal D}$
. We will prove that we can create such a member of
${\mathcal D}$
. We will prove that we can create such a member of
![]() ${\mathcal D}^*$
without losing the ‘nice’ properties of Y.
${\mathcal D}^*$
without losing the ‘nice’ properties of Y.
Note first that condition (iv) says that
![]() $L" \cdot {\mathfrak {e}}_8 \neq L" \cdot {\mathfrak {e}}_9$
. If
$L" \cdot {\mathfrak {e}}_8 \neq L" \cdot {\mathfrak {e}}_9$
. If
![]() $L"\cdot {\mathfrak {e}}_i=0$
for
$L"\cdot {\mathfrak {e}}_i=0$
for
![]() $i =8$
or
$i =8$
or
![]() $9$
, we may contract
$9$
, we may contract
![]() ${\mathfrak {e}}_i$
and reduce to the case studied in the previous proposition. We will therefore assume that
${\mathfrak {e}}_i$
and reduce to the case studied in the previous proposition. We will therefore assume that
Fix now, general
![]() $y_1,y_2,y_3,y_5,y_6,y_7 \in T$
. Varying
$y_1,y_2,y_3,y_5,y_6,y_7 \in T$
. Varying
![]() $(x_4,x_8,x_9)$
in
$(x_4,x_8,x_9)$
in
![]() $T^3$
, we obtain a 3-dimensional family of surfaces of the form
$T^3$
, we obtain a 3-dimensional family of surfaces of the form
together with a family of line bundles
![]() $(L',L")$
. There exists a relative Hilbert scheme
$(L',L")$
. There exists a relative Hilbert scheme
![]() $\mathcal H$
of effective Cartier divisors
$\mathcal H$
of effective Cartier divisors
![]() $C'\cup _TD'$
on these surfaces, such that on each surface the line bundle
$C'\cup _TD'$
on these surfaces, such that on each surface the line bundle
![]() $(C',D')$
is in the numerical equivalence class
$(C',D')$
is in the numerical equivalence class
![]() $[L',L"]$
, cf. Remark 2.1 (considering
$[L',L"]$
, cf. Remark 2.1 (considering
![]() $L'$
and
$L'$
and
![]() $L"$
as relative line bundles, see section 3.1). By our assumptions, we have a nonempty subscheme
$L"$
as relative line bundles, see section 3.1). By our assumptions, we have a nonempty subscheme
![]() ${\mathcal W}$
of
${\mathcal W}$
of
![]() $\mathcal H$
with a dominating morphism
$\mathcal H$
with a dominating morphism
![]() ${\mathcal W} \to T^3$
whose fibre over a point
${\mathcal W} \to T^3$
whose fibre over a point
![]() $(x_4,x_8,x_9)$
consists of pairs
$(x_4,x_8,x_9)$
consists of pairs
![]() $(X',Y')$
, such that
$(X',Y')$
, such that
-
•
 $X'=R'\cup _TP'$
with
$X'=R'\cup _TP'$
with
 $R'=\operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
and
$R'=\operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
and
 $P' =\operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
,
$P' =\operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
, -
•
 $Y'=C' \cup _T D'$
, where
$Y'=C' \cup _T D'$
, where  $$ \begin{align*} C' & = C^{\prime}_0+{\mathfrak{e}}_1+{\mathfrak{e}}_2+{\mathfrak{e}}_3\equiv L' \\ D' & = D^{\prime}_0+{\mathfrak{e}}_5+{\mathfrak{e}}_6+{\mathfrak{e}}_7\sim L", \\ &\mbox{with } C^{\prime}_0\in V^{**}_{1,m}(R',T,L^{\prime}_0), D^{\prime}_0\in V^*_{0,m}(P',T,L^{\prime\prime}_0) \mbox{ intersecting all } {\mathfrak{e}}_i \mbox{ transversely,} \\ C^{\prime}_0 \cap T & = mx'+y_5+y_6+y_7, \\ D^{\prime}_0 \cap T & = mx'+y_1+y_2+y_3,\\ &\mbox{for a point } x' \in T\setminus \{y_1,y_2,y_3, y_5,y_6,y_7\}. \end{align*} $$
$$ \begin{align*} C' & = C^{\prime}_0+{\mathfrak{e}}_1+{\mathfrak{e}}_2+{\mathfrak{e}}_3\equiv L' \\ D' & = D^{\prime}_0+{\mathfrak{e}}_5+{\mathfrak{e}}_6+{\mathfrak{e}}_7\sim L", \\ &\mbox{with } C^{\prime}_0\in V^{**}_{1,m}(R',T,L^{\prime}_0), D^{\prime}_0\in V^*_{0,m}(P',T,L^{\prime\prime}_0) \mbox{ intersecting all } {\mathfrak{e}}_i \mbox{ transversely,} \\ C^{\prime}_0 \cap T & = mx'+y_5+y_6+y_7, \\ D^{\prime}_0 \cap T & = mx'+y_1+y_2+y_3,\\ &\mbox{for a point } x' \in T\setminus \{y_1,y_2,y_3, y_5,y_6,y_7\}. \end{align*} $$
We once and for all substitute
![]() ${\mathcal W}$
with a dominating component containing
${\mathcal W}$
with a dominating component containing
![]() $[(X,Y)]$
and will henceforth assume
$[(X,Y)]$
and will henceforth assume
![]() ${\mathcal W}$
is irreducible. Taking the closure in
${\mathcal W}$
is irreducible. Taking the closure in
![]() $\mathcal H$
, we obtain a closed scheme with a surjective morphism
$\mathcal H$
, we obtain a closed scheme with a surjective morphism
If
![]() $[(X',Y')]\in \overline {{\mathcal W}}$
, then
$[(X',Y')]\in \overline {{\mathcal W}}$
, then
![]() $Y'$
looks like
$Y'$
looks like
![]() $C' \cup _T D'$
as above, except that
$C' \cup _T D'$
as above, except that
![]() $C^{\prime }_0\in \overline {V}_{1,m}(R',T,L^{\prime }_0)$
and
$C^{\prime }_0\in \overline {V}_{1,m}(R',T,L^{\prime }_0)$
and
![]() $D^{\prime }_0\in \overline {V}_{0,m}(P',T,L^{\prime \prime }_0)$
, the intersection with the
$D^{\prime }_0\in \overline {V}_{0,m}(P',T,L^{\prime \prime }_0)$
, the intersection with the
![]() ${\mathfrak {e}}_i$
s need not be transversal and
${\mathfrak {e}}_i$
s need not be transversal and
![]() $x'$
may coincide with one of the points
$x'$
may coincide with one of the points
![]() $y_i$
s (this follows from Lemmas 3.6(i) and 3.10(i)). In any event,
$y_i$
s (this follows from Lemmas 3.6(i) and 3.10(i)). In any event,
![]() $(X',Y')$
comes equipped with a point
$(X',Y')$
comes equipped with a point
![]() $x' \in T$
, which is the only point of intersection between the nonexceptional members of
$x' \in T$
, which is the only point of intersection between the nonexceptional members of
![]() $Y'$
. We will call this the tacnodal point of
$Y'$
. We will call this the tacnodal point of
![]() $[(X',Y')]$
(although it may be a worse singularity of
$[(X',Y')]$
(although it may be a worse singularity of
![]() $Y'$
for special pairs). We therefore have a natural map
$Y'$
for special pairs). We therefore have a natural map
sending a pair to its tacnodal point. For
![]() $x' \in T$
, we set
$x' \in T$
, we set
![]() $\overline {{\mathcal W}}_{x'}:=p^{-1}(x')$
; this is the locus of pairs
$\overline {{\mathcal W}}_{x'}:=p^{-1}(x')$
; this is the locus of pairs
![]() $[(X',Y')]$
of
$[(X',Y')]$
of
![]() $\overline {{\mathcal W}}$
with tacnodal point
$\overline {{\mathcal W}}$
with tacnodal point
![]() $x'$
.
$x'$
.
Claim 4.4. The map g is finite and
![]() $\dim (\overline {{\mathcal W}})=3$
.
$\dim (\overline {{\mathcal W}})=3$
.
Proof of claim.
Since g is surjective, we only need to prove that g is finite. Fix any
![]() $X'=R' \cup _T P'$
as above, with
$X'=R' \cup _T P'$
as above, with
![]() $R'=\operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
and
$R'=\operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
and
![]() $P' =\operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
, and assume
$P' =\operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
, and assume
![]() $[(X',Y')] \in \overline {{\mathcal W}}$
. Let
$[(X',Y')] \in \overline {{\mathcal W}}$
. Let
![]() $\overline {C_0} \subset R'$
and
$\overline {C_0} \subset R'$
and
![]() $\overline {D_0} \subset P'$
be the nonexceptional irreducible components of
$\overline {D_0} \subset P'$
be the nonexceptional irreducible components of
![]() $Y'$
, elliptic and rational, respectively. They intersect only at the tacnodal point
$Y'$
, elliptic and rational, respectively. They intersect only at the tacnodal point
![]() $x' \in T$
, and otherwise, they intersect T in fixed points, as the
$x' \in T$
, and otherwise, they intersect T in fixed points, as the
![]() $(-1)$
-curves are fixed on each component of
$(-1)$
-curves are fixed on each component of
![]() $X'$
. Therefore, by Lemma 3.10(ii), there are finitely many possibilities for the point
$X'$
. Therefore, by Lemma 3.10(ii), there are finitely many possibilities for the point
![]() $x'$
and the curve
$x'$
and the curve
![]() $\overline {D_0}$
, and consequently, finitely many possibilities for the intersection
$\overline {D_0}$
, and consequently, finitely many possibilities for the intersection
![]() $\overline {C_0} \cap T$
. As
$\overline {C_0} \cap T$
. As
![]() $\overline {C_0}$
is odd by assumption (ii), there are, by Lemma 3.6(ii), only finitely many possibilities for
$\overline {C_0}$
is odd by assumption (ii), there are, by Lemma 3.6(ii), only finitely many possibilities for
![]() $\overline {C_0}$
as well. This proves that g is finite.
$\overline {C_0}$
as well. This proves that g is finite.
Let
![]() $\left (T^3\right )^*$
denote the two-dimensional subset of triples
$\left (T^3\right )^*$
denote the two-dimensional subset of triples
![]() $(x_4,x_8,x_9) \in T^3$
, such that
$(x_4,x_8,x_9) \in T^3$
, such that
and let
![]() $\overline {{\mathcal W}}^*=g^{-1}(\left (T^3\right )^*)$
. This is the locus of pairs
$\overline {{\mathcal W}}^*=g^{-1}(\left (T^3\right )^*)$
. This is the locus of pairs
![]() $[(X',Y')]$
of
$[(X',Y')]$
of
![]() $\overline {{\mathcal W}}$
, such that
$\overline {{\mathcal W}}$
, such that
![]() $X'$
is semistable. For
$X'$
is semistable. For
![]() $x' \in T$
, we set
$x' \in T$
, we set
![]() $\overline {{\mathcal W}}^*_{x'}:=\overline {{\mathcal W}}^*\cap \overline {{\mathcal W}}_{x'}$
.
$\overline {{\mathcal W}}^*_{x'}:=\overline {{\mathcal W}}^*\cap \overline {{\mathcal W}}_{x'}$
.
We write
![]() $g_1:\overline {{\mathcal W}} \to T$
and
$g_1:\overline {{\mathcal W}} \to T$
and
![]() $g_2:\overline {{\mathcal W}} \to T \times T$
for the composition of g with the projections onto the first factor and onto the product of the second and third factors, respectively. In other words,
$g_2:\overline {{\mathcal W}} \to T \times T$
for the composition of g with the projections onto the first factor and onto the product of the second and third factors, respectively. In other words,
![]() $g_1$
maps a pair
$g_1$
maps a pair
![]() $(X'=R' \cup _T P',Y')$
as above to
$(X'=R' \cup _T P',Y')$
as above to
![]() $x_4$
, whereas
$x_4$
, whereas
![]() $g_2$
maps it to
$g_2$
maps it to
![]() $(x_8,x_9)$
.
$(x_8,x_9)$
.
Claim 4.5. For all
![]() $x'\in T$
, the following hold:
$x'\in T$
, the following hold:
-
(i)
 $\overline {{\mathcal W}}^*_{x'} \neq \emptyset $
(hence,
$\overline {{\mathcal W}}^*_{x'} \neq \emptyset $
(hence,
 $\overline {{\mathcal W}}_{x'}\neq \emptyset $
),
$\overline {{\mathcal W}}_{x'}\neq \emptyset $
), -
(ii)
 $\left (g_1\right )|_{\overline {{\mathcal W}}_{x'}^*}$
is surjective (hence, also
$\left (g_1\right )|_{\overline {{\mathcal W}}_{x'}^*}$
is surjective (hence, also
 $\left (g_1\right )|_{\overline {{\mathcal W}}_{x'}}$
is surjective).
$\left (g_1\right )|_{\overline {{\mathcal W}}_{x'}}$
is surjective).
Proof of claim.
Fix any
![]() $x_4\in T$
and consider
$x_4\in T$
and consider
![]() $R'= \operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
. By Lemma 3.6(ii), there are finitely many curves
$R'= \operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
. By Lemma 3.6(ii), there are finitely many curves
![]() $C^{\prime }_0\in \overline {V}_{1,m}(R',T,L^{\prime }_0)$
, such that
$C^{\prime }_0\in \overline {V}_{1,m}(R',T,L^{\prime }_0)$
, such that
![]() $C_0' \cap T = mx'+y_5+y_6+y_7$
. On the other hand, by Lemma 3.11(ii), taking property (17) into account, and considering the linear series
$C_0' \cap T = mx'+y_5+y_6+y_7$
. On the other hand, by Lemma 3.11(ii), taking property (17) into account, and considering the linear series
of type
![]() $g^1_2$
on T, there exist finitely many curves
$g^1_2$
on T, there exist finitely many curves
![]() $D^{\prime }_0\in \overline {V}_{0,m}(P',T,L^{\prime \prime }_0)$
, with
$D^{\prime }_0\in \overline {V}_{0,m}(P',T,L^{\prime \prime }_0)$
, with
![]() $P'=\operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
for some
$P'=\operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
for some
![]() $x_8+x_9 \in \mathfrak {g}(x_4)$
, such that
$x_8+x_9 \in \mathfrak {g}(x_4)$
, such that
![]() $D_0"\cap T = mx'+y_1+y_2+y_3$
. Thus
$D_0"\cap T = mx'+y_1+y_2+y_3$
. Thus
which proves (i) and (ii) (note, in particular, that the condition that
![]() $x_8+x_9 \in \mathfrak {g}(x_4)$
is equivalent to (18)).
$x_8+x_9 \in \mathfrak {g}(x_4)$
is equivalent to (18)).
Note that Claim 4.5 also implies that p is surjective, whence all fibres
![]() $\overline {{\mathcal W}}_{x'}$
are two-dimensional by Claim 4.4.
$\overline {{\mathcal W}}_{x'}$
are two-dimensional by Claim 4.4.
Now consider the map
 $$ \begin{align*} \sigma: T \times T & \longrightarrow \operatorname{Sym}^2(T), \\ (x,y) & \mapsto x+y \end{align*} $$
$$ \begin{align*} \sigma: T \times T & \longrightarrow \operatorname{Sym}^2(T), \\ (x,y) & \mapsto x+y \end{align*} $$
and recall that there is a fibration
![]() $u:\operatorname {Sym}^2(T) \to T$
with fibres being the
$u:\operatorname {Sym}^2(T) \to T$
with fibres being the
![]() $g^1_2$
s on T.
$g^1_2$
s on T.
For all
![]() $x_4 \in T$
, we consider the linear series
$x_4 \in T$
, we consider the linear series
![]() $\mathfrak {g}(x_4) \subset \operatorname {Sym}^2(T)$
defined in (19) above; it is a
$\mathfrak {g}(x_4) \subset \operatorname {Sym}^2(T)$
defined in (19) above; it is a
![]() $g^1_2$
, hence, a fibre of u.
$g^1_2$
, hence, a fibre of u.
Claim 4.6. For all
![]() $x'\in T$
, one has
$x'\in T$
, one has
![]() $u(\sigma (g_2(\overline {{\mathcal W}}_{x'})))=T$
, that is,
$u(\sigma (g_2(\overline {{\mathcal W}}_{x'})))=T$
, that is,
![]() $\sigma (g_2(\overline {{\mathcal W}}_{x'}))$
is not a union of fibres of u.
$\sigma (g_2(\overline {{\mathcal W}}_{x'}))$
is not a union of fibres of u.
Proof of claim.
Suppose to the contrary that
![]() $\sigma (g_2(\overline {{\mathcal W}}_{x'}))$
is a union of fibres of u. Then, for general
$\sigma (g_2(\overline {{\mathcal W}}_{x'}))$
is a union of fibres of u. Then, for general
![]() $x_4 \in T$
, we would have
$x_4 \in T$
, we would have
![]() $\sigma (g_2(\overline {{\mathcal W}}_{x'})) \cap \mathfrak {g}(x_4) = \emptyset $
, contradicting Claim 4.5(ii).
$\sigma (g_2(\overline {{\mathcal W}}_{x'})) \cap \mathfrak {g}(x_4) = \emptyset $
, contradicting Claim 4.5(ii).
Let now
![]() $x'\in T$
be general. Set
$x'\in T$
be general. Set
![]() ${\mathcal W}_{x'}=\overline {{\mathcal W}}_{x'} \cap {\mathcal W}$
, which is nonempty, as
${\mathcal W}_{x'}=\overline {{\mathcal W}}_{x'} \cap {\mathcal W}$
, which is nonempty, as
![]() $[(X,Y)] \in {\mathcal W}_x$
. Since
$[(X,Y)] \in {\mathcal W}_x$
. Since
![]() $\overline {{\mathcal W}}_{x'}$
is a general fibre of p and
$\overline {{\mathcal W}}_{x'}$
is a general fibre of p and
![]() $\overline {{\mathcal W}}$
is irreducible,
$\overline {{\mathcal W}}$
is irreducible,
![]() ${\mathcal W}_{x'}$
is dense in any component of
${\mathcal W}_{x'}$
is dense in any component of
![]() $\overline {{\mathcal W}}_{x'}$
. It follows that
$\overline {{\mathcal W}}_{x'}$
. It follows that
![]() $g_2({\mathcal W}_{x'})$
is dense in any component of
$g_2({\mathcal W}_{x'})$
is dense in any component of
![]() $g_2(\overline {{\mathcal W}}_{x'})$
. By the last claim,
$g_2(\overline {{\mathcal W}}_{x'})$
. By the last claim,
![]() $\sigma (g_2({\mathcal W}_{x'})) \cap \mathfrak {g}(x_4) \neq \emptyset $
for general
$\sigma (g_2({\mathcal W}_{x'})) \cap \mathfrak {g}(x_4) \neq \emptyset $
for general
![]() $x_4 \in T$
. Pick any
$x_4 \in T$
. Pick any
![]() $(x_8,x_9) \in g_2({\mathcal W}_{x'}) \cap \sigma ^{-1}(\mathfrak {g}(x_4))$
. Then, by definition, there exists a pair
$(x_8,x_9) \in g_2({\mathcal W}_{x'}) \cap \sigma ^{-1}(\mathfrak {g}(x_4))$
. Then, by definition, there exists a pair
![]() $[(X^1,Y^1=C^1 \cup _T D^1)] \in {\mathcal W}_{x'}$
, such that
$[(X^1,Y^1=C^1 \cup _T D^1)] \in {\mathcal W}_{x'}$
, such that
 $$ \begin{align*} & X^1=\operatorname{Bl}_{y_1,y_2,y_3,x^{\prime}_4}(R) \cup_T \operatorname{Bl}_{y_5,y_6,y_7,x_8,x_9}(P) \; \; \mbox{for some} \; \; x^{\prime}_4 \in T, \text{and} \\ & y_1+y_2+y_3+x_4+y_5+y_6+y_7+x_8+x_9 \in |{\mathcal N}_{T/R} \otimes {\mathcal N}_{T/P}|. \end{align*} $$
$$ \begin{align*} & X^1=\operatorname{Bl}_{y_1,y_2,y_3,x^{\prime}_4}(R) \cup_T \operatorname{Bl}_{y_5,y_6,y_7,x_8,x_9}(P) \; \; \mbox{for some} \; \; x^{\prime}_4 \in T, \text{and} \\ & y_1+y_2+y_3+x_4+y_5+y_6+y_7+x_8+x_9 \in |{\mathcal N}_{T/R} \otimes {\mathcal N}_{T/P}|. \end{align*} $$
In particular,
![]() $D^1\subset \operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
satisfies the conditions of Proposition 4.1 and
$D^1\subset \operatorname {Bl}_{y_5,y_6,y_7,x_8,x_9}(P)$
satisfies the conditions of Proposition 4.1 and
As
![]() $x_4$
is general in T, one has
$x_4$
is general in T, one has
![]() $x_4 \in g_1({\mathcal W}_{x'})$
(since
$x_4 \in g_1({\mathcal W}_{x'})$
(since
![]() $\left (g_1\right )|_{\overline {{\mathcal W}}_{x'}}$
is surjective, by Claim 4.5(ii)). Then, by definition, there exists a pair
$\left (g_1\right )|_{\overline {{\mathcal W}}_{x'}}$
is surjective, by Claim 4.5(ii)). Then, by definition, there exists a pair
![]() $[(X^2,Y^2=C^2 \cup _T D^2)] \in {\mathcal W}_{x'}$
, such that
$[(X^2,Y^2=C^2 \cup _T D^2)] \in {\mathcal W}_{x'}$
, such that
In particular,
![]() $C^2 \subset \operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
satisfies the conditions of Proposition 4.1 and
$C^2 \subset \operatorname {Bl}_{y_1,y_2,y_3,x_4}(R)$
satisfies the conditions of Proposition 4.1 and
Consider the pair
Recall that
![]() $y_1,y_2,y_3, y_5,y_6,y_7$
were chosen general to start with, and
$y_1,y_2,y_3, y_5,y_6,y_7$
were chosen general to start with, and
![]() $x_4$
and
$x_4$
and
![]() $x'$
are also general by construction. Lemma 3.11(ii) implies that we may choose
$x'$
are also general by construction. Lemma 3.11(ii) implies that we may choose
![]() $x_8+x_9$
general in
$x_8+x_9$
general in
![]() $\mathfrak g(x_4)$
. It follows that
$\mathfrak g(x_4)$
. It follows that
![]() $\overline X$
is a general member of
$\overline X$
is a general member of
![]() $\mathcal D_{[4]}^*$
, that is, (b) holds. Properties (20) and (21) imply that the pair
$\mathcal D_{[4]}^*$
, that is, (b) holds. Properties (20) and (21) imply that the pair
![]() $(\overline X, \overline Y)$
satisfies the conditions of Proposition 4.1 and therefore (c) holds. It is, moreover, clear that also (a) holds.
$(\overline X, \overline Y)$
satisfies the conditions of Proposition 4.1 and therefore (c) holds. It is, moreover, clear that also (a) holds.
5 Isotropic
 $10$
-sequences and simple isotropic decompositions
$10$
-sequences and simple isotropic decompositions
An important tool for identifying the various components of the moduli spaces of polarised Enriques surfaces is the decomposition of line bundles as sums of effective isotropic divisors. In this section, we will recall some notions and results from [Reference Ciliberto, Dedieu, Galati and Knutsen10, Reference Knutsen23].
Definition 5.1 [Reference Cossec and Dolgachev13, p. 122].
An isotropic
![]() $10$
-sequence on an Enriques surface S is a sequence of isotropic effective divisors
$10$
-sequence on an Enriques surface S is a sequence of isotropic effective divisors
![]() $\{E_1, \ldots , E_{10}\}$
, such that
$\{E_1, \ldots , E_{10}\}$
, such that
![]() $E_i \cdot E_j=1$
for
$E_i \cdot E_j=1$
for
![]() $i \neq j$
.
$i \neq j$
.
It is well-known that any Enriques surface contains isotropic
![]() $10$
-sequences. Note that we, contrary to [Reference Cossec and Dolgachev13], require the divisors to be effective, which can always be arranged by changing signs. We also recall the following result:
$10$
-sequences. Note that we, contrary to [Reference Cossec and Dolgachev13], require the divisors to be effective, which can always be arranged by changing signs. We also recall the following result:
Lemma 5.2 ([Reference Ciliberto, Dedieu, Galati and Knutsen10, Lemma 3.4(a)], [13, Corollary 2.5.5]).
Let
![]() $\{E_1,\ldots ,E_{10}\}$
be an isotropic
$\{E_1,\ldots ,E_{10}\}$
be an isotropic
![]() $10$
-sequence. Then there exists a divisor D on S, such that
$10$
-sequence. Then there exists a divisor D on S, such that
![]() $D^2=10$
and
$D^2=10$
and
![]() $3D \sim E_1+\cdots +E_{10}$
. Furthermore, for any
$3D \sim E_1+\cdots +E_{10}$
. Furthermore, for any
![]() $i \neq j$
, we have
$i \neq j$
, we have
and
![]() $E_k \cdot E_{i,j}=1 \; \; \mbox {for} \; \; k \neq i,j$
. Moreover,
$E_k \cdot E_{i,j}=1 \; \; \mbox {for} \; \; k \neq i,j$
. Moreover,
 $E_{i,j} \cdot E_{k,l}= \begin {cases} 1, \; \mbox {if} \; \{i,j\} \cap \{k,l\} \neq \emptyset , \\ 2, \; \mbox {if} \; \{i,j\} \cap \{k,l\} = \emptyset. \end {cases}$
$E_{i,j} \cdot E_{k,l}= \begin {cases} 1, \; \mbox {if} \; \{i,j\} \cap \{k,l\} \neq \emptyset , \\ 2, \; \mbox {if} \; \{i,j\} \cap \{k,l\} = \emptyset. \end {cases}$
The next result yields a ‘canonical’ way of decomposing line bundles:
Proposition 5.3 [Reference Knutsen23, Theorem 5.7].
Let L be an effective line bundle on an Enriques surface S, such that
![]() $L^2>0$
. Then there are unique nonnegative integers
$L^2>0$
. Then there are unique nonnegative integers
![]() $a_0,a_1,\ldots ,a_7,a_9$
,
$a_0,a_1,\ldots ,a_7,a_9$
,
![]() $a_{10}$
, depending on L, satisfying
$a_{10}$
, depending on L, satisfying
such that L can be written as
for an isotropic
![]() $10$
-sequence
$10$
-sequence
![]() $\{E_1,\ldots ,E_{10}\}$
(depending on L) and
$\{E_1,\ldots ,E_{10}\}$
(depending on L) and
 $$ \begin{align} \varepsilon_L= \begin{cases} 0, & \mbox{if } L+K_S \mbox{ is not } 2\mbox{-divisible in } \operatorname{Pic} (S), \\ 1, & \mbox{if } L+K_S \mbox{ is } 2\mbox{-divisible in } \operatorname{Pic} (S). \end{cases} \end{align} $$
$$ \begin{align} \varepsilon_L= \begin{cases} 0, & \mbox{if } L+K_S \mbox{ is not } 2\mbox{-divisible in } \operatorname{Pic} (S), \\ 1, & \mbox{if } L+K_S \mbox{ is } 2\mbox{-divisible in } \operatorname{Pic} (S). \end{cases} \end{align} $$
Remark 5.4. Although the coefficients
![]() $a_i$
are unique, the isotropic
$a_i$
are unique, the isotropic
![]() $10$
-sequence in Proposition 5.3 is not unique, not even up to numerical equivalence or permutation, and nor is the presentation (25) (see [Reference Knutsen23, Remark 5.6]).
$10$
-sequence in Proposition 5.3 is not unique, not even up to numerical equivalence or permutation, and nor is the presentation (25) (see [Reference Knutsen23, Remark 5.6]).
Definition 5.5 [Reference Knutsen23, Definitions 5.1, 5.8].
Let L be any effective line bundle on an Enriques surface S, such that
![]() $L^2>0$
. A decomposition of the form (25) with coefficients satisfying (23), (24) and (26) is called a fundamental presentation of L. The coefficients
$L^2>0$
. A decomposition of the form (25) with coefficients satisfying (23), (24) and (26) is called a fundamental presentation of L. The coefficients
![]() $a_i=a_i(L)$
,
$a_i=a_i(L)$
,
![]() $i \in \{0,1,\ldots ,7,9,10\}$
and
$i \in \{0,1,\ldots ,7,9,10\}$
and
![]() $\varepsilon _L$
appearing in any fundamental presentation are called fundamental coefficients of L or of
$\varepsilon _L$
appearing in any fundamental presentation are called fundamental coefficients of L or of
![]() $(S,L)$
.
$(S,L)$
.
Remark 5.6. By [Reference Ciliberto, Dedieu, Galati and Knutsen10, Lemma 4.8] (or [Reference Knutsen23, Theorem 1.3(f) and Proposition 5.5]), a line bundle L is
![]() $2$
-divisible in
$2$
-divisible in
![]() $\operatorname {Num} (S)$
if and only if all
$\operatorname {Num} (S)$
if and only if all
![]() $a_i=a_i(L)$
are even,
$a_i=a_i(L)$
are even,
![]() $i \in \{0,1,\ldots ,7,9,10\}$
. In particular, by (26) or [Reference Ciliberto, Dedieu, Galati and Knutsen10, Corollary 4.7], the number
$i \in \{0,1,\ldots ,7,9,10\}$
. In particular, by (26) or [Reference Ciliberto, Dedieu, Galati and Knutsen10, Corollary 4.7], the number
![]() $\varepsilon =\varepsilon _L$
satisfies
$\varepsilon =\varepsilon _L$
satisfies
 $$ \begin{align} \varepsilon= \begin{cases} 0, & \mbox{if some } a_i \mbox{ is odd,} \\ 0 \; \mbox{or} \; 1, & \mbox{if all } a_i \mbox{ are even.} \end{cases} \end{align} $$
$$ \begin{align} \varepsilon= \begin{cases} 0, & \mbox{if some } a_i \mbox{ is odd,} \\ 0 \; \mbox{or} \; 1, & \mbox{if all } a_i \mbox{ are even.} \end{cases} \end{align} $$
This means that any
![]() $11$
-tuple
$11$
-tuple
![]() $(a_0,a_1,\ldots ,a_7,a_9,a_{10},\varepsilon )$
occurring as fundamental coefficients satisfies the conditions (23), (24) and (27). Conversely, for any such
$(a_0,a_1,\ldots ,a_7,a_9,a_{10},\varepsilon )$
occurring as fundamental coefficients satisfies the conditions (23), (24) and (27). Conversely, for any such
![]() $11$
-tuple, we can choose any isotropic
$11$
-tuple, we can choose any isotropic
![]() $10$
-sequence on any Enriques surface and write down the line bundle (25) having this
$10$
-sequence on any Enriques surface and write down the line bundle (25) having this
![]() $11$
-tuple as fundamental coefficients.
$11$
-tuple as fundamental coefficients.
For any integer
![]() $g \geq 2$
, let
$g \geq 2$
, let
![]() ${\mathcal E}_{g}$
denote the moduli space of complex polarised Enriques surfaces
${\mathcal E}_{g}$
denote the moduli space of complex polarised Enriques surfaces
![]() $(S,L)$
of genus g, which is a quasiprojective variety by [Reference Viehweg38, Theorem 1.13]. Its irreducible components are determined by the fundamental coefficients, by the following:
$(S,L)$
of genus g, which is a quasiprojective variety by [Reference Viehweg38, Theorem 1.13]. Its irreducible components are determined by the fundamental coefficients, by the following:
Theorem 5.7 [Reference Knutsen23, Theorem 5.9].
Given an irreducible component
![]() ${\mathcal E}$
of
${\mathcal E}$
of
![]() ${\mathcal E}_{g}$
, all pairs
${\mathcal E}_{g}$
, all pairs
![]() $(S,L)$
in
$(S,L)$
in
![]() ${\mathcal E}$
have the same fundamental coefficients. Different components correspond to different fundamental coefficients.
${\mathcal E}$
have the same fundamental coefficients. Different components correspond to different fundamental coefficients.
The following technical result will be useful for our purposes:
Lemma 5.8. Let
![]() $(S,L)$
be an element of
$(S,L)$
be an element of
![]() ${\mathcal E}_{g} \setminus {\mathcal E}_g[2]$
. Set
${\mathcal E}_{g} \setminus {\mathcal E}_g[2]$
. Set
![]() $a_i=a_i(L)$
. Then one of the following holds:
$a_i=a_i(L)$
. Then one of the following holds:
-
(i) There are three distinct
 $k,l,m \in \{1,\ldots ,7\}$
, such that
$k,l,m \in \{1,\ldots ,7\}$
, such that
 $a_i+a_k+a_l+a_m$
is odd for
$a_i+a_k+a_l+a_m$
is odd for
 $i=9$
or
$i=9$
or
 $10$
.
$10$
. -
(ii)
 $a_0>0$
is odd, and all
$a_0>0$
is odd, and all
 $a_i$
for
$a_i$
for
 $i \neq 0$
are even.
$i \neq 0$
are even. -
(iii)
 $a_0>0$
, and all
$a_0>0$
, and all
 $a_i$
for
$a_i$
for
 $i \neq 0$
are odd.
$i \neq 0$
are odd.
Proof. We first show that if
![]() $a_0=0$
, then we end up in case (i). We have
$a_0=0$
, then we end up in case (i). We have
![]() $a_9=a_{10}=0$
by condition (24). Moreover, by Remark 5.6, the set
$a_9=a_{10}=0$
by condition (24). Moreover, by Remark 5.6, the set
![]() $I:=\{i \in \{1,\ldots ,7\} \; | \; a_i \; \mbox {is odd}\}$
is nonempty. If
$I:=\{i \in \{1,\ldots ,7\} \; | \; a_i \; \mbox {is odd}\}$
is nonempty. If
![]() $\sharp I \geq 3$
, then for any distinct
$\sharp I \geq 3$
, then for any distinct
![]() $k,l,m \in I$
, we have that
$k,l,m \in I$
, we have that
![]() $a_i+a_k+a_l+a_m=a_k+a_l+a_m$
is odd for
$a_i+a_k+a_l+a_m=a_k+a_l+a_m$
is odd for
![]() $i=9$
and
$i=9$
and
![]() $10$
. If
$10$
. If
![]() $\sharp I \leq 2$
, we may pick
$\sharp I \leq 2$
, we may pick
![]() $k \in I$
and two distinct
$k \in I$
and two distinct
![]() $l,m \in \{1,\ldots ,7\}\setminus I$
; then again,
$l,m \in \{1,\ldots ,7\}\setminus I$
; then again,
![]() $a_i+a_k+a_l+a_m=a_k+a_l+a_m$
is odd for
$a_i+a_k+a_l+a_m=a_k+a_l+a_m$
is odd for
![]() $i=9$
and
$i=9$
and
![]() $10$
.
$10$
.
We may therefore assume that
![]() $a_0>0$
.
$a_0>0$
.
Assume next that (i) does not hold; then we have
This clearly implies that
![]() $a_9$
and
$a_9$
and
![]() $a_{10}$
have the same parity.
$a_{10}$
have the same parity.
Assume that
![]() $a_9$
and
$a_9$
and
![]() $a_{10}$
are even. Then (28) implies that
$a_{10}$
are even. Then (28) implies that
![]() $a_k+a_l+a_m$
is even for all distinct
$a_k+a_l+a_m$
is even for all distinct
![]() $k,l,m \in \{1,\ldots ,7\}$
. Hence,
$k,l,m \in \{1,\ldots ,7\}$
. Hence,
![]() $a_i$
is even for all
$a_i$
is even for all
![]() $i\in \{1,\ldots ,7\}$
. Then
$i\in \{1,\ldots ,7\}$
. Then
![]() $a_0$
is odd by Remark 5.6, and we end up in case (ii).
$a_0$
is odd by Remark 5.6, and we end up in case (ii).
Assume that
![]() $a_9$
and
$a_9$
and
![]() $a_{10}$
are odd. Then (28) implies that
$a_{10}$
are odd. Then (28) implies that
![]() $a_k+a_l+a_m$
is odd for all distinct
$a_k+a_l+a_m$
is odd for all distinct
![]() $k,l,m \in \{1,\ldots ,7\}$
. Hence,
$k,l,m \in \{1,\ldots ,7\}$
. Hence,
![]() $a_i$
is odd for all
$a_i$
is odd for all
![]() $i\in \{1,\ldots ,7\}$
, yielding case (iii).
$i\in \{1,\ldots ,7\}$
, yielding case (iii).
6 Isotropic
 $10$
-sequences on members of
$10$
-sequences on members of
 ${\mathcal D}$
${\mathcal D}$
The notions of isotropic divisors and isotropic
![]() $10$
-sequences can be extended in the obvious way to all members of
$10$
-sequences can be extended in the obvious way to all members of
![]() ${\mathcal D}$
. Referring to [Reference Knutsen23, Section 3] for more details, we will in Example 6.1 below construct one such 10-sequence that we will use in the proof of Theorem 1.1 in the next section.
${\mathcal D}$
. Referring to [Reference Knutsen23, Section 3] for more details, we will in Example 6.1 below construct one such 10-sequence that we will use in the proof of Theorem 1.1 in the next section.
Recall that we have the points
![]() $y_1,\ldots ,y_9 \in T$
, which are the blownup points on either R or P. We will now assume that
$y_1,\ldots ,y_9 \in T$
, which are the blownup points on either R or P. We will now assume that
![]() $y_1,\ldots ,y_9$
are distinct, though the case of coinciding points can be treated similarly. Denote by
$y_1,\ldots ,y_9$
are distinct, though the case of coinciding points can be treated similarly. Denote by
![]() ${\mathfrak {e}}_j$
the exceptional divisor over
${\mathfrak {e}}_j$
the exceptional divisor over
![]() $y_j$
, without fixing whether it lies on
$y_j$
, without fixing whether it lies on
![]() $\widetilde {R}$
or
$\widetilde {R}$
or
![]() $\widetilde {P}$
. View
$\widetilde {P}$
. View
![]() $y_j \in T \subset P$
. The linear system of lines in P through
$y_j \in T \subset P$
. The linear system of lines in P through
![]() $y_j$
is a pencil inducing a
$y_j$
is a pencil inducing a
![]() $g^1_2$
on T, which has, by Riemann-Hurwitz, two members that are also two fibres of
$g^1_2$
on T, which has, by Riemann-Hurwitz, two members that are also two fibres of
![]() $\pi _{|T}: T \to E$
. In other words, there are two fibres
$\pi _{|T}: T \to E$
. In other words, there are two fibres
![]() $\mathfrak {f}_{\alpha _j}$
and
$\mathfrak {f}_{\alpha _j}$
and
![]() $\mathfrak {f}_{\alpha ^{\prime }_j}$
of
$\mathfrak {f}_{\alpha ^{\prime }_j}$
of
![]() $\pi :R \to E$
, such that the intersection divisors
$\pi :R \to E$
, such that the intersection divisors
![]() $\mathfrak {f}_{\alpha _j} \cap T$
and
$\mathfrak {f}_{\alpha _j} \cap T$
and
![]() $\mathfrak {f}_{\alpha ^{\prime }_j} \cap T$
belong to this
$\mathfrak {f}_{\alpha ^{\prime }_j} \cap T$
belong to this
![]() $g^1_2$
. Since
$g^1_2$
. Since
![]() $\mathfrak {f}_{\alpha _j}-\mathfrak {f}_{\alpha _i}$
restricts trivially to T, one has
$\mathfrak {f}_{\alpha _j}-\mathfrak {f}_{\alpha _i}$
restricts trivially to T, one has
![]() $\alpha ^{\prime }_j=\alpha _j \oplus \eta $
(see Remark 2.1). In particular, there are two uniquely defined points
$\alpha ^{\prime }_j=\alpha _j \oplus \eta $
(see Remark 2.1). In particular, there are two uniquely defined points
![]() $\alpha _j$
and
$\alpha _j$
and
![]() $\alpha _j \oplus \eta $
on E, such that the pairs
$\alpha _j \oplus \eta $
on E, such that the pairs
 $$ \begin{align*} (\mathfrak{f}_{\alpha_j}+{\mathfrak{e}}_j,\ell) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_j\oplus\eta}+{\mathfrak{e}}_j,\ell),\; \; \mbox{if} \; \; {\mathfrak{e}}_j \subset \widetilde{R}, \\ (\mathfrak{f}_{\alpha_j},\ell-{\mathfrak{e}}_j) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_j\oplus\eta},\ell-{\mathfrak{e}}_j),\; \; \mbox{if} \; \; {\mathfrak{e}}_j \subset \widetilde{P}, \end{align*} $$
$$ \begin{align*} (\mathfrak{f}_{\alpha_j}+{\mathfrak{e}}_j,\ell) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_j\oplus\eta}+{\mathfrak{e}}_j,\ell),\; \; \mbox{if} \; \; {\mathfrak{e}}_j \subset \widetilde{R}, \\ (\mathfrak{f}_{\alpha_j},\ell-{\mathfrak{e}}_j) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_j\oplus\eta},\ell-{\mathfrak{e}}_j),\; \; \mbox{if} \; \; {\mathfrak{e}}_j \subset \widetilde{P}, \end{align*} $$
define distinct numerically equivalent Cartier divisors on
![]() $X:=\widetilde {R} \cup _T \widetilde {P}$
. Hence, their difference is
$X:=\widetilde {R} \cup _T \widetilde {P}$
. Hence, their difference is
![]() $K_{X}$
(see, again, Remark 2.1).
$K_{X}$
(see, again, Remark 2.1).
Similarly, for four distinct (general)
![]() $y_i,y_j,y_k,y_l \in T$
, the linear system of plane conics through
$y_i,y_j,y_k,y_l \in T$
, the linear system of plane conics through
![]() $y_i,y_j,y_k,y_l$
is again a pencil inducing a
$y_i,y_j,y_k,y_l$
is again a pencil inducing a
![]() $g^1_2$
on T. As above, there are two fibres
$g^1_2$
on T. As above, there are two fibres
![]() $\mathfrak {f}_{\alpha _{ijkl}}$
and
$\mathfrak {f}_{\alpha _{ijkl}}$
and
![]() $\mathfrak {f}_{\alpha _{ijkl} \oplus \eta }$
of
$\mathfrak {f}_{\alpha _{ijkl} \oplus \eta }$
of
![]() $\pi :R \to E$
, such that the divisors
$\pi :R \to E$
, such that the divisors
![]() $\mathfrak {f}_{\alpha _{ijkl}} \cap T$
and
$\mathfrak {f}_{\alpha _{ijkl}} \cap T$
and
![]() $\mathfrak {f}_{\alpha _{ijkl} \oplus \eta } \cap T$
belong to this
$\mathfrak {f}_{\alpha _{ijkl} \oplus \eta } \cap T$
belong to this
![]() $g^1_2$
. In particular, the pairs
$g^1_2$
. In particular, the pairs
 $$ \begin{align*} &(\mathfrak{f}_{\alpha_{ijkl}}+{\mathfrak{e}}_i+{\mathfrak{e}}_j+{\mathfrak{e}}_k+{\mathfrak{e}}_l,2\ell) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_{ijkl}\oplus\eta}+{\mathfrak{e}}_i+{\mathfrak{e}}_j+{\mathfrak{e}}_k+{\mathfrak{e}}_l,2\ell),\; \; \mbox{if} \; \; {\mathfrak{e}}_i,{\mathfrak{e}}_j,{\mathfrak{e}}_k,{\mathfrak{e}}_l \subset \widetilde{R}, \\ &(\mathfrak{f}_{\alpha_{ijkl}},2\ell-{\mathfrak{e}}_i-{\mathfrak{e}}_j-{\mathfrak{e}}_k-{\mathfrak{e}}_l) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_{ijkl}\oplus\eta},2\ell-{\mathfrak{e}}_i-{\mathfrak{e}}_j-{\mathfrak{e}}_k-{\mathfrak{e}}_l),\; \; \mbox{if} \; \; {\mathfrak{e}}_i,{\mathfrak{e}}_j,{\mathfrak{e}}_k,{\mathfrak{e}}_l \subset \widetilde{P}, \end{align*} $$
$$ \begin{align*} &(\mathfrak{f}_{\alpha_{ijkl}}+{\mathfrak{e}}_i+{\mathfrak{e}}_j+{\mathfrak{e}}_k+{\mathfrak{e}}_l,2\ell) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_{ijkl}\oplus\eta}+{\mathfrak{e}}_i+{\mathfrak{e}}_j+{\mathfrak{e}}_k+{\mathfrak{e}}_l,2\ell),\; \; \mbox{if} \; \; {\mathfrak{e}}_i,{\mathfrak{e}}_j,{\mathfrak{e}}_k,{\mathfrak{e}}_l \subset \widetilde{R}, \\ &(\mathfrak{f}_{\alpha_{ijkl}},2\ell-{\mathfrak{e}}_i-{\mathfrak{e}}_j-{\mathfrak{e}}_k-{\mathfrak{e}}_l) \; \; \mbox{and} \; \; (\mathfrak{f}_{\alpha_{ijkl}\oplus\eta},2\ell-{\mathfrak{e}}_i-{\mathfrak{e}}_j-{\mathfrak{e}}_k-{\mathfrak{e}}_l),\; \; \mbox{if} \; \; {\mathfrak{e}}_i,{\mathfrak{e}}_j,{\mathfrak{e}}_k,{\mathfrak{e}}_l \subset \widetilde{P}, \end{align*} $$
together with similar pairs when
![]() ${\mathfrak {e}}_i,{\mathfrak {e}}_j,{\mathfrak {e}}_k,{\mathfrak {e}}_l$
are distributed differently, define Cartier divisors on X. One may again check that their difference is
${\mathfrak {e}}_i,{\mathfrak {e}}_j,{\mathfrak {e}}_k,{\mathfrak {e}}_l$
are distributed differently, define Cartier divisors on X. One may again check that their difference is
![]() $K_{X}$
.
$K_{X}$
.
Considering instead,
![]() $y_i \in T \subset R=\operatorname {Sym}^2(E)$
, we may write
$y_i \in T \subset R=\operatorname {Sym}^2(E)$
, we may write
![]() $y_i=p_i+(p_i \oplus \eta )$
, for some
$y_i=p_i+(p_i \oplus \eta )$
, for some
![]() $p_i \in E$
. There are two sections in R passing through
$p_i \in E$
. There are two sections in R passing through
![]() $y_i$
, namely,
$y_i$
, namely,
![]() $\mathfrak {s}_{p_i}$
and
$\mathfrak {s}_{p_i}$
and
![]() $\mathfrak {s}_{p_i \oplus \eta }$
, cf. (1). Thus, the pairs
$\mathfrak {s}_{p_i \oplus \eta }$
, cf. (1). Thus, the pairs
 $$ \begin{align*} &(\mathfrak{s}_{p_i}-{\mathfrak{e}}_i,0) \; \; \mbox{and} \; \; (\mathfrak{s}_{p_i\oplus \eta}-{\mathfrak{e}}_i,0), \; \; \mbox{if} \; \; {\mathfrak{e}}_i \subset \widetilde{R}, \\ &(\mathfrak{s}_{p_i},{\mathfrak{e}}_i) \; \; \mbox{and} \; \; (\mathfrak{s}_{p_i\oplus \eta},{\mathfrak{e}}_i), \; \; \mbox{if} \; \; {\mathfrak{e}}_i \subset \widetilde{P} \end{align*} $$
$$ \begin{align*} &(\mathfrak{s}_{p_i}-{\mathfrak{e}}_i,0) \; \; \mbox{and} \; \; (\mathfrak{s}_{p_i\oplus \eta}-{\mathfrak{e}}_i,0), \; \; \mbox{if} \; \; {\mathfrak{e}}_i \subset \widetilde{R}, \\ &(\mathfrak{s}_{p_i},{\mathfrak{e}}_i) \; \; \mbox{and} \; \; (\mathfrak{s}_{p_i\oplus \eta},{\mathfrak{e}}_i), \; \; \mbox{if} \; \; {\mathfrak{e}}_i \subset \widetilde{P} \end{align*} $$
define Cartier divisors on
![]() ${X}$
. Again, one may check that their difference is
${X}$
. Again, one may check that their difference is
![]() $K_{X}$
.
$K_{X}$
.
Example 6.1. We consider
![]() $\widetilde {R}=\operatorname {Bl}_{y_1,y_2,y_3,y_4}(R)$
and
$\widetilde {R}=\operatorname {Bl}_{y_1,y_2,y_3,y_4}(R)$
and
![]() $\widetilde {P}=\operatorname {Bl}_{y_5,\ldots ,y_9}({\mathbb {P}}^2)$
. Define
$\widetilde {P}=\operatorname {Bl}_{y_5,\ldots ,y_9}({\mathbb {P}}^2)$
. Define
 $$ \begin{align*} E^0_i&:= (\mathfrak{s}_{p_i}-{\mathfrak{e}}_i,0) \; \; \mbox{for} \; \; i \in\{1,2,3,4\},\\ E^0_i &:= (\mathfrak{f}_{\alpha_i},\ell-{\mathfrak{e}}_i) \; \; \mbox{for} \; \; i \in\{5,6,7,8\}, \\ E^0_9&:= (\mathfrak{s}_{p_9},{\mathfrak{e}}_9), \\ E^0_{10} &:= (\mathfrak{f}_{\alpha_{5678}}, 2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*} $$
$$ \begin{align*} E^0_i&:= (\mathfrak{s}_{p_i}-{\mathfrak{e}}_i,0) \; \; \mbox{for} \; \; i \in\{1,2,3,4\},\\ E^0_i &:= (\mathfrak{f}_{\alpha_i},\ell-{\mathfrak{e}}_i) \; \; \mbox{for} \; \; i \in\{5,6,7,8\}, \\ E^0_9&:= (\mathfrak{s}_{p_9},{\mathfrak{e}}_9), \\ E^0_{10} &:= (\mathfrak{f}_{\alpha_{5678}}, 2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*} $$
These are all Cartier divisors on
![]() $X=\widetilde {R} \cup _T \widetilde {P}$
by the above considerations. One may check that
$X=\widetilde {R} \cup _T \widetilde {P}$
by the above considerations. One may check that
![]() $(E^0_i)^2=0$
for all i and
$(E^0_i)^2=0$
for all i and
![]() $E^0_i \cdot E^0_j=1$
for all
$E^0_i \cdot E^0_j=1$
for all
![]() $i \neq j$
. If X is a member of
$i \neq j$
. If X is a member of
![]() ${\mathcal D}^*$
, then, arguing as in the proof of [Reference Knutsen23, Lemma 3.6], one may show that
${\mathcal D}^*$
, then, arguing as in the proof of [Reference Knutsen23, Lemma 3.6], one may show that
with
![]() $\xi $
as in (7) and
$\xi $
as in (7) and
Thus, we may similarly to (22) define
In particular, letting
![]() $y_{78}\in T\subset {\mathbb {P}}^2$
be the third intersection point of the line through
$y_{78}\in T\subset {\mathbb {P}}^2$
be the third intersection point of the line through
![]() $y_7$
and
$y_7$
and
![]() $y_8$
with T, and writing
$y_8$
with T, and writing
![]() $y_{78}=p_{78}+(p_{78}\oplus \eta )\in T\subset \mathrm {Sym}^2(E)$
for some
$y_{78}=p_{78}+(p_{78}\oplus \eta )\in T\subset \mathrm {Sym}^2(E)$
for some
![]() $p_{78}\in E$
, we will use that
$p_{78}\in E$
, we will use that
Note that
![]() $E^0_{9,10}$
and
$E^0_{9,10}$
and
![]() $E^0_{5,6}$
are Cartier divisors on any X in
$E^0_{5,6}$
are Cartier divisors on any X in
![]() ${\mathcal D}$
.
${\mathcal D}$
.
Remark 6.2. If
![]() $X=\widetilde {R} \cup _T \widetilde {P}$
belongs to
$X=\widetilde {R} \cup _T \widetilde {P}$
belongs to
![]() ${\mathcal D}^*$
, then, by Theorem 2.2, as it deforms to a general Enriques surface S, the sequence
${\mathcal D}^*$
, then, by Theorem 2.2, as it deforms to a general Enriques surface S, the sequence
![]() $(E^0_1,\ldots ,E^0_{10})$
deforms to an isotropic
$(E^0_1,\ldots ,E^0_{10})$
deforms to an isotropic
![]() $10$
-sequence
$10$
-sequence
![]() $(E_1,\ldots ,E_{10})$
on S and each
$(E_1,\ldots ,E_{10})$
on S and each
![]() $E^0_{i,j}$
deforms to
$E^0_{i,j}$
deforms to
![]() $E_{i,j}$
, satisfying (22).
$E_{i,j}$
, satisfying (22).
7 Proof of Theorem 1.1
We are now ready to finish the proof of our main result, Theorem 1.1. Keeping in mind that the various irreducible components of
![]() ${\mathcal E}_g$
are determined by the fundamental coefficients of the line bundles they parametrise (cf. Theorem 5.7), the proof will be divided in various cases depending on parity properties of the fundamental coefficients. Also recall that since we assume that we are not in
${\mathcal E}_g$
are determined by the fundamental coefficients of the line bundles they parametrise (cf. Theorem 5.7), the proof will be divided in various cases depending on parity properties of the fundamental coefficients. Also recall that since we assume that we are not in
![]() ${\mathcal E}_g[2]$
, at least one of the fundamental coefficients
${\mathcal E}_g[2]$
, at least one of the fundamental coefficients
![]() $a_i$
is odd and
$a_i$
is odd and
![]() $\varepsilon =0$
(cf. Remark 5.6). In particular, the components we consider contain both
$\varepsilon =0$
(cf. Remark 5.6). In particular, the components we consider contain both
![]() $(S,L)$
and
$(S,L)$
and
![]() $(S,L+K_S)$
, so there is no need to distinguish between linear and numerical equivalence classes (cf. also [Reference Knutsen23, Theorem 1.1]).
$(S,L+K_S)$
, so there is no need to distinguish between linear and numerical equivalence classes (cf. also [Reference Knutsen23, Theorem 1.1]).
The proof strategy will be as follows: given fundamental coefficients
![]() $a_i$
, find a suitable line bundle with the same fundamental decomposition on some limit surface in terms of the isotropic divisors in Example 6.1, and apply Proposition 4.2 or 4.3 (and Remark 6.2). As mentioned in the beginning of Section 4, the existence of a rigid nodal elliptic curve will prove Theorem 1.1.
$a_i$
, find a suitable line bundle with the same fundamental decomposition on some limit surface in terms of the isotropic divisors in Example 6.1, and apply Proposition 4.2 or 4.3 (and Remark 6.2). As mentioned in the beginning of Section 4, the existence of a rigid nodal elliptic curve will prove Theorem 1.1.
We will first treat three special cases in Sections 7.1–7.3 and then the three cases of Lemma 5.8 in Sections 7.4–7.6.
7.1 The case
 $a_1=a_2=1$
and
$a_1=a_2=1$
and
 $a_i=0$
otherwise
$a_i=0$
otherwise
Consider the limit line bundle
![]() $L^0= E^0_8+E^0_9$
, with
$L^0= E^0_8+E^0_9$
, with
![]() $E^0_8$
and
$E^0_8$
and
![]() $E^0_9$
as in Example 6.1 (where we consider a general surface
$E^0_9$
as in Example 6.1 (where we consider a general surface
![]() $\widetilde R\cup _T\widetilde P$
in
$\widetilde R\cup _T\widetilde P$
in
![]() $\mathcal D^*$
). Note that the order in an isotropic 10-sequence does not matter, hence, we can choose
$\mathcal D^*$
). Note that the order in an isotropic 10-sequence does not matter, hence, we can choose
![]() $E^0_8$
and
$E^0_8$
and
![]() $E^0_9$
instead of
$E^0_9$
instead of
![]() $E^0_1$
and
$E^0_1$
and
![]() $E^0_2$
. This fact will be used throughout the rest of the proof, without further mention. Then
$E^0_2$
. This fact will be used throughout the rest of the proof, without further mention. Then
In this case, there is no need to invoke Proposition 4.2 or 4.3: indeed, the linear system
![]() $|L|$
contains the following curve:
$|L|$
contains the following curve:

Here,
![]() $\mathfrak {f}'$
is the unique fibre passing through the point
$\mathfrak {f}'$
is the unique fibre passing through the point
![]() $y_9={\mathfrak {e}}_9\cap T$
and D is the unique element of
$y_9={\mathfrak {e}}_9\cap T$
and D is the unique element of
![]() $|\ell -{\mathfrak {e}}_8|$
passing through the point
$|\ell -{\mathfrak {e}}_8|$
passing through the point
![]() $y^{\prime }_9$
, such that
$y^{\prime }_9$
, such that
![]() $y_9+y^{\prime }_9= T \cap \mathfrak {f}'$
; finally
$y_9+y^{\prime }_9= T \cap \mathfrak {f}'$
; finally
![]() $\mathfrak {s}'$
is one of the two sections
$\mathfrak {s}'$
is one of the two sections
![]() $\mathfrak {s}$
passing through the remaining intersection point of D with T.
$\mathfrak {s}$
passing through the remaining intersection point of D with T.
Arguing as in the proof of Proposition 4.1, this curve can be deformed to a one-nodal rigid elliptic curve of arithmetic genus
![]() $2$
in the linear system
$2$
in the linear system
![]() $|L|$
as
$|L|$
as
![]() $(\widetilde {R} \cup _T \widetilde {P},L^0)$
deforms to
$(\widetilde {R} \cup _T \widetilde {P},L^0)$
deforms to
![]() $(S,L)$
.
$(S,L)$
.
7.2 The case
 $a_0=a_9$
and
$a_0=a_9$
and
 $a_i=0$
otherwise
$a_i=0$
otherwise
Both
![]() $a_0$
and
$a_0$
and
![]() $a_9$
are odd.
$a_9$
are odd.
7.2.1 Subcase
 $a_0=a_9=1$
$a_0=a_9=1$
Consider the limit line bundle
![]() $L^0 = E^0_{9,10}+E^0_9$
, with
$L^0 = E^0_{9,10}+E^0_9$
, with
![]() $E^0_{9,10}$
and
$E^0_{9,10}$
and
![]() $E^0_9$
as in Example 6.1 (as above). Then
$E^0_9$
as in Example 6.1 (as above). Then
There is, again, no need to invoke Proposition 4.2 or 4.3: indeed, the linear system
![]() $|L|$
contains the following curve, constructed as in the previous case:
$|L|$
contains the following curve, constructed as in the previous case:

Arguing, again, as in the proof of Proposition 4.1, this curve can be deformed to a rigid elliptic two-nodal curve of arithmetic genus
![]() $3$
in the linear system
$3$
in the linear system
![]() $|L|$
as
$|L|$
as
![]() $(\widetilde {R} \cup _T \widetilde {P},L^0)$
deforms to
$(\widetilde {R} \cup _T \widetilde {P},L^0)$
deforms to
![]() $(S,L)$
.
$(S,L)$
.
7.2.2 Subcase
 $a_0=a_9 \geq 3$
$a_0=a_9 \geq 3$
Consider the limit line bundle
![]() $L^0 = a_0(E^0_{5,6}+E^0_5)$
, with
$L^0 = a_0(E^0_{5,6}+E^0_5)$
, with
![]() $E^0_{5,6}$
and
$E^0_{5,6}$
and
![]() $E^0_5$
as in Example 6.1. Then
$E^0_5$
as in Example 6.1. Then
We see that we might as well substitute
![]() $\widetilde {R}$
with R and
$\widetilde {R}$
with R and
![]() $\widetilde {P}$
with
$\widetilde {P}$
with
![]() $P'=\operatorname {Bl}_{y_5,y_7,y_8}(P)$
and consider
$P'=\operatorname {Bl}_{y_5,y_7,y_8}(P)$
and consider
![]() $L^0=(L',L")$
as a line bundle on
$L^0=(L',L")$
as a line bundle on
![]() $R \cup _T P'$
. We apply Proposition 4.2 with
$R \cup _T P'$
. We apply Proposition 4.2 with
![]() $k=0$
,
$k=0$
,
![]() $s=0$
and
$s=0$
and
![]() $t=3$
.
$t=3$
.
Clearly
![]() $L'$
satisfies condition
$L'$
satisfies condition
![]() $(\star )$
and is odd and
$(\star )$
and is odd and
![]() $L"$
is big and nef. Moreover,
$L"$
is big and nef. Moreover,
![]() ${\mathfrak {e}}_i \cdot L">0$
for
${\mathfrak {e}}_i \cdot L">0$
for
![]() $i \in \{5,7,8\}$
. The conditions of Proposition 4.2 are satisfied, and we are done.
$i \in \{5,7,8\}$
. The conditions of Proposition 4.2 are satisfied, and we are done.
7.3 The cases
 $a_7=a_9=a_{10}=a_0=0$
$a_7=a_9=a_{10}=a_0=0$
At least one of the
![]() $a_i$
is odd. Pick the minimal such and call it
$a_i$
is odd. Pick the minimal such and call it
![]() $c_1$
. Reordering the remaining
$c_1$
. Reordering the remaining
![]() $a_i$
s, we have that a limit line bundle is of type
$a_i$
s, we have that a limit line bundle is of type
 $$\begin{align*}L^0 \equiv c_1E^0_1+\sum_{i=5}^8c_iE^0_i+c_{10}E^0_{10}, \end{align*}$$
$$\begin{align*}L^0 \equiv c_1E^0_1+\sum_{i=5}^8c_iE^0_i+c_{10}E^0_{10}, \end{align*}$$
with the
![]() $E^0_i$
as in Example 6.1, where
$E^0_i$
as in Example 6.1, where
![]() $c_1$
is the minimal odd coefficient, and we may also assume that
$c_1$
is the minimal odd coefficient, and we may also assume that
![]() $c_5>0$
. Then
$c_5>0$
. Then
 $$ \begin{align*} L':=L^0|_{\widetilde{R}} & \equiv c_1(\mathfrak{s}-{\mathfrak{e}}_1)+\sum_{i=5}^8c_i \mathfrak{f}+c_{10}\mathfrak{f}=c_1\mathfrak{s}+(c_5+c_6+c_7+c_8+c_{10})\mathfrak{f}-c_1{\mathfrak{e}}_1, \\ L":=L^0|_{\widetilde{P}} & \sim \sum_{i=5}^8c_i(\ell-{\mathfrak{e}}_i)+c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*} $$
$$ \begin{align*} L':=L^0|_{\widetilde{R}} & \equiv c_1(\mathfrak{s}-{\mathfrak{e}}_1)+\sum_{i=5}^8c_i \mathfrak{f}+c_{10}\mathfrak{f}=c_1\mathfrak{s}+(c_5+c_6+c_7+c_8+c_{10})\mathfrak{f}-c_1{\mathfrak{e}}_1, \\ L":=L^0|_{\widetilde{P}} & \sim \sum_{i=5}^8c_i(\ell-{\mathfrak{e}}_i)+c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*} $$
We see that we might as well substitute
![]() $\widetilde {R}$
with
$\widetilde {R}$
with
![]() $R'=\operatorname {Bl}_{y_1}(R)$
and
$R'=\operatorname {Bl}_{y_1}(R)$
and
![]() $\widetilde {P}$
with
$\widetilde {P}$
with
![]() $P'=\operatorname {Bl}_{y_5,y_6,y_7,y_8}(P)$
and consider
$P'=\operatorname {Bl}_{y_5,y_6,y_7,y_8}(P)$
and consider
![]() $L^0=(L',L")$
as a line bundle on
$L^0=(L',L")$
as a line bundle on
![]() $R' \cup _T P'$
. We apply Proposition 4.2 with
$R' \cup _T P'$
. We apply Proposition 4.2 with
![]() $s=1$
,
$s=1$
,
![]() $t=4$
and
$t=4$
and
![]() $k=0$
. Conditions (i)–(iii) of
$k=0$
. Conditions (i)–(iii) of
![]() $(\star )$
are verified by
$(\star )$
are verified by
![]() $L'$
; condition (iv) is equivalent to
$L'$
; condition (iv) is equivalent to
![]() $c_5+c_6+c_7+c_8+c_{10}\geq 2$
, which is verified unless
$c_5+c_6+c_7+c_8+c_{10}\geq 2$
, which is verified unless
![]() $c_5=1$
and
$c_5=1$
and
![]() $c_6=c_7=c_8=c_{10}=0$
. Since
$c_6=c_7=c_8=c_{10}=0$
. Since
![]() $c_1$
was assumed to be a minimal odd fundamental coefficient, we must have
$c_1$
was assumed to be a minimal odd fundamental coefficient, we must have
![]() $c_1=1$
as well. This case is the one treated in Section 7.1. We may therefore assume that
$c_1=1$
as well. This case is the one treated in Section 7.1. We may therefore assume that
![]() $L'$
satisfies
$L'$
satisfies
![]() $(\star )$
. One readily checks that
$(\star )$
. One readily checks that
![]() $L'$
is odd (since
$L'$
is odd (since
![]() $c_1$
is odd), and that
$c_1$
is odd), and that
![]() $L"$
is big and nef (all components have square zero, intersect and can be represented by irreducible curves). This verifies conditions (i)–(iv) in Proposition 4.2. Since, for instance,
$L"$
is big and nef (all components have square zero, intersect and can be represented by irreducible curves). This verifies conditions (i)–(iv) in Proposition 4.2. Since, for instance,
![]() ${\mathfrak {e}}_5 \cdot L"=c_5+c_{10} \geq c_5>0$
, also condition (v) therein is satisfied. Hence, we are done by Proposition 4.2.
${\mathfrak {e}}_5 \cdot L"=c_5+c_{10} \geq c_5>0$
, also condition (v) therein is satisfied. Hence, we are done by Proposition 4.2.
7.4 Case where there are three distinct
 $k,l,m \in \{1,\ldots ,7\}$
, such that
$k,l,m \in \{1,\ldots ,7\}$
, such that
 $a_i+a_k+a_l+a_m$
is odd for
$a_i+a_k+a_l+a_m$
is odd for
 $i=9$
or
$i=9$
or
 $10$
(case (i) in Lemma 5.8)
$10$
(case (i) in Lemma 5.8)
Note that the cases among these with
![]() $a_0=0$
(whence also
$a_0=0$
(whence also
![]() $a_9=a_{10}=0$
) and
$a_9=a_{10}=0$
) and
![]() $a_7=0$
fall into the cases treated in Section 7.3. We can therefore assume that
$a_7=0$
fall into the cases treated in Section 7.3. We can therefore assume that
Similarly, the cases among these with
![]() $a_0=a_9$
and all remaining
$a_0=a_9$
and all remaining
![]() $a_i=0$
fall into the cases treated in Section 7.2. We can therefore assume that
$a_i=0$
fall into the cases treated in Section 7.2. We can therefore assume that
We know that for
![]() $i=9$
or
$i=9$
or
![]() $10$
, we can find indices
$10$
, we can find indices
![]() $k,l,m$
so that
$k,l,m$
so that
![]() $a_i+ a_k+a_l+a_m$
is odd. In this case, we take
$a_i+ a_k+a_l+a_m$
is odd. In this case, we take
![]() $k,l,m$
so that
$k,l,m$
so that
![]() $a_k+a_l+a_m$
is minimal with respect to this property. If we can do this for both
$a_k+a_l+a_m$
is minimal with respect to this property. If we can do this for both
![]() $i=9$
and
$i=9$
and
![]() $10$
(with possibly different triples of indices
$10$
(with possibly different triples of indices
![]() $k,l,m$
), we will pick
$k,l,m$
), we will pick
![]() $i \in \{9,10\}$
so that
$i \in \{9,10\}$
so that
![]() $a_i+ a_k+a_l+a_m$
is minimal. We rename these coefficients
$a_i+ a_k+a_l+a_m$
is minimal. We rename these coefficients
![]() $a_i,a_k,a_l,a_m$
as
$a_i,a_k,a_l,a_m$
as
![]() $c_9,c_2,c_3,c_4$
, making sure that
$c_9,c_2,c_3,c_4$
, making sure that
set
![]() $c_0=a_0$
,
$c_0=a_0$
,
 $c_{10}=\begin {cases} a_{10}, & \mbox {if} \; i=9 \\ a_{9}, & \mbox {if} \; i=10 \end {cases}$
, and rename the remaining
$c_{10}=\begin {cases} a_{10}, & \mbox {if} \; i=9 \\ a_{9}, & \mbox {if} \; i=10 \end {cases}$
, and rename the remaining
![]() $a_i$
as
$a_i$
as
![]() $c_5,c_6,c_7,c_8$
in such a way that
$c_5,c_6,c_7,c_8$
in such a way that
We thus have a limit line bundle
 $$\begin{align*}L^0 \equiv c_0E_{9,10}^0+c_9E^0_9+c_{10}E^0_{10}+\sum_{i=2}^8c_iE^0_i, \end{align*}$$
$$\begin{align*}L^0 \equiv c_0E_{9,10}^0+c_9E^0_9+c_{10}E^0_{10}+\sum_{i=2}^8c_iE^0_i, \end{align*}$$
with the
![]() $E^0_i$
and
$E^0_i$
and
![]() $E^0_{9,10}$
as in Example 6.1, where, besides (31) and (32), one has
$E^0_{9,10}$
as in Example 6.1, where, besides (31) and (32), one has
 $$\begin{align*} & \qquad\qquad\qquad\qquad\quad c_i+c_k+c_l+c_m \mbox{ is odd and} \nonumber \\ & \begin{cases} c_k+c_l+c_m < c_2+c_3+c_4, \mbox{or} \\ c_k+c_l+c_m = c_2+c_3+c_4 \; \; \mbox{and} \; \; c_i+ c_k+c_l+c_m < c_9 + c_2+c_3+c_4. \end{cases} \notag \end{align*}$$
$$\begin{align*} & \qquad\qquad\qquad\qquad\quad c_i+c_k+c_l+c_m \mbox{ is odd and} \nonumber \\ & \begin{cases} c_k+c_l+c_m < c_2+c_3+c_4, \mbox{or} \\ c_k+c_l+c_m = c_2+c_3+c_4 \; \; \mbox{and} \; \; c_i+ c_k+c_l+c_m < c_9 + c_2+c_3+c_4. \end{cases} \notag \end{align*}$$
Furthermore, (29) gives
and (30) yields
We define
Claim 7.1. The following hold:
-
(i) If
 $c_0=0$
, then
$c_0=0$
, then
 $(\kappa ,\lambda )=(3,4)$
.
$(\kappa ,\lambda )=(3,4)$
. -
(ii) If
 $\lambda \leq 2$
, then
$\lambda \leq 2$
, then
 $\kappa \leq 1$
; moreover,
$\kappa \leq 1$
; moreover,
 $\kappa =1$
implies
$\kappa =1$
implies
 $c_{10} \geq 2$
.
$c_{10} \geq 2$
. -
(iii) If
 $(\kappa ,\lambda ,c_{10})=(0,0,0)$
, then
$(\kappa ,\lambda ,c_{10})=(0,0,0)$
, then
 $c_0 \neq c_9$
.
$c_0 \neq c_9$
.
Proof. Property (i) follows from condition (36).
Next assume
![]() $\lambda \leq 2$
, that is,
$\lambda \leq 2$
, that is,
![]() $c_7=c_8=0$
. Then properties (34) and (35) yield that
$c_7=c_8=0$
. Then properties (34) and (35) yield that
![]() $c_3=c_4=0$
, that is,
$c_3=c_4=0$
, that is,
![]() $\kappa \leq 1$
, as we now explain. Indeed, if
$\kappa \leq 1$
, as we now explain. Indeed, if
![]() $c_4$
is even and positive, we have that
$c_4$
is even and positive, we have that
![]() $c_9+c_2+c_3+c_8$
is odd and
$c_9+c_2+c_3+c_8$
is odd and
![]() $c_2+c_3+c_8<c_2+c_3+c_4$
, contradicting (35) (similarly for the cases where
$c_2+c_3+c_8<c_2+c_3+c_4$
, contradicting (35) (similarly for the cases where
![]() $c_i$
is even and positive with
$c_i$
is even and positive with
![]() $i=2,3$
). From this, it follows that none among
$i=2,3$
). From this, it follows that none among
![]() $c_2,c_3, c_4$
can be even and positive.
$c_2,c_3, c_4$
can be even and positive.
If
![]() $c_3$
and
$c_3$
and
![]() $c_4$
are odd, then
$c_4$
are odd, then
![]() $c_9+c_2+c_7+c_8$
is odd and
$c_9+c_2+c_7+c_8$
is odd and
![]() $c_2+c_7+c_8<c_2+c_3+c_4$
, contradicting (35) (similarly if
$c_2+c_7+c_8<c_2+c_3+c_4$
, contradicting (35) (similarly if
![]() $c_2$
and
$c_2$
and
![]() $c_3$
or
$c_3$
or
![]() $c_2$
and
$c_2$
and
![]() $c_4$
are odd). Hence, at most one among
$c_4$
are odd). Hence, at most one among
![]() $c_2,c_3, c_4$
is odd.
$c_2,c_3, c_4$
is odd.
In conclusion, at least two among
![]() $c_2,c_3, c_4$
must be zero, hence,
$c_2,c_3, c_4$
must be zero, hence,
![]() $c_3=c_4=0$
by (31), as we claimed.
$c_3=c_4=0$
by (31), as we claimed.
If
![]() $\kappa =1$
, we have
$\kappa =1$
, we have
![]() $c_2>0$
and
$c_2>0$
and
![]() $c_9+c_2$
is odd by (34). Condition (35) yields that
$c_9+c_2$
is odd by (34). Condition (35) yields that
![]() $c_9$
is even (whence
$c_9$
is even (whence
![]() $c_2$
is odd), for otherwise,
$c_2$
is odd), for otherwise,
![]() $c_9=c_9+c_3+c_4+c_8$
would be odd with
$c_9=c_9+c_3+c_4+c_8$
would be odd with
![]() $0=c_3+c_4+c_8<c_2=c_2+c_3+c_4$
. For the same reason,
$0=c_3+c_4+c_8<c_2=c_2+c_3+c_4$
. For the same reason,
![]() $c_{10}$
is even, and condition (35) yields that
$c_{10}$
is even, and condition (35) yields that
![]() $c_{10} \geq c_9$
. By (33) and the fact that
$c_{10} \geq c_9$
. By (33) and the fact that
![]() $c_0>0$
from (i), we must have
$c_0>0$
from (i), we must have
![]() $c_{10}>0$
. This proves (ii).
$c_{10}>0$
. This proves (ii).
Finally, (iii) is a reformulation of property (37).
Consider
 $$ \begin{align*} L' := L^0|_{\widetilde{R}} & \equiv c_0\mathfrak{f}+c_9\mathfrak{s}+c_{10}\mathfrak{f} +\sum_{i=2}^4 c_i(\mathfrak{s}-{\mathfrak{e}}_i)+\sum_{i=5}^8c_i\mathfrak{f} \\ & = (c_2+c_3+c_4+c_9)\mathfrak{s}+(c_0+c_5+c_6+c_7+c_8+c_{10})\mathfrak{f} - \sum_{i=2}^4 c_i{\mathfrak{e}}_i\\ & = L^{\prime}_0 + \sum_{i=2}^{\kappa+1}(\mathfrak{f}-{\mathfrak{e}}_i), \end{align*} $$
$$ \begin{align*} L' := L^0|_{\widetilde{R}} & \equiv c_0\mathfrak{f}+c_9\mathfrak{s}+c_{10}\mathfrak{f} +\sum_{i=2}^4 c_i(\mathfrak{s}-{\mathfrak{e}}_i)+\sum_{i=5}^8c_i\mathfrak{f} \\ & = (c_2+c_3+c_4+c_9)\mathfrak{s}+(c_0+c_5+c_6+c_7+c_8+c_{10})\mathfrak{f} - \sum_{i=2}^4 c_i{\mathfrak{e}}_i\\ & = L^{\prime}_0 + \sum_{i=2}^{\kappa+1}(\mathfrak{f}-{\mathfrak{e}}_i), \end{align*} $$
where
 $$\begin{align*}L^{\prime}_0 :=(c_2+c_3+c_4+c_9)\mathfrak{s}+(c_0+c_5+c_6+c_7+c_8+c_{10}-\kappa)\mathfrak{f}-\sum_{i=2}^{\kappa+1} (c_i-1){\mathfrak{e}}_i \end{align*}$$
$$\begin{align*}L^{\prime}_0 :=(c_2+c_3+c_4+c_9)\mathfrak{s}+(c_0+c_5+c_6+c_7+c_8+c_{10}-\kappa)\mathfrak{f}-\sum_{i=2}^{\kappa+1} (c_i-1){\mathfrak{e}}_i \end{align*}$$
and
![]() $\sum _{i=2}^{\kappa +1}(\mathfrak {f}-{\mathfrak {e}}_i)$
is the sum of
$\sum _{i=2}^{\kappa +1}(\mathfrak {f}-{\mathfrak {e}}_i)$
is the sum of
![]() $\kappa $
disjoint
$\kappa $
disjoint
![]() $(-1)$
-curves. We note that we may consider
$(-1)$
-curves. We note that we may consider
![]() $L'$
as a line bundle on the blowup of R at
$L'$
as a line bundle on the blowup of R at
![]() $\kappa $
points. Hence, we will eventually apply Proposition 4.2 with
$\kappa $
points. Hence, we will eventually apply Proposition 4.2 with
![]() $k=s=\kappa $
.
$k=s=\kappa $
.
Claim 7.2.
![]() $L^{\prime }_0$
verifies condition
$L^{\prime }_0$
verifies condition
![]() $(\star )$
and is odd.
$(\star )$
and is odd.
Proof. Oddness is equivalent to condition (34). Conditions (i)–(iii) of
![]() $(\star )$
are easily checked. Condition (iv) is equivalent to
$(\star )$
are easily checked. Condition (iv) is equivalent to
 $$ \begin{align} 2c_0+c_9+2c_{10}+2\sum_{i=5}^8c_i -\kappa \geq 4. \end{align} $$
$$ \begin{align} 2c_0+c_9+2c_{10}+2\sum_{i=5}^8c_i -\kappa \geq 4. \end{align} $$
If
![]() $c_0=0$
, then
$c_0=0$
, then
![]() $c_9=c_{10}=0$
by (33) and
$c_9=c_{10}=0$
by (33) and
![]() $(\kappa ,\lambda )=(3,4)$
by Claim 7.1(i), whence the left-hand side of (38) equals
$(\kappa ,\lambda )=(3,4)$
by Claim 7.1(i), whence the left-hand side of (38) equals
![]() $2\sum _{i=5}^8c_i -\kappa \geq 8 -3=5$
, and we are done. Hence, we may assume that
$2\sum _{i=5}^8c_i -\kappa \geq 8 -3=5$
, and we are done. Hence, we may assume that
![]() $c_0>0$
for the rest of the proof.
$c_0>0$
for the rest of the proof.
We note that, by (33),
 $$\begin{align*}2c_0+c_9+2c_{10}+2\sum_{i=5}^8c_i -\kappa \geq 3c_0+c_{10}+2\lambda-\kappa \geq 3+c_{10}+2\lambda-\kappa.\end{align*}$$
$$\begin{align*}2c_0+c_9+2c_{10}+2\sum_{i=5}^8c_i -\kappa \geq 3c_0+c_{10}+2\lambda-\kappa \geq 3+c_{10}+2\lambda-\kappa.\end{align*}$$
This, together with Claim 7.1(ii) tells us that (38) is always satisfied if
![]() $\lambda \geq 1$
. Assume, therefore, that
$\lambda \geq 1$
. Assume, therefore, that
![]() $\lambda =0$
. Then
$\lambda =0$
. Then
![]() $\kappa \leq 1$
, by Claim 7.1(ii). If
$\kappa \leq 1$
, by Claim 7.1(ii). If
![]() $\kappa =1$
, then
$\kappa =1$
, then
![]() $c_{10} \geq 2$
, by Claim 7.1(ii), and (38) is again satisfied. If
$c_{10} \geq 2$
, by Claim 7.1(ii), and (38) is again satisfied. If
![]() $\kappa =0$
, we have that
$\kappa =0$
, we have that
![]() $c_9$
is odd by (34). If
$c_9$
is odd by (34). If
![]() $c_{10}>0$
, (38) is satisfied. Otherwise, Claim 7.1(iii) yields
$c_{10}>0$
, (38) is satisfied. Otherwise, Claim 7.1(iii) yields
![]() $c_0 \geq 2$
, whence (38) is again satisfied.
$c_0 \geq 2$
, whence (38) is again satisfied.
Consider
 $$ \begin{align*} L" := L^0|_{\widetilde{P}} & \sim c_0(\ell-{\mathfrak{e}}_9)+c_9{\mathfrak{e}}_9+c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^8 c_i(\ell-{\mathfrak{e}}_i) \\ & = (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^8 c_i(\ell-{\mathfrak{e}}_i). \end{align*} $$
$$ \begin{align*} L" := L^0|_{\widetilde{P}} & \sim c_0(\ell-{\mathfrak{e}}_9)+c_9{\mathfrak{e}}_9+c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^8 c_i(\ell-{\mathfrak{e}}_i) \\ & = (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^8 c_i(\ell-{\mathfrak{e}}_i). \end{align*} $$
The idea is now to apply Proposition 4.2 with
![]() $k=\kappa $
.
$k=\kappa $
.
7.4.1 Subcase
 $\lambda =3,4$
$\lambda =3,4$
We have
![]() $c_5 \geq c_6 \geq c_7>0$
, by (32). Define
$c_5 \geq c_6 \geq c_7>0$
, by (32). Define
 $$ \begin{align} L_0"(3) & := (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \\& \quad + \sum_{i=5}^7 (c_i-1) (\ell-{\mathfrak{e}}_i) + c_8(\ell-{\mathfrak{e}}_8) +(\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6)+(\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7)+(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8), \nonumber\\L_0"(2) & = L_0"(3)+{\mathfrak{e}}_6, \nonumber\\L_0"(1) & = L_0"(3)+{\mathfrak{e}}_6+{\mathfrak{e}}_7, \nonumber\\L_0"(0) & = L_0"(3)+{\mathfrak{e}}_6+{\mathfrak{e}}_7+{\mathfrak{e}}_8. \nonumber\end{align} $$
$$ \begin{align} L_0"(3) & := (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \\& \quad + \sum_{i=5}^7 (c_i-1) (\ell-{\mathfrak{e}}_i) + c_8(\ell-{\mathfrak{e}}_8) +(\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6)+(\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7)+(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8), \nonumber\\L_0"(2) & = L_0"(3)+{\mathfrak{e}}_6, \nonumber\\L_0"(1) & = L_0"(3)+{\mathfrak{e}}_6+{\mathfrak{e}}_7, \nonumber\\L_0"(0) & = L_0"(3)+{\mathfrak{e}}_6+{\mathfrak{e}}_7+{\mathfrak{e}}_8. \nonumber\end{align} $$
Then one may check that
 $$\begin{align*}L" = L_0"(\kappa)+ \begin{cases} 0, & \mbox{if} \; \; \kappa=0, \\ {\mathfrak{e}}_8, & \mbox{if} \; \; \kappa=1, \\ {\mathfrak{e}}_7+{\mathfrak{e}}_8, & \mbox{if} \; \; \kappa=2, \\ {\mathfrak{e}}_6+{\mathfrak{e}}_7+{\mathfrak{e}}_8, & \mbox{if} \; \; \kappa=3. \\ \end{cases} \end{align*}$$
$$\begin{align*}L" = L_0"(\kappa)+ \begin{cases} 0, & \mbox{if} \; \; \kappa=0, \\ {\mathfrak{e}}_8, & \mbox{if} \; \; \kappa=1, \\ {\mathfrak{e}}_7+{\mathfrak{e}}_8, & \mbox{if} \; \; \kappa=2, \\ {\mathfrak{e}}_6+{\mathfrak{e}}_7+{\mathfrak{e}}_8, & \mbox{if} \; \; \kappa=3. \\ \end{cases} \end{align*}$$
Claim 7.3.
![]() $L_0"(\kappa )$
is big and nef for all
$L_0"(\kappa )$
is big and nef for all
![]() $\kappa \in \{0,1,2,3\}$
.
$\kappa \in \{0,1,2,3\}$
.
Proof. Since
![]() ${\mathfrak {e}}_i \cdot L_0"(3)>0$
, for
${\mathfrak {e}}_i \cdot L_0"(3)>0$
, for
![]() $i\in \{6,7,8\}$
, it suffices to verify that
$i\in \{6,7,8\}$
, it suffices to verify that
![]() $L_0"(3)$
is big and nef. All divisors in the sum (39) are nef, except for the last three, which are irreducible. Nefness follows if the latter three intersect
$L_0"(3)$
is big and nef. All divisors in the sum (39) are nef, except for the last three, which are irreducible. Nefness follows if the latter three intersect
![]() $L_0"(3)$
nonnegatively. We have
$L_0"(3)$
nonnegatively. We have
 $$ \begin{align*} L_0"(3) \cdot (\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6) & = c_0+(c_7-1)+c_8-1+0+1 \geq 0, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8) & = c_0+(c_5-1)+(c_6-1)+1+0-1 \geq 0. \end{align*} $$
$$ \begin{align*} L_0"(3) \cdot (\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6) & = c_0+(c_7-1)+c_8-1+0+1 \geq 0, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8) & = c_0+(c_5-1)+(c_6-1)+1+0-1 \geq 0. \end{align*} $$
Finally
which is nonnegative, since, by Claim 7.1(i), either
![]() $c_0>0$
, or
$c_0>0$
, or
![]() $\lambda =4$
(whence
$\lambda =4$
(whence
![]() $c_8>0$
). This proves nefness. Bigness is easily checked.
$c_8>0$
). This proves nefness. Bigness is easily checked.
We apply Proposition 4.2 with
![]() $k=s=\kappa $
,
$k=s=\kappa $
,
![]() $t=5$
and
$t=5$
and
![]() $L^{\prime \prime }_0=L_0(\kappa )$
. What is left to be checked is condition (v). The set of additional
$L^{\prime \prime }_0=L_0(\kappa )$
. What is left to be checked is condition (v). The set of additional
![]() $t-k=5-\kappa $
disjoint
$t-k=5-\kappa $
disjoint
![]() $(-1)$
-curves on
$(-1)$
-curves on
![]() $\widetilde {P}$
is
$\widetilde {P}$
is
 $$\begin{align*}\begin{cases} {\mathfrak{e}}_5,{\mathfrak{e}}_6,{\mathfrak{e}}_7,{\mathfrak{e}}_8,{\mathfrak{e}}_9, & \mbox{if} \; \; \kappa=0, \\ {\mathfrak{e}}_5,{\mathfrak{e}}_6,{\mathfrak{e}}_7,{\mathfrak{e}}_9, & \mbox{if} \; \; \kappa=1, \\ {\mathfrak{e}}_5,{\mathfrak{e}}_6,{\mathfrak{e}}_9 & \mbox{if} \; \; \kappa=2, \\ {\mathfrak{e}}_5,{\mathfrak{e}}_9 & \mbox{if} \; \; \kappa=3, \\ \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} {\mathfrak{e}}_5,{\mathfrak{e}}_6,{\mathfrak{e}}_7,{\mathfrak{e}}_8,{\mathfrak{e}}_9, & \mbox{if} \; \; \kappa=0, \\ {\mathfrak{e}}_5,{\mathfrak{e}}_6,{\mathfrak{e}}_7,{\mathfrak{e}}_9, & \mbox{if} \; \; \kappa=1, \\ {\mathfrak{e}}_5,{\mathfrak{e}}_6,{\mathfrak{e}}_9 & \mbox{if} \; \; \kappa=2, \\ {\mathfrak{e}}_5,{\mathfrak{e}}_9 & \mbox{if} \; \; \kappa=3, \\ \end{cases} \end{align*}$$
and
![]() ${\mathfrak {e}}_5 \cdot L"(\kappa ) = c_{10}+c_5 \geq c_5>0$
, as
${\mathfrak {e}}_5 \cdot L"(\kappa ) = c_{10}+c_5 \geq c_5>0$
, as
![]() $\lambda>0$
, verifying condition (v) in Proposition 4.2.
$\lambda>0$
, verifying condition (v) in Proposition 4.2.
7.4.2 Subcase
 $\lambda \leq 2$
$\lambda \leq 2$
We have
![]() $c_0>0$
,
$c_0>0$
,
![]() $c_7=c_8=0$
, and
$c_7=c_8=0$
, and
![]() $\kappa \leq 1$
, by Claim 7.1(i)–(ii).
$\kappa \leq 1$
, by Claim 7.1(i)–(ii).
If
![]() $\kappa =0$
, we apply Proposition 4.2 with
$\kappa =0$
, we apply Proposition 4.2 with
![]() $k=s=0$
and
$k=s=0$
and
![]() $t=5$
. Condition (v) therein is satisfied, as for instance,
$t=5$
. Condition (v) therein is satisfied, as for instance,
![]() ${\mathfrak {e}}_5 \cdot L"=c_{10}+c_5$
and
${\mathfrak {e}}_5 \cdot L"=c_{10}+c_5$
and
![]() ${\mathfrak {e}}_9 \cdot L"=c_0-c_9$
; indeed, if
${\mathfrak {e}}_9 \cdot L"=c_0-c_9$
; indeed, if
![]() ${\mathfrak {e}}_5 \cdot L"=0$
, then
${\mathfrak {e}}_5 \cdot L"=0$
, then
![]() $c_{10}=c_5=0$
, whence
$c_{10}=c_5=0$
, whence
![]() $\lambda =0$
, so Claim 7.1(iii) yields
$\lambda =0$
, so Claim 7.1(iii) yields
![]() ${\mathfrak {e}}_9 \cdot L">0$
.
${\mathfrak {e}}_9 \cdot L">0$
.
If
![]() $\kappa =1$
, then
$\kappa =1$
, then
![]() $c_{10} \geq 2$
, by Claim 7.1(ii). Write
$c_{10} \geq 2$
, by Claim 7.1(ii). Write
![]() $L"=L^{\prime \prime }_0+ {\mathfrak {e}}_9$
, with
$L"=L^{\prime \prime }_0+ {\mathfrak {e}}_9$
, with
 $$ \begin{align*} L^{\prime\prime}_0:= (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ (c_{10}-1)(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \\ \sum_{i=5}^6 c_i(\ell-{\mathfrak{e}}_i) +(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8-{\mathfrak{e}}_9), \end{align*} $$
$$ \begin{align*} L^{\prime\prime}_0:= (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ (c_{10}-1)(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \\ \sum_{i=5}^6 c_i(\ell-{\mathfrak{e}}_i) +(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8-{\mathfrak{e}}_9), \end{align*} $$
which is big and nef, since the only term with negative square is the last one, and one checks that
![]() $(2\ell -{\mathfrak {e}}_5-{\mathfrak {e}}_6-{\mathfrak {e}}_7-{\mathfrak {e}}_8-{\mathfrak {e}}_9) \cdot L^{\prime \prime }_0=c_0+c_9+c_5+c_6-1 \geq 0$
. We apply Proposition 4.2 with
$(2\ell -{\mathfrak {e}}_5-{\mathfrak {e}}_6-{\mathfrak {e}}_7-{\mathfrak {e}}_8-{\mathfrak {e}}_9) \cdot L^{\prime \prime }_0=c_0+c_9+c_5+c_6-1 \geq 0$
. We apply Proposition 4.2 with
![]() $k=s=1$
and
$k=s=1$
and
![]() $t=5$
. Condition (v), therein, is satisfied, as for instance,
$t=5$
. Condition (v), therein, is satisfied, as for instance,
![]() ${\mathfrak {e}}_5 \cdot L"=c_{10}+c_5 \geq c_{10} \geq 2$
.
${\mathfrak {e}}_5 \cdot L"=c_{10}+c_5 \geq c_{10} \geq 2$
.
7.5 Case where
 $a_0>0$
is odd and all remaining
$a_0>0$
is odd and all remaining
 $a_i$
are even (case (ii) in Lemma 5.8)
$a_i$
are even (case (ii) in Lemma 5.8)
Since
![]() $a_9,a_{10}$
are even and
$a_9,a_{10}$
are even and
![]() $a_0$
is odd, we have
$a_0$
is odd, we have
which implies
![]() $a_0 \geq 3$
and
$a_0 \geq 3$
and
![]() $a_9,a_{10} \geq 2$
. Rearranging indices, we have a limit line bundle
$a_9,a_{10} \geq 2$
. Rearranging indices, we have a limit line bundle
 $$\begin{align*}L^0 \equiv c_0E_{5,6}^0+\sum_{i=1}^8c_iE^0_i+c_{10}E^0_{10}, \end{align*}$$
$$\begin{align*}L^0 \equiv c_0E_{5,6}^0+\sum_{i=1}^8c_iE^0_i+c_{10}E^0_{10}, \end{align*}$$
with the
![]() $E^0_i$
and
$E^0_i$
and
![]() $E^0_{5,6}$
, as in Example 6.1, where
$E^0_{5,6}$
, as in Example 6.1, where
We define
Consider
 $$ \begin{align*} L' := L^0|_{\widetilde{R}} & \equiv c_0\mathfrak{s}+\sum_{i=1}^4 c_i(\mathfrak{s}-{\mathfrak{e}}_i)+\sum_{i=5}^8c_i\mathfrak{f}+c_{10}\mathfrak{f} \\ & = (c_0+c_1+c_2+c_3+c_4)\mathfrak{s}+\left(c_5+c_6+c_7+c_8+c_{10}\right)\mathfrak{f} - \sum_{i=1}^{\kappa} c_i{\mathfrak{e}}_i \\ & = L^{\prime}_0 + \sum_{i=2}^{\kappa}(\mathfrak{f}-{\mathfrak{e}}_i), \end{align*} $$
$$ \begin{align*} L' := L^0|_{\widetilde{R}} & \equiv c_0\mathfrak{s}+\sum_{i=1}^4 c_i(\mathfrak{s}-{\mathfrak{e}}_i)+\sum_{i=5}^8c_i\mathfrak{f}+c_{10}\mathfrak{f} \\ & = (c_0+c_1+c_2+c_3+c_4)\mathfrak{s}+\left(c_5+c_6+c_7+c_8+c_{10}\right)\mathfrak{f} - \sum_{i=1}^{\kappa} c_i{\mathfrak{e}}_i \\ & = L^{\prime}_0 + \sum_{i=2}^{\kappa}(\mathfrak{f}-{\mathfrak{e}}_i), \end{align*} $$
where
 $$\begin{align*}L^{\prime}_0 :=(c_0+c_1+c_2+c_3+c_4)\mathfrak{s}+ \left(c_5+c_6+c_7+c_8+c_{10}-\kappa+1\right)\mathfrak{f} -c_1{\mathfrak{e}}_1 -\sum_{i=2}^{\kappa} (c_i-1){\mathfrak{e}}_i \end{align*}$$
$$\begin{align*}L^{\prime}_0 :=(c_0+c_1+c_2+c_3+c_4)\mathfrak{s}+ \left(c_5+c_6+c_7+c_8+c_{10}-\kappa+1\right)\mathfrak{f} -c_1{\mathfrak{e}}_1 -\sum_{i=2}^{\kappa} (c_i-1){\mathfrak{e}}_i \end{align*}$$
and
![]() $\sum _{i=2}^{\kappa }(\mathfrak {f}-{\mathfrak {e}}_i)$
is the sum of
$\sum _{i=2}^{\kappa }(\mathfrak {f}-{\mathfrak {e}}_i)$
is the sum of
![]() $\max \{0,\kappa -1\}$
disjoint
$\max \{0,\kappa -1\}$
disjoint
![]() $(-1)$
-curves. We note that we may consider
$(-1)$
-curves. We note that we may consider
![]() $L'$
as a line bundle on the blowup of R at
$L'$
as a line bundle on the blowup of R at
![]() $\kappa $
points. Hence, we will eventually apply Proposition 4.2 with
$\kappa $
points. Hence, we will eventually apply Proposition 4.2 with
![]() $s=\kappa $
and
$s=\kappa $
and
![]() $k=\max \{0,\kappa -1\}$
.
$k=\max \{0,\kappa -1\}$
.
Claim 7.4.
![]() $L^{\prime }_0$
verifies condition
$L^{\prime }_0$
verifies condition
![]() $(\star )$
and is odd.
$(\star )$
and is odd.
Proof. Oddness follows since
![]() $c_0+c_1+c_2+c_3+c_4$
is odd by our assumptions (40) and (41). Conditions (i)–(iii) of
$c_0+c_1+c_2+c_3+c_4$
is odd by our assumptions (40) and (41). Conditions (i)–(iii) of
![]() $(\star )$
are easily checked. Condition (iv) is equivalent to
$(\star )$
are easily checked. Condition (iv) is equivalent to
This is verified since, by (40), the left-hand side is
![]() $\geq c_0+2c_5+2c_6 \geq 3+4+4=11$
.
$\geq c_0+2c_5+2c_6 \geq 3+4+4=11$
.
We have
 $$\begin{align*}L" := L^0|_{\widetilde{P}} \sim c_0(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^8 c_i(\ell-{\mathfrak{e}}_i) +c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*}$$
$$\begin{align*}L" := L^0|_{\widetilde{P}} \sim c_0(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^8 c_i(\ell-{\mathfrak{e}}_i) +c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*}$$
We can view
![]() $L"$
as a line bundle on
$L"$
as a line bundle on
![]() $\operatorname {Bl}_{y_5,y_6,y_7,y_8}(P)$
. The idea is now to apply Proposition 4.2 with
$\operatorname {Bl}_{y_5,y_6,y_7,y_8}(P)$
. The idea is now to apply Proposition 4.2 with
![]() $k=\max \{0,\kappa -1\}$
,
$k=\max \{0,\kappa -1\}$
,
![]() $s=\kappa $
and
$s=\kappa $
and
![]() $t=4$
.
$t=4$
.
7.5.1 Subcase
 $c_7=0$
$c_7=0$
By (41), we have
![]() $c_1=c_2=c_3=c_4=0$
, whence
$c_1=c_2=c_3=c_4=0$
, whence
![]() $\kappa =0$
. We apply Proposition 4.2 with
$\kappa =0$
. We apply Proposition 4.2 with
![]() $s=k=0$
and
$s=k=0$
and
![]() $t=4$
. Condition (v), therein, is satisfied, as for instance,
$t=4$
. Condition (v), therein, is satisfied, as for instance,
![]() ${\mathfrak {e}}_5 \cdot L"=c_5+c_{10} \geq c_{5}>0$
by (40).
${\mathfrak {e}}_5 \cdot L"=c_5+c_{10} \geq c_{5}>0$
by (40).
7.5.2 Subcase
 $c_7>0$
$c_7>0$
By (41), we have
![]() $c_7,c_8,c_{10} \geq 2$
.
$c_7,c_8,c_{10} \geq 2$
.
Define
 $$ \begin{align} L_0"(3) &:= c_0(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ c_5(\ell-{\mathfrak{e}}_5) +\sum_{i=6}^8 (c_i-1)(\ell-{\mathfrak{e}}_i) + \\& \quad +c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8) +(\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7)+(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_5)+ (\ell-{\mathfrak{e}}_8-{\mathfrak{e}}_6),\notag \\L_0"(2) & = L"(3)+{\mathfrak{e}}_5, \nonumber \\L_0"(1) & = L"(3)+{\mathfrak{e}}_5+{\mathfrak{e}}_6, \nonumber \\L_0"(0) & = L"(3)+{\mathfrak{e}}_5+{\mathfrak{e}}_6+{\mathfrak{e}}_7. \nonumber \end{align} $$
$$ \begin{align} L_0"(3) &:= c_0(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ c_5(\ell-{\mathfrak{e}}_5) +\sum_{i=6}^8 (c_i-1)(\ell-{\mathfrak{e}}_i) + \\& \quad +c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8) +(\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7)+(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_5)+ (\ell-{\mathfrak{e}}_8-{\mathfrak{e}}_6),\notag \\L_0"(2) & = L"(3)+{\mathfrak{e}}_5, \nonumber \\L_0"(1) & = L"(3)+{\mathfrak{e}}_5+{\mathfrak{e}}_6, \nonumber \\L_0"(0) & = L"(3)+{\mathfrak{e}}_5+{\mathfrak{e}}_6+{\mathfrak{e}}_7. \nonumber \end{align} $$
Then one may check that, for
![]() $j \in \{0,1,2,3\}$
:
$j \in \{0,1,2,3\}$
:
 $$\begin{align*}L" = L_0"(j)+ \begin{cases} 0, & \mbox{if} \; \; j=0, \\ {\mathfrak{e}}_7, & \mbox{if} \; \; j=1, \\ {\mathfrak{e}}_6+{\mathfrak{e}}_7, & \mbox{if} \; \; j=2, \\ {\mathfrak{e}}_5+{\mathfrak{e}}_6+{\mathfrak{e}}_7, & \mbox{if} \; \; j=3. \\ \end{cases} \end{align*}$$
$$\begin{align*}L" = L_0"(j)+ \begin{cases} 0, & \mbox{if} \; \; j=0, \\ {\mathfrak{e}}_7, & \mbox{if} \; \; j=1, \\ {\mathfrak{e}}_6+{\mathfrak{e}}_7, & \mbox{if} \; \; j=2, \\ {\mathfrak{e}}_5+{\mathfrak{e}}_6+{\mathfrak{e}}_7, & \mbox{if} \; \; j=3. \\ \end{cases} \end{align*}$$
Claim 7.5.
![]() $L_0"(j)$
is big and nef for all
$L_0"(j)$
is big and nef for all
![]() $j \in \{0,1,2,3\}$
.
$j \in \{0,1,2,3\}$
.
Proof. Since
![]() ${\mathfrak {e}}_i \cdot L_0"(3)>0$
, for
${\mathfrak {e}}_i \cdot L_0"(3)>0$
, for
![]() $i\in \{5,6,7\}$
, it suffices to verify that
$i\in \{5,6,7\}$
, it suffices to verify that
![]() $L_0"(3)$
is big and nef. All divisors in the sum (42) are of nonnegative square, except for the first and the last three. We have, using (40) and the fact that
$L_0"(3)$
is big and nef. All divisors in the sum (42) are of nonnegative square, except for the first and the last three. We have, using (40) and the fact that
![]() $c_5,c_6,c_7,c_8,c_{10} \geq 2$
:
$c_5,c_6,c_7,c_8,c_{10} \geq 2$
:
 $$ \begin{align*} L_0"(3) \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8) & = -c_0+c_5+(c_6-1) \geq 0, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7) & = c_5+(c_8-1)-1 \geq 2+1-1=2, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_5) & = (c_6-1)+(c_8-1)-1+1 \geq 1+1+0 \geq 2, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_8-{\mathfrak{e}}_6) & = c_5+(c_7-1)+1-1 \geq 2+1+0=3, \end{align*} $$
$$ \begin{align*} L_0"(3) \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8) & = -c_0+c_5+(c_6-1) \geq 0, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7) & = c_5+(c_8-1)-1 \geq 2+1-1=2, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_5) & = (c_6-1)+(c_8-1)-1+1 \geq 1+1+0 \geq 2, \\ L_0"(3) \cdot (\ell-{\mathfrak{e}}_8-{\mathfrak{e}}_6) & = c_5+(c_7-1)+1-1 \geq 2+1+0=3, \end{align*} $$
which proves that
![]() $L_0"(3)$
is nef. It is easily verified that it is big.
$L_0"(3)$
is nef. It is easily verified that it is big.
Now we apply Proposition 4.2 with
![]() $k=\max \{0,\kappa -1\} \leq 3$
,
$k=\max \{0,\kappa -1\} \leq 3$
,
![]() $s=\kappa $
,
$s=\kappa $
,
![]() $t=4$
and
$t=4$
and
![]() $L^{\prime \prime }_0=L_0(k)$
. What is left to be checked is condition (v). This is satisfied because
$L^{\prime \prime }_0=L_0(k)$
. What is left to be checked is condition (v). This is satisfied because
![]() ${\mathfrak {e}}_8 \cdot L_0"(k)=c_0+c_{8}-1+c_{10}+1=c_0+c_8+c_{10}>0$
.
${\mathfrak {e}}_8 \cdot L_0"(k)=c_0+c_{8}-1+c_{10}+1=c_0+c_8+c_{10}>0$
.
7.6 Case where
 $a_0>0$
and all remaining
$a_0>0$
and all remaining
 $a_i$
are odd (case (iii) in Lemma 5.8)
$a_i$
are odd (case (iii) in Lemma 5.8)
Rearranging indices, we have a limit line bundle
 $$\begin{align*}L^0 \equiv c_0E_{9,10}^0+c_9E^0_9+c_{10}E^0_{10}+\sum_{i=1}^7c_iE^0_i, \end{align*}$$
$$\begin{align*}L^0 \equiv c_0E_{9,10}^0+c_9E^0_9+c_{10}E^0_{10}+\sum_{i=1}^7c_iE^0_i, \end{align*}$$
with the
![]() $E^0_i$
and
$E^0_i$
and
![]() $E_{9,10}^0$
, as in Example 6.1, where
$E_{9,10}^0$
, as in Example 6.1, where
Consider
 $$ \begin{align*} L' & := L^0|_{\widetilde{R}} \equiv c_0\mathfrak{f} +c_9\mathfrak{s}+c_{10}\mathfrak{f} +\sum_{i=1}^4 c_i(\mathfrak{s}-{\mathfrak{e}}_i)+\sum_{i=5}^7c_i\mathfrak{f} \\ & = (c_1+c_2+c_3+c_4+c_9)\mathfrak{s}+(c_0+c_5+c_6+c_7+c_{10})\mathfrak{f}-\sum_{i=1}^4 c_i{\mathfrak{e}}_i \\ & = L^{\prime}_0 + \sum_{i=2}^{4}(\mathfrak{f}-{\mathfrak{e}}_i), \end{align*} $$
$$ \begin{align*} L' & := L^0|_{\widetilde{R}} \equiv c_0\mathfrak{f} +c_9\mathfrak{s}+c_{10}\mathfrak{f} +\sum_{i=1}^4 c_i(\mathfrak{s}-{\mathfrak{e}}_i)+\sum_{i=5}^7c_i\mathfrak{f} \\ & = (c_1+c_2+c_3+c_4+c_9)\mathfrak{s}+(c_0+c_5+c_6+c_7+c_{10})\mathfrak{f}-\sum_{i=1}^4 c_i{\mathfrak{e}}_i \\ & = L^{\prime}_0 + \sum_{i=2}^{4}(\mathfrak{f}-{\mathfrak{e}}_i), \end{align*} $$
where
 $$\begin{align*}L^{\prime}_0 := (c_1+c_2+c_3+c_4+c_9)\mathfrak{s} +\left(c_0+c_5+c_6+c_7+c_{10}-3\right)\mathfrak{f}-c_1{\mathfrak{e}}_1-\sum_{i=2}^4 (c_i-1){\mathfrak{e}}_i \end{align*}$$
$$\begin{align*}L^{\prime}_0 := (c_1+c_2+c_3+c_4+c_9)\mathfrak{s} +\left(c_0+c_5+c_6+c_7+c_{10}-3\right)\mathfrak{f}-c_1{\mathfrak{e}}_1-\sum_{i=2}^4 (c_i-1){\mathfrak{e}}_i \end{align*}$$
and
![]() $\sum _{i=2}^{4}(\mathfrak {f}-{\mathfrak {e}}_i)$
is the sum of three disjoint
$\sum _{i=2}^{4}(\mathfrak {f}-{\mathfrak {e}}_i)$
is the sum of three disjoint
![]() $(-1)$
-curves. We will eventually apply Proposition 4.3.
$(-1)$
-curves. We will eventually apply Proposition 4.3.
Claim 7.6.
![]() $L^{\prime }_0$
verifies condition
$L^{\prime }_0$
verifies condition
![]() $(\star )$
and is odd.
$(\star )$
and is odd.
Proof. Oddness follows since
![]() $c_9+c_1+c_2+c_3+c_4$
is odd by our assumptions (43)–(44). Conditions (i)–(iv) of
$c_9+c_1+c_2+c_3+c_4$
is odd by our assumptions (43)–(44). Conditions (i)–(iv) of
![]() $(\star )$
easily follow from properties (43)–(44).
$(\star )$
easily follow from properties (43)–(44).
We have
 $$ \begin{align*} L" := L^0|_{\widetilde{P}} & \sim c_0(\ell-{\mathfrak{e}}_9)+c_9{\mathfrak{e}}_9+c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^7 c_i(\ell-{\mathfrak{e}}_i) \\ & = L_0"+{\mathfrak{e}}_6+{\mathfrak{e}}_7+{\mathfrak{e}}_8, \end{align*} $$
$$ \begin{align*} L" := L^0|_{\widetilde{P}} & \sim c_0(\ell-{\mathfrak{e}}_9)+c_9{\mathfrak{e}}_9+c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^7 c_i(\ell-{\mathfrak{e}}_i) \\ & = L_0"+{\mathfrak{e}}_6+{\mathfrak{e}}_7+{\mathfrak{e}}_8, \end{align*} $$
with
 $$ \begin{align*} L_0" & := (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^7 (c_i-1)(\ell-{\mathfrak{e}}_i)+\\ &\quad +(\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6)+(\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7)+(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*} $$
$$ \begin{align*} L_0" & := (c_0-c_9)(\ell-{\mathfrak{e}}_9)+c_9 \ell+ c_{10}(2\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6-{\mathfrak{e}}_7-{\mathfrak{e}}_8)+ \sum_{i=5}^7 (c_i-1)(\ell-{\mathfrak{e}}_i)+\\ &\quad +(\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6)+(\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7)+(\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8). \end{align*} $$
Claim 7.7.
![]() $L^{\prime \prime }_0$
is big and nef.
$L^{\prime \prime }_0$
is big and nef.
Proof. All terms in the expression of
![]() $L_0"$
right above have nonnegative square, except for the last three. One computes
$L_0"$
right above have nonnegative square, except for the last three. One computes
 $$ \begin{align*} L_0" \cdot (\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6) & = c_0+(c_7-1)-1+0+1 \geq c_0>0, \\ L_0" \cdot (\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7) & = c_0+(c_5-1)-1 \geq 0, \\ L_0" \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8) & = c_0+(c_5-1)+(c_6-1)+1-1 \geq c_0>0, \\ \end{align*} $$
$$ \begin{align*} L_0" \cdot (\ell-{\mathfrak{e}}_5-{\mathfrak{e}}_6) & = c_0+(c_7-1)-1+0+1 \geq c_0>0, \\ L_0" \cdot (\ell-{\mathfrak{e}}_6-{\mathfrak{e}}_7) & = c_0+(c_5-1)-1 \geq 0, \\ L_0" \cdot (\ell-{\mathfrak{e}}_7-{\mathfrak{e}}_8) & = c_0+(c_5-1)+(c_6-1)+1-1 \geq c_0>0, \\ \end{align*} $$
which shows that
![]() $L_0"$
is nef. One easily computes that it is big.
$L_0"$
is nef. One easily computes that it is big.
We apply Proposition 4.3. What is left to be checked is condition (iv): The additional disjoint
![]() $(-1)$
-curves on
$(-1)$
-curves on
![]() $\widetilde {P}$
are
$\widetilde {P}$
are
![]() ${\mathfrak {e}}_5$
and
${\mathfrak {e}}_5$
and
![]() ${\mathfrak {e}}_9$
, and we have
${\mathfrak {e}}_9$
, and we have
This concludes the proof of Theorem 1.1.
Acknowledgments
The authors would like to thank Johannes Schmitt for useful correspondence and two referees for useful remarks. The authors acknowledge funding from Ministero dell’Università e della Ricerca (MIUR) Excellence Department Project CUP E83C180 00100006 (Ciro Ciliberto [CC]), project Families of Subvarieties in Complex Algebraic Varieties (FOSICAV) within the European Community (EU) Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement n. 652782 (CC, Thomas Dedieu [ThD]), Gruppo Nazionale per le Strutture Algebriche, Geometriche e le loro Applicazioni (GNSAGA) of Istituto Nazionale di Alta Matematica Francesco Severi (INDAM) (CC, Concettina Galati [CG]), the Trond Mohn Foundation Project “Pure Mathematics in Norway” (Andreas Leopold Knutsen [ALK], CG) and grant 261756 of the Research Council of Norway (ALK).
Competing interest
The authors have no competing interest to declare.