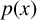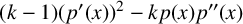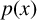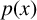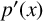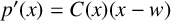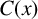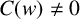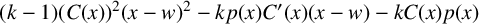1 Introduction
The assertion that if a real polynomial
![]() $p(x)$
has only simple real zeros, then the function
$p(x)$
has only simple real zeros, then the function
![]() $p(x)$
is (locally) strictly monotone was known to Gauss (see [Reference Sheil-Small3]). We can reformulate it in the form of the classical Laguerre inequality: if
$p(x)$
is (locally) strictly monotone was known to Gauss (see [Reference Sheil-Small3]). We can reformulate it in the form of the classical Laguerre inequality: if
![]() $p(x)$
has only simple real zeros, then the polynomial
$p(x)$
has only simple real zeros, then the polynomial
![]() $p_1(x)=(p{'}(x))^{2}-p(x)p{"}(x)$
is strictly positive. A refinement of the Laguerre inequality constitutes the Hawaiian conjecture (see [Reference Csordas, Craven and Smith1]), where if
$p_1(x)=(p{'}(x))^{2}-p(x)p{"}(x)$
is strictly positive. A refinement of the Laguerre inequality constitutes the Hawaiian conjecture (see [Reference Csordas, Craven and Smith1]), where if
![]() $p(x)$
is a real polynomial, then the number of real zeros of
$p(x)$
is a real polynomial, then the number of real zeros of
![]() $({p{'}(x)}/{p(x)}){'}$
does not exceed the number of nonreal zeros of
$({p{'}(x)}/{p(x)}){'}$
does not exceed the number of nonreal zeros of
![]() $p(x)$
. The Hawaiian conjecture was settled in 2011 by Tyaglov [Reference Tyaglov4]. Shapiro proposed three conjectures around the Hawaiian conjecture (see Conjectures 11, 12 and 13 in [Reference Shapiro2]). Conjecture 11 is discussed in [Reference Tyaglov and Atia5].
$p(x)$
. The Hawaiian conjecture was settled in 2011 by Tyaglov [Reference Tyaglov4]. Shapiro proposed three conjectures around the Hawaiian conjecture (see Conjectures 11, 12 and 13 in [Reference Shapiro2]). Conjecture 11 is discussed in [Reference Tyaglov and Atia5].
We consider Conjecture 12 which states: for any real polynomial
![]() $p(x)$
of even degree k, we have
$p(x)$
of even degree k, we have
![]() $\Delta := \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
. Here,
$\Delta := \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
. Here,
![]() $\sharp _r p(x)$
stands for the number of real zeros of a polynomial
$\sharp _r p(x)$
stands for the number of real zeros of a polynomial
![]() $p(x)$
with real coefficients.
$p(x)$
with real coefficients.
Our first result shows that, in most cases, the conjecture is true.
Theorem 1.1. Let
![]() $p(x)$
be a real polynomial of even degree k. Then the quantity
$p(x)$
be a real polynomial of even degree k. Then the quantity
![]() $\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
if and only if one of the following four cases holds:
$\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
if and only if one of the following four cases holds:
-
(1) the polynomial
 $p(x)$
has real zeros;
$p(x)$
has real zeros; -
(2) the polynomial
 $p(x)$
has no real zeros and the polynomial
$p(x)$
has no real zeros and the polynomial
 $p{'}(x)$
has at least three distinct real zeros;
$p{'}(x)$
has at least three distinct real zeros; -
(3) the polynomial
 $p(x)$
has no real zeros and the polynomial
$p(x)$
has no real zeros and the polynomial
 $p{'}(x)$
has one real zero with exponent larger than 1;
$p{'}(x)$
has one real zero with exponent larger than 1; -
(4) the polynomial
 $p(x)$
has no real zeros, the polynomial
$p(x)$
has no real zeros, the polynomial
 $p{'}(x)$
has one real zero which is simple, that is,
$p{'}(x)$
has one real zero which is simple, that is,
 $p{'}(x)=C(x)(x-w)$
, where
$p{'}(x)=C(x)(x-w)$
, where
 $C(x)$
is a polynomial with
$C(x)$
is a polynomial with
 $C(w)\ne 0$
, and the polynomial
$C(w)\ne 0$
, and the polynomial
 $(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has at least one real zero.
$(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has at least one real zero.
The only case in which the conjecture is false is described in our second result.
Theorem 1.2. Let
![]() $p(x)$
be a real polynomial of even degree k. Then the quantity
$p(x)$
be a real polynomial of even degree k. Then the quantity
![]() $\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)=0$
if and only if the polynomial
$\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)=0$
if and only if the polynomial
![]() $p(x)$
has no real zeros, the polynomial
$p(x)$
has no real zeros, the polynomial
![]() $p{'}(x)$
has one real zero which is simple, that is,
$p{'}(x)$
has one real zero which is simple, that is,
![]() $p{'}(x)=C(x)(x-w)$
, where
$p{'}(x)=C(x)(x-w)$
, where
![]() $C(x)$
is a polynomial with
$C(x)$
is a polynomial with
![]() $C(w)\ne 0$
, and the polynomial
$C(w)\ne 0$
, and the polynomial
![]() $(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has no real zeros.
$(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has no real zeros.
At the end of the paper, we give some examples to show that the case described in Theorem 1.2 does occur.
2 Proofs of the theorems
We derive Theorem 1.1 from a series of lemmas.
Lemma 2.1. For a real polynomial
![]() $p(x)$
of even degree k, the real zeros of the polynomial
$p(x)$
of even degree k, the real zeros of the polynomial
![]() $kp{"}(x)p(x)-(k-1)(p{'}(x))^2$
are all included in the critical points of the rational fraction
$kp{"}(x)p(x)-(k-1)(p{'}(x))^2$
are all included in the critical points of the rational fraction
![]() $P(x)={(p{'}(x))^{k}}/{(p(x))^{k-1}} $
.
$P(x)={(p{'}(x))^{k}}/{(p(x))^{k-1}} $
.
Proof. Observe that
 $$ \begin{align*} P{'}(x)=\bigg(\frac{(p{'}(x))^{k}}{(p(x))^{k-1}}\bigg)' & =\frac{k(p{'}(x))^{k-1}p{"}(x)(p(x))^{k-1}-(k-1)(p{'}(x))^{k}(p(x))^{k-2}p{'}(x)}{(p(x))^{2k-2}} \\ & =\frac{k(p{'}(x))^{k-1}p{"}(x)(p(x))^{k-1}-(k-1)(p{'}(x))^{k+1}(p(x))^{k-2} }{(p(x))^{2k-2}} \\ & =\frac{(p{'}(x))^{k-1}(kp{"}(x)p(x)-(k-1)(p{'}(x))^2)}{(p(x))^{k}}.\\[-3.3pc] \end{align*} $$
$$ \begin{align*} P{'}(x)=\bigg(\frac{(p{'}(x))^{k}}{(p(x))^{k-1}}\bigg)' & =\frac{k(p{'}(x))^{k-1}p{"}(x)(p(x))^{k-1}-(k-1)(p{'}(x))^{k}(p(x))^{k-2}p{'}(x)}{(p(x))^{2k-2}} \\ & =\frac{k(p{'}(x))^{k-1}p{"}(x)(p(x))^{k-1}-(k-1)(p{'}(x))^{k+1}(p(x))^{k-2} }{(p(x))^{2k-2}} \\ & =\frac{(p{'}(x))^{k-1}(kp{"}(x)p(x)-(k-1)(p{'}(x))^2)}{(p(x))^{k}}.\\[-3.3pc] \end{align*} $$
Lemma 2.2. When the real polynomial
![]() $p(x)$
of even degree has real zeros, we have
$p(x)$
of even degree has real zeros, we have
![]() $ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
$ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
Now suppose
![]() $p(x)$
is a real polynomial of even degree with no real zeros, so that
$p(x)$
is a real polynomial of even degree with no real zeros, so that
![]() $\sharp _r p(x)=0$
. The derivative polynomial
$\sharp _r p(x)=0$
. The derivative polynomial
![]() $p{'}(x)$
has odd degree. A real polynomial of odd degree has an odd number of real zeros. In particular, it has at least one real zero.
$p{'}(x)$
has odd degree. A real polynomial of odd degree has an odd number of real zeros. In particular, it has at least one real zero.
Lemma 2.3. Let
![]() $p(x)$
be a real polynomial of even degree with no real zeros. If
$p(x)$
be a real polynomial of even degree with no real zeros. If
![]() $p{'}(x)$
has at least three distinct real zeros, then
$p{'}(x)$
has at least three distinct real zeros, then
![]() $ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
$ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
Proof. The rational function
![]() $P(x)$
is a real function. Since
$P(x)$
is a real function. Since
![]() $p(x)$
has no real zeros and
$p(x)$
has no real zeros and
![]() $p{'}(x)$
has no real poles, the rational function
$p{'}(x)$
has no real poles, the rational function
![]() $P(x)$
has no real poles and so satisfies the conditions of Rolle’s theorem. By the hypothesis, the polynomial
$P(x)$
has no real poles and so satisfies the conditions of Rolle’s theorem. By the hypothesis, the polynomial
![]() $p{'}(x)$
has at least three real zeros. By Rolle’s theorem, between two adjacent real zeros of
$p{'}(x)$
has at least three real zeros. By Rolle’s theorem, between two adjacent real zeros of
![]() $P(x)$
, there is at least one real critical point. So,
$P(x)$
, there is at least one real critical point. So,
![]() $P(x)$
has at least two real critical points. These two real critical points of
$P(x)$
has at least two real critical points. These two real critical points of
![]() $P(x)$
are not zeros of
$P(x)$
are not zeros of
![]() $p{'}(x)$
. So, by Lemma 2.1, at least two real critical points of
$p{'}(x)$
. So, by Lemma 2.1, at least two real critical points of
![]() $P(x)$
are real zeros of the polynomial
$P(x)$
are real zeros of the polynomial
![]() $(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)$
. So,
$(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)$
. So,
![]() $ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]\ge 2>0$
.
$ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]\ge 2>0$
.
Example 2.4. Let
![]() $p_1(x)=x^4-2x^2+5=(x^2-1)^2+1$
, so
$p_1(x)=x^4-2x^2+5=(x^2-1)^2+1$
, so
![]() $k=4$
.
$k=4$
.
Obviously,
![]() $p_1(x) $
has four distinct complex zeros and it has no real zeros. Further,
$p_1(x) $
has four distinct complex zeros and it has no real zeros. Further,
![]() $p_1^{\prime }(x)=4x^3-4x=4x(x^2-1)$
has three real zeros. In each of the intervals
$p_1^{\prime }(x)=4x^3-4x=4x(x^2-1)$
has three real zeros. In each of the intervals
![]() $(-1,0)$
and
$(-1,0)$
and
![]() $(0,1)$
, there is one critical point of the rational fraction
$(0,1)$
, there is one critical point of the rational fraction
![]() $P_1(x)={(p{'}(x))^{k}}/{p^{k-1}(x)}={(4x^3-4x)^4}/{(x^4-2x^2+5)^3}$
and
$P_1(x)={(p{'}(x))^{k}}/{p^{k-1}(x)}={(4x^3-4x)^4}/{(x^4-2x^2+5)^3}$
and
![]() $ \sharp _r [(k-1)(p_1^{\prime }(x))^{2}-kp_1(x)p_1^{\prime \prime }(x)]=2>0$
. This is in accord with Lemma 2.3.
$ \sharp _r [(k-1)(p_1^{\prime }(x))^{2}-kp_1(x)p_1^{\prime \prime }(x)]=2>0$
. This is in accord with Lemma 2.3.
Lemma 2.5. Let
![]() $p(x)$
be a real polynomial of even degree with no real zeros. If
$p(x)$
be a real polynomial of even degree with no real zeros. If
![]() $p{'}(x)$
has one real zero with exponent larger than 1, then
$p{'}(x)$
has one real zero with exponent larger than 1, then
![]() $ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
$ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
Proof. By hypothesis,
![]() $p{'}(x)=C(x)(x-w)^l$
, where
$p{'}(x)=C(x)(x-w)^l$
, where
![]() $C(x)$
is a polynomial, w is real,
$C(x)$
is a polynomial, w is real,
![]() $C(w)\ne 0$
and
$C(w)\ne 0$
and
![]() $l>1$
. Then,
$l>1$
. Then,
 $$ \begin{align*} &(k -1)(p{'}(x))^{2}-kp(x)p{"}(x) \\ &\quad=(k-1)(C(x))^2(x-w)^{2l}-kp(x)C{'}(x)(x-w)^l-klC(x)p(x)(x-w)^{l-1} \\ &\quad=(x-w)^{l-1}((k-1)(C(x))^2(x-w)^{l+1}-kp(x)C{'}(x)(x-w)-klC(x)p(x)) \end{align*} $$
$$ \begin{align*} &(k -1)(p{'}(x))^{2}-kp(x)p{"}(x) \\ &\quad=(k-1)(C(x))^2(x-w)^{2l}-kp(x)C{'}(x)(x-w)^l-klC(x)p(x)(x-w)^{l-1} \\ &\quad=(x-w)^{l-1}((k-1)(C(x))^2(x-w)^{l+1}-kp(x)C{'}(x)(x-w)-klC(x)p(x)) \end{align*} $$
and this polynomial has a zero at
![]() $z=w$
with exponent
$z=w$
with exponent
![]() $l-1$
. From this, it follows that
$l-1$
. From this, it follows that
![]() $ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)\ge l-1>0$
.
$ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)\ge l-1>0$
.
Lemma 2.6. Let
![]() $p(x)$
be a real polynomial of even degree with no real zeros. If
$p(x)$
be a real polynomial of even degree with no real zeros. If
![]() $p{'}(x)$
has one real zero which is simple, that is,
$p{'}(x)$
has one real zero which is simple, that is,
![]() $p{'}(x)=C(x)(x-w)$
, where
$p{'}(x)=C(x)(x-w)$
, where
![]() $C(x)$
is a polynomial with
$C(x)$
is a polynomial with
![]() $C(w)\ne 0$
, and
$C(w)\ne 0$
, and
![]() $(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has real zeros, then
$(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has real zeros, then
![]() $ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
$ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
Proof. By hypothesis, the polynomial
has real zeros. Consequently,
![]() $ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
$ \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)>0$
.
Proof of Theorem 1.1
Let
![]() $\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)$
. The four cases of Theorem 1.1 arise as follows.
$\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)$
. The four cases of Theorem 1.1 arise as follows.
-
(1) If
 $p(x)$
has real zeros, then
$p(x)$
has real zeros, then
 $\Delta>0$
by Lemma 2.2.
$\Delta>0$
by Lemma 2.2. -
(2) If
 $p(x)$
has no real zeros and
$p(x)$
has no real zeros and
 $p{'}(x)$
has at least three distinct real zeros, then
$p{'}(x)$
has at least three distinct real zeros, then
 $\Delta>0$
by Lemma 2.3.
$\Delta>0$
by Lemma 2.3. -
(3) Suppose
 $p{'}(x)$
has fewer than three distinct real zeros. Because
$p{'}(x)$
has fewer than three distinct real zeros. Because
 $p'(x)$
is a polynomial of odd degree, it must have just one real zero. If
$p'(x)$
is a polynomial of odd degree, it must have just one real zero. If
 $p(x)$
has no real zeros and
$p(x)$
has no real zeros and
 $p{'}(x)$
has one real zero with exponent larger than 1, then
$p{'}(x)$
has one real zero with exponent larger than 1, then
 $\Delta>0$
by Lemma 2.5.
$\Delta>0$
by Lemma 2.5. -
(4) If
 $p(x)$
has no real zeros,
$p(x)$
has no real zeros,
 $p{'}(x)=C(x)(x-w)$
has one real zero which is simple, and the polynomial
$p{'}(x)=C(x)(x-w)$
has one real zero which is simple, and the polynomial
 $(k-1)(C(x))^2 (x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has real zeros, then
$(k-1)(C(x))^2 (x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has real zeros, then
 $\Delta>0$
by Lemma 2.6.
$\Delta>0$
by Lemma 2.6.
The only remaining case is when
![]() $p(x)$
has no real zeros,
$p(x)$
has no real zeros,
![]() $p{'}(x)=C(x)(x-w)$
has one real zero which is simple, that is,
$p{'}(x)=C(x)(x-w)$
has one real zero which is simple, that is,
![]() $C(x)$
is a polynomial with
$C(x)$
is a polynomial with
![]() $C(w)\ne 0$
, and the polynomial
$C(w)\ne 0$
, and the polynomial
![]() $(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has no real zeros. In this case, the calculation in Lemma 2.6 shows that
$(k-1)(C(x))^2(x-w)^{2}-kp(x)C{'}(x)(x-w)-kC(x)p(x)$
has no real zeros. In this case, the calculation in Lemma 2.6 shows that
![]() $\Delta = 0$
. This completes the proof of Theorem 1.1.
$\Delta = 0$
. This completes the proof of Theorem 1.1.
Proof of Theorem 1.2
Let
![]() $\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)$
. From the proof of Theorem 1.1, the hypotheses of Theorem 1.2 describe the only case in which
$\Delta = \sharp _r [(k-1)(p{'}(x))^{2}-kp(x)p{"}(x)]+\sharp _r p(x)$
. From the proof of Theorem 1.1, the hypotheses of Theorem 1.2 describe the only case in which
![]() $\Delta =0$
; in all other cases,
$\Delta =0$
; in all other cases,
![]() $\Delta>0$
.
$\Delta>0$
.
Example 2.7. Let
![]() $p_2(x)=x^2+ax+b$
with
$p_2(x)=x^2+ax+b$
with
![]() $a,b$
real, so
$a,b$
real, so
![]() $k=2$
.
$k=2$
.
For this example,
![]() $(k-1)(p_2^{\prime }(x))^{2}-kp_2(x)p{"}(x)= (2x+a)^2-4(x^2+ax+b)= a^2-4b$
. If
$(k-1)(p_2^{\prime }(x))^{2}-kp_2(x)p{"}(x)= (2x+a)^2-4(x^2+ax+b)= a^2-4b$
. If
![]() $a^2-4b<0$
, then the polynomials
$a^2-4b<0$
, then the polynomials
![]() $(k-1)(p_2^{\prime }(x))^{2}-kp_2(x)p_2^{\prime \prime }(x)$
and
$(k-1)(p_2^{\prime }(x))^{2}-kp_2(x)p_2^{\prime \prime }(x)$
and
![]() $p_2(x)$
have no real zeros, that is,
$p_2(x)$
have no real zeros, that is,
![]() $ \sharp _r [(k-1)(p_2^{\prime }(x))^{2}-kp_2(x)p_2^{\prime \prime }(x)]+\sharp _r p_2(x)=0$
, in contrast to Shapiro’s conjecture.
$ \sharp _r [(k-1)(p_2^{\prime }(x))^{2}-kp_2(x)p_2^{\prime \prime }(x)]+\sharp _r p_2(x)=0$
, in contrast to Shapiro’s conjecture.
Example 2.8. Let
![]() $p_3(x)=x^4+x^2+1$
, so
$p_3(x)=x^4+x^2+1$
, so
![]() $k=4$
. For this example,
$k=4$
. For this example,
![]() $(k-1)(p_3^{\prime }(x))^{2}- kp_3(x)p_3^{\prime \prime } (x){\kern-1pt}={\kern-1pt}3(4x^3{\kern-1pt}+{\kern-1pt}2x)^2{\kern-1pt}-4(x^4{\kern-1pt}+{\kern-1pt}x^2{\kern-1pt}+{\kern-1pt}1)(12x^2{\kern-1pt}+{\kern-1pt}2)=-4(2x^4{\kern-1pt}+{\kern-1pt}11x^2{\kern-1pt}+{\kern-1pt}2)$
. The zeros of the polynomial
$(k-1)(p_3^{\prime }(x))^{2}- kp_3(x)p_3^{\prime \prime } (x){\kern-1pt}={\kern-1pt}3(4x^3{\kern-1pt}+{\kern-1pt}2x)^2{\kern-1pt}-4(x^4{\kern-1pt}+{\kern-1pt}x^2{\kern-1pt}+{\kern-1pt}1)(12x^2{\kern-1pt}+{\kern-1pt}2)=-4(2x^4{\kern-1pt}+{\kern-1pt}11x^2{\kern-1pt}+{\kern-1pt}2)$
. The zeros of the polynomial
![]() $2t^2+11t+2$
are
$2t^2+11t+2$
are
![]() $\tfrac 12(-11\pm \sqrt {105})$
which are both negative real zeros. So, the polynomial
$\tfrac 12(-11\pm \sqrt {105})$
which are both negative real zeros. So, the polynomial
![]() $2x^4+11x^2+2$
has four complex zeros and no real zeros. So,
$2x^4+11x^2+2$
has four complex zeros and no real zeros. So,
![]() $ \sharp _r [(k-1)(p_3^{\prime }(x))^{2}-kp_3(x)p_3^{\prime \prime }(x)]+\sharp _r p_3(x)=0$
.
$ \sharp _r [(k-1)(p_3^{\prime }(x))^{2}-kp_3(x)p_3^{\prime \prime }(x)]+\sharp _r p_3(x)=0$
.