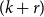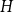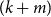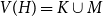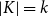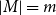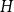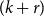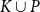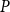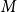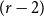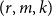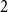On the Ramsey numbers of daisies II

Abstract

A $(k+r)$-uniform hypergraph $H$ on $(k+m)$ vertices is an $(r,m,k)$-daisy if there exists a partition of the vertices $V(H)=K\cup M$ with $|K|=k$, $|M|=m$ such that the set of edges of $H$ is all the $(k+r)$-tuples $K\cup P$, where $P$ is an $r$-tuple of $M$. We obtain an $(r-2)$-iterated exponential lower bound to the Ramsey number of an $(r,m,k)$-daisy for $2$-colours. This matches the order of magnitude of the best lower bounds for the Ramsey number of a complete $r$-graph.

1. Introduction

For a natural number $N$ , we set $[N]=\{1,\ldots,N\}$ . Given a set $X$ , we denote by $X^{(r)}$ the set of $r$ -tuples of $X$ . For two sets $X$ , $Y$ we say that $X\lt Y$ if $\max (X) \lt \min (Y)$ . Unless stated otherwise, the elements of a set $X$ will be always displayed in increasing order. That is, if $X=\{x_1,\ldots,x_t\}$ , then $x_1\lt \ldots \lt x_t$ .

A $(k+r)$ -uniform hypergraph $H$ on $k+m$ vertices is an $(r,m,k)$ -daisy if there exists a partition of the vertices $V(H)=K\cup M$ with $|K|=k$ and $|M|=m$ such that

\begin{align*} H=\{K\cup P\;:\; P \in M^{(r)}\} \end{align*}

We say that the set $K$ is the kernel of $H$ , the elements of $M^{(r)}$ are the petals of $H$ and $M$ is the universe of petals. We will often refer to an edge of $H$ by $X$ and its correspondent petal by $P$ .

Daisies were first introduced by Bollobás, Leader, and Malvenuto in [1]. They were interested in Turán-type questions related to $(r,m,k)$ -daisies, i.e., the maximum number of edges that an $(r+k)$ -graph has with no copy of an $(r,m,k)$ -daisy. In this paper we will study the Ramsey number $D_r(m,k)$ of an $(r,m,k)$ -daisy. The number $D_r(m,k)$ is defined as the minimum integer $N$ such that any $2$ -colouring of the complete hypergraph $[N]^{(k+r)}$ contains a monochromatic $(r,m,k)$ -daisy.

Those numbers were already studied in [5]. Although the main focus of their paper is on daisies with kernel of non fixed size, they noted that

(1) \begin{align} R_{r-k}(\lceil m/(k+1) \rceil -k)\leqslant D_r(m,k)\leqslant R_r(m)+k, \end{align}

where $R_r(m)$ is the Ramsey number of the complete graph $K_m^{(r)}$ , i.e., the minimum integer $N$ such that any $2$ -colouring of $[N]^{(r)}$ contains a monochromatic set $X$ of size $m$ .

A natural question raised in [5] is whether $D_r(m,k)$ behaves similarly $R_r(m)$ . Erdős, Hajnal, and Rado (see [3, 4]) and Conlon, Fox, and Sudakov [2] showed that there exists absolute constants $c_1,c_2$ such that for sufficiently large $m$ ,

(2) \begin{align} t_{r-2}(c_1m^2)\leqslant R_r(m)\leqslant t_{r-1}(c_2m), \end{align}

where $t_i(x)$ is the tower function defined by $t_0(x)=x$ and $t_{i+1}(x)=2^{t_i(x)}$ . In this paper, we provide for $k\geqslant 1$ a lower bound of $D_r(m,k)$ in the same order of magnitude as the best current bounds of the Ramsey number $R_r(m)$ for sufficiently large $m$ . We remark here that for $k=0$ , the problem is equivalent to the Ramsey number, since an $(r,m,0)$ -daisy is just the complete graph $K_m^{(r)}$ .

Theorem 1.1. Let $r\geqslant 3$ and $k\geqslant 1$ be integers. There exist integer $m_0=m_0(r,k)$ and absolute constant $c$ such that

\begin{align*} D_r(m,k)\geqslant t_{r-2}(ck^{-2}m^{2^{4-r}}) \end{align*}

holds for $m\geqslant m_0$ .

In order to prove Theorem 1.1 we will actually study the Ramsey number of a subfamily of daisies. We say that a hypergraph $H$ is a simple $(r,m,k)$ -daisy if $H$ is an $(r,m,k)$ -daisy and its kernel $K$ can be partitioned into $K=K_0\cup K_1$ such that $K_0\lt M\lt K_1$ . We define the Ramsey number of simple $(r,m,k)$ -daisies $D_r^{{\textrm{smp}}}(m,k)$ as the minimum integer $N$ such that any $2$ -colouring of the complete hypergraph $[N]^{(k+r)}$ yields a monochromatic copy of a simple $(r,m,k)$ -daisy.

In [5], the authors observed that the Ramsey number of daisies can be bounded from below by the Ramsey number of simple daisies.

Proposition 1.2 ([5], Proposition 5.3). $D_r(m,k)\geqslant D_r^{{\textrm{smp}}}\left (\lceil m/(k+1) \rceil, k\right )$ .

Our main technical result is an $(r-2)$ -iterated exponential lower bound for the Ramsey number of simple $(r,m,k)$ -daisies. Note that Theorem 1.1 is a corollary from Proposition 1.2 and Theorem 1.3.

Theorem 1.3. Let $r \geqslant 3$ and $k\geqslant 1$ be integers. There exist integer $m_0=m_0(r,k)$ and absolute positive constant $c$ such that

\begin{align*} D_r^{{\textrm{smp}}}(m,k)\geqslant t_{r-2}(ck^{2^{4-r}-2}m^{2^{4-r}}) \end{align*}

holds for $m\geqslant m_0$ .

Our proof is a variant of the stepping-up lemma of Erdős, Hajnal and Rado [3, 4]. There are $k+1$ distinct simple $(r,m,k)$ -daisies depending on the sizes of $K_0$ and $K_1$ . While it is not hard to construct a colouring avoiding a monochromatic copy of one of these simple daisies, the main challenge is to define a colouring that avoids all $k+1$ simple $(r,m,k)$ -daisies simultaneously. To this end, we will introduce in Section 2 some auxiliary trees using the vertices of our ground set. A big portion of the paper consists on the study of those trees and how to use them to obtain a stepping-up lemma.

The paper is organized as follows. We introduce some auxiliary trees and most of the terminology in Section 2. Section 3 is devoted to give a general overview of the proof. We briefly describe the stepping-up lemma in [3, 4] with our setup and later describe the colouring of the variant. Sections 4 and 5 are the heart of the proof. We prove a key lemma (Lemma 5.1) that allows us to identify an important auxiliary tree containing the petal of an edge and then show how to reduce the stepping-up argument to this tree. We finish the proof of the stepping-up lemma and Theorem 1.3 in Section 6.

2. Auxiliary trees

Given an integer $N$ , we construct a binary tree $T_{[2^N]}$ of height $N$ with $2^{N+1}-1$ vertices and identify its leaves with the set $[2^N]$ . We also identify each level of the tree with the set $[N+1]$ , where the root is at level $1$ , while the leaves are at level $N+1$ (see Figure 1). For a vertex $u \in T_{[2^N]}$ we denote its level by $\pi (u)$ .

Figure 1. An example of a binary tree $T_{[2^3]}$ with its $4$ levels.

Given two vertices $u,v$ in $T_{[2^N]}$ , we say that $u$ is an ancestor of $v$ if $\pi (u)\lt \pi (v)$ and there is a path $u=x_1,x_2,\ldots,x_{\ell }=v$ in $T_{[2^N]}$ such that $\pi (x_i)\neq \pi (x_j)$ for every $1\leqslant i,j \leqslant \ell$ . For two vertices $x,y \in [2^N]$ we define the $\textit{greatest common ancestor}$ $a(x,y)$ of $x$ and $y$ as the vertex of $T_{[2^N]}$ of highest level that is an ancestor of both $x$ and $y$ . Also define

\begin{align*} \delta (x,y)=\pi (a(x,y)). \end{align*}

Let $X=\{x_1,\ldots,x_t\} \subseteq [2^N]$ with $x_1\lt \ldots \lt x_t$ be a subset of the leaves of our binary tree. We define the auxiliary tree $T_X$ of $X$ as the subtree of $T_{[2^N]}$ whose vertices are $X$ and all their common ancestors. That is,

\begin{align*} T_X=X \cup \{a(x_i,x_{i+1})\;:\:1\leqslant i \leqslant t-1\}. \end{align*}

Note that $T_X$ is a tree of $2t-1$ vertices (see Figure 2). Moreover, we denote the set of non-leaves by $a(X)$ and its projection by $\delta (X)$ , i.e.,

\begin{align*} a(X)&=\{a(x_i,x_{i+1})\;:\:1\leqslant i \leqslant t-1\} \\[5pt] \delta (X)&=\{\delta (x_i,x_{i+1})\;:\: 1\leqslant i \leqslant t-1\}. \end{align*}

Since the auxiliary tree $T_X$ is uniquely determined by its ground set $X$ , sometimes we will denote $T_X$ by $X$ .

Figure 2. The auxiliary tree $T_X$ for $X=\{2,3,7\}$ .

Given a vertex $u \in a(X)$ , we can define the set $X(u)$ of descendants of $u$ as the leaves of $T_X$ that have $u$ as an ancestor. That is,

\begin{align*} X(u)=\{x \in X\;:\: u \text{ is an ancestor of } x\}. \end{align*}

The set of descendants of $u$ can be partitioned into the left descendants and right descendants as follows: Since $T_X$ is a binary tree, the vertex $u$ has two children $u^L$ and $u^R$ . Let $u^L$ be the left children of $u$ and $u^R$ be the right children of $u$ . Then we define the left descendants of $u$ by

\begin{align*} X_L(u)=\begin{cases} u^L &\quad \text{if } u^L \in X,\\[5pt] X(u^L) &\quad \text{if } u^L\in a(X), \end{cases} \end{align*}

and the right descendants of $u$ by

\begin{align*} X_R(u)=\begin{cases} u^R &\quad \text{if } u^R \in X,\\[5pt] X(u^R) &\quad \text{if } u^R\in a(X), \end{cases} \end{align*}

Note that by this definition $X_L(u), X_R(u)\neq \emptyset$ and $\max X_L(u)\lt \min X_R(u)$ .

Figure 3. The interval $\{2,3,4\}$ is closed, since $X(u)=\{2,3,4\}$ for $u=a(2,4)$ . The interval $\{4,5\}$ is not closed, since $X(v)=\{1,2,3,4,5\}\neq \{4,5\}$ for $v=a(4,5)$ .

Although an auxiliary tree is not uniquely determined by its ancestors, we can at least determine the “shape” of the tree $T_X$ by looking at $a(X)$ . In a more precise way, the following can be proved by a simple induction.

Fact 2.1. If $X$ and $Y$ are subsets of $[2^N]$ such that $a(X)=a(Y)$ , then $|X|=|Y|$ . Moreover, if $X=\{x_1,\ldots,x_t\}$ and $Y=\{y_1,\ldots,y_t\}$ , then $a(x_i,x_{i+1})=a(y_i,y_{i+1})$ for every $1\leqslant i \leqslant t-1$ .

Now we devote the rest of the section on classifying our auxiliary trees.

Definition 2.2. Given $X=\{x_1,\ldots,x_t\}\subseteq [2^N]$ . We say that an interval $I=\{x_p,\ldots,x_q\} \subseteq X$ for some $1\leqslant p\leqslant q \leqslant t$ is closed in $X$ if the following condition holds:

1. ( $\star$ ) $I=X(a(x_p,x_q))$ .

In Figure 3, one can see examples of a closed interval and a not closed one. Alternatively, one can replace ( $\star$ ) by the useful equivalent condition:

1. ( $\star \star$ ) For every vertex $y\in X\setminus I$ , the vertex $a(x_p,x_q)$ is not an ancestor of $y$ .

The following proposition shows that closed intervals cannot have proper intersections.

Proposition 2.3. Let $I_1$ , $I_2$ be two intervals in $X$ with $|I_1|\leqslant |I_2|$ . If $I_1$ and $I_2$ are closed, then either $I_1 \cap I_2=\emptyset$ or $I_1\subseteq I_2$ .

Proof. Suppose that $I_1\cap I_2$ is a proper intersection. That is, $I_1\cap I_2 \neq \emptyset$ , $I_1\setminus I_2\neq \emptyset$ and $I_2\setminus I_1\neq \emptyset$ . Write $X=\{x_1,\ldots,x_t\}$ and $I_1=\{x_{p_1},x_{p_1+1},\ldots,x_{q_1}\}$ , $I_2=\{x_{p_2},x_{p_2+1},\ldots,x_{q_2}\}$ for $1\leqslant p_1\lt p_2\leqslant q_1\lt q_2\leqslant t$ . Let $u=a(x_{p_1},x_{q_1})$ and $v=a(x_{p_2},x_{q_2})$ . We claim that either $u$ is an ancestor of $v$ or $v$ is an ancestor of $u$ . Let $z\in I_1\cap I_2$ . By definition, both $u$ and $v$ are ancestors of $z$ . This means that there exists descending paths connecting $z$ to $u$ and $z$ to $v$ in $T_X$ with vertices in different levels. However, every vertex in $T_X$ has at most one father. Therefore, either the path $z$ to $u$ contains the path $z$ to $v$ or vice-versa. If the path $z$ to $u$ contains the path $z$ to $v$ , then $u$ is an ancestor of $v$ . Hence $u$ is an ancestor of $I_2\setminus I_1$ , which contradicts the fact that $I_1$ is closed (Condition ( $\star \star$ ) of Definition 2.2). The other case is analogous.

We classify the closed intervals of $X$ by three classes: left combs, right combs, and broken combs (see also Figure 4).

Definition 2.4. Given a closed interval $I$ in $X$ we say that

1. (a) $I$ is a $\ell$ -left comb if $\ell$ is the least positive integer such that there exists a partition $I=A\cup B$ with $|A|=\ell$ and $B\neq \emptyset$ and

   1. (a1) $A\lt B$ .

   2. (a2) $A$ is a closed interval in $X$

   3. (a3) If $z=\max (A)$ and $B=\{b_1,\ldots,b_s\}$ , then $\delta (z,b_1)\gt \delta (b_1,b_2)\gt \ldots \gt \delta (b_{s-1},b_s)$ .

2. (b) $I$ is a $\ell$ -right comb if $\ell$ is the least positive integer such that there exists a partition $I=A\cup B$ with $|A|=\ell$ and $B\neq \emptyset$ and

   1. (b1) $B\lt A$ .

   2. (b2) $A$ is a closed interval in $X$

   3. (b3) If $z=\min (A)$ and $B=\{b_1,\ldots,b_s\}$ , then $\delta (b_1,b_2)\lt \ldots \lt \delta (b_{s-1},b_s)\lt \delta (b_t,z)$ .

3. (c) $I$ is a broken comb if it is neither a left or right comb.

We will use the convention that an $\ell$ -left/right comb will be described by its partition $I=A\cup B$ with $|A|=\ell$ that verifies the condition on Definition 2.4. As we can see in the picture above, the set $A$ should be thought as the “handle” of the comb, while the set $B$ should be thought as the “teeth” of the comb. For broken combs we will adopt the same convention by assuming that $B= \emptyset$ .

Figure 4. An example of a left, right, and broken comb, respectively.

Figure 5. A left and right $1$ -comb.

One may remove the use of the projection $\delta (b_i,b_{i+1})$ in conditions (a3) and (b3) of the right/left comb by using the following equivalent alternative conditions:

1. (a3*) If $B=\{b_1,\ldots,b_s\}$ , then the intervals $A\cup \{b_1,\ldots,b_i\}$ are closed in $X$ for every $1\leqslant i \leqslant s$

2. (b3*) If $B=\{b_1,\ldots,b_s\}$ , then the intervals $\{b_i,\ldots,b_s\}\cup A$ are closed in $X$ for every $1\leqslant i \leqslant s$ .

Those conditions have the advantage of describing a comb only using closed intervals. This will be useful later in the proof.

Example 2.5. A important type of comb in the stepping-up lemma [3, 4] is the $1$ -left/right comb (see Figure 5). Those are the combs $I=\{y_1,\ldots,y_t\}$ satisfying that the sequence $\{\delta (y_i,y_{i+1})\}_{1\leqslant i \leqslant t}$ is monotone. Indeed, the interval $I$ is a $1$ -left comb if $\delta (y_1,y_2)\gt \ldots \gt \delta (y_{t-1},y_t)$ , while it is a $1$ -right comb if $\delta (y_1,y_2)\lt \ldots \lt \delta (y_{t-1},y_t)$ .

For the proof of Theorem 1.3 we will be interested in maximal comb structures inside our auxiliary trees.

Definition 2.6. Given $X=\{x_1,\ldots,x_t\} \subseteq [2^N]$ , a interval $I=\{x_p,\ldots,x_q\}$ is a

1. (a) Maximal left comb in $X$ if $I$ is a left comb and $I\cup \{x_{q+1}\}$ is not a closed interval in $X$ .

2. (b) Maximal right comb in $X$ if $I$ is a right comb and $I\cup \{x_{p-1}\}$ is not a closed interval in $X$ .

3. (c) Maximal broken comb in $X$ if $I$ is a broken comb and neither $I\cup \{x_{p-1}\}$ or $I\cup \{x_{q+1}\}$ are closed.

Figure 6 illustrates Definition 2.6. The next proposition shows that given two maximal combs they are either disjoint or one is contained in the “handle” of the other.

Proposition 2.7. Given a closed inteval $I_1$ and a maximal comb $I_2=A_2\cup B_2$ with $|I_1|\leqslant |I_2|$ in a set $X\subseteq [2^N]$ , then one of the following holds:

1. 1. $I_1\cap I_2=\emptyset$

2. 2. $I_1\subseteq A_2$ .

3. 3. $I_1=A_2\cup B_1$ for some initial segment $B_1\subseteq B_2$

Figure 6. An example of a maximal left, right, and broken comb, respectively.

Moreover, condition (3) only holds if $I_1$ is not a maximal comb.

Proof. By Proposition 2.3 we obtain that either $I_1\cap I_2=\emptyset$ or $I_1\subseteq I_2$ . If the first case happens, then $I_1$ and $I_2$ satisfy condition (1) and we are done. Hence, we may assume that $I_1\subseteq I_2$ . If $I_2$ is a broken comb, then by definition $A_2=I_2$ . Thus in this case $I_1\subseteq A_2$ , satsifying condition (2). Now suppose without loss of generality that $I_2=A_2\cup B_2$ is a left maximal comb and write $A_2=\{x_1,\ldots, x_{\ell }\}$ , $B_2=\{y_1,\ldots, y_s\}$ . If $I_1\cap B_2=\emptyset$ , then $I_1\subseteq A_2$ and again condition (2) holds.

At last, it remains to deal with the case that $I_1\cap B_2\neq \emptyset$ . Since $I_1$ is an interval of $X$ and $I_1\subseteq I_2$ , then in particular $I_1$ is an interval of $I_2$ . Write $I_1=\{x_p,\ldots,x_\ell \}\cup \{y_1,\ldots, y_q\}$ for $1\leqslant p \leqslant \ell$ and $1\leqslant q \leqslant s$ . By condition (a3*) of Definition 2.4, the set $A_2\cup \{y_1,\ldots,y_{q-1}\}$ is closed. Therefore for any $z \in A_2\cup \{y_1,\ldots,y_{q-1}\}$ the greatest ancestor $a(z,y_q)$ of $z$ and $y_q$ is the same as the greatest ancestor of $a(x_1,y_q)$ . In particular, this implies that $a(x_p,y_q)$ is an ancestor for the entire set $A_2$ . Hence $A_2\subseteq I_1$ and consequently $I_1=A_1\cup B_1$ is a left comb satisfying condition (3), because $A_1=A_2$ and $B_1$ is an initial segment of $B_2$ . Note that $I_1$ is not maximal in this case, since the set $I_1\cup \{y_{q+1}\}$ is also a left comb. Thus if $I_1$ is a maximal comb, then it either satisfies (1) or (2).

3. Stepping-up lemma and our colouring

3.1 Erdős–Hajnal–Rado stepping-up lemma

For instructional purposes, we will briefly go over the stepping-up lemma in [3, 4] using our notation. For $k\geqslant 4$ , let $N=R_{k-1}((n-k+4)/2)-1$ and $\varphi \;:\; [N]^{(k-1)} \rightarrow \{0,1\}$ be a colouring of the $(k-1)$ -tuples in $[N]$ with no monochromatic subset of size $(n-k+4)/2$ . Our goal is to find a colouring $\psi \;:\; [2^N]^{(k)}\rightarrow \{0,1\}$ with no monochromatic subset of size $n$ . This will give us that $R_k(n)\gt 2^N=2^{R_{k-1}((n-k+4)/2)-1}$ .

Fix an edge $X=\{x_1,\ldots,x_k\} \in [2^N]^{(k)}$ and let $\delta _i=\delta (x_i,x_{i+1})$ . We describe the colouring $\psi$ by the structure of $T_X$ and the colouring of the vertical projection $\varphi$ of $[N]$ in the following way

\begin{align*} \psi (X)=\begin{cases} 0,& \quad \text{if }\delta _{k-3}\gt \delta _{k-2}\lt \delta _{k-1}\\[5pt] 1,& \quad \text{if }\delta _{k-3}\lt \delta _{k-2}\gt \delta _{k-1}\\[5pt] \varphi (\{\delta _1,\ldots,\delta _{k-1}\}),& \quad \text{otherwise if } |\delta (X)|=k-1\\[5pt] 0,& \quad \text{otherwise if } |\delta (X)|\lt k-1. \end{cases} \end{align*}

Suppose by contradiction that $\psi$ contains a monochromatic subset $Y\subset [2^N]$ of size $n$ . We can use the structure of $Y$ to find a large $1$ -comb.

Proposition 3.1. There exists an interval $I$ of $Y$ with $|I|\geqslant (n-k+6)/2$ such that $I$ is a $1$ -comb

Proof. We may assume without loss of generality that $Y$ is monochromatic of colour $0$ . Write $Y=\{y_1,\ldots,y_n\}$ and let $\delta ^Y_i=\delta (y_i,y_{i+1})$ for $1\leqslant i \leqslant n-1$ . Since all edges in $Y$ are of colour $0$ , then for any edge $X=\{x_1,\ldots,x_k\}\in Y^{(k)}$ we do not have that

(3) \begin{align} \delta (x_{k-3},x_{k-2})\lt \delta (x_{k-2},x_{k-1})\gt \delta (x_{k-1},x_k). \end{align}

In particular, by taking the edge $\{y_{\ell -k+1},\ldots,y_\ell \}$ , inequality (3) implies that $\delta ^Y_{\ell -3}\lt \delta ^Y_{\ell -2}\gt \delta ^Y_{\ell -1}$ does not hold fore every $k\leqslant \ell \leqslant n$ . Hence, the sequence $\{\delta ^Y_i\}_{i=k-3}^{n-1}$ has no local maximum.

A standard calculus argument says that between two local minimums there is always a local maximum. Therefore, the sequence $\{\delta ^Y_i\}_{i=k-3}^{n-1}$ has at most one local minimum, which means that there exists an interval $[p,q]$ of size $(n-k+4)/2$ such that $\{\delta ^Y_i\}_{i\in [p,q]}$ is monotone. Thus by definition the interval $I=\{x_p,x_{p+1},\ldots,x_{q+1}\}$ is a $1$ -comb of size $(n-k+6)/2$ .

Let $I=\{z_1,\ldots,z_{t}\}$ be the $1$ -comb of $Y$ obtained by Proposition 3.1 and denote $\delta _i^I=\delta (z_i,z_{i+1})$ for $1\leqslant i \leqslant i-1$ . Note that because $\{\delta _i^I\}_{i=1}^{t-1}$ is a monotone sequence, every edge $X\in I^{(k)}$ will be also a $1$ -comb. Moreover, for every $(k-1)$ -tuple $Z\in \delta (I)$ there exists an edge $X\in I^{(k)}$ such that $\delta (X)=Z$ .

Finally, by the definition of the colouring $\psi$ , if $X$ is a $1$ -comb, then $\psi (X)=\varphi (\delta (X))$ . Thus if $I^{(k)}$ coloured by $\psi$ is monochromatic, then $\delta (I)^{(k-1)}$ coloured by $\varphi$ is also monochromatic. This implies that $[N]$ has a monochromatic set of size $(n-k+4)/2$ , which contradicts our assumption on $\varphi$ .

3.2 Overview of the proof

In order to obtain a lower bound for simple daisies, we will define a variant of the stepping-up lemma described in the previous subsection. Suppose for a moment that our goal is to avoid a monochromatic simple $(r,m,k)$ -daisy with in $[2^N]$ with $|K_0|=k_0$ and $|K_1|=k_1$ fixed. Then for every edge $X=\{x_1,\ldots,x_{k+r}\}$ of the daisy, we know that the petal of size $r$ of $X$ is $P=\{x_{k_0+1},\ldots,x_{k_0+r}\}$ . That is, we know the exact location of the petal prior defining the colouring in our stepping-up lemma. In this case a natural way to define the colouring would be to just assign for every edge $X$ with petal $P\subseteq X$ the colour $\chi (X)=\psi (P)$ , where $\psi (P)$ is exactly the stepping-up colouring defined in the previous subsection. Since the petal is the only part of the edge changing when we run through all edges, a similar proof as in the previous subsection works.

Unfortunately, in the original problem we want to avoid all possible monochromatic simple $(r,m,k)$ -daisies, which means that we need to avoid simple daisies for all the values of $|K_0|$ and $|K_1|$ . The obstruction now is that the location of the petal within the edge is no longer clear to us. To fix that we are going to pre-process our potentially monochromatic simple daisy (Lemma 5.1) to satisfy the following property: Every petal $P$ of an edge $X$ is either a closed interval in $X$ or is in the “teeth” of a maximal comb in $X$ . This gives us partial information about the location of the petal. A good strategy then is to define an auxiliary colouring $\chi _0$ for every maximal comb in $X$ and use those colourings to define a colouring for $X$ . This is the content of Section 3.3.

Some technical challenges remain. By Proposition 2.7, the maximal combs in $X$ do not need to be disjoint. Therefore, it might happen that for the colouring $\chi$ different maximal combs interfere with each other. To solve that we need to construct a careful colouring taking the issue into consideration. In Section 4 we provide an analysis showing that distinct maximal combs do not interfere with each other in our colouring. Section 5 is devoted to the pre-processing described in the last paragraph. One of the consequences of the section is that for an edge $X$ the colouring $\chi (X)$ is essentially determined by a unique maximal comb inside of it. Finally, we finish the proof in Section 6, by showing, similarly as in Subsection 3.1, that a monochromatic simple daisy in $[2^N]$ corresponds to a monochromatic simple daisy in the vertical colouring of $[N]$ .

3.3 A variant of the stepping-up lemma

Let $N=\min _{0\leqslant t \leqslant k-1}\left \{D_{r-1}^{{\textrm{smp}}}(c_k\sqrt{m},t)-1\right \}$ for $r\geqslant 4$ and $c_k$ some constant depending on $k$ to be defined later and let $\{\varphi _i\}_{r-1\leqslant i \leqslant k+r-1}$ be a family of colourings such that $\varphi _i\;:\;[N]^{(i)}\rightarrow \{0,1\}$ is a $2$ -colouring of the $i$ -tuples without a monochromatic simple $(r-1,c_k\sqrt{m},i-r+1)$ -daisy. Note that by the choice of $N$ is always possible to find such a family.

Given an $(k+r)$ -tuple $X \in [2^N]^{(k+r)}$ we define

\begin{align*}{\mathcal{I}}_X=\{I\subseteq X\;:\: I \text{ is a maximal comb in } X\} \end{align*}

as the set of maximal combs of $X$ . We will construct now an auxiliary colouring $\chi _0\;:\;{\mathcal{I}}_X \rightarrow \{0,1\}$ depending on the structure of $T_X$ and in the family of colourings $\{\varphi _t\}_{0\leqslant t \leqslant k}$ . The colouring is divided in several cases depending on the type of the maximal comb $I$ .

Remember that a maximal $\ell$ -comb is always identified with the partition $I=A\cup B$ , where $|A|=\ell$ is the handle and $B$ is the set of teeth of the comb. Also write $I=\{x_1,\ldots,x_s\}$ and let $\delta _{i}^I=\delta (x_i,x_{i+1})$ for $1\leqslant i \leqslant s-1$ . Aiming to simplify the discussion, we will only describe $\chi _0$ for left and broken maximal combs. We define $\chi _0$ for right combs by symmetry. Some Figures are provided to illustrate some of the types (see Figures 7–9).

Type 1: $I$ is broken or left comb, $|I|=r$ and there is no maximal comb $I'=A'\cup B'$ such that $I=A'$ .

\begin{align*} \chi _0(I)=\begin{cases} 0,& \quad \text{if }\delta ^I_{r-3}\gt \delta ^I_{r-2}\lt \delta ^I_{r-1}\\[5pt] 1,& \quad \text{if }\delta ^I_{r-3}\lt \delta ^I_{r-2}\gt \delta ^I_{r-1}\\[5pt] \varphi _{|\delta (I)|}(\{\delta ^I_1,\ldots,\delta ^I_{r-1}\}),& \quad \text{otherwise if } |\delta (I)|=r-1\\[5pt] 0,& \quad \text{otherwise if } |\delta (I)|\lt r-1 \end{cases} \end{align*}

Type 2: $I$ is left comb, $|I|=r$ and there exists a maximal comb $I'=A'\cup B'$ such that $I=A'$

\begin{align*} \chi _0(I)=0 \end{align*}

Figure 7. An example of left comb of type 2.

Type 3: $I$ is left comb, $\ell =|A|\leqslant r$ and $r+1\leqslant |I|\leqslant 2r-2$ .

\begin{align*} \chi _0(I)=\begin{cases} 0,& \quad \text{if }\delta ^I_{r-3}\gt \delta ^I_{r-2}\lt \delta ^I_{r-1}\\[5pt] 1,& \quad \text{if }\delta ^I_{r-3}\lt \delta ^I_{r-2}\gt \delta ^I_{r-1}\\[5pt] \varphi _{|\delta (I)|}(\{\delta ^I_1,\ldots,\delta ^I_{s-1}\}),& \quad \text{otherwise if } |\delta (I)|\geqslant r-1\\[5pt] 0,& \quad \text{otherwise if } |\delta (I)|\lt r-1 \end{cases} \end{align*}

Type 4: $I$ is left comb, $\ell =|A|\leqslant r$ and $|I|\geqslant 2r-1$ .

\begin{align*} \chi _0(I)=\begin{cases} \varphi _{s-r}(\{\delta _r^I,\ldots,\delta _{s-1}^I\}),& \quad \text{if }\delta ^I_{r-3}\gt \delta ^I_{r-2}\lt \delta ^I_{r-1}\\[5pt] 1-\varphi _{s-r}(\{\delta _r^I,\ldots,\delta _{s-1}^I\}),& \quad \text{if }\delta ^I_{r-3}\lt \delta ^I_{r-2}\gt \delta ^I_{r-1}\\[5pt] \varphi _{|\delta (I)|}(\{\delta ^I_1,\ldots,\delta ^I_{s-1}\}),& \quad \text{otherwise} \end{cases} \end{align*}

Figure 8. A left comb of Type $4$ and its projections.

Figure 9. A left comb of Type $5$ and its projections.

Type 5: $I$ is left comb, $\ell =|A|\gt r$ and $|B|\geqslant r$ .

\begin{align*} \chi _0(I)=\varphi _{|B|}(\delta _{\ell }^I,\ldots,\delta _{s-1}^I) \end{align*}

Type 6: All other broken or left maximal combs.

\begin{align*} \chi _0(I)=0 \end{align*}

Finally, the auxiliary colouring $\chi _0$ define a colouring $\chi \;:\;[2^N]^{(k+r)}\rightarrow \{0,1\}$ as follows:

\begin{align*} \chi (X)=\sum _{I\in{\mathcal{I}}_X}\chi _0(I) \pmod{2} \end{align*}

4. Colouring data

Given an edge $X$ and a maximal comb $I \subseteq X$ , one can determine the colour $\chi _0(I)$ by looking at the type of the maximal comb $I$ . Some of the types do not use information on the ancestors to determine its colouring. For instance, if $I$ is of type $2$ , then its colour will be always $0$ . The projection of the ancestors $\delta _i^I$ has no influence in defining $\chi _0(I)$ . However, if $I$ is of type $1$ , then the colour crucially depends on the projection of the ancestors.

This observation suggests the following definition. Given an edge $X \in [2^N]^{(k+r)}$ and a maximal comb $I\subseteq X$ , let the colouring data $F(I)$ of $I$ be defined as the ordered set of ancestors whose projection determine the colouring $\chi _0(I)$ . More explicitly, we can define directly the colouring data of $I$ by looking its types. We may assume here that $I=\{x_1,\ldots,x_s\}$ is a broken or left maximal comb.

• Type 1,3 and 4: $F(I)=\{a(x_i,x_{i+1})\}_{1\leqslant i \leqslant s-1}$

• Type 2 and 6: $F(I)=\emptyset$

• Type 5: $F(I)=\{a(x_i,x_{i+1})\}_{\ell \leqslant i \leqslant s-1}$

Our first observation is that maximal combs with same data have same colour. We say that two combs have the same orientation if they are of the same class (e.g., both are left combs).

Proposition 4.1. Let $X$ , $X' \in [2^N]^{(k+r)}$ be two edges. If $I$ and $I'$ are maximal combs of same type and orientation in $X$ and $X'$ , respectively, such that $F(I)=F(I')$ , then $\chi _0(I)=\chi _0(I')$ .

Proof. The proof basically consists of checking the consistency of our definition. If $F(I)=F(I')=\emptyset$ , then $I$ and $I'$ are either of type $2$ or $6$ . In both cases $\chi _0(I)=\chi _0(I')=0$ .

If $I=\{x_1,\ldots,x_s\}$ and $I'=\{x'_1,\ldots,x'_{s'}\}$ are of type $1$ , $3$ or $4$ , then since $a(I)=F(I)=F(I')=a(I')$ we obtain by Fact 2.1 that $s=s'$ and $a(x_i,x_{i+1})=a(x'_i,x'_{i+1})$ for every $1\leqslant i \leqslant s$ . Therefore $\delta (x_i,x_{i+1})=\delta (x'_i,x'_{i+1})$ for every $1\leqslant i \leqslant s$ and by the colouring defined in Section 3.3, it follows that $\chi _0(I)=\chi _0(I')$ .

The last case that we need to check is when $I=A\cup B=\{x_1,\ldots,x_{s}\}$ and $I'=A'\cup B'=\{x'_1,\ldots,x'_{s'}\}$ are of type $5$ , where $|A|=\ell$ and $|A'|=\ell '$ . As usual, we assume that $I$ and $I'$ are left combs. Since $a(\{x_\ell,\ldots,x_s\})=F(I)=F(I')=a(\{x'_{\ell '},\ldots,x'_{s'}\})$ , it follows again by Fact 2.1 that $s-\ell =|B|=|B'|=s'-\ell '$ and $a(x_i,x_{i+1})=a(x'_i,x'_{i+1})$ for $\ell \leqslant i\leqslant s-1$ . Thus $\delta (x_i,x_{i+1})=\delta (x'_i,x'_{i+1})$ for $\ell \leqslant i \leqslant s-1$ and by the colouring of type 5 we obtain that $\chi _0(I)=\chi _0(I')$ .

Although maximal combs in the same edge do not need to be disjoint, the next result shows that they do not share the same colouring data.

Proposition 4.2. Let $X \in [2^N]^{(k+r)}$ be an edge. If $I=A\cup B$ and $I'=A'\cup B'$ are maximal combs in $X$ , then $F(I)\cap F(I')=\emptyset$ .

Proof. Suppose without loss of generality that $|I|\leqslant |I'|$ . By Proposition 2.7 either $I\cap I'=\emptyset$ or $I\subseteq A'$ . If $I\cap I'=\emptyset$ , then by the fact that $I, I'$ are closed we obtain that $a(I)\cap a(I')=\emptyset$ . Since $F(I)\subseteq a(I)$ by definition, it follows that $F(I)\cap F(I')=\emptyset$ .

Now suppose that $I\subseteq A'$ . We may assume that $F(I), F(I')\neq \emptyset$ and consequently that $I,I'$ are of type $1$ , $3$ , $4$ or $5$ . Since maximal combs of types $1$ , $3$ , $4$ and $5$ have size at least $r$ , our assumption implies that $|I'|\geqslant |I|\geqslant r$ .

We claim that $|A'|\gt r$ . Suppose that $|A'|=r$ . Since $r\leqslant |I|\leqslant |A'|$ we obtain that $I=A'$ and $|I|=r$ . The maximality of $I$ implies that it is either a left or right maximal comb (otherwise we could extend the comb to $I\cup B$ ). However, in this case $I$ is of type $2$ . Thus $F(I)=\emptyset$ , which contradicts our assumption on $I$ . Therefore, $|A'|\gt r$ and consequently $I'$ is of type $5$ . Write $I'=\{x'_1,\ldots,x'_{s'}\}$ with $|A'|=\ell '$ and assume that $I'$ is a left comb. Then by definition

\begin{align*} F(I')=\{a(x'_i,x'_{i+1})\}_{\ell '\leqslant i \leqslant s'-1}. \end{align*}

Since $I\subseteq A'$ we obtain that $F(I)\subseteq a(A')$ . By the structure of a left comb (see Figure 10) we have that

\begin{align*} \delta (x'_1,x'_{\ell '})\gt \delta (x'_{\ell '},x'_{\ell '+1})\gt \delta (x'_{\ell '+1},x'_{\ell '+2})\gt \ldots \gt \delta (x'_{s'-1},x'_{s'}). \end{align*}

Figure 10. A picture of $I$ and $\{a(x_i,x_{i+1})\}_{\ell '\leqslant i \leqslant s-1}$ .

Thus $a(I)\cap \{a(x'_i,x'_{i+1})\}_{\ell '\leqslant i \leqslant s'-1}=\emptyset$ and consequently $F(I)\cap F(I')=\emptyset$ .

5. Pre-processing

As discussed in Subsection 3.2, we now turn our focus to show that a simple daisy $H$ can be pre-processed in a smaller simple subdaisy $H'$ with the property that for every edge $X$ with petal $P$ we have that either $P$ is a closed interval in $X$ or is part of the “teeth” of a maximal comb in $X$ .

Lemma 5.1. For any simple $(r,m,k)$ -daisy $H$ with vertex set $V(H)\subseteq [2^N]$ , $K_0\lt M\lt K_1$ , $|K_0\cup K_1|=k$ and $|M|=m$ , there exists a subset $M'\subseteq M$ of size $|M'|=\frac{1}{2}k^{-1/2}m^{1/2}$ such that the simple $(r,\frac{1}{2}k^{-1/2}m^{1/2},k)$ -daisy $H'=H[K_0\cup M'\cup K_1]$ satisfies one of the following (see Figure 11):

1. 1. $M'$ is a closed interval in $V(H')$ .

2. 2. There exists a maximal comb $I=A\cup B$ in $V(H')$ such that $M'\subseteq B$ .

Figure 11. An example of $H'$ satisfying statement (1) and (2).

Proof. Let $V\;:\!=\;V(H)$ . Given a closed interval $I\subseteq V$ , by condition (ii) of Definition 2.2 there exists a vertex $u \in a(I)$ such that $I=V(u)$ . Consider the partition of $I$ given by $I=I^L\cup I^R$ , where $I^L=V_L(u)$ are the left descendants of $u$ and $I^R=V_R(u)$ are the right descendants of $u$ . Let $u^L$ be the left child of $u$ and $u^R$ be the right child. Hence, $I^L=V(u^L)$ and $I^R=V(u^R)$ and consequently $I=I^L \cup I^R$ is a partition of a closed interval in $V$ into two non empty closed intervals in $V$ (see Figure 12).

Figure 12. Partition of a closed interval into two other closed intervals.

We will construct our set $M'$ iteratively. This is done in two stages. In the first stage we start with the closed interval $Y_0=V$ and proceed recursively as follows: For a closed interval $Y_i\subseteq V$ , let $Y_i=Y_i^L\cup Y_i^R$ be the partition described above in two closed intervals. The choice of $Y_{i+1}$ is determined by the conditions below

1. (P1) Set $Y_{i+1}\;:\!=\;Y_i^L$ if $|Y_i^L\cap M|\geqslant |Y_i^R\cap M|$ .

2. (P2) Set $Y_{i+1}\;:\!=\;Y_i^R$ if $|Y_i^L\cap M|\lt |Y_i^R\cap M|$ .

We stop the process whenever $Y_{i}\cap K_0=\emptyset$ or $Y_{i}\cap K_1=\emptyset$ . Note that since $Y_i^L$ and $Y_i^R$ are non empty, at each iteration of the process the size of $|(K_0\cup K_1)\cap Y_i|$ reduces at least by one. Thus, in a finite amount of time the process terminates. Let $Y$ be the closed interval obtained in the end. We may assume without loss of generality that $Y\cap K_1=\emptyset$ . Write $Y=K_Y\cup M_Y$ , where $K_Y\subseteq K_0$ and $M_Y\subseteq M$ . It is not hard to check by the construction that $|M_Y|\geqslant m/2$ .

For the second stage, let $Z_0=Y$ . Given a closed interval $Z_i \subseteq V$ , let $Z_i=Z_i^L\cup Z_i^R$ be the partition into two non empty closed intervals. By definition we have that $Z_i^L\lt Z_i^R$ . We say that a partition $Z_i^L\cup Z_i^R$ is of type $A$ if $Z_i^R\cap K_0=\emptyset$ and of type $B$ if $Z_i^R\cap K_0\neq \emptyset$ . The choice of $Z_{i+1}$ will depend on the type of partition as follows:

Type A: $Z_i^R\cap K_0 = \emptyset$ .

1. (A1) Set $Z_{i+1}\;:\!=\;Z_i^L$ if $|Z_i^R|\lt \frac{1}{2}k^{-1/2}m^{1/2}$ .

2. (A2) Set $Z_{i+1}\;:\!=\;Z_I^R$ if $|Z_i^R|\geqslant \frac{1}{2}k^{-1/2}m^{1/2}$ and stop the process.

Type B: $Z_i^R\cap K_0 \neq \emptyset$ .

1. (B) Set $Z_{i+1}\;:\!=\;Z_i^R$ .

We terminate the process if we either reach condition (A2) or if $Z_{i+1}$ is a singleton. Since $|Z_{i+1}|\lt |Z_i|$ , the process is finite. Let $Z$ be the closed interval obtained at the end. We split into two cases.

If the process terminates after some instance of condition (A2), then it means that $Z=Z_i^R$ is a closed interval in $V$ with $|Z|\geqslant \frac{1}{2}k^{-1/2}m^{1/2}$ for some index $i$ . Because we are in a partition of type $A$ we also obtain that $Z\subseteq M$ . Thus, if we set $M'=Z$ the simple subdaisy $H[K_0\cup M'\cup K_1]$ satisfies condition (1) of the statement.

Now suppose that the process terminates with $|Z|=1$ . Then it means that for every partition of type A we had an instance of condition (A1). If $Z_{i+1}$ is a set obtained after condition (A1), then $|Z_{i+1}\cap M|\gt |Z_i\cap M|-\frac{1}{2}k^{-1/2}m^{1/2}$ and $|Z_{i+1}\cap K_0|=|Z_{i+1}\cap K_0|$ . That is, condition (A1) removes less than $\frac{1}{2}k^{-1/2}m^{1/2}$ element of $M$ from $Z_i$ and no elements of $K_0$ from it. Moreover, if $Z_{i+1}$ is obtained after condition (B), then $|Z_{i+1}\cap M|=|Z_i\cap M|$ and $|Z_{i+1}\cap K_0|\lt |Z_i\cap K_0|$ . That is, $M$ remains unaffected, but $K_0$ loses at least one element from $K_i$ to $K_{i+1}$ .

Consider the sequence of operations applied to $Z_0$ in order to obtain $Z$ . Since we start with a set $Z_0=Y$ with $|Z_0\cap M|=|M_Y|\geqslant m/2$ , we obtain that during our process we had at least

\begin{align*} \frac{\frac{m}{2}}{\frac{1}{2}k^{-1/2}m^{1/2}}=k^{1/2}m^{1/2} \end{align*}

instances of condition (A1) in the sequence. Similarly, since $|Z_0\cap K_0|=|K_Y|\leqslant k$ , we obtain that we had at most $k$ instances of condition (B) in the sequence. Hence, by the pigeonhole principle there exists a sequence of consecutive applications of condition (A1) of length at least $m^{\prime}=k^{1/2}m^{1/2}/(k+1)\geqslant \frac{1}{2}k^{-1/2}m^{1/2}$ .

Figure 13. Sequence of closed intervals $Z_j^R,\ldots, Z_{j+m^{\prime}-1}^R$ .

Let $Z_j, Z_{j+1},\ldots, Z_{j+m^{\prime}}$ be the closed intervals involved in the sequence. That is, $Z_{i+1}$ is obtained from $Z_i$ by a condition (A1) for every $j\leqslant i \leqslant j+m^{\prime}-1$ . By the algorithm, we obtain closed intervals $Z_j^R,\ldots,Z_{j+m^{\prime}-1}^R \subseteq M$ all of them with size less than $\frac{1}{2}k^{-1/2}m^{1/2}$ (Figure 13). For every $j\leqslant i \leqslant j+m^{\prime}-1$ , choose a point $z_i\in Z_i^R$ .

Set $M'=\{z_j,\ldots,z_{j+m^{\prime}-1}\}$ . We claim that $M'$ is a set satisfying condition (2) of the statement. Let $H'=H[K_0\cup M'\cup K_1]$ and $V'=V(H')$ . To see that condition (2) is satisfied we just need to find a maximal comb $I=A\cup B \subseteq V'$ such that $M'\subseteq B$ . Let $K'=K_0\cap Z_{j+m^{\prime}}$ and consider the interval $I'=K' \cup M'$ in $V'$ . By construction, the intervals $K'$ and $K'\cup \{z_{j+i},\ldots,z_{j+m^{\prime}-1}\}$ are closed in $V'$ for every $0\leqslant i\leqslant m^{\prime}-1$ . Therefore, by condition (a3*) of Definition 2.4, the interval $I'=A'\cup B'$ is a left comb and $M' \subseteq B'$ . Since every comb can be extended to a maximal one, there exists a maximal left comb $I=A\cup B$ with $A=A'$ and $B'\subseteq B$ such that $M'\subseteq B$ and we are done.

One of the main consequences of our pre-processing is that it allows us to identify certain closed and non-closed intervals in an arbitrary edge of $H'$ . To be more precise, given an edge $X \in E(H')$ with petal $P$ and $V'=V(H')$ , let

\begin{align*}{\mathcal{C}}_{V',M'}&=\{I\;:\: I \textrm{ is an interval in}\; V' \textrm{ and either } M'\subseteq I \textrm{ or } M'\cap I=\emptyset \} \\[5pt] {\mathcal{C}}_{X,P}&=\{I\;:\: I \textrm{ is an interval in } X \textrm{ and either } P\subseteq I \textrm{ or }P\cap I=\emptyset \} \end{align*}

be the set of intervals in $V'$ and $X$ such that the intervals either contain or are disjoint of $M'$ and $P$ , respectively. The next proposition shows that there is a one-to-one correspondence between ${\mathcal{C}}_{V',M'}$ and ${\mathcal{C}}_{X,P}$ preserving the property of being closed.

Proposition 5.2. For a given edge $X\in E(H')$ with petal $P$ , there exists a bijection $\Psi \;:\;{\mathcal{C}}_{V',M'}\rightarrow{\mathcal{C}}_{X,P}$ given by

\begin{align*} \Psi (I)=I\cap X \end{align*}

such that $I$ is a closed interval in $V'$ if and only if $\Psi (I)$ is a closed interval in $X$ .

Proof. If $I\in{\mathcal{C}}_{V',M'}$ is such that $I\cap M'=\emptyset$ , then either $I\subseteq K_0$ or $I\subseteq K_1$ . Since $X=K_0\cup P\cup K_1$ for some $P\in M'^{(r)}$ , we obtain that $\Psi (I)=I\cap X=I$ . This shows that $\Psi$ is a bijection from the intervals of $V'$ disjoint of $M'$ to the intervals of $X$ disjoint of $P$ .

Now suppose that $I \in{\mathcal{C}}_{V',M'}$ is such that $M'\subseteq I$ . Then $I$ can be written as $I=K_I\cup M'$ with $K_I\subseteq K_0\cup K_1$ . Thus $\Psi (I)=I\cap X=K_I \cup P$ . Since $K_I\neq K_{I'}$ for $I\neq I'$ , we obtain that $\Psi$ is an injection from the intervals of $V'$ containing $M'$ to the intervals of $X$ containing $P$ . To check surjectivity, just notice that $K_I\cup P$ is an interval if and only if $K_I\cup M'$ is an interval.

It remains to prove that $I$ is closed if and only if $\Psi (I)$ is closed. Throughout the rest of the proof, for a set $S\subseteq V$ we define

\begin{align*} x_S=\min (S), \quad y_S=\max (S), \quad u_S=a(x_S,y_S). \end{align*}

Note that the backwards direction is straightforward from the definition of being closed.

Proposition 5.3. If $I$ is closed in $V'$ , then $I\cap X$ is closed in $X$ .

Proof. Suppose by contradiction that $I\cap X$ is not closed in $X$ . Then by condition ( $\star \star$ ) of Definition 2.2, there exists $y \in X\setminus I$ such that $u_{I\cap X}$ is an ancestor of $y$ . Since $I\cap X \subseteq I$ , we have that $u_I$ is an ancestor of $u_{I\cap X}$ . Therefore, $y\in X\setminus I \subseteq V'\setminus I$ is an ancestor of $u_I$ which contradicts the fact that $I$ is closed in $V'$ .

The following observation will be useful for the rest of the proof.

Fact 5.4. Let $W=V(u_W)$ be a closed interval in $V$ . If $x$ and $y$ are two vertices such that $x\in W$ and $y\notin W$ , then $a(x,y)=a(y,u_W)$ (see Figure 14).

In particular, Fact 5.4 applied to $W=M'$ says that an element $y\notin M'$ have the same common ancestor with any $x\in M'$ . We split the proof of the forward implication depending on the structure of $H'$ given by Lemma 5.1.

Case 1: $M'$ is a closed interval in $V'$ .

The proof of Case 1 is slightly different depending on the location of the interval $I$ in $V'$ .

Figure 14. A picture of Fact 5.4.

Case 1.1: $I \in{\mathcal{C}}_{V',M'}$ such that $I\cap M'=\emptyset$ .

As seen before, we have that $\Psi (I)=I$ . By condition ( $\star \star$ ) of Definition 2.2 there is no vertex $x\in X\setminus I$ such that $u_I$ is an ancestor of $x$ . If there is a descendant of $u_I$ in $V'\setminus I$ , then the descendant is in the set $V'\setminus X=M'\setminus P$ . Since $I\cap M'=\emptyset$ , Fact 5.4, applied to the closed interval $M'$ , implies that for every $y\in I'$ and $x\in M'$ we have $a(x,y)=a(y,u_{M'})$ . Thus, if $u_I$ is an ancestor of some $x \in M'$ , then $u_I$ is an ancestor of $u_{M'}$ . This implies that $u_I$ is an ancestor for the entire set $M'$ and in particular of $P$ , which contradicts the fact that $I$ is closed in $X$ . Therefore, $I$ is a closed interval in $V'$ .

Case 1.2: $I \in{\mathcal{C}}_{V',M'}$ such that $M'\subseteq I$ .

Suppose that $I=K_I\cup M'$ is a interval in $V'$ containing $M'$ . We need to prove that $I=K_I\cup M'$ is closed in $V'$ if $\Psi (I)=I\cap X=K_I\cup P$ is closed in $X$ . If $K_I=\emptyset$ , then $I=M'$ which is by assumption closed in $V'$ . Otherwise, we claim that $u_I=u_{\Psi (I)}$ . That is $I$ and $\Psi (I)$ have the same common ancestor.

The assumption that $K_I\neq \emptyset$ gives us that either $x_I\lt \min (M')$ or $y_I\gt \max (M')$ . Assume without loss of generality that $y_I\gt \max (M')$ . Thus, $y_I\in K_I$ and we have that $y_I=y_{\Psi (I)}=\max (K_I)$ . If $x_I \notin M'$ , then similarly we have $x_I=x_{\Psi (I)}$ and consequently $u_I=a(x_I,y_I)=a(x_{\Psi (I)},y_{\Psi (I)})=u_{\Psi (I)}$ . Now if $x_I \in M'$ , then $x_I\notin K_I$ . This implies that $x_{\Psi (I)} \in P\subseteq M'$ . Since both $x_I,x_{\Psi (I)} \in M'$ and $y_I=y_{\Psi (I)}\notin M'$ , by Fact 5.4 we obtain that $u_I=a(x_I,y_I)=a(u_{M'},y_I)=a(u_{M'},y_{\Psi (I)})=a(x_{\Psi (I)},y_{\Psi (I)})=u_{\Psi (I)}$ . Hence, $I=K_I\cup M'$ and $\Psi (I)=K_I\cup P$ have the same common ancestor.

To finish the proof note that by condition ( $\star \star$ ) of Definition 2.2 there are no descendants of $u_{\Psi (I)}$ in $X\setminus \Psi (I)$ . Since $u_I=u_{\Psi (I)}$ and $V\setminus I'=K\setminus K_I=X\setminus \Psi (I)$ , we conclude that there are no descendants of $u_I$ in $V'\setminus I$ and consequently $I$ is closed in $V'$ .

Case 2: $M'\subseteq Q$ for some maximal comb $Q=A^Q\cup B^Q$ in $V'$ with $M'\subseteq B^Q$ .

We may assume without loss of generality that $Q$ is a maximal left comb. Let $K_0^Q=K_0\cap Q$ and $K_1^Q=K_1\cap Q$ . Clearly, $Q=K_0^Q\cup M'\cup K_1^Q$ with $K_0^Q\lt M'\lt K_1^Q$ . Moreover, $Q=A^Q\cup B^Q$ with $A^Q\lt B^Q$ and $M'\subseteq B^Q$ (Figure 15). Thus, $A^Q\subseteq K_0^Q$ and by condition (a3*) of Definition 2.4, we obtain that $K_0^Q$ is closed in $V'$ . As in the first case, we split into two cases depending on the type of the interval.

Case 2.1: $I \in{\mathcal{C}}_{V',M'}$ such that $I\cap M'=\emptyset$ .

Suppose that $I$ is a closed interval in $X$ . We claim that $V'(u_I)\cap M' = \emptyset$ , i.e., the descendants of $u_I$ are disjoint of $M'$ . Applying Proposition 2.3 to the closed interval $V'(u_I)$ and maximal comb $Q$ gives us that either $V'(u_I)\cap Q=\emptyset$ , $V'(u_I)\subseteq Q$ or $Q\subseteq V'(u_I)$ . If $V'(u_I)\cap Q=\emptyset$ , then we immediately obtain that $V'(u_I)\cap M'=\emptyset$ , since $M'\subseteq Q$ . If $Q\subseteq V'(u_I)$ , then $M'\subseteq V'(u_I)$ and consequently $P=M'\cap X\subseteq V'(u_I)\cap X=X(u_I)$ . This implies that $X(u_I)\neq I$ , which contradicts $I$ being closed in $X$ .

Thus, we may assume that $V'(u_I)\subseteq Q$ and $M' \not \subseteq V'(u_I)$ . Then, by Proposition 2.7, we have that $V'(u_I)=A^{V'(u_i)}\cup B^{V'(u_I)}$ where either $V'(u_I) \subseteq A^Q$ or $A^{V'(u_i)}=A^Q$ and $B^{V'(u_I)}\subseteq B^Q$ . For the first case, note that $A^Q\cap M'=\emptyset$ and therefore $V'(u_I)\cap M'=\emptyset$ . For the second case, note that since $M'\not \subseteq V'(u_I)$ , then $M'\not \subseteq B^{V'(u_I)}$ . This implies that $V'(u_I)\subseteq K_0\cup M'$ . Together with the fact that $I\cap M'=\emptyset$ and $I\subseteq V'(u_I)$ , we obtain that $I\subseteq K_0^Q$ . Since $K_0^Q$ is closed in $V'$ , we have that the common ancestor $u_{K_0^Q}=a(\!\min (K_0^Q),\max (K_0^Q))$ is an ancestor of the entire $I$ and therefore of $u_I$ . Hence, $V'(u_I)\subseteq K_0^Q$ , which implies that $V'(u_I)\cap M'=\emptyset$ . The fact that $I$ is closed in $V'$ now follows because $V'(u_I)=X(u_I)=I$ .

Figure 15. Maximal comb $Q$ and sets $K_0^Q$ and $K_1^Q$ .

Case 2.2: $I \in{\mathcal{C}}_{V',M'}$ such that $M'\subseteq I$ .

Let $I=K_0^I\cup M'\cup K_1^I$ be an interval in $V'$ containing $M'$ with $K_0^I\subseteq K_0$ and $K_1^I\subseteq K_1$ . Suppose that $\psi (I)=K_0^I\cup P\cup K_1^I$ is closed in $X$ . Since $K_0^Q\cup M'$ is closed, by the same argument of Case 1.2 (by considering $K_0^Q\cup M'$ instead of $M'$ ), we can show that if $x_I\lt \min (K_0^Q)$ or $y_I \gt \max (M')$ , then $u_I=a(x_I,y_I)=a(x_{\Psi (I)},y_{\Psi (I)})=u_{\Psi (I)}$ and consequently $I$ is closed in $V'$ .

Now suppose that $\min (K_0^Q)\leqslant x_I \leqslant \min (M')$ and $y_I=\max (M')$ . Since both $M'$ and $P$ are not closed intervals in their respective ground sets, we have that $x_I\neq \min (M')$ and consequently $x_{\Psi (I)}=x_I$ and $y_{\Psi (I)}=\max (P)$ . Hence, in this case, $K_0^I\subseteq K_0^Q$ and $K_I=\emptyset$ , which implies that $I=K_0^I\cup M'$ and $\Psi (I)=K_0^I\cup P$ . Because $Q$ is a maximal left comb with $M'\subseteq Q$ , then both sets $K_0^Q$ and $K_0^Q\cup M'$ are closed in $V'$ . Therefore, by Proposition 5.3 the intervals $K_0^Q$ and $K_0^Q\cup P$ are closed in $X$ . Fact 5.4 applied to $K_0^Q$ gives us that $a(z,y_{\Psi (I)})=a(z',y_{\Psi (I)})$ for every $z,z' \in K_0^Q$ . This implies that $u_{\Psi (I)}=a(x_{\Psi (I)},y_{\Psi (I)})=a(\!\min (K_0^Q),y_{\Psi (I)})$ , i.e., $K_0^Q\cup P$ and $\Psi (I)=K_0^I\cup P$ have $u_{\Psi (I)}$ as the same common ancestor. Since $K_0^Q\cup P$ and $K_0^I\cup P$ are both closed in $X$ , we obtain that $K_0^Q=K_0^I$ . Thus $I=K_0^Q\cup M'$ , which is closed in $V'$ .

The next result shows that we can always find in an edge the location of the maximal comb with colouring data containing $a(P)$ . This will be extremely important, since the comb will be the only maximal comb such that colouring data changes while we run through different edges of $H'$ .

Proposition 5.5. Let $H'$ be a fixed pre-processed daisy obtained by Lemma 5.1 . There exists a unique interval $J \subseteq [k+r]$ such that for every edge $X=K_0\cup P\cup K_1=\{x_1,\ldots,x_{k+r}\}$ in $H'$ , the interval $X_J=\{x_j\}_{j\in J}$ is a maximal comb of type depending only on $H'$ with

\begin{align*} a(P)\subseteq F(X_J). \end{align*}

Moreover, writing $X_J=A^{X_J}\cup B^{X_J}$ we have one of the following:

1. 1. If $H'$ satisfies statement $(1)$ of Lemma 5.1 , then $A^{X_J}\subseteq P$ and $X_J$ is the smallest maximal comb containing $P$ with non-empty colouring data.

2. 2. If $H'$ satisfies statement $(2)$ of Lemma 5.1 , then $X_J=I\cap X$ , where $I=A\cup B$ is the maximal comb in $V'$ such that $M'\subseteq B$ , and $X_J$ satisfies $P\subseteq B^{X_J}$ .

Proof. The idea of the proof is to identify certain maximal combs in $V'$ with maximal combs in an edge $X$ . Because the structure of those maximal combs in $V'$ only depends on $H'$ , we will obtain the same for the corresponding combs in $X$ . Proposition 5.2 will be useful here, since by condition (a3*) and (b3*) of Definition 2.4 a comb can be defined by looking at certain closed subintervals. The proof is split into cases depending on the structure of the tree $T_{V'}$

Case 1: $M'$ is a closed interval in $V'$ .

We will construct a maximal comb in $X$ by looking at a maximal comb in $V'$ containing $M'$ . Write $K_0=\{x_1,\ldots,x_{k_0}\}$ , $M'=\{y_1,\ldots, y_{m^{\prime}}\}$ and $K_1=\{z_1,\ldots,z_{k_1}\}$ . There are two possibilities here:

Case 1.1: Either $M'\cup \{z_1\}$ is a closed interval in $V'$ or $M'\cup \{x_{k_0}\}$ is a closed interval in $V'$ .

Suppose without loss of generality that $M'\cup \{z_1\}$ is closed in $V'$ . In this case $M'\cup \{z_1\}$ is a left comb. Let $M'\cup \{z_1,\ldots,z_t\}$ be the maximal left comb obtained by extending $M'\cup \{z_1\}$ . We will assume during the entire proof that $t\lt k_1$ . For $t=k_1$ , the same proof work by removing any claims and sets involving $z_{t+1}$ . By condition (a3*) of Definition 2.4 and Definition 2.6, $M'\cup \{z_1,\ldots,z_t\}$ being a maximal left comb is the same as saying that the intervals $M'$ and $M'\cup \{z_1,\ldots,z_i\}$ are closed for every $1\leqslant i \leqslant t$ , but the interval $M'\cup \{z_1,\ldots,z_{t+1}\}$ is not closed.

Set $J=\{k_0+1,\ldots,k_0+r+t\}$ . Let $X$ be an edge of $H'$ with petal $P$ . We claim that $X_J$ is a maximal left comb in $X$ with $A^{X_J}\subseteq P$ . To see that consider the intervals

\begin{align*} J_i=\{k_0+1,\ldots,k_0+r+i\}, \quad 0\leqslant i \leqslant t+1. \end{align*}

In particular $J_t=J$ . Note that $X_{J_0}=M'\cap X=P$ and $X_{J_i}=(M'\cap \{z_1,\ldots,z_i\})\cap X$ for $1\leqslant i \leqslant t+1$ . Thus, by applying Proposition 5.2 with $I=M'$ and $I=M'\cup \{z_1,\ldots,z_i\}$ , we obtain that $X_{J_i}$ is closed in $X$ for $0\leqslant i \leqslant t$ and $X_{J_{t+1}}$ is not closed in $X$ . Hence, by condition (a3*) of Definition 2.4 and Definition 2.6, we have that $X_J=X_{J_t}$ is a maximal left comb. Since $P=X_{J_0}\subseteq X_{J_1}\subseteq \ldots \subseteq X_{J_t}=X_J$ are all closed intervals, we have that $A^{X_J}\subseteq P$ . Thus, $|A^{X_J}|\leqslant |P| =r$ and we have that either $X_J$ is a maximal comb of type 3 or type 4 depending on the size of $|X_J|=r+t$ . Because $t$ is a parameter that depends on the size of the maximal comb in $V'$ , i.e., on the structure of $H'$ , we conclude that the type of $X_J$ is independent of our choice of edge $X$ .

It remains to show that $a(P)\subseteq F(X_J)$ and $X_J$ is the smallest maximal comb containing $P$ with non-empty data colouring. For the first, note that $F(X_J)=a(X_J)$ because $X_J$ is of type $3$ or $4$ . Thus, $a(P)\subseteq a(X_J)=F(X_J)$ . For the latter, note that the only potential maximal comb smaller than $X_J$ containing $P$ is $P$ itself. However, if $P$ is a maximal comb, then it is a comb of type $2$ and therefore $F(P)=\emptyset$ . Hence, $X_J$ is the smallest maximal comb containing $P$ with non-empty colouring data.

Case 1.2: Both $M'\cup \{z_1\}$ and $M'\cup \{x_{k_0}\}$ are not closed in $V'$ .

By Definition 2.6, $M'$ is a maximal comb. Set $J=\{k_0+1,\ldots,k_0+r\}$ . Note that $X_J=P$ . By Proposition 5.2, the set $P=M'\cap X$ is closed in $X$ and $P\cup \{z_1\}=(M'\cup \{z_1\})\cap X$ and $P\cup \{x_{k_0}\}=(M'\cup \{x_{k_0}\})\cap X$ are not closed in $X$ . Thus, $P$ is a maximal comb in $X$ . It is clear that $A^{X_J}\subseteq X_J=P$ . Since $|P|=r$ and $P\cup \{z_1\}$ , $P\cup \{x_{k_0}\}$ are not closed, we have that $X_J=P$ is of type $1$ . Therefore, the type of $X_J$ does not depend on $X$ . Moreover, the fact that $X_J$ is of type 1 gives us that $a(P)=a(X_J)=F(X_J)$ . The minimality of $X_J$ is immediate from the fact that all combs with non-empty data has size at least $r$ .

Case 2: $M'\subseteq B$ for a maximal comb $I=A\cup B$ in $V'$ .

Suppose without loss of generality that $I=A\cup B$ is a maximal left comb. Let $A=\{x_{k_0-p-\ell +1},\ldots,x_{k_0-p}\}$ , $B\cap K_0=\{x_{k_0-p+1},\ldots,x_{k_0}\}$ and $B\cap K_1=\{z_1,\ldots,z_t\}$ . Set $J=\{k_0-p-\ell +1,\ldots,k_0+r+t\}$ . Let $X$ be an edge of $H'$ with petal $P$ (see Figure 16). Clearly, $X_J=I\cap X$ . We claim that $X_J$ is a maximal left comb with $P\subseteq B^{X_J}$ . By Definition 2.4 and 2.6 we have that $A$ is a closed interval in $V'$ , $A\setminus \{x_{k_0-p}\}$ and $I\cup \{z_{t+1}\}$ are not closed in $V'$ and

\begin{align*} \delta (x_{k_0-p},x_{k_0-p+1})&\gt \ldots \gt \delta (x_{k_0-1},x_{k_0})\gt \delta (x_{k_0},y_1)\gt \delta (y_1,y_2)\gt \ldots \gt \delta (y_{m^{\prime}-1},y_{m^{\prime}})\\[5pt] &\gt \delta (y_{m^{\prime}},z_1)\gt \delta (z_1,z_2)\gt \ldots \gt \delta (z_{t-1},z_t). \end{align*}

Figure 16. Case $2$ of Proposition 5.5.

Let $P=\{y_{i_1},\ldots,y_{i_r}\}$ . By Proposition 5.2, the set $A=A\cap X$ is closed in $X$ and the sets $A\setminus \{x_{k_0-p}\}=(A\setminus \{x_{k_0-p}\})\cap X$ and $X_J\cup \{z_{t_1}\}=(I\cup \{z_{t+1}\})\cap X$ are not closed in $X$ . Moreover, since $P\subseteq M'$ , we have that

\begin{align*} \delta (x_{k_0-p},x_{k_0-p+1})&\gt \ldots \gt \delta (x_{k_0-1},x_{k_0})\gt \delta (x_{k_0},y_{i_1})\gt \delta (y_{i_1},y_{i_2})\gt \ldots \gt \delta (y_{i_{r-1}},y_{i_r})\\[5pt] &\gt \delta (y_{i_r},z_1)\gt \delta (z_1,z_2)\gt \ldots \gt \delta (z_{t-1},z_t). \end{align*}

Thus, by Definition 2.4 and Definition 2.6, the interval $X_J$ is a maximal left comb in $X$ with $A^{X_J}=A$ and $|B^{X_J}|=r+t+p$ . Since $A\subseteq K_0$ , we obtain that $P\subseteq B^{X_J}$ . Note that to determine the type of $X_J$ we need to know the sizes of $X_J$ , $A^{X_J}$ and $B^{X_J}$ . None of this parameters depends on the choice of $X$ . Hence, the type of $X_J$ is independent of $X$ . Finally, because $|B^{X_J}|\geqslant |P|\geqslant r$ , we obtain that $|X_J|\geqslant r+1$ and consequently the comb $X_J$ is of type $3$ , $4$ or $5$ . If it is of type $3$ or $4$ , then $a(P)\subseteq a(X_J)=F(X_J)$ . If it is of type $5$ , then $a(P)\subseteq a(\max (A^{X_J})\cup B^{X_J})=F(X_J)$ .

To finish the section we prove that the maximal comb determined by the set $J$ is the comb that essentially determines the colour of the entire edge.

Proposition 5.6. Let $X=\{x_1,\ldots,x_{k+r}\}$ , $X'=\{x'_1,\ldots,x'_{k+r}\}$ be two edges in $H'$ and let $X_J=\{x_j\}_{j\in J}$ , $X'_J=\{x'_j\}_{j\in J}$ . If $\chi (X)=\chi (X')$ , then $\chi _0(X_J)=\chi _0(X'_J)$ .

Proof. Let $P, P'\subseteq M'$ be the petals of $X$ and $X'$ , respectively. By definition, $\chi (X)=\chi (X')$ implies that

\begin{align*} \sum _{I\in{\mathcal{I}}_X}\chi _0(I)=\sum _{I'\in{\mathcal{I}}_{X'}}\chi _0(I') \pmod{2}. \end{align*}

By the definition of colouring data, if $F(I)=\emptyset$ , then $\chi _0(I)=0$ . Thus, we may rewrite the equality above as

(4) \begin{align} \sum _{\substack{I\in{\mathcal{I}}_X\\[5pt] F(I)\neq \emptyset }}\chi _0(I)=\sum _{\substack{I'\in{\mathcal{I}}_{X'}\\[5pt] F(I')\neq \emptyset }} \chi _0(I) \pmod{2}. \end{align}

We claim that if $I=A\cup B$ is a maximal comb of $X$ with $F(I)\neq \emptyset$ , then either $I\cap P=\emptyset$ or $P\subseteq I$ . Note that, in the colouring defined in Subsection 3.3, whenever $F(I)=\emptyset$ , we have that $|I|\geqslant |P|=r$ . By Lemma 5.1, the daisy $H'$ satisfies one of the following conditions: Either $M'$ is a closed interval in $V'\;:\!=\;V(H')$ or there exists a maximal comb $Q=A^Q\cup B^Q$ such that $M'\subseteq B^Q$ . If $M'$ is closed in $V'$ , then by Proposition 5.2 the petal $P=M'\cap X$ is a closed interval in $X$ . Thus, Proposition 2.3 applied to the closed intervals $I$ and $P$ gives the desired result that either $I\cap P=\emptyset$ or $P\subseteq I$ . Now suppose that we are in Condition (2) of Lemma 5.1. By Proposition 5.5, we have that $P\subseteq B^{X_J}$ , where $B^{X_J}$ is the “teeth” part of the comb $X_J=A^{X_J}\cup B^{X_J}$ . Thus, Proposition 2.7 applied to the maximal combs $I$ and $X_J$ implies that $I\cap X_J=\emptyset$ , $I\subseteq A^{X_J}$ or $X_J\subseteq A \subseteq I$ . In the first two cases we obtain $I\cap P=\emptyset$ , while in the latter we have $P\subseteq I$ .

The idea of the proof of Proposition 5.6 is to show that there exists a bijection between $\{I\in{\mathcal{I}}_X\;:\: F(I)\neq \emptyset \}$ and $\{I'\in{\mathcal{I}}_{X'}\;:\: F(I')\neq \emptyset \}$ such that $X_J$ is sent to $X'_J$ and every $I\neq X_J$ is sent to an $I'\neq X'_J$ with $\chi _0(I)=\chi _0(I')$ . Hence, after some cancellation, we obtain from equation (4) that $\chi _0(X_J)=\chi _0(X'_J)$ . Based on the last paragraph, we construct such a bijection by splitting $\{I\in{\mathcal{I}}_X\;:\: F(I)\neq \emptyset \}$ into two parts:

Case 1: $I\in{\mathcal{I}}_X$ is a maximal comb of $X$ with $F(I)\neq \emptyset$ and $I\cap P=\emptyset$ .

We claim that $I\in{\mathcal{I}}_{X'}$ is a maximal comb in $X'$ of the same type and consequently $\chi _0(I)$ is the same in $X$ and $X'$ . Assume without loss of generality that $I\subseteq K_0$ . Let $x$ be the element preceding $\min (I)$ in $X$ (In the case that such $x$ does not exists, we simply take $x=\min (I)$ ). Let $y$ be the element after $\max (I)$ in $X$ . Similarly, define $x'$ as the element before $\min (I)$ in $X'$ and $y'$ as the element after $\max (I)$ in $X'$ . Since $I\subseteq K_0$ , clearly $x=x'$ . However, $y$ and $y'$ are not necessarily the same. By conditions (a3*) and (b3*) of Definition 2.4 and Definition 2.6, to prove that $I\in{\mathcal{I}}_{X'}$ is enough to check that $I\cup \{x\}$ , $L\subseteq I$ , $I\cup \{y\}$ are closed intervals in $X$ if and only if $I\cup \{x'\}$ , $L\subseteq I$ and $I\cup \{y'\}$ are closed intervals in $X'$ , respectively. Since $F(I)=\neq \emptyset$ , we have that $I$ is of type 1, 3, 4 or 5. Note that one can distinguish between this types by determining the size of the “handle” and ‘teeth” of $I$ . Thus, by checking the properties above, we also obtain that $I$ have the same type in $X$ and $X'$ .

For an interval $L\subseteq I$ , by Proposition 5.2 we have that $L=L\cap X$ is a closed interval in $X$ if and only if it is a closed interval in $V'$ . Another application of Proposition 5.2 gives us that $L=L\cap X'$ is a closed interval if it is closed in $V'$ . Hence, $L$ is closed in $X$ if and only if it is closed in $X'$ . Similarly, the same argument works for $I\cup \{x\}$ and $I\cup \{x'\}$ , because $x=x'\notin M'$ . Moreover, if $y\in K_0$ , then $y'=y\notin M'$ and we also obtain that $I\cup \{y\}$ is closed in $X$ if and only if $I\cup \{y'\}$ is closed in $X'$ . Hence, the only case remaining is when $y\notin K_0$ , i,e, $y=\min (P)$ and $y'=\min (P')$ .

We split the argument into two cases depending on the structure given by Lemma 5.1. Suppose that $M'$ is closed in $V'$ and let $u=a(\!\min (M'),\max (M'))$ be the common ancestor of $M'$ . By Fact 5.4, we have that $a(z,y)=a(z,y')=a(z,u)$ for every $z\in I$ . Therefore, the entire set $M'$ is descendant of the common ancestors of $I\cup \{y\}$ and $I\cup \{y'\}$ , which by condition (ii*) of Definition 2.2 implies that both sets are not closed. Now suppose that $M'\subseteq B^Q$ for some maximal comb $Q=A^Q\cup B^Q$ . Since $I$ is a closed interval in $X$ , then by Proposition 5.2 it is a closed interval in $V'$ . Thus, by Proposition 2.3, applied to $I$ and the maximal comb $Q$ , one of the following three possibilities holds: $I\cap Q=\emptyset$ , $I\subseteq Q$ or $Q\subseteq I$ . Clearly, the last possibility cannot hold, since $P\subseteq Q$ and $I\cap P=\emptyset$ . Suppose that $I\cap Q=\emptyset$ . By Proposition 5.2, the interval $Q\cap X$ is a closed interval in $X$ . Since $(I\cup \{y\})\cap (Q\cap X)=\{y\}\neq \emptyset$ and $\{y\}\neq Q\cap X$ , we obtain by Proposition 2.3 that $I\cup \{y\}$ is not closed in $X$ . Similarly, $I\cup \{y'\}$ is not closed in $X'$ .

Now we handle with the case that $I\subseteq Q$ . By Proposition 2.7, either $I\subseteq A^Q$ or $I=A\cup B$ is a comb with $A=A^Q$ and $B\subseteq B^Q$ . Since $I\subseteq K_0$ , we have that $Q$ is a maximal left comb. Let $K_0^Q=K_0\cap Q$ , $B^Q=\{z_1,\ldots,z_b\}$ and let $Q_{z_i}=A^Q\cup \{z_1,\ldots,z_i\}$ be the subcomb of $Q$ ending in $z_i$ . By condition (a3*) of Definition 2.4, we have that $A^Q$ and $Q_z$ are closed in $V'$ for every $z\in B^Q$ . Moreover, note that $\min (I)\in A^Q$ . Let $v=a(\!\min (A^Q),\max (A^Q)$ and $w=a(\!\min (I),y)$ be the common ancestor of $A^Q$ and $I\cup \{y\}$ , respectively. By Fact 5.4 applied to $A^Q$ , we have that $a(\!\min (I),x)=a(v,x)=a(\!\min (A^Q),x)$ for every $x\in M'$ . Thus, $X(w)=V'(w)\cap X=Q_y\cap X=K_0^Q\cup \{y\}$ , which implies that $I\cup \{y\}$ is a closed interval in $X$ if and only if $I=K_0^Q$ . Similarly, $I\cup \{y'\}$ is a closed interval in $X'$ if and only if $I=K_0^Q$ . Hence, $I\cup \{y\}$ is closed in $X$ if and only if $I\cup \{y'\}$ is closed in $X'$ .

Case 2: $I\in{\mathcal{I}}_X$ is a maximal comb of $X$ with $F(I)\neq \emptyset$ , $P\subseteq I$ and $I\neq X_J$ .

In this case, by Proposition 4.2 and Proposition 5.5, we have that $F(I)\cap a(P)=\emptyset$ and consequently $F(I)\neq a(I)$ . Thus, by our colouring, we obtain that $I$ is of type $5$ , i.e., $I=A\cup B$ is a maximal left/right comb with $|A|\gt r$ and $|B|\geqslant r$ . We may assume that $I$ is a maximal left comb. Hence, $F(I)=a(\{\max (A)\}\cup B)$ and the fact that $F(I)\cap a(P)=\emptyset$ implies that $P\subseteq A$ . Write $A=K_A\cup P$ with $K_A\subseteq K_0\cup K_1$ . We claim that $I'=K_A\cup P'\cup B$ is a maximal comb of type $5$ with set of “teeth” $B'=B$ and “handle” $A'=K_A\cup P'$ .

Write $B=\{y_1,\ldots,y_t\}$ . Let $x=\max (A)$ , $x'=\max (A')$ and let $z$ be the element coming after $B$ in $V'$ (In case that such element does note exist, we take $z=\max (B)$ ). By condition (a3*) of Definition 2.4 and Definition 2.6 to prove that $I=A'\cup B'$ is a maximal comb of type $5$ with $A'=K_A\cup P$ and $B'=B$ it is enough to prove that $A'$ and $A'\cup \{y_1,\ldots,y_i\}$ are closed in $X'$ for every $1\leqslant i \leqslant t$ , $A'\setminus \{x'\}$ is not closed in $X'$ and $A'\cup \{y_1,\ldots, y_t,z\}$ is closed if and only if $A\cup \{y_1,\ldots,y_t,z\}$ is closed in $X$ . Applying Proposition 5.2 with $X$ and $V'$ and then $V'$ and $X'$ gives us that $A$ , $A\cup \{y_1,\ldots,y_i\}$ and $A\cup \{y_1,\ldots,y_t,z\}$ are closed in $X$ if and only if $A'$ , $A'\cup \{y_1,\ldots,y_i\}$ and $A'\cup \{y_1,\ldots,y_t,z\}$ are closed in $X'$ , respectively. Since $I$ is a maximal comb in $X$ , this implies that $A'$ , $A'\cup \{y_1,\ldots,y_i\}$ are closed in $X'$ for $1\leqslant i \leqslant t$ . If $x\notin P$ , then $x=x'$ and by the same argument $A'\setminus \{x'\}$ is not closed in $X'$ .

It remains to deal with the case that $x\in P$ , i.e., $x=\max (P)$ and $x'=\max (P')$ . The proof is split into two cases depending on the structure of $H'$ given by Lemma 5.1. If $M'$ is a closed interval in $V'$ , then by Proposition 5.2 the interval $P'$ is closed in $X'$ . The intersection $A'\setminus \{x'\}$ is proper since $|A'|=|A|\gt r=|P'|$ and $x'\in P'$ . Therefore, by Proposition 2.3, we have that $A'\setminus \{x'\}$ is not closed in $X'$ .

Now suppose that $M'\subseteq B^Q$ for some maximal comb $Q=A^Q\cup B^Q$ . By Proposition 5.5, the maximal combs $X_J$ and $X'_J$ satisfies $P\subseteq B^{X_J}$ and $P'\subseteq B^{X'_J}$ . Applying Proposition 2.7 to the maximal combs $I$ and $X_J$ gives us that either $I\subseteq A^{X_J}$ or $X_J\subseteq A$ . Since $P\cap A^{X_J}=\emptyset$ , it follows that $X_J\subseteq A$ . Because $x=\max (A)\in P$ , we have that $\max (K_A)\lt \min (P)$ . This implies that $X_J$ is a maximal left comb. Hence, by Proposition 5.5 both $Q$ and $X'_J$ are maximal left combs.

We claim that $A'\setminus \{x'\} \cap X'_J$ is a proper intersection. Since $|X'_J|=|X_J|\leqslant |A|=|A'|$ , by Proposition 2.3 applied to $A'$ and $X'_J$ , we have that $X'_J\subseteq A'$ . Note that we already proved for $1\leqslant i \leqslant t$ that $A'$ and $A'\cup \{y_1,\ldots,y_i\}$ are closed in $X'$ . Hence, by the maximality of $X'_J$ we have that $A'\neq X'_J$ (otherwise we could extend to the left comb $X'_J\cup B$ ). Thus, $X'_J$ is strictly contained in $A'$ , which implies that $K_A\setminus X'_J\neq \emptyset$ . This concludes that $A'\setminus \{x'\}\cap X'_J$ is proper and by Proposition 2.3 the interval $A\setminus \{x\}$ is not closed in $X'$ .

Therefore, the interval $I'=A'\cup B'$ is a maximal left comb in $X'$ of type $5$ with $A'=K_A\cup P'$ and $B'=B$ . It is not difficult to check (by Proposition 5.2) that the correspondence between $I$ and $I'$ is a bijection. Moreover, since $A=K_A\cup P$ is closed in $X$ , we obtain by Proposition 5.2 that $K_A\cup M'$ is closed in $V'$ . It follows by Fact 5.4 that $a(x,y_1)=a(x',y_1)$ and consequently thar $F(I)=a(B\cup \{x\})=a(B'\cup \{x'\})=F(I')$ . Hence, by Proposition 4.1 we have $\chi _0(I)=\chi _0(I')$ .

6. Main proof

The proof of Theorem 1.3 follows by a simple induction of the following stepping up theorem.

Theorem 6.1. Let $m\geqslant 100kr^2$ , $N=\min _{0\leqslant j\leqslant k}\{ D_{r-1}^{{\textrm{smp}}}(\frac{1}{5}k^{-1/2}m^{1/2},j)\}$ be integers and let $\{\varphi _i\}_{r-1\leqslant i \leqslant k+r-1}$ be a family of colourings $\varphi _i\;:\;[N]^{(i)}\rightarrow \{0,1\}$ without a monochromatic copy of a simple $(r-1,\frac{1}{5}k^{-1/2}m^{1/2},i-r+1)$ -daisy. Then, the colouring $\chi \;:\;[2^N]^{(k+r)}\rightarrow \{0,1\}$ described in Subsection 3.3 does not contain a monochromatic simple $(r,m,k)$ -daisy.

Proof. Suppose by contradiction that there exists a monochromatic simple $(r,m,k)$ -daisy $H$ in $[2^N]^{(k+r)}$ with kernel $K=K_0\cup K_1$ of size $k$ , universe of petals $M$ of size $m$ and $K_0\lt M\lt K_1$ . By Lemma 5.1, we obtain a monochromatic simple $(r,\frac{1}{2}k^{-1/2}m^{1/2},k)$ -daisy $H'$ with same kernel and universe of petals $M'=\{y_1,\ldots,y_{m^{\prime}}\} \subseteq M$ of size $m^{\prime}=\frac{1}{2}k^{-1/2}m^{1/2}$ satisfying that either $M'$ is a closed interval in $V'=V(H')$ or $M'$ is part of the “teeth” of a maximal comb $I=A\cup B$ , i.e., $M'\subseteq B$ .

Note that every edge $X\in H'$ can be written in the form $X=K_0\cup P\cup K_1$ where $P\in (M')^{(r)}$ is a petal of $H'$ . Since $H'$ is monochromatic, we have that

\begin{align*} \chi (X)=\sum _{I\subseteq{\mathcal{I}}_X} \chi _0(I) \pmod{2} \end{align*}

is constant, for every $X \in H'$ . Thus, by Propositions 5.5 and 5.6, there exists a unique interval $J\subseteq [k+r]$ such that for every $X \in E(H')$ the interval $X_{J}=\{x_j\}_{j\in J}$ is maximal comb with colour $\chi _0(X_J)$ constant.

As in the proof give in Subsection 3.1, our goal is to use the fact that the combs $X_J$ are monochromatic with respect to $\chi _0$ to find a large $1$ -comb. Let $t=|J|-r$ and let $G$ be the simple $(r,\frac{1}{2}k^{-1/2}m^{1/2},t)$ -daisy constructed by taking as edges the combs $X_J$ for every edge $X \in H'$ . To be more precise, let $K_J$ be the subset of $t$ vertices of $K_0\cup K_1$ in the interval $J$ . Note that every comb $X_J$ can be partitioned into $X_J=K_J\cup P$ , where $P\subseteq M'$ is the petal of $X$ . We define $G$ as the simple $(r,\frac{1}{2}k^{-1/2}m^{1/2},t)$ -daisy given by

\begin{align*} V(G)&=K_J\cup M'\\[5pt] G&=\{X_{J}\;:\: X\in H'\} \end{align*}

As discussed in the last paragraph the $(t+r)$ -graph $G$ is monochromatic under the colouring $\chi _0$ . The following lemma is a variant of Proposition 3.1 for simple daisies.

Proposition 6.2. If $M'$ is a closed interval in $V(H')$ and $G$ is monochromatic with respect to the colouring $\chi _0$ , then there exists an interval $M''\subseteq M'$ of size $|M''|\geqslant (|M'|-r+6)/2$ such that $M''$ is a $1$ -comb in $V'$ .

Proof. By Proposition 5.5, all the edges $X_J$ of $G$ are combs of the same type. Thus we may assume without loss of generality that $X_J$ is either a broken comb or a $\ell$ -left comb in $X$ . Since $M'$ is closed, by the same proposition we obtain that $A^{X_J}\subseteq P$ and consequently $K_J \subseteq B^{X_J}$ for every edge $X \in H'$ . Therefore, we either have $K_J=\emptyset$ (and $X_J$ is a broken comb) or $P\lt K_J$ for every $X$ , which implies that $K_J\subseteq K_1$ , i.e., $M'\lt K_J$ . Moreover, if $X_J$ is an $\ell$ -left comb, then $A^{X_J}\subseteq P$ implies that $\ell \leqslant r$ . This implies that $X_J$ is either of type $1$ , $3$ or $4$ .

We split the proof into two cases according to the size of $t=|K_J|$ . Write $M'=\{y_1,\ldots,y_{m^{\prime}}\}$ , $K_J=\{y_{m^{\prime}+1},\ldots,y_{m^{\prime}+t}\}$ (if $K_J\neq \emptyset$ ) and $\delta _i^G=\delta (y_i,y_{i+1})$ for $1\leqslant i \leqslant m^{\prime}+t-1$ .

Case 1: $0\leqslant t\leqslant r-2$ .

Since $|X_J|=r+t\leqslant 2r-2$ , we obtain that $X_J$ is either of type $1$ or $3$ . The proof follow the same lines of the proof of Proposition 3.1. Write $P=\{y_{i_1},\ldots,y_{i_r}\}\subseteq M'$ for indices $1\leqslant i_1\lt \ldots \lt i_r\leqslant m^{\prime}$ . Suppose without loss of generality that $G$ is monochromatic of colour $0$ , i.e., $\chi _0(X_J)=0$ for every $X_J \in G$ . Thus, by the definition of $\chi _0$ for combs of type $1$ and $3$ , we do not have that $\delta _{i_{r-3}}^G\lt \delta _{i_{r-2}}^G\gt \delta _{i_{r-1}}^G$ . In particular, because $X_J$ is arbitrary, this implies that there are no indices $r-3\leqslant p\lt q\lt s \leqslant m^{\prime}-1$ such that $\delta _p^G\lt \delta _q^G\gt \delta _s^G$ . That is, the sequence $\{\delta _i^G\}_{i=r-3}^{m^{\prime}-1}$ has no local maximum.

Now the same argument as in Proposition 3.1 gives that there exists an interval $M''=\{y_p,\ldots,y_q\}\subseteq M'$ such that $\{\delta _i^G\}_{i=p}^{q-1}$ is monotone and $|M''|\geqslant (|M'|-r+6)/2$ . By the definition given in Example 2.5, it follows that $M''$ is a $1$ -comb.

Case 2: $t\geqslant r-1$ .

In this case $X_J$ is a left comb of type 4 for every $X_J\in G$ , since $|X_J|=|P|+|K_J|=r+t\geqslant 2r-1$ . Suppose without loss of generality that $G$ is monochromatic of colour $0$ and that $\varphi _t(\{\delta _{m^{\prime}}^G,\ldots,\delta _{m^{\prime}+t-1}^G\})=0$ . Let $u=a(\!\min (M'),\max (M'))$ . Fact 5.4 applied to $M'$ gives us that $\delta (z,y_{m^{\prime}+1})=\delta (u,y_{m^{\prime}+1})$ for every $z\in M'$ . In particular, this implies that $\delta (z,y_{m^{\prime}+1})=\delta _{m^{\prime}}^G$ for every $z\in M'$ .

Write $P=\{y_{i_1},\ldots,y_{i_r}\}\subseteq M'$ with $1\leqslant i_1\lt \ldots \lt i_r\leqslant m^{\prime}$ and $X_J=P\cup K_J=\{y_{i_1},\ldots,y_{i_r},y_{m^{\prime}},\ldots,y_{m^{\prime}+t-1}\}$ . Since $\chi _0(X_J)=0$ , $\delta (y_{i_j},y_{m^{\prime}+1})=\delta _{m^{\prime}}^G$ for every $1\leqslant j\leqslant r$ and $\varphi _t(\{\delta _{m^{\prime}}^G,\ldots,\delta _{m^{\prime}+t-1}^G\})+1=1$ we obtain by the definition of $\chi _0$ for combs of type $4$ that the inequality $\delta _{i_{r-3}}^G\lt \delta _{i_{r-2}}^G\gt \delta _{i_{r-1}}^G$ cannot hold. Because $X_J$ is arbitrary, we have that there are no indices $r-3\leqslant p\lt q\lt s \leqslant m^{\prime}-1$ such that $\delta _p^G\lt \delta _q^G\gt \delta _s^G$ . Hence, similarly as in Case $1$ we find an interval $M''\subseteq M'$ of size at least $(|M'|-r+6)/2$ such that $M''$ is a $1$ -comb in $V'$ .

To finish the proof of Theorem 1.3 we are going to show now that if $G$ is monochromatic with respect to $\chi _0$ , then there exists a monochromatic simple $(r-1,\frac{1}{5}k^{-1/2}m^{1/2},j)$ -daisy in $\delta (G)\subseteq [N]$ with respect to some colouring $\varphi _{j+r-1}$ . The proof is split into several cases depending on the structure of $H'$ given by Lemma 5.1 and on the possible types of $X_J$ .

Case 1: $M'$ is a closed interval in $V'$ .

As usual, we may assume that an edge of $G$ is either a broken comb or a left comb. By Proposition 6.2, there exists an interval $M''\subseteq M'$ of size $h=(|M'|-r+6)/2$ such that $M''$ is a $1$ -comb. Consider the colouring $\chi _0$ over the monochromatic subdaisy $G'\;:\!=\;G[K_J\cup M'']\subseteq G$ . As in the proof of Proposition 6.2, we have that either $X_J$ is a broken comb and $t=|K_J|=0$ or $X_J$ is an $\ell$ -left comb with $\ell \leqslant r$ and $M'\lt K_J$ . Write $M''=\{y_{i_1},\ldots,y_{i_h}\}$ with $1\leqslant i_1\lt \ldots \lt i_h\lt m^{\prime}$ , $K_J=\{y_{m^{\prime}+1},\ldots,y_{m^{\prime}+t}\}$ (if $K_J\neq \emptyset$ ) and $\delta _i^G=\delta (y_i,y_{i+1})$ .

Let $X_J=P\cup K_J=\{x_1,\ldots,x_r\}\cup \{y_{m^{\prime}+1},\ldots,y_{m^{\prime}+t}\}$ be an arbitrary edge from $G'$ with $P\subseteq (M'')^{(r)}$ . Note that since $M''$ is a $1$ -comb, then $\delta (x_{r-3},x_{r-2})$ , $\delta (x_{r-2},x_{r-1})$ , $\delta (x_{r-1},x_r)$ forms a monotone sequence. Moreover, as discussed in Proposition 6.2, the comb $X_J$ is of type $1$ , $3$ or $4$ . Thus, by the colouring defined in Subsection 3.3, we have $\chi _0(X_J)=\varphi _{r+t-1}(\delta (X_J))$ , i.e., the colour of $X_J$ is determined by its full projection on the levels $[N]$ .

Let $u=a(\!\min (M'),\max (M'))$ . Note that since $M'$ is closed, by Fact 5.4 we have that $a(x_r,y_{m^{\prime}+1})=a(u,y_{m^{\prime}+1})=a(y_{m^{\prime}},y_{m^{\prime}+1})$ . Consequently, we have that $\delta (x_r,y_{m^{\prime}+1})=\delta ^G_{m^{\prime}}$ , which implies that $\delta (X_J)=\{\delta (x_1,x_2),\ldots,\delta (x_{r-1},x_r)\}\cup \{\delta _{m^{\prime}}^G,\ldots,\delta _{m^{\prime}+t-1}^G\}$ . Therefore the projection of all the edges of $X_J$ forms a simple $(r-1,h-1,t)$ -daisy $D\subseteq [N]$ with universe of petals $\delta (M'')$ an kernel $K_D=\{\delta _{m^{\prime}}^G,\ldots,\delta _{m^{\prime}+t-1}^G\}$ satisfying $K_D\lt \delta (M'')$ (see Figure 17). By the fact that $G'$ is monochromatic with respect to $\chi _0$ , we have that $D$ is a monochromatic simple $(r-1,h-1,t)$ -daisy with respect to the colouring $\varphi _{r+t-1}$ . This leads to a contradiction since $h-1\geqslant (m^{\prime}-r+4)/2\geqslant \frac{1}{5}k^{-1/2}m^{1/2}$ for $m\geqslant 100kr^2$ and $\varphi _{r+t-1}$ has no monochromatic simple $(r-1,\frac{1}{5}k^{-1/2}m^{1/2},t)$ -daisy.

Case 2: There exists a maximal comb $I=A\cup B$ in $V(H')$ such that $M'\subseteq B$

We may assume without loss of generality that $I=A\cup B$ is a left comb. Write $A=\{y_1,\ldots,y_{\ell }\}$ , $B_0=B\cap K_0=\{y_{\ell +1},\ldots,y_{\ell +p}\}$ , $M'=\{y_{\ell +p+1},\ldots,y_{\ell +p+m^{\prime}}\}$ and $B_1=B\cap K_1=\{y_{\ell +p+m^{\prime}+1},\ldots,y_{\ell +p+m^{\prime}+t}\}$ (as in Figure 18). By Proposition 5.5, $V(G)=I$ and all the edges $X_J=A^{X_J}\cup B^{X_J} \in G$ are maximal left comb of same type with $A^{X_J}=A$ , $B^{X_J}=B_0\cup P\cup B_1$ and $A\lt B_0\lt P\lt B_1$ . In particular, this implies that $|B^{X_J}|\geqslant r$ and $X_J$ is of type $3$ , $4$ or $5$ . We split the cases depending on the type of $X_J$ . Let $\delta _i^G=\delta (y_i,y_{i+1})$ for $1\leqslant i \leqslant \ell +p+m^{\prime}+t-1$ . For an arbitrary edge $X_J\in G$ , write $X_J=\{x_1,\ldots,x_{\ell +p+r+t}\}$ with $x_i=y_i$ for $1\leqslant i \leqslant \ell +p$ , $P=\{x_{\ell +p+1},\ldots,x_{\ell +p+r}\}\subseteq M'$ and $x_{\ell +p+r+i}=y_{\ell +p+m^{\prime}+i}$ for $1\leqslant i \leqslant t$ and let $\delta _i^{X_J}=\delta (x_i,x_{i+1})$ for $1\leqslant i \leqslant \ell +p+r+t-1$ .

Figure 17. Case 1 of Theorem 6.1.

Figure 18. Auxiliary tree of $G$ in Case $2$ .

Case 2.1: $X_J$ is of type $3$ .

Recall that if $X_J$ is of type $3$ , then $|A^{X_J}|\leqslant r$ and $r\leqslant |X_J|=|A^{X_J}|+|B^{X_J}|\leqslant 2r-2$ . Because $|B^{X_J}|\geqslant r$ , we obtain that $|A^{X_J}|\leqslant r-2$ . This implies that $\{x_{r-1},x_{r}\}\subseteq B^{X_J}$ and consequently $\delta _{r-3}^{X_J}\gt \delta _{r-2}^{X_J}\gt \delta _{r-1}^{X_J}$ . Therefore, by the fact that $|\delta (X_J)|\geqslant |\delta (\{x_\ell,\ldots,x_{\ell +p+r+t}\})|=p+r+t\geqslant r$ , we obtain that $\chi _0(X_J)=\varphi _{|\delta (X_J)|}(\delta (X_J))$ .

Note that

\begin{align*} \delta (X_J)&=\{\delta _1^G, \ldots, \delta _{\ell +p-1}^G\}\cup \{\delta _{\ell +p}^{X_J},\ldots,\delta _{\ell +p+r-1}^{X_J}\}\cup \{\delta _{\ell +p+m^{\prime}}^G,\ldots,\delta _{\ell +p+m^{\prime}+t-1}^G\}\\[5pt] &=\delta (A\cup B_0)\cup \{\delta _{\ell +p}^{X_J},\ldots,\delta _{\ell +p+r-1}^{X_J}\}\cup \delta (\{y_{\ell +p+m^{\prime}}\}\cup B_1). \end{align*}

Hence, the projection of the edges of $G$ is a simple $(r,m^{\prime},|\delta (A\cup B_0)|+t)$ -daisy with kernel $\delta (A\cup B_0)\cup \delta (\{y_{\ell +p+m^{\prime}}\}\cup B_1)$ (as in Figure 19). Since $G$ is monochromatic with respect to $\chi _0$ , we obtain that $\delta (G)\subseteq [N]$ is monochromatic with respect to the projection colouring, which is a contradiction because any simple $(r,m^{\prime},|\delta (A\cup B_0)|+t)$ -daisy contains a simple $(r-1,m^{\prime}-1,|\delta (A\cup B_0)|+t+1)$ -subdaisy and $m^{\prime}-1\geqslant \frac{1}{5}k^{-1/2}m^{1/2}$ .

Figure 19. Case $2.1$ of Theorem 6.1.

Case 2.2: $X_J$ is of type $4$ .

If $X_J$ is of type 4, then $|A^{X_J}|\leqslant r$ and $|X_J|=|A^{X_J}|+|B^{X_J}|\geqslant 2r-1$ . We split the proof into two subcases depending on the sequence formed by $\{\delta _{r-3}^{X_J},\delta _{r-2}^{X_J},\delta _{r-1}^{X_J}\}$ :

Case 2.2.a: Either $\delta _{r-3}^{X_J}\gt \delta _{r-2}^{X_J}\lt \delta _{r-1}^{X_J}$ or $\delta _{r-3}^{X_J}\lt \delta _{r-2}^{X_J}\gt \delta _{r-1}^{X_J}$ .

Suppose without loss of generality that $\delta _{r-3}^{X_J}\gt \delta _{r-2}^{X_J}\lt \delta _{r-1}^{X_J}$ . Hence, by the colouring definition, we have $\chi _0(X_J)=\varphi _{\ell +p+t}(\{\delta _r^{X_J},\ldots,\delta _{\ell +p+r+t-1}^{X_J}\})$ . Thus, we just need to look at the projection $\{\delta _r^{X_J},\ldots,\delta _{\ell +p+r+t-1}^{X_J}\}$ for every $X_J \in G$ . Note that $\delta _{r-3}^{X_J}\gt \delta _{r-2}^{X_J}\lt \delta _{r-1}^{X_J}$ implies that $|A^{X_J}|\geqslant r-1$ . Indeed, by the same argument made in Case 2.1, if $|A^{X_J}|\leqslant r-2$ , then $\delta _{r-3}^{X_J}\gt \delta _{r-2}^{X_J}\gt \delta _{r-1}^{X_J}$ , which is a contradiction. So, it follows that $r-1\leqslant |A^{X_J}|=\ell \leqslant r$ .

Suppose that $|A^{X_J}|=r-1$ and $B_0=\emptyset$ , i.e., $\ell =r-1$ , $p=0$ and $M'=\{y_r,\ldots,y_{r+m^{\prime}-1}\}$ . Then the projection of the relevant part of an edge $X_J$ can be written as

\begin{align*} \{\delta _r^{X_J},\ldots,\delta _{\ell +p+r+t-1}^{X_J}\}&=\{\delta _r^{X_J}. \ldots, \delta _{2r-2}^{X_J}\}\cup \{\delta _{r+m^{\prime}-1}^G,\ldots,\delta _{r+m^{\prime}+t-2}^G\}\\[5pt] &=\delta (P)\cup \{\delta _{r+m^{\prime}-1}^G,\ldots,\delta _{r+m^{\prime}+t-2}^G\}, \end{align*}

since $\delta _{2r-1+i}^{X_J}=\delta _{\ell +p+r+i}^{X_J}=\delta _{\ell +p+m^{\prime}+i}^G=\delta _{2r+m^{\prime}-1+i}^G$ for $0\leqslant i \leqslant t-1$ . Therefore, the projection of the edges $X_J$ is a simple $(r-1,m^{\prime}-1,t)$ -daisy with kernel $\{\delta _{r+m^{\prime}-1}^G,\ldots,\delta _{r+m^{\prime}+t-2}^G\}$ (see Figure 20). Because $G$ is monochromatic under $\chi _0$ , the projection is also monochromatic under $\varphi _{r+t-1}$ , which is a contradiction.

Now suppose that $|A^{X_J}\cup B_0|=\ell +p\geqslant r$ . The relevant projection of $X_J$ in this case would be

\begin{align*} \{\delta _r^{X_J},\ldots,\delta _{\ell +p+r+t-1}^{X_J}\}=\{\delta _r^G,\ldots, \delta _{\ell +p-1}^G\}&\cup \{\delta _{\ell +p}^{X_J},\ldots,\delta _{\ell +p+r-1}^{X_J}\}\\[5pt] &\cup \{\delta _{\ell +p+m^{\prime}}^G,\ldots,\delta _{\ell +p+m^{\prime}+t-1}^G\}, \end{align*}

where the set $\{\delta _r^G,\ldots,\delta _{\ell +p-1}^G\}$ is empty for $\ell +p=r$ . Since $\{\delta _{\ell +p}^{X_J},\ldots,\delta _{\ell +p+r-1}^{X_J}\}=\delta (\{y_{\ell +p}\}\cup P)$ , we obtain that the projection of all edges $X_J$ is a simple $(r,m^{\prime}, \ell +p+t-r)$ -daisy with kernel $\{\delta _r^G,\ldots,\delta _{\ell +p-1}^G\} \cup \{\delta _{\ell +p+m^{\prime}}^G,\ldots,\delta _{\ell +p+m^{\prime}+t-1}^G\}$ . Because every simple $(r,m^{\prime},\ell +p+t-r)$ -daisy contains an $(r-1,m^{\prime}-1,\ell +p+t-r+1)$ -daisy and the projection is monochromatic with respect to $\varphi _{\ell +p+t-1}$ , we obtain a monochromatic simple $(r-1,\frac{1}{5}k^{-1/2}m^{1/2},\ell +p+t-r+1)$ -daisy, which is a contradiction.

Case 2.2.b: Either $\delta _{r-3}^{X_J}\lt \delta _{r-2}^{X_J}\lt \delta _{r-1}^{X_J}$ or $\delta _{r-3}^{X_J}\gt \delta _{r-2}^{X_J}\gt \delta _{r-1}^{X_J}$ .

In this case we obtain that $\chi _0(X_J)=\varphi _{|\delta (X_J)|}(\delta (X_J))$ , i.e., the colouring of $\chi _0$ is just the colouring of the projection of $X_J$ . The proof now follows similarly as in Case 2.1.

Case 2.3: $X_J$ is of type $5$ .

Figure 20. Case $2.2$ of Theorem 6.1 when $|A|=r-1$ .

Figure 21. Case $2.3$ of Theorem 6.1.

If $X_J$ is of type $5$ , then $|A^{X_J}|\gt r$ and $|B^{X_J}|=p+r+t\geqslant r$ . By the colouring definition, we have $\chi _0(X_J)=\varphi _{p+r+t}(\{\delta _{\ell }^{X_J},\ldots,\delta _{\ell +p+r+t-1}^{X_J}\})$ . The projection here can be rewritten as

\begin{align*} \{\delta _{\ell }^{X_J},\ldots,\delta _{\ell +p+r+t-1}^{X_J}\}=\{\delta _{\ell }^G,\ldots,\delta _{\ell +p-1}^G\}&\cup \{\delta (\{y_{\ell +p}\}\cup P) \\[5pt] &\cup \{\delta _{\ell +p+m^{\prime}}^G,\ldots, \delta _{\ell +p+m^{\prime}+t-1}^G\}. \end{align*}

Thus, the relevant projection over all edges $X_J$ is a simple $(r,m^{\prime},p+t)$ -daisy with kernel $\{\delta _{\ell }^G,\ldots,\delta _{\ell +p-1}^G\}\cup \{\delta _{\ell +p+m^{\prime}}^G,\ldots, \delta _{\ell +p+m^{\prime}+t-1}^G\}$ (see Figure 21). Therefore, by the same argument did in the previous cases, we reach a contradiction since there is no monochromatic simple $(r-1,\frac{1}{5}k^{-1/2}m^{1/2},p+t+1)$ -daisy in the colouring $\varphi _{p+r+t}$ .

Proof of Theorem 1.3. We will prove by induction on the size of $r$ that there exists an absolute positive constants $c$ and $c'$ not depending on $k$ and $r$ such that

\begin{align*} D_r^{{\textrm{smp}}}(m,k)=t_{r-2}(c'(5\sqrt{k})^{2^{5-r}-4}m^{2^{4-r}})\geqslant t_{r-2}(ck^{2^{4-r}-2}m^{2^{4-r}}) \end{align*}

holds for $k\geqslant 1$ and $m\geqslant (25k)^{2^{r}-1}$ . For $r=3$ , the result follows by the next proposition given in [5].

Proposition 6.3 ([5], Proposition 1.2). There exists a positive constant $c'$ not depending on $k$ such that

\begin{align*} D_3(m,k)\geqslant 2^{c'm^2} \end{align*}

holds for $m\gt 3$ .

Now suppose that $r\geqslant 4$ and that for any integer $\ell \lt r$ the induction hypothesis is satisfied, i.e.,

\begin{align*} D_{\ell }^{{\textrm{smp}}} (m,k)\geqslant t_{\ell -2}(c'(5\sqrt{k})^{2^{5-\ell }-4}m^{2^{4-\ell }}) \end{align*}

for $m\geqslant (25k)^{2^{\ell }-1}$ and $k\geqslant 1$ . Let $N=\min _{0\leqslant i \leqslant k-1}{D_{r-1}^{{\textrm{smp}}}(\frac{1}{5}k^{-1/2}m^{1/2},i)}$ . For $i=0$ , by equation (2) we have that

\begin{align*} D_{r-1}^{{\textrm{smp}}}\left (\frac{1}{5}k^{-1/2}m^{1/2},0\right )\geqslant R_{r-1}\left (\frac{1}{5}k^{-1/2}m^{1/2}\right )\geqslant t_{r-2}(c_1k^{-1}m) \end{align*}

for a positive constant $c_1$ . Since $m\geqslant (25k)^{2^r-1}$ , we obtain that $\frac{1}{5}k^{-1/2}m^{1/2}\geqslant (25k)^{2^{r-1}-1}$ . Thus, by induction hypothesis we also have that

\begin{align*} D_{r-1}^{{\textrm{smp}}}\left (\frac{1}{5}k^{-1/2}m^{1/2},i\right )\geqslant t_{r-3}\left (c'(5\sqrt{i})^{2^{6-r}-4}\left (\frac{1}{5}k^{-1/2}m^{1/2}\right )^{2^{5-r}}\right ), \end{align*}

for $i\geqslant 1$ . Therefore,

\begin{align*} N &\geqslant \min \left \{t_{r-2}(c_1k^{-1}m),\min _{1\leqslant i \leqslant k}\left \{t_{r-3}\left (c'(5\sqrt{i})^{2^{6-r}-4}\left (\frac{1}{5}k^{-1/2}m^{1/2}\right )^{2^{5-r}}\right )\right \}\right \}\\[5pt] &\geqslant t_{r-3}(c'(5\sqrt{k})^{2^{5-r}-4}m^{2^{4-r}}). \end{align*}

Finally, Theorem 6.1, applied to $m\geqslant (25k)^{2^r-1}\geqslant 100kr^2$ , gives us that

\begin{align*} D_r^{{\textrm{smp}}}(m,k)\geqslant 2^N\geqslant t^{r-2}(c'(5\sqrt{k})^{2^{5-r}-4}m^{2^{4-r}}). \end{align*}