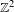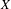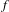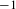Survey Article
Open problems and questions about geodesics
- Part of:
-
- Published online by Cambridge University Press:
- 06 December 2019, pp. 641-684
-
- Article
- Export citation
Sobolev regularity of solutions of the cohomological equation
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2020, pp. 685-789
-
- Article
- Export citation
Original Article
A family of minimal and renormalizable rectangle exchange maps
-
- Published online by Cambridge University Press:
- 27 November 2019, pp. 790-817
-
- Article
- Export citation
On Baire measurable colorings of group actions
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2020, pp. 818-845
-
- Article
- Export citation
Frequent universality criterion and densities
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2019, pp. 846-868
-
- Article
- Export citation
Support stability of maximizing measures for shifts of finite type
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2019, pp. 869-880
-
- Article
- Export citation
A construction of subshifts and a class of semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2020, pp. 881-905
-
- Article
-
- You have access
- Open access
- Export citation
An autocorrelation and a discrete spectrum for dynamical systems on metric spaces
- Part of:
-
- Published online by Cambridge University Press:
- 27 November 2019, pp. 906-922
-
- Article
-
- You have access
- Open access
- Export citation
An example of a planar Anosov diffeomorphism without fixed points
- Part of:
-
- Published online by Cambridge University Press:
- 06 December 2019, pp. 923-934
-
- Article
- Export citation
The Ellis semigroup of certain constant-length substitutions
- Part of:
-
- Published online by Cambridge University Press:
- 06 December 2019, pp. 935-960
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 41 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 February 2021, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 41 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 February 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation