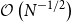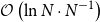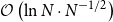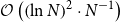1. Introduction
We consider the following two-block separable convex optimization problem with linear equality constraints:
where
![]() $A \in \mathbb{R}^{n \times n_1}, B \in \mathbb{R}^{n \times n_2}, b \in \mathbb{R}^n, \mathcal{X} \subseteq \mathbb{R}^{n_1}$
, and
$A \in \mathbb{R}^{n \times n_1}, B \in \mathbb{R}^{n \times n_2}, b \in \mathbb{R}^n, \mathcal{X} \subseteq \mathbb{R}^{n_1}$
, and
![]() $\mathcal{Y} \subseteq \mathbb{R}^{n_2}$
are closed convex sets, and
$\mathcal{Y} \subseteq \mathbb{R}^{n_2}$
are closed convex sets, and
![]() ${\theta _2}:{\mathbb{R}^{{n_2}}} \to \mathbb{R} \cup \left\{ { + \infty } \right\}$
is a convex function (not necessarily smooth).
${\theta _2}:{\mathbb{R}^{{n_2}}} \to \mathbb{R} \cup \left\{ { + \infty } \right\}$
is a convex function (not necessarily smooth).
![]() ${\theta _1}:{\mathbb{R}^{{n_1}}} \to \mathbb{R}$
is a convex function and is smooth on an open set containing
${\theta _1}:{\mathbb{R}^{{n_1}}} \to \mathbb{R}$
is a convex function and is smooth on an open set containing
![]() $\mathcal{X}$
, but has its specific structure; in particular, we assume that there is a stochastic first-order oracle (SFO) for
$\mathcal{X}$
, but has its specific structure; in particular, we assume that there is a stochastic first-order oracle (SFO) for
![]() $\theta_1$
, which returns a stochastic gradient
$\theta_1$
, which returns a stochastic gradient
![]() $G\left( {x,\xi } \right)$
at x, where
$G\left( {x,\xi } \right)$
at x, where
![]() $\xi$
is a random variable whose distribution is supported on
$\xi$
is a random variable whose distribution is supported on
![]() $\Xi \subseteq \mathbb{R}^d$
, satisfying
$\Xi \subseteq \mathbb{R}^d$
, satisfying
 \begin{equation*} \begin{aligned} {\rm (a}) \ &\mathbb{E}\left[ {G\left( {x,\xi } \right)} \right] = \nabla {\theta _1}\left( x \right) , \text{and}\\ {\rm (b}) \ &\mathbb{E}\left[ {{{\left\| {G\left( {x,\xi } \right) - \nabla {\theta _1}\left( x \right)} \right\|}^2}} \right] \le {\sigma ^2}, \end{aligned}\end{equation*}
\begin{equation*} \begin{aligned} {\rm (a}) \ &\mathbb{E}\left[ {G\left( {x,\xi } \right)} \right] = \nabla {\theta _1}\left( x \right) , \text{and}\\ {\rm (b}) \ &\mathbb{E}\left[ {{{\left\| {G\left( {x,\xi } \right) - \nabla {\theta _1}\left( x \right)} \right\|}^2}} \right] \le {\sigma ^2}, \end{aligned}\end{equation*}
where
![]() $\sigma > 0$
is some constant. In addition, we make the following assumptions throughout the paper: (i) The solution set of (1) is assumed to be nonempty, (ii) the gradient of
$\sigma > 0$
is some constant. In addition, we make the following assumptions throughout the paper: (i) The solution set of (1) is assumed to be nonempty, (ii) the gradient of
![]() $\theta_1$
is L-Lipschitz continuous for some
$\theta_1$
is L-Lipschitz continuous for some
![]() $L > 0$
, i.e.,
$L > 0$
, i.e.,
![]() $\left\| \nabla{\theta _1}\left( x \right) - \nabla{\theta _2}\left( y \right) \right\|$
$\left\| \nabla{\theta _1}\left( x \right) - \nabla{\theta _2}\left( y \right) \right\|$
![]() $\le L\left\| {x - y} \right\|$
for any
$\le L\left\| {x - y} \right\|$
for any
![]() $x, y \in \mathcal{X}$
, (iii) y-subproblem has a minimizer at each iteration. As a linearly constrained convex optimization problem, though the model (1) is special, it is rich enough to characterize many optimization problems arising from various application fields, such as machine learning, image processing, and signal processing. In these fields, a typical scenario is that one of the functions represents a data fidelity term and the other function is a regularization term.
$x, y \in \mathcal{X}$
, (iii) y-subproblem has a minimizer at each iteration. As a linearly constrained convex optimization problem, though the model (1) is special, it is rich enough to characterize many optimization problems arising from various application fields, such as machine learning, image processing, and signal processing. In these fields, a typical scenario is that one of the functions represents a data fidelity term and the other function is a regularization term.
Without considering the specific structure of
![]() $\theta_1$
, i.e., the function value and gradient information is readily available, a classical method for solving problem (1) is the alternating direction method of multipliers (ADMM). ADMM was originally proposed by Glowinski and Marroco (Reference Glowinski and Marroco1975), and Gabay and Mercier (Reference Gabay and Mercier1976), which is a Gauss-Seidel implementation of augmented Lagrangian method (Glowinski, Reference Glowinski2014) or an application of Douglas-Rachford splitting method on the dual problem of (1) (Eckstein and Bertsekas, Reference Eckstein and Bertsekas1992). For both convex and non-convex problems, there are extensive studies on the theoretical properties of ADMM. In particular, for convex optimization problems, theoretical results on convergence behavior are abundant, whether global convergence, sublinear convergence rate, or linear convergence rate, see, e.g., Eckstein and Bertsekas (Reference Eckstein and Bertsekas1992); He and Yuan (Reference He and Yuan2012); Monteiro and Svaiter (Reference Monteiro and Svaiter2013); He and Yuan (Reference He and Yuan2015); Deng and Yin (Reference Deng and Yin2016); Yang and Han (Reference Yang and Han2016); Han et al. (2016). Recently, ADMM has been studied on non-convex models satisfying the KL inequality or other similar properties, see, e.g., Li and Pong (Reference Li and Pong2015); Wang et al. (Reference Wang, Yin and Zeng2019); Jiang et al. (Reference Jiang, Lin, Ma and Zhang2019); Zhang and Luo (Reference Zhang and Luo2020). For a thorough understanding on some recent developments of ADMM, one can refer to a survey (Han, Reference Han2022). However, when the objective function value (or its gradient) in (1) is computationally costly or even impossible to compute, we can only access some noisy information and deterministic ADMM does not work. Such a setting is exactly what the stochastic programming (SP) model considers. In SP, the objective function is often in the form of expectation. In this case, getting the full function value or gradient information is impractical. To tackle this problem, Robbins and Monro originally introduced the stochastic approximation (SA) approach in 1951 (Robbins and Monro, Reference Robbins and Monro1951). Since then, SA has gone through many developments; for more detail, readers are referred to a series of works by Nemirovski, Ghadimi, and Lan, etc, see, e.g., Nemirovski et al. (Reference Nemirovski, Juditsky, Lan and Shapiro2009); Ghadimi and Lan (Reference Ghadimi and Lan2012); Lan (Reference Lan2012); Ghadimi and Lan (Reference Ghadimi and Lan2013); Ghadimi et al. (Reference Ghadimi, Lan and Zhang2016). As for solving problem (1), motivated by the SA, some stochastic ADMM type algorithms have been proposed recently, see, e.g., Ouyang et al. (Reference Ouyang, He, Tran and Gray2013); Suzuki (Reference Suzuki2013, Reference Suzuki2014); Zhao et al. (Reference Zhao, Yang, Zhang and Li2015); Gao et al. (Reference Gao, Jiang and Zhang2018). Note that in these works, only the basic iterative scheme of ADMM was considered. It is well-known that incorporating an acceleration factor into the subproblem and the update on the dual variables often improves the algorithmic performance, which is the idea of generalized ADMM (Eckstein and Bertsekas, Reference Eckstein and Bertsekas1992, Fang et al., Reference Fang, He, Liu and Yuan2015). In this paper, we study generalized ADMM in the stochastic setting. In particular, we propose a stochastic linearized generalized ADMM (SLG-ADMM) for solving two-block separable stochastic optimization problem (1) and analyze corresponding worst-case convergence rate by means of the framework of variational inequality. Moreover, we establish the large deviation properties of SLG-ADMM under certain light-tail assumptions.
$\theta_1$
, i.e., the function value and gradient information is readily available, a classical method for solving problem (1) is the alternating direction method of multipliers (ADMM). ADMM was originally proposed by Glowinski and Marroco (Reference Glowinski and Marroco1975), and Gabay and Mercier (Reference Gabay and Mercier1976), which is a Gauss-Seidel implementation of augmented Lagrangian method (Glowinski, Reference Glowinski2014) or an application of Douglas-Rachford splitting method on the dual problem of (1) (Eckstein and Bertsekas, Reference Eckstein and Bertsekas1992). For both convex and non-convex problems, there are extensive studies on the theoretical properties of ADMM. In particular, for convex optimization problems, theoretical results on convergence behavior are abundant, whether global convergence, sublinear convergence rate, or linear convergence rate, see, e.g., Eckstein and Bertsekas (Reference Eckstein and Bertsekas1992); He and Yuan (Reference He and Yuan2012); Monteiro and Svaiter (Reference Monteiro and Svaiter2013); He and Yuan (Reference He and Yuan2015); Deng and Yin (Reference Deng and Yin2016); Yang and Han (Reference Yang and Han2016); Han et al. (2016). Recently, ADMM has been studied on non-convex models satisfying the KL inequality or other similar properties, see, e.g., Li and Pong (Reference Li and Pong2015); Wang et al. (Reference Wang, Yin and Zeng2019); Jiang et al. (Reference Jiang, Lin, Ma and Zhang2019); Zhang and Luo (Reference Zhang and Luo2020). For a thorough understanding on some recent developments of ADMM, one can refer to a survey (Han, Reference Han2022). However, when the objective function value (or its gradient) in (1) is computationally costly or even impossible to compute, we can only access some noisy information and deterministic ADMM does not work. Such a setting is exactly what the stochastic programming (SP) model considers. In SP, the objective function is often in the form of expectation. In this case, getting the full function value or gradient information is impractical. To tackle this problem, Robbins and Monro originally introduced the stochastic approximation (SA) approach in 1951 (Robbins and Monro, Reference Robbins and Monro1951). Since then, SA has gone through many developments; for more detail, readers are referred to a series of works by Nemirovski, Ghadimi, and Lan, etc, see, e.g., Nemirovski et al. (Reference Nemirovski, Juditsky, Lan and Shapiro2009); Ghadimi and Lan (Reference Ghadimi and Lan2012); Lan (Reference Lan2012); Ghadimi and Lan (Reference Ghadimi and Lan2013); Ghadimi et al. (Reference Ghadimi, Lan and Zhang2016). As for solving problem (1), motivated by the SA, some stochastic ADMM type algorithms have been proposed recently, see, e.g., Ouyang et al. (Reference Ouyang, He, Tran and Gray2013); Suzuki (Reference Suzuki2013, Reference Suzuki2014); Zhao et al. (Reference Zhao, Yang, Zhang and Li2015); Gao et al. (Reference Gao, Jiang and Zhang2018). Note that in these works, only the basic iterative scheme of ADMM was considered. It is well-known that incorporating an acceleration factor into the subproblem and the update on the dual variables often improves the algorithmic performance, which is the idea of generalized ADMM (Eckstein and Bertsekas, Reference Eckstein and Bertsekas1992, Fang et al., Reference Fang, He, Liu and Yuan2015). In this paper, we study generalized ADMM in the stochastic setting. In particular, we propose a stochastic linearized generalized ADMM (SLG-ADMM) for solving two-block separable stochastic optimization problem (1) and analyze corresponding worst-case convergence rate by means of the framework of variational inequality. Moreover, we establish the large deviation properties of SLG-ADMM under certain light-tail assumptions.
The rest of this paper is organized as follows. We present the iterative scheme of SLG-ADMM and summarize some preliminaries which will be used in the theoretical analysis in Section 2. In Section 3, we analyze the worst-case convergence rate and the high probability guarantees for objective error and constraint violation for the SLG-ADMM. Finally, we make some conclusions in Section 4.
Notation. 1. For two matrices A and B, the ordering relation
![]() $A \succ B$
(
$A \succ B$
(
![]() $A \succeq B$
) means
$A \succeq B$
) means
![]() $A-B$
is positive definite (semidefinite).
$A-B$
is positive definite (semidefinite).
![]() $I_m$
denotes the
$I_m$
denotes the
![]() $m \times m$
identity matrix. For a vector x,
$m \times m$
identity matrix. For a vector x,
![]() $\left\| x \right\|$
denotes its Euclidean norm; for a matrix X,
$\left\| x \right\|$
denotes its Euclidean norm; for a matrix X,
![]() $\left\| X \right\|$
denotes its spectral norm. For any symmetric matrix G, define
$\left\| X \right\|$
denotes its spectral norm. For any symmetric matrix G, define
![]() $\left\| x \right\|_G^2: = {x^T}Gx$
and
$\left\| x \right\|_G^2: = {x^T}Gx$
and
![]() ${\left\| x \right\|_G}: = \sqrt {{x^T}Gx} $
if
${\left\| x \right\|_G}: = \sqrt {{x^T}Gx} $
if
![]() $G \succeq 0$
.
$G \succeq 0$
.
![]() $\mathbb{E}\left[ \cdot \right]$
denotes the mathematical expectation of a random variable.
$\mathbb{E}\left[ \cdot \right]$
denotes the mathematical expectation of a random variable.
![]() ${\rm Pr}\left\{\cdot\right\}$
denotes the probability value of an event.
${\rm Pr}\left\{\cdot\right\}$
denotes the probability value of an event.
![]() $\partial$
and
$\partial$
and
![]() $\nabla$
denote the subdifferential and gradient operator of a function, respectively. We also sometimes use
$\nabla$
denote the subdifferential and gradient operator of a function, respectively. We also sometimes use
![]() $\left( {x,y} \right)$
and
$\left( {x,y} \right)$
and
![]() $\left( {x,y,\lambda } \right)$
to denote the vectors
$\left( {x,y,\lambda } \right)$
to denote the vectors
![]() ${\left( {{x^T},{y^T}} \right)^T}$
and
${\left( {{x^T},{y^T}} \right)^T}$
and
![]() ${\left( {{x^T},{y^T},{\lambda ^T}} \right)^T}$
, respectively.
${\left( {{x^T},{y^T},{\lambda ^T}} \right)^T}$
, respectively.
2. Stochastic Linearized Generalized ADMM
In this section, we first present the iterative scheme of SLG-ADMM for solving (1), and then, we introduce some preliminaries that will be frequently used in the later analysis.

We give some remarks on this algorithm. Algorithm 1 is an ADMM type algorithm, which alternates through one x-subproblem, one y-subproblem, and an update on the dual variables (multipliers). The algorithm is stochastic since at each iteration SFO is called to obtain a stochastic gradient
![]() $G\left(x^k , \xi\right)$
which is an unbiased estimation of
$G\left(x^k , \xi\right)$
which is an unbiased estimation of
![]() $\nabla {\theta _1}\left( x^k \right)$
and is bounded relative to
$\nabla {\theta _1}\left( x^k \right)$
and is bounded relative to
![]() $\nabla {\theta _1}\left( x^k \right)$
in expectation. The algorithm is linearized because of the following two aspects: (i) The term
$\nabla {\theta _1}\left( x^k \right)$
in expectation. The algorithm is linearized because of the following two aspects: (i) The term
![]() $G\left(x^k , \xi\right)^T\left(x - x^k\right)$
in the x-subproblem of SLG-ADMM is a stochastic version of linearization of
$G\left(x^k , \xi\right)^T\left(x - x^k\right)$
in the x-subproblem of SLG-ADMM is a stochastic version of linearization of
![]() ${\theta _1}\left( x^k \right)$
. (ii) x-subproblem and y-subproblem are added proximal terms
${\theta _1}\left( x^k \right)$
. (ii) x-subproblem and y-subproblem are added proximal terms
![]() $\frac{1}{{2}}\left\| {x - {x^k}} \right\|_{{G_{1,k}}}^2 $
and
$\frac{1}{{2}}\left\| {x - {x^k}} \right\|_{{G_{1,k}}}^2 $
and
![]() $\frac{1}{2}\left\| {y - {y^k}} \right\|_{{G_{2,k,}}}^2$
respectively, where
$\frac{1}{2}\left\| {y - {y^k}} \right\|_{{G_{2,k,}}}^2$
respectively, where
![]() $\left\{G_{1,k}\right\} \text{and} \left\{G_{2,k}\right\}$
are two sequences of symmetric and positive definite matrices that can be changed with iteration; with the choice of
$\left\{G_{1,k}\right\} \text{and} \left\{G_{2,k}\right\}$
are two sequences of symmetric and positive definite matrices that can be changed with iteration; with the choice of
![]() ${G_{2,k}} \equiv \tau {I_{{n_2}}} - \beta {B^T}B,\tau > \beta \left\| {{B^T}B} \right\|$
, the quadratic term in the y-subproblem is linearized. The same fact applies to the x-subproblem. Furthermore, SLG-ADMM incorporates an acceleration factor
${G_{2,k}} \equiv \tau {I_{{n_2}}} - \beta {B^T}B,\tau > \beta \left\| {{B^T}B} \right\|$
, the quadratic term in the y-subproblem is linearized. The same fact applies to the x-subproblem. Furthermore, SLG-ADMM incorporates an acceleration factor
![]() $\alpha$
; generally, the case with
$\alpha$
; generally, the case with
![]() $\alpha \in \left(1,2\right)$
could lead to better numerical results than the special case with
$\alpha \in \left(1,2\right)$
could lead to better numerical results than the special case with
![]() $\alpha = 1$
. When
$\alpha = 1$
. When
![]() $\alpha = 1$
,
$\alpha = 1$
,
![]() $G_{1,k} \equiv I_{n_1}$
, and the term
$G_{1,k} \equiv I_{n_1}$
, and the term
![]() $\frac{1}{2}\left\| {y - {y^k}} \right\|_{{G_{2,k}}}^2$
vanishes, SLG-ADMM reduces to the algorithm appeared in earlier literatures (Ouyang et al., Reference Ouyang, He, Tran and Gray2013; Gao et al., Reference Gao, Jiang and Zhang2018).
$\frac{1}{2}\left\| {y - {y^k}} \right\|_{{G_{2,k}}}^2$
vanishes, SLG-ADMM reduces to the algorithm appeared in earlier literatures (Ouyang et al., Reference Ouyang, He, Tran and Gray2013; Gao et al., Reference Gao, Jiang and Zhang2018).
Let the Lagrangian function of the problem (1) be
defined on
![]() $\mathcal{X} \times \mathcal{Y} \times \mathbb{R}^n$
. We call
$\mathcal{X} \times \mathcal{Y} \times \mathbb{R}^n$
. We call
![]() $\left( {{x^ * },{y^ * },{\lambda ^ * }} \right)$
a saddle point of
$\left( {{x^ * },{y^ * },{\lambda ^ * }} \right)$
a saddle point of
![]() $L\left(x, y, \lambda \right) \in \mathcal{X} \times \mathcal{Y} \times \mathbb{R}^n$
if the following inequalities are satisfied:
$L\left(x, y, \lambda \right) \in \mathcal{X} \times \mathcal{Y} \times \mathbb{R}^n$
if the following inequalities are satisfied:
Obviously, a saddle point
![]() $\left( {{x^ * },{y^ * },{\lambda ^ * }} \right)$
can be characterized by the following inequalities
$\left( {{x^ * },{y^ * },{\lambda ^ * }} \right)$
can be characterized by the following inequalities
 \[\left\{ \begin{array}{l} {x^ * } \in \mathcal{X},L\left( {x,{y^ * },{\lambda ^ * }} \right) - L\left( {{x^ * },{y^ * },{\lambda ^ * }} \right) \ge 0 \ \forall x \in \mathcal{X},\\ {y^ * } \in \mathcal{Y},L\left( {{x^ * },y,{\lambda ^ * }} \right) - L\left( {{x^ * },{y^ * },{\lambda ^ * }} \right) \ge 0 \ \forall y \in \mathcal{Y},\\ {\lambda ^ * } \in {\mathbb{R}^n},L\left( {{x^ * },{y^ * },{\lambda ^ * }} \right) - L\left( {{x^ * },{y^ * },\lambda } \right) \ge 0 \ \forall \lambda \in {\mathbb{R}^n}.\end{array} \right. .\]
\[\left\{ \begin{array}{l} {x^ * } \in \mathcal{X},L\left( {x,{y^ * },{\lambda ^ * }} \right) - L\left( {{x^ * },{y^ * },{\lambda ^ * }} \right) \ge 0 \ \forall x \in \mathcal{X},\\ {y^ * } \in \mathcal{Y},L\left( {{x^ * },y,{\lambda ^ * }} \right) - L\left( {{x^ * },{y^ * },{\lambda ^ * }} \right) \ge 0 \ \forall y \in \mathcal{Y},\\ {\lambda ^ * } \in {\mathbb{R}^n},L\left( {{x^ * },{y^ * },{\lambda ^ * }} \right) - L\left( {{x^ * },{y^ * },\lambda } \right) \ge 0 \ \forall \lambda \in {\mathbb{R}^n}.\end{array} \right. .\]
Below we invoke a proposition which characterize the optimality condition of an optimization model by a variational inequality. The proof can be found in He (Reference He2017).
Proposition. 2. Let
![]() $\mathcal{X} \subset \mathbb{R}^n$
be a closed convex set and let
$\mathcal{X} \subset \mathbb{R}^n$
be a closed convex set and let
![]() $\theta \left( x \right):{\mathbb{R}^n} \to \mathbb{R}$
and
$\theta \left( x \right):{\mathbb{R}^n} \to \mathbb{R}$
and
![]() $f \left( x \right):{\mathbb{R}^n} \to \mathbb{R}$
be convex functions. In addition,
$f \left( x \right):{\mathbb{R}^n} \to \mathbb{R}$
be convex functions. In addition,
![]() $f\left(x\right)$
is differentiable. Assuming that the solution set of the minimization problem
$f\left(x\right)$
is differentiable. Assuming that the solution set of the minimization problem
![]() $\min \left\{ {\theta \left( x \right) + f\left( x \right)\left| {x \in \mathcal{X}} \right.} \right\}$
is nonempty, then we have the assertion that
$\min \left\{ {\theta \left( x \right) + f\left( x \right)\left| {x \in \mathcal{X}} \right.} \right\}$
is nonempty, then we have the assertion that
if and only if
Hence with this proposition, solving (1) is equivalent to solving the following variational inequality problem under the assumption that the solution set of problem (1) is nonempty: Finding
![]() ${w^ * } = \left( {{x^ * },{y^ * },{\lambda ^ * }} \right) \in \Omega : = \mathcal{X} \times \mathcal{Y} \times {\mathbb{R}^n}$
such that
${w^ * } = \left( {{x^ * },{y^ * },{\lambda ^ * }} \right) \in \Omega : = \mathcal{X} \times \mathcal{Y} \times {\mathbb{R}^n}$
such that
where
 \begin{align*} u = \begin{pmatrix} x \\ y \end{pmatrix} , w = \begin{pmatrix} x \\ y \\ \lambda \end{pmatrix}, F\left( w \right) = \begin{pmatrix} - {A^T}\lambda \\ - {B^T}\lambda \\ Ax + By - b \end{pmatrix}, \ {\rm and} \ \theta \left( u \right) = {\theta _1}\left( x \right) + {\theta _2}\left( y \right).\end{align*}
\begin{align*} u = \begin{pmatrix} x \\ y \end{pmatrix} , w = \begin{pmatrix} x \\ y \\ \lambda \end{pmatrix}, F\left( w \right) = \begin{pmatrix} - {A^T}\lambda \\ - {B^T}\lambda \\ Ax + By - b \end{pmatrix}, \ {\rm and} \ \theta \left( u \right) = {\theta _1}\left( x \right) + {\theta _2}\left( y \right).\end{align*}
The variables with superscript or subscript such as
![]() $u^k, w^k, {\bar{u}_k}, {\bar{w}_k}$
are denoted similarly. In addition, we define two auxiliary sequences for the convergence analysis. More specifically, for the sequence
$u^k, w^k, {\bar{u}_k}, {\bar{w}_k}$
are denoted similarly. In addition, we define two auxiliary sequences for the convergence analysis. More specifically, for the sequence
![]() $\left\{ {{w^k}} \right\}$
generated by the SLG-ADMM, let
$\left\{ {{w^k}} \right\}$
generated by the SLG-ADMM, let
 \begin{equation} \begin{aligned} \tilde{w}^k = \begin{pmatrix} \tilde{x}^k \\ \tilde{y}^k \\ \tilde{\lambda}^k \end{pmatrix} = \begin{pmatrix} x^{k+1} \\ y^{k+1} \\ {\lambda ^k} - \beta \left( {A{x^{k + 1}} + B{y^k} - b} \right) \end{pmatrix} \ {\rm and} \ \tilde{u}^k = \begin{pmatrix} \tilde{x}^k \\ \tilde{y}^k \end{pmatrix}. \end{aligned}\end{equation}
\begin{equation} \begin{aligned} \tilde{w}^k = \begin{pmatrix} \tilde{x}^k \\ \tilde{y}^k \\ \tilde{\lambda}^k \end{pmatrix} = \begin{pmatrix} x^{k+1} \\ y^{k+1} \\ {\lambda ^k} - \beta \left( {A{x^{k + 1}} + B{y^k} - b} \right) \end{pmatrix} \ {\rm and} \ \tilde{u}^k = \begin{pmatrix} \tilde{x}^k \\ \tilde{y}^k \end{pmatrix}. \end{aligned}\end{equation}
Based on the above notations and the update scheme of
![]() $\lambda ^ k$
in SLG-ADMM, we have
$\lambda ^ k$
in SLG-ADMM, we have
and
Then, we get
where M is defined as
 \begin{equation} \begin{pmatrix} I_{n_1}\;\;\;\; & 0\;\;\;\; & 0 \\ 0\;\;\;\; & I_{n_2}\;\;\;\; & 0 \\ 0\;\;\;\; & -\beta B\;\;\;\; & \alpha I_n \end{pmatrix}.\end{equation}
\begin{equation} \begin{pmatrix} I_{n_1}\;\;\;\; & 0\;\;\;\; & 0 \\ 0\;\;\;\; & I_{n_2}\;\;\;\; & 0 \\ 0\;\;\;\; & -\beta B\;\;\;\; & \alpha I_n \end{pmatrix}.\end{equation}
For notational simplicity, we define two sequences of matrices that will be used later: for
![]() $k = 0, 1, \ldots$
$k = 0, 1, \ldots$
 \begin{equation} H_k = \begin{pmatrix} G_{1,k}\;\;\;\; & 0\;\;\;\; & 0 \\ 0\;\;\;\; & \frac{\beta}{\alpha}B^TB+G_{2,k}\;\;\;\; & \frac{1-\alpha}{\alpha}B^T \\ 0\;\;\;\; & \frac{1-\alpha}{\alpha}B\;\;\;\; & \frac{1}{\beta \alpha}I_n \end{pmatrix}, Q_k = \begin{pmatrix} G_{1,k}\;\;\;\; & 0\;\;\;\; & 0 \\ 0\;\;\;\; & \beta B^TB+G_{2,k}\;\;\;\; & \left( {1 - \alpha } \right)B^T \\ 0\;\;\;\; & -B\;\;\;\; & \frac{1}{\beta}I_n \end{pmatrix}.\end{equation}
\begin{equation} H_k = \begin{pmatrix} G_{1,k}\;\;\;\; & 0\;\;\;\; & 0 \\ 0\;\;\;\; & \frac{\beta}{\alpha}B^TB+G_{2,k}\;\;\;\; & \frac{1-\alpha}{\alpha}B^T \\ 0\;\;\;\; & \frac{1-\alpha}{\alpha}B\;\;\;\; & \frac{1}{\beta \alpha}I_n \end{pmatrix}, Q_k = \begin{pmatrix} G_{1,k}\;\;\;\; & 0\;\;\;\; & 0 \\ 0\;\;\;\; & \beta B^TB+G_{2,k}\;\;\;\; & \left( {1 - \alpha } \right)B^T \\ 0\;\;\;\; & -B\;\;\;\; & \frac{1}{\beta}I_n \end{pmatrix}.\end{equation}
Obviously, for any k, the matrices
![]() $M, H_k$
, and
$M, H_k$
, and
![]() $Q_k$
satisfy
$Q_k$
satisfy
![]() $Q_k = H_k M$
.
$Q_k = H_k M$
.
Throughout the paper, we need the following assumptions:
Assumption. (i) The primal-dual solution set
![]() $\Omega ^*$
of problem (1) is nonempty.
$\Omega ^*$
of problem (1) is nonempty.
(ii)
![]() $\theta_1 \left(x\right)$
is differentiable, and its gradient satisfies the L-Lipschitz condition
$\theta_1 \left(x\right)$
is differentiable, and its gradient satisfies the L-Lipschitz condition
for all
![]() $x_1, x_2 \in \mathcal{X}$
.
$x_1, x_2 \in \mathcal{X}$
.
(iii)
where
![]() $\sigma > 0$
is some constant.
$\sigma > 0$
is some constant.
Under the second assumption, it holds that for all
![]() $x, y \in \mathcal{X}$
,
$x, y \in \mathcal{X}$
,
A direct result of combining this property with convexity is shown in the following lemma.
Lemma. 3 Suppose function f is convex and differentiable, and its gradient is L-Lipschitz continuous, then for any x, y, z, we have
In addition, if f is
![]() $\mu$
-strongly convex, then for any x, y, z we have
$\mu$
-strongly convex, then for any x, y, z we have
Proof. Since the gradient of f is L-Lipschitz continuous, then for any y, z we have
![]() $f\left( y \right) \le f\left( z \right) + {\left( {y - z} \right)^T}\nabla f\left( z \right) + \frac{L}{2}{\left\| {y - z} \right\|^2}.$
Also, due to the convexity of f, we have for any x, z,
$f\left( y \right) \le f\left( z \right) + {\left( {y - z} \right)^T}\nabla f\left( z \right) + \frac{L}{2}{\left\| {y - z} \right\|^2}.$
Also, due to the convexity of f, we have for any x, z,
![]() $f\left( x \right) \ge f\left( z \right) + {\left( {x - z} \right)^T}\nabla f\left( z \right).$
Adding the above two inequalities, we get the conclusion. If f is
$f\left( x \right) \ge f\left( z \right) + {\left( {x - z} \right)^T}\nabla f\left( z \right).$
Adding the above two inequalities, we get the conclusion. If f is
![]() $\mu$
-strongly convex, then for any x, z,
$\mu$
-strongly convex, then for any x, z,
![]() $f\left( x \right) \ge f\left( z \right) + {\left( {x - z} \right)^T}\nabla f\left( z \right) + \frac{\mu }{2}{\left\| {x - z} \right\|^2}.$
Then, we combine this inequality with
$f\left( x \right) \ge f\left( z \right) + {\left( {x - z} \right)^T}\nabla f\left( z \right) + \frac{\mu }{2}{\left\| {x - z} \right\|^2}.$
Then, we combine this inequality with
![]() $f\left( y \right) \le f\left( z \right) + {\left( {y - z} \right)^T}\nabla f\left( z \right) + \frac{L}{2}{\left\| {y - z} \right\|^2}$
, and the proof is completed.
$f\left( y \right) \le f\left( z \right) + {\left( {y - z} \right)^T}\nabla f\left( z \right) + \frac{L}{2}{\left\| {y - z} \right\|^2}$
, and the proof is completed. ![]()
3. Theoretical Analysis of SLG-ADMM
In this section, we shall establish theoretical properties of SLG-ADMM. More specifically, in Subsection 3.1, we analyze the expected convergence rates of SLG-ADMM. And, we analyze the large deviation properties of SLG-ADMM in Subsection 3.2.
3.1 Expected convergence rate
First, this subsection considers that the function
![]() $\theta_1$
is convex. The next several lemmas are to obtain an upper bound of
$\theta_1$
is convex. The next several lemmas are to obtain an upper bound of
![]() $\theta \left( {{{\tilde u}^k}} \right) - \theta \left( u \right) + {\left( {{{\tilde w}^k} - w} \right)^T}F\left( {{{\tilde w}^k}} \right)$
. With such a bound, it is possible to estimate the worst-case convergence rate of SLG-ADMM.
$\theta \left( {{{\tilde u}^k}} \right) - \theta \left( u \right) + {\left( {{{\tilde w}^k} - w} \right)^T}F\left( {{{\tilde w}^k}} \right)$
. With such a bound, it is possible to estimate the worst-case convergence rate of SLG-ADMM.
Lemma. 4. Let the sequence
![]() $\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM and the associated
$\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM and the associated
![]() $\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2). Then, we have
$\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2). Then, we have
 \begin{equation} \begin{aligned} \theta \left( u \right) - \theta \left( {{{\tilde u}^k}} \right) + {\left( {w - {{\tilde w}^k}} \right)^T}F\left( {{{\tilde w}^k}} \right) \ge& {\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} \\ &- \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2}, \forall w \in \Omega, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \theta \left( u \right) - \theta \left( {{{\tilde u}^k}} \right) + {\left( {w - {{\tilde w}^k}} \right)^T}F\left( {{{\tilde w}^k}} \right) \ge& {\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} \\ &- \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2}, \forall w \in \Omega, \end{aligned} \end{equation}
where
![]() $Q_k$
is defined in (7), and
$Q_k$
is defined in (7), and
![]() $\delta ^ k = G\left( {{x^k},\xi } \right) - \nabla {\theta _1}\left( {{x^k}} \right)$
, similarly hereinafter.
$\delta ^ k = G\left( {{x^k},\xi } \right) - \nabla {\theta _1}\left( {{x^k}} \right)$
, similarly hereinafter.
Proof. The optimality condition of the x-subproblem in SLG-ADMM is
 \begin{equation} \begin{aligned} &{\left( {x - {x^{k + 1}}} \right)^T}\left( {G\left( {{x^k},\xi } \right) - {A^T}{\lambda ^k} + \beta {A^T}\left( {A{x^{k + 1}} + B{y^k} - b} \right) + G_{1,k}\left( {{x^{k + 1}} - {x^k}} \right)} \right) \\ &\ge 0,\forall x \in \mathcal{X}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &{\left( {x - {x^{k + 1}}} \right)^T}\left( {G\left( {{x^k},\xi } \right) - {A^T}{\lambda ^k} + \beta {A^T}\left( {A{x^{k + 1}} + B{y^k} - b} \right) + G_{1,k}\left( {{x^{k + 1}} - {x^k}} \right)} \right) \\ &\ge 0,\forall x \in \mathcal{X}. \end{aligned} \end{equation}
Using
![]() $\tilde{x}^k$
and
$\tilde{x}^k$
and
![]() $\tilde{\lambda}^k$
defined in (2) and notation of
$\tilde{\lambda}^k$
defined in (2) and notation of
![]() $\delta^k$
, (9) can be rewritten as
$\delta^k$
, (9) can be rewritten as
In lemma 1, letting
![]() $y = \tilde{x}^k$
,
$y = \tilde{x}^k$
,
![]() $z = x^k$
, and
$z = x^k$
, and
![]() $f = \theta_1$
, we get
$f = \theta_1$
, we get
Combining (10) and (11), we obtain
 \begin{equation} \begin{aligned} &{\theta _1}\left( x \right) - {\theta _1}\left( {{{\tilde x}^k}} \right) + {\left( {x - {{\tilde x}^k}} \right)^T}\left( { - {A^T}{{\tilde \lambda }^k}} \right) \\ &\ge {\left( {x - {{\tilde x}^k}} \right)^T}G_{1,k}\left( {{x^k} - {{\tilde x}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} - \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &{\theta _1}\left( x \right) - {\theta _1}\left( {{{\tilde x}^k}} \right) + {\left( {x - {{\tilde x}^k}} \right)^T}\left( { - {A^T}{{\tilde \lambda }^k}} \right) \\ &\ge {\left( {x - {{\tilde x}^k}} \right)^T}G_{1,k}\left( {{x^k} - {{\tilde x}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} - \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2}. \end{aligned} \end{equation}
Similarly, the optimality condition of y-subproblem is
Substituting (3) into (13), we obtain that
 \begin{equation} \begin{aligned} &{\theta _2}\left( y \right) - {\theta _2}\left( {{{\tilde y}^k}} \right) + {\left( {y - {{\tilde y}^k}} \right)^T}\left( { - {B^T}{{\tilde \lambda }^k}} \right) \\ &\ge \left( {1 - \alpha } \right){\left( {y - {{\tilde y}^k}} \right)^T}{B^T}\left( {{\lambda ^k} - {{\tilde \lambda }^k}} \right) + {\left( {y - {{\tilde y}^k}} \right)^T}\left( {\beta {B^T}B + {G_{2,k}}} \right)\left( {{y^k} - {{\tilde y}^k}} \right),\forall y \in \mathcal{Y}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &{\theta _2}\left( y \right) - {\theta _2}\left( {{{\tilde y}^k}} \right) + {\left( {y - {{\tilde y}^k}} \right)^T}\left( { - {B^T}{{\tilde \lambda }^k}} \right) \\ &\ge \left( {1 - \alpha } \right){\left( {y - {{\tilde y}^k}} \right)^T}{B^T}\left( {{\lambda ^k} - {{\tilde \lambda }^k}} \right) + {\left( {y - {{\tilde y}^k}} \right)^T}\left( {\beta {B^T}B + {G_{2,k}}} \right)\left( {{y^k} - {{\tilde y}^k}} \right),\forall y \in \mathcal{Y}. \end{aligned} \end{equation}
At the same time,
 \begin{align*} {{\tilde \lambda }^k} &= {\lambda ^k} - \beta \left( {A{x^{k + 1}} + B{y^{k + 1}} - b} \right) + \beta B\left( {{y^{k + 1}} - {y^k}} \right) \\ &= {\lambda ^k} - \beta \left( {A{{\tilde x}^k} + B{{\tilde y}^k} - b} \right) + \beta B\left( {{{\tilde y}^k} - {y^k}} \right). \end{align*}
\begin{align*} {{\tilde \lambda }^k} &= {\lambda ^k} - \beta \left( {A{x^{k + 1}} + B{y^{k + 1}} - b} \right) + \beta B\left( {{y^{k + 1}} - {y^k}} \right) \\ &= {\lambda ^k} - \beta \left( {A{{\tilde x}^k} + B{{\tilde y}^k} - b} \right) + \beta B\left( {{{\tilde y}^k} - {y^k}} \right). \end{align*}
That is,
Combining (12), (14), and (15), we get
 \begin{equation} \begin{aligned} \theta& \left( u \right) - \theta \left( {{{\tilde u}^k}} \right) + \begin{pmatrix} {x - {{\tilde x}^k}} \\ {y - {{\tilde y}^k}} \\ {\lambda - {{\tilde \lambda}^k}} \end{pmatrix} ^T \begin{pmatrix} { - {A^T}{{\tilde \lambda }^k}} \\ { - {B^T}{{\tilde \lambda }^k}} \\ {A{{\tilde x}^k} + B{{\tilde y}^k} - b} \end{pmatrix} \\ \ge& {\left( {x - {{\tilde x}^k}} \right)^T}G_{1,k}\left( {{x^k} - {{\tilde x}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} - \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2} \\ & + \left( {1 - \alpha } \right){\left( {y - {{\tilde y}^k}} \right)^T}{B^T}\left( {{\lambda ^k} - {{\tilde \lambda }^k}} \right) + {\left( {y - {{\tilde y}^k}} \right)^T}\left( {\beta {B^T}B + {G_{2,k}}} \right)\left( {{y^k} - {{\tilde y}^k}} \right) \\ & + \frac{1}{\beta }{\left( {\lambda - {{\tilde \lambda }^k}} \right)^T}\left( {{\lambda ^k} - {{\tilde \lambda }^k}} \right) + {\left( {\lambda - {{\tilde \lambda }^k}} \right)^T}B\left( {{{\tilde y}^k} - {y^k}} \right),\forall w \in \Omega. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \theta& \left( u \right) - \theta \left( {{{\tilde u}^k}} \right) + \begin{pmatrix} {x - {{\tilde x}^k}} \\ {y - {{\tilde y}^k}} \\ {\lambda - {{\tilde \lambda}^k}} \end{pmatrix} ^T \begin{pmatrix} { - {A^T}{{\tilde \lambda }^k}} \\ { - {B^T}{{\tilde \lambda }^k}} \\ {A{{\tilde x}^k} + B{{\tilde y}^k} - b} \end{pmatrix} \\ \ge& {\left( {x - {{\tilde x}^k}} \right)^T}G_{1,k}\left( {{x^k} - {{\tilde x}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} - \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2} \\ & + \left( {1 - \alpha } \right){\left( {y - {{\tilde y}^k}} \right)^T}{B^T}\left( {{\lambda ^k} - {{\tilde \lambda }^k}} \right) + {\left( {y - {{\tilde y}^k}} \right)^T}\left( {\beta {B^T}B + {G_{2,k}}} \right)\left( {{y^k} - {{\tilde y}^k}} \right) \\ & + \frac{1}{\beta }{\left( {\lambda - {{\tilde \lambda }^k}} \right)^T}\left( {{\lambda ^k} - {{\tilde \lambda }^k}} \right) + {\left( {\lambda - {{\tilde \lambda }^k}} \right)^T}B\left( {{{\tilde y}^k} - {y^k}} \right),\forall w \in \Omega. \end{aligned} \end{equation}
Finally, by the definition of F and
![]() $Q_k$
, we come to the conclusion.
$Q_k$
, we come to the conclusion. ![]()
Next, we need to further explore the terms on the right-hand side of (8).
Lemma. 5. Let the sequence
![]() $\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM and the associated
$\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM and the associated
![]() $\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2). Then for any
$\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2). Then for any
![]() $w \in \mathcal{X} \times \mathcal{Y} \times {\mathbb{R}^n}$
, we have
$w \in \mathcal{X} \times \mathcal{Y} \times {\mathbb{R}^n}$
, we have
 \begin{equation} \begin{aligned} &{\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) \\ =& \frac{1}{2}\left( {\left\| {w - {w^{k + 1}}} \right\|_{{H_k}}^2 - \left\| {w - {w^k}} \right\|_{{H_k}}^2} \right) + \left\| {{x^k} - {{\tilde x}^k}} \right\|_{{G_{1,k}}}^2 + \frac{1}{2}\left\| {{y^k} - {{\tilde y}^k}} \right\|_{{G_{2,k}}}^2 \\ &- \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^k} - {{\tilde \lambda }^k}} \right\|^2}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &{\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) \\ =& \frac{1}{2}\left( {\left\| {w - {w^{k + 1}}} \right\|_{{H_k}}^2 - \left\| {w - {w^k}} \right\|_{{H_k}}^2} \right) + \left\| {{x^k} - {{\tilde x}^k}} \right\|_{{G_{1,k}}}^2 + \frac{1}{2}\left\| {{y^k} - {{\tilde y}^k}} \right\|_{{G_{2,k}}}^2 \\ &- \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^k} - {{\tilde \lambda }^k}} \right\|^2}. \end{aligned} \end{equation}
Proof. Using
![]() $Q_k = H_k M$
and
$Q_k = H_k M$
and
![]() ${w^k} - {w^{k + 1}} = M\left( {{w^k} - {{\tilde w}^k}} \right)$
in (5), we have
${w^k} - {w^{k + 1}} = M\left( {{w^k} - {{\tilde w}^k}} \right)$
in (5), we have
 \begin{equation} \begin{aligned} {\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) =& {\left( {w - {{\tilde w}^k}} \right)^T}{H_k}M\left( {{w^k} - {{\tilde w}^k}} \right) \\ =& {\left( {w - {{\tilde w}^k}} \right)^T}{H_k}\left( {{w^k} - {w^{k + 1}}} \right). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} {\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) =& {\left( {w - {{\tilde w}^k}} \right)^T}{H_k}M\left( {{w^k} - {{\tilde w}^k}} \right) \\ =& {\left( {w - {{\tilde w}^k}} \right)^T}{H_k}\left( {{w^k} - {w^{k + 1}}} \right). \end{aligned} \end{equation}
Now applying the identity: for the vectors a, b, c, d and a matrix H with appropriate dimension,
In this identity, letting
![]() $a = w$
,
$a = w$
,
![]() $b = \tilde{w}^k$
,
$b = \tilde{w}^k$
,
![]() $c = w^k$
,
$c = w^k$
,
![]() $d = \tilde{w}^k$
, and
$d = \tilde{w}^k$
, and
![]() $H = Q_k$
, we have
$H = Q_k$
, we have
 \begin{equation*} \begin{aligned} {\left( {w - {{\tilde w}^k}} \right)^T}{H_k}\left( {{w^k} - {w^{k + 1}}} \right) =& \frac{1}{2}\left( {\left\| {w - {w^{k + 1}}} \right\|_{{H_k}}^2 - \left\| {w - {w^k}} \right\|_{{H_k}}^2} \right)\\ & + \frac{1}{2}\left( {\left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {{\tilde w}^k}} \right\|_{{H_k}}^2} \right). \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} {\left( {w - {{\tilde w}^k}} \right)^T}{H_k}\left( {{w^k} - {w^{k + 1}}} \right) =& \frac{1}{2}\left( {\left\| {w - {w^{k + 1}}} \right\|_{{H_k}}^2 - \left\| {w - {w^k}} \right\|_{{H_k}}^2} \right)\\ & + \frac{1}{2}\left( {\left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {{\tilde w}^k}} \right\|_{{H_k}}^2} \right). \end{aligned} \end{equation*}
Next, we simplify the term
![]() ${\left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {{\tilde w}^k}} \right\|_{{H_k}}^2}$
.
${\left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {{\tilde w}^k}} \right\|_{{H_k}}^2}$
.
 \begin{equation*} \begin{aligned} &\left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {{\tilde w}^k}} \right\|_{{H_k}}^2 \\ &= \left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {w^k} + {w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 \\ &= \left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {\left( {{I_{{n_1} + {n_2} + n}} - M} \right)\left( {{w^k} - {{\tilde w}^k}} \right)} \right\|_{{H_k}}^2 \\ &= {\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {{H_k} - {{\left( {{I_{{n_1} + {n_2} + n}} - M} \right)}^T}{H_k}\left( {{I_{{n_1} + {n_2} + n}} - M} \right)} \right)\left( {{w^k} - {{\tilde w}^k}} \right) \\ &= {\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {{H_k}M + {M^T}{H_k} - {M^T}{H_k}M} \right)\left( {{w^k} - {{\tilde w}^k}} \right) \\ &= {\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {\left( {2I_{n_1+n_2+n} - {M^T}} \right){Q_k}} \right)\left( {{w^k} - {{\tilde w}^k}} \right), \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} &\left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {{\tilde w}^k}} \right\|_{{H_k}}^2 \\ &= \left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {{w^{k + 1}} - {w^k} + {w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 \\ &= \left\| {{w^k} - {{\tilde w}^k}} \right\|_{{H_k}}^2 - \left\| {\left( {{I_{{n_1} + {n_2} + n}} - M} \right)\left( {{w^k} - {{\tilde w}^k}} \right)} \right\|_{{H_k}}^2 \\ &= {\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {{H_k} - {{\left( {{I_{{n_1} + {n_2} + n}} - M} \right)}^T}{H_k}\left( {{I_{{n_1} + {n_2} + n}} - M} \right)} \right)\left( {{w^k} - {{\tilde w}^k}} \right) \\ &= {\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {{H_k}M + {M^T}{H_k} - {M^T}{H_k}M} \right)\left( {{w^k} - {{\tilde w}^k}} \right) \\ &= {\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {\left( {2I_{n_1+n_2+n} - {M^T}} \right){Q_k}} \right)\left( {{w^k} - {{\tilde w}^k}} \right), \end{aligned} \end{equation*}
where the second equality uses
![]() ${w^k} - {w^{k + 1}} = M\left( {{w^k} - {{\tilde w}^k}} \right)$
in (5), and the last equality holds since the transpose of
${w^k} - {w^{k + 1}} = M\left( {{w^k} - {{\tilde w}^k}} \right)$
in (5), and the last equality holds since the transpose of
![]() $M^TH_k$
is
$M^TH_k$
is
![]() $H_kM,$
and hence,
$H_kM,$
and hence,
 \begin{equation*} \begin{aligned} {\left( {{w^k} - {{\tilde w}^k}} \right)^T}{H_k}M\left( {{w^k} - {{\tilde w}^k}} \right) =& {\left( {{w^k} - {{\tilde w}^k}} \right)^T}{M^T}{H_k}\left( {{w^k} - {{\tilde w}^k}} \right)\\ =& {\left( {{w^k} - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right). \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} {\left( {{w^k} - {{\tilde w}^k}} \right)^T}{H_k}M\left( {{w^k} - {{\tilde w}^k}} \right) =& {\left( {{w^k} - {{\tilde w}^k}} \right)^T}{M^T}{H_k}\left( {{w^k} - {{\tilde w}^k}} \right)\\ =& {\left( {{w^k} - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right). \end{aligned} \end{equation*}
The remaining task is to prove
 \begin{equation} \begin{aligned} &{\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {\left( {2I_{n_1+n_2+n} - {M^T}} \right){Q_k}} \right)\left( {{w^k} - {{\tilde w}^k}} \right) \\ &= \left\| {{x^k} - {{\tilde x}^k}} \right\|_{{G_{1,k}}}^2 + \left\| {{y^k} - {{\tilde y}^k}} \right\|_{{G_{2,k}}}^2 - \frac{{\alpha - 2}}{\beta }{\left\| {{\lambda ^k} - {{\tilde \lambda }^k}} \right\|^2}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &{\left( {{w^k} - {{\tilde w}^k}} \right)^T}\left( {\left( {2I_{n_1+n_2+n} - {M^T}} \right){Q_k}} \right)\left( {{w^k} - {{\tilde w}^k}} \right) \\ &= \left\| {{x^k} - {{\tilde x}^k}} \right\|_{{G_{1,k}}}^2 + \left\| {{y^k} - {{\tilde y}^k}} \right\|_{{G_{2,k}}}^2 - \frac{{\alpha - 2}}{\beta }{\left\| {{\lambda ^k} - {{\tilde \lambda }^k}} \right\|^2}. \end{aligned} \end{equation}
By simple algebraic operation,
 \begin{align*} \left( {2I_{n_1+n_2+n} - {M^T}} \right){Q_k} = \begin{pmatrix} G_{1,k} & 0 & 0 \\ 0 & G_{2,k} & \left(2 - \alpha\right)B^T \\ 0 & \left(\alpha - 2\right)B & \frac{2-\alpha}{\beta}I_n \end{pmatrix}. \end{align*}
\begin{align*} \left( {2I_{n_1+n_2+n} - {M^T}} \right){Q_k} = \begin{pmatrix} G_{1,k} & 0 & 0 \\ 0 & G_{2,k} & \left(2 - \alpha\right)B^T \\ 0 & \left(\alpha - 2\right)B & \frac{2-\alpha}{\beta}I_n \end{pmatrix}. \end{align*}
With this result, (19) holds and the proof is completed. ![]()
Now, we are ready to establish the first main theorem for SLG-ADMM. In this theorem, we take
![]() $G_{1,k}$
of the form
$G_{1,k}$
of the form
![]() $\tau _k I_{n_1} - \beta A^TA, \tau_k > 0$
, which simplifies the system of linear equation in x-subproblem, and
$\tau _k I_{n_1} - \beta A^TA, \tau_k > 0$
, which simplifies the system of linear equation in x-subproblem, and
![]() $G_{2,k} \equiv G_2$
. Of course,
$G_{2,k} \equiv G_2$
. Of course,
![]() $G_2$
can also take the similar form as
$G_2$
can also take the similar form as
![]() $G_{1,k}$
. In particular, if
$G_{1,k}$
. In particular, if
![]() $G_2 = \eta I_{n_2} - \beta B^TB, \eta \ge \beta \left\| {{B^T}B} \right\|$
, then y-subproblem reduces to the proximal mapping of g.
$G_2 = \eta I_{n_2} - \beta B^TB, \eta \ge \beta \left\| {{B^T}B} \right\|$
, then y-subproblem reduces to the proximal mapping of g.
Theorem. Let the sequence
![]() $\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
$\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
![]() $\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
$\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
 $${\bar w_N} = \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\tilde w}^t}}, $$
$${\bar w_N} = \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\tilde w}^t}}, $$
for some pre-selected integer N. Choosing
![]() $ {{\tau _k}} \equiv \sqrt{N} + M$
, where M is a constant satisfying the ordering relation
$ {{\tau _k}} \equiv \sqrt{N} + M$
, where M is a constant satisfying the ordering relation
![]() $MI_{n_1} \succeq LI_{n_1} + \beta A^TA $
, then we have
$MI_{n_1} \succeq LI_{n_1} + \beta A^TA $
, then we have
 \begin{equation} \begin{aligned} &\theta \left( {{{\bar u}_N}} \right) - \theta \left( {u} \right) + {\left( {{{\bar w}_N} - w} \right)^T}F\left( {w} \right) \\ \le& \frac{1}{{2\left( {N + 1} \right)}} \left\| {{w^0} - w} \right\|_{{H_0}}^2 + \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\left( {x - {x^t}} \right)}^T}{\delta ^t}} + \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {\frac{{1}}{2\sqrt{N}}{{\left\| {{\delta ^t}} \right\|}^2}} . \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\theta \left( {{{\bar u}_N}} \right) - \theta \left( {u} \right) + {\left( {{{\bar w}_N} - w} \right)^T}F\left( {w} \right) \\ \le& \frac{1}{{2\left( {N + 1} \right)}} \left\| {{w^0} - w} \right\|_{{H_0}}^2 + \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\left( {x - {x^t}} \right)}^T}{\delta ^t}} + \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {\frac{{1}}{2\sqrt{N}}{{\left\| {{\delta ^t}} \right\|}^2}} . \end{aligned} \end{equation}
Proof. Combining lemma 2 and lemma 3, we get
 \begin{equation} \begin{aligned} &\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {\left( {{{\tilde w}^t} - w} \right)^T}F\left( {{{\tilde w}^t}} \right) \\ \le& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) - \frac{1}{{2}}\left\| {{x^t} - {{\tilde x}^t}} \right\|_{{G_{1,t}}}^2 - \frac{1}{2}\left\| {{y^t} - {{\tilde y}^t}} \right\|_{{G_{2,t}}}^2 \\ &+ \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^t} - {{\tilde \lambda }^t}} \right\|^2} + {\left( {x - {{\tilde x}^t}} \right)^T}{\delta ^t} + \frac{L}{2}{\left\| {{x^t} - {{\tilde x}^t}} \right\|^2} \\ =& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + {\left( {{x^t} - {{\tilde x}^t}} \right)^T}{\delta ^t} \\ &+ \frac{1}{2}{\left( {{x^t} - {{\tilde x}^t}} \right)^T}\left( {L{I_{{n_1}}} - {G_{1,t}}} \right)\left( {{x^t} - {{\tilde x}^t}} \right) - \frac{1}{2}\left\| {{y^t} - {{\tilde y}^t}} \right\|_{{G_{2,t}}}^2 + \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^t} - {{\tilde \lambda }^t}} \right\|^2} \\ \le& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + \frac{{1}}{2\sqrt{N}}{\left\| {{\delta ^t}} \right\|^2} \\ &+ \frac{1}{2}{\left( {{x^t} - {{\tilde x}^t}} \right)^T}\left( LI_{n_1} - MI_{n_1} + \beta A^TA \right)\left( {{x^t} - {{\tilde x}^t}} \right) \\ \le& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + \frac{{1}}{2\sqrt{N}}{\left\| {{\delta ^t}} \right\|^2}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {\left( {{{\tilde w}^t} - w} \right)^T}F\left( {{{\tilde w}^t}} \right) \\ \le& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) - \frac{1}{{2}}\left\| {{x^t} - {{\tilde x}^t}} \right\|_{{G_{1,t}}}^2 - \frac{1}{2}\left\| {{y^t} - {{\tilde y}^t}} \right\|_{{G_{2,t}}}^2 \\ &+ \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^t} - {{\tilde \lambda }^t}} \right\|^2} + {\left( {x - {{\tilde x}^t}} \right)^T}{\delta ^t} + \frac{L}{2}{\left\| {{x^t} - {{\tilde x}^t}} \right\|^2} \\ =& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + {\left( {{x^t} - {{\tilde x}^t}} \right)^T}{\delta ^t} \\ &+ \frac{1}{2}{\left( {{x^t} - {{\tilde x}^t}} \right)^T}\left( {L{I_{{n_1}}} - {G_{1,t}}} \right)\left( {{x^t} - {{\tilde x}^t}} \right) - \frac{1}{2}\left\| {{y^t} - {{\tilde y}^t}} \right\|_{{G_{2,t}}}^2 + \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^t} - {{\tilde \lambda }^t}} \right\|^2} \\ \le& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + \frac{{1}}{2\sqrt{N}}{\left\| {{\delta ^t}} \right\|^2} \\ &+ \frac{1}{2}{\left( {{x^t} - {{\tilde x}^t}} \right)^T}\left( LI_{n_1} - MI_{n_1} + \beta A^TA \right)\left( {{x^t} - {{\tilde x}^t}} \right) \\ \le& \frac{1}{2}\left( {\left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + \frac{{1}}{2\sqrt{N}}{\left\| {{\delta ^t}} \right\|^2}, \end{aligned} \end{equation}
where the second inequality holds owing to the Young’s inequality and
![]() $\alpha \in \left(0,2\right)$
. Meanwhile,
$\alpha \in \left(0,2\right)$
. Meanwhile,
 \begin{equation} \begin{aligned} &\frac{1}{{N + 1}}\sum\limits_{t = 0}^N {\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {{\left( {{{\tilde w}^t} - w} \right)}^T}F\left( {{{\tilde w}^t}} \right)} \\ &= \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {{\left( {{{\tilde w}^t} - w} \right)}^T}F\left( {w} \right)} \\ &\ge \theta \left( {{{\bar u}_N}} \right) - \theta \left( {u} \right) + {\left( {{{\bar w}_N} - w} \right)^T}F\left( {w} \right) , \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\frac{1}{{N + 1}}\sum\limits_{t = 0}^N {\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {{\left( {{{\tilde w}^t} - w} \right)}^T}F\left( {{{\tilde w}^t}} \right)} \\ &= \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {{\left( {{{\tilde w}^t} - w} \right)}^T}F\left( {w} \right)} \\ &\ge \theta \left( {{{\bar u}_N}} \right) - \theta \left( {u} \right) + {\left( {{{\bar w}_N} - w} \right)^T}F\left( {w} \right) , \end{aligned} \end{equation}
where the equality holds since for any
![]() $w_1$
and
$w_1$
and
![]() $w_2$
,
$w_2$
,
and the inequality follows from the convexity of
![]() $\theta$
. Now summing both sides of (21) from 0 to N and then taking the average, and using (22), the assertion of this theorem follows directly.
$\theta$
. Now summing both sides of (21) from 0 to N and then taking the average, and using (22), the assertion of this theorem follows directly. ![]()
Corollary. 6. Let the sequence
![]() $\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
$\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
![]() $\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
$\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
 $${\bar w_N} = \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\tilde w}^t}}, $$
$${\bar w_N} = \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\tilde w}^t}}, $$
for some pre-selected integer N. Choosing
![]() $ {{\tau _k}} \equiv \sqrt{N} + M$
, where M is a constant satisfying the ordering relation
$ {{\tau _k}} \equiv \sqrt{N} + M$
, where M is a constant satisfying the ordering relation
![]() $MI_{n_1} \succeq LI_{n_1} + \beta A^TA $
, then we have
$MI_{n_1} \succeq LI_{n_1} + \beta A^TA $
, then we have
and
where e is an unit vector satisfying
![]() $ - {e^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right) = \left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|$
.
$ - {e^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right) = \left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|$
.
Proof. In (20), let
![]() $w = \left( {{x^ * },{y^ * },\lambda } \right)$
, where
$w = \left( {{x^ * },{y^ * },\lambda } \right)$
, where
![]() $\lambda = {\lambda ^ * } + e$
. Obviously,
$\lambda = {\lambda ^ * } + e$
. Obviously,
![]() $\left\| e \right\| = 1$
. Then, the left-hand side of (20) is
$\left\| e \right\| = 1$
. Then, the left-hand side of (20) is
Such a result is attributed to
 \begin{equation*} \begin{aligned} &{\left( {{{\bar w}_N} - w} \right)^T}F\left( w \right) \\ =& {\left( {{{\bar x}_N} - {x^ * }} \right)^T}\left( { - {A^T}\lambda } \right) + {\left( {{{\bar y}_N} - {y^ * }} \right)^T}\left( { - {B^T}\lambda } \right) + {\left( {{{\bar \lambda }_N} - \lambda } \right)^T}\left( {A{x^ * } + B{y^ * } - b} \right) \\ =& {\lambda ^T}\left( {A{x^ * } + B{y^ * } - b} \right) - \left( {{\lambda ^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right)} \right) \\ =& - {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right) + \left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|, \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} &{\left( {{{\bar w}_N} - w} \right)^T}F\left( w \right) \\ =& {\left( {{{\bar x}_N} - {x^ * }} \right)^T}\left( { - {A^T}\lambda } \right) + {\left( {{{\bar y}_N} - {y^ * }} \right)^T}\left( { - {B^T}\lambda } \right) + {\left( {{{\bar \lambda }_N} - \lambda } \right)^T}\left( {A{x^ * } + B{y^ * } - b} \right) \\ =& {\lambda ^T}\left( {A{x^ * } + B{y^ * } - b} \right) - \left( {{\lambda ^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right)} \right) \\ =& - {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right) + \left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|, \end{aligned} \end{equation*}
where the first equality follows from the definition of F, and the second and last equalities hold due to
![]() ${A{x^ * } + B{y^ * } - b} = 0$
and the choice of
${A{x^ * } + B{y^ * } - b} = 0$
and the choice of
![]() $\lambda$
. On the other hand, substituting
$\lambda$
. On the other hand, substituting
![]() $w = \bar w_N$
into the variational inequality associated with (1), we get
$w = \bar w_N$
into the variational inequality associated with (1), we get
Combining (25) and (26), we obtain that the left-hand side of (20) is no less than
![]() $\left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|$
when letting
$\left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|$
when letting
![]() $w = \left(x^*, y^*, \lambda^* + e\right)$
. Hence,
$w = \left(x^*, y^*, \lambda^* + e\right)$
. Hence,
where in the first inequality we use
![]() $\mathbb{E}\left[ {{\delta ^k}} \right] = 0$
and
$\mathbb{E}\left[ {{\delta ^k}} \right] = 0$
and
![]() $\mathbb{E}\left[ {{{\left\| {{\delta ^k}} \right\|}^2}} \right] \le {\sigma ^2}$
. The first part of this corollary is proved. Next, we prove the second part. Substituting
$\mathbb{E}\left[ {{{\left\| {{\delta ^k}} \right\|}^2}} \right] \le {\sigma ^2}$
. The first part of this corollary is proved. Next, we prove the second part. Substituting
![]() $w = \bar w_N$
into the variational inequality associated with (1), we get
$w = \bar w_N$
into the variational inequality associated with (1), we get
 \begin{equation*} \begin{aligned} &\theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) + {\left( {{{\bar w}_N} - {w^ * }} \right)^T}F\left( {{w^ * }} \right) \\ =& \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) - {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right) \\ \ge& \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) - \left\| {{\lambda ^ * }} \right\|\left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|, \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} &\theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) + {\left( {{{\bar w}_N} - {w^ * }} \right)^T}F\left( {{w^ * }} \right) \\ =& \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) - {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right) \\ \ge& \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) - \left\| {{\lambda ^ * }} \right\|\left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|, \end{aligned} \end{equation*}
i.e.,
Take expectation on both sides of (28), and hence, (24) is proved. ![]()
Remark. 7. (i) In the above theorem or corollary, N needs to be selected in advance, and hence,
![]() $\tau_k$
s are constant. In fact,
$\tau_k$
s are constant. In fact,
![]() $\tau_k$
can also vary with the number of iterations. In the case of
$\tau_k$
can also vary with the number of iterations. In the case of
![]() $\tau_k = \sqrt{k} + M$
, if the distance between
$\tau_k = \sqrt{k} + M$
, if the distance between
![]() $w^k$
and
$w^k$
and
![]() $w^*$
is bounded, i.e.,
$w^*$
is bounded, i.e.,
![]() ${\left\| {{w^k} - {w^ * }} \right\|^2} \le {R^2}$
for any k, we can also obtain a worst-case convergence rate. The main difference with that proof idea in the above theorem or corollary is bounding the term
${\left\| {{w^k} - {w^ * }} \right\|^2} \le {R^2}$
for any k, we can also obtain a worst-case convergence rate. The main difference with that proof idea in the above theorem or corollary is bounding the term
![]() $\sum\nolimits_{t = 0}^k {\left( {\left\| {{x^t} - {x^ * }} \right\|_{G_{1,t}}^2 - \left\| {{x^{t + 1}} - {x^ * }} \right\|_{G_{1,t}}^2} \right)} $
, which is now bounded as follows.
$\sum\nolimits_{t = 0}^k {\left( {\left\| {{x^t} - {x^ * }} \right\|_{G_{1,t}}^2 - \left\| {{x^{t + 1}} - {x^ * }} \right\|_{G_{1,t}}^2} \right)} $
, which is now bounded as follows.
 \begin{equation*} \begin{aligned} &\sum\limits_{t = 0}^k {\left( {\left\| {{x^t} - {x^ * }} \right\|_{G_{1,t}}^2 - \left\| {{x^{t + 1}} - {x^ * }} \right\|_{G_{1,t}}^2} \right)} \\ =& M{\left\| {{x^0} - {x^ * }} \right\|^2} + \sum\limits_{i = 0}^{k - 1} {\left( {{\tau _{i + 1}} - {\tau _i}} \right){{\left\| {{x^{i + 1}} - {x^ * }} \right\|}^2}} - \left\| {{x^{k + 1}} - {x^ * }} \right\|_{{G_{1,k}}}^2 \\ \le& \left( {M + \sum\limits_{i = 0}^{k - 1} {\left( {{\tau _{i + 1}} - {\tau _i}} \right)} } \right){R^2} \\ =& \left( {M + \sqrt k } \right){R^2} . \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} &\sum\limits_{t = 0}^k {\left( {\left\| {{x^t} - {x^ * }} \right\|_{G_{1,t}}^2 - \left\| {{x^{t + 1}} - {x^ * }} \right\|_{G_{1,t}}^2} \right)} \\ =& M{\left\| {{x^0} - {x^ * }} \right\|^2} + \sum\limits_{i = 0}^{k - 1} {\left( {{\tau _{i + 1}} - {\tau _i}} \right){{\left\| {{x^{i + 1}} - {x^ * }} \right\|}^2}} - \left\| {{x^{k + 1}} - {x^ * }} \right\|_{{G_{1,k}}}^2 \\ \le& \left( {M + \sum\limits_{i = 0}^{k - 1} {\left( {{\tau _{i + 1}} - {\tau _i}} \right)} } \right){R^2} \\ =& \left( {M + \sqrt k } \right){R^2} . \end{aligned} \end{equation*}
(ii) The above corollary reveals that the worst-case expected convergence rate of SLG-ADMM for solving general convex problems is
![]() $\mathcal{O}\left(\frac{1}{\sqrt{N}}\right)$
, where N is the iteration number.
$\mathcal{O}\left(\frac{1}{\sqrt{N}}\right)$
, where N is the iteration number.
At end of this subsection, we assume that
![]() $\theta_1$
is
$\theta_1$
is
![]() $\mu$
-strongly convex, i.e.,
$\mu$
-strongly convex, i.e.,
![]() ${\theta _1}\left( x \right) \ge {\theta _1}\left( y \right) + \left\langle {\nabla {\theta _1}\left( y \right),x - y} \right\rangle + \frac{\mu }{2}{\left\| {x - y} \right\|^2}, \mu > 0$
for all
${\theta _1}\left( x \right) \ge {\theta _1}\left( y \right) + \left\langle {\nabla {\theta _1}\left( y \right),x - y} \right\rangle + \frac{\mu }{2}{\left\| {x - y} \right\|^2}, \mu > 0$
for all
![]() $x, y \in \mathcal{X}$
. With the strong convexity, we can obtain not only the objective function value gap and constraint violation converge to zero in expectation but also the convergence of ergodic iterates of SLG-ADMM.
$x, y \in \mathcal{X}$
. With the strong convexity, we can obtain not only the objective function value gap and constraint violation converge to zero in expectation but also the convergence of ergodic iterates of SLG-ADMM.
Theorem. Let the sequence
![]() $\left\{ {{w^k}} \right\}$
be generated by the SSL-ADMM and the associated
$\left\{ {{w^k}} \right\}$
be generated by the SSL-ADMM and the associated
![]() $\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
$\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
 \[{{\bar w}_k} = \frac{1}{k}\sum\limits_{t = 1}^k {{{\tilde w}^t}} .\]
\[{{\bar w}_k} = \frac{1}{k}\sum\limits_{t = 1}^k {{{\tilde w}^t}} .\]
Choosing
![]() $\tau_k = \mu\left(k+1\right) + M$
, where M is a constant satisfying the ordering relation
$\tau_k = \mu\left(k+1\right) + M$
, where M is a constant satisfying the ordering relation
![]() $M{I_{{n_1}}} \succeq L{I_{{n_1}}} + \beta {A^T}A$
, then SLG-ADMM has the following properties
$M{I_{{n_1}}} \succeq L{I_{{n_1}}} + \beta {A^T}A$
, then SLG-ADMM has the following properties
 \begin{equation} \begin{aligned} &\mathbb{E}\left[ {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} \right] \\ \le& \frac{1}{2\left ( k+1 \right ) }\left \| \left ( y^{0},\lambda ^{0} \right ) - \left ( y^{\ast },\lambda ^{\ast } + e \right ) \right \| _{H_{1;2\times 2} }^{2} + \frac{1 }{2\left ( k+1 \right ) } \left \| x^{0} - x^{\ast } \right \|_{MI_{n_1}-\beta A^TA} ^{2} \\ &+ \frac{\sigma ^{2} }{2\mu \left ( k+1 \right ) }\left ( 1+{\ln}\left ( k+1 \right ) \right ) , \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\mathbb{E}\left[ {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} \right] \\ \le& \frac{1}{2\left ( k+1 \right ) }\left \| \left ( y^{0},\lambda ^{0} \right ) - \left ( y^{\ast },\lambda ^{\ast } + e \right ) \right \| _{H_{1;2\times 2} }^{2} + \frac{1 }{2\left ( k+1 \right ) } \left \| x^{0} - x^{\ast } \right \|_{MI_{n_1}-\beta A^TA} ^{2} \\ &+ \frac{\sigma ^{2} }{2\mu \left ( k+1 \right ) }\left ( 1+{\ln}\left ( k+1 \right ) \right ) , \end{aligned} \end{equation}
and
 \begin{equation} \begin{aligned} &\mathbb{E}\left[ {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} \right] \\ \le& \frac{\left \| \lambda ^{\ast } \right \|+1 }{2\left ( k+1 \right ) }\left \| \left ( y^{0},\lambda ^{0} \right ) - \left ( y^{\ast },\lambda ^{\ast } + e \right ) \right \| _{H_{1;2\times 2} }^{2} + \frac{ \left \| \lambda ^{\ast } \right \|+1 }{2\left ( k+1 \right ) } \left \| x^{0} - x^{\ast } \right \|_{MI_{n_1}-\beta A^TA} ^{2} \\ & + \frac{\sigma ^{2}\left ( \left \| \lambda ^{\ast } \right \|+1 \right ) }{2\mu \left ( k+1 \right ) }\left ( 1+\ln\left ( k+1 \right ) \right ) , \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\mathbb{E}\left[ {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} \right] \\ \le& \frac{\left \| \lambda ^{\ast } \right \|+1 }{2\left ( k+1 \right ) }\left \| \left ( y^{0},\lambda ^{0} \right ) - \left ( y^{\ast },\lambda ^{\ast } + e \right ) \right \| _{H_{1;2\times 2} }^{2} + \frac{ \left \| \lambda ^{\ast } \right \|+1 }{2\left ( k+1 \right ) } \left \| x^{0} - x^{\ast } \right \|_{MI_{n_1}-\beta A^TA} ^{2} \\ & + \frac{\sigma ^{2}\left ( \left \| \lambda ^{\ast } \right \|+1 \right ) }{2\mu \left ( k+1 \right ) }\left ( 1+\ln\left ( k+1 \right ) \right ) , \end{aligned} \end{equation}
where e is an unit vector satisfying
![]() $ - {e^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right) = \left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|$
, and
$ - {e^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right) = \left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|$
, and
 \begin{equation*} H_{1;2\times2} = \begin{pmatrix} \frac{\beta}{\alpha}\beta B^TB+G_2 & \frac{1-\alpha}{\alpha}B^T \\ \frac{1-\alpha}{\alpha}B & \frac{1}{\beta \alpha} I_n \\ \end{pmatrix}.\end{equation*}
\begin{equation*} H_{1;2\times2} = \begin{pmatrix} \frac{\beta}{\alpha}\beta B^TB+G_2 & \frac{1-\alpha}{\alpha}B^T \\ \frac{1-\alpha}{\alpha}B & \frac{1}{\beta \alpha} I_n \\ \end{pmatrix}.\end{equation*}
Proof. First, similar to the proof of lemma 2, using the
![]() $\mu$
-strong convexity of f, we conclude that for any
$\mu$
-strong convexity of f, we conclude that for any
![]() $w \in \Omega$
$w \in \Omega$
 \begin{equation} \begin{aligned} &\theta \left( u \right) - \theta \left( {{{\tilde u}^k}} \right) + {\left( {w - {{\tilde w}^k}} \right)^T}F\left( {{{\tilde w}^k}} \right) \\ \ge& {\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} - \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2} + \frac{\mu }{2}{\left\| {x - {x^k}} \right\|^2}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\theta \left( u \right) - \theta \left( {{{\tilde u}^k}} \right) + {\left( {w - {{\tilde w}^k}} \right)^T}F\left( {{{\tilde w}^k}} \right) \\ \ge& {\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) - {\left( {x - {{\tilde x}^k}} \right)^T}{\delta ^k} - \frac{L}{2}{\left\| {{x^k} - {{\tilde x}^k}} \right\|^2} + \frac{\mu }{2}{\left\| {x - {x^k}} \right\|^2}, \end{aligned} \end{equation}
where
![]() $Q_k$
is defined in (7). Then using the result in lemma 3,
$Q_k$
is defined in (7). Then using the result in lemma 3,
 \begin{equation} \begin{aligned} &{\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) \\ =& \frac{1}{2}\left( {\left\| {w - {w^{k + 1}}} \right\|_{{H_k}}^2 - \left\| {w - {w^k}} \right\|_{{H_k}}^2} \right) + \frac{1}{{2}}\left\| {{x^k} - {{\tilde x}^k}} \right\|_{{G_{1,k}}}^2 + \frac{1}{2}\left\| {{y^k} - {{\tilde y}^k}} \right\|_{{G_2}}^2 \\ &- \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^k} - {{\tilde \lambda }^k}} \right\|^2}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &{\left( {w - {{\tilde w}^k}} \right)^T}{Q_k}\left( {{w^k} - {{\tilde w}^k}} \right) \\ =& \frac{1}{2}\left( {\left\| {w - {w^{k + 1}}} \right\|_{{H_k}}^2 - \left\| {w - {w^k}} \right\|_{{H_k}}^2} \right) + \frac{1}{{2}}\left\| {{x^k} - {{\tilde x}^k}} \right\|_{{G_{1,k}}}^2 + \frac{1}{2}\left\| {{y^k} - {{\tilde y}^k}} \right\|_{{G_2}}^2 \\ &- \frac{{\alpha - 2}}{{2\beta }}{\left\| {{\lambda ^k} - {{\tilde \lambda }^k}} \right\|^2}. \end{aligned} \end{equation}
Combining (31) and (32), we get
 \begin{equation} \begin{aligned} &\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {\left( {{{\tilde w}^t} - w} \right)^T}F\left( {{{\tilde w}^t}} \right) \\ \le& \frac{1}{2}\left( \left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2 - {\mu }{\left\| {x^t - x} \right\|^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + \frac{1}{2\mu\left(t+1\right)}{\left\| {{\delta ^t}} \right\|^2} . \end{aligned}\end{equation}
\begin{equation} \begin{aligned} &\theta \left( {{{\tilde u}^t}} \right) - \theta \left( {u} \right) + {\left( {{{\tilde w}^t} - w} \right)^T}F\left( {{{\tilde w}^t}} \right) \\ \le& \frac{1}{2}\left( \left\| {{w^t} - w} \right\|_{{H_t}}^2 - \left\| {{w^{t + 1}} - w} \right\|_{{H_t}}^2 - {\mu }{\left\| {x^t - x} \right\|^2} \right) + {\left( {x - {x^t}} \right)^T}{\delta ^t} + \frac{1}{2\mu\left(t+1\right)}{\left\| {{\delta ^t}} \right\|^2} . \end{aligned}\end{equation}
Now using (22) and (33), we have

Finally, taking expectation on both sides of (32) and following the proof for getting (27) and (28), we obtain

and
Therefore, (29) and (30) are proved. ![]()
This theorem implies that under the assumption that
![]() $\theta_1$
is strongly convex, the worst-case expected convergence rate for the SLG-ADMM can be improved to
$\theta_1$
is strongly convex, the worst-case expected convergence rate for the SLG-ADMM can be improved to
![]() $\mathcal{O}\left(\ln k / k\right)$
with the choice of diminishing size. The following theorem shows the convergence of ergodic iterates of SLG-ADMM, which is not covered in some earlier literatures (Ouyang et al., Reference Ouyang, He, Tran and Gray2013; Gao et al., Reference Gao, Jiang and Zhang2018). Furthermore, if
$\mathcal{O}\left(\ln k / k\right)$
with the choice of diminishing size. The following theorem shows the convergence of ergodic iterates of SLG-ADMM, which is not covered in some earlier literatures (Ouyang et al., Reference Ouyang, He, Tran and Gray2013; Gao et al., Reference Gao, Jiang and Zhang2018). Furthermore, if
![]() $\theta_2$
is also strongly convex, the assumption that B is full column rank can be removed.
$\theta_2$
is also strongly convex, the assumption that B is full column rank can be removed.
Theorem. Let the sequence
![]() $\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
$\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
![]() $\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
$\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
 \[{{\bar w}_k} = \frac{1}{k}\sum\limits_{t = 1}^k {{{\tilde w}^t}} .\]
\[{{\bar w}_k} = \frac{1}{k}\sum\limits_{t = 1}^k {{{\tilde w}^t}} .\]
Choosing
![]() $\tau_k = \mu\left(k+1\right) + M$
, where M is a constant satisfying the ordering relation
$\tau_k = \mu\left(k+1\right) + M$
, where M is a constant satisfying the ordering relation
![]() $M{I_{{n_1}}} \succeq L{I_{{n_1}}} + \beta {A^T}A$
, and assuming B is full column rank and
$M{I_{{n_1}}} \succeq L{I_{{n_1}}} + \beta {A^T}A$
, and assuming B is full column rank and
![]() $\lambda_{\min}$
denotes the minimum eigenvalue of
$\lambda_{\min}$
denotes the minimum eigenvalue of
![]() $B^TB$
, then we have
$B^TB$
, then we have
 \begin{equation} \begin{aligned} &\mathbb{E}\left[{\left\| {{{\bar x}_k} - {x^ * }} \right\|} + {\left\| {{{\bar y}_k} - {y^ * }} \right\|}\right] \\ \le& \left(1+\frac{\left\|A\right\|}{\sqrt{\lambda_{\min}}}\right) \sqrt{\left[\frac{2}{\mu}\left( {\mathbb{E}\left[\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)\right]} + \left\| {{\lambda ^ * }} \right\|\mathbb{E}\left[\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|\right]\right)\right]} \\ &+ \frac{1}{{\sqrt{\lambda_{\min}}}}\mathbb{E}{\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|}, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} &\mathbb{E}\left[{\left\| {{{\bar x}_k} - {x^ * }} \right\|} + {\left\| {{{\bar y}_k} - {y^ * }} \right\|}\right] \\ \le& \left(1+\frac{\left\|A\right\|}{\sqrt{\lambda_{\min}}}\right) \sqrt{\left[\frac{2}{\mu}\left( {\mathbb{E}\left[\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)\right]} + \left\| {{\lambda ^ * }} \right\|\mathbb{E}\left[\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|\right]\right)\right]} \\ &+ \frac{1}{{\sqrt{\lambda_{\min}}}}\mathbb{E}{\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|}, \end{aligned} \end{equation}
where the bounds for
![]() $\mathbb{E}\left[ {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} \right]$
and
$\mathbb{E}\left[ {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} \right]$
and
![]() $\mathbb{E}\left[ {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} \right]$
are the same as in (29) and (30), respectively.
$\mathbb{E}\left[ {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} \right]$
are the same as in (29) and (30), respectively.
Proof. Since
![]() $\left(x^*, y^*, \lambda^*\right)$
is a solution of (1), we have
$\left(x^*, y^*, \lambda^*\right)$
is a solution of (1), we have
![]() ${A^T}{\lambda ^ * } = \nabla {\theta _1}\left( {{x^ * }} \right) \ {\rm and} \ {B^T}{\lambda ^ * } \in \partial {\theta _2}\left( {{y^ * }} \right).$
Hence, since
${A^T}{\lambda ^ * } = \nabla {\theta _1}\left( {{x^ * }} \right) \ {\rm and} \ {B^T}{\lambda ^ * } \in \partial {\theta _2}\left( {{y^ * }} \right).$
Hence, since
![]() $\theta_1$
is strongly convex and
$\theta_1$
is strongly convex and
![]() $\theta_2$
is convex, we have
$\theta_2$
is convex, we have
and
Adding up (36) and (37), we get
![]() $\theta \left( {{{\bar u}_k}} \right) \ge \theta \left( {{u^ * }} \right) + {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right) + \frac{\mu }{2}{\left\| {{{\bar x}_k} - {x^ * }} \right\|^2},$
that is
$\theta \left( {{{\bar u}_k}} \right) \ge \theta \left( {{u^ * }} \right) + {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right) + \frac{\mu }{2}{\left\| {{{\bar x}_k} - {x^ * }} \right\|^2},$
that is
 \begin{equation} \begin{aligned} {\left\| {{{\bar x}_k} - {x^ * }} \right\|} \le& \sqrt{\frac{2}{\mu}\left({\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} - {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right)\right)} \\ \le& \sqrt{\frac{2}{\mu}\left( {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} + \left\| {{\lambda ^ * }} \right\|\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|\right)}. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} {\left\| {{{\bar x}_k} - {x^ * }} \right\|} \le& \sqrt{\frac{2}{\mu}\left({\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} - {\left( {{\lambda ^ * }} \right)^T}\left( {A{{\bar x}_k} + B{{\bar y}_k} - b} \right)\right)} \\ \le& \sqrt{\frac{2}{\mu}\left( {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} + \left\| {{\lambda ^ * }} \right\|\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|\right)}. \end{aligned} \end{equation}
On the other hand,
 \begin{equation*} \begin{aligned} {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} =& {\left\| {A\left( {{{\bar x}_k} - {x^ * }} \right) + B\left( {{{\bar y}_k} - {y^ * }} \right)} \right\|} \\ \ge& \left\| {B\left( {{{\bar y}_k} - {y^ * }} \right)} \right\| - \left\| A \right\|\left\| {{{\bar x}_k} - {x^ * }} \right\|, \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} =& {\left\| {A\left( {{{\bar x}_k} - {x^ * }} \right) + B\left( {{{\bar y}_k} - {y^ * }} \right)} \right\|} \\ \ge& \left\| {B\left( {{{\bar y}_k} - {y^ * }} \right)} \right\| - \left\| A \right\|\left\| {{{\bar x}_k} - {x^ * }} \right\|, \end{aligned} \end{equation*}
this implies
![]() ${\left\| {B\left( {{{\bar y}_k} - {y^ * }} \right)} \right\|} \le {\left\| A \right\|}{\left\| {{{\bar x}_k} - {x^ * }} \right\|} + {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|,}$
and hence,
${\left\| {B\left( {{{\bar y}_k} - {y^ * }} \right)} \right\|} \le {\left\| A \right\|}{\left\| {{{\bar x}_k} - {x^ * }} \right\|} + {\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|,}$
and hence,
Adding (38) and (39), using Jensen’s inequality
![]() $\mathbb{E}X^{\frac{1}{2}} \le \left(\mathbb{E}X\right)^{\frac{1}{2}}$
for a random variable X, and taking expectation imply
$\mathbb{E}X^{\frac{1}{2}} \le \left(\mathbb{E}X\right)^{\frac{1}{2}}$
for a random variable X, and taking expectation imply
 \begin{equation*} \begin{aligned} &\mathbb{E}\left[{\left\| {{{\bar x}_k} - {x^ * }} \right\|} + {\left\| {{{\bar y}_k} - {y^ * }} \right\|}\right] \\ \le& \left(1+\frac{\left\|A\right\|}{\sqrt{\lambda_{\min}}}\right) \sqrt{\mathbb{E}\left[\frac{2}{\mu}\left( {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} + \left\| {{\lambda ^ * }} \right\|\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|\right)\right]} \\ &+ \frac{1}{{\sqrt{\lambda_{\min}}}}\mathbb{E}{\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} . \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} &\mathbb{E}\left[{\left\| {{{\bar x}_k} - {x^ * }} \right\|} + {\left\| {{{\bar y}_k} - {y^ * }} \right\|}\right] \\ \le& \left(1+\frac{\left\|A\right\|}{\sqrt{\lambda_{\min}}}\right) \sqrt{\mathbb{E}\left[\frac{2}{\mu}\left( {\theta \left( {{{\bar u}_k}} \right) - \theta \left( {{u^ * }} \right)} + \left\| {{\lambda ^ * }} \right\|\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|\right)\right]} \\ &+ \frac{1}{{\sqrt{\lambda_{\min}}}}\mathbb{E}{\left\| {A{{\bar x}_k} + B{{\bar y}_k} - b} \right\|} . \end{aligned} \end{equation*}
The proof is completed. ![]()
3.2 High probability performance analysis
In this subsection, we shall establish the large deviation properties of SLG-ADMM. By (23) and (24), and Markov’s inequality, we have for any
![]() $\varepsilon_1 > 0$
and
$\varepsilon_1 > 0$
and
![]() $\varepsilon_2 > 0$
that
$\varepsilon_2 > 0$
that
and
However, these bounds are not strong. In the following, we will show these high probability bounds can be significantly improved when imposing standard “light-tail” assumption, see, e.g., Nemirovski et al. (Reference Nemirovski, Juditsky, Lan and Shapiro2009); Lan (Reference Lan2020). Specifically, assume that for any
![]() $x \in \mathcal{X}$
$x \in \mathcal{X}$
ʼ
This assumption is a little bit stronger than b) in Assumption (iii), which can be explained by Jensen’s inequality. For further analysis, we assume that
![]() $\mathcal{X}$
is bounded and its diameter is denoted by
$\mathcal{X}$
is bounded and its diameter is denoted by
![]() $D_X$
, defined as
$D_X$
, defined as
![]() $\max _{x_1,x_2\in \mathcal{X} } \left \| x_1 - x_2 \right \| $
. The following theorem shows the high probability bound for objective error and constraint violation of SLG-ADMM.
$\max _{x_1,x_2\in \mathcal{X} } \left \| x_1 - x_2 \right \| $
. The following theorem shows the high probability bound for objective error and constraint violation of SLG-ADMM.
Theorem. Let the sequence
![]() $\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
$\left\{ {{w^k}} \right\}$
be generated by the SLG-ADMM, the associated
![]() $\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
$\left\{ {{{\tilde w}^k}} \right\}$
be defined in (2), and
 $${\bar w_N} = \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\tilde w}^t}} $$
$${\bar w_N} = \frac{1}{{N + 1}}\sum\limits_{t = 0}^N {{{\tilde w}^t}} $$
for some pre-selected integer N. Choosing
![]() $ {{\tau _k}} \equiv \sqrt{N} + M$
, where M is a constant satisfying the ordering relation
$ {{\tau _k}} \equiv \sqrt{N} + M$
, where M is a constant satisfying the ordering relation
![]() $MI_{n_1} \succeq LI_{n_1} + \beta A^TA $
, then SLG-ADMM has the following properties
$MI_{n_1} \succeq LI_{n_1} + \beta A^TA $
, then SLG-ADMM has the following properties
(i)
 \begin{equation} \!\!\!\!\!\begin{aligned} {\rm Pr}\left \{ \left \| A\bar{x}_{N} + B\bar{y}_{N} - b \right \| \le \frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2} \right \} \\ \ge 1 - {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} - {\rm exp}\left \{ -\Theta \right \} , \end{aligned} \end{equation}
\begin{equation} \!\!\!\!\!\begin{aligned} {\rm Pr}\left \{ \left \| A\bar{x}_{N} + B\bar{y}_{N} - b \right \| \le \frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2} \right \} \\ \ge 1 - {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} - {\rm exp}\left \{ -\Theta \right \} , \end{aligned} \end{equation}
(ii)
 \begin{equation} \!\!\!\!\!\begin{aligned} {\rm Pr}\left \{ \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) \le \left(\left\| {{\lambda ^ * }} \right\| + 1\right)\left(\frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } \right. \right. \\ \left. \left. + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2}\right) \right \} \ge 1 - {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} - {\rm exp}\left \{ -\Theta \right \} , \end{aligned} \end{equation}
\begin{equation} \!\!\!\!\!\begin{aligned} {\rm Pr}\left \{ \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) \le \left(\left\| {{\lambda ^ * }} \right\| + 1\right)\left(\frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } \right. \right. \\ \left. \left. + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2}\right) \right \} \ge 1 - {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} - {\rm exp}\left \{ -\Theta \right \} , \end{aligned} \end{equation}
where e is an unit vector satisfying
![]() $ - {e^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right) = \left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|$
.
$ - {e^T}\left( {A{{\bar x}_N} + B{{\bar y}_N} - b} \right) = \left\| {A{{\bar x}_N} + B{{\bar y}_N} - b} \right\|$
.
Proof. Let
![]() $\zeta^t = \frac{1}{N}\left ( x^* - x^{t} \right ) ^{T} \delta ^{t} $
. Clearly,
$\zeta^t = \frac{1}{N}\left ( x^* - x^{t} \right ) ^{T} \delta ^{t} $
. Clearly,
![]() $\left \{ \zeta ^{t} \right \} _{t\ge 1} $
is a martingale-difference sequence. Moreover, it follows from the definition of
$\left \{ \zeta ^{t} \right \} _{t\ge 1} $
is a martingale-difference sequence. Moreover, it follows from the definition of
![]() $D_X$
and that light-tail assumption that
$D_X$
and that light-tail assumption that
 $$\mathbb{E}\left [ {\rm exp}\left \{ {\left ( \zeta ^{t} \right )^{2} / \left ( \frac{1}{N}D_{X}\sigma \right ) ^{2} } \right \} \right ] \le \mathbb{E}\left [ {\rm exp}\left \{ \left ( \frac{1}{N}D_{X}\left \| \delta ^{t} \right \| \right ) ^{2} / \left ( \frac{1}{N}D_{X}\sigma \right ) ^{2} \right \} \right ] \le {\rm exp}\left \{ 1 \right \} .$$
$$\mathbb{E}\left [ {\rm exp}\left \{ {\left ( \zeta ^{t} \right )^{2} / \left ( \frac{1}{N}D_{X}\sigma \right ) ^{2} } \right \} \right ] \le \mathbb{E}\left [ {\rm exp}\left \{ \left ( \frac{1}{N}D_{X}\left \| \delta ^{t} \right \| \right ) ^{2} / \left ( \frac{1}{N}D_{X}\sigma \right ) ^{2} \right \} \right ] \le {\rm exp}\left \{ 1 \right \} .$$
Now using a well-known result (see Lemma 4.1 in Lan (Reference Lan2020)) for the martingale-difference sequence, we have for any
![]() $\Theta \ge 0$
$\Theta \ge 0$
 \begin{equation} {\rm Pr}\left \{ \sum_{t=1}^{N}\zeta ^{t} > \frac{\Theta D_{X} \sigma}{\sqrt{N} } \right \} \le {\rm exp}\left \{ -\Theta ^{2} /3 \right \} . \end{equation}
\begin{equation} {\rm Pr}\left \{ \sum_{t=1}^{N}\zeta ^{t} > \frac{\Theta D_{X} \sigma}{\sqrt{N} } \right \} \le {\rm exp}\left \{ -\Theta ^{2} /3 \right \} . \end{equation}
Also, observe that by Jensen’s inequality
 $${\rm exp}\left \{ \frac{1}{N} \sum_{t=1}^{N} \left ( \left \| \delta ^{t} \right \|^{2} / \sigma ^{2} \right ) \right \}\le \frac{1}{N}\sum_{t=1}^{N}{\rm exp}\left \{ \left \| \delta ^{t} \right \|^{2} /\sigma ^{2} \right \} , $$
$${\rm exp}\left \{ \frac{1}{N} \sum_{t=1}^{N} \left ( \left \| \delta ^{t} \right \|^{2} / \sigma ^{2} \right ) \right \}\le \frac{1}{N}\sum_{t=1}^{N}{\rm exp}\left \{ \left \| \delta ^{t} \right \|^{2} /\sigma ^{2} \right \} , $$
whence, taking expectation,
 $$\mathbb{E}\left [ {\rm exp}\left \{ \frac{1}{N} \sum_{t=1}^{N} \left \| \delta ^{t} \right \|^{2} / \sigma^{2} \right \} \right ] \le \frac{1}{N}\sum_{t=1}^{N} \mathbb{E}\left [ {\rm exp}\left \{ \left \| \delta ^{t} \right \|^{2} / \sigma ^{2} \right \} \right ] \le {\rm exp} \left\{1\right\} .$$
$$\mathbb{E}\left [ {\rm exp}\left \{ \frac{1}{N} \sum_{t=1}^{N} \left \| \delta ^{t} \right \|^{2} / \sigma^{2} \right \} \right ] \le \frac{1}{N}\sum_{t=1}^{N} \mathbb{E}\left [ {\rm exp}\left \{ \left \| \delta ^{t} \right \|^{2} / \sigma ^{2} \right \} \right ] \le {\rm exp} \left\{1\right\} .$$
It then follows from Markov’s inequality that for any
![]() $\Theta \ge 0$
$\Theta \ge 0$
 \begin{equation} {\rm Pr}\left \{ \frac{1}{N} \sum_{t=1}^{N}\left \| \delta ^{t} \right \|^{2} \ge \left ( 1 + \Theta \right ) \sigma ^{2} \right \}\le {\rm exp}\left \{ -\Theta \right \} . \end{equation}
\begin{equation} {\rm Pr}\left \{ \frac{1}{N} \sum_{t=1}^{N}\left \| \delta ^{t} \right \|^{2} \ge \left ( 1 + \Theta \right ) \sigma ^{2} \right \}\le {\rm exp}\left \{ -\Theta \right \} . \end{equation}
Using (44) and (45) in (20) for
![]() $w = \left(x^*, y^*, \lambda ^* + e\right)$
, we conclude that
$w = \left(x^*, y^*, \lambda ^* + e\right)$
, we conclude that
 \begin{equation} \begin{aligned} {\rm Pr}\left \{ \left \| A\bar{x}_{N} + B\bar{y}_{N} - b \right \| > \frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2} \right \} \\ \le {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} + {\rm exp}\left \{ -\Theta \right \} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} {\rm Pr}\left \{ \left \| A\bar{x}_{N} + B\bar{y}_{N} - b \right \| > \frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2} \right \} \\ \le {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} + {\rm exp}\left \{ -\Theta \right \} \end{aligned} \end{equation}
and
 \begin{equation} \begin{aligned} {\rm Pr}\left \{ \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) > \left(\left\| {{\lambda ^ * }} \right\| + 1\right) \left(\frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } \right. \right. \\ \left. \left. + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2}\right) \right \} \le {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} + {\rm exp}\left \{ -\Theta \right \} . \end{aligned} \end{equation}
\begin{equation} \begin{aligned} {\rm Pr}\left \{ \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) > \left(\left\| {{\lambda ^ * }} \right\| + 1\right) \left(\frac{1}{{2\left(N+1\right)}}\left\| {{w^0} - \left( {{x^ * },{y^ * },{\lambda ^ * } + e} \right)} \right\|_{{H_0}}^2 + \frac{\Theta D_{X} \sigma }{\sqrt{N} } \right. \right. \\ \left. \left. + \frac{1}{2\sqrt{N} } \left ( 1 + \Theta \right ) \sigma ^{2}\right) \right \} \le {\rm exp}\left \{ -\Theta ^{2} / 3 \right \} + {\rm exp}\left \{ -\Theta \right \} . \end{aligned} \end{equation}
The result immediately follows from the above inequalities. ![]()
Remark.8. In view of the last Theorem, if we take
![]() $\Theta = {\rm ln} \ N$
, then we have
$\Theta = {\rm ln} \ N$
, then we have
and
For strongly convex case, using similar derivation, the high probability bound for objective error and constraint violation of SLG-ADMM is
 $${\rm Pr}\left \{ \left \| A\bar{x}_{N} + B\bar{y}_{N} - b \right \| \le \mathcal{O}\left ( \frac{\left(\ln N\right)^2}{N} \right ) \right \}\ge 1 - \frac{1}{N^{2/3} } - \frac{1}{N}, $$
$${\rm Pr}\left \{ \left \| A\bar{x}_{N} + B\bar{y}_{N} - b \right \| \le \mathcal{O}\left ( \frac{\left(\ln N\right)^2}{N} \right ) \right \}\ge 1 - \frac{1}{N^{2/3} } - \frac{1}{N}, $$
and
 $${\rm Pr}\left \{ \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) \le \mathcal{O}\left ( \frac{\left(\ln N\right)^2}{N} \right ) \right \}\ge 1 - \frac{1}{N^{2/3} } - \frac{1}{N} . $$
$${\rm Pr}\left \{ \theta \left( {{{\bar u}_N}} \right) - \theta \left( {{u^ * }} \right) \le \mathcal{O}\left ( \frac{\left(\ln N\right)^2}{N} \right ) \right \}\ge 1 - \frac{1}{N^{2/3} } - \frac{1}{N} . $$
Observe that the convergence rate of ergodic iterates of SLG-ADMM is obtained in (35). The high probability bound can be also established, which is shown as follows
where N is the iteration number. In contrast to (40) and (41), we can observe that the results in the last theorem are much finer.
4. Conclusion
In this paper, we analyze the expected convergence rates and the large deviation properties of a stochastic variant of generalized ADMM using the variational inequality framework. By means of this framework, the proof is very clear. When the model is deterministic and SFO is not needed, our proposed algorithm reduces to a generalized proximal ADMM, and the convergence region of
![]() $\alpha$
is the same as that in the corresponding literature.
$\alpha$
is the same as that in the corresponding literature.