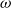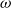Robustness is a property of system analyses, namely monotonic maps from the complete lattice of subsets of a (system’s state) space to the two-point lattice. The definition of robustness requires the space to be a metric space. Robust analyses cannot discriminate between a subset of the metric space and its closure; therefore, one can restrict to the complete lattice of closed subsets. When the metric space is compact, the complete lattice of closed subsets ordered by reverse inclusion is 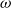 $\omega$-continuous, and robust analyses are exactly the Scott-continuous maps. Thus, one can also ask whether a robust analysis is computable (with respect to a countable base). The main result of this paper establishes a relation between robustness and Scott continuity when the metric space is not compact. The key idea is to replace the metric space with a compact Hausdorff space, and relate robustness and Scott continuity by an adjunction between the complete lattice of closed subsets of the metric space and the
$\omega$-continuous, and robust analyses are exactly the Scott-continuous maps. Thus, one can also ask whether a robust analysis is computable (with respect to a countable base). The main result of this paper establishes a relation between robustness and Scott continuity when the metric space is not compact. The key idea is to replace the metric space with a compact Hausdorff space, and relate robustness and Scott continuity by an adjunction between the complete lattice of closed subsets of the metric space and the 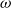 $\omega$-continuous lattice of closed subsets of the compact Hausdorff space. We demonstrate the applicability of this result with several examples involving Banach spaces.
$\omega$-continuous lattice of closed subsets of the compact Hausdorff space. We demonstrate the applicability of this result with several examples involving Banach spaces.