SPHERICAL REPRESENTATIONS FOR $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS

Abstract

We apply Takesaki’s and Connes’s ideas on structure analysis for type III factors to the study of links (a short term of Markov kernels) appearing in asymptotic representation theory.

1 Introduction

Asymptotic representation theory was initiated by Vershik and Kerov in around 1980, and investigates unitary characters of inductive limits of finite/compact groups. The theory has involved several operator algebraic tools such as AF-algebras with their dimension groups since its birth; see for example, [9]. The main classification problem (on factor representations) in the theory is described in terms of links (or equivalently, Markov kernels) on branching graphs; see for example, [1, 9]. (See Section 2 too for the definition of links.) For the infinite symmetric group, that is, the inductive limit of symmetric groups, the branching graph is a Young poset and the link is obtained from the multiplicity function that describes its branching rule. In this way, the study of asymptotic representation theory for ordinary groups can be studied by looking at only branching graphs. However, one can consider links that do not match multiplicity functions. Such a link naturally arises in the quantum group setting as an effect of q-deformation (see [7, 12]), and we have developed, in [18, 19], an abstract framework to discuss those from the viewpoint of Olshanski’s spherical representation theory in the general operator algebraic setting. The purpose of this paper is to introduce a new method of studying general links on branching graphs, which admits a K-theoretic interpretation.

Our operator algebraic, abstract framework is rather general, but it starts, in the context of this paper, with an inductive sequence $A_n$ of atomic $W^*$ -algebras with continuous flows $\alpha _n^t : \mathbb {R} \curvearrowright A_n$ , and then takes its ( $C^*$ -algebraic) inductive limit $(A,\alpha ^t) = \varinjlim (A_n,\alpha _n^t)$ . Such an inductive limit naturally arises when one considers the inductive limit of quantum unitary groups $\mathrm {U}_q(n)$ , that is, $A_n = W^*(\mathrm {U}_q(n))$ , the group $W^*$ -algebra of $\mathrm {U}_q(n)$ , and $\alpha _n^t$ is given by the so-called scaling automorphism group arising as a consequence of q-deformation. See [18, Section 4] for more details.

In our previous paper [19], we introduced the notion of $(\alpha ^t,\beta )$ -spherical representations with $\beta \in {\mathbb {R}}$ . An $(\alpha ^t,\beta )$ -spherical representation of A is a $*$ -representation $\Pi : A\otimes _{\mathrm {\max }} A^{\mathrm {op}} \curvearrowright {\mathcal {H}}_\Pi $ ( $\otimes _{\mathrm {\max }}$ denotes the maximal $C^*$ -tensor product and $A^{\mathrm {op}}$ the opposite algebra of A) together with a unit vector $\xi \in {\mathcal {H}}_\Pi $ with the following KMS-like property: for each $a \in A$ and each $\eta \in {\mathcal {H}}_\Pi $ , there is a bounded continuous function $F(z)$ on $0 \wedge (\beta /2) \leq \mathrm {Im}z \leq 0 \vee (\beta /2)$ such that $F(z)$ is holomorphic in its interior and

$$ \begin{align*} F(t) = (\Pi(\alpha^t(a)\otimes 1^{\mathrm{op}})\xi\,|\,\eta)_{{\mathcal{H}}_\Pi}, \quad F(t+i\beta/2) = (\Pi(1\otimes (\alpha^t(a))^{\mathrm{op}})\xi\,|\,\eta)_{{\mathcal{H}}_\Pi} \end{align*} $$

for all $t \in \mathbb {R}$ . See [19, Definition 5.1]. This definition may look technical but is equivalent to that

$$ \begin{align*} \Pi(a\otimes1^{\mathrm{op}})\xi = \Pi(1\otimes a^{\mathrm{op}})\xi, \quad a \in A \end{align*} $$

when $\alpha ^t$ is the trivial flow. Thus, the notion of $(\alpha ^t,\beta )$ -spherical representations is a natural abstraction of that of spherical representations for spherical pairs of ordinary (topological) groups $G < G\times G$ in the sense due to Olshanski. See the first several paragraphs of [19, Section 3] (and also see [18, Corollary 4.11]). The natural class of $(\alpha ^t,\beta )$ -spherical representations in the present context is given by locally bi-normal ones, that is, $(a,b^{\mathrm {op}}) \mapsto \Pi (a\otimes b^{\mathrm {op}})$ is separately normal on $A_n\times A_n^{\mathrm {op}}$ for each n. We have established a one-to-one correspondence between the equivalence classes of locally bi-normal $(\alpha ^t,\beta )$ -spherical representations and the locally normal $(\alpha ^t,\beta )$ -KMS states $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ (see [19, Theorem 5.7]). This correspondence explains that $K_{-1}^{\mathrm {ln}}(\alpha ^t)$ can naturally be understood as a counterpart of the space of unitary characters when $(A,\alpha ^t) = \varinjlim (A_n,\alpha _n^t)$ arises from an inductive limit of compact quantum groups; see [19, Section 6] and [18, Sections 4.1, 4.2]. Therefore, the analysis of Vershik–Kerov type should be the study of $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ in our abstract setup, and we work with $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ rather than $(\alpha ^t,\beta )$ -spherical representations themselves in this paper because the main focus here is to develop an analog of Vershik–Kerov’s theory.

Our framework naturally leads us to the use of Takesaki’s idea [13] on general structure analysis for type III factors (based on his celebrated duality theorem) and Connes’ idea [4] on almost-periodic weights in the study of links that do not match multiplicity functions. We apply the construction of Takesaki duals to the inductive sequence $(A_n,\alpha _n^t)$ and obtain a new inductive sequence $\widetilde {A}_n$ of atomic $W^*$ -algebras again equipped with actions $\widetilde {\alpha }_n^\gamma $ of discrete subgroup $\Gamma $ of the multiplicative group $\mathbb {R}_+^\times $ . We take the new ( $C^*$ -algebraic) inductive limit $(\widetilde {A},\widetilde {\alpha }^\gamma ) = \varinjlim (\widetilde {A}_n,\widetilde {\alpha }_n^\gamma )$ , and then $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ are shown to be affine-isomorphic to the tracial weights $\tau $ on $\widetilde {A}$ that are locally normal semifinite and suitably scaling under $\widetilde {\alpha }^\gamma $ . This procedure is explained in Section 3. We then interpret this procedure in terms of links on branching graphs. This is done in Section 4. A consequence is that the study of a general link on a branching graph is reduced to that of the link arising from the multiplicity function on an extended branching graph with group action. This new approach allows us to use the notion of dimension groups explicitly. The reader who is only interested in the study of links may directly go to Section 4.3, where the present method is given without appealing to any operator algebras. In Section 5, we examine a relation between the present method and K-theory. A consequence is to give a way to connect the study of general links to $K_0$ -groups. In Section 6, we examine the present method with the infinite dimensional quantum unitary group $\mathrm {U}_q(\infty )$ , whose formulation was precisely given in part II of this series of papers. The consequence there explains that the present method is closed in the class of inductive limits of compact quantum groups and should be regarded as a way to make the special positive elements $\rho _n \in \mathcal {U}(\mathrm {U}_q(n))$ , $n=0,1,\ldots $ (see, for example, [18, equation (4.5)]) form an inductive sequence by enlarging the algebras in question. See Section 6.2.

We use the following notation rule: $\mathcal {F} \Subset \Gamma $ means that $\mathcal {F}$ is a finite subset of a set  $\Gamma $ . For a $C^*$ -algebra C, we denote by $C_+$ the cone of its positive elements. We also mention that our main references on operator algebras are still Bratteli and Robinson’s books [2, 3] as well as our previous two papers [18, 19], but we have to refer to Takesaki’s book vol.II [15] concerning weights on $C^*$ -/ $W^*$ -algebras and the so-called Tomita–Takesaki theory with its applications to type III factors.

2 General setup and necessary concepts

Let $A_n$ , $n=1,2,\ldots $ be atomic $W^*$ -algebras with separable preduals, and put ${A_0=\mathbb {C}1}$ . We assume that the $A_n$ form an inductive sequence by unital normal embeddings $A_n \hookrightarrow A_{n+1}$ , $n=0,1,\ldots .$ Let $A = \varinjlim A_n$ be the inductive (direct) limit $C^*$ -algebra. For each n, we denote by $\mathfrak {Z}_n$ all the minimal projections in the center $\mathcal {Z}(A_n)$ .

Assume that we have a flow $\alpha : \mathbb {R} \curvearrowright A$ such that $\alpha ^t(A_n) = A_n$ holds for every $t\in \mathbb {R}$ and $n\geq 0$ (that is, $\alpha ^t$ is an inductive flow) and moreover that the restriction of $\alpha ^t$ to each $A_n$ , denoted by $\alpha _n^t : \mathbb {R} \curvearrowright A_n$ , is continuous in the u-topology, that is, ${\Vert \omega \circ \alpha _n^t - \omega \Vert \to 0}$ as $t\to 0$ for all $\omega \in A_n{}_*$ (note that the u-topology is the most natural topology on automorphisms of $W^*$ -algebras and dates back to Haagerup’s work [8, Definition 3.4]). The u-continuity assumption makes every flow $\alpha _n^t$ fix elements in $\mathcal {Z}(A_n)$ . See [19, Lemma 7.1] for details. Thus, for each $z \in \mathfrak {Z}_n$ , $n \geq 0$ , the restriction of $\alpha _n^t$ to $zA_n$ defines a ‘local’ flow $\alpha _z^t$ .

For each $z\in \mathfrak {Z}_n$ , $zA_n$ is identified with all the bounded operators $B({\mathcal {H}}_z)$ on a Hilbert space ${\mathcal {H}}_z$ , since $A_n$ is atomic. Then, for each $z \in \mathfrak {Z}_n$ , $n \geq 0$ , we can find a unique (up to positive scaling) nonsingular positive self-adjoint operator $\rho _z$ affiliated with $zA_n = B({\mathcal {H}}_z)$ such that $\alpha _z^t = \mathrm {Ad}\rho _z^{it}$ for every $t \in \mathbb {R}$ . Throughout this paper, we consider only the case when all $\rho _z$ are diagonalizable. This is fulfilled when all the dimensions $\dim (z) := \dim ({\mathcal {H}}_z)<\infty $ .

To the inductive sequence $A_n$ , we associate a branching graph together with multiplicity function as follows. The vertex set is $\mathfrak {Z} = \bigsqcup _{n\geq 0}\mathfrak {Z}_n$ , and the multiplicity function $m : \bigsqcup _{n\geq 0} \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n \to \mathbb {N}\cup \{0,\infty \}$ is defined to be the multiplicity of ${z' A_n = B({\mathcal {H}}_{z'})}$ in $zA_{n+1} = B({\mathcal {H}}_z)$ via $A_n \hookrightarrow A_{n+1}$ for $(z,z') \in \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ . We observe that

$$ \begin{align*} \bigcup_{z'\in\mathfrak{Z_n}} \{z \in \mathfrak{Z}_{n+1}; m(z,z')> 0\} = \mathfrak{Z}_{n+1}, \quad \bigcup_{z\in\mathfrak{Z}_{n+1}} \{z' \in \mathfrak{Z}_n; m(z,z') > 0\} = \mathfrak{Z}_n \end{align*} $$

for all $n\geq 0$ , and

$$ \begin{align*} \mathrm{Tr}(zz') = m(z,z')\,\dim(z'), \quad (z,z') \in \bigsqcup_{n\geq0} \mathfrak{Z}_{n+1}\times\mathfrak{Z}_n \end{align*} $$

hold, where $\mathrm {Tr}$ stands for the nonnormalized trace on $zA_{n+1} = B({\mathcal {H}}_z)$ . We also remark that

$$ \begin{align*} \dim(z) = \sum_{z' \in \mathfrak{Z}_{n-1}} m(z,z') \dim(z') = \cdots = \sum_{z_i \in \mathfrak{Z}_i (i=1,\ldots,n-1)} m(z,z_{n-1})\cdots m(z_2,z_1) m(z_1,1) \end{align*} $$

for every $z \in \mathfrak {Z}_n$ . The edge set is defined to be all the $(z,z') \in \bigsqcup _{n\geq 0} \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ with $m(z,z')> 0$ . We have shown (see [19, Section 9]) that the graph $(\mathfrak {Z},m)$ completely remembers the inductive sequence $A_n$ .

Let an inverse temperature $\beta \in \mathbb {R}$ be fixed throughout in such a way that $\mathrm {Tr}(\rho _z^{-\beta }) < \infty $ for all $z \in \mathfrak {Z}_n$ , $n\geq 1$ . For each $z \in \mathfrak {Z}_n$ , $n\geq 0$ , a unique (faithful, normal) $(\alpha _z^t,\beta )$ -KMS state $\tau _z^\beta = \tau ^{(\alpha _z^t,\beta )}$ on $zA_n = B({\mathcal {H}}_z)$ is given by

$$ \begin{align*} x \in B({\mathcal{H}}_z) \mapsto \tau_z^\beta(x) := \frac{\mathrm{Tr}(\rho_z^{-\beta} x)}{\mathrm{Tr}(\rho_z^{-\beta})} \in \mathbb{C}. \end{align*} $$

In what follows, we write $\dim _\beta (z) = \dim _{(\alpha ^t,\beta )}(z) := \mathrm {Tr}(\rho _z^{-\beta })$ .

We discussed, in [18, 19], locally normal $(\alpha ^t,\beta )$ -spherical representations, or equivalently, locally normal $(\alpha ^t,\beta )$ -KMS states for $A = \varinjlim A_n$ , whose classification problem can be discussed in terms of links over $\mathfrak {Z} = \bigsqcup _{n\geq 0}\mathfrak {Z}_n$ . See Section 1 too on this point. Here we recall the notion of links. A function $\lambda : \bigsqcup _{n\geq 0} \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n \to [0,1]$ is called a link (a synonym of a Markov kernel) if $\lambda (z,\,\cdot \,)$ gives a (discrete) probability measure on $\mathfrak {Z}_n$ for every $z \in \mathfrak {Z}_{n+1}$ .

In the present setting, the link $\kappa = \kappa _{(\alpha ^t,\beta )} : \bigsqcup _{n\geq 0} \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n \to [0,1]$ is given by

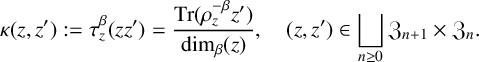(2-1) $$ \begin{align} \kappa(z,z') := \tau_z^\beta(zz') = \frac{\mathrm{Tr}(\rho_z^{-\beta}z')}{\dim_\beta(z)}, \quad (z,z') \in \bigsqcup_{n\geq0} \mathfrak{Z}_{n+1}\times\mathfrak{Z}_n. \end{align} $$

If $\beta =0$ and all $\dim (z) < \infty $ , then $\dim _\beta (z) = \dim (z)$ holds for every $z \in \mathfrak {Z}$ and the link $\kappa (z,z')$ is nothing less than

$$ \begin{align*} \mu(z,z') := \frac{1}{\dim(z)}\,m(z,z')\,\dim(z'), \quad (z,z') \in \bigsqcup_{n\geq0} \mathfrak{Z}_{n+1}\times\mathfrak{Z}_n. \end{align*} $$

We call this special link $\mu : \bigsqcup _{n\geq 0} \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n \to [0,1]$ the standard link (this is available only when all $\dim (z)<\infty $ ). The standard link fits the notion of dimension groups, but other links do not. Consequently, to a given branching graph $(\mathfrak {Z},m)$ , we associate the standard link $\mu $ under all the $\dim (z)<\infty $ , but a nonstandard link on $(\mathfrak {Z},m)$ can also be considered even when $\mu $ cannot. Moreover, we illustrated in [19, Section 9] how any nonstandard link arises in the spherical representation theory for a certain class of $C^*$ -flows.

3 $\rho $ -Extension

We fix a family $\rho = \{\rho _z\}_{z\in \mathfrak {Z}}$ as in Section 2, that is, each $\rho _z^{it}$ implements the restriction $\alpha _z^t$ of $\alpha _n^t$ to $zA_n$ , $z \in \mathfrak {Z}_n \subset \mathfrak {Z}$ , and all $\rho _z$ are diagonalizable. Let $\Gamma =\Gamma (\rho )$ be the discrete (countable) subgroup generated by all the eigenvalues of $\rho _z$ in the multiplicative group $\mathbb {R}_+^\times = (0,\infty )$ . Let $G = \widehat {\Gamma }$ be the dual compact abelian group of $\Gamma $ . There is a continuous homomorphism from $\mathbb {R}$ into G with dense image such that $\langle \gamma ,t\rangle = \gamma ^{it}$ holds for every $\gamma \in \Gamma $ when $t \in \mathbb {R}$ is regarded as an element of G via the homomorphism, where $\langle \,\cdot \,,\,\cdot \,\rangle : \Gamma \times G \to \mathbb {T}$ is the dual pairing. It is evident that every unitary representation $t\mapsto u_z(t) = \rho _z^{it}$ of the real numbers $\mathbb {R}$ uniquely extends to G by using the spectral decomposition of $\rho _z$ , and hence so does every flow $\alpha _n^t$ .

For each $n=0,1,\ldots ,$ we take the $W^*$ -crossed product $\widetilde {A}_n := A_n\bar {\rtimes }_{\alpha _n^g} G$ , whose construction (see for example, [2, Definition 2.7.3]) is reviewed in our convenient way as follows. Since $A_n$ has separable predual and thus is $\sigma $ -finite, $A_n$ acts on a Hilbert space $\mathcal {K}_n$ with a separating and cyclic vector. (See for example, [2, Proposition 2.5.6].) Let $L^2(G;\mathcal {K}_n)$ be the $\mathcal {K}_n$ -valued $L^2$ -space over G with respect to the Haar probability measure $dg$ , which can be identified with the completion of the $\mathcal {K}_n$ -valued continuous functions $C(G;\mathcal {K}_n)$ equipped with inner product

$$ \begin{align*} (\xi\,|\,\eta) := \int_G (\xi(g)\,|\,\eta(g))_{\mathcal{K}_n}\,dg, \quad \xi, \eta \in C(G;\mathcal{K}_n). \end{align*} $$

We define an injective normal $*$ -homomorphism $\pi _{\alpha _n} : A_n \to B(L^2(G;\mathcal {K}_n))$ by

$$ \begin{align*} (\pi_{\alpha_n}(a)\xi)(g) := \alpha_n^{g^{-1}}(a)\xi(g), \quad a \in A_n, \quad \xi \in C(G;\mathcal{K}_n) \subset L^2(G;\mathcal{K}_n). \end{align*} $$

Let $\lambda : G \curvearrowright L^2(G;\mathcal {K}_n)$ be the unitary representation defined by

$$ \begin{align*} (\lambda(g_1)\xi)(g_2):=\xi(g_1^{-1}g_2), \quad g_1,g_2 \in G, \quad \xi \in C(G;\mathcal{K}_n) \subset L^2(G;\mathcal{K}_n). \end{align*} $$

We have a natural identification $L^2(G;\mathcal {K}_n) = \mathcal {K}_n\,\bar {\otimes }\,L^2(G)$ by

$$ \begin{align*} (\xi\otimes f)(g) = f(g)\xi, \quad \xi \in \mathcal{K}_n, \quad f \in C(G) \subset L^2(G), \end{align*} $$

where $C(G) \subset L^2(G)$ denote the continuous functions on G and the $L^2$ -space over G with respect to $dg$ , respectively. Via the identification, we set

$$ \begin{align*} \lambda(g) := 1\otimes\lambda_g, \quad g \in G \end{align*} $$

with the left regular representation $\lambda _g$ of G. Then, the $W^*$ -crossed product $A_n\bar {\rtimes }_{\alpha _n^g} G$ is the $W^*$ -subalgebra of $A_n\,\bar {\otimes }\,B(L^2(G))$ generated by $\pi _{\alpha _n}(A_n)$ and $\lambda (G)$ in $A_n\,\bar {\otimes }\,B(L^2(G))$ with the covariant relation

$$ \begin{align*} \lambda(g)\pi_{\alpha_n}(a) = \pi_{\alpha_n}(\alpha_n^g(a))\lambda(g), \quad a \in A_n, \quad g \in G. \end{align*} $$

Note that (the algebraic structure of) the resulting $W^*$ -algebra $A_n\bar {\rtimes }_{\alpha _n^g} G$ is known to be independent of the choice of representation $A_n \subset B(\mathcal {K}_n)$ ; see [15, Section X.1].

We observe that $\widetilde {A}_0 = \mathbb {C}1\bar {\rtimes }G \cong \ell ^\infty (\Gamma )$ is given by

$$ \begin{align*} e_\gamma = \int_G \overline{\langle \gamma, g\rangle}\,\lambda(g)\,dg \longleftrightarrow \delta_\gamma, \end{align*} $$

where $\delta _\gamma $ is the Dirac function at $\gamma $ . The so-called dual action $\widetilde {\alpha }_n : \Gamma \curvearrowright \widetilde {A}_n$ (see for example, [2, Definition 2.7.3]) can be constructed in such a way that

$$ \begin{align*} \widetilde{\alpha}_n^\gamma(\pi_{\alpha_n}(a)) = \pi_{\alpha_n}(a), \quad \widetilde{\alpha}_n^\gamma(\lambda(g)) = \overline{\langle \gamma,g\rangle}\,\lambda(g) \quad a \in A_n, \quad \gamma \in \Gamma, \quad g \in G, \end{align*} $$

and the latter relation is rephrased as

(3-1) $$ \begin{align} \widetilde{\alpha}_n^\gamma(e_{\gamma'}) = e_{\gamma\gamma'}, \quad \gamma,\gamma' \in \Gamma. \end{align} $$

Since $\alpha _{n+1}^g = \alpha _n^g$ holds on $A_n$ for every $g \in G$ , we have a normal embedding ${\widetilde {A}_n \hookrightarrow \widetilde {A}_{n+1}}$ determined by

(3-2) $$ \begin{align} \pi_{\alpha_n}(a) \mapsto \pi_{\alpha_{n+1}}(a), \quad a \in A_n. \end{align} $$

Hence, the $\widetilde {A}_n$ form an inductive sequence, and let $\widetilde {A} := \varinjlim \widetilde {A}_n$ be the inductive limit $C^*$ -algebra. Moreover, since

there is a unique injective $*$ -homomorphism $\pi _\alpha := \varinjlim \pi _{\alpha _n} : A = \varinjlim A_n \to \widetilde {A} = \varinjlim \widetilde {A}_n$ such that $\pi _\alpha (a) = \pi _{\alpha _m}(a)$ in $\widetilde {A}$ for every $a \in A_n$ and $m\geq n$ . By (3-1) and (3-2), we can take the inductive limit action $\widetilde {\alpha } := \varinjlim \widetilde {\alpha }_n : \Gamma \curvearrowright \widetilde {A}$ , which acts on $\pi _\alpha (A)$ trivially.

Definition 3.1. We call $(\widetilde {\alpha } : \Gamma \curvearrowright \widetilde {A} = \varinjlim \widetilde {A}_n)$ as above the $\rho $ -extension of ${(A,\alpha ^t) = \varinjlim (A_n,\alpha _n^t)}$ .

We remark that $\Gamma $ is not a canonical object of the flow $\alpha ^t$ because it depends on the choice of $\rho _z$ . In the next section, we select $\Gamma $ to be a canonical object under an additional assumption on $A = \varinjlim A_n$ .

Following a standard strategy in operator algebras dating back to Takesaki’s structure theorem for type III factors (see for example, [15, Section XII.1]), we interpret $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ as a suitable class of tracial weights on $\widetilde {A}$ .

We start with necessary concepts/facts on (tracial) weights on $C^*$ -algebras (see [15, Ch. VII] as well as [14, Section V.2]). A weight $\psi $ on a $C^*$ -algebra C means a map from $C_+$ to $[0,+\infty ]$ such that

$$ \begin{align*} \psi(c_1+c_2) &= \psi(c_1)+\psi(c_2), \quad c_1,c_2 \in C_+, \\ \psi(t c) &= t\psi(c), \quad t \in [0,+\infty), \quad c \in C_+ \end{align*} $$

with the convention $0\times (+\infty )=0$ . We call $\psi $ a tracial weight if, in addition, ${\psi (c^* c) = \psi (cc^*)}$ holds for any $c \in C$ . The definition domain $\mathfrak {m}_\psi $ of $\psi $ is defined to be the linear span of all the $c_1^* c_2$ with $\psi (c_k^* c_k) < +\infty $ , $k=1,2$ . By the polarization identity, we can extend $\psi $ to $\mathfrak {m}_\psi $ as a linear functional. When $\psi $ is tracial, $\psi $ satisfies that $\psi (c_1 c_2) = \psi (c_2 c_1)$ if one of $c_i \in C$ falls into $\mathfrak {m}_\psi $ ; see the proof of [14, Lemma V.2.16]. When C is a $W^*$ -algebra, $\psi $ is said to be normal if $c_i \nearrow c$ in $C_+$ implies $\psi (c_i) \nearrow \psi (c)$ , and also semifinite if C is generated as a $W^*$ -algebra by all the $c \in C_+$ with $\psi (c) < +\infty $ .

Definition 3.2. (1) An $(\widetilde {\alpha }^\gamma ,\beta )$ -scaling trace is defined to be a tracial weight ${\tau : (\widetilde {A})_+ \to [0,\infty ]}$ such that:

1. (i) for each $x \in \widetilde {A}$ and each n, the mapping $y \in (\widetilde {A}_n)_+ \mapsto \tau (xyx^*) \in [0,+\infty ]$ is normal;

2. (ii) $\tau \circ \widetilde {\alpha }^\gamma = \gamma ^\beta \,\tau $ for all $\gamma \in \Gamma $ ;

3. (iii) $\tau (e_1) = 1$ .

The set of all $(\widetilde {\alpha }^\gamma ,\beta )$ -scaling traces is denoted by $TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ .

(2) We define a normal semifinite weight $\mathrm {tr}_\beta : (\widetilde {A}_0)_+ \to [0,\infty ]$ by $\mathrm {tr}_\beta (e_\gamma ) = \gamma ^\beta $ for every $\gamma \in \Gamma $ .

Note that items (ii), (iii) in part (1) imply that $\tau (e_\gamma ) = \gamma ^\beta $ for every $\gamma \in \Gamma $ so that $\tau $ is semifinite on each $\widetilde {A}_n$ . In fact, letting $e_{\mathcal {F}} := \sum _{\gamma \in \mathcal {F}} e_\gamma $ with $\mathcal {F} \Subset \Gamma $ , we see that $\bigcup _{\gamma \in \mathcal {F}} e_{\mathcal {F}} (\widetilde {A}_n)_+ e_{\mathcal {F}}$ is $\sigma $ -weakly dense in $(\widetilde {A}_n)_+$ and items (ii), (iii) imply $0\leq \tau (e_{\mathcal {F}} x e_{\mathcal {F}}) \leq \Vert x\Vert \,\sum _{\gamma \in \mathcal {F}}\gamma ^\beta < +\infty $ for any $x \in (\widetilde {A}_n)_+$ .

Lemma 3.3. For each $\omega \in K_\beta ^{\mathrm {ln}}(\alpha ^t)$ , the restriction of $\omega \,\bar {\otimes }\,\mathrm {id} : A_n\,\bar {\otimes }\,B(L^2(G)) \to \mathbb {C}1\,\bar {\otimes }\,B(L^2(G))$ (the composition of $x \mapsto 1\otimes x$ and the normal slice map $R_\omega : A\,\bar {\otimes }\,B(L^2(G))$ sending $a\otimes x$ to $\omega (a)x$ ; see for example, [16]) to $\widetilde {A}_n = A_n\,\bar {\rtimes }_{\alpha _n}\,G$ defines a unique normal conditional expectation $\widetilde {E}_{\omega ,n} : \widetilde {A}_n \twoheadrightarrow \widetilde {A}_0$ such that $\widetilde {E}_{\omega ,n}(\pi _{\alpha _n}(a)) = \omega (a)1$ for every $a \in A_n$ . Then, $\widetilde {E}_{\omega ,n+1}$ coincides with $\widetilde {E}_{\omega ,n}$ on $\widetilde {A}_n$ , and the inductive limit conditional expectation $\widetilde {E}_\omega := \varinjlim \widetilde {E}_{\omega ,n}$ from $\widetilde {A}=\varinjlim \widetilde {A}_n$ onto $\widetilde {A}_0$ is well defined.

Proof. Since the image of $\mathbb {R}$ in G is dense and $\omega \circ \alpha ^t = \omega $ for all $t \in \mathbb {R}$ , we have $\omega \circ \alpha _n^g(a) = \omega (a)$ for all $g \in G$ and $a \in A_n$ . By [2, Theorem 2.5.31(a)], we can choose a representing vector $\xi \in \mathcal {K}_n$ of the restriction of $\omega $ to $A_n$ , so that $\omega (a) = (a\,\xi \,|\,\xi )_{\mathcal {K}_n}$ holds for every $a \in A_n$ . We observe that $(R_\omega (x)f_1\,|\,f_2)_{L^2(G)} = (x\,\xi \otimes f_1\,|\,\xi \otimes f_2)_{\mathcal {K}_n\,f_2\bar {\otimes }\,L^2(G)}$ by definition, for all $x \in A_n\,\bar {\otimes }\,B(L^2(G))$ and $f_1,f_2 \in L^2(G)$ . By the identification $L^2(G;\mathcal {K}_n) = \mathcal {K}_n\,\bar {\otimes }\,L^2(G)$ ,

$$ \begin{align*} (\pi_{\alpha_n}(a)\,\xi\otimes f_1\,|\,\xi\otimes f_2)_{\mathcal{K}_n\,\bar{\otimes}\,L^2(G)} &= \int_G (\alpha_n^{g^{-1}}(a)\xi\,|\,\xi)_{\mathcal{K}_n}\,f_1(g)\overline{f_2(g)}\,dg \\ &= \int_G \omega(\alpha_n^{g^{-1}}(a))\,f_1(g)\overline{f_2(g)}\,dg \\ &= \omega(a)\,(f_1\,|\,f_2)_{L^2(G)} \end{align*} $$

for all $a \in A_n$ and $f_1,f_2 \in C(G) \subset L^2(G)$ . We conclude that $R_\omega (\pi _{\alpha _n}(a)) = \omega (a)\,1_{L^2(G)}$ and hence $(\omega \,\bar {\otimes }\,\mathrm {id})(\pi _{\alpha _n}(a)) = \omega (a)\,1$ for all $a \in A_n$ . Since the $\pi _{\alpha _n}(a)\lambda (g)$ form a $\sigma $ -weakly total subset of $\widetilde {A}_n$ , it follows that $(\omega \,\bar {\otimes }\,\mathrm {id})(\widetilde {A}_n) = \widetilde {A}_0$ and hence the restriction of $\omega \,\bar {\otimes }\,\mathrm {id}$ to $\widetilde {A}_n$ gives the desired conditional expectation $\widetilde {E}_{\omega ,n}$ . The rest of the assertion is now obvious.

Lemma 3.4. For each $\omega \in K_\beta ^{\mathrm {ln}}(\alpha ^t)$ , the weight $\tau _\omega := \mathrm {tr}_\beta \circ \widetilde {E}_\omega : \widetilde {A}_+ \to [0,\infty ]$ becomes an $(\widetilde {\alpha }^\gamma ,\beta )$ -scaling trace.

Proof. We have to confirm that $\tau _\omega $ satisfies items (i)–(iii) of Definition 3.2(1).

We remark that the restriction of $\omega $ to $A_n$ becomes $\sum _{z \in \mathfrak {Z}_n} \omega (z)\,\tau _z^\beta $ (see [19, Lemma 7.3]). We set $s := \sum _{z \in \mathfrak {Z}_n} \mathbf {1}_{(0,1]}(\omega (z))\,z \in \mathcal {Z}(A_n)$ , which is the support projection of the restriction of $\omega $ to $A_n$ , that is, $\omega $ is faithful on $sA_n$ and identically zero on $(1-s)A_n$ . One can easily confirm that $\omega $ enjoys the $(\alpha _n^{-\beta t},-1)$ -KMS condition, and hence the restriction of $\alpha _n^{-\beta t}$ to $sA_n$ gives the modular automorphism group associated with the restriction of $\omega $ to $sA_n$ by [3, Theorem 5.3.10].

We observe that $\pi _{\alpha _n}(s) \kern1.3pt{=}\kern1.3pt s\otimes 1 \kern1.3pt{\in}\kern1.3pt \mathcal {Z}(\widetilde {A}_n)$ ; so, $\pi _{\alpha _n}(s)\widetilde {A}_n \kern1.3pt{=}\kern1.3pt (sA_n)\bar {\rtimes }_{\alpha _n}G \subset (sA_n)\kern1.3pt{\bar {\otimes} }\kern1.3pt B(L^2(G))$ by its construction. We have a bijective $*$ -homomorphism $\iota : \pi _{\alpha _n}(s)\widetilde {A}_0 \to \widetilde {A}_0$ sending $\lambda ^{(0)}(g) := \pi _{\alpha _n}(s)\lambda (g) = s\otimes \lambda _g$ to $1\otimes \lambda _g = \lambda (g)$ for any $g \in G$ . With

$$ \begin{align*} e_\gamma^{(00)} := \int_G \overline{\langle \gamma,g\rangle}\lambda_g\,dg, \quad \gamma \in \Gamma, \end{align*} $$

we observe that the bijective $*$ -homomorphism $\iota $ sends $e_\gamma ^{(0)} := s\otimes e^{(00)}_\gamma $ to $1\otimes e^{(00)}_\gamma = e_\gamma $ for every $\gamma \in \Gamma $ . For a while, we work with $\pi _{\alpha _n}(s)\widetilde {A}_n = (sA_n)\bar {\rtimes }_{\alpha _n^g}G$ whose generators are $\pi _{\alpha _n}(a)$ ( $a \in sA_n$ ) as well as $\lambda ^{(0)}(g)$ ( $g \in G$ ) or $e^{(0)}_\gamma $ ( $\gamma \in \Gamma $ ) along the lines of proof of [17, Theorem 1].

Let $\tilde {\omega }$ be the dual weight on $(sA_n)\bar {\rtimes }_{\alpha _n^g}G$ constructed out of the restriction of $\omega $ to $sA_n$ (see [15, Definition X.1.16, Lemma X.1.18]), which satisfies that

$$ \begin{align*} \tilde{\omega}\bigg(\bigg(\int_G \lambda^{(0)}(g)\pi_{\alpha_n}(a(g))\,dg\bigg)^*\bigg(\int_G \lambda^{(0)}(g)\pi_{\alpha_n}(a(g))\,dg\bigg)\bigg) = \int_G \omega(a(g)^* b(g))\,dg \end{align*} $$

for any $\sigma $ -strong $^*$ -continuous functions $a,b : G \to sA_n$ , where $\tilde {\omega }$ extends to its definition domain $\mathfrak {m}_{\tilde {\omega }}$ . Moreover, its modular automorphism $\sigma _t^{\tilde {\omega }}$ satisfies that

$$ \begin{align*} \sigma_t^{\tilde{\omega}}(\pi_{\alpha_n}(a)) = \pi_{\alpha_n}(\alpha_n^{-\beta t}(a)), \quad \sigma_t^{\tilde{\omega}}(\lambda^{(0)}(g)) = \lambda^{(0)}(g) \end{align*} $$

for all $a \in sA_n$ and $g \in G$ . In particular, we obtain $\sigma _t^{\widetilde {\omega }} = \mathrm {Ad}\lambda ^{(0)}(-\beta t)$ for every ${t \in \mathbb {R}}$ . Also, we have $\tilde {\omega }(e^{(0)}_\gamma ) = \tilde {\omega }(e^{(0)}_\gamma e^{(0)}_\gamma ) = \int _G dg = 1$ , and hence the restriction of $\tilde {\omega }$ to $\lambda ^{(0)}(G)"$ is semifinite. Thus, Takesaki’s theorem [15, Theorem IX.4.2] guarantees that there is a unique faithful normal conditional expectation $E : (sA_n) \bar {\rtimes }_{\alpha _n^g}G \to \lambda ^{(0)}(G)"$ with $\tilde {\omega }\circ E = \tilde {\omega }$ . Then

$$ \begin{align*} \tilde{\omega}(E(\pi_{\alpha_n}(a)) e^{(0)}_\gamma) &= \tilde{\omega}\circ E(e^{(0)}_\gamma \pi_{\alpha_n}(a) e^{(0)}_\gamma) = \tilde{\omega}(e^{(0)}_\gamma\pi_{\alpha_n}(a) e^{(0)}_\gamma)\\ &= \int_G \omega(a)\,dg = \omega(a)\,\tilde{\omega}(e^{(0)}_\gamma), \end{align*} $$

implying that $E(\pi _{\alpha _n}(a)) = \omega (a)1$ for every $a \in sA_n$ because $\tilde {\omega }(e^{(0)}_\gamma ) = 1$ . Since

$$ \begin{align*} \lambda^{(0)}(-\beta t) = \sum_{\gamma \in \Gamma} \langle\gamma,-\beta t\rangle e^{(0)}_\gamma = \sum_{\gamma \in \Gamma} \gamma^{i(-\beta t)}\,e^{(0)}_\gamma = \bigg(\sum_{\gamma\in\Gamma}\gamma^{-\beta}\,e^{(0)}_\gamma\bigg)^{it} =: H^{it} \end{align*} $$

(H is a nonsingular positive self-adjoint operator affiliated with $\lambda ^{(0)}(G)"$ ), [15, Theorem VIII.3.14] and its proof show that a semifinite normal tracial weight on $(sA_n)\bar {\rtimes }_{\alpha _n^g}G$ can be defined to be $\tilde {\omega }(H^{-1}(\,\cdot \,))$ (which needs some justification; see [15, Lemma VIII.2.8]). Then we can easily verify $\tilde {\omega }(H^{-1}E(\,\cdot \,)) = \tilde {\omega }(H^{-1}(\,\cdot \,))$ , since H is affiliated with $\lambda ^{(0)}(G)"$ . We observe that $H^{-1}e^{(0)}_\gamma = \gamma ^\beta \,e^{(0)}_\gamma $ and hence $\tilde {\omega }(H^{-1}e^{(0)}_\gamma ) = \gamma ^\beta \,\tilde {\omega }(e^{(0)}_\gamma ) = \gamma ^\beta $ for every $\gamma \in \Gamma $ .

Since

$$ \begin{align*} \widetilde{E}_{\omega,n}(\pi_{\alpha_n}(a)\lambda(g)) = \omega(a)\lambda(g) = \omega(sa)\iota(\lambda^{(0)}(g)) = \iota(E(\pi_{\alpha_n}(s)\pi_{\alpha_n}(a)\lambda^{(0)}(g))) \end{align*} $$

for any $a \in A_n$ and $g \in G$ , we have $\widetilde {E}_{\omega ,n}(x) = \iota (E(\pi _{\alpha _n}(s)x))$ for every $x \in \widetilde {A}_n$ . Since $\mathrm {tr}_\beta (\iota (e^{(0)}_\gamma )) = \mathrm {tr}_\beta (e_\gamma ) = \gamma ^\beta = \tilde {\omega }(H^{-1} e^{(0)}_\gamma )$ for every $\gamma \in \Gamma $ , we also have $\mathrm {tr}_\beta \circ \iota = \tilde {\omega }(H^{-1}(\,\cdot \,))$ on $(\widetilde {A}_0)_+$ . Therefore,

$$ \begin{align*} \mathrm{tr}_\beta\circ\widetilde{E}_{\omega,n}(x) = \mathrm{tr}_\beta(\iota(E(\pi_{\alpha_n}(s)x))) = \tilde{\omega}(H^{-1}E(\pi_{\alpha_n}(s)x)) = \tilde{\omega}(H^{-1}\pi_{\alpha_n}(s)x) \end{align*} $$

for every $x \in (\widetilde {A}_n)_+$ . Since $\tau _\omega $ coincides with $\mathrm {tr}_\beta \circ \widetilde {E}_{\omega ,n}$ on $\widetilde {A}_n$ , it must be a normal semifinite tracial weight on $\widetilde {A}_n$ .

Let $x \in \widetilde {A}$ be arbitrarily chosen. Choose a sequence $x_k \in \bigcup _{n\geq 0}\widetilde {A}_n$ in such a way that $\Vert x_k - x\Vert \to 0$ as $k\to \infty $ .

For any net $y_\lambda \nearrow y$ in $(\widetilde {A}_n)_+$ ,

$$ \begin{align*} \limsup_\lambda |\phi(E_\omega(x y_\lambda x^*) - E_\omega(x y x^*))| \leq 2\Vert\phi\Vert\,\Vert y\Vert\,(\Vert x\Vert + \Vert x_k\Vert)\,\Vert x_k - x\Vert \overset{k\to\infty}{\to} 0 \end{align*} $$

for every normal linear functional $\phi $ on $\widetilde {A}_0$ , since the $x_k y_\lambda x_k^*$ and $x_k y x_k^*$ fall into some $\widetilde {A}_m$ with $m \geq n$ for a fixed k, and since the restriction of $E_\omega $ to $\widetilde {A}_m$ is normal. Hence, we conclude that $E_\omega (x y_\lambda x^*) \nearrow E_\omega (xyx^*)$ , that is, $y \in \widetilde {A}_0 \mapsto E_\omega (xyx^*) \in \widetilde {A}_0$ is a normal map. It follows that $\tau _\omega = \mathrm {tr}_\beta \circ E_\omega $ satisfies item (i) thanks to the normality of $\mathrm {tr}_\beta $ .

Let $\mathcal {F}_1,\mathcal {F}_2 \Subset \Gamma $ be arbitrarily given. For each k, $e_{\mathcal {F}_2}x_k e_{\mathcal {F}_1}$ falls in some $\widetilde {A}_n$ , and what we have proved above shows that $\tau _\omega (e_{\mathcal {F}_1}x_k^* e_{\mathcal {F}_2} x_k e_{\mathcal {F}_1}) = \tau _\omega (e_{\mathcal {F}_2} x_k e_{\mathcal {F}_1} x_k^* e_{\mathcal {F}_2})$ , since $\tau _\omega $ coincides with $\mathrm {tr}_\beta \circ \widetilde {E}_{\omega ,n}$ on $\widetilde {A}_n$ . By the dominated convergence theorem (note, $\widetilde {A}_0 \cong \ell ^\infty (\Gamma )$ is pointed out before),

$$ \begin{align*} \tau_\omega(e_{\mathcal{F}_1}x_k^* e_{\mathcal{F}_2} x_k e_{\mathcal{F}_1}) = \mathrm{tr}_\beta(\widetilde{E}_\omega(x_k^* e_{\mathcal{F}_2} x_k) e_{\mathcal{F}_1}) &\to \mathrm{tr}_\beta(\widetilde{E}_\omega(x^* e_{\mathcal{F}_2} x) e_{\mathcal{F}_1}) = \tau_\omega(e_{\mathcal{F}_1}x^* e_{\mathcal{F}_2} x e_{\mathcal{F}_1}), \\ \tau_\omega(e_{\mathcal{F}_2}x_k e_{\mathcal{F}_1} x_k^* e_{\mathcal{F}_2}) = \mathrm{tr}_\beta(\widetilde{E}_\omega(x_k e_{\mathcal{F}_1} x_k^*) e_{\mathcal{F}_2}) &\to \mathrm{tr}_\beta(\widetilde{E}_\omega(x e_{\mathcal{F}_1} x^*) e_{\mathcal{F}_2}) = \tau_\omega(e_{\mathcal{F}_2}x e_{\mathcal{F}_1} x^* e_{\mathcal{F}_2}) \end{align*} $$

as $k\to \infty $ . Consequently, we obtain that $\tau _\omega (e_{\mathcal {F}_1}x^* e_{\mathcal {F}_2} x e_{\mathcal {F}_1}) = \tau _\omega (e_{\mathcal {F}_2}x e_{\mathcal {F}_1} x^* e_{\mathcal {F}_2})$ for any $\mathcal {F}_1,\mathcal {F}_2 \Subset \Gamma $ .

By the normality of $\mathrm {tr}_\beta $ ,

$$ \begin{align*} \tau_\omega(e_{\mathcal{F}_1}x^* e_{\mathcal{F}_2} x e_{\mathcal{F}_1}) = \mathrm{tr}_\beta(\widetilde{E}_\omega(x^* e_{\mathcal{F}_2} x) e_{\mathcal{F}_1}) \nearrow \mathrm{tr}_\beta(\widetilde{E}_\omega(x^* e_{\mathcal{F}_2} x)) = \tau_\omega(x^* e_{\mathcal{F}_2} x) \end{align*} $$

as $\mathcal {F}_1 \nearrow \Gamma $ . However, we have, by item (i), $\tau _\omega (e_{\mathcal {F}_2}x e_{\mathcal {F}_1} x^* e_{\mathcal {F}_2}) \nearrow \tau _\omega (e_{\mathcal {F}_2}xx^* e_{\mathcal {F}_2})$ as ${\mathcal {F}_1 \nearrow \Gamma} $ . Hence, $\tau _\omega (x^* e_{\mathcal {F}_2} x) = \tau _\omega (e_{\mathcal {F}_2}xx^* e_{\mathcal {F}_2})$ for any $\mathcal {F}_2 \Subset \Gamma $ . Similarly, taking the limit as $\mathcal {F}_2 \nearrow \Gamma $ , we obtain $\tau _\omega (x^* x) = \tau _\omega (xx^*)$ . Hence, $\tau _\omega $ is a tracial weight.

We have

$$ \begin{align*} \widetilde{E}_\omega\circ\widetilde{\alpha}^\gamma(\pi_\alpha(a)\lambda(g)) &= \overline{\langle \gamma,g\rangle}\,\widetilde{E}_\omega(\pi_\alpha(a)\lambda(g)) = \overline{\langle \gamma,g\rangle}\,\widetilde{E}_{\omega,n}(\pi_{\alpha_n}(a)\lambda(g)) \\ &= \overline{\langle \gamma,g\rangle}\,\omega(a)\,\lambda(g) = \widetilde{\alpha}^\gamma(\widetilde{E}_{\omega,n}(\pi_{\alpha_n}(a)\lambda(g))) = \widetilde{\alpha}^\gamma\circ\widetilde{E}_\omega(\pi_\alpha(a)\lambda(g)) \end{align*} $$

for any $a \in A_n$ and $g \in G$ . Hence, we obtain $\widetilde {E}_\omega \circ \widetilde {\alpha }^\gamma = \widetilde {\alpha }^\gamma \circ \widetilde {E}_\omega $ for every $\gamma \in \Gamma $ . Moreover, we observe that $ \mathrm {tr}_\beta \circ \widetilde {\alpha }^\gamma (e_{\gamma '}) = \mathrm {tr}_\beta (e_{\gamma \gamma '}) = \gamma ^\beta \gamma '{}^\beta = \gamma ^\beta \,\mathrm {tr}_\beta (e_{\gamma '}) $ for all ${\gamma , \gamma ' \in \Gamma }$ . Therefore, we obtain that $\mathrm {tr}_\beta \circ \widetilde {\alpha }^\gamma = \gamma ^\beta \,\mathrm {tr}_\beta $ and, thus, $\tau _\omega $ satisfies item (ii). Item (iii) is trivial by Definition 3.2(2).

Lemma 3.5. For each $\tau \in TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ , the mapping

$$ \begin{align*} a \in A_+ \mapsto \tau(e_1\pi_\alpha(a)) = \tau(\pi_\alpha(a)e_1) = \tau(e_1\pi_\alpha(a)e_1) \in [0,\infty) \end{align*} $$

extends to the whole of A and defines an element of $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ .

Proof. Since $\tau (e_1) < +\infty $ , $\tau (e_1 \pi _{\alpha _n}(a)) = \tau (\pi _{\alpha _n}(a)e_1) = \tau (e_1 \pi _{\alpha _n}(a) e_1)$ makes sense for all $a \in A$ . By the standard Phragmen–Lindelöf method, it suffices to show that $\tau (e_1 \pi _{\alpha _n}(ab)) = \tau (\pi _{\alpha _n}(b\alpha _n^{i\beta }(a))e_1)$ ( $=\tau (e_1\pi _{\alpha _n}(b\alpha _n^{i\beta }(a)))$ ) for any $\alpha _n^t$ -analytic $a \in A_n$ and any $b \in A_n$ .

For each $\gamma \in \Gamma $ , we define $E_\gamma ^{(n)} : A_n \to A_n$ by

$$ \begin{align*} E_\gamma^{(n)}(a) := \int_G \overline{\langle \gamma,g\rangle}\, \alpha_n^g(a)\,dg, \quad a \in A_n. \end{align*} $$

Then,

(3-3) $$ \begin{align} E_\gamma^{(n)}(a)^* = E_{\gamma^{-1}}^{(n)}(a^*) \end{align} $$

for every $a \in A_n$ . Observe that $E_\gamma ^{(n)}(\alpha _n^t(a)) = \gamma ^{it}\,E_\gamma ^{(n)}(a)$ for every $a \in A_n$ , and moreover that $z \mapsto E_\gamma ^{(n)}(\alpha _n^z(a))$ is entire for every $\alpha _n^t$ -analytic $a \in A_n$ (note, this can easily be confirmed by using [15, Appendix A1]). By the unicity theorem in complex analysis, we conclude that

(3-4) $$ \begin{align} \gamma^{-\beta}E_\gamma^{(n)}(a) = E_\gamma^{(n)}(\alpha_n^{i\beta}(a)) \end{align} $$

for every $\alpha _n^t$ -analytic $a \in A_n$ . We also observe that

(3-5) $$ \begin{align} e_1\pi_{\alpha_n}(a)e_\gamma = \pi_{\alpha_n}(E_{\gamma^{-1}}^{(n)}(a))e_\gamma \end{align} $$

for every $a \in A_n$ . Taking the adjoint of this identity together with (3-3),

(3-6) $$ \begin{align} e_\gamma \pi_{\alpha_n}(a) e_1 = e_\gamma \pi_{\alpha_n}(E_\gamma^{(n)}(a)) \end{align} $$

for every $a \in A_n$ .

Let $a \in A_n$ be an arbitrary $\alpha _n^t$ -analytic element, and $b \in A_n$ be an arbitrary element of $A_n$ . Then,

$$ \begin{align*} \tau(e_1 \pi_{\alpha_n}(ab)) &= \tau(e_1\pi_{\alpha_n}(a)\pi_{\alpha_n}(b)e_1) = \tau(\pi_{\alpha_n}(b) e_1 \pi_{\alpha_n}(a)) \quad \text{(trace property)}\\ &= \sum_{\gamma \in \Gamma} \tau(\pi_{\alpha_n}(b) e_1 \pi_{\alpha_n}(a) e_\gamma) \\ &= \sum_{\gamma \in \Gamma} \tau(\pi_{\alpha_n}(b E_{\gamma^{-1}}^{(n)}(a)) e_\gamma) \quad \text{(use}\ (3\text{-}5))\\ &= \sum_{\gamma \in \Gamma} \tau\circ\widetilde{\alpha}^\gamma(\pi_{\alpha_n}(b E_{\gamma^{-1}}^{(n)}(a)) e_1) \quad \text{(use}\ (3\text{-}1))\\ &= \sum_{\gamma \in \Gamma} \gamma^\beta\,\tau(\pi_{\alpha_n}(b E_{\gamma^{-1}}^{(n)}(a)) e_1) \quad \text{(use item (ii) in Definition}\ 3.2(1))\\ &= \sum_{\gamma \in \Gamma} \tau(\pi_{\alpha_n}(b (\gamma^\beta\,E_{\gamma^{-1}}^{(n)}(a))) e_1) \\ &= \sum_{\gamma \in \Gamma} \tau(\pi_{\alpha_n}(b E_{\gamma^{-1}}^{(n)}(\alpha_n^{i\beta}(a)) e_1) \quad \text{(use}\ (3\text{-}4))\\ &= \sum_{\gamma \in \Gamma} \tau(\pi_{\alpha_n}(b) e_{\gamma^{-1}}\pi_{\alpha_n}(\alpha_n^{i\beta}(a)) e_1) \quad \text{(use}\ (3\text{-}6))\\ &= \tau(\pi_{\alpha_n}(b\alpha_n^{i\beta}(a)) e_1). \end{align*} $$

Hence, we are done.

So far, we have constructed two maps

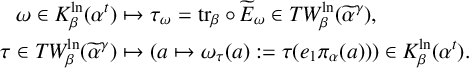(3-7) $$ \begin{align}\begin{aligned} \omega \in K_\beta^{\mathrm{ln}}(\alpha^t) &\mapsto \tau_\omega = \mathrm{tr}_\beta\circ \widetilde{E}_\omega \in TW_\beta^{\mathrm{ln}}(\widetilde{\alpha}^\gamma), \\ \tau \in TW_\beta^{\mathrm{ln}}(\widetilde{\alpha}^\gamma) &\mapsto (a \mapsto \omega_\tau(a):=\tau(e_1 \pi_\alpha(a))) \in K_\beta^{\mathrm{ln}}(\alpha^t). \end{aligned}\end{align} $$

Since $\tau _\omega (e_1 \pi _\alpha (a)) = \omega (a)$ for all $a \in A$ , it follows that the first map in (3-7) is injective. We also remark that $\omega _\tau $ in (3-7) makes sense on the whole A since $\tau (e_1)<+\infty $ .

Lemma 3.6. We have $\tau = \tau _{\omega _\tau }$ for every $\tau \in TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ .

Proof. For any $a\in A_+$ , $g \in G$ , and $\gamma \in \Gamma $ ,

$$ \begin{align*} \tau(\pi_\alpha(a)\lambda(g) e_\gamma) &= \tau(\pi_\alpha(a)\,\langle \gamma,g\rangle\,e_\gamma) = \langle \gamma,g\rangle\,\tau(e_\gamma \pi_\alpha(a)e_\gamma) \\ &= \langle \gamma,g\rangle\,\tau\circ\widetilde{\alpha}^\gamma(e_1 \pi_\alpha(a)e_1) = \langle \gamma,g\rangle\,\gamma^\beta\,\tau(e_1 \pi_\alpha(a)e_1) \\ &= \langle \gamma,g\rangle\,\gamma^\beta\,\omega_\tau(a) = \langle \gamma,g\rangle\,\omega_\tau(a)\,\mathrm{tr}_\beta(e_\gamma) = \mathrm{tr}_\beta(\widetilde{E}_{\omega_\tau}(\pi_\alpha(a))\lambda(g)e_\gamma). \end{align*} $$

It follows that $\tau (x e_\gamma ) = \tau _{\omega _\tau }(x e_\gamma )$ holds for any $x \in \widetilde {A}$ and $\gamma \in \Gamma $ . Therefore, we have $\tau (x e_{\mathcal {F}}) = \tau _{\omega _\tau }(x e_{\mathcal {F}})$ for any $x \in \widetilde {A}$ and any finite $\mathcal {F} \Subset \Gamma $ . By the trace property together with $\tau (e_{\mathcal {F}}) < +\infty $ , we have, by item (i) of Definition 3.2(1),

$$ \begin{align*} \tau(x e_{\mathcal{F}}) = \tau(e_{\mathcal{F}} x e_{\mathcal{F}}) = \tau(x^{1/2}e_{\mathcal{F}} x^{1/2}) \nearrow \tau(x) \end{align*} $$

as $\mathcal {F} \nearrow \Gamma $ for every $x \in \widetilde {A}_+$ . We also have $\tau _{\omega _\tau }(xe_{\mathcal {F}}) = \mathrm {tr}_\beta (\widetilde {E}_{\omega _\tau }(x)e_{\mathcal {F}}) \nearrow \mathrm {tr}_\beta (\widetilde {E}_{\omega _\tau }(x)) = \tau _{\omega _\tau }(x)$ as $\mathcal {F} \nearrow \Gamma $ for every $x \in \widetilde {A}_+$ . We conclude that $\tau = \tau _{\omega _\tau }$ holds.

Summing up the discussion so far, we have obtained the following theorem.

Theorem 3.7. The maps in (3-7) are inverse to each other. Therefore, $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ and $TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ are affine-isomorphic.

Thanks to the theorem, a natural topology on $TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ is defined by the following convergence: $\tau _i \to \tau $ in $TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ means that $\tau _i(e_1\pi _\alpha (a))\to \tau (e_1\pi _\alpha (a))$ for every $a \in A$ . By item (ii) of Definition 3.2(1), we have $\tau _i \to \tau $ in $TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ implies that $\tau _i(e_{\mathcal {F}} x) \to \tau (e_{\mathcal {F}}x)$ for any $\mathcal {F} \Subset \Gamma $ and $x \in \widetilde {A}$ , and hence $\liminf _i \tau _i(x) \geq \tau (x)$ for all $x \in \widetilde {A}_+$ .

4 Weight-extended branching graph

In the previous section, we transferred the study of locally normal $(\alpha ^t,\beta )$ -KMS states to that of $(\widetilde { \alpha }^\gamma ,\beta )$ -scaling traces on $\widetilde {A}=\varinjlim \widetilde {A}_n$ . Here, we translate this procedure into the terminology of standard links. For this purpose, we have to assume that all ${\dim (z) < \infty }$ . Then we can select each $\rho _z$ in such a way that $\mathrm {Tr}(\rho _z) = \mathrm {Tr}(\rho _z^{-1})$ . Under this selection, the $\rho = \{\rho _z\}_{z\in \mathfrak {Z}}$ is uniquely determined from the flow $\alpha ^t$ , and hence both $\Gamma =\Gamma (\rho )$ and $G=\widehat {\Gamma }$ are canonical objects associated with $\alpha ^t$ . Hence, we call this $\Gamma $ the weight group, and the $\rho $ -extension $(\widetilde {\alpha } : \Gamma \curvearrowright \widetilde {A}=\varinjlim \widetilde {A}_n)$ the weight-extension in this case. Note that this choice of $\Gamma $ is not exactly the same as that in the so-called discrete decomposition for type III factors due to Connes (see for example, [17] whose treatment aligns the present discussion).

4.1 Weight-extended branching graph

Let

$$ \begin{align*} \rho_z = \sum_{\gamma\in\Gamma} \gamma\,p_z(\gamma) \end{align*} $$

be the spectral decomposition (note, the support of $p_z(\,\cdot \,)$ is a finite subset of $\Gamma $ due to $\dim (z)<+\infty $ ). Then,

$$ \begin{align*} u_z(g) = \sum_{\gamma\in\Gamma} \langle \gamma,g\rangle\,p_z(\gamma), \quad g\in G, \end{align*} $$

and regarding $p_z(\gamma )$ , $u_z(g)$ as elements of $zA_n \subset A_n$ ,

$$ \begin{align*} u_n(g) = \sum_{z\in\mathfrak{Z}_n} u_z(g) = \sum_{z\in\mathfrak{Z}_n}\sum_{\gamma \in \Gamma} \langle\gamma,g\rangle\,p_z(\gamma) \in A_n, \quad g \in G. \end{align*} $$

The unitary operator U on $L^2(G;\mathcal {K}_n)$ defined by

$$ \begin{align*} (U\xi)(g) = u_n(g)\xi(g), \quad \xi\in C(G;\mathcal{K}_n) \subset L^2(G;\mathcal{K}_n) \end{align*} $$

satisfies

(4-1) $$ \begin{align} U\pi_{\alpha_n}(a)U^* = a\otimes1, \quad U\lambda(g)U^* = u_n(g)\otimes\lambda_g \end{align} $$

for any $a \in A_n$ and $g \in G$ , where we identify $L^2(G;\mathcal {K}_n) = \mathcal {K}_n\,\bar {\otimes }\,L^2(G)$ as in Section 3. See for example, [15, Theorem X.1.7(ii)]. We observe that

(4-2) $$ \begin{align} U e_\gamma U^* = \sum_{z\in\mathfrak{Z}_n}\sum_{\gamma_1,\gamma_2\in\Gamma} \int_G \langle \gamma^{-1}\gamma_1\gamma_2,g\rangle\,dg\,p_z(\gamma_1)\otimes e^{(00)}_{\gamma_2} = \sum_{z\in\mathfrak{Z}_n}\sum_{\gamma' \in \Gamma} p_z(\gamma \gamma'{}^{-1})\otimes e^{(00)}_{\gamma'} \end{align} $$

for every $\gamma \in \Gamma $ .

Lemma 4.1. There is a unique bijective $*$ -homomorphism

$$ \begin{align*} \Phi_n : \widetilde{A}_n \longrightarrow \bigoplus_{(z,\gamma) \in \mathfrak{Z}_n\times\Gamma} zA_n \, \bigg(\cong \bigoplus_{(z,\gamma) \in \mathfrak{Z}_n\times\Gamma} B({\mathcal{H}}_z)\bigg) \end{align*} $$

such that

(4-3) $$ \begin{align} \Phi_n(\pi_{\alpha_n}(a))(z,\gamma') := za, \quad \Phi_n(e_\gamma)(z,\gamma') := p_z(\gamma\gamma'{}^{-1}) \end{align} $$

hold for any $a \in A_n$ , $z \in \mathfrak {Z}_n$ , and $\gamma ,\gamma ' \in \Gamma $ . The map $\Phi _n$ intertwines the dual action $\widetilde {\alpha }^\gamma $ with the translation action of $\Gamma $ on the right coordinate, that is,

(4-4) $$ \begin{align} \Phi_n(\widetilde{\alpha}^\gamma(x))(z,\gamma') = \Phi_n(x)(z,\gamma^{-1}\gamma') \end{align} $$

holds for any $x \in \widetilde {A}_n$ and $z \in \mathfrak {Z}_n$ , and $\gamma ,\gamma ' \in \Gamma $ .

Proof. Note that $A_n\,\bar {\otimes }\,L(G) \cong A_n\,\bar {\otimes }\,\ell ^\infty (\Gamma ) \cong \bigoplus _{\gamma \in \Gamma }A_n \cong \bigoplus _{(z,\gamma )\in \mathfrak {Z}_n\times \Gamma } zA_n$ by

$$ \begin{align*} a\otimes\lambda_g \leftrightarrow \sum_{\gamma \in \Gamma} \langle\gamma,g\rangle\,a\otimes\delta_\gamma \leftrightarrow (\langle \gamma,g\rangle\,a)_{\gamma\in\Gamma} = (\langle \gamma,g\rangle\,za)_{(z,\gamma)\in\mathfrak{Z}_n\times\Gamma}, \quad a \in A_n, \quad g \in G \end{align*} $$

with $L(G) := \lambda (G)"$ on $L^2(G)$ . Therefore, the composition of $\mathrm {Ad}U$ and this bijective $*$ -homomorphism gives the desired $\Phi _n$ . By (4-1) and (4-2),

$$ \begin{align*} \Phi_n(e_\gamma)(z,\gamma') = (Ue_\gamma U^*)(z,\gamma') = p_z(\gamma\gamma'{}^{-1}) \end{align*} $$

for every $\gamma \in \Gamma $ . Hence, we have confirmed that (4-3) actually holds true. Since the $e_\gamma $ are the spectral projections of $\lambda (g)$ ( $g \in G$ ), it is clear that (4-3) determines $\Phi _n$ completely.

We have

$$ \begin{align*} \Phi_n(\widetilde{\alpha}_n^\gamma(\pi_{\alpha_n}(a)))(z,\gamma') &= \Phi_n(\pi_{\alpha_n}(a))(z,\gamma') = za = \Phi_n(\pi_{\alpha_n}(a))(z,\gamma^{-1}\gamma'), \\ \Phi_n(\widetilde{\alpha}_n^\gamma(e_{\gamma"}))(z,\gamma') &= \Phi_n(e_{\gamma\gamma"})(z,\gamma') = p_z(\gamma\gamma"\gamma'{}^{-1}) = p_z(\gamma"(\gamma^{-1}\gamma')^{-1})\\ &= \Phi_n(e_{\gamma"})(z,\gamma^{-1}\gamma') \end{align*} $$

(note, $\Gamma $ is commutative). Hence, (4-4) holds true.

We then investigate the inclusion $\widetilde {A}_n \hookrightarrow \widetilde {A}_{n+1}$ in the description of Lemma 4.1. Note that the lemma, in particular, says that the inductive sequence $\widetilde {A}_n$ consists of finite, atomic $W^*$ -algebras again.

Since $\alpha _{n+1}^g= \alpha _n^g$ holds on $A_n$ for every $g \in G$ thanks to the density of $\mathbb {R}$ in G, we observe that $g \in G \mapsto w_{n+1,n}(g) := u_n(g)^* u_{n+1}(g) \in (A_n)'\cap A_{n+1}$ gives a unitary representation. Since all the $zz' \neq 0$ with $(z,z') \in \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ form a complete set of minimal central projections of $(A_n)'\cap A_{n+1}$ , we obtain the unitary representation

$$ \begin{align*} g \in G \mapsto w_{z,z'}(g) := zz' w_{n+1,n}(g) = u_{z}(g) u_{z'}(g)^* = u_{z'}(g)^* u_{z}(g) \in zz'((A_n)'\cap A_{n+1}) \end{align*} $$

for each $(z,z') \in \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ with $zz' \neq 0$ . Since $w_{z,z'}(g)$ is a unitary representation of a compact abelian group, it admits a spectral decomposition of the following form:

(4-5) $$ \begin{align} w_{(z,z')}(g) = \sum_{\gamma \in \Gamma} \langle \gamma,g\rangle\,q_{(z,z')}(\gamma), \quad g \in G, \end{align} $$

where the $q_{(z,z')}(\gamma )$ form a partition of unity of $zz'((A_n)'\cap A_{n+1})$ consisting of projections. Since $\alpha _{n+1}^t = \alpha _n^t$ holds on $A_n$ for every $t \in \mathbb {R}$ , we see that $\rho _z\rho _{z'} = \rho _{z'}\rho _z$ holds in $zA_{n+1}$ for each $(z,z') \in \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ with $zz'\neq 0$ . Hence, the generator of $w_{z,z'}(t)$ should be $\rho _z\rho _{z'}^{-1}=\rho _{z'}^{-1}\rho _z$ , and thus we have the following explicit description of $q_{(z,z')}(\gamma )$ in terms of $p_z(\gamma )$ :

(4-6) $$ \begin{align} q_{(z,z')}(\gamma) = \sum_{\gamma'\in\Gamma} p_z(\gamma\gamma')p_{z'}(\gamma') = \sum_{\gamma'\in\Gamma} p_{z'}(\gamma')p_z(\gamma'\gamma), \quad \gamma \in \Gamma. \end{align} $$

We define an element $a \otimes \delta _\gamma \in \Phi _n(\widetilde {A}_n)$ with $a \in A_n$ and $\gamma \in \Gamma $ by

$$ \begin{align*} (a\otimes \delta_\gamma)(z',\gamma') := \delta_\gamma(\gamma')\,z' a, \quad (z',\gamma') \in \mathfrak{Z}_n\times\Gamma, \end{align*} $$

where $\delta _\gamma $ denotes the Dirac function at $\gamma $ . We remark that the $z\otimes \delta _\gamma $ , $(z,\gamma ) \in \mathfrak {Z}_n\times \Gamma $ , form a complete set of minimal central projections of $\Phi _n(\widetilde {A}_n)$ .

Lemma 4.2. The embedding $\iota _{n+1,n} = \Phi _{n+1}\circ \Phi _n^{-1} : \Phi _n(\widetilde {A}_n) \hookrightarrow \Phi _{n+1}(\widetilde {A}_{n+1})$ obtained from $\widetilde {A}_n \hookrightarrow \widetilde {A}_{n+1}$ sends each $z'\otimes \delta _{\gamma '}$ with $(z',\gamma ') \in \mathfrak {Z}_n\times \Gamma $ to

(4-7) $$ \begin{align} \iota_{n+1,n}(z'\otimes\delta_{\gamma'}) = \sum_{\substack{z \in \mathfrak{Z}_{n+1} \\ m(z,z')> 0}} \sum_{\gamma \in \Gamma} q_{(z,z')}(\gamma'\gamma^{-1})\otimes\delta_\gamma. \end{align} $$

In particular,

(4-8) $$ \begin{align} (z\otimes\delta_\gamma)\,\iota_{n+1,n}(z'\otimes\delta_{\gamma'}) = \begin{cases} q_{(z,z')}(\gamma'\gamma^{-1})\otimes\delta_\gamma & (m(z,z')> 0), \\ 0 & (m(z,z') = 0) \end{cases} \end{align} $$

for each pair $((z,\gamma ),(z',\gamma ')) \in (\mathfrak {Z}_{n+1}\times \Gamma )\times (\mathfrak {Z}_n\times \Gamma )$ .

Proof. Choose an arbitrary pair $(z',\gamma ') \in \mathfrak {Z}_n\times \Gamma $ . By the proof of Lemma 4.1,

$$ \begin{align*} \Phi_n\bigg(\int_G \overline{\langle\gamma',g\rangle}\,\pi_{\alpha_n}(u_{z'}(g)^*)\,\lambda(g)\,dg\bigg) = z'\otimes\delta_{\gamma'}. \end{align*} $$

Observe that

We have, by (4-5) and the proof of Lemma 3.4 (formula $\lambda _g e_\gamma ^{(00)} = \langle \gamma ,g\rangle \,e_\gamma ^{(00)}$ ),

$$ \begin{align*} \int_G \overline{\langle\gamma',g\rangle}\,(u_{z'}(g)^* u_{n+1}(g))\otimes\lambda_g\,dg &= \sum_{\substack{z \in \mathfrak{Z}_{n+1} \\ m(z,z')> 0}} \int_G \overline{\langle\gamma',g\rangle}\,w_{(z,z')}(g)\otimes\lambda_g\,dg \\ &= \sum_{\substack{z \in \mathfrak{Z}_{n+1} \\ m(z,z') > 0}} \sum_{\gamma_1, \gamma_2 \in \Gamma} \int_G \langle \gamma'{}^{-1} \gamma_1\gamma_2,g\rangle\,q_{(z,z')}(\gamma_1)\otimes e_{\gamma_2}^{(00)}\,dg \\ &= \sum_{\substack{z \in \mathfrak{Z}_{n+1} \\ m(z,z') > 0}} \sum_{\gamma \in \Gamma} q_{(z,z')}(\gamma'\gamma^{-1})\otimes e_\gamma^{(00)}. \end{align*} $$

It follows that

$$ \begin{align*} \Phi_{n+1}\bigg(\int_G \overline{\langle\gamma',g\rangle}\,\pi_{\alpha_n}(u_{z'}(g)^*)\,\lambda(g)\,dg\bigg) = \sum_{\substack{z \in \mathfrak{Z}_{n+1} \\ m(z,z')> 0}} \sum_{\gamma \in \Gamma} q_{(z,z')}(\gamma'\gamma^{-1})\otimes\delta_\gamma. \end{align*} $$

Consequently, we obtain (4-7), which trivially implies (4-8).

The lemmas above immediately imply the following proposition.

Proposition 4.3. The minimal central projections of $\widetilde {A}_n$ are labeled by ${\widetilde {\mathfrak {Z}}_n := \mathfrak {Z}_n\times \Gamma }$ , and the dimension corresponding to a $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_n$ becomes $\dim (z)$ (that is, being independent of $\gamma $ ).

The branching graph $(\widetilde {\mathfrak {Z}},\tilde {m})$ of the inductive sequence $\widetilde {A}_n$ is given by $\widetilde {\mathfrak {Z}} := \bigsqcup _{n\geq 0} \widetilde {\mathfrak {Z}}_n$ and

$$ \begin{align*} \tilde{m}((z,\gamma),(z',\gamma')) &= \frac{\mathrm{Tr}(\iota_{n+1,n}(z'\otimes\delta_{\gamma'})(z,\gamma))}{\dim(z')} \\ &= \begin{cases} \dfrac{\mathrm{Tr}(q_{(z,z')}(\gamma^{-1}\gamma'))}{\dim(z')} & (m(z,z')> 0), \\ 0 & (m(z,z') = 0) \end{cases} \end{align*} $$

for any $((z,\gamma ),(z',\gamma ')) \in \widetilde {\mathfrak {Z}}_{n+1}\times \widetilde {\mathfrak {Z}}_n$ , $n \geq 0$ . In particular, the standard link $\tilde {\mu }$ over $(\widetilde {\mathfrak {Z}},\tilde {m})$ becomes

$$ \begin{align*} \tilde{\mu}((z,\gamma),(z',\gamma')) &= \tilde{m}((z,\gamma),(z',\gamma'))\,\frac{\dim(z')}{\dim(z)} \\ &= \begin{cases} \dfrac{\mathrm{Tr}(q_{(z,z')}(\gamma^{-1}\gamma'))}{\dim(z)} & (m(z,z')> 0), \\ 0 & (m(z,z') = 0) \end{cases} \end{align*} $$

for any $((z,\gamma ),(z',\gamma ')) \in \widetilde {\mathfrak {Z}}_{n+1}\times \widetilde {\mathfrak {Z}}_n$ , $n \geq 0$ .

In particular, the multiplicity function $\tilde {m}$ and the standard link $\tilde {\mu }$ are invariant under the translation action $T: \Gamma \curvearrowright \widetilde {\mathfrak {Z}}$ defined by $T_\gamma (z,\gamma ') := (z,\gamma \gamma ')$ , that is,

$$ \begin{align*} \tilde{\mu}\circ(T_\gamma^{-1}\times T_\gamma^{-1}) = \tilde{\mu}, \quad \tilde{m}\circ(T_\gamma^{-1}\times T_\gamma^{-1}) = \tilde{m}, \quad \gamma \in \Gamma. \end{align*} $$

Remark 4.4. Lemma 4.1 says that

$$ \begin{align*} \widetilde{A}_n \cong \Phi_n(\widetilde{A}_n) = \bigoplus_{(z,\gamma)\in\mathfrak{Z}_n\times\Gamma} \overset{\tiny z\otimes\delta_\gamma}{zA_n} \quad \text{with}\ zA_n = B({\mathcal{H}}_z), \end{align*} $$

where the symbol $z\otimes \delta _\gamma $ over $zA_n$ indicates the central support projection of direct summand $zA_n$ . Then its center-valued trace $\mathrm {ctr}_n$ is given by

$$ \begin{align*} \mathrm{ctr}_n(x)(z,\gamma) = \frac{\mathrm{Tr}(x(z,\gamma))}{\dim(z)}, \quad x \in \Phi_n(\widetilde{A}_n),\quad (z,\gamma) \in \mathfrak{Z}_n\times\Gamma, \end{align*} $$

where $\mathrm {Tr}$ stands for the nonnormalized trace on $zA_n = B({\mathcal {H}}_z)$ . (See [14, Theorem V.2.6]; its uniqueness guarantees that the above map is indeed the center-valued trace.) We observe that

(4-9) $$ \begin{align} \mathrm{ctr}_{n+1}(\iota_{n+1,n}(z'\otimes\delta_{\gamma'}))(z,\gamma) = \tilde{\mu}((z,\gamma),(z',\gamma')) \end{align} $$

holds for every pair $((z,\gamma ),(z',\gamma ')) \in \widetilde {\mathfrak {Z}}_{n+1}\times \widetilde {\mathfrak {Z}}_n$ , $n \geq 0$ . This is consistent with [18, Equation (3.7)] and the natural conditional expectations playing the role of $E^{(\alpha _n^t,\beta )}$ in [18] are the center-valued traces of $\widetilde {A}_n$ in the present context.

4.2 Harmonic functions corresponding to $(\widetilde {\alpha }^\gamma ,\beta )$ -scaling traces

So far, we have described the branching graph $(\widetilde {\mathfrak {Z}},\tilde {m})$ associated with the $\widetilde {A}_n$ , $n\geq 0$ . With the description, we translate the $(\widetilde {\alpha }^\gamma ,\beta )$ -traces $TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ into a certain class of harmonic functions on $(\widetilde {\mathfrak {Z}},\tilde {m})$ .

Lemma 4.5. For each $\tau \in TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ , there is a unique function $\tilde {\nu } = \tilde {\nu }[\tau ] : \widetilde {\mathfrak {Z}} := \bigsqcup _{n\geq 0}\widetilde {\mathfrak {Z}}_n \to [0,+\infty )$ such that

(4-10) $$ \begin{align} \tau(x) = \sum_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_n} \tilde{\nu}(z,\gamma)\,\frac{\mathrm{Tr}(\Phi_n(x)(z,\gamma))}{\dim(z)}, \quad x \in \widetilde{A}_n. \end{align} $$

The function $\tilde {\nu }$ has the following properties:

1. (i) $ \tilde {\nu }(z',\gamma ') = \sum _{(z,\gamma ) \in \widetilde {\mathfrak {Z}}_{n+1}}\tilde {\nu }(z,\gamma )\,\tilde {\mu }((z,\gamma ),(z',\gamma '))$ for all $(z',\gamma ') \in \widetilde {\mathfrak {Z}}_n$ , $n \geq 0$ ;

2. (ii) $ \tilde {\nu }(z,\gamma ) = \gamma ^\beta \tilde {\nu }(z,1)$ for all $(z,\gamma ) \in \widetilde {\mathfrak {Z}}$ ;

3. (iii) $\tilde {\nu }(1,1) = 1$ .

Proof. Write $\tau _n := \tau \circ \Phi _n^{-1}$ for simplicity, and it should be a normal semifinite tracial weight on $\Phi _n(\widetilde {A}_n)$ . Since all the $z \otimes \delta _\gamma $ form a complete orthogonal family of minimal central projections of $\Phi _n(\widetilde {A}_n)$ , we observe that $\tau _n(z\otimes \delta _\gamma ) < +\infty $ for any $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_n$ . Thus,

$$ \begin{align*} a \in \overset{z\otimes\delta_\gamma}{(zA_n)_+} (\subset \Phi_n(\widetilde{A}_n)_+) \mapsto \tau_n(a) \in [0,+\infty) \end{align*} $$

(see Remark 4.4 for this notation of direct summands) coincides with a unique nonnegative scalar multiple of the normalized trace $\mathrm {Tr}(\,\cdot \,)/\dim (z)$ on $zA_n = B({\mathcal {H}}_z)$ . Then, the nonnegative scalar gives the desired number $\tilde {\nu }(z,\gamma )$ , that is, by semifiniteness and normality,

$$ \begin{align*} \tau_n(x) = \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_n} \tau_n((z\otimes\delta_\gamma)x) = \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_n} \tilde{\nu}(z,\gamma)\frac{\mathrm{Tr}(x(z,\gamma))}{\dim(z)}\ (= \tau_n(\mathrm{ctr}_n(x)) ) \end{align*} $$

for all $x \in \Phi _n(\widetilde {A}_n)_+$ . Hence, (4-10) follows.

Item (i): we have

$$ \begin{align*} \tilde{\nu}(z',\gamma') &= \tau_n(z'\otimes\delta_{\gamma'}) \\ &= \tau_{n+1}(\iota_{n+1,n}(z'\otimes\delta_{\gamma'})) \\ &= \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\frac{\mathrm{Tr}(\iota_{n+1,n}(z'\otimes\delta_{\gamma'})(z,\gamma))}{\dim(z)} \\ &= \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\,\tilde{\mu}((z,\gamma),(z',\gamma')) \end{align*} $$

by Proposition 4.3 (and Remark 4.4).

Item (ii): we observe that

$$ \begin{align*} \Phi_n(\widetilde{\alpha}^\gamma(\Phi_n^{-1}(z\otimes\delta_1)))(z',\gamma') = \Phi_n(\Phi_n^{-1}(z\otimes\delta_1))(z',\gamma^{-1}\gamma') = (z\otimes\delta_\gamma)(z',\gamma') \end{align*} $$

for $(z',\gamma ') \in \widetilde {\mathfrak {Z}}_n$ . Hence, we have $\widetilde {\alpha }^\gamma (\Phi _n^{-1}(z\otimes \delta _1)) = \Phi _n^{-1}(z\otimes \delta _\gamma )$ and, thus,

$$ \begin{align*} \tilde{\nu}(z,\gamma) = \tau(\Phi_n^{-1}(z\otimes\delta_\gamma)) = \tau(\widetilde{\alpha}^\gamma(\Phi_n^{-1}(z\otimes\delta_1))) = \gamma^\beta\,\tau(\Phi_n^{-1}(z\otimes\delta_1)) = \gamma^\beta\,\tilde{\nu}(z,1) \end{align*} $$

by item (ii) of Definition 3.2(1).

Item (iii): this is nothing but item (iii) of Definition 3.2(1), that is, $\tau (e_1) = 1$ .

We remark that

$$ \begin{align*} \sum_{z\in\mathfrak{Z}_n} \frac{\dim_\beta(z)}{\dim(z)}\,\tilde{\nu}(z,1) = 1, \quad n \geq 0, \end{align*} $$

which follows from items (i)–(iii) above thanks to Proposition 4.3.

Definition 4.6. A normalized, $\beta $ -power scaling $\tilde {\mu }$ -harmonic function is a function $\tilde {\nu } : \widetilde {\mathfrak {Z}} \to [0,+\infty )$ such that items (i)–(iii) in Proposition 4.5 hold. We denote by $H_1^+(\tilde {\mu })_\beta $ all the normalized, $\beta $ -power scaling $\tilde {\mu }$ -harmonic functions.

We also need to recall the notion of $\kappa $ -harmonic functions and notation $H_1^+(\kappa )$ . A function $\nu : \mathfrak {Z} = \bigsqcup _{n\geq 0}\mathfrak {Z}_n \to \mathbb {C}$ is $\kappa $ -harmonic if

$$ \begin{align*} \nu(z') = \sum_{z \in \mathfrak{Z}_{n+1}} \nu(z)\kappa(z,z'), \quad z' \in \mathfrak{Z}_n \end{align*} $$

holds for every $n \neq 0$ . A $\kappa $ -harmonic function $\nu $ is positive if $\nu (z) \geq 0$ for all $z \in \mathfrak {Z}$ , and normalized if $\nu (1) = 1$ , where one must remember $\mathfrak {Z}_0 = \{1\}$ . We denote by $H_1^+(\kappa )$ all the normalized, positive $\kappa $ -harmonic functions on $\mathfrak {Z}$ . See [19, Section 7] for more details.

Theorem 4.7. There is a unique affine-isomorphism $\nu \in H_1^+(\kappa ) \longleftrightarrow \tilde {\nu } \in H_1^+(\tilde {\mu })_\beta $ with

$$ \begin{align*} \dim_\beta(z)\,\tilde{\nu}(z,\gamma) = \dim(z)\,\nu(z)\,\gamma^\beta, \quad (z,\gamma) \in \widetilde{\mathfrak{Z}}. \end{align*} $$

Proof. We first claim that

(4-11) $$ \begin{align} \frac{\mathrm{Tr}(\rho_z^{-\beta}x)}{\mathrm{Tr}(\rho_z^{-\beta}z')} = \frac{\mathrm{Tr}(\rho_{z'}^{-\beta}x)}{\dim_\beta(z')}, \quad x \in z'A_n = B({\mathcal{H}}_{z'}) \hookrightarrow zA_{n+1} = B({\mathcal{H}}_z) \end{align} $$

holds for any pair $(z,z') \in \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ with $m(z,z')> 0$ . In fact, the left-hand side defines an $(\alpha _{z'}^t,\beta )$ -KMS state on $z'A_n = B({\mathcal {H}}_{z'})$ , and the uniqueness of $(\alpha _{z'}^t,\beta )$ -KMS states shows the claim.

Let $\nu \in H_1^+(\kappa )$ be arbitrarily chosen. We show that

$$ \begin{align*} \tilde{\nu}(z,\gamma) := \frac{\dim(z)}{\dim_\beta(z)}\,\nu(z)\,\gamma^\beta \end{align*} $$

defines an element of $H_1^+(\tilde {\mu })_\beta $ . Item (ii) of Lemma 4.5 trivially holds, and the normalization property of $\nu $ trivially implies item (iii) of Lemma 4.5. Hence, it suffices to show item (i) of Lemma 4.5.

We have

$$ \begin{align*} \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\,\tilde{\mu}((z,\gamma),(z',\gamma)) &= \sum_{\substack{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1} \\ m(z,z')>0}} \frac{\dim(z)}{\dim_\beta(z)}\,\nu(z)\,\gamma^\beta\,\frac{\mathrm{Tr}(q_{(z,z')}(\gamma^{-1}\gamma'))}{\dim(z)} \\ &= \frac{1}{\dim_\beta(z)}\sum_{\substack{z \in \mathfrak{Z}_{n+1} \\ m(z,z')>0}} \nu(z)\sum_{\gamma \in \Gamma}\gamma^\beta\,\mathrm{Tr}(q_{(z,z')}(\gamma^{-1}\gamma')). \end{align*} $$

Now, we observe that

$$ \begin{align*} \sum_{\gamma \in \Gamma}\gamma^\beta\,\mathrm{Tr}(q_{(z,z')}(\gamma^{-1}\gamma')) &= \sum_{\gamma \in \Gamma}\gamma^\beta \sum_{\gamma" \in \Gamma} \mathrm{Tr}(p_z(\gamma^{-1}\gamma'\gamma")p_{z'}(\gamma")) \\ &= \gamma'{}^\beta\sum_{\gamma_1,\gamma_2 \in \Gamma} \gamma_1^{-\beta}\gamma_2^\beta\mathrm{Tr}(p_z(\gamma_1)p_{z'}(\gamma_2)) \\ &= \gamma'{}^\beta\,\mathrm{Tr}(\rho_z^{-\beta}\rho_{z'}^\beta) \\ &= \dim_\beta(z)\,\tau_z^\beta(zz')\frac{\dim(z')\,\gamma'{}^\beta}{\dim_\beta(z')} \end{align*} $$

by (4-11). Since $\kappa (z,z') = \tau _z^\beta (zz')$ and since $zz' = 0$ if and only if $m(z,z') = 0$ , we conclude that

$$ \begin{align*} \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\,\tilde{\mu}((z,\gamma),(z',\gamma)) &= \frac{\dim(z')\,\gamma'{}^\beta}{\dim_\beta(z')}\sum_{z \in \mathfrak{Z}_{n+1}} \nu(z)\,\tau_z^\beta(zz') \\ &= \frac{\dim(z')\,\gamma'{}^\beta}{\dim_\beta(z')}\nu(z') = \tilde{\nu}(z',\gamma'). \end{align*} $$

Hence, $\tilde {\nu }$ satisfies item (i) of Lemma 4.5.

Let $\tilde {\nu } \in H_1^+(\tilde {\mu })_\beta $ be arbitrarily chosen. We show that

$$ \begin{align*} \nu(z) := \frac{\dim_\beta(z)}{\dim(z)}\tilde{\nu}(z,1) \end{align*} $$

defines an element of $H_1^+(\kappa )$ .

We first observe that

$$ \begin{align*} \sum_{z\in\mathfrak{Z}_{n+1}} \nu(z)\kappa(z,z') &= \sum_{z\in\mathfrak{Z}_{n+1}} \tilde{\nu}(z,1) \frac{\mathrm{Tr}(\rho_z^{-\beta}z')}{\dim(z)} \\ &= \sum_{z\in\mathfrak{Z}_{n+1}} \tilde{\nu}(z,1) \frac{\mathrm{Tr}(\rho_z^{-\beta}\rho_{z'}^\beta)\dim_\beta(z')}{\dim(z)\,\mathrm{Tr}(\rho_{z'}^{-\beta}\rho_{z'}^\beta)} \quad \text{(use}\ (4\text{-}11)) \\ &= \sum_{z\in\mathfrak{Z}_{n+1}} \tilde{\nu}(z,1) \sum_{\gamma \in \Gamma} \gamma^{-\beta}\frac{\mathrm{Tr}(q_{(z,z')}(\gamma))}{\dim(z)}\frac{\dim_\beta(z')}{\dim(z')} \\ &= \frac{\dim_\beta(z')}{\dim(z')}\sum_{z\in\mathfrak{Z}_{n+1}} \tilde{\nu}(z,1) \sum_{\gamma \in \Gamma} \gamma^\beta\,\frac{\mathrm{Tr}(q_{(z,z')}(\gamma^{-1}))}{\dim(z)} \\ &= \frac{\dim_\beta(z')}{\dim(z')}\sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\tilde{\mu}((z,\gamma),(z',1)) \quad \text{(by Proposition}\ 4.3)\\ &= \frac{\dim_\beta(z')}{\dim(z')}\tilde{\nu}(z',1) = \nu(z'). \end{align*} $$

Hence, $\nu $ is $\kappa $ -harmonic. Moreover, item (iii) of Lemma 4.5, a requirement of $\tilde {\nu }$ , clearly shows that $\nu $ is normalized. Hence, we are done.

So far, we have obtained the following diagram:

where the correspondences (a)–(d) have been established as follows:

1. (a) Theorem 3.7;

2. (b) [19, Proposition 3.7];

3. (c) Lemma 4.5;

4. (d) Theorem 4.7.

We examine the composition of maps (d) $\to $ (b) $\to $ (a).

Let $\tilde {\nu } \in H_1^+(\tilde {\mu },\beta )$ be arbitrarily chosen. By Theorem 4.7, we have a unique $\nu \in H_1^+(\kappa )$ with

$$ \begin{align*} \nu(z) = \frac{\dim_\beta(z)}{\dim(z)}\tilde{\nu}(z,1), \quad z \in \mathfrak{Z}. \end{align*} $$

Then, by [19, Proposition 3.7], we have a unique $\omega \in K_\beta ^{\mathrm {ln}}(\alpha ^t)$ so that

$$ \begin{align*} \omega(a) = \sum_{z \in \mathfrak{Z}_n} \nu(z)\,\tau_z^\beta(za)=\sum_{z \in \mathfrak{Z}_n}\frac{\dim_\beta(z)}{\dim(z)}\tilde{\nu}(z,1)\,\tau_z^\beta(za), \quad a \in A_n,\ n\geq0. \end{align*} $$

Finally, with this $\omega $ , we obtain a unique $\tau _\omega = \mathrm {tr}_\beta \circ \widetilde {E}_\omega \in TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma )$ by Theorem 3.7. Consequently, the resulting $\tau _\omega $ enjoys

$$ \begin{align*} \tilde{\nu}[\tau_\omega](z,\gamma) = \tau_\omega(\Phi_n^{-1}(z\otimes\delta_\gamma)) = \mathrm{tr}_\beta(E_\omega(\Phi_n^{-1}(z\otimes\delta_\gamma))). \end{align*} $$

By the proof of Lemma 4.2, we observe that

$$ \begin{align*} \Phi_n^{-1}(z\otimes\delta_\gamma) = \int_G \overline{\langle\gamma,g\rangle}\,\pi_{\alpha_n}(u_z(g)^*)\,\lambda(g)\,dg = \sum_{\gamma_1^{-1}\gamma_2 = \gamma} \pi_{\alpha_n}(p_z(\gamma_1)) e_{\gamma_2}. \end{align*} $$

Consequently, we obtain that

$$ \begin{align*} \tilde{\nu}[\tau_\omega](z,\gamma) &= \sum_{\gamma_1^{-1}\gamma_2=\gamma} \dim_\beta(z)\,\tilde{\nu}(z,1)\frac{1}{\dim(z)} \tau_z^\beta(p_z(\gamma_1))\,\gamma_2^\beta \\ &= \sum_{\gamma_1^{-1}\gamma_2=\gamma} \dim_\beta(z)\,\tilde{\nu}(z,1)\frac{1}{\dim(z)}\,\frac{\gamma_1^{-\beta}\mathrm{Tr}(p_z(\gamma_1))}{\dim_\beta(z)}\,\gamma_2^\beta \\ &= \tilde{\nu}(z,1)\,\gamma^\beta\,\sum_{\gamma_1} \frac{\mathrm{Tr}(p_z(\gamma_1))}{\dim(z)} \\ &= \tilde{\nu}(z,1)\gamma^\beta = \tilde{\nu}(z,\gamma). \end{align*} $$

It follows that the composition of maps (d) $\to $ (b) $\to $ (a) is exactly inverse to map (c). Hence, we have arrived at the following theorem.

Theorem 4.8. The mapping $\tau \in TW_\beta ^{\mathrm {ln}}(\widetilde {\alpha }^\gamma ) \mapsto \tilde {\nu }[\tau ] \in H_1^+(\tilde {\mu })_\beta $ obtained in Lemma 4.5 is an affine-isomorphism.

4.3 Weights and weight-extended branching graphs of links

The reader might ask how to construct the branching graph $(\widetilde {\mathfrak {Z}},\tilde {m})$ with a $\Gamma $ -action from a given link $(\mathfrak {Z},\kappa )$ rather than an inductive $C^*$ -flow $\alpha ^t$ . See Section 2 for the notion of links. Such a construction can be given by using [19, Section 9]; namely, one first constructs an inductive $C^*$ -flow from $(\mathfrak {Z},\kappa )$ , and then applies the discussions so far in this paper to it. Here, we translate this procedure without appealing to any $C^*$ -flows. This seems to be of independent interest.

We first remark that the analysis of links does not depend on multiplicities on edges; hence, we ignore, for simplicity, the multiplicity function over $\mathfrak {Z}$ . Here, one should remark that $m(z,z')> 0$ if and only if $\kappa (z,z')>0$ , and hence the edges $(z,z') \in \bigsqcup _{n\geq 0}\mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ are determined by the positivity of $\kappa (z,z')$ . Moreover, we have assumed that

$$ \begin{align*} \bigcup_{z' \in \mathfrak{Z}_n}\{z \in \mathfrak{Z}_{n+1}; \kappa(z,z')> 0\} = \mathfrak{Z}_{n+1}, \quad \bigcup_{z \in \mathfrak{Z}_{n+1}}\{z' \in \mathfrak{Z}_n; \kappa(z,z') > 0\} = \mathfrak{Z}_n \end{align*} $$

for all $n\geq 0$ . (Informally, this assumption corresponds to that $A_n \hookrightarrow A_{n+1}$ is a unital embedding for every $n\geq 0$ .) We assume that our link satisfies these requirements.

Since the definition of $\kappa $ in (2-1) involves the inverse temperature $\beta $ , we have to specify this $\beta $ . In what follows, we informally think that the inverse temperature has been selected to be $\beta =-1$ .

Definition 4.9. For each $z \in \mathfrak {Z}_n$ , $n \geq 0$ , we define its $\kappa $ -dimension by

$$ \begin{align*} \kappa\text{-}\kern-1.2pt\dim(z) := \sqrt{\sum_{\substack{z_k \in \mathfrak{Z}_k (k=0,1\ldots,n) \\ z_0=1, z_n=z \\ \kappa(z_{k+1},z_k)> 0\, (k=0,1,\ldots,n-1)}} \frac{1}{\kappa(z_n,z_{n-1})\kappa(z_{n-1},z_{n-2})\cdots\kappa(z_1,z_0)}} \end{align*} $$

with $\kappa \text{-}\kern-1.2pt\dim (1) := 1$ . We then define the weight at $(z,z') \in \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ , $n \geq 0$ , by

$$ \begin{align*} \rho(z,z') := \kappa \text{-}\kern-1.2pt\dim(z)\,\kappa(z,z')\frac{1}{\kappa \text{-}\kern-1.2pt\dim(z')}. \end{align*} $$

The countable discrete subgroup $\Gamma (\kappa )$ of $\mathbb {R}_+^\times $ generated by all the positive weights $\rho (z,z')>0$ with $(z,z') \in \mathfrak {Z}_{n+1}\times \mathfrak {Z}_n$ , $n\geq 0$ , is called the weight group of $\kappa $ .

By definition, $\rho (z,z')> 0$ if and only if $\kappa (z,z') = 1$ . This construction is motivated by that in [19, Proposition 9.5] together with (4-5), (4-6).

Here is a claim, which informally corresponds to $\mathrm {Tr}(\rho _z) = \mathrm {Tr}(\rho _z^{-1})$ .

Lemma 4.10. We have

$$ \begin{align*} \kappa \text{-}\kern-1.2pt\dim(z) &= \sum_{\substack{z_k \in \mathfrak{Z}_k (k=0,1\ldots,n) \\ z_0=1, z_n=z}} \rho(z_n,z_{n-1})\rho(z_{n-1},z_{n-2})\cdots\rho(z_1,z_0) \\ &= \sum_{\substack{z_k \in \mathfrak{Z}_k (k=0,1\ldots,n) \\ z_0=1, z_n=z \\ \kappa(z_{k+1},z_k)>0\,(k=0,1\ldots,n-1)}} \frac{1}{\rho(z_n,z_{n-1})\rho(z_{n-1},z_{n-2})\cdots\rho(z_1,z_0)} \end{align*} $$

for every $z \in \mathfrak {Z}_n$ , $n\geq 1$ .

Proof. This is easily shown by induction on n. Clearly, $\kappa \text{-}\kern-1.2pt\dim (z) = \kappa (z,1) = \rho (z,1) = 1$ holds for every $z \in \mathfrak {Z}_1$ . The induction procedure from n to $n+1$ goes as follows. Using $\sum _{z' \in \mathfrak {Z}_n} \kappa (z,z') = 1$ for every $z \in \mathfrak {Z}_{n+1}$ , a property of links, we easily see that the first identity holds true. Compute

$$ \begin{align*} &\sum_{\substack{z_k \in \mathfrak{Z}_k (k=0,1\ldots,n+1) \\ z_0=1, z_{n+1}=z \\ \kappa(z_{k+1},z_k)>0\,(k=0,1\ldots,n)}} \frac{1}{\rho(z_{n+1},z_n)\rho(z_n,z_{n-1})\cdots\rho(z_1,z_0)} \\ &\qquad= \frac{1}{\kappa \text{-}\kern-1.2pt\dim(z)}\sum_{\substack{ z_n \in \mathfrak{Z}_n \\ \kappa(z,z_n) > 0}} \frac{\kappa \text{-}\kern-1.2pt\dim(z_n)}{\kappa(z,z_n)} \sum_{\substack{z_k \in \mathfrak{Z}_k (k=0,1\ldots,n-1) \\ z_0=1 \\ \kappa(z_{k+1},z_k)>0\, (k=0,1\ldots,n-1)}} \frac{1}{\rho(z_n,z_{n-1})\cdots\rho(z_1,z_0)} \\ &\qquad= \frac{1}{\kappa \text{-}\kern-1.2pt\dim(z)}\sum_{\substack{ z_n \in \mathfrak{Z}_n \\ \kappa(z,z_n) > 0}} \frac{\kappa \text{-}\kern-1.2pt\dim(z_n)^2}{\kappa(z,z_n)} \quad \text{(by induction hypothesis)} \\ &\qquad= \frac{1}{\kappa \text{-}\kern-1.2pt\dim(z)}\sum_{\substack{ z_n \in \mathfrak{Z}_n \\ \kappa(z,z_n) > 0}} \frac{1}{\kappa(z,z_n)} \sum_{\substack{z_k \in \mathfrak{Z}_k (k=0,1\ldots,n-1) \\ z_0=1 \\\kappa(z_{k+1},z_k)>0\, (k=0,1\ldots,n-1)}} \frac{1}{\kappa(z_n,z_{n-1})\cdots\kappa(z_1,z_0)} \\ &\qquad= \frac{1}{\kappa \text{-}\kern-1.2pt\dim(z)} \sum_{\substack{z_k \in \mathfrak{Z}_k (k=0,1\ldots,n+1) \\ z_0=1, z_{n+1}=z \\ \kappa(z_{k+1},z_k)>0\, (k=0,1\ldots,n)}} \frac{1}{\kappa(z_{n+1},z_n)\kappa(z_n,z_{n-1})\cdots\kappa(z_1,z_0)} \\ &\qquad= \kappa \text{-}\kern-1.2pt\dim(z). \end{align*} $$

Hence, we are done.

Proposition 4.3 suggests that we define the desired new branching graph as follows.

Definition 4.11. The weight-extended branching graph $(\widetilde {\mathfrak {Z}},\tilde {m})$ of $\kappa $ is defined to be $\widetilde {\mathfrak {Z}} = \bigsqcup _{n\geq 0} \widetilde {\mathfrak {Z}}_n$ with $\widetilde {\mathfrak {Z}}_n := \mathfrak {Z}_n\times \Gamma $ and

$$ \begin{align*} \tilde{m}((z,\gamma),(z',\gamma')) := \begin{cases} 1 & (\gamma^{-1}\gamma' = \rho(z,z')>0), \\ 0 & (\text{otherwise}). \end{cases} \end{align*} $$

This multiplicity function $\tilde {m}$ is invariant under the translation action of $\Gamma $ on the right coordinate, that is, $\tilde {m}\circ (T_\gamma ^{-1}\times T_\gamma ^{-1}) = \tilde {m}$ for every $\gamma \in \Gamma $ .

Since we have implicitly assumed that all $m(z,z')$ are either $0$ or $1$ , the dimension $\dim (z)$ of $z \in \mathfrak {Z}_n \subset \mathfrak {Z}$ in this context should be the total number of paths $(z_n,\ldots ,z_1,1)$ with $z_k \in \mathfrak {Z}_k$ , $z_n=z$ and $\kappa (z_{k+1},z_k)> 0$ . The dimension $\dim (z,\gamma )$ of $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_n$ is defined to be the total number of paths ending at $(z,\gamma )$ and starting in the $0$  th stage $\widetilde {\mathfrak {Z}}_0$ (which is no longer a singleton). Here is a lemma.

Lemma 4.12. $\dim (z,\gamma ) = \dim (z)$ always holds.

Proof. Let $((z_n,\gamma _n),\ldots ,(z_1,\gamma _1),(1,\gamma _0))$ be a path in $\widetilde {\mathfrak {Z}}$ ending at $(z_n,\gamma _n)$ and starting in $\widetilde {\mathfrak {Z}}_0$ . Then, $m(z_{k+1},z_k) =1$ holds for every $k=0,\ldots ,n-1$ with ${z_0:=1}$ . Moreover, the equations $\gamma _1 = \gamma _0/\rho (z_1,1)$ , $\gamma _2 = \gamma _1/\rho (z_2,z_1) = \gamma _0/\rho (z_2,z_1)\rho (z_1,1)$ , … , $\gamma _n = \gamma _0/\rho (z_n,z_{n-1})\cdots \rho (z_1,1)$ should hold. This means that each path is uniquely determined by the path $(z_n,\ldots ,z_1,1)$ in $\mathfrak {Z}$ and the relation $\gamma _0=\gamma _n\rho (z_n,z_{n-1})\cdots \rho (z_1,1)$ . Hence, the desired assertion must hold.

This lemma shows that the standard link $\tilde {\mu }$ over $(\widetilde {\mathfrak {Z}},\tilde {m})$ should be

$$ \begin{align*} \tilde{\mu}((z,\gamma),(z',\gamma')) = \begin{cases} \dfrac{\dim(z')}{\dim(z)} & (\tilde{m}((z,\gamma),(z',\gamma'))=1), \\ 0 & (\text{otherwise}). \end{cases} \end{align*} $$

With the preparation so far, Theorem 4.7 actually holds as it is with $\beta =-1$ and $\dim _\beta (z) = \kappa \text{-}\kern-1.2pt\dim (z)$ in the present setup. Its proof is an easy exercise now.

5 Relation to $K_0$ -groups

$K_0$ -groups or dimension groups play a role of representation rings in asymptotic representation theory, but they are not applicable to spherical representations for $C^*$ -flows (nor general links). Thus, we introduced, in our previous paper [18], a certain replacement of $K_0$ -groups by means of operator systems to investigate inductive $C^*$ -flows. Here, we give a way to connect the locally normal $(\alpha ^t,\beta )$ -KMS states $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ to K-theory of the $\rho $ -extension $(\widetilde {\alpha } : \Gamma \curvearrowright \widetilde {A} = \varinjlim \widetilde {A}_n)$ under the assumption that all $\dim (z) < +\infty $ .

We investigate the $K_0$ -group $K_0(\widetilde {A})$ and its positive cone $K_0(\widetilde {A})_+$ of $\widetilde {A}=\varinjlim \widetilde {A}_n$ . By a standard fact on K-theory (see for example, [6, Proposition 8.1]), we have $K_0(\widetilde {A}) = \varinjlim K_0(\widetilde {A}_n)$ and $K_0(\widetilde {A}_n)_+ =\varinjlim K_0(\widetilde {A}_n)_+$ . Thus, we first have to calculate each pair $K_0(\widetilde {A}_n)_+ \subset K_0(\widetilde {A}_n)$ and then have to do each embedding $K_0(\widetilde {A}_n) \hookrightarrow K_0(\widetilde {A}_{n+1})$ .

The first task was completed by just using [11, Proposition 6.1] as follows. It is convenient to transform each $\widetilde {A}_n$ to

$$ \begin{align*} \Phi_n(\widetilde{A}_n) = \bigoplus_{(z,\gamma)\in\mathfrak{Z}_n} \overset{z\otimes\delta_\gamma}{B({\mathcal{H}}_z)} \end{align*} $$

by Lemma 4.1 with the notation in Remark 4.4. By [11, Proposition 6.1(iv)], the $K_0$ -group $K_0(\Phi _n(\widetilde {A}_n))$ is isomorphic, by the dimension function $\mathrm {cdim}_n := \dim _{\mathcal {Z}(\Phi _n(\widetilde {A}_n))}$ induced from the center-valued trace $\mathrm {ctr}_n$ ( $=\mathrm {tr}_{\mathcal {Z}(\Phi _n(\widetilde {A}_n))}$ in [11]), to

(5-1) $$ \begin{align} \nonumber &\tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)} \\ &\quad:= \bigg\{ f : \widetilde{\mathfrak{Z}}_n \to \mathbb{Q}\ ;\ \displaystyle f(z,\gamma) \in \frac{\mathbb{Z}}{\dim(z)}\ \text{for each}\ (z,\gamma) \in \widetilde{\mathfrak{Z}}_n\ \text{and} \displaystyle \sup_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_n} |f(z,\gamma)| < +\infty \bigg\}, \end{align} $$

which sits in the center $\ell ^\infty (\widetilde {\mathfrak {Z}}_n)=\mathcal {Z}(\Phi _n(\widetilde {A}_n))$ . Here, this identification of the center is given by $\delta _{(z,\gamma )} = z\otimes \delta _\gamma $ . We take a closer look at $\mathrm {cdim}_n$ . In this case, the $K_0$ -group is the Grothendieck group of the Murray–von Neumann equivalence classes $[P]_n$ of projections in $\mathbb {M}_\infty (\Phi _n(\widetilde {A}_n)) := \bigcup _{m\geq 1} M_m(\mathbb {C})\otimes \Phi _n(\widetilde {A}_n)$ , where the embedding $M_m(\mathbb {C})\otimes \Phi _n(\widetilde {A}_n) \hookrightarrow M_{m+1}(\mathbb {C})\otimes \Phi _n(\widetilde {A}_n)$ is the upper corner one. The addition (semigroup operation) on it is given by

$$ \begin{align*} [P]_n+[Q]_n := \left[ \begin{bmatrix} P \\ & Q \end{bmatrix} \right]_n. \end{align*} $$

Then, the mapping $[P]_n \mapsto (\mathrm {Tr}\otimes \mathrm {ctr}_n)(P)$ is well defined because $\mathrm {Tr}$ is the nonnormalized trace. This mapping is nothing less than the dimension function $\mathrm {cdim}_n$ . The commutative diagram in [11, Proposition 6.1(ii)] and the finiteness of the $W^*$ -algebra in question show that the order arising from the positive cone $K_0(\Phi _n(\widetilde {A}_n))_+$ is the natural, point-wise one on $\ell ^\infty (\widetilde {\mathfrak {Z}}_n)$ . Hence, $K_0(\Phi _n(\widetilde {A}_n))_+$ ( $\subset K_0(\Phi _n(\widetilde {A}_n))$ ) is isomorphic via $\mathrm {cdim}_n$ to

$$ \begin{align*} \bigg[\tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)}\bigg]_+ := \bigg\{ f \in \tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)} ;\quad f(z,\gamma) \geq 0\ \text{for each}\ (z,\gamma) \in \widetilde{\mathfrak{Z}}_n \bigg\}. \end{align*} $$

We then investigate the embedding $K_0(\Phi _n(\widetilde {A}_n)) \hookrightarrow K_0(\Phi _n(\widetilde {A}_{n+1}))$ in description (5-1). The embedding is $\iota _{n+1,n}^*$ with $\iota _{n+1,n} = \Phi _{n+1}\circ \Phi _n^{-1}$ in Lemma 4.2. Hence, we need to compute

$$ \begin{align*} \iota_{n+1,n}^{**} := \mathrm{cdim}_{n+1}\circ\iota_{n+1,n}^*\circ(\mathrm{cdim}_{n})^{-1} : \tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)} \to \tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_{n+1}}} \frac{\mathbb{Z}}{\dim(z)}. \end{align*} $$

Let $x \in K_0(\Phi _n(\widetilde {A}_n))$ be arbitrarily chosen. Then there are $m \in \mathbb {N}$ and projections $P,Q \in M_m(\mathbb {C})\otimes \Phi _n(\widetilde {A}_n)$ such that $x = [P]_n - [Q]_n$ . Then,

$$ \begin{align*} &\mathrm{cdim}_n(x)=(\mathrm{Tr}\otimes\mathrm{ctr}_n)(P-Q)=\sum_{(z',\gamma') \in \widetilde{\mathfrak{Z}}_n} \frac{\mathrm{Tr}((1\otimes (z'\otimes\delta_{\gamma'}))(P-Q))}{\dim(z')}(z'\otimes\delta_{\gamma'}), \\ &\mathrm{cdim}_{n+1}\circ\iota_{n+1,n}^*(x) = (\mathrm{Tr}\otimes\mathrm{ctr}_{n+1}) ((\mathrm{id}\otimes\iota_{n+1,n})(P-Q)) \\ &\quad =\!\!\sum_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_{n+1}} \sum_{(z',\gamma')\in\widetilde{\mathfrak{Z}}_n}\! \frac{1}{\dim(z)}\mathrm{Tr}((1\!\otimes(z\!\otimes\delta_\gamma)) (\mathrm{id}\otimes\iota_{n+1,n})((1\otimes(z'\otimes\delta_{\gamma'}))(P\!-\!Q)))(z\otimes\delta_\gamma) \\ &\quad =\sum_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_{n+1}}\sum_{(z',\gamma')\in\widetilde{\mathfrak{Z}}_n} \frac{\mathrm{Tr}((z\otimes\delta_\gamma)\iota_{n+1,n}(z'\otimes\delta_{\gamma'}))}{\dim(z)\dim(z')}\mathrm{Tr}((1\otimes(z'\otimes\delta_{\gamma'}))(P-Q))(z\otimes\delta_\gamma) \end{align*} $$

by using the uniqueness of traces. Thus,

$$ \begin{align*} &\mathrm{cdim}_{n+1}\circ\iota_{n+1,n}^*(x) \\ &\quad= \sum_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_{n+1}}\sum_{(z',\gamma')\in\widetilde{\mathfrak{Z}}_n} \frac{\mathrm{Tr}((1\otimes(z'\otimes\delta_{\gamma'}))(P-Q))}{\dim(z')}\,\mathrm{ctr}_{n+1}(\iota_{n+1,n}(z'\otimes\delta_{\gamma'}))(z\otimes\delta_\gamma) \\ &\quad= \sum_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_{n+1}} \mathrm{ctr}_{n+1}(\iota_{n+1,n}(\mathrm{ctr}_n(x))) (z'\otimes\delta_{\gamma'})) \\ &\quad= \mathrm{ctr}_{n+1}(\iota_{n+1,n}(\mathrm{ctr}_n(x))). \end{align*} $$

Therefore, we conclude that the desired embedding map $\iota _{n+1,n}^{**}$ is just the restriction of the normal map $\mathrm {ctr}_{n+1}\circ \iota _{n+1,n} : \mathcal {Z}(\Phi _n(\widetilde {A}_n)) \to \mathcal {Z}(\Phi _{n+1}(\widetilde {A}_{n+1}))$ to the range of $\mathrm {cdim}_n(K_0(\Phi _n(\widetilde {A}_n)))$ . Actually, for an $f \in \tilde {\prod }_{(z,\gamma )\in \widetilde {\mathfrak {Z}}_n} ({\mathbb {Z}}/{\dim (z)})$ ,

(5-2) $$ \begin{align} \iota_{n+1,n}^{**}(f)(z,\gamma) &= \sum_{(z',\gamma')\in\widetilde{\mathfrak{Z}}_n}f(z',\gamma')\,\mathrm{ctr}_{n+1}(\iota_{n+1,n}(z'\otimes\delta_{\gamma'}))(z,\gamma)\nonumber\\ &= \sum_{(z',\gamma')\in\widetilde{\mathfrak{Z}}_n}\tilde{\mu}((z,\gamma),(z',\gamma'))\,f(z',\gamma') \end{align} $$

by (4-9). This computation shows that the embedding $\iota _{n+1,n}^{**}$ is the left-multiplication of the $\infty \times \infty $ matrix

$$ \begin{align*} \begin{bmatrix} \tilde{\mu}((z,\gamma),(z',\gamma'))\end{bmatrix}_{\widetilde{\mathfrak{Z}}_{n+1}\times\widetilde{\mathfrak{Z}}_n} \end{align*} $$

in Description (5-1). Since $\tilde {\mu }((z,\gamma ),(z',\gamma ')) \geq 0$ , the embedding preserves the positivity. Summing up the discussion so far, we conclude as follows.

Proposition 5.1. The triple $(K_0(\widetilde {A}) \supset K_0(\widetilde {A})_+,[1])$ is computed as

$$ \begin{align*} (\mathfrak{D} \supset \mathfrak{D}_+,1) := \varinjlim\bigg(\tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)}\supset\bigg[\tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)}\bigg]_+,\mathbf{1}\bigg) \end{align*} $$

along the embeddings $\iota _{n+1,n}^{**} = \mathrm {ctr}_{n+1}\circ \iota _{n+1,n}$ , $n=0,1,\ldots ,$ where $\mathbf {1}$ is the constant function, that is, $\mathbf {1}(z,\gamma ) = 1$ for all $(z,\gamma )\in \widetilde {\mathfrak {Z}}_n$ .

Remark 5.2. For each n, the mapping

$$ \begin{align*} f \in \tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)} \mapsto \{(z,\gamma) \mapsto \dim(z)f(z,\gamma)\} \in \mathbb{Z}^{\widetilde{\mathfrak{Z}}_n} \end{align*} $$

is an injective group homomorphism, whose image is exactly

$$ \begin{align*} \langle\mathbb{Z}^{\widetilde{\mathfrak{Z}}_n}\rangle := \bigg\{ h \in \mathbb{Z}^{\widetilde{\mathfrak{Z}}_n}\,;\, \sup_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_n} \frac{|h(z,\gamma)|}{\dim(z)} <+\infty\bigg\}. \end{align*} $$

With these mappings, $(K_0(\widetilde {A}) \supset K_0(\widetilde {A})_+,[1])$ is identified with

$$ \begin{align*} \varinjlim (\langle\mathbb{Z}^{\widetilde{\mathfrak{Z}}_n}\rangle,\langle\mathbb{Z}^{\widetilde{\mathfrak{Z}}_n}\rangle_+,\dim) \end{align*} $$

along the mapping from $\langle \mathbb {Z}^{\widetilde {\mathfrak {Z}}_n}\rangle $ to $\langle \mathbb {Z}^{\widetilde {\mathfrak {Z}}_{n+1}}\rangle $ given as the left-multiplication of an $\infty \times \infty $ matrix

$$ \begin{align*} \begin{bmatrix} \tilde{m}((z,\gamma),(z',\gamma'))\end{bmatrix}_{\widetilde{\mathfrak{Z}}_{n+1}\times\widetilde{\mathfrak{Z}}_n}, \end{align*} $$

where

$$ \begin{align*} \langle\mathbb{Z}^{\widetilde{\mathfrak{Z}}_n}\rangle_+ := \{ h \in \langle\mathbb{Z}^{\widetilde{\mathfrak{Z}}_n}\rangle\,;\, h(z,\gamma)\geq0\ \text{for all}\ (z,\gamma)\in\widetilde{\mathfrak{Z}}_n\} \end{align*} $$

and $\dim (z,\gamma ) = \dim (z)$ holds for every $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_n$ . This description is completely consistent with dimension groups of AF-algebras. An additional feature here is that $\langle \mathbb {Z}^{\widetilde {\mathfrak {Z}}_n}\rangle $ is a much smaller set than $\mathbb {Z}^{\widetilde {\mathfrak {Z}}_n}$ except for the case when $\widetilde {\mathfrak {Z}}_n$ is a finite set.

We then investigate how the action $\widetilde {\alpha }^\gamma : \Gamma \curvearrowright \widetilde {A}$ behaves on $\mathfrak {D}$ . Let $(\widetilde {\alpha }^\gamma )^*$ be the automorphism of $K_0(\widetilde {A})$ induced from $\widetilde {\alpha }^\gamma $ canonically.

Proposition 5.3. The automorphism $(\widetilde {\alpha }^\gamma )^{**}$ of $\mathfrak {D}$ obtained from $(\widetilde {\alpha }^\gamma )^*$ via $K_0(\widetilde {A}) \cong \mathfrak {D}$ is given as follows. For each $n \geq 0$ ,

$$ \begin{align*} (\widetilde{\alpha}^\gamma)^{**}(\iota_n^{**}(f)) = \iota_n^{**}(f\circ T_\gamma^{-1}), \quad \gamma \in\Gamma, \quad f \in\tilde{\prod_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_n}}\frac{\mathbb{Z}}{\dim(z)}, \end{align*} $$

where $\iota _n^{**} : \tilde {\prod }_{(z,\gamma )\in \widetilde {\mathfrak {Z}}_n}({\mathbb {Z}}/{\dim (z)}) \to \mathfrak {D}$ is the canonical group-homomorphism.

Proof. Since $\widetilde {\alpha }^\gamma $ is an inductive action, the restriction of $\widetilde {\alpha }^\gamma $ to each $\widetilde {A}_n$ makes sense and induces an automorphism $(\widetilde {\alpha }^\gamma )_n^{**}$ of

$$ \begin{align*} (K_0(\widetilde{A}_n) \overset{\Phi_n^*}{\rightarrow} K_0(\Phi_n(\widetilde{A}_n)) \overset{\mathrm{cdim}_n}{\rightarrow})\quad \tilde{\prod_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_n}}\frac{\mathbb{Z}}{\dim(z)} \quad (\subset \mathcal{Z}(\Phi_n(\widetilde{A}_n))), \end{align*} $$

which we have to compute. This is nothing but $\mathrm {cdim}_n\circ (\widetilde {\alpha }^\gamma )^*\circ (\mathrm {cdim}_n)^{-1}$ , and can be shown in the same way as above to coincide with the restriction of $\Phi _n\circ \widetilde {\alpha }^\gamma \circ \Phi _n^{-1}$ to $ \tilde {\prod }_{(z,\gamma )\in \widetilde {\mathfrak {Z}}_n}({\mathbb {Z}}/{\dim (z)})$ ( $\subset \mathcal {Z}(\Phi _n(\widetilde {A}_n))$ ). By (4-4),

$$ \begin{align*} (\Phi_n\circ\widetilde{\alpha}^\gamma\circ\Phi_n^{-1})(z'\otimes\delta_\gamma) = z'\otimes\delta_{\gamma\gamma'}, \end{align*} $$

and hence, we conclude that

$$ \begin{align*} (\widetilde{\alpha}^\gamma)_n^{**}(f) = f\circ T^{-1}_\gamma, \quad \gamma \in \Gamma, \quad f \in \tilde{\prod_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_n}}\frac{\mathbb{Z}}{\dim(z)}. \end{align*} $$

Since

$$ \begin{align*} &(\iota_{n+1,n}^{**}\circ(\widetilde{\alpha}^{\gamma"})_n^{**}(f))(z,\gamma)\\ &\quad= \sum_{(z',\gamma') \in \widetilde{\mathfrak{Z}}_n} \tilde{\mu}((z,\gamma),(z',\gamma'))\,f(T_{\gamma"}^{-1}(z',\gamma')) \quad \text{(by}\ (5\text{-}2)) \\ &\quad= \sum_{(z',\gamma') \in \widetilde{\mathfrak{Z}}_n} \tilde{\mu}(T_{\gamma"}^{-1}(z,\gamma),T_{\gamma"}^{-1}(z',\gamma'))\,f(T_{\gamma"}^{-1}(z',\gamma')) \quad \text{(by Proposition}\ 4.3) \\ &\quad= \iota_{n+1,n}^{**}(f)(T_{\gamma"}^{-1}(z,\gamma)) \\ &\quad= ((\widetilde{\alpha}^{\gamma"})_{n+1}^{**}\circ\iota_{n+1,n}^{**}(f))(z,\gamma) \end{align*} $$

for every $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_{n+1}$ and $\gamma " \in \Gamma $ , the inductive limit $\varinjlim (\widetilde {\alpha }^\gamma )_n^{**}$ is well defined on $\mathfrak {D}$ . Then, it is not difficult to see that this coincides with $(\widetilde {\alpha }^\gamma )^{**}$ .

Here is a proposition.

Proposition 5.4. Let $\mathcal {W}_\beta ^{\mathrm {ln}}(\tilde {\mu })$ be all the additive maps $\psi : \mathfrak {D}_+ \to [0,\infty ]$ such that:

1. (i) $\psi \circ (\widetilde {\alpha }^\gamma )^{**} = \gamma ^\beta \,\psi $ for all $\gamma \in \Gamma $ ;

2. (ii) for each n, if $f_k \nearrow f$ in $[\tilde {\prod }_{(z,\gamma )\in \widetilde {\mathfrak {Z}}_n} ({\mathbb {Z}}/{\dim (z)})]_+$ pointwise as functions over $\widetilde {\mathfrak {Z}}_n$ , then $\psi \circ \iota _n^{**}(f_k) \nearrow \psi \circ \iota _n^{**}(f)$ as $k \to \infty $ ;

3. (iii) $\psi (\iota _0^{**}(\delta _{(1,1)})) = 1$ .

Then there is a unique affine bijection $\tilde {\nu } \in H_1^+(\tilde {\mu })_\beta \mapsto \psi _{\tilde {\nu }} \in \mathcal {W}_\beta ^{\mathrm {ln}}(\tilde {\mu })$ so that

$$ \begin{align*} \psi_{\tilde{\nu}}(\iota_n^{**}(\delta_{(z,\gamma)})) = \tilde{\nu}(z,\gamma) \end{align*} $$

for all $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_n$ , $n \geq 0$ .

Proof. Let $\tilde {\nu } \in H_1^+(\tilde {\mu })_\beta $ be arbitrarily chosen. We observe that

$$ \begin{align*} \sum_{(z',\gamma') \in \widetilde{\mathfrak{Z}}_n} \tilde{\nu}(z',\gamma')\,f(z',\gamma') &= \sum_{(z',\gamma') \in \widetilde{\mathfrak{Z}}_n} \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\,\tilde{\mu}((z,\gamma),(z',\gamma'))\,f(z',\gamma') \\ &= \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\,\sum_{(z',\gamma') \in \widetilde{\mathfrak{Z}}_n} \tilde{\mu}((z,\gamma),(z',\gamma'))\,f(z',\gamma') \\ &= \sum_{(z,\gamma) \in \widetilde{\mathfrak{Z}}_{n+1}} \tilde{\nu}(z,\gamma)\,\iota_{n+1,n}^{**}(f)(z,\gamma) \end{align*} $$

for every $f \in [\tilde {\prod }_{(z,\gamma )\in \widetilde {\mathfrak {Z}}_n} ({\mathbb {Z}}/{\dim (z)})]_+$ . Hence,

$$ \begin{align*} \iota_n^{**}(f) \quad \text{with} \quad f \in \bigg[\tilde{\prod_{(z,\gamma)\in \widetilde{\mathfrak{Z}}_n}} \frac{\mathbb{Z}}{\dim(z)}\bigg]_+ \quad \mapsto \quad \sum_{(z,\gamma)\in\widetilde{\mathfrak{Z}}_n} \tilde{\nu}(z,\gamma)\,f(z,\gamma) \end{align*} $$

defines a well-defined additive map $\psi _\nu $ from $\mathfrak {D}_+$ to $[0,\infty ]$ . That the $\tilde {\nu }$ satisfies item (ii) of Definition 4.6 implies that the $\psi _{\tilde {\nu }}$ does item (i) here. That $\psi _{\tilde {\nu }}$ satisfies items (ii), (iii) is clear from its definition.

Let $\psi \in \mathcal {W}_\beta ^{\mathrm {ln}}(\tilde {\nu })$ be arbitrarily chosen. Define $\tilde {\nu }_\psi (z,\gamma ) := \psi (\iota _n^{**}(\delta _{(z,\gamma )}))$ for each $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_n \subset \widetilde {\mathfrak {Z}}$ . Using (5-2) and item (ii) here, we can easily confirm that this $\tilde {\nu }_\psi $ satisfies item (i) of Definition 4.6. We also have, for every $(z,\gamma ) \in \widetilde {\mathfrak {Z}}_n$ , $n\geq 0$ ,

$$ \begin{align*} \tilde{\nu}_\psi(z,\gamma) &= \psi(\iota_n^{**}(\delta_{(z,\gamma)})) = \psi(\iota_n^{**}(T_\gamma^{-1}(\delta_{(z,1)}))) = \psi((\widetilde{\alpha}^\gamma)^{**}(\iota_n^{**}(\delta_{(z,1)})))\\ &= \gamma^\beta\,\psi(\iota_n^{**}(\delta_{(z,1)})) = \gamma^\beta\,\tilde{\nu}_\psi(z,1), \end{align*} $$

implying that the $\tilde {\nu }_\psi $ satisfies item (ii) of Definition 4.6. Finally, $\tilde {\nu }_\psi (1,1) = \psi (\iota _0^{**}(\delta _{(1,1)}))~=~1$ . Hence, we are done.

This proposition together with Theorem 4.7 gives an interpretation of $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ or $H_1^+(\kappa )$ in terms of $K_0$ -group. In fact, we have the following theorem.

Theorem 5.5. The correspondence $\omega \in K_\beta ^{\mathrm {ln}}(\alpha ^t) \mapsto \psi _\omega \in \mathcal {W}_\beta ^{\mathrm {ln}}(\tilde {\mu })$ defined by

$$ \begin{align*} \psi_\omega(\iota_n^{**}(\delta_{(z,\gamma)})) = \frac{\dim(z)}{\dim_\beta(z)}\,\omega(z)\,\gamma^\beta, \quad (z,\gamma) \in \widetilde{\frak{Z}}_n, \quad n =0,1,\ldots \end{align*} $$

is an affine-isomorphism. In particular, each $\psi \in \mathcal {W}^{\mathrm {ln}}_\beta (\tilde {\mu })$ gives a unique $\omega _\psi \in K_\beta ^{\mathrm {ln}}(\alpha ^t)$ in such a way that

$$ \begin{align*} \omega_\psi(a) = \sum_{z\in\mathfrak{Z}_n} \psi(\iota_n^{**}(\delta_{(z,1)}))\,\frac{\mathrm{Tr}(\rho_z^{-\beta}za)}{\dim(z)}, \quad a \in A_n, \quad n=0,1,\ldots, \end{align*} $$

and any element of $K_\beta ^{\mathrm {ln}}(\alpha ^t)$ arises in this way.

Remark 5.6. Let $\mathcal {W}_\beta (K_0(\widetilde {A}))$ be all the additive maps $\psi : K_0(\widetilde {A})_+ \to [0,\infty ]$ so that $\psi \circ ( \widetilde {\alpha} ^\gamma )^* = \gamma ^\beta \,\psi $ for all $\gamma \in \Gamma $ . Then we see that $\mathcal {W}_\beta ^{\mathrm {ln}}(\tilde {\mu })$ sits in $\mathcal {W}_\beta (K_0(\widetilde {A}))$ via ${\mathfrak {D} \cong K_0(\widetilde {A})}$ . Note that $\mathcal {W}_\beta (K_0(\widetilde {A}))$ depends only on $\widetilde {A}$ , but $\mathcal {W}_\beta ^{\mathrm {ln}}(\tilde {\mu })$ does not.

6 A concrete example: ${\mathbf{U}}_{\boldsymbol {q}}\boldsymbol {(\infty )}$

We illustrate the present method with the infinite dimensional quantum unitary group $\mathrm {U}_q(\infty )$ , for whose formulation we follow our previous paper [18] (note, the convention of q-deformation in both [7, 12] does not fit standard references on the quantum unitary group $\mathrm {U}_q(n)$ , although the difference in the consequences is minor, that is, $q \rightsquigarrow q^{-1/2}$ in [7] and $q \rightsquigarrow q^{-1}$ in [12]). Namely, we freely use the notation in [18, Section 4.2]. However, the Greek letter $\Gamma $ was used there with a different meaning from in this paper.

6.1 Weight group and weight-extended branching system

We first have to find the eigenvalues of $\rho _\lambda $ to determine the weight group $\Gamma $ in Section 4. Here, we remark that the $\rho _\lambda $ , $\lambda \in \mathbb {S}_n$ , naturally satisfy $\mathrm {Tr}(\rho _\lambda ) = \mathrm {Tr}(\rho _\lambda ^{-1})$ .

Lemma 6.1. The weight group $\Gamma $ is $q^{\mathbb {Z}} := \{q^k; k \in \mathbb {Z}\}$ .

Proof. By [18, equation (4.17)],

$$ \begin{align*} \rho_\lambda = \pi_\lambda(K_1^{-n+1}K_2^{-n+3}\cdots K_n^{n-1}), \quad \lambda \in \mathbb{S}_n. \end{align*} $$

The irreducible representations $\pi _\lambda $ , $\lambda \in \mathbb {S}_n$ , must satisfy that the $\pi _\lambda (K_i)$ are commonly diagonalized with eigenvalues of the form $q^k$ including at least $q^{\lambda _i}$ for $\pi _\lambda (K_i)$ . Thus, $\rho _{(1,0)}$ ( $(1,0) \in \mathbb {S}_2$ ) has eigenvalue $q^{-1}$ . This shows $\Gamma = q^{\mathbb {Z}}$ .

The dual of $q^{\mathbb {Z}}$ is identified with the $1$ -dimensional torus $\mathbb {T} = \{\zeta \in \mathbb {C}; |\zeta | = 1\}$ with dual pairing $\langle q^k, \zeta \rangle = \zeta ^k$ for any $k \in \mathbb {Z}$ and $\zeta \in \mathbb {T}$ . The canonical surjective group-homomorphism from $\mathbb {R}$ to $\mathbb {T}$ is given by $t \mapsto q^{it}$ .

The inductive sequence $\widetilde {W^*(\mathrm {U}_q(n))}$ , $n=0,1,\ldots ,$ is given as the $W^*$ -crossed products $W^*(\mathrm {U}_q(n))\,\bar {\rtimes }_{\vartheta _n^\zeta }\mathbb {T}$ . By Proposition 4.3, its branching graph is given by $\bigsqcup _{n\geq 0} \mathbb {S}_n\times q^{\mathbb {Z}}$ and the multiplicity function is computed by finding the spectral decomposition $\rho _\lambda \rho _{\lambda '}^{-1}$ on ${\mathcal {H}}_\lambda \overset {\pi _\lambda }{\curvearrowleft } U_q\mathfrak {gl}(n+1)$ with $(\lambda ,\lambda ') \in \mathbb {S}_{n+1}\times \mathbb {S}_n$ , $\lambda ' \prec \lambda $ , $n \geq 0$ . As in [18, Section 4.4.5], we obtain

$$ \begin{align*} \rho_\lambda\rho_{\lambda'}^{-1} = \pi_{\lambda'}(K_1^{-1}\cdots K_n^{-1})\otimes\pi_{(|\lambda|-|\lambda'|)}(K_1^n) \end{align*} $$

(up to unitary equivalence), where the right-hand side is the representation of $U_q\mathfrak {gl}(n)\otimes U_q\mathfrak {gl}(1)$ . Since the branching rule from $U_q\mathfrak {gl}(n) \hookrightarrow U_q\mathfrak {gl}(n+1)$ is the same as the classical case and hence multiplicity-free, we obtain that $\rho _\lambda \rho _{\lambda '}^{-1}$ is of the form $\gamma \,z_\lambda z_{\lambda '}$ with positive scalar $\gamma> 0$ and also that

$$ \begin{align*} \mathrm{Tr}(z_\lambda z_{\lambda'}) &= s_{\lambda'}(1,\ldots,1)\,s_{(|\lambda|-|\lambda'|)}(1) = s_{\lambda'}(1,\ldots,1) = \dim(\lambda'), \\ \mathrm{Tr}(\rho_\lambda\rho_{\lambda'}^{-1}) &= s_{\lambda'}(q^{-1},\ldots,q^{-1})\,s_{(|\lambda|-|\lambda'|)}(q^n) \\ &= q^{n|\lambda|-(n+1)|\lambda'|} s_{\lambda'}(1,\ldots,1) = q^{n|\lambda|-(n+1)|\lambda'|}\dim(\lambda'). \end{align*} $$

It follows that $\gamma = q^{n|\lambda |-(n+1)|\lambda '|}$ and hence,

$$ \begin{align*} q_{(\lambda,\lambda')}(q^k) = \begin{cases} z_\lambda z_{\lambda'} & (k = n|\lambda|-(n+1)|\lambda'|), \\ 0 & \text{(otherwise)}. \end{cases} \end{align*} $$

Therefore,

$$ \begin{align*} \tilde{m}((\lambda,q^k),(\lambda',q^\ell)) = \begin{cases} 1 & (\ell-k = n|\lambda|-(n+1)|\lambda'|), \\ 0 & \text{(otherwise)} \end{cases} \end{align*} $$

(note $n|\lambda |-(n+1)|\lambda '| = [\lambda ', (|\lambda |-|\lambda '|)]$ ; see [18, Section 4.4.5] for this terminology). Hence, we have determined the branching graph of the $\widetilde {W^*(\mathrm {U}_q(n))}$ , $n=0,1,\ldots ,$ completely. With [18, (4.16)], we remark that this computation is consistent with the construction in Section 4.3. This is not a surprise, because this computation as well as the computation of the link [18, (4.16)] were done by using only the branching rule.

6.2 Quantum group interpretation of weight-extensions

We clarify that the algebra $\widetilde {W^*(\mathrm {U}_q(n))} = W^*(\mathrm {U}_q(n))\,\bar {\rtimes }_{\vartheta _n^\zeta }\mathbb {T}$ comes from a compact quantum group. A similar (but not the same) algebra appeared in an unpublished manuscript of De Commer [5], where $q^{\mathbb {Z}}$ is replaced with $q^{2\mathbb {Z}}$ .

Let $(\mathbb {C}[\mathbb {T}],\Delta _{\mathbb {T}},S_{\mathbb {T}},\varepsilon _{\mathbb {T}})$ be the Hopf $*$ -algebra associated with the $1$ -dimensional torus $\mathbb {T}$ , that is, $\mathbb {C}[\mathbb {T}]$ denotes all the Laurent polynomials $\sum _k c_k \chi _k$ ( $c_k \in \mathbb {C}$ ) in the continuous functions $C(\mathbb {T})$ with $\chi _k(\zeta ) = \zeta ^k$ in $\zeta \in \mathbb {T}$ ( $k \in \mathbb {Z}$ ), and

$$ \begin{align*} \Delta_{\mathbb{T}}(\chi_k) = \chi_k\otimes\chi_k, \quad S_{\mathbb{T}}(\chi_k) = \chi_{-k}, \quad \varepsilon_{\mathbb{T}}(\chi_k) = 1. \end{align*} $$

Since $S_{\mathbb {T}}^2 = \mathrm {id}$ , the Woronowicz character or the special positive element of $\mathcal {U}(\mathbb {T})$ , the algebraic dual of $\mathbb {C}[\mathbb {T}]$ , must be trivial by [10, Proposition 1.7.9].

We define the new Hopf $*$ -algebra $(\mathbb {C}[\mathrm {U}_q(n)\times \mathbb {T}], \Delta _{n,\mathbb {T}}, S_{n,\mathbb {T}}, \varepsilon _{n,\mathbb {T}})$ to be the algebraic tensor product $\mathbb {C}[\mathrm {U}_q(n)\times \mathbb {T}] := \mathbb {C}[\mathrm {U}_q(n)]\otimes \mathbb {C}[\mathbb {T}]$ and

$$ \begin{align*} \Delta_{n,\mathbb{T}} := \Sigma_{23}\circ(\Delta_n\otimes\Delta_{\mathbb{T}}), \quad S_{n,\mathbb{T}} := S_n\otimes S_{\mathbb{T}}, \quad \varepsilon_{n,\mathbb{T}} := \varepsilon_n\otimes\varepsilon_{\mathbb{T}}, \end{align*} $$

where $\Sigma $ is the tensor-flip map and we use the leg-notation. The matrix elements of unitary representations $U\otimes \chi _k$ with finite dimensional unitary representations U of $(\mathbb {C}[\mathrm {U}_q(n)],\Delta _n)$ and $k\in \mathbb {Z}$ clearly generate $\mathbb {C}[\mathrm {U}_q(n)\times \mathbb {T}]$ as algebra, and hence the Hopf $*$ -algebra indeed defines a compact quantum group by [10, Theorem 1.6.7]. The corresponding $C^*$ -algebra is trivially $C(\mathrm {U}_q(n))\otimes C(\mathbb {T})$ with unique $C^*$ -tensor product due to nuclearity. Moreover, the unitary irreducible representations $U_\lambda \otimes \chi _k$ , $(\lambda ,k)\in \mathbb {S}_n\times \mathbb {Z}$ , are easily shown to be mutually inequivalent, and we can prove that they form a complete family of inequivalent, unitary irreducible representations by appealing to the famous orthogonal relation and the Peter–Weyl type theorem (see [10, Theorem 1.4.3(ii) and the discussion following Corollary 1.5.5]). Consequently,

$$ \begin{align*} \mathcal{U}(\mathrm{U}_q(n)\times\mathbb{T}) = \prod_{(\lambda,m)\in\mathbb{S}_n\times\mathbb{Z}} B({\mathcal{H}}_{(\lambda,m)}) \quad \text{with } {\mathcal{H}}_{(\lambda,m)}:={\mathcal{H}}_\lambda, \end{align*} $$

and hence,

(6-1) $$ \begin{align} W^*(\mathrm{U}_q(n)\times\mathbb{T}) = \bigoplus_{(\lambda,m)\in\mathbb{S}_n\times\mathbb{Z}} B({\mathcal{H}}_{(\lambda,m)}) = W^*(\mathrm{U}_q(n))\,\bar{\otimes}\,\ell^\infty(\mathbb{Z}), \end{align} $$

which is clearly isomorphic to $\widetilde {W^*(\mathrm {U}_q(n))}$ via $\Phi _n$ of Lemma 4.1.

Choose an $x \in W^*(\mathrm {U}_q(n)) \subset \mathcal {U}(\mathrm {U}_q(n))$ and a $\zeta \in \mathbb {T}$ . We regard $\zeta $ as an element of $\mathcal {U}(\mathbb {T})$ by $\zeta (f) := f(\zeta )$ for every $f \in C(\mathbb {T})$ , in which $\mathbb {C}[\mathbb {T}]$ sits. For any $a,b \in \mathbb {C}[\mathrm {U}_q(n)]$ and $k,\ell \in \mathbb {Z}$ ,

$$ \begin{align*} (\hat{\Delta}_{n,\mathbb{T}}(x\otimes\zeta))((a\otimes\chi_k)\otimes(b\otimes\chi_\ell)) &= (x\otimes\zeta)(ab\otimes\chi_{k+\ell}) \\ &= x(ab) \zeta^{k+\ell} \\ &= \hat{\Delta}_n(x)(a\otimes b)\,\hat{\Delta}_{\mathbb{T}}(\chi_k\otimes\chi_\ell) \\ &= (\hat{\Delta}_n(x)_{13}\hat{\Delta}_{\mathbb{T}}(\zeta)_{24})((a\otimes\chi_k)\otimes(b\otimes\chi_\ell)), \end{align*} $$

and hence,

$$ \begin{align*} \hat{\Delta}_{n,\mathbb{T}}(x\otimes\zeta) = \hat{\Delta}_n(x)_{13}\hat{\Delta}_{\mathbb{T}}(\zeta)_{24} = \hat{\Delta}_n(x)_{13}(1\otimes\zeta\otimes1\otimes\zeta) \in \mathcal{U}((\mathrm{U}_q(n)\times\mathbb{T})^2). \end{align*} $$

We observe that

$$ \begin{align*} \zeta = \sum_{k\in\mathbb{Z}} \zeta(\chi_k)\,\delta_k = \sum_{k\in\mathbb{Z}} \zeta^k\,\delta_k \in \ell^\infty(\mathbb{Z}) \subset \mathbb{C}^{\mathbb{Z}} = \mathcal{U}(\mathbb{T}). \end{align*} $$

Since $\hat {\Delta }_n(x) \in W^*(\mathrm {U}_q(n))\,\bar {\otimes }\,W^*(\mathrm {U}_q(n))$ and since the $\zeta \in \mathbb {T}$ generate $\ell ^\infty (\mathbb {Z})$ as a $W^*$ -algebra, we conclude that the restriction of $\hat {\Delta }_{n,\mathbb {T}}$ to $W^*(\mathrm {U}_q(n)\times \mathbb {T})$ coincides with the injective normal $*$ -homomorphism

$$ \begin{align*} \Sigma_{23}\circ(\hat{\Delta}_n\,\bar{\otimes}\,\hat{\Delta}_{\mathbb{T}}) : W^*(\mathrm{U}_q(n)\times\mathbb{T}) \to (W^*(\mathrm{U}_q(n)\times\mathbb{T}))^{\bar{\otimes}2}. \end{align*} $$

It is also easy to see that the restrictions of $\hat {\varepsilon }_{n,\mathbb {T}}$ and $\hat {S}_{n,\mathbb {T}}$ to $\mathcal {U}(\mathrm {U}_q(n))\otimes \mathcal {U}(\mathbb {T})$ (sitting in $\mathcal {U}(\mathrm {U}_q(n)\times \mathbb {T})$ naturally) are exactly $\hat {\varepsilon }_n\otimes \hat {\varepsilon }_{\mathbb {T}}$ and $\hat {S}_n\otimes \hat {S}_{\mathbb {T}}$ , respectively. In particular, the restriction of $\hat {\varepsilon }_{n,\mathbb {T}}$ to $W^*(\mathrm {U}_q(n)\times \mathbb {T})$ is $\hat {\varepsilon }_n\,\bar {\otimes }\,\hat {\varepsilon }_{\mathbb {T}}$ . Since the algebraic tensor product $\mathcal {F}(\mathrm {U}_q(n)\times \mathbb {T}) = \mathcal {F}(\mathrm {U}_q(n))\otimes c_{\mathrm {fin}}(\mathbb {Z})$ with all the finitely supported bi-sequences $c_{\mathrm {fin}}(\mathbb {Z})$ , we have $\hat {S}_{n,\mathbb {T}}^2 = \hat {S}_n^2\otimes \mathrm {id}$ on $\mathcal {F}(\mathrm {U}_q(n)\times \mathbb {T})$ .

We observe that $(U_\lambda \otimes \chi _k)^{\mathrm {cc}} = U_\lambda ^{\mathrm {cc}}\otimes \chi _k$ by definition and hence $\rho _{(\lambda ,k)} = \rho _\lambda \otimes 1$ by [10, Proposition 1.4.4] for every $(\lambda ,k) \in \mathbb {S}_n\times \mathbb {Z}$ . Therefore, the special positive element for $\mathrm {U}_q(n)\times \mathbb {T}$ must be $\rho _n\otimes 1 \in \mathcal {U}(\mathrm {U}_q(n))\otimes \mathbb {C}1 \subset \mathcal {U}(\mathrm {U}_q(n)\times \mathbb {T})$ . It follows that the restriction of the unitary antipode $\hat {R}_{n,\mathbb {T}}$ to $W^*(\mathrm {U}_q(n)\times \mathbb {T})$ coincides with $\hat {R}_n\,\bar {\otimes }\,\hat {S}_{\mathbb {T}}$ .

Regarding the $\Phi _n$ in Lemma 4.1 as a map from $\widetilde {W^*(\mathrm {U}_q(n))}$ onto $W^*(\mathrm {U}_q(n)\times \mathbb {T}) = W^*(\mathrm {U}_q(n))\,\bar {\otimes }\,\ell ^\infty (\mathbb {Z})$ (see (6-1)), we observe that

$$ \begin{align*} \Phi_n(\pi_{\vartheta_n}(x)) = x\otimes1, \quad \Phi_n(\lambda(q^{it})) = \rho_n^{it}\otimes q^{it}, \quad x \in W^*(\mathrm{U}_q(n)), \quad t\in\mathbb{R}. \end{align*} $$

Hence, via $\Phi _n$ , the Hopf $*$ -algebra structure $(\hat {\Delta }_{n,\mathbb {T}},\hat {R}_{n,\mathbb {T}},\vartheta _{n,\mathbb {T}}^t = \mathrm {Ad}(\rho _n^{it}\otimes 1),\varepsilon _{n,\mathbb {T}})$ on $W^*(\mathrm {U}_q(n)\times \mathbb {T})$ is transferred to that on $\widetilde {W^*(\mathrm {U}_q(n))}$ as follows. Write

$$ \begin{align*} \tilde {\Delta }_n := (\Phi _n^{\bar {\otimes }2})^{-1}\circ \hat {\Delta }_{n,\mathbb {T}}\circ \Phi _n, \tilde {R}_n := \Phi _n^{-1}\circ \hat {R}_{n,\mathbb {T}}\circ \Phi _n,\tilde {\vartheta }_n^t := \Phi _n^{-1}\circ \vartheta _{n,\mathbb {T}}^t\circ \Phi _n\end{align*} $$

(note, this does not correspond to $\widetilde {\alpha }_n^\gamma $ in Section 3) and $\tilde {\varepsilon }_n^t := \hat {\varepsilon }_{n,\mathbb {T}}\circ \Phi _n$ for simplicity. Then,

$$ \begin{align*} \tilde{\Delta}_n(\pi_{\vartheta_n}(x)\lambda(q^{it})) &= \pi_{\vartheta_n}^{\bar{\otimes}2}(\hat{\Delta}_n(x))\,(\lambda(q^{it})\otimes\lambda(q^{it})), \\ \tilde{R}_n(\pi_{\vartheta}(x)\lambda(q^{it})) &= \lambda(q^{-it})\,\pi_{\vartheta_n}(\hat{R}_n(x)), \\ \tilde{\vartheta}_n^t(\pi_{\vartheta_n}(x)\lambda(q^{it})) &= \pi_{\vartheta_n}(\vartheta_n^t(x))\lambda(q^{it})), \\ \tilde{\varepsilon}_n(\pi_{\vartheta_n}(x)\lambda(q^{it})) &= \hat{\varepsilon}_n(x) \end{align*} $$

for any $x \in W^*(\mathrm {U}_q(n))$ and $t \in \mathbb {R}$ . Thus, $\widetilde {W^*(\mathrm {U}_q(n))}$ is equipped with the natural structure of the group $W^*$ -algebra of the compact quantum group $\mathrm {U}_q(n)\times \mathbb {T}$ .

It is easy to see that the dual action of $q^k \in q^{\mathbb {Z}}$ acts on a generator $x\otimes \delta _m \in W^*(\mathrm {U}_q(n))\,\bar {\otimes }\,\ell ^\infty (\mathbb {Z}) = W^*(\mathrm {U}_q(n)\times \mathbb {T})$ as $x\otimes \delta _m \mapsto x\otimes \delta _{m+k}$ .

So far, we have seen that each $\widetilde {W^*(\mathrm {U}_q(n))}$ becomes a ‘compact quantum group’. Moreover, the above computations show that the resulting quantum group structure is compatible with the embedding $\widetilde {W^*(\mathrm {U}_q(n))} \hookrightarrow \widetilde {W^*(\mathrm {U}_q(n+1))}$ , $n\geq 0$ . The embedding is interpreted, on the $W^*(\mathrm {U}_q(n)\times \mathbb {T})$ , $n=0,1,\ldots ,$ as

$$ \begin{align*} x\otimes1 = \Phi_n(\pi_{\vartheta_n}(x)) &\mapsto \Phi_{n+1}(\pi_{\vartheta_{n+1}}(x)) = x\otimes1 \quad (x \in W^*(\mathrm{U}_q(n))), \\ \rho_n^{it}\otimes q^{it} = \Phi_n(\lambda(q^{it})) &\mapsto \Phi_{n+1}(\lambda(q^{it})) = \rho_{n+1}^{it}\otimes q^{it} \quad (t \in \mathbb{R}), \end{align*} $$

or other words,

$$ \begin{align*} x\otimes q^{it} \mapsto (x(\rho_n^{-1}\rho_{n+1})^{it})\otimes q^{it} \quad (x \in W^*(\mathrm{U}_q(n)),\ t \in \mathbb{R}). \end{align*} $$

Here, we remark (see [18, Section 4.2.1]) that

$$ \begin{align*} (\rho_n^{-1}\rho_{n+1})^{it} = (\rho_{n+1}\rho_n^{-1})^{it} = \rho_n^{-it}\rho_{n+1}^{it} = \rho_{n+1}^{it}\rho_n^{-it} \in W^*(\mathrm{U}_q(n))' \cap W^*(\mathrm{U}_q(n+1)) \end{align*} $$

for every $t \in \mathbb {R}$ . Namely, the choice of embedding of $\mathrm {U}_q(n)\times \mathbb {T} \hookrightarrow \mathrm {U}_q(n+1)\times \mathbb {T}$ is not standard. Thus, although the $\rho _n$ , $n=0,1,\ldots ,$ do not form an inductive sequence in any sense, the $\rho _n^{it}\otimes q^{it}$ , $n=0,1,\ldots ,$ do, thanks to the weight-extension of $\mathcal {B}(\mathrm {U}_q(\infty )) = \varinjlim W^*(\mathrm {U}_q(n))$ . This became possible by the famous Fell absorption principle!

Finally, the projection $e_{q^k}(n)$ in $L(\mathbb {T}) := \lambda (\mathbb {T})" \subset \widetilde {W^*(\mathrm {U}_q(n))}$ becomes

$$ \begin{align*} e_{q^k}(n) := \sum_{\ell \in \mathbb{Z}} \sum_{\lambda \in \mathbb{S}_n} p_\lambda(q^{k-\ell})\otimes \delta_\ell \end{align*} $$

in $W^*(\mathrm {U}_q(n)\times \mathbb {T})$ , where the double sums can be interchanged and $\rho _\lambda = \sum _{k \in \mathbb {Z}} q^k\,p_\lambda (q^k)$ (a finite sum; note, all but finitely many $p_\lambda (q^k)=0$ ) is the spectral decomposition as in Section 4. In fact, for any $x \in z_\lambda W^*(\mathrm {U}_q(n))$ ,

$$ \begin{align*} e_1(n)(x\otimes 1)e_1(n) = \sum_{\ell \in \mathbb{Z}} (p_\lambda(q^{-\ell}) x p_\lambda(q^{-\ell}))\otimes\delta_\ell, \end{align*} $$

and

$$ \begin{align*} \mathrm{ctr}_n(e_1(n)(x\otimes 1)e_1(n)) = \sum_{\ell\in\mathbb{Z}} \frac{\mathrm{Tr}(p_\lambda(q^{-\ell})\,x)}{\dim(\lambda)}(1\otimes\delta_\ell). \end{align*} $$

Hence, if we assign $q^{-\ell }$ at $1\otimes \delta _\ell $ , then the above element becomes $\mathrm {Tr}(\rho _\lambda x)/\dim (\lambda )$ . This is a closer look at the trick behind Theorem 3.7 in the quantum group setting.

Remark 6.2. The discussion in this subsection is completely general. Actually, the same interpretation in terms of quantum groups is applicable to any inductive sequence of compact quantum groups, where the $1$ -dimensional torus $\mathbb {T}$ and its dual $\mathbb {Z} = \widehat {\mathbb {T}}$ in the above should be replaced with the dual G of the weight group $\Gamma $ and $\Gamma $ itself, respectively.