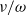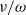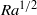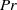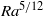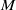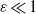Papers
High frequency oscillatory flows in a slightly rarefied gas according to the Boltzmann–BGK equation
-
- Published online by Cambridge University Press:
- 19 July 2013, pp. 1-46
-
- Article
- Export citation
Turbulence during the reflection of internal gravity waves at critical and near-critical slopes
-
- Published online by Cambridge University Press:
- 19 July 2013, pp. 47-68
-
- Article
- Export citation
The Eliassen–Palm flux tensor
-
- Published online by Cambridge University Press:
- 16 July 2013, pp. 69-102
-
- Article
- Export citation
A bound on the vertical transport of heat in the ‘ultimate’ state of slippery convection at large Prandtl numbers
-
- Published online by Cambridge University Press:
- 18 July 2013, pp. 103-122
-
- Article
- Export citation
The primary instability of falling films in the presence of soluble surfactants
-
- Published online by Cambridge University Press:
- 16 July 2013, pp. 123-150
-
- Article
- Export citation
Large eddy simulation of flow around a reverse rotating propeller
-
- Published online by Cambridge University Press:
- 18 July 2013, pp. 151-179
-
- Article
- Export citation
Spin-up of a two-component superfluid: analytic theory in arbitrary geometry
-
- Published online by Cambridge University Press:
- 18 July 2013, pp. 180-213
-
- Article
- Export citation
Modelling spreading dynamics of nematic liquid crystals in three spatial dimensions
-
- Published online by Cambridge University Press:
- 16 July 2013, pp. 214-230
-
- Article
- Export citation
Flow physics and RANS modelling of oblique shock/turbulent boundary layer interaction
-
- Published online by Cambridge University Press:
- 19 July 2013, pp. 231-284
-
- Article
- Export citation
Low-dimensional modelling of high-Reynolds-number shear flows incorporating constraints from the Navier–Stokes equation
-
- Published online by Cambridge University Press:
- 18 July 2013, pp. 285-308
-
- Article
- Export citation
Coherent structures and the saturation of a nonlinear dynamo
-
- Published online by Cambridge University Press:
- 19 July 2013, pp. 309-329
-
- Article
- Export citation
Range of validity of an extended WKB theory for atmospheric gravity waves: one-dimensional and two-dimensional case
-
- Published online by Cambridge University Press:
- 19 July 2013, pp. 330-363
-
- Article
- Export citation
Casimir cascades in two-dimensional turbulence
-
- Published online by Cambridge University Press:
- 19 July 2013, pp. 364-376
-
- Article
- Export citation
Topology-induced effect in biomimetic propulsive wakes
-
- Published online by Cambridge University Press:
- 24 July 2013, pp. 377-387
-
- Article
- Export citation
Measurements of the budgets of the subgrid-scale stress and temperature flux in a convective atmospheric surface layer
-
- Published online by Cambridge University Press:
- 24 July 2013, pp. 388-422
-
- Article
- Export citation
Induced diffusion of tracers in a bacterial suspension: theory and experiments
-
- Published online by Cambridge University Press:
- 24 July 2013, pp. 423-444
-
- Article
- Export citation
Meridional trapping and zonal propagation of inertial waves in a rotating fluid shell
-
- Published online by Cambridge University Press:
- 24 July 2013, pp. 445-470
-
- Article
- Export citation
On the thinnest steady threads obtained by gravitational stretching of capillary jets
-
- Published online by Cambridge University Press:
- 24 July 2013, pp. 471-483
-
- Article
- Export citation
Dual role of friction in granular flows: attenuation versus enhancement of instabilities
-
- Published online by Cambridge University Press:
- 24 July 2013, pp. 484-495
-
- Article
- Export citation
The Faraday threshold in small cylinders and the sidewall non-ideality
-
- Published online by Cambridge University Press:
- 24 July 2013, pp. 496-523
-
- Article
- Export citation