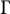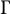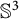Discrete group actions on 3-manifolds and embeddable Cayley complexes

Abstract

We prove that a group $\Gamma $ admits a discrete, topological (equivalently, smooth) action on some simply connected 3-manifold if and only if $\Gamma $ has a Cayley complex embeddable—with certain natural restrictions—in one of the following four 3-manifolds: (i) $\mathbb {S}^3$, (ii) $\mathbb {R}^3$, (iii) $\mathbb {S}^2 \times \mathbb R$, and (iv) the complement of a tame Cantor set in $\mathbb {S}^3$. The fact that these are the only simply connected 3-manifolds that allow such actions is a consequence of the Thurston–Perelman geometrization theorem.

1 Introduction

It is a classical fact that a finite group admits a faithful action on $\mathbb S^2$ if and only if it has a planar Cayley graph [6]. This paper proves an analogous statement for actions on 3-manifolds, by finite or infinite groups. We prove (Theorem 1.5 below) that a group $\Gamma $ admits a discrete topological action on some simply connected 3-manifold if and only if $\Gamma $ has a Cayley complex embeddable —with certain natural restrictions—in one of the following four 3-manifolds: (i) $\mathbb {S}^3$ , (ii) $\mathbb {R}^3$ , (iii) $\mathbb {S}^2 \times \mathbb R$ , and (iv) the complement of a tame Cantor set in $\mathbb {S}^3$ . Which of these four cases occurs is determined by the number of ends of $\Gamma $ [28], and the fact that these are the only simply connected 3-manifolds admitting such actions (Theorem 1.1) is interesting per se. By a discrete action, here we mean a faithful, properly discontinuous, cocompact action. All our manifolds and actions are topological, but they can be smoothed by a classical result of Bing and Moise [7, 37] and a recent result of Pardon [39, 40] (see Theorem A.1). The 1-ended case of our result is related to Cannon’s conjecture (Section 1.3).

A homeomorphic image C of the Cantor set in $\mathbb S^3$ is called tame, if it is contained in a piecewise linear arc. It is known that if $C'$ is another tame Cantor set in $\mathbb S^3$ , then $\mathbb S^3 - C$ is homeomorphic to $\mathbb S^3 - C'$ ; see [44] and references therein. A topological space homeomorphic to $\mathbb S^3 - C$ will be called a Cantor 3-sphere. Its importance is established by the following result:

Theorem 1.1 Let M be a connected, simply connected, topological 3-manifold. Suppose M admits a properly discontinuous, cocompact action by homeomorphisms. Then M is homeomorphic to one of the following four spaces:

(i) $\mathbb S^3$ , (ii) $\mathbb R^3$ , (iii) $\mathbb S^2 \times \mathbb R$ , or (iv) the Cantor 3-sphere.

The special case of Theorem 1.1 when the action is smooth and free became well known to experts in the aftermath of the Thurston–Perelman geometrization theorem [41, 42, 45]. A proof for the general case, assembled from ingredients provided by others, can be found in the Appendix.

Theorem 1.1 can be thought of as a generalization of the Poincaré conjecture to open 3-manifolds, since the case where M is acted upon by the trivial group implies it.

Like our other results below, it adds to the many purely topological statements that have been obtained via geometrization in the aftermath of Perelman’s work.

One could be tempted to try to avoid using the geometrization theorem by dropping the simple-connectedness condition and instead assuming that M is a subspace of $\mathbb S^3$ . However, Freedman & Skora [19] constructed a properly discontinuous, cocompact action of the free group of rank 2 by homeomorphisms on $\mathbb S^3 -W$ where W is homeomorphic to a Cantor set. They remark that $\mathbb S^3 -W$ is not simply connected, and in particular W is not tame. This shows that the simple connectedness assumption in Theorem 1.1 cannot be relaxed.

1.1 Finite group actions on $\mathbb S^2$ and $\mathbb S^3$

The following is a classical theorem, essentially going back to a 1896 paper of Maschke [33]; for modern references, see, e.g., [6, Theorem 1.16.] and [23].

Theorem 1.2 (Folklore)

A finite group admits a faithful action (by homeomorphisms or isometries) on $\mathbb S^2$ if and only if it has a planar Cayley graph.

The finite case of our result is a 3-dimensional version of Theorem 1.2, replacing $\mathbb S^2$ by $\mathbb S^3$ . We will prove that a finite group $\Gamma $ admits a faithful—topological, smooth, or isometric—action on $\mathbb S^3$ , if and only if it has a Cayley complex X that embeds topologically in $\mathbb S^3$ so that the canonical action $\Gamma \curvearrowright X$ maps each chamber boundary to a chamber boundary. Before clarifying the details, we recall that this class of groups is now well-understood:

Theorem 1.3 A finite group admits a faithful action by homeomorphisms/smooth maps/isometries on $\mathbb S^3$ if and only if it is isomorphic to a subgroup of the orthogonal group $O(4)$ .

Indeed, using the geometrization theorem, Dinkelbach and Leeb [17] showed that every finite smooth action on $\mathbb S^3$ is conjugate to an isometric action. Pardon [40] complemented this by proving that every topological action on $\mathbb {S}^3$ is the uniform limit of smooth actions. Since any isometry of $\mathbb S^3$ extends to an element of $O(4)$ , these two facts combined establish that the finite groups admitting faithful, topological actions on $\mathbb S^3$ coincide, up to isomorphism, with the finite subgroups of $O(4)$ , as anticipated by Zimmermann [48]. This forms a quite rich family of groups, described explicitly in [15]. Theorem 1.3 is the culmination of a long effort, the history of which is surveyed, e.g., in [16, 18, 27, 47]. In contrast, the groups of Theorem 1.2 were described by Maschke in 1986: they are just the finite cyclic and dihedral groups, and 8 sporadic ones [33, Figures 1–10], [25].

For an analogue of Theorem 1.2 for actions on $\mathbb S^3$ , Cayley graphs are unlikely to suffice: every finite graph embeds in $\mathbb S^3$ . As we will see, the key is to consider Cayley complexes instead. Define a generalized Cayley complex of a group $\Gamma $ to be a simply connected 2-dimensional cell-complex X, such that there is an action of $\Gamma $ on X that is regular on the 0-skeleton $X^0$ . This generalizes the standard notion of Cayley complex, in that we allow the action to fix 1-cells and 2-cells.

Any embedding $\phi $ of a 2-dimensional cell-complex X into $\mathbb S^3$ —more generally, into an orientable 3-manifold—induces a cyclic ordering $\sigma _e$ of the 2-cells containing a given 1-cell e of X, e.g., by considering the clockwise cyclic order in which these 2-cells intersect a disc locally perpendicular to e. This family of cyclic orderings $\sigma (\phi ):= \{\sigma _e\}_{e\in X^1}$ will be called a planar rotation system, defined more carefully in Section 2.6. Importantly, $\sigma (\phi )$ contains all the information needed to determine which sets of 2-cells of X bound a chamber of $\phi (X)$ ; these sets will be called prechambers. Given a cellular group action $\Gamma \curvearrowright X$ , e.g., when X is a Cayley complex of $\Gamma $ , we say that $\sigma (\phi )$ is $\Gamma $ -invariant if $\Gamma \curvearrowright X$ preserves $\sigma (\phi )$ (see Section 2.7 for details).

Our 3-dimensional analogue of Theorem 1.2 is the equivalence of items (i) and (iii) of

Theorem 1.4 For a finite group $\Gamma $ , the following are equivalent:

1. (i) $\Gamma $ is one of the groups of Theorem 1.3;

2. (ii) $\Gamma $ admits a generalized Cayley complex X with a $\Gamma $ -invariant planar rotation system;

3. (iii) $\Gamma $ admits a generalized Cayley complex X with an embedding $\phi : X \to \mathbb S^3$ with $\Gamma $ -invariant planar rotation system.

As an example, let $\Gamma $ be the cartesian product of two finite cyclic groups $C_k, C_\ell $ , and consider its generalized Cayley complex X with respect to the standard presentation $\left < a,b \mid a^k, b^\ell , [ab] \right>$ . Thus, X is a quadrangulated torus T, united with 2-cells bounding its essential cycles spanned by each one of the generators $a,g$ . It is easy to see a topological embedding of X in $\mathbb S^3$ , with all a-colored 2-cells inside T and all b-colored 2-cells outside it. Notice that the planar rotation system induced by this embedding is $\Gamma $ -invariant, as required by item (iii). The reader will be able to see a topological action of $\Gamma $ that preserves this embedding as postulated by (i). While the implication (iii) $\to $ (ii) is trivial, its converse (ii) $\to $ (iii) says that we could have specified the planar rotation system abstractly, as a combinatorial set of cyclic orderings, without mention to a particular embedding. This implication makes use of the validity of the Poincaré conjecture via a result of Carmesin [13] (Theorem 3.1 below). In Section 3, we observe that Carmesin’s result fails in general for infinite 2-complexes but remains true for Cayley complexes, a fact that relies on the geometrization theorem via Theorem 1.1.

1.2 Infinite discrete actions on open 3-manifolds

Our main theorem extends Theorem 1.4 to infinite groups and adds detailed information on the interplay between the action of (i) and the embedding of (iii). We call the four 3-manifolds featuring in Theorem 1.1 the special 3-manifolds. They also feature in our main theorem:

Theorem 1.5 For a finitely generated group $\Gamma ,$ the following are equivalent:

1. (i) $\Gamma $ admits a faithful, properly discontinuous, cocompact, topological action on a simply connected 3-manifold;

2. (ii) $\Gamma $ admits a generalized Cayley complex X with a $\Gamma $ -invariant planar rotation system with finite prechambers;

3. (iii) $\Gamma $ admits a generalized Cayley complex X with an embedding $\phi : X \to \mathbb S^3$ such that $\sigma (\phi )$ is $\Gamma $ -invariant and has finite prechambers;

4. (iv) $\Gamma $ admits a generalized Cayley complex X with an embedding $\phi $ into a special 3-manifold M such that $\phi (X)$ is invariant under some faithful, properly discontinuous, cocompact, topological action of $\Gamma $ on M, which acts regularly on the vertices of X. Moreover, $\phi (X)$ has finite prechambers.

A 2-dimensional statement analogous to Theorem 1.5, generalizing Theorem 1.2, can be found in [23, Theorem 1.1]. It says that the infinite groups acting discretely on a planar surface are exactly the Kleinian function groups. They also coincide with those groups admitting a Cayley graph with invariant planar rotation system. Details can be found in [10, 23, 30].

We saw examples of discrete actions on $\mathbb S^3$ above. Groups acting discretely on $\mathbb R^3$ include lattices in the Thurston geometries homeomorphic to $\mathbb R^3$ , such as euclidean and hyperbolic crystalographic groups, and the discrete Heisenberg group. On the contrary, $\mathbb Z^4$ cannot act discretely on $\mathbb R^3$ , by a theorem of Stallings saying that it is not isomorphic to any subgroup of a 3-manifold group [8]. Groups acting discretely on $\mathbb {S}^2 \times \mathbb R$ include $\mathbb Z$ , and its cartesian product with any of the groups of Theorem 1.2. An example of a group acting discretely on the Cantor 3-sphere is the free group $F_r$ of rank $r \geq 2$ . The universal cover of any closed 3-manifold with fundamental group $F_r$ provides an example, and such manifolds can be easily obtained using connect sums of copies of $\mathbb S^2 \times \mathbb S^1$ .

Actions like those of Theorems 1.1 and 1.5 but with the manifold M being a—not necessarily simply connected—subspace of $\mathbb S^3$ are a classical topic in the context of convergence group actions on $\mathbb S^3$ , where we can let M be the domain of discontinuity; see [29, 31] and the references therein. Some of our results, e.g., Theorem 5.2, apply to the nonsimply connected case and therefore to such actions.

1.3 Relationship to Cannon’s conjecture

A famous conjecture of Cannon [12, Conjecture 5.1] postulates that if $\Gamma $ is a Gromov-hyperbolic group with hyperbolic boundary $\partial \Gamma $ homeomorphic to $\mathbb S^2$ , then $\Gamma $ admits a properly discontinuous, cocompact action by isometries on $\mathbb {H}^3$ . A similar conjecture of Martin & Skora [32] postulates that every action of a discrete convergence group on $\mathbb S^2$ extends to a convergence group action on the 3-dimensional ball. The lower-dimensional version of this conjecture, i.e., with $\partial \Gamma $ homeomorphic to $\mathbb S^1$ , is an important theorem of Gabai [21, 22] and Casson & Jungreis [14]. The implication (iii) $\to $ (i) of Theorem 1.5, restricted to 1-ended groups, provides the 3-dimensional analogue of a fact that Gabai uses in his aforementioned proof. Specifically, Gabai uses the action of $\Gamma $ on its boundary $\mathbb S^1$ to obtain an 1-complex G embedded in the interior $\mathbb {D}$ of $\mathbb S^1$ to which the action extends [21, Figure 1]. He then notices that if each face of this embedding of G is compact—equivalently, if it is bounded by finitely many edges of G—then the induced action of $\Gamma $ on G extends to a discrete action of $\Gamma $ on $\mathbb {D}$ [21, p. 4]. This is the lower-dimensional analogue of the implication (iii) $\to $ (i) of Theorem 1.5. It should be noted, however, that the difficult part of Gabai’s proof was to ensure that G has compact faces, and so the progress toward Cannon’s conjecture that this remark makes is modest. Nevertheless, we have had to use the geometrization theorem to make this step.

In the converse direction, Theorem 1.5 establishes that a suspected counterexample $\Gamma $ to Cannon’s conjecture can be proved to be one by checking that no Cayley complex of $\Gamma $ admits an invariant planar rotation system, or an embedding as in (iii).

1.4 Tightness of the conditions

We now discuss the tightness of the various conditions of Theorem 1.5. Item (iv) provides the most detailed information about these groups, and it trivially implies the other three (Section 6). The conditions in the other three items are necessary in the sense that dropping any one of them would violate at least one of the equivalences. To see that the condition of finite prechambers is necessary for the implications (ii), (iii) $\to $ (iv), (i), consider the group $\mathbb Z^2$ . Its standard Cayley complex embeds in $\mathbb R^3$ with invariant planar rotation system, but with two infinite prechambers, and it is well-known that $\mathbb Z^2$ is not one of the groups of Theorem 1.5 [2, 20]. We do not have an explicit example of a group with a Cayley complex that embeds in $\mathbb S^3$ with finite prechambers but only with noninvariant planar rotation system but expect that such a group can be found using ideas of [23, Section 10].

Dropping some of our conditions in pairs can lead to interesting statements, some of which are implicit in our proofs. A notable example is that the implication (i) $\to $ (iii) generalizes to group actions on nonsimply connected 3-manifolds, resulting to embedded 2-complexes with an appropriate action by the same group; see Theorem 5.2. Dropping the condition of finiteness of prechambers leads to an interesting class of groups; see Section 6 for related open problems.

In items (i) and (iv) of Theorem 1.5, we can assume that the action is in addition smooth.

This paper is structured as follows. Section 2 provides all the necessary definitions. The implication (ii) $\to $ (iv) of Theorem 1.5 is proved in Section 3. Since the implication (iii) $\to $ (ii) is trivial, this also establishes the implication (iii) $\to $ (iv). The implication (i) $\to $ (iv) is proved in Section 5, while (iv) trivially implies the other three statements. Section 6 puts the pieces together to conclude the proof of Theorem 1.5.

In Section 4, we provide a separate proof of the implication (iii) $\to $ (i) of Theorem 1.4 avoiding the Poincaré conjecture. This allows us to prove the equivalence of items (i) and (iii) of Theorem 1.4 without relying on Perelman’s work. This is not the case for Theorem 1.5, where we do not see a way to avoid using the geometrization theorem.

2 Definitions and preliminary results

2.1 Group actions

A 3-manifold is a topological space each point of which has a neighborhood homeomorphic to an open subset of $\mathbb R^3$ .

A (topological) action $\Gamma \curvearrowright M$ of a group $\Gamma $ on a topological space M is a homomorphism from $\Gamma $ into the group of homeomorphisms of M. Given such an action, the images of a point $x\in M$ under $\Gamma \curvearrowright M$ form the orbit of x.

An action $\Gamma \curvearrowright M$ is faithful, if for every two distinct $g,h \in \Gamma $ there exists an $x \in M$ such that $gx \neq hx$ ; or equivalently, if for each $g \neq e \in \Gamma $ there exists an $x \in M$ such that $gx \neq x$ . It is free if $gx \neq hx$ for every $g,h\in \Gamma $ and $x\in M$ . It is transitive if for every $x,y\in M$ there is $g\in \Gamma $ with $gx =y$ (we will only encounter transitive actions on discrete spaces M). Finally, $\Gamma \curvearrowright M$ is regular if it is free and transitive.

An action $\Gamma \curvearrowright M$ is properly discontinuous, if for every compact subspace K of M, the set $\{g\in \Gamma \mid g K \cap K \neq \emptyset \}$ is finite. It is cocompact, if the quotient space $M/\Gamma $ is compact. If M is locally compact, then an equivalent condition is that there is a compact subset K of M such that $\bigcup \Gamma K =M$ .

2.2 Graphs

A (simple) graph G is a pair $(V,E)$ of sets, where V is called the set of vertices, and E is a set of two-element subsets of V, called the set of edges. We will write $uv$ instead of $\{u,v\}$ to denote an edge. A multigraph is defined similarly, except that E is a multiset, and it can have elements consisting of just one vertex.

We let $V(G)$ denote the set of vertices of a graph G, and $E(G)$ denote the set of edges of G.

Every (multi-)graph $G\ =(V,E)$ gives rise to a $1$ -complex, by letting V be the set of 0-cells, and for each $uv\in E$ introducing an arc with its endpoints identified with u and v. Thus, we will sometimes interpret the word graph as a 1-complex. In particular, when discussing embeddings of graphs we will mean topological embeddings of 1-complexes.

A generalized Cayley graph of a group $\Gamma $ is a graph G endowed with an action $\Gamma \curvearrowright G$ by isomorphisms which action is regular on $V(G)$ . This is analogous to our definition of a generalized Cayley complex in the introduction. Again the difference to the standard notion of a Cayley graph is that we allow the action to fix edges.

2.3 2-complexes

A $2$ -complex is a topological space X obtained as follows. We start with a $1$ -complex $X^1$ as defined above, called the 1-skeleton of X. We then introduce a set $X^2$ of copies of the closed unit disc $\mathbb {D} \subseteq \mathbb R^2$ , called the 2-cells or faces of X, and for each $f\in X^2$ we attach f to $X^1$ via a map $\phi _f: \mathbb S^1 \to X^1$ , called the attachment map, where we think of $\mathbb S^1$ as the boundary of $\mathbb {D}$ . Attaching here means that we consider the quotient space where each point x of $\mathbb S^1\subset f$ is identified with $\phi _f(x)$ . We let $X^0:= V(X^1)$ be the set of vertices, or 0-cells, of X.

We say that X is regular, if $\phi _f$ is a homeomorphism onto its image for every $f\in X^2$ . We say that X is edge-regular, if each $\phi _f$ is injective on 1-cells, that is, $x\in X^0$ holds for every point $x\in X$ with more than one preimage under $\phi _f$ .

For $f\in X^2$ , we write $f =[x_1,\dots , x_k]$ if $x_1,\dots , x_k$ is the cyclic sequence of vertices appearing in the image of $\phi _f$ .

To each 2-cell $f=[x_1,\dots , x_k] \in X^2$ , we associate two distinct directed 2-cells $f_1,f_2$ , also denoted by $\langle x_1,\dots , x_k\rangle $ and $\langle x_k,\dots , x_1\rangle ,$ respectively. Their reverses are defined as $f_1^{-1}:= f_2$ and $f_2^{-1}:= f_1$ .

If X is not regular, then it is always possible to produce a regular complex $X'$ homeomorphic to X using the barycentric subdivision defined as follows. For each edge $e=uv\in X^1$ , we subdivide e by adding a new vertex m at its midpoint. For each occurrence of e in a 2-cell f of X, we replace that occurrence by the pair $um, mv$ or $vm, mu$ as appropriate. We then triangulate each 2-cell $h=x_1,\ldots ,x_k$ of the resulting $2$ -complex by adding a new vertex c in its interior, adding the edges $c x_1,\ldots , cx_k$ to the 1-skeleton, and replacing h by the 2-cells $[c, x_1, x_2], [c, x_2, x_3], \ldots , [c,x_k, x_1]$ .

Note that the barycentric subdivision $X'$ of X is a simplicial complex, in particular a regular one, and its 1-skeleton is a simple graph. Here, a 2-complex X is simplicial, if its 1-skeleton is a simple graph and each $F\in X^2$ is of the form $f=[x_1, x_2, x_3]$ where $x_1,x_2,x_3$ are distinct vertices.

For each $v\in X^0$ , the link graph $L_X(v)$ is the graph on the neighborhood of v in $X^1$ with $uw \in E(L_X(v))$ if and only if $u,v,w$ are consecutive in a 2-cell of X. Alternatively, we can define $L_X(v)$ so that its vertices are the edges incident with v, and two edges $vu,vw$ are joined by an edge of $L_X(v)$ whenever $u,v,w$ are consecutive in a 2-cell of X. These two definitions yield isomorphic graphs when $X^1$ is a simple graph, and it is a matter of convenience to use the one or the other. In general, link graphs are more naturally defined as multigraphs, as $u,v,w$ may be consecutive in more than one 2-cells of X.

2.4 Embeddings and Chambers

An embedding of a space X in a space Y is homeomorphism between X and a subspace of Y.

For an embedding $\phi :X\rightarrow M$ of a $2$ -complex X into a 3-manifold M, we call each connected component of $M \setminus \phi (X)$ a chamber. The boundary $\partial C$ of a chamber C is the set of points $x \in \phi (X)$ in the closure of C that are not in the interior of C. Indeed, as C is an open set, $\partial C$ is disjoint from C. The following basic fact helps to further explain the notion.

Proposition 2.1 ([24, Proposition 2.1])

Let $\phi :X\rightarrow \mathbb S^3$ be an embedding of a finite, $2$ -complex X, such that every 0-cell and 1-cell of X is contained in a 2-cell. Then $\partial C$ is a union of 2-cells of X for every $\phi $ -chamber C.

2.5 Local flatness

We recall the standard notion of local flatness. An embedding $\phi : \mathbb S^2 \to M$ , where M is a 3-manifold, is locally flat, if for each $x\in \phi (\mathbb S^2)$ there exists a neighborhood $U_x$ of x such that the topological pair $(U_x,U_x\cap \phi (X))$ is homeomorphic to $(\mathbb {R}^3, \mathbb {R}^2)$ , by which we mean that there is a homeomorphism from $U_x$ to $\mathbb {R}^3$ mapping $U_x\cap \phi (X)$ to $\mathbb {R}^2 \subset \mathbb {R}^3$ . (A topological pair $(X,A)$ consists of a topological space X and a subspace $A\subseteq X$ .)

We can extend the notion of local flatness to an embedding $\phi : X \to M$ of a $2$ -complex X instead of $\mathbb S^2$ : we say that $\phi $ is locally flat, if the restriction of $\phi $ to each homeomorphic image of $\mathbb S^2$ in X is locally flat, as defined above.

2.6 Rotation systems

A rotation system of a graph G is a family $(\sigma _v)_{v\in V(G)}$ of cyclic orderings of the edges incident with each vertex $v\in V(G)$ . Every embedding of G on an orientable surface defines a rotation system, by taking $\sigma _v$ to be the clockwise cyclic ordering in which the edges incident to v appear in the embedding. The rotation system $(\sigma _v)_{v\in V(G)}$ is said to be planar, if it can be defined by an embedding of G in the sphere $\mathbb S^2$ .

Let X be an edge-regular $2$ -complex, and let $\overleftrightarrow {E}(X)$ denote the set of directions of its 1-cells, that is, the set of directed pairs $\overrightarrow {xy}:= \left <x,y \right>$ such that $xy\in X^1$ . Thus, every 1-cell gives rise to two elements of $\overleftrightarrow {E}(X)$ . A rotation system of X is a family $(\sigma _e)_{e \in \overleftrightarrow {E}(X)}$ of cyclic orderings $\sigma _e$ of the 2-cells incident with each $e = \overrightarrow {xy} \in \overleftrightarrow {E}(X)$ , such that if $e'=\overrightarrow {yx}$ , then $\sigma _{e'}$ is the reverse of $\sigma _e$ . A rotation system $(\sigma _e)_{e \in \overleftrightarrow {E}(X)}$ of X induces a rotation system $\sigma ^v$ at each of its link graphs $L_X(v)$ by restricting to the directions of 1-cells emanating from v: for every $u\in V(L_X(v))$ we let $\sigma ^v_{u}$ be the cyclic order obtained from $\sigma _{\overrightarrow {vu}}$ by replacing each 2-cell f appearing in the latter by the edge $uw$ where w is the unique neighbor u in $V(L_X(v))$ such that $w,v,u$ appear consecutively in f.

A rotation system of a regular $2$ -complex X is planar, if it induces a planar rotation system on each of its link graphs. Note that once, we fix an orientation, every locally flat embedding $\phi $ of X into $\mathbb S^3$ or $\mathbb R^3$ defines a planar rotation system, by letting $\sigma _e$ be the cyclic order in which the images of the 2-cells incident with e appear in $U_x$ , where x is any interior point of $\phi (e)$ , and $U_x$ is as in the definition of local flatness (Section 2.5).

2.7 Invariant rotation systems

Suppose that a group $\Gamma $ acts on a $2$ -complex X by a faithful action $\Gamma \curvearrowright X$ . Let $\Sigma $ be the set of all rotation systems $\boldsymbol {\sigma }= (\sigma _e)_{e \in \overleftrightarrow {E}(X)}$ on X as defined in the previous subsection. Then we can let $\Gamma $ act on $\Sigma $ by elementwise multiplication as follows. Recall that $\sigma _e$ is formally a ternary “betweenness” relation on the set $F(e)$ of 2-cells containing e for every 1-cell e. For $g\in \Gamma $ , we define the product $g \cdot \sigma _e:= \{ [ga,gb,gc]\mid [a,b,c]\in \sigma _e\}$ , which is a cyclic ordering on $F(ge)$ . This defines our action $g \cdot \boldsymbol {\sigma }:= (g \cdot \sigma _e)_{e \in E(X)}$ of $\Gamma $ on $\Sigma $ . We will say that $\boldsymbol {\sigma }$ is $\Gamma $ -invariant, if $g \cdot \boldsymbol {\sigma }$ coincides with $ \boldsymbol {\sigma }$ up to a global change of orientation. To make this more precise, let $\eta : \Gamma \to \mathbb Z_2$ be a homomorphism from $\Gamma $ to the group $\mathbb Z_2$ ; we will use $\eta $ to carry the information of which $g\in \Gamma $ preserve/reverse the orientation. We say that ${\boldsymbol {\sigma }}$ is invariant with respect to $\eta $ , if

(1) $$ \begin{align} g \cdot \sigma_e =(-1)^{\eta(g)} \sigma_{ge}, \end{align} $$

holds for every $e \in \overleftrightarrow {E}(X)$ and $g\in \Gamma $ . We say that $\boldsymbol {\sigma }$ is $\Gamma $ -invariant if it is invariant with respect to some homomorphism $\eta $ . Note that $\eta $ is uniquely determined by $\boldsymbol {\sigma }$ if it exists.

3 From invariant planar rotation systems to invariant Cayley complex embeddings

The implication (ii) $\to $ (iii) of Theorem 1.4 is an immediate consequence of the following result of Carmesin:

Theorem 3.1 ([13])

A finite, simply connected, simplicial 2-complex admits an embedding $\phi $ in $\mathbb S^3$ if and only if it admits a planar rotation system $\sigma $ . Moreover, $\phi $ can be chosen so that $\sigma (\phi )$ coincides with $\sigma $ . ¹

Indeed, if X is a generalized Cayley complex of $\Gamma $ , and $\sigma $ a $\Gamma $ -invariant planar rotation system on X, then we can apply the barycentric subdivision to turn X into a simplicial 2-complex $X'$ , extend $\sigma $ to $X'$ in the obvious way, and apply Theorem 3.1 to $X'$ to obtain an embedding of $X'$ , which induces an embedding $\phi : X \to \mathbb S^3$ with $\sigma (\phi )= \sigma $ .

Remark 1 If a locally finite 2-complex X admits an embedding $\phi $ in $\mathbb S^3$ (or any 3-dimensional submanifold of $\mathbb S^3$ ), then we may assume $\phi $ to be locally flat (as defined in Section 2.5). Indeed, we can modify $\phi $ to make it piecewise-linear (PL) [34, Appendix C], and it is easy to see that any PL embedding of X in $\mathbb S^3$ is locally flat.

The implication (ii) $\to $ (iii) of Theorem 1.5 is more difficult, because Theorem 3.1 does not extend to infinite 2-complexes:

Theorem 3.2 There is a locally finite, simply connected, simplicial 2-complex which admits a planar rotation system but does not admit an embedding in $\mathbb S^3$ .

Proof It is known that there is a contractible, hence simply connected, open 3-manifold W which does not embed in any compact 3-manifold, let alone in $\mathbb S^3$ ; see, e.g. [26] and references therein. Let T be a triangulation of such a manifold W. It is easy to see that if a simplicial complex X has a topological embedding into some oriented 3-dimensional manifold, then it has a planar rotation system [13]. Letting X be the 2-skeleton of T, we thus deduce that X has a planar rotation system, since it embeds in W.

We may assume without loss of generality that there is no 3-cell C of T the boundary $\partial C$ of which separates W, because even if T does not have this property its barycentric subdivision $T'$ will, and we could have chosen $T'$ instead of T. Thus, no $\partial C$ separates X.

Suppose now that X admits an embedding f in $\mathbb S^3$ . By Remark 1, we may assume that f is locally flat. Then we can extend f into an embedding of W in $\mathbb S^3$ as follows. For every 3-cell C of T, we observe that $\partial C \subset X$ is homeomorphic to $\mathbb S^2$ , hence it separates $\mathbb S^3$ into two components. One of these components A is disjoint from $f(X)$ , because $\partial C$ does not separate X as mentioned above. Since f is locally flat, A is homeomorphic to $\mathbb R^3$ by the generalized Schoenflies theorem [11, 35]. Thus, we can embed C onto A. Doing so for each 3-cell C of T, we obtain an embedding of W into $\mathbb S^3$ , contradicting the choice of W.

Despite the fact that Theorem 3.1 fails for infinite 2-complexes in general, it does hold for Cayley-complexes, and proving it requires the Thurston–Perelman geometrization theorem. This is the content of the following theorem.

Theorem 3.3 Let C be a finitely presented Cayley complex admitting an invariant planar rotation system $\sigma $ with finite prechambers. Then C admits an embedding $\phi $ into $\mathbb S^3$ such that $\sigma (\phi )$ coincides with $\sigma $ .

Proof We follow the lines of the proof of Theorem 3.1 in [13], the main difference being that we apply Theorem 1.1 instead of the Poincaré conjecture. This starts by defining a 3-manifold $M=T(C,\sigma )$ , with 2-skeleton C as follows. The planar rotation system $\sigma $ induces a relation on the directed 2-cells of C, where two directed 2-cells $f,f'$ are related via a directed 1-cell $\overrightarrow {uv}$ , if $f,f'$ appear consecutively is $\sigma _{\overrightarrow {uv}}$ , and u appears right before v in f and v appears right before u in $f'$ . The equivalence classes induced by this relation are called pre-chambers. The intuition is that prechambers will coincide with the boundaries of chambers of the embedding of C that we are constructing. It is a good exercise to check that if T is a triangulation of $\mathbb S^3$ , and $T^2$ its 2-skeleton, then the prechambers of $T^2$ with respect to the rotation system that $T^2$ naturally inherits from its inclusion in $\mathbb S^3$ are exactly the boundaries of the 3-cells of T.

For each prechamber S of C as above, we attach a solid surface $\hat {S}$ to C, so that the attachment map—which is not always injective—maps the boundary of $\hat {S}$ onto S. This completes the definition of $M=T(C,\sigma )$ , which Carmesin proves to be an oriented topological 3-manifold [13, Lemma 4.5] (Carmesin works with finite C, but this proof extends verbatim to the infinite case). He then observes that M is simply connected if C is ([13, Lemma 4.6]); indeed, any loop in M can be homotoped to one in C by the construction of M. Finally, Carmesin observes that when C is finite then M is compact, hence homeomorphic to $\mathbb S^3$ by the Poincaré conjecture! By construction, C is embedded in $M\cong \mathbb S^3$ , and the rotation system of this embedding coincides with $\sigma $ .

We now handle the case where C is infinite. Let us first assume that every prechamber of C with respect to $\sigma $ is homeomorphic to a surface; we will consider the general case later. Under this assumption, we claim that

(2) $$ \begin{align} \text{the union of 2-cells in each pre-chamber }S\text{ of }C\text{ is homeomorphic to }\mathbb S^2. \end{align} $$

When C is finite then this is not hard and has been observed in [24, Lemma 5.1.]: it is proved there that if X is a finite, simply-connected, 2-complex, and $\phi : X \to \mathbb S^3$ an embedding, then for every chamber Y of $\phi $ such that $\partial Y$ is a surface, we have $\partial Y \cong \mathbb S^2$ . (To see this, think of Y as a solid surface in $\mathbb S^3$ .) We can reduce (2) to this finite setup as follows. Let $C'$ be a finite subcomplex of C containing S, and contract each component of $C - C'$ into a vertex, to obtain the (finite) 2-complex $C^*$ . Notice that $C^*$ is simply connected, because for every simply connected space X, and every path-connected subspace Y, the quotient $X/Y$ is simply connected. Moreover, $\sigma $ induces a planar rotation system $\sigma ^*$ on $C^*$ by restricting $\sigma $ to the 1-cells that have not been contracted. Clearly, S is a prechamber of $C^*$ . Repeat the above construction of $M^*=T(C^*,\sigma ^*)$ , and recall that $M^*\cong \mathbb S^3$ by the Poincaré conjecture. We can now apply the aforementioned result [24, Lemma 5.1.], using our assumption that S is a surface, to deduce that $S \cong \mathbb S^2$ .

Notice that the group $\Gamma $ of C acts properly discontinuous and cocompactly on C. We can use (2) to extend this action to M: since each prechamber S of C is a 2-sphere, each of the solid surfaces $\hat {S}$ that we attached to C to obtain M is a 3-ball. Therefore, using the fact that $\sigma $ is invariant, it is easy to extend $\Gamma \curvearrowright C$ to M as any automorphism of $\mathbb S^2 \subset \mathbb R^3$ extends to an automorphism of the 3-ball bounded by $\mathbb S^2$ .

Easily, the resulting action $\Gamma \curvearrowright C$ is still properly discontinuous and cocompact. As above, M is simply connected because C is. Thus, M is homeomorphic to one of the 3-manifolds of Theorem 1.1, each of which embeds in $\mathbb S^3$ . Again, since C embeds in M with rotation system $\sigma $ by construction, the statement follows.

It remains to consider the general case where some prechambers of C with respect to $\sigma $ may fail to be homeomorphic to a surface. In this case, we can still follow the lines of the proof of (2) to conclude that $\hat {S}$ is still homeomorphic to an open 3-ball, although its attachment map $\alpha _S: \partial \hat {S} \to S$ is noninjective. We then extend $\Gamma \curvearrowright C$ to $\Gamma \curvearrowright M$ as above, noting that whenever $\Gamma $ maps a prechamber S to a prechamber Q, this induces a homeomorphism from $\alpha _S^{-1}(S)$ to $\alpha _Q^{-1}(Q)$ , which can be extended to a homeomorphism from the 3-ball $\hat {S}$ to the 3-ball $\hat {Q}$ .

This establishes the implication (ii) $\to $ (iii) of Theorem 1.5. However, a closer inspection of the last proof reveals that we can obtain the stronger implication (ii) $\to $ (iv) (of both Theorem 1.5 and Theorem 1.4):

Corollary 3.4 Let C be a finitely presented Cayley complex of a group $\Gamma $ , admitting a $\Gamma $ -invariant planar rotation system $\sigma $ with finite prechambers. Then C admits an embedding $\phi : C \to M$ into a special 3-manifold M such that $\phi (C)$ is invariant under some properly discontinuous, cocompact action $\Gamma \curvearrowright M$ .

Proof Define $M=T(C,\sigma )$ as in the proof of Theorem 3.3. Notice that prechambers are defined using $\sigma $ , and so the action of $\Gamma $ on C preserves prechambers. Moreover, the action of $\Gamma $ on C was extended there to an action on M by homeomorphisms. As already observed, M is a special 3-manifold, and this action is properly discontinuous and cocompact.

4 From invariant Cayley complex embeddings to group actions

Since the implication (iii) $\to $ (ii) of Theorem 1.5 is trivial, the previous section also establishes the implication (iii) $\to $ (iv) and hence (iii) $\to $ (i). The aim of this section is to reprove the latter implication (iii) $\to $ (i) of Theorem 1.4 by a more elementary method that avoids the Poincaré conjecture. (We do not have a proof of the analogous implication of Theorem 1.5 avoiding the geometrization theorem.)

The purpose of this section is a proof of the following theorem without using the Poincaré conjecture.

Theorem 4.1 Let $\Gamma $ be a finite group, let X be a generalized Cayley complex of $\Gamma $ , and $\phi :X \to \mathbb S^3$ an embedding with $\Gamma $ -invariant rotation system $\sigma (\phi )$ . Then there is a faithful topological action $\Gamma \curvearrowright \mathbb S^3$ fixing $\phi (X)$ as a set, and acting regularly on its vertices.

The idea is to reduce this to the following result of [24]. We say that a 2-complex X is locally k-connected, if each of its link graphs is k-connected. Recall that a graph is k-connected, if it has more than k vertices and remains connected after removing any set of at most $k-1$ vertices.

Theorem 4.2 ([24, Theorem 1.3])

Let Y be a finite, simply connected, locally 3-connected $2$ -complex. Then, for every two locally flat embeddings $\chi ,\psi : Y \to \mathbb S^3$ , there exists a homeomorphism $\alpha : \mathbb S^3 \to \mathbb S^3$ such that $\psi = \alpha \circ \chi $ .

Moreover, we may assume that $\alpha $ is determined by its restriction to $\chi (Y)$ . ²

Every finite Cayley complex automatically satisfies the simple connectedness condition, and it is locally 1-connected (Lemma 4.3), but it is not necessarily locally $3$ -connected. With the lemmas that follow we will be able to increase the local connectedness of a complex X as in Theorem 4.1 by extending it to a supercomplex. This supercomplex $X'$ will inherit the canonical action of $\Gamma $ , and its rotation system will still be $\Gamma $ -invariant. This will allow us to apply Theorem 4.2 to $X'$ to prove Theorem 4.1.

We start with the following basic fact about finite Cayley complexes.

Lemma 4.3 Every finite generalized Cayley complex X is locally 1-connected, unless X has fewer than 3 vertices.

This is well known (see, e.g., [13, Lemma 5.1]), but we provide a proof for completeness:

Proof Recall that the 1-skeleton $X^1$ of X is a generalized Cayley graph, and so $X^1$ is 2-connected as it is finite. Thus, any two incident edges of $X^1$ are contained in a cycle.

To prove that the link graph $L=L(o)$ of the identity element o of X is connected, pick two edges $e,f$ of X incident with o. By the above remark, there is a cycle C in $X^1$ containing both $e,f$ . Consider a van Kampen diagram K proving that C is null homotopic in X using the 2-cells of X. Let $K_o$ denote the set of 2-cells appearing in K that contain o. These 2-cells yield an e–f path in L. Since $e,f$ where arbitrary edges of o, this proves that L, and hence every link graph of X, is connected.

Next, we show how to increase the local connectivity of an embedded 2-complex from 1 to 2 by passing to a supercomplex:

Lemma 4.4 Let X be a locally 1-connected $2$ -complex, and let $\phi : X \to \mathbb S^3$ be a locally flat embedding. Then there is a locally $2$ -connected $2$ -complex $X'$ containing X as a topological subspace, and a locally flat embedding $\phi ': X' \to \mathbb S^3$ , such that $\phi '(X)= \phi (X)$ .

Moreover, any action $\Gamma \curvearrowright X$ with respect to which $\sigma (\phi )$ is invariant extends to an action $\Gamma \curvearrowright X'$ with respect to which $\sigma (\phi ')$ is invariant.

Furthermore, $\pi _1(X')\cong \pi _1(X)$ .

Before giving the formal proof, let us explain the intuition by going one dimension down. Recall that a plane graph is a 1-complex embedded in $\mathbb S^2$ or $\mathbb R^2$ . Given a connected plane graph G that has some cut-vertices, it is easy to extend G into a plane supergraph $G^\otimes $ that is 2-connected by “fattening” it, i.e., adding new vertices and edges near each face boundary; see Figure 1 and Definition 4.5 for details. To prove Lemma 4.4, we will add new 2-cells to X to “fatten” it in such a way that the effect on each of its link graphs will be the same as the above modification of G into $G^\otimes $ :

Definition 4.5 Let G be a finite, connected, plane graph. Let $G"$ be a plane multigraph obtained from G by adding two parallel edges $e',e"$ to each edge $e\in E(G)$ , and embedding them so that the circle $e' \cup e"$ separates e from the rest of G. Then, for each e of $G"$ with end-vertices $u,v$ , subdivide e into a path of length 3 by placing two new vertices $e_u,e_v$ inside e. Finally, for each vertex v of $G"$ , and each two edges $e,f$ incident with v that appear consecutively in the plane, add an edge between $e_v$ and $f_v$ . We embed these edges in such a way that they form a circle separating v from any other vertex of G. Let $G^\otimes $ denote the resulting plane graph; see Figure 1.

Figure 1: A portion of a graph G (left half), and the corresponding part of $G^\otimes $ (right half).

We remark that G is a topological minor of $G^\otimes $ .

Lemma 4.6 Let G be a connected, plane graph. Then $G^\otimes $ is $2$ -connected.

Proof This is straightforward and boils down to checking that neither an original vertex of G nor one of the new vertices can be a cut vertex of $G^\otimes $ .

Using this we can now prove Lemma 4.4.

Proof of Lemma 4.4

We may assume that X is regular, for otherwise we can work with its barycentric subdivision, which preserves all assumptions we have made on X as well as $\pi _1(X)$ .

We begin the construction of $X'$ by “tripling” each 2-cell of X as follows. For every $f\in X^2$ , we introduce two new 2-cells $f^-,f^+$ with the same boundary and attaching map as f, and embed $f^-,f^+$ in $\mathbb S^3$ locally flat and in such a way that their images bound a 3-ball that contains f and is otherwise disjoint from X. Let $X^\pm $ be the resulting $2$ -complex, and $\phi ^\pm : X^\pm \to \mathbb S^3$ the resulting locally flat embedding.

Next, we modify $X^\pm $ into $X'$ by engulfing each 1-cell $e\in X^1$ inside a copy of $\mathbb S^2$ . To make this more precise, we pick a locally flat homeomorph $S_e$ of $\mathbb S^2$ in $\mathbb S^3$ , such that $S_e$ intersects $X^0$ at the endpoints of e, it intersects each 2-cell f incident with e along an arc, which we denote by $f_e$ , and $S_e$ is otherwise disjoint from $X^\pm $ and all other $S_{e'}, e'\neq e$ . It is easy to find such an $S_e$ inside a small neighborhood of e.

To turn the resulting subspace of $\mathbb S^3$ into a 2-complex, we declare $f_e$ to be an 1-cell for every pair $e,f$ as above, and we replace f by the two 2-cells into which $f_e$ dissects it (one of which 2-cells will be further dissected by the other edges incident with f). Moreover, for every two 2-cells $f,g$ that are consecutive in the rotation system of e, the 1-cells $f_e, g_e$ cut a “slice” of $S_e$ , which we also declare to be a 2-cell of $X'$ , and denote it by $s_{feg}$ . This completes the construction of $X'$ , and the PL embedding $\phi '$ . As X is a subspace of $X'$ , we have $\phi '(X)= \phi (X)$ . Notice that $X'$ has the same vertex set as X, and so to check that $X'$ is locally $2$ -connected we just need to consider the effect of the newly added cells to each link graph $L_X(v), v \in X^0$ . It is straightforward to check that the new link graph $L_{X'}(v)$ coincides with $L_X(v)^\otimes $ as in Definition 4.5 below. Thus, $X'$ is locally $2$ -connected by Lemma 4.6 below.

For the second statement, we first extend the action $\Gamma \curvearrowright X$ to $X^\pm $ as follows. For every $\gamma \in \Gamma $ and $f\in X^2$ , we let $\gamma $ map the new 2-cells $f^-,f^+$ bijectively to $(\gamma f)^-,(\gamma f)^+$ . There are two ways to do so, and we choose the unique option that retains the invariance of the rotation system $\sigma :=\sigma (\phi )$ , i.e. the choice that ensures that $\gamma \sigma _d = (-1)^{\eta (\gamma )} \sigma _{\gamma d}$ for some, hence every, directed edge d incident with f, where $\eta : \Gamma \to \mathbb Z_2$ is a homomorphism as in (1), witnessing the fact that $\sigma $ is invariant. This ensures that the rotation system of $\phi ^\pm $ is invariant with respect to the resulting action $\Gamma \curvearrowright X^\pm $ . Extending further to $\Gamma \curvearrowright X'$ is straightforward: we just let $\gamma \in \Gamma $ map each $s_{feg}$ to $s_{(\gamma f)(\gamma e)(\gamma g)}$ .

Finally, it is easy to prove $\pi _1(X')\cong \pi _1(X^\pm )\cong \pi _1(X)$ by applying van Kampen’s theorem whenever a new 2-cell is introduced, using the fact that every new 2-cell forms a copy of $\mathbb S^2$ with existing 2-cells.

Remark Lemma 4.6 would remain true if instead of tripling each edge we just doubled it. The reason we triple is that in Lemma 4.4 we have to triple each 2-cell in order to maintain the invariance of the action.

Next, we observe that we can increase the local connectivity further from 2 to 3, using a construction of [24]. It was shown in [24, Section 6] how given a locally 2-connected, simplicial, $2$ -complex X, and an embedding $\phi : X \to \mathbb S^3$ , one can construct a supercomplex $\mathrm {fat}(X)=\mathrm {fat}(X,\phi )$ with improved properties:

Lemma 4.7 ([24, Lemma 6.3])

Suppose that X is a locally 2-connected, simplicial, $2$ -complex, and $\phi : X \to \mathbb S^3$ is a locally flat embedding. Then $\mathrm {fat}(X)$ is locally $3$ -connected.

Moreover, $\phi $ extends to a locally flat embedding $\phi ': \mathrm {fat}(X) \to \mathbb S^3$ ([24, Lemma 6.1]). As the construction of $\mathrm {fat}(X)$ is canonical, any group action $\Gamma \curvearrowright X$ extends to an action $\Gamma \curvearrowright \mathrm {fat}(X)$ . Finally, any loop in $\mathrm {fat}(X)$ is homotopic to a loop in X by the construction, and so $\mathrm {fat}(X)$ is simply connected if X is.

We now have all the ingredients needed for the main result of this section:

Proof of Theorem 4.1

By Remark 1, we may assume without loss of generality that $\phi $ is locally flat. By Lemma 4.3, X satisfies the conditions of Lemma 4.4, and we let $X'$ be the locally 2-connected 2-complex provided by the latter, and $\phi ': X' \to \mathbb S^3$ the corresponding locally flat embedding (the case where X has fewer than 3 vertices is trivial). Since the rotation system of $\phi $ is $\Gamma $ -invariant by assumption, the second sentence of Lemma 4.4 yields an action $\Gamma \curvearrowright X'$ with respect to which $\sigma (\phi ')$ is $\Gamma $ -invariant. By the third sentence of Lemma 4.4 $X'$ is simply connected since X is. By applying a barycentric subdivision (twice) if needed, we may assume that $X'$ is in addition a simplicial complex.

Next, we consider $Y:= \mathrm {fat}(X')=\mathrm {fat}(X',\phi ')$ , which is locally 3-connected by Lemma 4.7. By the remarks following Lemma 4.7, we also obtain a locally flat embedding $\chi : Y \to \mathbb S^3$ , and an extension $\Gamma \curvearrowright Y$ of the above action. Moreover, Y is still simply connected.

We finish by applying Theorem 4.2 to Y, and pairs of embeddings of the form $\chi , \chi \circ a$ for each $a\in \Gamma $ . To make this precise, we recall that $\Gamma $ acts on $\chi (Y)\subset \mathbb S^3$ , and we want to extend each $a\in \Gamma $ into a homeomorphism $h_a: \mathbb S^3 \to \mathbb S^3$ . We let $h_a$ be the homeomorphism $\alpha $ obtained from Theorem 4.2 when applied to the two embeddings $\chi $ and $\psi := \chi \circ a$ of Y. In order for this map $a \mapsto h_a$ to be an action on $\mathbb S^3$ , we need it to be a homomorphism from $\Gamma $ to $Aut(\mathbb S^3)$ . This will not be the case in general if we let Theorem 4.2 output any $h_a$ satisfying $\psi = h_a \circ \chi $ , because, for example, $h_{a^{-1}}$ may differ from $(h_a)^{-1}$ . But we can control the output of Theorem 4.2 by exploiting its second statement. This ensures that $g \mapsto h_a$ is a homomorphism from $\Gamma $ to $Aut(\mathbb S^3)$ as desired, because restricting each $h_a$ to Y recovers the action of $\Gamma $ on Y, which is a homomorphism. (This idea is spelt out in more detail in [23, Lemma 5.6].)

Notice that $h_a \circ \chi = \psi = \chi \circ a$ , i.e., $\chi (Y),$ is invariant with respect to the action we just defined.

5 From group actions to invariant embedded generalized Cayley complexes

In this section, we prove the implication (i) $\to $ (iv) of Theorem 1.5. An embedded 2-complex in a 3-manifold M is a homeomorphic image of a 2-complex in M. Given an action $\Gamma \curvearrowright M$ , we say that an embedded 2-complex X is $\Gamma $ -invariant if $\Gamma \curvearrowright M$ preserves X setwise.

Theorem 5.1 Let $\Gamma $ be a finite group, and $\Gamma \curvearrowright \mathbb S^3$ a faithful action by homeomorphisms. Then $\Gamma $ admits an embedded, $\Gamma $ -invariant, generalized Cayley complex.

In fact, we will prove the following more general statement, which yields a generalization of the implication (i) $\to $ (iv) of Theorem 1.5. We say that a chamber C of an embedded 2-complex $Y\subset M$ is finitary, if $\partial C$ is a finite subcomplex of Y.

Theorem 5.2 Let M be a 3-manifold, let $\Gamma $ be a finitely generated group, and $\Gamma \curvearrowright M$ a faithful, properly discontinuous, cocompact action by homeomorphisms. Then there is a $\Gamma $ -invariant embedded 2-complex $Y\subset M$ with finitary chambers such that $\Gamma $ acts regularly on $Y^0$ , and $\pi _1(Y)\cong \pi _1(M)$ .

In particular, when M is simply connected, then $\Gamma $ admits a $\Gamma $ -invariant generalized Cayley complex embedded in M.

Notice that the statement that Y has finitary chambers implies in particular that the vertices of Y have no accumulation point in M.

Recall that a $2$ -complex C is a generalized Cayley complex of $\Gamma $ if C is simply connected and $\Gamma $ admits an action on C that is regular on $C^0$ . We will construct such a 2-complex embedded in M in two steps. In the first step, we construct an embedded $2$ -complex $X \subset M$ such that our action $\Gamma \curvearrowright M$ is regular on the chambers of X (Lemma 5.3). In the second step, we perform local modifications on X to transform regularity on the chambers into regularity of the action on the vertices.

5.1 Step 1: Constructing an embedded $2$ -complex with a regular action on its chambers

The following lemma performs the first step of our construction of a generalized Cayley complex of $\Gamma $ as mentioned above:

Lemma 5.3 Let M be a topological 3-manifold, and let $\Gamma \curvearrowright M$ be a faithful, properly discontinuous, cocompact group action by homeomorphisms. Then there is a $\Gamma $ -invariant, embedded 2-complex $X\subset M$ , such that $\pi _1(X)\cong \pi _1(M)$ , and $\Gamma $ acts regularly on the chambers of X, each of which is finitary and homeomorphic to $\mathbb R^3$ .

For the proof of this, we will use the following basic fact:

Lemma 5.4 Let M be a topological 3-manifold, and let $X\subset M$ be an embedded 2-complex such that each chamber of X is homeomorphic to $\mathbb R^3$ , and it is bounded by a finite subcomplex of X. Let $f\in X^2$ be a 2-cell contained in the boundary of two distinct chambers. Then $\pi _1(X)\cong \pi _1(X - f)$ .

Proof Let $C_1,C_2$ denote the two chambers having f in their boundaries. We can continuously deform f via the closure of $C_1$ (or $C_2$ ) onto a continuous image $f'\subset \partial C_1 - f$ of a topological disc using the fact that $C_1$ is homeomorphic to a ball in $\mathbb R^3$ , and $f\subset \partial C_1$ is homeomorphic to a disc. We can use $f'$ to show that the circle $\partial f$ is 0-homotopic in $X - f$ . Thus, we have $\pi _1(X)\cong \pi _1(X - f)$ by van Kampen’s theorem since f is simply connected.

Proof of Lemma 5.3

We may assume without loss of generality that our action $\Gamma \curvearrowright M$ is smooth by Pardon’s theorem, A.1.

It is known that for every such action, the quotient space $M/\Gamma $ —which is a 3-orbifold, but the reader will not need to know what this means—admits a triangulation T [36, Proposition 1.2.1], which is adapted to the action in the sense that for each simplex $\sigma $ of T, the stabilizers under $\Gamma $ of all preimages of points in $\sigma $ are isomorphic to each other. Since $\Gamma \curvearrowright M$ is cocompact, $M/\Gamma $ is compact, and thus T is finite. Let $\pi : M \to M/\Gamma $ be the quotient projection. Its inverse $\pi ^{-1}$ lifts T to a triangulation $\tilde {T}$ of M, as proved in [36, Lemma 1.2.2], which is $\Gamma $ -invariant by construction. We think of the 2-skeleton $\tilde {T}^2$ of $\tilde {T}$ as an embedded 2-complex in M. It is straightforward to check that the chambers of $\tilde {T}$ are exactly its 3-cells. It is easy to show that $\pi _1(\tilde {T}^2)\cong \pi _1(M)$ by applying van Kampen’s theorem to the 3-cells of $\tilde {T}$ .

Notice that the action $\Gamma \curvearrowright M$ is free on the 3-cells of $\tilde {T}$ and therefore on the chambers of $\tilde {T}^2$ , because it is faithful. Indeed, if an element g of $\Gamma $ fixed a 3-cell C setwise, then g would have to fix C pointwise. This would force g to also fix the 3-cells incident with C, hence all of M by its connectedness, implying that g can only be the identity of $\Gamma $ .

If the action is not transitive on the chambers of $\tilde {T}^2$ , then we can find a subcomplex X of $\tilde {T}^2$ which maintains the other desired properties and such that $\Gamma $ acts transitively on the chambers of X, by finding an appropriate fundamental domain of 3-cells of $\tilde {T}^2$ and joining them into one chamber. To do so, we introduce the following notion.

Say that two chamber-boundaries $C,D$ of a 2-complex H are adjacent, if their boundaries share a 2-cell of H. Say that $C,D$ are tight-connected, if there is a sequence $C_1,\ldots C_k$ of chamber-boundaries such that $C_1=C, C_k=D$ , and $C_i$ is adjacent to $C_{i+1}$ for every $1\leq i<k$ . A tight-component is a maximal tight-connected set of chamber-boundaries of H. It is straightforward to check that

(3) $$ \begin{align} &\text{the boundaries of 3-cells of a triangulation of any connected 3-manifold}\nonumber\\ &\text{form a single tight-component. }\end{align} $$

Let F be a maximal tight-connected set of boundaries of 3-cells of $\tilde {T}^2$ that contains at most one representative from each $\Gamma $ -orbit of 3-cells of $\tilde {T}$ . The maximality of F, combined with (3), easily implies that F contains a representative from each $\Gamma $ -orbit of 3-cells, for otherwise we could add to F a 3-cell adjacent with one of its elements (this is a well-known idea, appearing, e.g., in [5]). Thus, F contains exactly one representative of each $\Gamma $ -orbit of 3-cells, in other words, the action of $\Gamma $ on the translates of F is regular. Moreover, F is finite since $\Gamma \curvearrowright M$ is cocompact.

We claim that there is a set D of 2-cells of $\bigcup F$ such that $\bigcup F \backslash D$ has only one chamber C, and moreover C is homeomorphic to $\mathbb S^3$ . Indeed, we can construct D recursively as follows. As long as $\bigcup F$ has more than one chamber (each homeomorphic to $\mathbb R^3$ ), we can find two of them $C_1,C_2$ sharing a 2-cell f by tight-connectedness. By removing f we join $C_1,C_2$ into one chamber, which is homeomorphic to $\mathbb R^3$ since both $C_1,C_2$ are. (The boundary of the new chamber need not be homeomorphic to $\mathbb S^2$ , however.) It is easy to see that the tight-connectedness of the chamber-boundaries of F is preserved. Since F is finite, this recursion terminates leaving a single chamber, proving our claim.

Let $X\subset M$ be the 2-complex obtained from $\tilde {T}^2$ by removing a set D as above along with all its $\Gamma $ -translates. Then $\bigcup F$ is contained in one chamber of X, and it follows that $\Gamma $ acts regularly on the chambers of X.

By construction, each chamber of X is still homeomorphic to $\mathbb R^3$ and finitary.

Notice that whenever we removed a 2-cell f of $\tilde {T}^2$ we joined two chambers $C_1,C_2$ into one, and so we did not change $\pi _1$ by Lemma 5.4. Thus, $\pi _1(X)\cong \pi _1(\tilde {T}^2)$ , which coincides with $\pi _1(M)$ as noticed above.

5.2 Step 2: From regularity of the action on the chambers to regularity on the vertices

Having constructed an embedded 2-complex $X\subset M$ such that the action $\Gamma \curvearrowright M$ of Theorem 5.1 or 5.2 is regular on the chambers of X, our aim now is to modify X locally so that the action becomes regular on the vertices. Most of the work will go into making the action free on the vertices, because having done so we will be able to use the standard trick of contracting a fundamental domain to achieve transitivity. To formulate this trick in our setup, given a graph G, and a subgroup $\Gamma $ of the automorphism group $Aut(G)$ of G, we call a subgraph $H\subseteq G$ a fundamental domain for $\Gamma $ , if H contains exactly one vertex from each $\Gamma $ -orbit.

Lemma 5.5 (Babai’s Contraction Lemma [5])

Let G be a connected graph, and suppose a group $\Gamma \leq Aut(G)$ acts freely on the vertex set $V(G)$ . Then there is a connected subgraph $D \subset G$ that is a fundamental domain for the action, and the graph $G / D$ obtained by contracting each $\Gamma $ -image of D into a point is a generalized Cayley graph of $\Gamma $ . In particular, $\Gamma $ acts transitively on $V(G / D)$ .

The graph we will later apply Lemma 5.5 to is the 1-skeleton of our 2-complex.

Thus, it remains to transform the freeness of the action on the chambers arising from Lemma 5.3 into freeness on the vertices. This is carried out by the following result.

Theorem 5.6 Let M be a topological 3-manifold, and let $\Gamma \curvearrowright M$ be a properly discontinuous group action by homeomorphisms. Let $X\subset M$ be a $\Gamma $ -invariant, embedded 2-complex, such that $\pi _1(X)\cong \pi _1(M)$ , the action of $\Gamma $ on the chambers of X is regular, and each chamber is finitary and homeomorphic to $\mathbb R^3$ . Then there is a $\Gamma $ -invariant, embedded 2-complex $F(X)\subset M$ with finitary chambers, such that the action of $\Gamma $ on $V(F(X))$ is free, and $\pi _1(F(X))\cong \pi _1(M)$ .

Our formal definition of the complex $F(X)$ that achieves this takes some time, but the idea is rather simple: given a vertex x of X stabilized by $\Gamma \curvearrowright M$ , we notice that we can pick a set $O_x$ of nearby points inside the chambers incident with x such that the action of $\Gamma $ on $O_x$ is regular, because $\Gamma $ acts freely on the chambers. The idea is to blow up each 2-cell, 1-cell, and 0-cell of X into a homeomorph of $\mathbb S^2$ , in order to modify X into a complex $F(X)$ with vertex set $\bigcup _{x\in X^0} O_x$ . An example is shown in Figure 2: if X is the standard cubic lattice embedded in $\mathbb R^3$ (top left), then a portion of $F(X)$ is displayed in the bottom right of the figure.

Figure 2: An example $F(X)$ , when X is the cubic lattice (top left). Each link graph is an octahedron (top right), and so each pineapple of $F(X)$ is a truncated cuboctahedron (bottom left). The pineapples are arranged as in the bottom right figure, which shows four of them in the front.

The reader will lose nothing by assuming that $M= \mathbb S^3$ and $\Gamma $ is finite throughout this section; this is enough for proving Theorem 1.4, and this assumption makes no difference for any of the proofs in this section.

We now prepare for the formal definition of $F(X)$ . Given an embedded 2-complex $X\subset M$ , and a homeomorphic image S of $\mathbb S^2$ in M which is locally flat, we say that S is adapted to X if

1. (i) for every 1-cell $e\in X^1$ the intersection $S \cap e$ is either a single point, or all of e, or empty;

2. (ii) for every 2-cell $f\in X^2$ , the intersection $S \cap f$ is either an arc between two points of the boundary of f (either 0-cells, or interior points of 1-cells) or empty, and

3. (iii) S separates M into two components.

If S is adapted to X, and A is one of the two components into which S separates M, then we can obtain an embedded 2-complex $X_A$ from X by removing $X \cap A$ and adding S to X; to make this more precise, we define the A-truncation of X to be the embedded 2-complex $X_A$ obtained as follows.

1. (i) For every 1-cell $e\in X^1$ that intersects S at a point p, we declare p to be a 0-cell of $X_A$ , we declare the subarc of e lying outside A to be a 1-cell of $X_A$ and discard the subarc of e lying inside A.

2. (ii) For every 2-cell $f\in X^2$ intersecting S along an arc P between two points $x,y$ of the boundary of f, we declare P to be a 1-cell of $X_A$ —its end-points $x,y$ must be 0-cells of $X_A$ by i. Notice that $f \backslash (S \cup A)$ is homeomorphic to a disc $f'$ , and we declare $f'$ to be a 2-cell of $X_A$ , discarding f.

3. (iii) The points p and arcs P as in i–iisubdivide S into topological discs, which we declare to be 2-cells of $X_A$ .

4. (iv) For every cell C of X that does not intersect S, we keep C in $X_A$ if it lies outside A, and discard it if it is contained in A.

We now construct the 2-complex $F(X)$ featuring in Theorem 5.6 by a combination of such truncations.

Definition 5.7 Given an embedded 2-complex $X\subset M$ , we construct another embedded 2-complex $F(X)\subset M$ as follows.

1. (i) We blow each 2-cell $f\in X^2$ up like a mango; that is, we replace f by two “parallel” copies $f',f"$ with the same boundary and attachment map, and embed $f',f"$ into M so that one of the sides of the 2-sphere $S_f:= f' \cup f"$ contains f and is otherwise disjoint from X. Moreover, we ensure that $S_f$ is locally flat, and disjoint from $g' \cup g"$ for every $g\neq f\in X^2$ except possibly for intersections along $X^1$ ; in other words, our mangos do not cross each other. Let $X_1$ denote the resulting 2-complex. We call $f' \cup f"$ the mango of f and imagine its side containing f as one.

2. (ii) Next, we blow each 1-cell $e\in X_1^1$ up like a banana. To define this formally, let $S_e$ be a homeomorph of $\mathbb S^2$ in M such that the end-vertices of e lie on $S_e$ , one side $A_e$ of $S_e$ contains the interior of e and is otherwise disjoint from the 1-skeleton of $X_1$ , and $S_e$ is adapted to $X_1$ and locally flat. It is easy to find such $S_e$ , and to ensure that they are pairwise disjoint except possibly at their vertices. We apply the $A_e$ -truncation of $X_1$ for each $e\in X_1^1$ to obtain a new embedded 2-complex $X_2$ . We call $S_e$ the banana of e.

3. (iii) Finally, we blow each vertex $v\in X_2^0=X^0$ up like a pineapple; that is, we pick a homeomorph $S_v$ of $\mathbb S^2$ in M, such that one side $A_v$ of $S_v$ contains v but no other vertices of $X_2$ , and $S_v$ is adapted to $X_2$ and locally flat. Moreover, we choose the $S_v, v\in X_2^0$ small enough that they are pairwise disjoint. We apply the $A_v$ -truncation of $X_2$ for each $v\in X_2^0$ to obtain the desired 2-complex $F(X)$ . We call $S_v$ the pineapple of v.

Remark 2 The 1-skeleton of the pineapple of v can be obtained from the link graph of v by doubling each edge by a parallel one, and then blowing up each vertex of the resulting plane graph into a cycle of vertices of degree 3.

Example When X is the cubic lattice in $\mathbb R^3$ , the link graph of each vertex is isomorphic to the 1-skeleton of the octahedron. Each pineapple of $F(X)$ is a truncated cuboctahedron. They are arranged as shown in Figure 2.

Remark 3 There is an alternative, more abstract, way to define $F(X)$ . A flag of X is a 4-tuple $(c_0,c_1,c_2,c_3)$ where $c_i$ is an i-cell of X, and $c_i$ is incident with $c_{i-1}$ for $1\leq i \leq 4$ , with the convention that the 3-cells of $X\subset M$ are its chambers. We can identify the set of 0-cells of $F(X)$ with the set of flags of X. We connect two flags with an 1-cell of $F(X)$ whenever they differ in exactly one coordinate. We can 4-color the 1-cells of $F(X)$ using the coordinate at which its end-vertices differ as a color. The 2-cells of $F(X)$ are bounded by the 2-colored cycles with respect to this coloring. Again Figure 2 can serve as an example. This definition generalizes in any dimension.

The letter F in our notation $F(X)$ stands for “fruit,” but also for “flag.”

Using van Kampen’s theorem, it will be easy to deduce that $F(X)$ preserves the fundamental group of X:

Lemma 5.8 For $F(X)$ as in Definition 5.7, we have $\pi _1(F(X))\cong \pi _1(X)$ .

Proof Notice that if we contract each pineapple $S_v$ in the construction of $F(X)$ to a point, we obtain a 2-complex homeomorphic to $X_2$ . Thus, $\pi _1(F(X))\cong \pi _1(X_2)$ by van Kampen’s theorem. Similarly, squeezing each banana $S_e$ in $X_2$ back to an edge with the same endpoints as e results into a 2-complex homeomorphic to $X_1$ , and so $\pi _1(X_2)\cong \pi _1(X_1)$ . Finally, squashing each mango $S_f$ of $X_1$ onto a disc with the same boundary as f results in a homeomorph of X, yielding $\pi _1(X_1)\cong \pi _1(X)$ .

In order to be able to use $F(X)$ to prove Theorem 5.6, we need to construct it more carefully so that $\Gamma \curvearrowright M$ extends to an action on $F(X)$ . This would be easy if $\Gamma $ acted freely on X, but in general we need to take some care to ensure that the stabilizer of each 2-cell, 1-cell, or 0-cell fixes the corresponding mango, banana, or pineapple, respectively. We will be able to achieve this by choosing a chamber C of X and using its closure $\overline {C}$ as a fundamental domain. More precisely, we will prove

Lemma 5.9 Let X and $\Gamma $ be as in the statement of Theorem 5.6, let C be a chamber of X, and let D be the subcomplex of X bounding C. Then there is a homeomorphic copy $F\subset M$ of $F(D)$ , such that $\Gamma (F \cap \overline {C})$ is homeomorphic to $F(X)$ .

Here, $\Gamma A$ denotes the image of a set $A\subset M$ under the action $\Gamma \curvearrowright M$ , and $F(D)$ is given by Definition 5.7.

Before proving Lemma 5.9, let us see how it implies Theorem 5.6.

Proof of Theorem 5.6

Given X as in the statement, we construct $F(X)$ as in Definition 5.7. By Lemma 5.8, $F(X)$ is simply connected since X is. Easily, $F(X)$ has finitary chambers since X does.

Let D be the subcomplex of X bounding a chamber C of X. Then Lemma 5.9 yields an embedded 2-complex $F\subset M$ such that $F':=\Gamma (F \cap \overline {C})$ is homeomorphic to $F(X)$ . Notice that $F'$ is $\Gamma $ -invariant by definition.

It remains to check that the action of $\Gamma $ on $V(F')$ is free. This is true because each vertex of $F'$ lies in the interior of a chamber of X, and $\Gamma $ acts freely on the chambers of X by assumption.

It remains to prove Lemma 5.9. To construct the desired copy F of $F(D)$ , we will first design the intersection of F with each 2-cell of $F(D)$ . To do so, we need to remember how the bananas and pineapples of $F(X)$ intersect each 2-cell of X (the mangos do not); these intersections are described in the following definition, but they are easier to see in Figure 3.

Figure 3: A topological 5-gon with a slice pattern. The $E_i$ are depicted in red (if color is shown), and the $V_i$ in blue.

A topological n-gon is a regular 2-complex P containing exactly one 2-cell f, and such that $P^1$ is homeomorphic to $\mathbb S^1$ (and coincides with the boundary of f).

Definition 5.10 Let P be a topological n-gon, with vertices $v_1,\ldots v_n$ , and edges $v_i v_{i+1\pmod n}$ . A slice pattern on P consists of two sets $\mathcal E:= \{E_1, \ldots , E_n\}$ and $\mathcal V:= \{V_1, \ldots , V_n\}$ of arcs on P, such that (Figure 3)

1. (i) the end-points of $E_i$ are $v_i$ and $v_{i+1\pmod n}$ ;

2. (ii) the end-points of $V_i$ are interior points of the edges $v_{i-1\pmod n} v_i$ and $v_i v_{i+1\pmod n}$ ;

3. (iii) each $E_i$ and $V_i$ meets the 1-skeleton of P at its end-points only;

4. (iv) the elements of $\mathcal E$ are pairwise disjoint, and so are the elements of $\mathcal V$ , and

5. (v) $V_i$ is disjoint from $E_j$ unless $j=i$ or $j=i-1\pmod n$ .

An automorphism of a topological n-gon P is a homeomorphism of P mapping each vertex to a vertex (and hence each edge to an edge). To prove Lemma 5.9, we will apply the following lemma to each 2-cell of D; this helps us by pushing the difficulty one dimension down.

Lemma 5.11 Let P be a topological n-gon, and $h: P \to P$ an automorphism such that $h^2$ is the identity. Then there is a slice pattern $(\mathcal E,\mathcal V)$ of P preserved by h. That is, h maps each element of $\mathcal E$ to an element of $\mathcal E$ , and each element of $\mathcal V$ to an element of $\mathcal V$ .

Proof Notice that h must fix some arc A joining two boundary points of P and exchange the two components into which A separates P. We can thus pick “half” a slice pattern on the quotient polygon $P/h$ and lift it back to P to obtain a slice pattern of P. We have assumed here that h in not the identity, in which case the statement is trivial.

Proof of Lemma 5.9

Notice that although $\Gamma \curvearrowright M$ is free on the chambers of X, some of the 2-cells of D may have a nontrivial stabilizer in $\Gamma $ . However, for every such 2-cell $f\in D^2$ , there is at most one nonidentity element $h_f$ of $\Gamma $ fixing f, because f is in the boundary of at most two chambers of X, and no nonidentity element of $\Gamma $ fixes a chamber. For the same reason, $h_f$ must be an involution. Applying Lemma 5.11 with $P=\overline {f}$ we obtain a slice pattern $(\mathcal E,\mathcal V)$ of $\overline {f}$ preserved by $h_f$ . Choosing such a slice pattern for one representative f of each $\Gamma $ -orbit of 2-cells of D, and translating it to the other representatives via the action of $\Gamma $ , we obtain a family $(\mathcal E_f,\mathcal V_f)_{f\in D^2}$ of slice patterns of all 2-cells of D, which family is compatible with our action $\Gamma \curvearrowright M$ , i.e., $(\mathcal E_f,\mathcal V_f)=(\mathcal E_{gf'},\mathcal V_{gf'})$ whenever $gf'=f$ for some $f,f'\in D^2$ and some $g\in \Gamma $ . Notice that this implies that the set of $\Gamma $ -translates of this family is $\Gamma $ -invariant.

To find the desired copy F of $F(D)$ , we can start by picking the mangoes arbitrarily as in (Definition 5.7 i). (The half-mango outside $\overline {C}$ will be irrelevant.) For each $e\in D^1$ , pick the corresponding banana $S_e$ (Definition 5.7 ii) so that its intersection with each 2-cell of D is contained in one of the $\mathcal E_f$ of the above family of slice patterns. Similarly, for each $v\in D^0$ , pick the corresponding pineapple $S_v$ (Definition 5.7 iii) so that its intersection with each 2-cell of D is contained in one of the $\mathcal V_f$ . This completes the construction of F.

It remains to check that $\Gamma (F \cap \overline {C})$ is homeomorphic to $F(X)$ as claimed. To see this, notice that $F \cap \overline {C}$ contains one half of each mango, a slice of each banana, and a sector of each pineapple of F. Moreover, when acted upon by $\Gamma $ , these portions combine well to produce a homeomorph of $F(X)$ . Indeed, for any $g,h\in \Gamma $ , the translates $g(F \cap \overline {C})$ and $h(F \cap \overline {C})$ are disjoint except possibly at the boundaries of $g \overline {C}$ and $h \overline {C}$ , where they meet along the $\Gamma $ -invariant family of slice patterns chosen above.

We are now ready to complete the main result of this section.

Proof of Theorems 5.1 and 5.2

Apply Lemma 5.3 to obtain an embedded 2-complex $X\subset M$ such that $\pi _1(X)\cong \pi _1(M)$ and X satisfies all the assumptions of Theorem 5.6. Then apply Theorem 5.6 to this X, to turn it into an embedded 2-complex $F(X)$ such that the action of $\Gamma $ on $V(F(X))$ is free.

Suppose that the action of $\Gamma $ on $V(F(X))$ is not transitive. Let $D\subset F(X)^1$ be a connected fundamental domain for the action as provided by Lemma 5.5. Notice that D is finite because $\Gamma \curvearrowright M$ is cocompact. Let T be a spanning tree of D, and let U be an open neighborhood of T in M homeomorphic to $\mathbb R^3$ . Easily, we can pick U small enough that its $\Gamma $ -translates are pairwise disjoint. Contracting each $\Gamma $ -translate of U into a point, we obtain a manifold homeomorphic to M, still acted upon by $\Gamma $ , into which manifold the 2-complex $Y:= F(X)/T$ is embedded $\Gamma $ -invariantly. These contractions preserve the property that all chambers are finitary. By the choice of T, the action of $\Gamma $ on $V(Y)$ is regular. Moreover, $\pi _1(Y) \cong \pi _1(F(X)) \cong \pi _1(X)\cong \pi _1(M)$ . In particular, when M is simply connected, then Y is a generalized Cayley complex of $\Gamma $ .

Notice that when M is simply connected in Theorem 5.2, then it is a special 3-manifold by Theorem 1.1. Thus, we have proved the implication $(i)\rightarrow (iv)$ of Theorem 1.5 and its analogue for Theorem 1.4. In particular, we deduce the implication $(i)\rightarrow (iii)$ of Theorem 1.4, and assuming, as we may, that the action of (i) is on $\mathbb S^2$ , we avoid using Theorem 1.1. Combined with Section 4, we thus obtain a proof of the equivalence of $(i)$ and (iii) of Theorem 1.4 without using Perelman’s work.

Remark 4 Since X, and hence $F(X)$ , are regular 2-complexes by construction, the 2-complex Y that the above proof provides is edge-regular (as defined in Section 2.3). We do not know if we can always obtain a regular Y in Theorems 5.1 and 5.2.

6 Concluding remarks

Our proofs of Theorems 1.4 and 1.5 are now complete. The implication $(iv)\rightarrow (i)$ is trivial because every special 3-manifold is simply connected. The implications $(iv)\rightarrow (iii) \rightarrow (ii)$ are trivial because every special 3-manifold embeds in $\mathbb S^3$ . The implications (ii) $\to $ (iv) and $(i)\rightarrow (iv)$ have been proved in Sections 3 and 5, respectively.

As mentioned in the introduction, there are groups admitting a Cayley complex embeddable in $\mathbb R^3$ with invariant planar rotation system, but only if we allow infinite prechambers. Examples include $\mathbb Z^2$ , and more generally any fundamental group of an orientable closed surface [1].

Question 6.1 Which infinite groups admit a Cayley complex embeddable in $\mathbb R^3$ with invariant planar rotation system?

This class of groups contains the fundamental groups of closed 3-manifolds (as proved by Theorem 1.4) and closed surfaces; more generally, it contains all Kleinian function groups [23, Section 12] ³ . It is easy to see that it also contains groups of the form $F \times \mathbb Z$ where F is free. It would be interesting to clarify the relationship between the groups of Question 6.1 and the Kleinian groups.

Question 6.2 Is there a finite set X of 3-manifolds, such that each of the groups of Question 6.1 admits a discrete action on an element of X?

This X should contain the three special open 3-manifolds of Theorem 1.1. It should also contain $\mathbb R^2 \times S^1$ , because of $\mathbb Z^2$ and other surface groups. Moreover, X should contain $C \times \mathbb R$ where C stands for the Cantor 2-sphere, i.e., $\mathbb S^2$ with a Cantor set removed; we include $C \times \mathbb R$ to let groups of the form $F \times \mathbb Z$ act. These 5 manifolds could suffice as far as we can tell.

One could enquire more generally about the class of groups admitting a Cayley complex embeddable in $\mathbb R^3$ with no further restrictions, though we do not expect an easy alternative description. An example of such a group is the Baumslag–Solitar group $BS(1,2)$ . Its standard Cayley complex defined by $\left < a,b \mid ba b^{-1}=a^2 \right>$ embeds in the cartesian product of a binary tree and $\mathbb R$ , as well-known figures show. It has been proved that $BS(1,2)$ cannot be mapped in a nondegenerate way into the fundamental group of an orientable 3-manifold [43], and so it is not one of the groups of Theorem 1.5.

Appendix: The universal covers of 3-manifolds and orbifolds

In this section, we provide a proof of Theorem 1.1. We emphasize that our only contribution to this proof was to ask the experts about it and put the pieces together.

For our proof of Theorem 1.1, and also in Section 5, we make use of Pardon’s theorem that topological actions on a 3-manifold can be smoothed:

Theorem A.1 ([39, 40])

Every properly discontinuous action of a finitely generated group $\Gamma $ on a 3-manifold M by homeomorphisms is the uniform limit of smooth actions of $\Gamma $ on M.

We will also need the following consequence of the Orbifold theorem of Boileau, Leeb, & Porti:

Theorem A.2 ([9, Corollary 1.3])

Every compact connected 3-orbifold which does not contain any bad 2-suborbifolds is the quotient of a compact 3-manifold by a finite group action.

Proof of Theorem 1.1

Suppose first that M admits an action $\Gamma \curvearrowright M$ as above, which is in addition free. Then $Q:= M / \Gamma $ is a closed 3-manifold, and M is its universal cover because it is simply connected. Moreover, $\Gamma \cong \pi _1(Q)$ .

We may assume without loss of generality that Q is orientable by replacing $\Gamma $ by its subgroup of orientation-preserving elements. Thus, Q is a closed, orientable, connected, 3-manifold. The fact that such a Q has special universal cover is apparently well-known to experts. We reproduce a proof by Ian Agol [3].

If $\pi _1(Q)$ is finite, then its universal cover M is homeomorphic to $\mathbb S^3$ by the validity of the Poincaré conjecture.

If $\pi _1(Q)$ is infinite and $\pi _2(Q)$ is trivial, then we claim that the universal cover M is homeomorphic to $\mathbb R^3$ . Indeed, in this case, Q has a geometric decomposition by the geometrization theorem [41, 42, 45]. If the decomposition is trivial, then Q is modeled on one of the six Thurston geometries homeomorphic to $\mathbb R^3$ , and hence the universal cover is $\mathbb R^3$ . Otherwise, we apply the virtually Haken conjecture, proved by Agol [4], which asserts that every compact, irreducible 3-manifold Q with infinite $\pi _1(Q)$ is finitely covered by a Haken manifold $Q'$ . The reader does not need to know what a Haken manifold is, all we need is a result of Waldhausen proving that any Haken manifold $Q'$ has universal cover homeomorphic to $\mathbb R^3$ [46, Theorem 8.1]. Since $Q'$ covers Q, we deduce that M is homeomorphic to $\mathbb R^3$ as claimed.

If $\pi _1(Q)$ is infinite and $\pi _2(Q)$ nontrivial, then it may be that Q is modeled on the $\mathbb S^2 \times \mathbb R$ geometry and Q is homeomorphic to $RP3 \# RP3$ or $\mathbb S^2 \times \mathbb S^1$ . In this case, the number of ends of $\pi _1(Q)$ , and M, is 2, and M is homeomorphic to $\mathbb S^2 \times \mathbb R$ . Otherwise, Q is a nontrivial connect sum by Papakyriakopoulos’ sphere theorem [38], and we claim that the universal cover M is a Cantor 3-sphere. Indeed, the connect summands have universal cover either $\mathbb S^3$ , or $\mathbb S^2 \times \mathbb R$ , or $\mathbb R^3$ by the above discussion. When forming connect sums, we remove open balls from each summand manifold and glue their sphere boundaries together. The universal cover is obtained by gluing the universal covers of each summand punctured along balls, either finitely many in $\mathbb S^3$ or infinitely many in $\mathbb S^2 \times \mathbb R$ or $\mathbb R^3$ . It is easy to see that such manifolds are built out of thrice punctured spheres, and hence the universal cover can be decomposed into thrice punctured spheres. It is not hard to see that such a manifold is homeomorphic to the Cantor 3-sphere.

It remains to consider the case where the action $\Gamma \curvearrowright M$ is nonfree, which we will be able to reduce to the free case. By Theorem A.1, we may assume that $\Gamma \curvearrowright M$ is smooth. Thus, the quotient $O:= M / \Gamma $ is endowed with the structure of an orbifold. Theorem A.2 implies that O is finitely covered by a manifold $M'$ . The universal cover of $M'$ covers O, and so it coincides with M by the uniqueness of a simply connected cover. Recall that $\pi _1(M')$ acts on its universal cover M freely, properly discontinuous, and cocompactly. We have reduced to the free case, and so we can deduce that M is special in all cases.