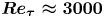1. Introduction
Turbulent flow in circular pipes has always attracted the interest of scientists, owing to its prominent importance in engineering practice and because of the beautiful simplicity of the set-up. The study of flows in circular pipes holds particular significance not only for its fundamental insights into fluid dynamics but also for its practical applications, especially in industries such as oil and gas transportation. Understanding the behaviour of turbulent flow in pipelines is crucial for optimising transport efficiency, ensuring structural integrity, and minimising energy consumption. As such, research into flows in circular pipes continues to be an active area of study, driving innovations in both theoretical understanding and engineering practice.
Specifically, the research on drag reduction techniques in pipe flow holds significant importance due to its potential for reducing energy consumption in the transportation of gases or liquids, thereby leading to decreased pollutant emissions into the atmosphere. The potential of axial rotation for drag reduction in turbulent pipe flow was first shown by White (Reference White1963). In those experiments, dye was injected from a hypodermic tube into the central core of the flow in a pipe, and then diffused radially outwards to fill the whole pipe. When rotation was imposed on the pipe wall, the dye moved along the central core of the pipe without as much radial diffusion. The rate of rotation is typically measured in terms of the rotation number, ![]() $N = \varOmega R / u_b$, where
$N = \varOmega R / u_b$, where ![]() $\varOmega$ is the rotational speed,
$\varOmega$ is the rotational speed, ![]() $R$ is the pipe radius and
$R$ is the pipe radius and ![]() $u_b$ is bulk velocity. The experiments of Kikuyama et al. (Reference Kikuyama, Murakami, Nishibori and Maeda1983) showed that as
$u_b$ is bulk velocity. The experiments of Kikuyama et al. (Reference Kikuyama, Murakami, Nishibori and Maeda1983) showed that as ![]() $N$ increases, the wall friction decreases, with the mean axial velocity profiles approaching the parabolic Poiseuille solution. These findings were subsequently confirmed from the direct numerical simulation (DNS) conducted by Orlandi & Fatica (Reference Orlandi and Fatica1997). Those authors mainly attributed the mechanism of drag reduction to the stabilising effect of the radially growing centrifugal force (or angular momentum). Indeed, according to the Rayleigh criterion (Reich & Beer Reference Reich and Beer1989; Drazin & Reid Reference Drazin and Reid2004), the radially growing pressure gradients impede the radial motion of fluid particles. Orlandi & Fatica (Reference Orlandi and Fatica1997) further pointed out that axial rotation induces a long columnar structure in the core region which transports the streamwise vortical structures away from the wall, while tilting and widening the near-wall streaks. Also, wall rotation disrupts the symmetry between right- and left-handed helical structures, and the resulting high helicity density yields less dissipation, with incurred drag reduction (Orlandi Reference Orlandi1997). Zhang & Wang (Reference Zhang and Wang2022) showed that the sweep events are systematically suppressed by rotation, which further impedes the formation of hairpin structures. However, they found that rotation amplifies the azimuthal and radial velocity variances, and that the pressure-strain and Coriolis production terms become the leading terms in the budget of these two Reynolds normal stresses.
$N$ increases, the wall friction decreases, with the mean axial velocity profiles approaching the parabolic Poiseuille solution. These findings were subsequently confirmed from the direct numerical simulation (DNS) conducted by Orlandi & Fatica (Reference Orlandi and Fatica1997). Those authors mainly attributed the mechanism of drag reduction to the stabilising effect of the radially growing centrifugal force (or angular momentum). Indeed, according to the Rayleigh criterion (Reich & Beer Reference Reich and Beer1989; Drazin & Reid Reference Drazin and Reid2004), the radially growing pressure gradients impede the radial motion of fluid particles. Orlandi & Fatica (Reference Orlandi and Fatica1997) further pointed out that axial rotation induces a long columnar structure in the core region which transports the streamwise vortical structures away from the wall, while tilting and widening the near-wall streaks. Also, wall rotation disrupts the symmetry between right- and left-handed helical structures, and the resulting high helicity density yields less dissipation, with incurred drag reduction (Orlandi Reference Orlandi1997). Zhang & Wang (Reference Zhang and Wang2022) showed that the sweep events are systematically suppressed by rotation, which further impedes the formation of hairpin structures. However, they found that rotation amplifies the azimuthal and radial velocity variances, and that the pressure-strain and Coriolis production terms become the leading terms in the budget of these two Reynolds normal stresses.
Davis et al. (Reference Davis, Ganju, Ashton, Bailey and Brehm2019) reported that the drag reduction effect increases with the bulk Reynolds number, ![]() $Re_b = u_b D/ \nu$, where
$Re_b = u_b D/ \nu$, where ![]() $D=2 R$ is the pipe diameter and
$D=2 R$ is the pipe diameter and ![]() $\nu$ is kinematic viscosity. However, their highest friction Reynolds number,
$\nu$ is kinematic viscosity. However, their highest friction Reynolds number, ![]() $Re_{\tau } = u_\tau R/\nu$ (with
$Re_{\tau } = u_\tau R/\nu$ (with ![]() $u_\tau =(\tau _w/\rho )^{1/2}$ the friction velocity), was approximately 540, at which extrapolation to real-world scenarios of fully developed turbulent flow is far from clear and well less than achieved in DNS of non-rotating pipe flow (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021).
$u_\tau =(\tau _w/\rho )^{1/2}$ the friction velocity), was approximately 540, at which extrapolation to real-world scenarios of fully developed turbulent flow is far from clear and well less than achieved in DNS of non-rotating pipe flow (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021).
Other techniques for drag reduction in turbulent pipe flow have been proposed based on more complex wall actuation. Quadrio & Sibilla (Reference Quadrio and Sibilla2000) studied turbulent flow in a circular pipe oscillating around its longitudinal axis through DNS and found that the maximum amount of drag reduction achievable with appropriate oscillations of the pipe wall is of the order of 40 %, comparable to what was found in planar geometries. They observed that the transverse shear layer induced by wall oscillation induces substantial modifications to the turbulence statistics in the near-wall region, indicating a strong effect on the vortical structures. Auteri et al. (Reference Auteri, Baron, Belan, Campanardi and Quadrio2010) assessed the practical use of travelling waves of spanwise velocity, as suggested by Quadrio, Ricco & Viotti (Reference Quadrio, Ricco and Viotti2009) and further analysed by Gatti & Quadrio (Reference Gatti and Quadrio2016), to achieve drag reduction in pipe flow. In their experiments, the pipe wall was subdivided into thin slabs that could rotate independently in the azimuthal direction, confirming the possibility of achieving drag reduction of up to 33 %.
In the present study, we leverage DNS data to explore drag reduction in turbulent pipe flow up to ![]() $Re_\tau \approx 3000$ through the use of steady axial rotation. The goal is to verify and quantify the drag reduction effects, and shed light on the underlying physical mechanisms.
$Re_\tau \approx 3000$ through the use of steady axial rotation. The goal is to verify and quantify the drag reduction effects, and shed light on the underlying physical mechanisms.
2. The numerical dataset
A second-order finite-difference solver is used to solve the incompressible Navier–Stokes equations in cylindrical coordinates (Orlandi & Fatica Reference Orlandi and Fatica1997; Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021). The current DNS pertains to fully developed turbulent flow, with periodic conditions along the axial direction. The DNS is carried out in a frame of reference rotating with the pipe, which has the advantage of allowing for larger time steps as compared with the inertial frame. Coriolis forces are then added as ![]() $-2\varOmega u_r$ and
$-2\varOmega u_r$ and ![]() $2\varOmega u_{\theta }$ to the azimuthal and radial momentum equations, where
$2\varOmega u_{\theta }$ to the azimuthal and radial momentum equations, where ![]() $u_\theta$ and
$u_\theta$ and ![]() $u_r$ are the velocity components in the azimuthal and radial directions. The simulations were conducted under conditions of constant mass flow rate. From now on, the subscript
$u_r$ are the velocity components in the azimuthal and radial directions. The simulations were conducted under conditions of constant mass flow rate. From now on, the subscript ![]() $0$ indicates non-rotating cases and the superscript
$0$ indicates non-rotating cases and the superscript ![]() $*$ is used to denote normalisation with wall units. Normalisation with wall units based on the non-rotating case is also used to better highlight the effects of pipe rotation, which we indicate with the
$*$ is used to denote normalisation with wall units. Normalisation with wall units based on the non-rotating case is also used to better highlight the effects of pipe rotation, which we indicate with the ![]() $+$ superscript. We performed DNS for various bulk Reynolds numbers, namely
$+$ superscript. We performed DNS for various bulk Reynolds numbers, namely ![]() $Re_b = 5300, 17\,000, 44\,000, 82\,500$ and
$Re_b = 5300, 17\,000, 44\,000, 82\,500$ and ![]() $133\,000$, corresponding to friction Reynolds numbers of
$133\,000$, corresponding to friction Reynolds numbers of ![]() $Re_{\tau,0} = 180$,
$Re_{\tau,0} = 180$, ![]() $495$,
$495$, ![]() $1137$,
$1137$, ![]() $1979$ and
$1979$ and ![]() $3020$, in the absence of rotation. For each Reynolds number, we have considered various rotation numbers, namely
$3020$, in the absence of rotation. For each Reynolds number, we have considered various rotation numbers, namely ![]() $N=0$,
$N=0$, ![]() $0.25$,
$0.25$, ![]() $0.5$,
$0.5$, ![]() $1.0$ and
$1.0$ and ![]() $2.0$ and
$2.0$ and ![]() $4.0$. A list including the flow parameters for all the simulations is provided in table 1. The pipe length is set to
$4.0$. A list including the flow parameters for all the simulations is provided in table 1. The pipe length is set to ![]() $L=15R$ and the mesh resolution for each of the Reynolds numbers is decided based on the non-rotating cases, which exhibit the highest wall friction. Specifically, the grid spacing is
$L=15R$ and the mesh resolution for each of the Reynolds numbers is decided based on the non-rotating cases, which exhibit the highest wall friction. Specifically, the grid spacing is ![]() $\Delta z^+ \approx 10$ and
$\Delta z^+ \approx 10$ and ![]() $R^+ \Delta \theta \approx 4$, along the axial and azimuthal directions, respectively. In the radial direction, the grid spacing is uniform up to
$R^+ \Delta \theta \approx 4$, along the axial and azimuthal directions, respectively. In the radial direction, the grid spacing is uniform up to ![]() $y^+ \approx 5$ and then proportional to the local Kolmogorov length scale (
$y^+ \approx 5$ and then proportional to the local Kolmogorov length scale (![]() $\eta ^+ \approx 0.8(y^+)^{1/4}$) in the outer layer. Approximately thirty grid points are allocated for
$\eta ^+ \approx 0.8(y^+)^{1/4}$) in the outer layer. Approximately thirty grid points are allocated for ![]() $y^+ \le 40$, with the first grid point located at
$y^+ \le 40$, with the first grid point located at ![]() $y^+ \approx 0.05$. Additional details can be found in previous publications (Pirozzoli & Orlandi Reference Pirozzoli and Orlandi2021). The sensitivity of the results to pipe length and mesh resolution is analysed in the Appendix. Hereafter, capital letters will be used to denote flow properties averaged in the homogeneous spatial directions and in time, brackets to denote the averaging operator, and lower-case letters to denote fluctuations from the mean.
$y^+ \approx 0.05$. Additional details can be found in previous publications (Pirozzoli & Orlandi Reference Pirozzoli and Orlandi2021). The sensitivity of the results to pipe length and mesh resolution is analysed in the Appendix. Hereafter, capital letters will be used to denote flow properties averaged in the homogeneous spatial directions and in time, brackets to denote the averaging operator, and lower-case letters to denote fluctuations from the mean.
Table 1. Flow parameters for DNS. ![]() $Re_b = 2 R u_b / \nu$ is the bulk Reynolds number;
$Re_b = 2 R u_b / \nu$ is the bulk Reynolds number; ![]() $Re_{\tau } = u_\tau R/\nu$ is the friction Reynolds number;
$Re_{\tau } = u_\tau R/\nu$ is the friction Reynolds number; ![]() $Re_{\tau,0}$ is the friction Reynolds number for the non-rotating case;
$Re_{\tau,0}$ is the friction Reynolds number for the non-rotating case; ![]() $N = \varOmega R / u_b$ is the rotation number;
$N = \varOmega R / u_b$ is the rotation number; ![]() $N_\theta$,
$N_\theta$, ![]() $N_r$ and
$N_r$ and ![]() $N_z$ are the number of grid points along the azimuthal, radial and axial directions, respectively;
$N_z$ are the number of grid points along the azimuthal, radial and axial directions, respectively; ![]() $N^+=\varOmega R/u_{\tau,0}$ is the inner-scaled rotational speed;
$N^+=\varOmega R/u_{\tau,0}$ is the inner-scaled rotational speed; ![]() $\lambda$ is the friction factor;
$\lambda$ is the friction factor; ![]() $DR$ is the percentage of drag reduction; and #ETT is the time-averaging interval, expressed in terms of the eddy turnover time,
$DR$ is the percentage of drag reduction; and #ETT is the time-averaging interval, expressed in terms of the eddy turnover time, ![]() $R/u_\tau$. The symbol
$R/u_\tau$. The symbol ![]() $*$ denotes DNS with pipe length
$*$ denotes DNS with pipe length ![]() $L = 30R$ and
$L = 30R$ and ![]() $**$ denotes DNS with doubled resolution in the radial direction. The standard uncertainty of the friction factor is estimated using a modified batch means method (Russo & Luchini Reference Russo and Luchini2017) and the uncertainty of drag reduction is evaluated by propagating the standard uncertainties of the friction factors.
$**$ denotes DNS with doubled resolution in the radial direction. The standard uncertainty of the friction factor is estimated using a modified batch means method (Russo & Luchini Reference Russo and Luchini2017) and the uncertainty of drag reduction is evaluated by propagating the standard uncertainties of the friction factors.

3. Results
3.1. Drag reduction
Before delving into the analysis of drag reduction, we compare our results with previous studies. Figure 1 displays the friction factor results. For the non-rotating cases, the DNS results exhibit minor derivations from Prandtl's friction law (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021). For the rotating cases, the DNS results for ![]() $Re_{\tau,0} = 180$ and
$Re_{\tau,0} = 180$ and ![]() $Re_{\tau,0} = 495$ agree well with the DNS data of Davis et al. (Reference Davis, Ganju, Ashton, Bailey and Brehm2019). However, all DNS results exhibit large discrepancies from the experimental data of Kikuyama et al. (Reference Kikuyama, Murakami, Nishibori and Maeda1983) at high rotation number, even accounting for differences in the Reynolds number (
$Re_{\tau,0} = 495$ agree well with the DNS data of Davis et al. (Reference Davis, Ganju, Ashton, Bailey and Brehm2019). However, all DNS results exhibit large discrepancies from the experimental data of Kikuyama et al. (Reference Kikuyama, Murakami, Nishibori and Maeda1983) at high rotation number, even accounting for differences in the Reynolds number (![]() $Re_{\tau,0} = 240$ and
$Re_{\tau,0} = 240$ and ![]() $570$ for those authors). Orlandi & Fatica (Reference Orlandi and Fatica1997) attributed discrepancies to the influence of the entrance conditions, and possible difficulties in achieving a constant pressure gradient in the experimental set-up. We note that differences could also be related to limited pipe length, which might prevent the achievement of a fully developed state in spatially developing flows. Indeed, as shown in the Appendix, see figure 11), the time interval needed to achieve a fully developed state is proportional to
$570$ for those authors). Orlandi & Fatica (Reference Orlandi and Fatica1997) attributed discrepancies to the influence of the entrance conditions, and possible difficulties in achieving a constant pressure gradient in the experimental set-up. We note that differences could also be related to limited pipe length, which might prevent the achievement of a fully developed state in spatially developing flows. Indeed, as shown in the Appendix, see figure 11), the time interval needed to achieve a fully developed state is proportional to ![]() $N$, for given
$N$, for given ![]() $Re_b$. The drag reduction coefficient
$Re_b$. The drag reduction coefficient ![]() $DR$ is here defined as
$DR$ is here defined as
where ![]() $\lambda = 4 C_{f}$ is the friction factor and again the subscript
$\lambda = 4 C_{f}$ is the friction factor and again the subscript ![]() $0$ indicates non-rotating cases. The average power expenditure to sustain wall rotation is
$0$ indicates non-rotating cases. The average power expenditure to sustain wall rotation is
where ![]() $\tau _{r\theta }$ is the tangential viscous shear stress and
$\tau _{r\theta }$ is the tangential viscous shear stress and ![]() $V_{\theta } = U_{\theta } + \varOmega r$ is the mean azimuthal velocity in the inertial frame of reference. As formally shown below, the mean momentum balance under the assumption of statistically steady flow implies that
$V_{\theta } = U_{\theta } + \varOmega r$ is the mean azimuthal velocity in the inertial frame of reference. As formally shown below, the mean momentum balance under the assumption of statistically steady flow implies that ![]() $\mathrm {d} (V_\theta /r)/ \mathrm {d} r$ is zero at the wall, i.e. there is no mean azimuthal friction. Hence, whereas energy must be spent to maintain the mass flow rate and to rotate the pipe during the initial transient, no energy must be spent to sustain wall rotation once statistically steady conditions are achieved, let alone mechanical losses in the actuation system. As a consequence, the drag reduction coefficient (3.1) is identical to the net power saving, which establishes an important difference and advantage from other types of wall manipulation requiring additional actuation energy (e.g. Ricco, Skote & Leschziner Reference Ricco, Skote and Leschziner2021).
$\mathrm {d} (V_\theta /r)/ \mathrm {d} r$ is zero at the wall, i.e. there is no mean azimuthal friction. Hence, whereas energy must be spent to maintain the mass flow rate and to rotate the pipe during the initial transient, no energy must be spent to sustain wall rotation once statistically steady conditions are achieved, let alone mechanical losses in the actuation system. As a consequence, the drag reduction coefficient (3.1) is identical to the net power saving, which establishes an important difference and advantage from other types of wall manipulation requiring additional actuation energy (e.g. Ricco, Skote & Leschziner Reference Ricco, Skote and Leschziner2021).

Figure 1. Global flow properties: (a) friction factor as a function of ![]() $N$; (b) friction factor as a function of
$N$; (b) friction factor as a function of ![]() $Re_b$; (c) drag reduction coefficient as a function of
$Re_b$; (c) drag reduction coefficient as a function of ![]() $N$; (d) drag reduction coefficient as a function of
$N$; (d) drag reduction coefficient as a function of ![]() $N^+$. In panels (a,c,d), we show data for
$N^+$. In panels (a,c,d), we show data for ![]() $Re_{\tau,0}= 180$ (black),
$Re_{\tau,0}= 180$ (black), ![]() $495$ (red),
$495$ (red), ![]() $1137$ (green),
$1137$ (green), ![]() $1979$ (blue) and
$1979$ (blue) and ![]() $3020$ (pink); in panel (b), we show
$3020$ (pink); in panel (b), we show ![]() $N=0$ (black),
$N=0$ (black), ![]() $0.25$ (red),
$0.25$ (red), ![]() $0.5$ (green),
$0.5$ (green), ![]() $1.0$ (cyan),
$1.0$ (cyan), ![]() $2.0$ (blue) and
$2.0$ (blue) and ![]() $4.0$ (pink). In panel (b), the brown dashed line denotes Prandtl's friction law (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021) and the orange dashed line denotes the laminar friction law
$4.0$ (pink). In panel (b), the brown dashed line denotes Prandtl's friction law (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021) and the orange dashed line denotes the laminar friction law ![]() $\lambda = 64/Re_b$. In panels (c,d), the horizontal dashed lines denote the laminar limits of drag reduction for various Reynolds numbers. The triangle symbols denote DNS data at
$\lambda = 64/Re_b$. In panels (c,d), the horizontal dashed lines denote the laminar limits of drag reduction for various Reynolds numbers. The triangle symbols denote DNS data at ![]() $Re_{\tau,0} \approx 180$ and
$Re_{\tau,0} \approx 180$ and ![]() $540$ (Davis et al. Reference Davis, Ganju, Ashton, Bailey and Brehm2019), and the circles denote experiments at
$540$ (Davis et al. Reference Davis, Ganju, Ashton, Bailey and Brehm2019), and the circles denote experiments at ![]() $Re_{\tau,0} \approx 240$ and
$Re_{\tau,0} \approx 240$ and ![]() $570$ (Kikuyama et al. Reference Kikuyama, Murakami, Nishibori and Maeda1983).
$570$ (Kikuyama et al. Reference Kikuyama, Murakami, Nishibori and Maeda1983).
Figure 1(c) shows the variation of the drag reduction coefficient with the rotation number at constant values of ![]() $Re_b$ (or
$Re_b$ (or ![]() $Re_{\tau,0}$). Pipe rotation consistently leads to drag reduction, and monotonic increase with both
$Re_{\tau,0}$). Pipe rotation consistently leads to drag reduction, and monotonic increase with both ![]() $N$ and
$N$ and ![]() $Re_{\tau,0}$ is observed, in agreement with previous studies (Davis et al. Reference Davis, Ganju, Ashton, Bailey and Brehm2019). At
$Re_{\tau,0}$ is observed, in agreement with previous studies (Davis et al. Reference Davis, Ganju, Ashton, Bailey and Brehm2019). At ![]() $N=4.0$ and
$N=4.0$ and ![]() $Re_{\tau,0} = 3020$, drag reduction is as high as 69 %, which clearly highlights the potential of rotation for curtailing energy consumption in high-
$Re_{\tau,0} = 3020$, drag reduction is as high as 69 %, which clearly highlights the potential of rotation for curtailing energy consumption in high-![]() $Re$ internal flows, such as fluid transportation in large-diameter pipelines, whose typical Reynolds number is
$Re$ internal flows, such as fluid transportation in large-diameter pipelines, whose typical Reynolds number is ![]() $Re_{\tau,0} = 10^5\unicode{x2013}10^6$ (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012). This is another important difference from other passive and active drag reduction strategies, for which the drag reduction effect typically decreases with the Reynolds number (Gatti & Quadrio Reference Gatti and Quadrio2016; Ricco et al. Reference Ricco, Skote and Leschziner2021). We note that full relaminarisation would result in a drag reduction of approximately
$Re_{\tau,0} = 10^5\unicode{x2013}10^6$ (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2012). This is another important difference from other passive and active drag reduction strategies, for which the drag reduction effect typically decreases with the Reynolds number (Gatti & Quadrio Reference Gatti and Quadrio2016; Ricco et al. Reference Ricco, Skote and Leschziner2021). We note that full relaminarisation would result in a drag reduction of approximately ![]() $97\,\%$ at
$97\,\%$ at ![]() $Re_{\tau,0} = 3020$, so at even
$Re_{\tau,0} = 3020$, so at even ![]() $N=4.0$, the flow remains distant from the laminar state. Figure 1(d) displays the drag reduction coefficient as a function of the inner-scaled wall rotational speed based on the non-rotating friction velocity,
$N=4.0$, the flow remains distant from the laminar state. Figure 1(d) displays the drag reduction coefficient as a function of the inner-scaled wall rotational speed based on the non-rotating friction velocity, ![]() $N^+ = \varOmega R /u_{\tau,0}$, which again confirms increased drag reduction with both
$N^+ = \varOmega R /u_{\tau,0}$, which again confirms increased drag reduction with both ![]() $N^+$ and
$N^+$ and ![]() $Re_{\tau,0}$. Notably, the drag reduction profiles tend to be much more universal when expressed as a function of
$Re_{\tau,0}$. Notably, the drag reduction profiles tend to be much more universal when expressed as a function of ![]() $N^+$, with deviations from a common trend occurring at increasingly higher
$N^+$, with deviations from a common trend occurring at increasingly higher ![]() $N^+$ as
$N^+$ as ![]() $Re_{\tau,0}$ increases. This suggests that the proper parameter to quantify drag reduction effects could be the ratio of the pipe peripheral velocity to the friction velocity, which is the typical scale for wall turbulence, in line with what is found in drag reduction studies based on the use of oscillating walls and travelling waves (Quadrio et al. Reference Quadrio, Ricco and Viotti2009; Touber & Leschziner Reference Touber and Leschziner2012).
$Re_{\tau,0}$ increases. This suggests that the proper parameter to quantify drag reduction effects could be the ratio of the pipe peripheral velocity to the friction velocity, which is the typical scale for wall turbulence, in line with what is found in drag reduction studies based on the use of oscillating walls and travelling waves (Quadrio et al. Reference Quadrio, Ricco and Viotti2009; Touber & Leschziner Reference Touber and Leschziner2012).
To analyse the flow modifications yielding drag reduction in greater detail, in figure 2(a), we display the inner-scaled mean axial velocity profiles at various rotation and Reynolds numbers. At zero and small rotation numbers, the mean axial velocity follows with good accuracy the logarithmic distribution observed in pipe flow (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021),
with ![]() $\kappa = 0.387$ and
$\kappa = 0.387$ and ![]() $B = 4.53$. Deviations from such universal behaviour occur increasingly farther from the wall as the Reynolds number increases. However, deviations tend to occur earlier as
$B = 4.53$. Deviations from such universal behaviour occur increasingly farther from the wall as the Reynolds number increases. However, deviations tend to occur earlier as ![]() $N$ increases, and at the same time, the wake is found to grow stronger. At
$N$ increases, and at the same time, the wake is found to grow stronger. At ![]() $N \gtrsim 1$, the whole logarithmic layer is eventually disrupted, consistent with the findings of Orlandi & Fatica (Reference Orlandi and Fatica1997) and Davis et al. (Reference Davis, Ganju, Ashton, Bailey and Brehm2019). This process is clearer when the logarithmic diagnostic function, namely
$N \gtrsim 1$, the whole logarithmic layer is eventually disrupted, consistent with the findings of Orlandi & Fatica (Reference Orlandi and Fatica1997) and Davis et al. (Reference Davis, Ganju, Ashton, Bailey and Brehm2019). This process is clearer when the logarithmic diagnostic function, namely ![]() $y^* \mathrm {d}U_z^*/\mathrm {d} y^*$, is considered, as shown in figure 2(b). Indeed, no plateau of this indicator is found at
$y^* \mathrm {d}U_z^*/\mathrm {d} y^*$, is considered, as shown in figure 2(b). Indeed, no plateau of this indicator is found at ![]() $N \gtrsim 1$, although one can speculate that a logarithmic behaviour is recovered at higher Reynolds numbers than we consider here.
$N \gtrsim 1$, although one can speculate that a logarithmic behaviour is recovered at higher Reynolds numbers than we consider here.

Figure 2. (a) Inner-scaled mean axial velocity profiles and (b) corresponding logarithmic diagnostic functions. The colour codes correspond to the same values of the rotation number: ![]() $N=0$ (black);
$N=0$ (black); ![]() $N=0.25$ (red);
$N=0.25$ (red); ![]() $N=0.5$ (green);
$N=0.5$ (green); ![]() $N=1$ (cyan);
$N=1$ (cyan); ![]() $N=2$ (blue) and
$N=2$ (blue) and ![]() $N=4$ (pink). The line patterns correspond to the same values of the nominal Reynolds number:
$N=4$ (pink). The line patterns correspond to the same values of the nominal Reynolds number: ![]() $Re_{\tau,0}=495$ (dash-dotted);
$Re_{\tau,0}=495$ (dash-dotted); ![]() $Re_{\tau,0}=1137$ (dotted);
$Re_{\tau,0}=1137$ (dotted); ![]() $Re_{\tau,0}=1979$ (dashed) and
$Re_{\tau,0}=1979$ (dashed) and ![]() $Re_{\tau,0}=3020$ (solid). The dashed black lines in panel (a) denote the expected logarithmic distribution given in (3.3), and in panel (b), the inverse of the Kármán constant (
$Re_{\tau,0}=3020$ (solid). The dashed black lines in panel (a) denote the expected logarithmic distribution given in (3.3), and in panel (b), the inverse of the Kármán constant (![]() $1/\kappa$).
$1/\kappa$).
The mean axial velocity profiles are then shown in defect form in figure 3. As known from previous studies (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021), normalisation by the friction velocity shown in panel (a) yields excellent universality of the profiles in the absence of rotation (![]() $N=0$). However, when rotation is introduced, a large scatter is observed when either the rotation number or the Reynolds number varies. Indeed, as noticed by Oberlack (Reference Oberlack1999), the pipe rotational speed is an independent velocity scale and it is a better candidate to achieve universality of the mean axial velocity profiles in the presence of pipe rotation. Hence, in panel (b), we show the velocity profiles normalised by the peripheral rotational speed. Excellent universality of the axial velocity profiles is then observed for any given (non-zero) rotation number; however, with obvious dependence on
$N=0$). However, when rotation is introduced, a large scatter is observed when either the rotation number or the Reynolds number varies. Indeed, as noticed by Oberlack (Reference Oberlack1999), the pipe rotational speed is an independent velocity scale and it is a better candidate to achieve universality of the mean axial velocity profiles in the presence of pipe rotation. Hence, in panel (b), we show the velocity profiles normalised by the peripheral rotational speed. Excellent universality of the axial velocity profiles is then observed for any given (non-zero) rotation number; however, with obvious dependence on ![]() $N$. Of course, this kind of normalisation cannot apply to the non-rotating case as
$N$. Of course, this kind of normalisation cannot apply to the non-rotating case as ![]() $\varOmega =0$. Based on these empirical observations, we then assume the following form for the defect velocity profiles,
$\varOmega =0$. Based on these empirical observations, we then assume the following form for the defect velocity profiles,
where fitting of the DNS data in the range ![]() $0 \leq r/R \leq 0.9$ yields
$0 \leq r/R \leq 0.9$ yields
It should be noted that previous experiments (Kikuyama et al. Reference Kikuyama, Murakami, Nishibori and Maeda1983) and DNS (Orlandi & Fatica Reference Orlandi and Fatica1997) also suggested values of the power-law exponent ![]() $\alpha \approx 2$; however, based on a much more limited set of data.
$\alpha \approx 2$; however, based on a much more limited set of data.

Figure 3. Mean axial velocity defect profiles (![]() $U_{CL}$ is the pipe centreline velocity), normalised (a) by the friction velocity,
$U_{CL}$ is the pipe centreline velocity), normalised (a) by the friction velocity, ![]() $u_{\tau }$, and (b) by the pipe rotational velocity,
$u_{\tau }$, and (b) by the pipe rotational velocity, ![]() $\varOmega R$. The colour codes correspond to the same values of rotation number:
$\varOmega R$. The colour codes correspond to the same values of rotation number: ![]() $N=0$ (black);
$N=0$ (black); ![]() $N=0.25$ (red);
$N=0.25$ (red); ![]() $N=0.5$ (green);
$N=0.5$ (green); ![]() $N=1$ (cyan);
$N=1$ (cyan); ![]() $N=2$ (green) and
$N=2$ (green) and ![]() $N=4$ (pink). The line patterns correspond to the same values of the nominal Reynolds number:
$N=4$ (pink). The line patterns correspond to the same values of the nominal Reynolds number: ![]() $Re_{\tau,0}=495$ (dash-dotted);
$Re_{\tau,0}=495$ (dash-dotted); ![]() $Re_{\tau,0}=1137$ (dotted);
$Re_{\tau,0}=1137$ (dotted); ![]() $Re_{\tau,0}=1979$ (dashed) and
$Re_{\tau,0}=1979$ (dashed) and ![]() $Re_{\tau,0}=3020$ (solid). The solid black lines in panel (b) indicate the power-law fitting function (3.4), with coefficients given in (3.5a,b).
$Re_{\tau,0}=3020$ (solid). The solid black lines in panel (b) indicate the power-law fitting function (3.4), with coefficients given in (3.5a,b).
The previous observations can be leveraged to obtain predictions for the friction coefficient. Indeed, integration of the defect profile (3.4) yields the following relationship between the centreline and bulk velocity:
Matching the wall-normal gradients of the inner profile (3.3) with the defect profile (3.4) yields the condition
where ![]() $\eta =y/R$. This condition can be numerically solved to determine the outer-scaled matching location
$\eta =y/R$. This condition can be numerically solved to determine the outer-scaled matching location ![]() $\eta _0$. Under the assumption
$\eta _0$. Under the assumption ![]() $\eta _0 \ll 1$, the approximate solution holds
$\eta _0 \ll 1$, the approximate solution holds
Finally, matching the pointwise values of (3.3) and (3.4) at ![]() $\eta = \eta _0$ yields
$\eta = \eta _0$ yields
Equation (3.9) can be numerically solved to obtain ![]() $u_b^*$ for a given
$u_b^*$ for a given ![]() $Re_b$ (as
$Re_b$ (as ![]() $Re_{\tau } = Re_b / (2 u_b^*)$) and
$Re_{\tau } = Re_b / (2 u_b^*)$) and ![]() $N$, and in turn obtain the friction factor,
$N$, and in turn obtain the friction factor, ![]() $f = 8 / {u_b^*}^2$.
$f = 8 / {u_b^*}^2$.
The charts of ![]() $u_b^*$ and
$u_b^*$ and ![]() $f$ as a function of the Reynolds number are shown in figure 4, where symbols denote the DNS data and lines represent the corresponding predictions of (3.9). The latter formula indeed captures the correct Reynolds number trends including the progressive departure of the friction curves from the non-rotating case, and it yields good quantitative predictions at low-to-moderate rotation numbers. However, the drag reduction effect becomes noticeably underestimated at
$f$ as a function of the Reynolds number are shown in figure 4, where symbols denote the DNS data and lines represent the corresponding predictions of (3.9). The latter formula indeed captures the correct Reynolds number trends including the progressive departure of the friction curves from the non-rotating case, and it yields good quantitative predictions at low-to-moderate rotation numbers. However, the drag reduction effect becomes noticeably underestimated at ![]() $N \gtrsim 1$, the reason being the previously noted breakdown of the logarithmic profile (3.3) at high rotation numbers, which we used for theoretical inference.
$N \gtrsim 1$, the reason being the previously noted breakdown of the logarithmic profile (3.3) at high rotation numbers, which we used for theoretical inference.

Figure 4. (a,b) Inner-scaled bulk velocity and (c,d) friction factor, as a function of the (a,c) friction Reynolds number and (b,d) bulk Reynolds number. The colour codes correspond to the same values of rotation number: ![]() $N=0$ (black);
$N=0$ (black); ![]() $N=0.25$ (red);
$N=0.25$ (red); ![]() $N=0.5$ (green);
$N=0.5$ (green); ![]() $N=1$ (cyan);
$N=1$ (cyan); ![]() $N=2$ (blue) and
$N=2$ (blue) and ![]() $N=4$ (pink). Symbols denote the DNS data, and lines the corresponding predictions of (3.9). The solid black line denotes the predictions of Prandtl's friction law for a non-rotating pipe (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021).
$N=4$ (pink). Symbols denote the DNS data, and lines the corresponding predictions of (3.9). The solid black line denotes the predictions of Prandtl's friction law for a non-rotating pipe (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021).
In figure 5, we further present the distributions of the absolute mean velocity in the azimuthal direction. Before analysing its scaling laws, it is informative to consider the momentum balance equation projected along the ![]() $\theta$ direction,
$\theta$ direction,
Multiplying (3.10) by ![]() $r^2$ and then integrating from
$r^2$ and then integrating from ![]() $0$ to
$0$ to ![]() $r$ yields
$r$ yields
which highlights the balance between the viscous and the turbulent shear stress. At the wall, ![]() $\langle u_r u_\theta \rangle = 0$, resulting in
$\langle u_r u_\theta \rangle = 0$, resulting in ![]() $V_\theta \overset {r\to R}{\operatorname *{\sim }}\varOmega r$. As one moves away from the wall, the presence of a nonlinear distribution of
$V_\theta \overset {r\to R}{\operatorname *{\sim }}\varOmega r$. As one moves away from the wall, the presence of a nonlinear distribution of ![]() $V_\theta$ becomes evident, due to positive values of
$V_\theta$ becomes evident, due to positive values of ![]() $\langle {{u}_{r}}{{u}_{\theta }} \rangle$. Oberlack (Reference Oberlack1999) suggested that for
$\langle {{u}_{r}}{{u}_{\theta }} \rangle$. Oberlack (Reference Oberlack1999) suggested that for ![]() $r/R \gtrsim 0.2$, the mean azimuthal velocity should follow a power-law variation, namely
$r/R \gtrsim 0.2$, the mean azimuthal velocity should follow a power-law variation, namely
with ![]() $\psi = 2.0$, as inferred from the set of data available at that time, which according to (3.11) would result in linear variation of the turbulent shear stress
$\psi = 2.0$, as inferred from the set of data available at that time, which according to (3.11) would result in linear variation of the turbulent shear stress ![]() $\langle {{u}_{r}}{{u}_{\theta }} \rangle$, with slope proportional to
$\langle {{u}_{r}}{{u}_{\theta }} \rangle$, with slope proportional to ![]() $N$. However, Orlandi & Fatica (Reference Orlandi and Fatica1997) reported that the slope of
$N$. However, Orlandi & Fatica (Reference Orlandi and Fatica1997) reported that the slope of ![]() $\langle u_r u_\theta \rangle$ is not strictly proportional to
$\langle u_r u_\theta \rangle$ is not strictly proportional to ![]() $N$, even in the core region, thereby preventing perfect collapse of the profiles in figure 5. In our simulations,
$N$, even in the core region, thereby preventing perfect collapse of the profiles in figure 5. In our simulations, ![]() $V_\theta /\varOmega R$ is found to gradually increase with
$V_\theta /\varOmega R$ is found to gradually increase with ![]() $N$, exhibiting a similar trend as other DNS (Orlandi & Fatica Reference Orlandi and Fatica1997; Feiz, Ould-Rouis & Lauriat Reference Feiz, Ould-Rouis and Lauriat2005; Davis et al. Reference Davis, Ganju, Ashton, Bailey and Brehm2019) and experimental studies (Kikuyama et al. Reference Kikuyama, Murakami, Nishibori and Maeda1983). We have checked the influence of pipe length on the azimuthal velocity profile and confirmed that using
$N$, exhibiting a similar trend as other DNS (Orlandi & Fatica Reference Orlandi and Fatica1997; Feiz, Ould-Rouis & Lauriat Reference Feiz, Ould-Rouis and Lauriat2005; Davis et al. Reference Davis, Ganju, Ashton, Bailey and Brehm2019) and experimental studies (Kikuyama et al. Reference Kikuyama, Murakami, Nishibori and Maeda1983). We have checked the influence of pipe length on the azimuthal velocity profile and confirmed that using ![]() $L=30R$ yields almost the same results as using
$L=30R$ yields almost the same results as using ![]() $L=15R$ (see figure 10b). It is worth mentioning that the experimental data of Reich & Beer (Reference Reich and Beer1989) for
$L=15R$ (see figure 10b). It is worth mentioning that the experimental data of Reich & Beer (Reference Reich and Beer1989) for ![]() $Re_b=5000$ with
$Re_b=5000$ with ![]() $N=1.0$ and
$N=1.0$ and ![]() $5.0$ are in good agreement with the quadratic law; however, they are likely affected by entrance effects, as pointed out by Orlandi & Fatica (Reference Orlandi and Fatica1997). Instead, our DNS data show that the exponent
$5.0$ are in good agreement with the quadratic law; however, they are likely affected by entrance effects, as pointed out by Orlandi & Fatica (Reference Orlandi and Fatica1997). Instead, our DNS data show that the exponent ![]() $\psi$ is clearly dependent on the rotation number, and also has weaker dependence on the bulk Reynolds number, as shown in panel (a). As the rotation number increases, the azimuthal velocity profiles become closer to the case of solid body rotation, corresponding to smaller values of
$\psi$ is clearly dependent on the rotation number, and also has weaker dependence on the bulk Reynolds number, as shown in panel (a). As the rotation number increases, the azimuthal velocity profiles become closer to the case of solid body rotation, corresponding to smaller values of ![]() $\psi$. This tendency is regarded to be reasonable, considering that as the rotation number increases, turbulent motions become increasingly suppressed due to the stronger centrifugal instability. The weak influence of the nominal bulk Reynolds number includes slightly higher values of
$\psi$. This tendency is regarded to be reasonable, considering that as the rotation number increases, turbulent motions become increasingly suppressed due to the stronger centrifugal instability. The weak influence of the nominal bulk Reynolds number includes slightly higher values of ![]() $\psi$ as
$\psi$ as ![]() $Re_b$ increases. This tendency is partly explained in terms of diminished viscous effects near the wall, which shortens the layer with approximately linear variation. Fitting the DNS data in the range
$Re_b$ increases. This tendency is partly explained in terms of diminished viscous effects near the wall, which shortens the layer with approximately linear variation. Fitting the DNS data in the range ![]() $0.2 \leq r/R \leq 0.9$, we get
$0.2 \leq r/R \leq 0.9$, we get
which is quite accurate as shown in figure 5. At ![]() $N \approx 1$, the formula yields
$N \approx 1$, the formula yields ![]() $\psi \approx 2.0$, corresponding to a quadratic power law. We would like to note that for
$\psi \approx 2.0$, corresponding to a quadratic power law. We would like to note that for ![]() $r/R \lesssim 0.2$, the azimuthal velocity profiles observed in the DNS exhibit deviations from the quadratic law and become closer to a linear distribution (see panel (b)) and thus indicate that the flow near the pipe axis is close to a solid-body rotation state.
$r/R \lesssim 0.2$, the azimuthal velocity profiles observed in the DNS exhibit deviations from the quadratic law and become closer to a linear distribution (see panel (b)) and thus indicate that the flow near the pipe axis is close to a solid-body rotation state.

Figure 5. Radial profiles of mean azimuthal velocity in (a) linear and (b) logarithmic scale. The colour codes correspond to the same values of rotation number: ![]() $N=0.25$ (red);
$N=0.25$ (red); ![]() $1.0$ (cyan);
$1.0$ (cyan); ![]() $2.0$ (blue) and
$2.0$ (blue) and ![]() $4.0$ (pink). The line patterns correspond to the same values of the nominal Reynolds number:
$4.0$ (pink). The line patterns correspond to the same values of the nominal Reynolds number: ![]() $Re_{\tau,0}=495$ (dash-dotted);
$Re_{\tau,0}=495$ (dash-dotted); ![]() $Re_{\tau,0}=1137$ (dotted);
$Re_{\tau,0}=1137$ (dotted); ![]() $Re_{\tau,0}=1979$ (dashed) and
$Re_{\tau,0}=1979$ (dashed) and ![]() $Re_{\tau,0}=3020$ (solid). The solid black lines denote (3.12), with the coefficient given in (3.13). The black dashed lines correspond to the case of solid body rotation.
$Re_{\tau,0}=3020$ (solid). The solid black lines denote (3.12), with the coefficient given in (3.13). The black dashed lines correspond to the case of solid body rotation.
3.2. Organisation of turbulence
A perspective view of the instantaneous axial velocity field is provided in figure 6 for two selected Reynolds numbers, including for reference the case of pipe flow in the absence of rotation (Pirozzoli et al. Reference Pirozzoli, Romero, Fatica, Verzicco and Orlandi2021). As the Reynolds number increases, finer scales are observed, but the flow in the cross-stream plane is always dominated by a limited number of bulges distributed along the azimuthal direction, which correspond to alternating intrusions of high-speed fluid from the pipe core and ejections of low-speed fluid from the wall. Streaks are clear in the near-wall cylindrical shell, whose pattern has a close association with the turbulence organisation in the cross-stream plane. The ![]() $R$-sized low-speed streaks are linked to the large-scale ejections, and
$R$-sized low-speed streaks are linked to the large-scale ejections, and ![]() $R$-sized high-speed streaks are associated with the large-scale inrush from the core flow. Simultaneously, smaller streaks scaled in wall units prevail very close to the wall, which is correlated with buffer-layer ejections and sweeps. Hence, the organisation of the flow at two characteristic length scales is apparent, whose separation increases with the Reynolds number.
$R$-sized high-speed streaks are associated with the large-scale inrush from the core flow. Simultaneously, smaller streaks scaled in wall units prevail very close to the wall, which is correlated with buffer-layer ejections and sweeps. Hence, the organisation of the flow at two characteristic length scales is apparent, whose separation increases with the Reynolds number.

Figure 6. Instantaneous fields of axial velocity on a near-wall cylindrical shell and cross-stream plane. The cylindrical shell is located at a wall distance ![]() $y^+ \approx 15$. The colour scale is from blue (low speed) to red (high speed). Rotation numbers
$y^+ \approx 15$. The colour scale is from blue (low speed) to red (high speed). Rotation numbers ![]() $N = 0, 0.5$ and
$N = 0, 0.5$ and ![]() $2.0$ are reported in panels (a,d), (b,e) and (c,f), respectively, for (a–c)
$2.0$ are reported in panels (a,d), (b,e) and (c,f), respectively, for (a–c) ![]() $Re_{\tau,0} = 495$ and (d–f)
$Re_{\tau,0} = 495$ and (d–f) ![]() $Re_{\tau,0} = 3020$. The arrows indicate the direction of rotation.
$Re_{\tau,0} = 3020$. The arrows indicate the direction of rotation.
When rotation is introduced, a distinctive axial coherence becomes apparent in the core region (White Reference White1963), reminiscent of the columnar structures observed in rotating homogeneous turbulence (Godeferd & Moisy Reference Godeferd and Moisy2015; Hu, Li & Yu Reference Hu, Li and Yu2022). Meanwhile, the ![]() $R$-sized structures in the cross-stream plane undergo deformation due to the decreasing angular velocity towards the core. The bulges gradually tend to lag behind the azimuthal motion of the wall as one moves away from it. For the low-
$R$-sized structures in the cross-stream plane undergo deformation due to the decreasing angular velocity towards the core. The bulges gradually tend to lag behind the azimuthal motion of the wall as one moves away from it. For the low-![]() $Re$ case, the turbulent fluctuations are intensified in the core region for
$Re$ case, the turbulent fluctuations are intensified in the core region for ![]() $N \gtrsim 1.0$, as highlighted by increased turbulence kinetic energy,
$N \gtrsim 1.0$, as highlighted by increased turbulence kinetic energy, ![]() $q = \langle u_r^2 + u_\theta ^2 + u_z^2 \rangle / 2$, in figure 7(a). Orlandi & Fatica (Reference Orlandi and Fatica1997) conjectured that such increase is due to a low-
$q = \langle u_r^2 + u_\theta ^2 + u_z^2 \rangle / 2$, in figure 7(a). Orlandi & Fatica (Reference Orlandi and Fatica1997) conjectured that such increase is due to a low-![]() $Re$ effect, whereby the fluctuations in the central part of the pipe are amplified by the near-wall enlarged vortical structures. This conjecture is corroborated herein as the phenomenon is much less evident in the high-
$Re$ effect, whereby the fluctuations in the central part of the pipe are amplified by the near-wall enlarged vortical structures. This conjecture is corroborated herein as the phenomenon is much less evident in the high-![]() $Re$ case, as substantiated by decreased turbulence kinetic energy shown in figure 7(b). It is nevertheless important to highlight that at sufficiently low rotation numbers, the fluctuations in the core region become consistently suppressed regardless of the Reynolds number. Turning to the near-wall region, a noticeable reduction in both the number and magnitude of the small-scale streaks is evident at both Reynolds numbers, which points to attenuation of sweeps and ejections in the buffer layer. This causes a distinct decrease in the axial velocity fluctuations compared with the other two components (see figure 7c), which is not unexpected as the production of
$Re$ case, as substantiated by decreased turbulence kinetic energy shown in figure 7(b). It is nevertheless important to highlight that at sufficiently low rotation numbers, the fluctuations in the core region become consistently suppressed regardless of the Reynolds number. Turning to the near-wall region, a noticeable reduction in both the number and magnitude of the small-scale streaks is evident at both Reynolds numbers, which points to attenuation of sweeps and ejections in the buffer layer. This causes a distinct decrease in the axial velocity fluctuations compared with the other two components (see figure 7c), which is not unexpected as the production of ![]() $q$ is associated with the axial velocity component. Moreover, the Taylor–Proudman theorem (Greenspan Reference Greenspan1968) implies that the vorticity component normal to the axis of rotation should be suppressed to reduce the axial velocity gradients. Noteworthy is the lack of discernible azimuthal tilting of the small-scale streaks. However, tilting of the footprints of the large-scale structures towards the direction of rotation is evident on the cylindrical shell in the low-
$q$ is associated with the axial velocity component. Moreover, the Taylor–Proudman theorem (Greenspan Reference Greenspan1968) implies that the vorticity component normal to the axis of rotation should be suppressed to reduce the axial velocity gradients. Noteworthy is the lack of discernible azimuthal tilting of the small-scale streaks. However, tilting of the footprints of the large-scale structures towards the direction of rotation is evident on the cylindrical shell in the low-![]() $Re$ case.
$Re$ case.

Figure 7. Distributions of: (a) turbulence kinetic energy for ![]() $Re_{\tau,0}=495$; (b) turbulence kinetic energy for
$Re_{\tau,0}=495$; (b) turbulence kinetic energy for ![]() $Re_{\tau,0}=3020$; (c) individual velocity variances for
$Re_{\tau,0}=3020$; (c) individual velocity variances for ![]() $Re_{\tau,0}=3020$. In panel (c), lines correspond to:
$Re_{\tau,0}=3020$. In panel (c), lines correspond to: ![]() $\langle u_\theta ^2 \rangle$ (solid);
$\langle u_\theta ^2 \rangle$ (solid); ![]() $\langle u_r^2 \rangle$ (dashed) and
$\langle u_r^2 \rangle$ (dashed) and ![]() $\langle u_z^2\rangle$ (dash-dot). Colour codes:
$\langle u_z^2\rangle$ (dash-dot). Colour codes: ![]() $N = 0$ (black);
$N = 0$ (black); ![]() $0.25$ (red);
$0.25$ (red); ![]() $0.5$ (green);
$0.5$ (green); ![]() $1.0$ (cyan) and
$1.0$ (cyan) and ![]() $2.0$ (blue).
$2.0$ (blue).
The modifications in the characteristic length scales can be quantified in terms of the pre-multiplied azimuthal energy spectra of the axial velocity, which we report in figure 8. In the non-rotating cases, the spectra exhibit a prominent ridge along ![]() $\lambda _\theta \sim y$, which should be interpreted as a hierarchy of wall-attached eddies as suggested by Townsend (Reference Townsend1976). Here,
$\lambda _\theta \sim y$, which should be interpreted as a hierarchy of wall-attached eddies as suggested by Townsend (Reference Townsend1976). Here, ![]() $\lambda _\theta$ is the wavelength in the azimuthal direction. The inner peak, associated with the near-wall turbulence regeneration cycle (Jiménez & Pinelli Reference Jiménez and Pinelli1999), and the outer site, linked with
$\lambda _\theta$ is the wavelength in the azimuthal direction. The inner peak, associated with the near-wall turbulence regeneration cycle (Jiménez & Pinelli Reference Jiménez and Pinelli1999), and the outer site, linked with ![]() $R$-sized large-scale motions (Hutchins & Marusic Reference Hutchins and Marusic2007), exhibit a more pronounced separation in the high-
$R$-sized large-scale motions (Hutchins & Marusic Reference Hutchins and Marusic2007), exhibit a more pronounced separation in the high-![]() $Re$ case. Upon imposition of rotation, the most remarkable modification is the progressive attenuation of the amplitude of the inner spectra. Concurrently, an outer-layer peak of
$Re$ case. Upon imposition of rotation, the most remarkable modification is the progressive attenuation of the amplitude of the inner spectra. Concurrently, an outer-layer peak of ![]() $\lambda _\theta /R=1.08$ emerges at
$\lambda _\theta /R=1.08$ emerges at ![]() $y/R=0.22$ for
$y/R=0.22$ for ![]() $N=2.0$ in the low-
$N=2.0$ in the low-![]() $Re$ case, which we believe to be linked to the
$Re$ case, which we believe to be linked to the ![]() $R$-sized distorted structures observed in figure 6(c). In contrast, the outer-layer peak of
$R$-sized distorted structures observed in figure 6(c). In contrast, the outer-layer peak of ![]() $\lambda _\theta /R=1.26$ at
$\lambda _\theta /R=1.26$ at ![]() $y/R=0.19$ in the high-
$y/R=0.19$ in the high-![]() $Re$, non-rotating case vanishes, and a subdominant peak is found instead at
$Re$, non-rotating case vanishes, and a subdominant peak is found instead at ![]() $\lambda _\theta /R={\rm \pi}$, at a wall distance
$\lambda _\theta /R={\rm \pi}$, at a wall distance ![]() $y^+ \lesssim 200$. At both Reynolds numbers, the inner peak undergoes a top-right shift, from approximately
$y^+ \lesssim 200$. At both Reynolds numbers, the inner peak undergoes a top-right shift, from approximately ![]() $y^+=13$ to
$y^+=13$ to ![]() $19$, with a concurrent increase in the typical streaks spacing from approximately
$19$, with a concurrent increase in the typical streaks spacing from approximately ![]() $\lambda _{\theta }^+=120$ to approximately
$\lambda _{\theta }^+=120$ to approximately ![]() $200$. Consequently, the spectral ridge becomes steeper, taking the form of a power law, with the exponent changing with
$200$. Consequently, the spectral ridge becomes steeper, taking the form of a power law, with the exponent changing with ![]() $Re$ and
$Re$ and ![]() $N$.
$N$.

Figure 8. Pre-multiplied azimuthal energy spectra of axial velocity ![]() $( \kappa _\theta E_{uu})^+$ for (a,d)
$( \kappa _\theta E_{uu})^+$ for (a,d) ![]() $N=0$, (b,e)
$N=0$, (b,e) ![]() $N=0.5$, (c,f)
$N=0.5$, (c,f) ![]() $N=2.0$, at (a–c)
$N=2.0$, at (a–c) ![]() $Re_{\tau,0} = 495$, (d–f)
$Re_{\tau,0} = 495$, (d–f) ![]() $Re_{\tau,0} = 3020$. The solid lines denote the trend
$Re_{\tau,0} = 3020$. The solid lines denote the trend ![]() $y = 0.14 \lambda _\theta$, and the dashed lines denote the trend
$y = 0.14 \lambda _\theta$, and the dashed lines denote the trend ![]() $\lambda _\theta /R = 2.35(y/R)^{0.52}$ in panel (c), and
$\lambda _\theta /R = 2.35(y/R)^{0.52}$ in panel (c), and ![]() $\lambda _\theta /R = 2.20(y/R)^{0.72}$ in panel (f). The crosses denote spectral peaks.
$\lambda _\theta /R = 2.20(y/R)^{0.72}$ in panel (f). The crosses denote spectral peaks.
3.3. Contributions to frictional drag
The Fukagata–Iwamoto–Kasagi (FIK) identity (Fukagata, Iwamoto & Kasagi Reference Fukagata, Iwamoto and Kasagi2002) is herein used to isolate the contributions of molecular viscosity and turbulence to the overall wall friction and to elucidate mechanisms contributing to the observed drag reduction. It can be shown that the form of the FIK identity for a rotating pipe is identical to the case of a non-rotating pipe as reported by Fukagata et al. (Reference Fukagata, Iwamoto and Kasagi2002), because its derivation originates from the momentum equation in the ![]() $z$ direction, which does not depend on the imposition of axial rotation. This results in the following expression for the relative drag reduction:
$z$ direction, which does not depend on the imposition of axial rotation. This results in the following expression for the relative drag reduction:
where
denotes the local contribution of turbulence at a given wall distance to the overall friction coefficient. It is noteworthy that the viscous contribution to wall friction (![]() $16/Re_b$) is the same at the various rotation numbers as the DNS were carried out at constant mass flow rate, hence it cancels out from (3.14). We have made sure that the relative errors between friction coefficients obtained from the direct calculation and the FIK identity are well below 1 %.
$16/Re_b$) is the same at the various rotation numbers as the DNS were carried out at constant mass flow rate, hence it cancels out from (3.14). We have made sure that the relative errors between friction coefficients obtained from the direct calculation and the FIK identity are well below 1 %.
Figure 9(a) clearly shows that the reduction of the turbulent shear stress is greater at higher Reynolds numbers. Whereas the maximum shear stress slowly increases asymptotically to unity as ![]() $Re_b$ increases, the peak decreases in the case of a rotating pipe, despite amplification of turbulence kinetic energy in the core region at high rotation numbers in the low-
$Re_b$ increases, the peak decreases in the case of a rotating pipe, despite amplification of turbulence kinetic energy in the core region at high rotation numbers in the low-![]() $Re$ cases (see figure 7a). This can be interpreted better by noticing that the inner-scaled wall rotational speed,
$Re$ cases (see figure 7a). This can be interpreted better by noticing that the inner-scaled wall rotational speed, ![]() $N^*=N/2(Re_b/Re_{\tau })$, increases with
$N^*=N/2(Re_b/Re_{\tau })$, increases with ![]() $Re_b$, with likely increased suppression of the near-wall turbulence. Figure 9(b) reports the wall-normal distribution of the local turbulence contribution to the overall friction. Note that the plot is reported in a semi-log scale and in pre-multiplied form to have a correct perception of the integrated contributions. The figure shows that at low Reynolds numbers, suppression of the turbulent contribution to friction mainly takes place in the core part of the flow, with a reduction of the absolute peak. At higher Reynolds numbers, a strong decrease of the peak value is still present and increasing, but substantial drag reduction is also coming from the near-wall layer. To have a quantification of the effects of the inner and outer layers, we then split the turbulent wall friction into integrated contributions from the inner layer (say,
$Re_b$, with likely increased suppression of the near-wall turbulence. Figure 9(b) reports the wall-normal distribution of the local turbulence contribution to the overall friction. Note that the plot is reported in a semi-log scale and in pre-multiplied form to have a correct perception of the integrated contributions. The figure shows that at low Reynolds numbers, suppression of the turbulent contribution to friction mainly takes place in the core part of the flow, with a reduction of the absolute peak. At higher Reynolds numbers, a strong decrease of the peak value is still present and increasing, but substantial drag reduction is also coming from the near-wall layer. To have a quantification of the effects of the inner and outer layers, we then split the turbulent wall friction into integrated contributions from the inner layer (say, ![]() $C_f^{T,I}$) and from the outer layer (say,
$C_f^{T,I}$) and from the outer layer (say, ![]() $C_f^{T,O}$), based on the position of the peak turbulent shear stress (say,
$C_f^{T,O}$), based on the position of the peak turbulent shear stress (say, ![]() $y_m$), as suggested by Hurst, Yang & Chung (Reference Hurst, Yang and Chung2014). Accordingly, we define
$y_m$), as suggested by Hurst, Yang & Chung (Reference Hurst, Yang and Chung2014). Accordingly, we define
 \begin{equation} \frac{C_{f}^{T,O}}{{{C}_{f,0}}} = \int_{\log y_m^+}^{\log Re_{\tau,0}} \left( \frac yR \right) {c_f^T}(y^+) \, \mathrm{d} \log y^+. \end{equation}
\begin{equation} \frac{C_{f}^{T,O}}{{{C}_{f,0}}} = \int_{\log y_m^+}^{\log Re_{\tau,0}} \left( \frac yR \right) {c_f^T}(y^+) \, \mathrm{d} \log y^+. \end{equation}
In non-rotating pipe flow, the turbulent shear stress attains a peak at ![]() $y_{m}^+\simeq c{{( Re_\tau /\kappa )}^{n}}$ (Chen, Hussain & She (Reference Chen, Hussain and She2018) recommended
$y_{m}^+\simeq c{{( Re_\tau /\kappa )}^{n}}$ (Chen, Hussain & She (Reference Chen, Hussain and She2018) recommended ![]() $n=1/3$ for
$n=1/3$ for ![]() $Re_{\tau } \le 3000$), and farther from the wall, it decays linearly, and hence
$Re_{\tau } \le 3000$), and farther from the wall, it decays linearly, and hence ![]() $\langle u_r u_z \rangle ^+ \sim r/R$. Under these assumptions, (3.16) yields
$\langle u_r u_z \rangle ^+ \sim r/R$. Under these assumptions, (3.16) yields
 \begin{equation} 1-\left( \frac{C_f^{T,O}}{C_f}\right)^{1/4} \approx 4.0 (\kappa Re_\tau ^ 2 ) ^{{-}1/3}. \end{equation}
\begin{equation} 1-\left( \frac{C_f^{T,O}}{C_f}\right)^{1/4} \approx 4.0 (\kappa Re_\tau ^ 2 ) ^{{-}1/3}. \end{equation}
Figure 9(c) shows that (3.17) also yields a satisfactory approximation in the case of rotating pipes, as long as ![]() $N \leq 2$. The formula also well underscores that
$N \leq 2$. The formula also well underscores that ![]() $C_{f}^{T,O}$ asymptotically approaches
$C_{f}^{T,O}$ asymptotically approaches ![]() $C_{f}$ with increasing
$C_{f}$ with increasing ![]() $Re_\tau$, as a result of the increasing influence of the very large turbulent structures that populate the outer layer and modulate the small near-wall structures (Hutchins & Marusic Reference Hutchins and Marusic2007). In (3.17), the splitting location for the rotating cases is based on the respective profiles of
$Re_\tau$, as a result of the increasing influence of the very large turbulent structures that populate the outer layer and modulate the small near-wall structures (Hutchins & Marusic Reference Hutchins and Marusic2007). In (3.17), the splitting location for the rotating cases is based on the respective profiles of ![]() $\langle u_r u_z \rangle$, but the asymptotic behaviour remains valid if
$\langle u_r u_z \rangle$, but the asymptotic behaviour remains valid if ![]() $y_m$ is determined based on the non-rotating cases, since
$y_m$ is determined based on the non-rotating cases, since ![]() $y_{m,0} \lesssim y_m$, as inferred from figure 9(a). In figure 9(d), we present the ratio of the drag reduction associated with the outer layer to the total drag reduction. This indicator is observed to exceed 90 % for
$y_{m,0} \lesssim y_m$, as inferred from figure 9(a). In figure 9(d), we present the ratio of the drag reduction associated with the outer layer to the total drag reduction. This indicator is observed to exceed 90 % for ![]() $N=4.0$ and
$N=4.0$ and ![]() $Re_{\tau,0} = 3020$, tending asymptotically to unity, consistent with theoretical expectations. We also emphasise that it becomes almost independent from
$Re_{\tau,0} = 3020$, tending asymptotically to unity, consistent with theoretical expectations. We also emphasise that it becomes almost independent from ![]() $N$ at high enough Reynolds numbers. It is important to note that the FIK identity per se does not imply any direct causality link between its right- and left-hand sides, meaning that the observed reduction of the turbulent shear stress in the outer layer could as well be a consequence of the reduced wall friction, rather than the opposite.
$N$ at high enough Reynolds numbers. It is important to note that the FIK identity per se does not imply any direct causality link between its right- and left-hand sides, meaning that the observed reduction of the turbulent shear stress in the outer layer could as well be a consequence of the reduced wall friction, rather than the opposite.

Figure 9. (a) Turbulent shear stress for ![]() $N=0$ (dashed lines) and
$N=0$ (dashed lines) and ![]() $N=2$ (solid lines); (b) local contributions to turbulent friction (as from (3.15)) for
$N=2$ (solid lines); (b) local contributions to turbulent friction (as from (3.15)) for ![]() $N=0$ (dashed lines) and
$N=0$ (dashed lines) and ![]() $N=2$ (solid lines); (c) turbulent contribution to friction as a function of
$N=2$ (solid lines); (c) turbulent contribution to friction as a function of ![]() $Re_\tau$; (d) fraction of drag reduction due to turbulence as a function of
$Re_\tau$; (d) fraction of drag reduction due to turbulence as a function of ![]() $Re_b$. In panels (a,b),
$Re_b$. In panels (a,b), ![]() $Re_{\tau,0} = 180$ (black),
$Re_{\tau,0} = 180$ (black), ![]() $495$ (red),
$495$ (red), ![]() $1137$ (green),
$1137$ (green), ![]() $1979$ (blue) and
$1979$ (blue) and ![]() $3020$ (pink). In panels (c,d),
$3020$ (pink). In panels (c,d), ![]() $N=0$ (black),
$N=0$ (black), ![]() $0.25$ (red),
$0.25$ (red), ![]() $0.5$ (green),
$0.5$ (green), ![]() $1.0$ (cyan),
$1.0$ (cyan), ![]() $2.0$ (blue) and
$2.0$ (blue) and ![]() $4.0$ (pink). In panel (c), the dash-dotted line indicates the prediction of (3.17).
$4.0$ (pink). In panel (c), the dash-dotted line indicates the prediction of (3.17).
4. Conclusions
Direct numerical simulation has been performed to study axially rotating pipe flow up to nominal friction Reynolds number ![]() $Re_{\tau,0} = 3020$. The drag reduction rate, which we show to be equivalent to net power saving in the fully developed scenario assuming no mechanical losses, increases with either
$Re_{\tau,0} = 3020$. The drag reduction rate, which we show to be equivalent to net power saving in the fully developed scenario assuming no mechanical losses, increases with either ![]() $N$ or
$N$ or ![]() $Re_{\tau,0}$, becoming a sole function of the inner-scaled wall rotational speed at high enough Reynolds numbers. The drag reduction is as high as approximately 70 % at
$Re_{\tau,0}$, becoming a sole function of the inner-scaled wall rotational speed at high enough Reynolds numbers. The drag reduction is as high as approximately 70 % at ![]() $N=4.0$ for
$N=4.0$ for ![]() $Re_{\tau,0}=3020$, although the flow is still far from full relaminarisation. We have developed a theoretical analysis informed with DNS data which allows for quantitative prediction of this effect, based on the observation that the rotational speed becomes the relevant velocity scale in the core flow. The analysis yields a predictive formula for the friction coefficient (3.9), which yields accurate approximation of the DNS data up to
$Re_{\tau,0}=3020$, although the flow is still far from full relaminarisation. We have developed a theoretical analysis informed with DNS data which allows for quantitative prediction of this effect, based on the observation that the rotational speed becomes the relevant velocity scale in the core flow. The analysis yields a predictive formula for the friction coefficient (3.9), which yields accurate approximation of the DNS data up to ![]() $N \approx 1$, regardless of the bulk Reynolds number, which however breaks down once the logarithmic layer in the mean axial velocity profile is disrupted.
$N \approx 1$, regardless of the bulk Reynolds number, which however breaks down once the logarithmic layer in the mean axial velocity profile is disrupted.
Analysis of the instantaneous velocity fields reveals the role of rotation in weakening the near-wall sweeps and ejections, and in the elongation and broadening of the streaks. In the core region, rotation leads to turbulence suppression at moderate rotation numbers and high Reynolds numbers, resulting in the disappearance of the outer-layer peak in the pre-multiplied spectra. Turbulence is instead intensified at moderate rotation numbers and low Reynolds numbers, and a distinct outer-layer peak or plateau, emerges in the pre-multiplied spectra. Nevertheless, a consistent decrease of the turbulent shear stress is observed. Use of the FIK identity reveals that the turbulent drag reduction originating from the outer layer asymptotically approaches the total turbulent drag reduction with increasing ![]() $Re_{\tau,0}$, consistent with a theoretically derived formula, and conveys that both the inner and outer layers increasingly contribute to drag reduction as
$Re_{\tau,0}$, consistent with a theoretically derived formula, and conveys that both the inner and outer layers increasingly contribute to drag reduction as ![]() $N$ increases.
$N$ increases.
It is finally important to acknowledge opportunities and challenges in applying wall rotation in practical contexts. On the positive side, it is clear from this paper that large drag reduction is possible without reverting to complicated wall actuation rules. In particular, we note that at a statistically steady state, the work required to sustain rotation is zero (leaving mechanical losses aside) and drag reduction effects increase with the Reynolds number, unlike in conventional wall actuation techniques. On the negative side, setting a full pipeline into rotation may not be an easy task. In addition, we find that the achievement of a fully developed state requires a longer distance than for non-rotating flows (typically, a few hundred diameters) and energy must be spent during this transient state to put the whole system into rotation. This energy expenditure should be accounted for in the evaluation of axial rotation for realistic applicative scenarios.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1103/APS.DFD.2023.GFM.V0080.
Acknowledgements
We acknowledge that the simulations were performed using the EuroHPC Research Infrastructure resource LEONARDO based at CINECA, Casalecchio di Reno, Italy, under a LEAP grant.
Funding
M.X. would like to acknowledge the financial support provided by the China Scholarship Council.
Declaration of interest
The authors report no conflict of interest.
Data availability statement
DNS data are available at http://newton.dma.uniroma1.it/.
Appendix. Numerical issues
The DNS herein reported assume a pipe length ![]() $L = 15R$. Figure 10 compares the profiles of axial velocity and azimuthal velocity obtained using
$L = 15R$. Figure 10 compares the profiles of axial velocity and azimuthal velocity obtained using ![]() $L=15R$ and
$L=15R$ and ![]() $30R$ for the case of
$30R$ for the case of ![]() $Re_{\tau,0} = 1137$ and
$Re_{\tau,0} = 1137$ and ![]() $N = 4.0$. The longer configuration predicts a more turbulent mean axial velocity profile. The friction factors for the two lengths have a relative difference of only approximately 3 %, which is much less than the drag reduction amount of approximately
$N = 4.0$. The longer configuration predicts a more turbulent mean axial velocity profile. The friction factors for the two lengths have a relative difference of only approximately 3 %, which is much less than the drag reduction amount of approximately ![]() $55\,\%$ for this case (see table 1). Note that the discrepancies would be smaller with decreasing
$55\,\%$ for this case (see table 1). Note that the discrepancies would be smaller with decreasing ![]() $N$ due to the weakened long columnar structures in the core region. Figure 10 also displays the results obtained using a grid with a higher resolution in the radial direction. The refined resolution results in a slightly less turbulent profile of the mean axial velocity, and it brings out a difference in the friction factor of only approximately
$N$ due to the weakened long columnar structures in the core region. Figure 10 also displays the results obtained using a grid with a higher resolution in the radial direction. The refined resolution results in a slightly less turbulent profile of the mean axial velocity, and it brings out a difference in the friction factor of only approximately ![]() $3\,\%$, which is again much lower than the drag reduction amount. Hence, we conclude that the current numerical settings could be considered enough especially when drag reduction is the primary focus. In our time-evolving simulations, the time interval needed to achieve a fully developed state becomes significantly longer with increasing
$3\,\%$, which is again much lower than the drag reduction amount. Hence, we conclude that the current numerical settings could be considered enough especially when drag reduction is the primary focus. In our time-evolving simulations, the time interval needed to achieve a fully developed state becomes significantly longer with increasing ![]() $N$ at a fixed Reynolds number. Figure 11 shows the time history of the axial pressure gradient for
$N$ at a fixed Reynolds number. Figure 11 shows the time history of the axial pressure gradient for ![]() $Re_{\tau,0} = 495$ at
$Re_{\tau,0} = 495$ at ![]() $N = 0$ and
$N = 0$ and ![]() $4.0$, showing that it takes a time interval of approximately
$4.0$, showing that it takes a time interval of approximately ![]() $100 R/u_b$ for the non-rotating case to become fully developed, whereas the rotating case needs approximately
$100 R/u_b$ for the non-rotating case to become fully developed, whereas the rotating case needs approximately ![]() $400 R/u_b$.
$400 R/u_b$.

Figure 10. Radial profiles for ![]() $Re_{\tau,0} = 1137$ and
$Re_{\tau,0} = 1137$ and ![]() $N=4.0$: (a) axial velocity and (b) azimuthal velocity. Pink,
$N=4.0$: (a) axial velocity and (b) azimuthal velocity. Pink, ![]() $L = 15R$ and
$L = 15R$ and ![]() $N_r=164$; blue,
$N_r=164$; blue, ![]() $L = 30R$ and
$L = 30R$ and ![]() $N_r=164$; green,
$N_r=164$; green, ![]() $L=15R$ and
$L=15R$ and ![]() $N_r=328$.
$N_r=328$.

Figure 11. Time history of axial pressure gradient for ![]() $Re_{\tau,0} = 495$. Black,
$Re_{\tau,0} = 495$. Black, ![]() $N = 0$ and pink,
$N = 0$ and pink, ![]() $N = 4.0$.
$N = 4.0$.