Research Article
Convergence of the zeta functions of prehomogeneous vector spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-31
-
- Article
-
- You have access
- Export citation
On uniqueness polynomials for meromorphic functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 33-46
-
- Article
-
- You have access
- Export citation
Character sheaves and generalized Springer correspondence
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 47-72
-
- Article
-
- You have access
- Export citation
Multiplier Hermitian structures on Kähler manifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 73-115
-
- Article
-
- You have access
- Export citation
Hardy spaces estimates for multilinear operators with homogeneous kernels
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 117-133
-
- Article
-
- You have access
- Export citation
On a generalized divisor problem II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 135-143
-
- Article
-
- You have access
- Export citation
The transcendence degree of an integral domain over a subfield and the dimension of the domain
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-162
-
- Article
-
- You have access
- Export citation
On Osgood-Yang’s conjecture and Mues conjecture
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 163-173
-
- Article
-
- You have access
- Export citation
Special tight closure
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 175-183
-
- Article
-
- You have access
- Export citation
The Hardy-Littlewood property of flag varieties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-211
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 170 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f4
-
- Article
-
- You have access
- Export citation

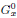 of the stabilizer of a generic point
of the stabilizer of a generic point