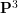1 Introduction
1.1 Introduction
Let
![]() $k$
be a field and
$k$
be a field and
![]() $X$
be a variety over
$X$
be a variety over
![]() $k$
. For nonnegative integers
$k$
. For nonnegative integers
![]() $i$
and
$i$
and
![]() $j$
, Bloch [Reference BlochB] defined the
$j$
, Bloch [Reference BlochB] defined the
![]() $j$
th higher Chow group
$j$
th higher Chow group
![]() $CH^{i}(X,j)$
of codimension
$CH^{i}(X,j)$
of codimension
![]() $i$
of
$i$
of
![]() $X$
. To study the higher Chow group, it is useful to consider the cycle map:
$X$
. To study the higher Chow group, it is useful to consider the cycle map:
for
![]() $\star$
-cohomology theory for
$\star$
-cohomology theory for
![]() $\star =et(\text{ale}),B\text{(etti)},dR\text{(ham)},{\mathcal{D}}\text{(eligne)}$
, when
$\star =et(\text{ale}),B\text{(etti)},dR\text{(ham)},{\mathcal{D}}\text{(eligne)}$
, when
![]() $X$
is smooth over
$X$
is smooth over
![]() $k$
. Rich arithmetic invariants are conjectured to appear from these cohomology theories. First natural question is how big the image of
$k$
. Rich arithmetic invariants are conjectured to appear from these cohomology theories. First natural question is how big the image of
![]() $c_{\star }^{i,j}(X)$
is. For a smooth surface
$c_{\star }^{i,j}(X)$
is. For a smooth surface
![]() $X$
in
$X$
in
![]() $\mathbf{P}^{3}$
over an algebraically closed field
$\mathbf{P}^{3}$
over an algebraically closed field
![]() $k$
, the map is trivial for
$k$
, the map is trivial for
![]() $\star =et$
and
$\star =et$
and
![]() $i=2$
,
$i=2$
,
![]() $j=1$
. We are mainly interested in the case where
$j=1$
. We are mainly interested in the case where
![]() $k$
is not algebraically closed. Concerning this question, there are some previous works, for example, [Reference Müller-StachM], [Reference Collino, Müller-Stach and SaitoCMS]. In this paper, we give an example of a surface over
$k$
is not algebraically closed. Concerning this question, there are some previous works, for example, [Reference Müller-StachM], [Reference Collino, Müller-Stach and SaitoCMS]. In this paper, we give an example of a surface over
![]() $\mathbf{C}((t))$
, whose image of the cycle map is of big dimension. We construct many elements in higher Chow group explicitly, which can be studied in detail.
$\mathbf{C}((t))$
, whose image of the cycle map is of big dimension. We construct many elements in higher Chow group explicitly, which can be studied in detail.
Let
![]() $S=\operatorname{Spec}(\mathbf{C}[t])$
and
$S=\operatorname{Spec}(\mathbf{C}[t])$
and
![]() ${\mathcal{L}}_{1},\ldots ,{\mathcal{L}}_{d},{\mathcal{M}}_{1},\ldots ,{\mathcal{M}}_{d}$
be linear forms on
${\mathcal{L}}_{1},\ldots ,{\mathcal{L}}_{d},{\mathcal{M}}_{1},\ldots ,{\mathcal{M}}_{d}$
be linear forms on
![]() $\mathbf{P}_{\mathbf{C}}^{3}$
. Let
$\mathbf{P}_{\mathbf{C}}^{3}$
. Let
![]() $l_{i}$
and
$l_{i}$
and
![]() $m_{i}$
be the zero loci of
$m_{i}$
be the zero loci of
![]() ${\mathcal{L}}_{i}$
and
${\mathcal{L}}_{i}$
and
![]() ${\mathcal{M}}_{i}$
, respectively. In the following, we assume that
${\mathcal{M}}_{i}$
, respectively. In the following, we assume that
![]() $\bigcup _{i=1}^{d}(l_{i}\cup m_{i})$
is a normal crossing divisor. Let
$\bigcup _{i=1}^{d}(l_{i}\cup m_{i})$
is a normal crossing divisor. Let
![]() $f:X\rightarrow S$
be a family of surfaces over
$f:X\rightarrow S$
be a family of surfaces over
![]() $S$
in
$S$
in
![]() $\mathbf{P}_{S}^{3}$
defined by
$\mathbf{P}_{S}^{3}$
defined by
Let
![]() $k=\mathbf{C}((t))$
and
$k=\mathbf{C}((t))$
and
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}(k)\rightarrow S$
the natural morphism. The fiber of
$\unicode[STIX]{x1D702}:\operatorname{Spec}(k)\rightarrow S$
the natural morphism. The fiber of
![]() $X$
at
$X$
at
![]() $\unicode[STIX]{x1D702}$
is denoted by
$\unicode[STIX]{x1D702}$
is denoted by
![]() $X_{\unicode[STIX]{x1D702}}$
. In this paper, we consider the image of the etale cycle map
$X_{\unicode[STIX]{x1D702}}$
. In this paper, we consider the image of the etale cycle map
The main theorem of the paper is as follows.
Theorem 1.1. Under the above notations, we have
As a corollary, we have the following:
Corollary 1.2.
Let us explain the contents of the paper. In Section 2, we construct elements in the higher Chow group of
![]() $X_{\unicode[STIX]{x1D702}}$
. Moreover, we give a relation between the image of these elements under the etale cycle map and the extension classes of relative homologies. In Section 3, we compare the etale extension classes and extension classes as representations of the (classical) fundamental group of a punctured disc. Thus we reduce the proof of Theorem 1.1 to the proof of the relevant statement for representations of fundamental groups. We recall how to compute the extension classes as representations of the fundamental group. In Section 4, we recall the monodromy weight spectral sequence and compute its terms for
$X_{\unicode[STIX]{x1D702}}$
. Moreover, we give a relation between the image of these elements under the etale cycle map and the extension classes of relative homologies. In Section 3, we compare the etale extension classes and extension classes as representations of the (classical) fundamental group of a punctured disc. Thus we reduce the proof of Theorem 1.1 to the proof of the relevant statement for representations of fundamental groups. We recall how to compute the extension classes as representations of the fundamental group. In Section 4, we recall the monodromy weight spectral sequence and compute its terms for
![]() $X_{\unicode[STIX]{x1D6E5}^{\ast }}$
. The monodromy weight spectral sequence is used to compute the cokernel of the logarithm of monodromy action. To compute every term of the monodromy weight spectral sequence explicitly, we use the model obtained by the blowing up of the original model. In Section 5, we execute a local computation for the extension class using a nice topological model. In this model, the extension class is computed by a topological lifting whose period map can be expressed by the dilogarithmic function. By these computations, we have the local description for the extensions, which will be used in the next section. In Section 6, we sum up the previous results to compute the lower bound for the dimension of the image of the cycle map.
$X_{\unicode[STIX]{x1D6E5}^{\ast }}$
. The monodromy weight spectral sequence is used to compute the cokernel of the logarithm of monodromy action. To compute every term of the monodromy weight spectral sequence explicitly, we use the model obtained by the blowing up of the original model. In Section 5, we execute a local computation for the extension class using a nice topological model. In this model, the extension class is computed by a topological lifting whose period map can be expressed by the dilogarithmic function. By these computations, we have the local description for the extensions, which will be used in the next section. In Section 6, we sum up the previous results to compute the lower bound for the dimension of the image of the cycle map.
2 Construction of elements in the higher Chow group and extension
From now on, we use the same notations for
![]() $X$
,
$X$
,
![]() $X_{\unicode[STIX]{x1D702}}$
in the previous section. In this section, we define an element
$X_{\unicode[STIX]{x1D702}}$
in the previous section. In this section, we define an element
![]() $\unicode[STIX]{x1D6E4}_{ijk.l}$
in
$\unicode[STIX]{x1D6E4}_{ijk.l}$
in
![]() $CH^{2}(X,1)$
, and study the extension class obtained by the generic fiber
$CH^{2}(X,1)$
, and study the extension class obtained by the generic fiber
![]() $\unicode[STIX]{x1D6E4}_{ijk,l,\unicode[STIX]{x1D702}}$
of
$\unicode[STIX]{x1D6E4}_{ijk,l,\unicode[STIX]{x1D702}}$
of
![]() $\unicode[STIX]{x1D6E4}_{ijk.l}$
at
$\unicode[STIX]{x1D6E4}_{ijk.l}$
at
![]() $\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}$
.
2.1 Elements in the higher Chow group of
 $X$
$X$
Let us briefly recall the definition of higher Chow group after Bloch [Reference BlochB]. Let
![]() $\unicode[STIX]{x1D6E5}^{j}$
be the scheme defined by
$\unicode[STIX]{x1D6E5}^{j}$
be the scheme defined by
Let
![]() $X$
be a variety over
$X$
be a variety over
![]() $\mathbf{C}$
. The simplicial faces of
$\mathbf{C}$
. The simplicial faces of
![]() $X\times \unicode[STIX]{x1D6E5}^{j}$
are defined in [Reference BlochB]. The Bloch cycle complex
$X\times \unicode[STIX]{x1D6E5}^{j}$
are defined in [Reference BlochB]. The Bloch cycle complex
![]() $Z^{i}(X,j)$
is defined by the group of
$Z^{i}(X,j)$
is defined by the group of
![]() $\mathbf{Z}$
-linear combinations of codimension
$\mathbf{Z}$
-linear combinations of codimension
![]() $i$
algebraic cycles in
$i$
algebraic cycles in
![]() $X\times \unicode[STIX]{x1D6E5}^{j}$
, which intersect properly to the simplicial faces. We consider the boundary operator
$X\times \unicode[STIX]{x1D6E5}^{j}$
, which intersect properly to the simplicial faces. We consider the boundary operator
using simplicial structure defined as in [Reference BlochB]. Then we have a complex
The
![]() $j$
th cohomology of
$j$
th cohomology of
![]() $Z^{i}(X,\bullet )$
is called the
$Z^{i}(X,\bullet )$
is called the
![]() $j$
th higher Chow group of codimension
$j$
th higher Chow group of codimension
![]() $i$
and denoted by
$i$
and denoted by
![]() $CH^{i}(X,j)$
.
$CH^{i}(X,j)$
.
We set
For integers
![]() $1\leqslant i$
,
$1\leqslant i$
,
![]() $l\leqslant d$
, the intersection
$l\leqslant d$
, the intersection
![]() $L_{i}\cap M_{l}$
is a family of projective lines over
$L_{i}\cap M_{l}$
is a family of projective lines over
![]() $S$
contained in
$S$
contained in
![]() $X$
. For
$X$
. For
![]() $i\neq j$
, we set
$i\neq j$
, we set
We fix
![]() $1\leqslant i<j<k\leqslant d$
and
$1\leqslant i<j<k\leqslant d$
and
![]() $1\leqslant l\leqslant d$
. The three lines
$1\leqslant l\leqslant d$
. The three lines
![]() $L_{i}\cap M_{l}$
,
$L_{i}\cap M_{l}$
,
![]() $L_{j}\cap M_{l}$
,
$L_{j}\cap M_{l}$
,
![]() $L_{k}\cap M_{l}$
form a family of triangles in
$L_{k}\cap M_{l}$
form a family of triangles in
![]() $X$
. Let
$X$
. Let
![]() $(l_{i}\cap m_{l})^{0}$
,
$(l_{i}\cap m_{l})^{0}$
,
![]() $(l_{j}\cap m_{l})^{0}$
and
$(l_{j}\cap m_{l})^{0}$
and
![]() $(l_{k}\cap m_{l})^{0}$
be one-dimensional affine spaces contained in
$(l_{k}\cap m_{l})^{0}$
be one-dimensional affine spaces contained in
![]() $(l_{i}\cap l_{l})$
,
$(l_{i}\cap l_{l})$
,
![]() $(l_{j}\cap m_{l})$
and
$(l_{j}\cap m_{l})$
and
![]() $(l_{k}\cap m_{l})$
such that
$(l_{k}\cap m_{l})$
such that
![]() $(l_{i}\cap m_{l})^{0}\cup (l_{j}\cap m_{l})^{0}\cup (l_{k}\cap m_{l})^{0}$
contains
$(l_{i}\cap m_{l})^{0}\cup (l_{j}\cap m_{l})^{0}\cup (l_{k}\cap m_{l})^{0}$
contains
![]() $p_{ij,l},p_{jk,l}$
and
$p_{ij,l},p_{jk,l}$
and
![]() $p_{ki,l}$
. We choose an isomorphism
$p_{ki,l}$
. We choose an isomorphism
![]() $\unicode[STIX]{x1D711}_{i,jk,l}:\unicode[STIX]{x1D6E5}^{1}\simeq (l_{i}\cap m_{l})^{0}$
such that
$\unicode[STIX]{x1D711}_{i,jk,l}:\unicode[STIX]{x1D6E5}^{1}\simeq (l_{i}\cap m_{l})^{0}$
such that
![]() $\unicode[STIX]{x1D711}_{i,jk,l}(0)=p_{ij,l},\unicode[STIX]{x1D711}_{i,jk,l}(1)=p_{ik,l}$
. The isomorphism
$\unicode[STIX]{x1D711}_{i,jk,l}(0)=p_{ij,l},\unicode[STIX]{x1D711}_{i,jk,l}(1)=p_{ik,l}$
. The isomorphism
![]() $\unicode[STIX]{x1D711}_{i,jk,l}$
induces an isomorphism
$\unicode[STIX]{x1D711}_{i,jk,l}$
induces an isomorphism
![]() $\unicode[STIX]{x1D6E5}^{1}\times S\simeq (l_{i}\cap m_{l})^{0}\times S$
over
$\unicode[STIX]{x1D6E5}^{1}\times S\simeq (l_{i}\cap m_{l})^{0}\times S$
over
![]() $S$
which is also denoted by
$S$
which is also denoted by
![]() $\unicode[STIX]{x1D711}_{i,jk,l}$
.
$\unicode[STIX]{x1D711}_{i,jk,l}$
.
Definition 2.1.
(1) We set
 $\unicode[STIX]{x1D6E4}_{i,jk,l}=\{(x,y)\in \unicode[STIX]{x1D6E5}^{1}\times X\mid \unicode[STIX]{x1D711}_{i,jk,l}(x)=y\}$
. Then it is an element in
$\unicode[STIX]{x1D6E4}_{i,jk,l}=\{(x,y)\in \unicode[STIX]{x1D6E5}^{1}\times X\mid \unicode[STIX]{x1D711}_{i,jk,l}(x)=y\}$
. Then it is an element in
 $Z^{2}(X,1)$
.
$Z^{2}(X,1)$
.(2) We define an element
 $\unicode[STIX]{x1D6E4}_{ijk,l}$
in
$\unicode[STIX]{x1D6E4}_{ijk,l}$
in
 $Z^{2}(X,1)$
by It is easy to see that
$Z^{2}(X,1)$
by It is easy to see that $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{ijk,l}=\unicode[STIX]{x1D6E4}_{i,jk,l}+\unicode[STIX]{x1D6E4}_{j,ki,l}+\unicode[STIX]{x1D6E4}_{k,ij,l}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{ijk,l}=\unicode[STIX]{x1D6E4}_{i,jk,l}+\unicode[STIX]{x1D6E4}_{j,ki,l}+\unicode[STIX]{x1D6E4}_{k,ij,l}.\end{eqnarray}$$
 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{ijk,l}=0$
. The class of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{ijk,l}=0$
. The class of
 $\unicode[STIX]{x1D6E4}_{ijk,l}$
in
$\unicode[STIX]{x1D6E4}_{ijk,l}$
in
 $CH^{2}(X,1)$
is also denoted by
$CH^{2}(X,1)$
is also denoted by
 $\unicode[STIX]{x1D6E4}_{ijk,l}$
.
$\unicode[STIX]{x1D6E4}_{ijk,l}$
.
For a point
![]() $x$
over
$x$
over
![]() $S$
, the fiber of
$S$
, the fiber of
![]() $f:X\rightarrow S$
is denoted by
$f:X\rightarrow S$
is denoted by
![]() $X_{x}$
. We set
$X_{x}$
. We set
Let
![]() $f_{T}:T\rightarrow S$
be the natural projection. The fiber of
$f_{T}:T\rightarrow S$
be the natural projection. The fiber of
![]() $T$
and
$T$
and
![]() $\unicode[STIX]{x1D6E4}_{ijk,l}$
at
$\unicode[STIX]{x1D6E4}_{ijk,l}$
at
![]() $x$
are written as
$x$
are written as
![]() $T_{x}$
and
$T_{x}$
and
![]() $\unicode[STIX]{x1D6E4}_{ijk,l,x}$
, respectively.
$\unicode[STIX]{x1D6E4}_{ijk,l,x}$
, respectively.
Let
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{i,jk,l}}$
be the graph of
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{i,jk,l}}$
be the graph of
![]() $\unicode[STIX]{x1D711}_{i,jk,l}$
. We define an element
$\unicode[STIX]{x1D711}_{i,jk,l}$
. We define an element
![]() $\unicode[STIX]{x1D6FF}$
by
$\unicode[STIX]{x1D6FF}$
by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF} & = & \displaystyle (P_{ij,l},P_{jk,l},P_{ki,l},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{i,jk,l}},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{j,ki,l}},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{k,ij,l}})\nonumber\\ \displaystyle & \in & \displaystyle (Z^{0}(P_{ij,l}\times \unicode[STIX]{x1D6E5}^{0})\oplus Z^{0}(P_{jk,l}\times \unicode[STIX]{x1D6E5}^{0})\oplus Z^{0}(P_{ki,l}\times \unicode[STIX]{x1D6E5}^{0}))\nonumber\\ \displaystyle & & \displaystyle \oplus \,(Z^{1}((L_{i}\cap M_{l})\times \unicode[STIX]{x1D6E5}^{1})\oplus Z^{1}((L_{j}\cap M_{l})\times \unicode[STIX]{x1D6E5}^{1})\oplus Z^{1}((L_{k}\cap M_{l})\times \unicode[STIX]{x1D6E5}^{1})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FF} & = & \displaystyle (P_{ij,l},P_{jk,l},P_{ki,l},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{i,jk,l}},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{j,ki,l}},\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D711}_{k,ij,l}})\nonumber\\ \displaystyle & \in & \displaystyle (Z^{0}(P_{ij,l}\times \unicode[STIX]{x1D6E5}^{0})\oplus Z^{0}(P_{jk,l}\times \unicode[STIX]{x1D6E5}^{0})\oplus Z^{0}(P_{ki,l}\times \unicode[STIX]{x1D6E5}^{0}))\nonumber\\ \displaystyle & & \displaystyle \oplus \,(Z^{1}((L_{i}\cap M_{l})\times \unicode[STIX]{x1D6E5}^{1})\oplus Z^{1}((L_{j}\cap M_{l})\times \unicode[STIX]{x1D6E5}^{1})\oplus Z^{1}((L_{k}\cap M_{l})\times \unicode[STIX]{x1D6E5}^{1})).\nonumber\end{eqnarray}$$
Then the sum of cycles
![]() $\unicode[STIX]{x1D6FF}$
determines an element in
$\unicode[STIX]{x1D6FF}$
determines an element in
![]() $CH^{1}(T,1)$
by the Mayer–Vietoris theorem. We have a natural map
$CH^{1}(T,1)$
by the Mayer–Vietoris theorem. We have a natural map
![]() $\unicode[STIX]{x1D70F}:CH^{1}(T,1)\rightarrow CH^{2}(X,1)$
. The cycle
$\unicode[STIX]{x1D70F}:CH^{1}(T,1)\rightarrow CH^{2}(X,1)$
. The cycle
![]() $\unicode[STIX]{x1D6E4}_{ijk.l}\in CH^{2}(X,1)$
is equal to
$\unicode[STIX]{x1D6E4}_{ijk.l}\in CH^{2}(X,1)$
is equal to
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF})$
.
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF})$
.
2.2 Cycle maps and connecting homomorphisms
Let
![]() $D_{T}=D_{T_{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D702}}$
be the
$D_{T}=D_{T_{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D702}}$
be the
![]() $\mathbf{Q}_{l}$
-dualizing complex of
$\mathbf{Q}_{l}$
-dualizing complex of
![]() $T_{\unicode[STIX]{x1D702}}$
over
$T_{\unicode[STIX]{x1D702}}$
over
![]() $\unicode[STIX]{x1D702}$
. For a subvariety
$\unicode[STIX]{x1D702}$
. For a subvariety
![]() $W$
in
$W$
in
![]() $X$
the restriction of
$X$
the restriction of
![]() $f$
to
$f$
to
![]() $W$
is denoted by
$W$
is denoted by
![]() $f_{W}$
. The restriction of
$f_{W}$
. The restriction of
![]() $f$
to
$f$
to
![]() $X_{\unicode[STIX]{x1D702}}$
is denoted by
$X_{\unicode[STIX]{x1D702}}$
is denoted by
![]() $f_{\unicode[STIX]{x1D702}}$
. For simplicity we consider the case
$f_{\unicode[STIX]{x1D702}}$
. For simplicity we consider the case
![]() $(i,j,k)=(1,2,3)$
. The complex
$(i,j,k)=(1,2,3)$
. The complex
![]() $\mathbf{R}f_{T_{\unicode[STIX]{x1D702}}\ast }D_{T}(1)[2]$
is quasi-isomorphic to
$\mathbf{R}f_{T_{\unicode[STIX]{x1D702}}\ast }D_{T}(1)[2]$
is quasi-isomorphic to
The homomorphism
![]() $\bigoplus _{1\leqslant i\leqslant 3}\mathbf{R}f_{(L_{i}\cap M_{l})_{\unicode[STIX]{x1D702}},\ast }\mathbf{Q}_{l}(1)[2]\rightarrow \mathbf{R}f_{\unicode[STIX]{x1D702}\ast }\mathbf{Q}_{l}(2)[4]$
induces a homomorphism
$\bigoplus _{1\leqslant i\leqslant 3}\mathbf{R}f_{(L_{i}\cap M_{l})_{\unicode[STIX]{x1D702}},\ast }\mathbf{Q}_{l}(1)[2]\rightarrow \mathbf{R}f_{\unicode[STIX]{x1D702}\ast }\mathbf{Q}_{l}(2)[4]$
induces a homomorphism
Its cone is denoted by
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D702}}$
. Let
${\mathcal{C}}_{\unicode[STIX]{x1D702}}$
. Let
![]() $S^{0}$
be the maximal open set of
$S^{0}$
be the maximal open set of
![]() $S$
over which
$S$
over which
![]() $f:X\rightarrow S$
is smooth. By the definition of the cone
$f:X\rightarrow S$
is smooth. By the definition of the cone
![]() ${\mathcal{C}}_{\unicode[STIX]{x1D702}}$
, we have the long exact sequence:
${\mathcal{C}}_{\unicode[STIX]{x1D702}}$
, we have the long exact sequence:
The same complex of (3) can be considered over
![]() $\overline{\unicode[STIX]{x1D702}}$
. The corresponding complex are denoted as
$\overline{\unicode[STIX]{x1D702}}$
. The corresponding complex are denoted as
![]() ${\mathcal{C}}_{\overline{\unicode[STIX]{x1D702}}}$
. We have the following similar long exact sequence of
${\mathcal{C}}_{\overline{\unicode[STIX]{x1D702}}}$
. We have the following similar long exact sequence of
![]() $G=\text{Gal}(\overline{k}/k)$
modules:
$G=\text{Gal}(\overline{k}/k)$
modules:
By the compatibility of cycle maps and the connecting homomorphisms, we have the following commutative diagram:
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}CH^{1}(T_{\unicode[STIX]{x1D702}},1) & \xrightarrow[{}]{\unicode[STIX]{x1D70F}} & CH^{2}(X_{\unicode[STIX]{x1D702}},1)\\ c_{et}^{1,1}\downarrow & & \downarrow c_{et}^{2,1}\\ H^{1}(T_{\unicode[STIX]{x1D702}},D(1)) & \rightarrow & H^{3}(X_{\unicode[STIX]{x1D702}},\mathbf{Q}_{l}(2)).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}CH^{1}(T_{\unicode[STIX]{x1D702}},1) & \xrightarrow[{}]{\unicode[STIX]{x1D70F}} & CH^{2}(X_{\unicode[STIX]{x1D702}},1)\\ c_{et}^{1,1}\downarrow & & \downarrow c_{et}^{2,1}\\ H^{1}(T_{\unicode[STIX]{x1D702}},D(1)) & \rightarrow & H^{3}(X_{\unicode[STIX]{x1D702}},\mathbf{Q}_{l}(2)).\end{array}\end{eqnarray}$$
The image of
![]() $\unicode[STIX]{x1D6FF}$
in
$\unicode[STIX]{x1D6FF}$
in
![]() $H^{1}(T_{\unicode[STIX]{x1D702}},D(1))$
under the cycle map is denoted by
$H^{1}(T_{\unicode[STIX]{x1D702}},D(1))$
under the cycle map is denoted by
![]() $\overline{\unicode[STIX]{x1D6FF}}$
. Then we have
$\overline{\unicode[STIX]{x1D6FF}}$
. Then we have
2.3 Cycle map and extension group
We study extensions arising from
![]() $\unicode[STIX]{x1D6E4}_{ijk,l}$
. Until the end of this section, we consider the fibers
$\unicode[STIX]{x1D6E4}_{ijk,l}$
. Until the end of this section, we consider the fibers
![]() $X_{\unicode[STIX]{x1D702}}$
over
$X_{\unicode[STIX]{x1D702}}$
over
![]() $\unicode[STIX]{x1D702}\rightarrow S$
. The varieties
$\unicode[STIX]{x1D702}\rightarrow S$
. The varieties
![]() $(L_{i}\cap M_{l})_{\unicode[STIX]{x1D702}}$
,
$(L_{i}\cap M_{l})_{\unicode[STIX]{x1D702}}$
,
![]() $T_{\unicode[STIX]{x1D702}}$
, etc. are subvarieties of
$T_{\unicode[STIX]{x1D702}}$
, etc. are subvarieties of
![]() $X_{\unicode[STIX]{x1D702}}$
. We set
$X_{\unicode[STIX]{x1D702}}$
. We set
![]() $\overline{\unicode[STIX]{x1D702}}=\operatorname{Spec}(\overline{k})$
. Since
$\overline{\unicode[STIX]{x1D702}}=\operatorname{Spec}(\overline{k})$
. Since
![]() $X_{\unicode[STIX]{x1D702}}$
is a hypersurface in
$X_{\unicode[STIX]{x1D702}}$
is a hypersurface in
![]() $\mathbf{P}^{3}$
, we have
$\mathbf{P}^{3}$
, we have
![]() $H^{0}(k_{et},H^{3}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))=0$
and by Hochschild–Serre spectral sequence, we have a map
$H^{0}(k_{et},H^{3}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))=0$
and by Hochschild–Serre spectral sequence, we have a map
Proposition 2.2. The image of
![]() $\unicode[STIX]{x1D6E4}_{ijk,l}\in CH^{2}(X_{\unicode[STIX]{x1D702}},1)$
under the map
$\unicode[STIX]{x1D6E4}_{ijk,l}\in CH^{2}(X_{\unicode[STIX]{x1D702}},1)$
under the map
is equal to the extension class of
as
![]() $G$
-module. In other words, the image of
$G$
-module. In other words, the image of
![]() $\overline{\unicode[STIX]{x1D6FF}}$
under the connecting homomorphism:
$\overline{\unicode[STIX]{x1D6FF}}$
under the connecting homomorphism:
Proof. We consider the long exact sequence (5). We obtain similar long exact sequence by replacing
![]() $k$
by
$k$
by
![]() $\overline{k}$
. Applying the functor
$\overline{k}$
. Applying the functor
![]() $H^{p}(G,\ast )$
, we have a complex
$H^{p}(G,\ast )$
, we have a complex
Since the cohomological dimension of
![]() $G$
is one, we have the following exact sequences by Hochschild–Serre spectral sequence.
$G$
is one, we have the following exact sequences by Hochschild–Serre spectral sequence.
 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle H^{1}(G,H^{i-2}(T_{\overline{\unicode[STIX]{x1D702}}},D(1)))\rightarrow H^{i-1}(T_{\unicode[STIX]{x1D702}},D(1))\nonumber\\ \displaystyle & \rightarrow & \displaystyle H^{0}(G,H^{i-1}(T_{\overline{\unicode[STIX]{x1D702}}},D(1)))\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle H^{1}(G,H^{i}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))\rightarrow H^{i+1}(X_{\unicode[STIX]{x1D702}},\mathbf{Q}_{l}(2))\nonumber\\ \displaystyle & \rightarrow & \displaystyle H^{0}(G,H^{i+1}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle H^{1}(G,H^{i}({\mathcal{C}}_{\overline{\unicode[STIX]{x1D702}}}))\rightarrow H^{i+1}({\mathcal{C}}_{\unicode[STIX]{x1D702}})\rightarrow H^{0}(G,H^{i+1}({\mathcal{C}}_{\overline{\unicode[STIX]{x1D702}}}))\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle H^{1}(G,H^{i-2}(T_{\overline{\unicode[STIX]{x1D702}}},D(1)))\rightarrow H^{i-1}(T_{\unicode[STIX]{x1D702}},D(1))\nonumber\\ \displaystyle & \rightarrow & \displaystyle H^{0}(G,H^{i-1}(T_{\overline{\unicode[STIX]{x1D702}}},D(1)))\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle H^{1}(G,H^{i}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))\rightarrow H^{i+1}(X_{\unicode[STIX]{x1D702}},\mathbf{Q}_{l}(2))\nonumber\\ \displaystyle & \rightarrow & \displaystyle H^{0}(G,H^{i+1}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))\rightarrow 0,\nonumber\\ \displaystyle 0 & \rightarrow & \displaystyle H^{1}(G,H^{i}({\mathcal{C}}_{\overline{\unicode[STIX]{x1D702}}}))\rightarrow H^{i+1}({\mathcal{C}}_{\unicode[STIX]{x1D702}})\rightarrow H^{0}(G,H^{i+1}({\mathcal{C}}_{\overline{\unicode[STIX]{x1D702}}}))\rightarrow 0.\nonumber\end{eqnarray}$$
Since the sequence (5) is exact, the homology of
and that of
are isomorphic. The following lemma is straight forward.
Lemma 2.3. Assume that
is exact. Then
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are zero maps.
$\unicode[STIX]{x1D6FD}$
are zero maps.
The homomorphism
induced by the isomorphism between cohomologies of (7) and (8) is equal to the connecting homomorphism arising from the exact sequence (9). The connecting homomorphism (6) is induced by the following zigzag.
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}} & & H^{1}(G,H^{2}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))\\ & & \downarrow \\ H^{1}(T_{\unicode[STIX]{x1D702}},D_{T^{0}}(1)) & \rightarrow & H^{3}(X_{\unicode[STIX]{x1D702}},\mathbf{Q}_{l}(2))\\ \downarrow & & \\ H^{0}(G,H^{1}(T_{\overline{\unicode[STIX]{x1D702}}},D(1))). & & \end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}} & & H^{1}(G,H^{2}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))\\ & & \downarrow \\ H^{1}(T_{\unicode[STIX]{x1D702}},D_{T^{0}}(1)) & \rightarrow & H^{3}(X_{\unicode[STIX]{x1D702}},\mathbf{Q}_{l}(2))\\ \downarrow & & \\ H^{0}(G,H^{1}(T_{\overline{\unicode[STIX]{x1D702}}},D(1))). & & \end{array}\end{eqnarray}$$
Therefore the image
![]() $c_{et}^{2,1}(\unicode[STIX]{x1D6E4}_{ijk,l})=c_{et}^{2,1}(\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}))$
of
$c_{et}^{2,1}(\unicode[STIX]{x1D6E4}_{ijk,l})=c_{et}^{2,1}(\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FF}))$
of
![]() $\unicode[STIX]{x1D6E4}_{ijk.l}$
under the cycle map is equal to the image of
$\unicode[STIX]{x1D6E4}_{ijk.l}$
under the cycle map is equal to the image of
![]() $\overline{\unicode[STIX]{x1D6FF}}\in H^{0}(G,H^{1}(T_{\overline{k}},D))$
under the connecting homomorphism.◻
$\overline{\unicode[STIX]{x1D6FF}}\in H^{0}(G,H^{1}(T_{\overline{k}},D))$
under the connecting homomorphism.◻
3 Comparison to classical cohomology theory
In this section, we compare extensions for etale cohomologies with those for classical cohomology theory.
3.1 Comparison to classical theory
Let
![]() $S^{0}$
be the maximal open set of
$S^{0}$
be the maximal open set of
![]() $S$
over which
$S$
over which
![]() $f:X\rightarrow S$
is smooth. Let
$f:X\rightarrow S$
is smooth. Let
![]() $\unicode[STIX]{x1D6E5}=\{t\in \mathbf{C}\mid |t|<\unicode[STIX]{x1D716}\}$
be a sufficiently small neighborhood of 0 in
$\unicode[STIX]{x1D6E5}=\{t\in \mathbf{C}\mid |t|<\unicode[STIX]{x1D716}\}$
be a sufficiently small neighborhood of 0 in
![]() $S(\mathbf{C})$
such that
$S(\mathbf{C})$
such that
![]() $\unicode[STIX]{x1D6E5}^{\ast }(=\unicode[STIX]{x1D6E5}-\{0\})\subset S^{0}(\mathbf{C})$
. We fix an element
$\unicode[STIX]{x1D6E5}^{\ast }(=\unicode[STIX]{x1D6E5}-\{0\})\subset S^{0}(\mathbf{C})$
. We fix an element
![]() $t_{0}$
in
$t_{0}$
in
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
.
$\unicode[STIX]{x1D6E5}^{\ast }$
.
The restrictions of
![]() $f$
and
$f$
and
![]() $f_{T}$
to
$f_{T}$
to
![]() $f^{-1}(S^{0})$
and
$f^{-1}(S^{0})$
and
![]() $f^{-1}(S^{0})\cap T$
are denoted by
$f^{-1}(S^{0})\cap T$
are denoted by
![]() $f_{S^{0}}$
and
$f_{S^{0}}$
and
![]() $f_{T,S^{0}}$
, respectively. We have the following short exact sequence of etale
$f_{T,S^{0}}$
, respectively. We have the following short exact sequence of etale
![]() $l$
-adic local systems on
$l$
-adic local systems on
![]() $S^{0}$
.
$S^{0}$
.
We set
![]() $\overline{\unicode[STIX]{x1D702}}=\operatorname{Spec}(\overline{k})$
. Let
$\overline{\unicode[STIX]{x1D702}}=\operatorname{Spec}(\overline{k})$
. Let
![]() $S^{st}$
be the strict Henselization under
$S^{st}$
be the strict Henselization under
![]() $\overline{\unicode[STIX]{x1D702}}$
of
$\overline{\unicode[STIX]{x1D702}}$
of
![]() $S$
at
$S$
at
![]() $t_{0}$
over
$t_{0}$
over
![]() $\unicode[STIX]{x1D702}$
. Then the diagram
$\unicode[STIX]{x1D702}$
. Then the diagram
![]() $t_{0}\leftarrow S^{st}\rightarrow \overline{\unicode[STIX]{x1D702}}$
defines an isomorphism
$t_{0}\leftarrow S^{st}\rightarrow \overline{\unicode[STIX]{x1D702}}$
defines an isomorphism
![]() $\unicode[STIX]{x1D70B}_{1}^{et}(S^{0},t_{0})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D70B}_{1}^{et}(S^{0},\overline{\unicode[STIX]{x1D702}})$
and isomorphism between the fiber of the exact sequence (11) at
$\unicode[STIX]{x1D70B}_{1}^{et}(S^{0},t_{0})\xrightarrow[{}]{\simeq }\unicode[STIX]{x1D70B}_{1}^{et}(S^{0},\overline{\unicode[STIX]{x1D702}})$
and isomorphism between the fiber of the exact sequence (11) at
![]() $t_{0}$
and that at
$t_{0}$
and that at
![]() $\overline{\unicode[STIX]{x1D702}}$
. We have the following diagram
$\overline{\unicode[STIX]{x1D702}}$
. We have the following diagram
 $$\begin{eqnarray}\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D70B}_{1}^{cl}(S^{0}(\mathbf{C}),t_{0}) & \rightarrow & \unicode[STIX]{x1D70B}_{1}^{et}(S^{0},t_{0}) & \xrightarrow[{}]{\simeq }\unicode[STIX]{x1D70B}_{1}(S^{0},\overline{\unicode[STIX]{x1D702}})\\ \cup & & & \cup \\ \unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },t_{0}) & & & \unicode[STIX]{x1D70B}_{1}^{et}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}}).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D70B}_{1}^{cl}(S^{0}(\mathbf{C}),t_{0}) & \rightarrow & \unicode[STIX]{x1D70B}_{1}^{et}(S^{0},t_{0}) & \xrightarrow[{}]{\simeq }\unicode[STIX]{x1D70B}_{1}(S^{0},\overline{\unicode[STIX]{x1D702}})\\ \cup & & & \cup \\ \unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },t_{0}) & & & \unicode[STIX]{x1D70B}_{1}^{et}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}}).\end{array}\end{eqnarray}$$
We can easily see that the above homomorphism induces a homomorphism
By composing the comparison map the fiber of the exact sequence (11) at
![]() $\overline{\unicode[STIX]{x1D702}}$
$\overline{\unicode[STIX]{x1D702}}$
is isomorphic to the exact sequence
This isomorphism is equivariant under the fundamental groups via the map
![]() $c_{\unicode[STIX]{x1D70B}}$
. As a consequence, we have the following proposition.
$c_{\unicode[STIX]{x1D70B}}$
. As a consequence, we have the following proposition.
Proposition 3.1. The extension class
![]() $\unicode[STIX]{x1D716}_{et}$
of (12) in
$\unicode[STIX]{x1D716}_{et}$
of (12) in
![]() $H^{1}(\unicode[STIX]{x1D70B}_{1}^{et}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}}),H^{2}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))$
goes to the extension class
$H^{1}(\unicode[STIX]{x1D70B}_{1}^{et}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}}),H^{2}(X_{\overline{\unicode[STIX]{x1D702}}},\mathbf{Q}_{l}(2)))$
goes to the extension class
![]() $\unicode[STIX]{x1D716}_{cl}$
of (13) in
$\unicode[STIX]{x1D716}_{cl}$
of (13) in
![]() $H^{1}(\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },\overline{t_{0}}),H^{2}(X_{t_{0}},\mathbf{Q}_{l}(2)))$
under the map
$H^{1}(\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },\overline{t_{0}}),H^{2}(X_{t_{0}},\mathbf{Q}_{l}(2)))$
under the map
![]() $c_{\unicode[STIX]{x1D70B}}$
.
$c_{\unicode[STIX]{x1D70B}}$
.
The short exact sequence (13) is isomorphic to the following short exact sequence
as a module over fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },t_{0})$
after tensoring with
$\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },t_{0})$
after tensoring with
![]() $\mathbf{Q}_{l}$
. Therefore, we have the following proposition.
$\mathbf{Q}_{l}$
. Therefore, we have the following proposition.
Proposition 3.2. The extension class
![]() $\unicode[STIX]{x1D716}_{cl}$
is equal to the extension class of (14) in
$\unicode[STIX]{x1D716}_{cl}$
is equal to the extension class of (14) in
![]() $H^{1}(\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },\overline{t_{0}}),H_{2}(X_{t_{0}},\mathbf{Q}))$
via the isomorphism
$H^{1}(\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },\overline{t_{0}}),H_{2}(X_{t_{0}},\mathbf{Q}))$
via the isomorphism
![]() $H^{2}(X_{t_{0}},\mathbf{Q}_{l}(2))\simeq H_{2}(X_{t_{0}},\mathbf{Q})\otimes \mathbf{Q}_{l}$
.
$H^{2}(X_{t_{0}},\mathbf{Q}_{l}(2))\simeq H_{2}(X_{t_{0}},\mathbf{Q})\otimes \mathbf{Q}_{l}$
.
3.2 Extensions from the topological side
The surface
![]() $X_{t_{0}}$
contains three affine lines
$X_{t_{0}}$
contains three affine lines
![]() $(l_{i}\cap m_{l})^{0},(l_{j}\cap m_{l})^{0},$
$(l_{i}\cap m_{l})^{0},(l_{j}\cap m_{l})^{0},$
![]() $(l_{k}\cap m_{l})^{0}$
. We choose a topological path
$(l_{k}\cap m_{l})^{0}$
. We choose a topological path
![]() $\unicode[STIX]{x1D6FE}_{jk,l}$
(resp.
$\unicode[STIX]{x1D6FE}_{jk,l}$
(resp.
![]() $\unicode[STIX]{x1D6FE}_{ki,l},\unicode[STIX]{x1D6FE}_{ij,l}$
) connecting
$\unicode[STIX]{x1D6FE}_{ki,l},\unicode[STIX]{x1D6FE}_{ij,l}$
) connecting
![]() $p_{ij,l}$
and
$p_{ij,l}$
and
![]() $p_{ik,l}$
(resp.
$p_{ik,l}$
(resp.
![]() $p_{jk,l}$
and
$p_{jk,l}$
and
![]() $p_{ji,l}$
,
$p_{ji,l}$
,
![]() $p_{ki,l}$
and
$p_{ki,l}$
and
![]() $p_{kj,l}$
) in
$p_{kj,l}$
) in
![]() $(l_{i}\cap m_{l})^{0}$
(resp.
$(l_{i}\cap m_{l})^{0}$
(resp.
![]() $(l_{j}\cap m_{l})^{0}$
and
$(l_{j}\cap m_{l})^{0}$
and
![]() $(l_{k}\cap m_{l})^{0}$
). Then we have a topological cycle
$(l_{k}\cap m_{l})^{0}$
). Then we have a topological cycle
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FE}_{ij,l}+\unicode[STIX]{x1D6FE}_{jk,l}+\unicode[STIX]{x1D6FE}_{ki,l}$
. Since
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FE}_{ij,l}+\unicode[STIX]{x1D6FE}_{jk,l}+\unicode[STIX]{x1D6FE}_{ki,l}$
. Since
![]() $X_{t_{0}}$
is simply connected, there exists a 2-chain
$X_{t_{0}}$
is simply connected, there exists a 2-chain
![]() $\unicode[STIX]{x1D70E}_{0}$
in
$\unicode[STIX]{x1D70E}_{0}$
in
![]() $X_{t_{0}}$
such that
$X_{t_{0}}$
such that
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}_{0})$
. Then the relative cycle
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}_{0})$
. Then the relative cycle
![]() $\unicode[STIX]{x1D70F}$
defines a relative homology class in
$\unicode[STIX]{x1D70F}$
defines a relative homology class in
![]() $H_{2}(X_{t_{0}},T_{t_{0}})$
. Let
$H_{2}(X_{t_{0}},T_{t_{0}})$
. Let
be a path in
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
beginning from
$\unicode[STIX]{x1D6E5}^{\ast }$
beginning from
![]() $t_{0}$
ending at
$t_{0}$
ending at
![]() $t_{0}$
turning around the origin, whose homotopy class is a positive generator
$t_{0}$
turning around the origin, whose homotopy class is a positive generator
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },t_{0})$
. We extend the relative two-cycle
$\unicode[STIX]{x1D70B}_{1}^{cl}(\unicode[STIX]{x1D6E5}^{\ast },t_{0})$
. We extend the relative two-cycle
![]() $\unicode[STIX]{x1D70E}_{0}$
to a continuous family on of relative two-cycle
$\unicode[STIX]{x1D70E}_{0}$
to a continuous family on of relative two-cycle
![]() $\unicode[STIX]{x1D70E}(s)$
in
$\unicode[STIX]{x1D70E}(s)$
in
![]() $X_{\unicode[STIX]{x1D713}(s)}$
.
$X_{\unicode[STIX]{x1D713}(s)}$
.
![]() $(0\leqslant s\leqslant 1)$
such that:
$(0\leqslant s\leqslant 1)$
such that:
(1)
 $\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}(s))=\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}(0))~(\subset T_{\unicode[STIX]{x1D713}(s)})$
for all
$\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}(s))=\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}(0))~(\subset T_{\unicode[STIX]{x1D713}(s)})$
for all
 $s\in [0,1]$
;
$s\in [0,1]$
;(2)
 $\unicode[STIX]{x1D70E}(0)=\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}(0)=\unicode[STIX]{x1D70E}$
.
We set
![]() $\unicode[STIX]{x1D70E}(1)=\unicode[STIX]{x1D70E}^{\prime }$
. Then the chain
$\unicode[STIX]{x1D70E}(1)=\unicode[STIX]{x1D70E}^{\prime }$
. Then the chain
![]() $\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70E}^{\prime }$
becomes a closed two-chain in
$\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70E}^{\prime }$
becomes a closed two-chain in
![]() $X_{t_{0}}$
and we have the homology class
$X_{t_{0}}$
and we have the homology class
![]() $[\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70E}^{\prime }]$
in
$[\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70E}^{\prime }]$
in
![]() $H_{2}(X_{t_{0}},\mathbf{Q})$
. The element
$H_{2}(X_{t_{0}},\mathbf{Q})$
. The element
![]() $[\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70E}^{\prime }]$
constructed as above defines an element in
$[\unicode[STIX]{x1D70E}-\unicode[STIX]{x1D70E}^{\prime }]$
constructed as above defines an element in
Here
![]() $N$
is the logarithm of
$N$
is the logarithm of
![]() $\unicode[STIX]{x1D6FE}$
. It is equal to
$\unicode[STIX]{x1D6FE}$
. It is equal to
![]() $\unicode[STIX]{x1D716}_{cl}$
introduced in the last subsection. Here
$\unicode[STIX]{x1D716}_{cl}$
introduced in the last subsection. Here
![]() $\unicode[STIX]{x1D6FE}$
denotes a positive generator of
$\unicode[STIX]{x1D6FE}$
denotes a positive generator of
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6E5}^{\ast },t_{0})$
. As a consequence, we have the following proposition.
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6E5}^{\ast },t_{0})$
. As a consequence, we have the following proposition.
Lemma 3.3. We have
![]() $c_{B}^{2,1}(\unicode[STIX]{x1D6E4}_{ijk,l})=\unicode[STIX]{x1D716}_{cl}$
.
$c_{B}^{2,1}(\unicode[STIX]{x1D6E4}_{ijk,l})=\unicode[STIX]{x1D716}_{cl}$
.
4 Monodromy weight spectral sequence
4.1 Blowing up and strata
From now on, we consider varieties in the category of complex analytic spaces. We use the same notations for the complex analytic space associated to
![]() $X$
and the morphism
$X$
and the morphism
![]() $f:X\rightarrow \mathbf{A}^{1}$
. Let
$f:X\rightarrow \mathbf{A}^{1}$
. Let
![]() $\unicode[STIX]{x1D6E5}$
be a sufficiently small disc around
$\unicode[STIX]{x1D6E5}$
be a sufficiently small disc around
![]() $t=0$
as in the previous section and
$t=0$
as in the previous section and
![]() $X_{\unicode[STIX]{x1D6E5}}$
the pull back
$X_{\unicode[STIX]{x1D6E5}}$
the pull back
![]() $f^{-1}(\unicode[STIX]{x1D6E5})$
.
$f^{-1}(\unicode[STIX]{x1D6E5})$
.
Then the total space
![]() $X_{D}$
has nodes at
$X_{D}$
has nodes at
![]() $p_{ij,l}=X_{0}\cap P_{ij,l}=\{{\mathcal{L}}_{i}={\mathcal{L}}_{j}={\mathcal{M}}_{l}=t=0\}$
for
$p_{ij,l}=X_{0}\cap P_{ij,l}=\{{\mathcal{L}}_{i}={\mathcal{L}}_{j}={\mathcal{M}}_{l}=t=0\}$
for
![]() $1\leqslant i<j\leqslant d$
,
$1\leqslant i<j\leqslant d$
,
![]() $1\leqslant l\leqslant d$
. For example, we can choose a local coordinate
$1\leqslant l\leqslant d$
. For example, we can choose a local coordinate
![]() $x,y,z,t$
at
$x,y,z,t$
at
![]() $p_{ij,l}$
such that
$p_{ij,l}$
such that
![]() $x={\mathcal{L}}_{i}$
,
$x={\mathcal{L}}_{i}$
,
![]() $y={\mathcal{L}}_{j}$
,
$y={\mathcal{L}}_{j}$
,
![]() $z={\mathcal{M}}_{l}$
. Under this coordinates,
$z={\mathcal{M}}_{l}$
. Under this coordinates,
![]() $X_{\unicode[STIX]{x1D6E5}}$
is defined by
$X_{\unicode[STIX]{x1D6E5}}$
is defined by
![]() $\{xy+tz=0\}$
around
$\{xy+tz=0\}$
around
![]() $p_{ij,l}$
. The blowing up along
$p_{ij,l}$
. The blowing up along
![]() $\bigcup _{i<j,l}\{(p_{ij,l},0)\}$
is denoted by
$\bigcup _{i<j,l}\{(p_{ij,l},0)\}$
is denoted by
![]() $\widetilde{X}$
and the induced morphism
$\widetilde{X}$
and the induced morphism
![]() $\widetilde{X}\rightarrow \unicode[STIX]{x1D6E5}$
is denoted by
$\widetilde{X}\rightarrow \unicode[STIX]{x1D6E5}$
is denoted by
![]() $\widetilde{f}$
.
$\widetilde{f}$
.
Let
![]() $h_{ij,k}$
be the exceptional divisor over
$h_{ij,k}$
be the exceptional divisor over
![]() $(p_{ij,l},0)$
(
$(p_{ij,l},0)$
(
![]() $1\leqslant i<j\leqslant d,1\leqslant l\leqslant d$
). Then the singular fiber
$1\leqslant i<j\leqslant d,1\leqslant l\leqslant d$
). Then the singular fiber
![]() $f^{-1}(0)$
consists of the following
$f^{-1}(0)$
consists of the following
![]() $d+(d^{2}(d-1))/2$
components.
$d+(d^{2}(d-1))/2$
components.
(1) Proper transforms
 $g_{1},\ldots ,g_{d}$
of
$g_{1},\ldots ,g_{d}$
of
 $l_{i}\times 0$
, where
$l_{i}\times 0$
, where
 $g_{i}$
is isomorphic to the blowing up of
$g_{i}$
is isomorphic to the blowing up of
 $\mathbf{P}^{2}$
along the points
$\mathbf{P}^{2}$
along the points
 $p_{ij,l}$
(
$p_{ij,l}$
(
 $j\neq i,1\leqslant l\leqslant d$
).
$j\neq i,1\leqslant l\leqslant d$
).(2)
 $(d^{2}(d-1))/2$
exceptional components
$(d^{2}(d-1))/2$
exceptional components
 $h_{ij,k}$
(
$h_{ij,k}$
(
 $1\leqslant i<j\leqslant d,1\leqslant k\leqslant d$
). Each component
$1\leqslant i<j\leqslant d,1\leqslant k\leqslant d$
). Each component
 $h_{ij,k}$
is isomorphic to
$h_{ij,k}$
is isomorphic to
 $\mathbf{P}^{1}\times \mathbf{P}^{1}$
.
$\mathbf{P}^{1}\times \mathbf{P}^{1}$
.
One-dimensional stratum of the singular fiber consists of the followings.
(1)
 $(d(d-1))/2$
intersections
$(d(d-1))/2$
intersections
 $l_{ij}=g_{i}\cap g_{j}$
(
$l_{ij}=g_{i}\cap g_{j}$
(
 $1\leqslant i<j\leqslant d$
).
$1\leqslant i<j\leqslant d$
).(2)
 $d^{2}(d-1)$
intersections of
$d^{2}(d-1)$
intersections of
 $m_{ij,k}=h_{ij,k}\cap g_{i}$
.
$m_{ij,k}=h_{ij,k}\cap g_{i}$
.
The zero-dimensional stratum consists of the following points:
(1)
 $(d(d-1)(d-2))/6$
intersection points
$(d(d-1)(d-2))/6$
intersection points
 $p_{ijk}=g_{i}\cap g_{j}\cap g_{k}$
;
$p_{ijk}=g_{i}\cap g_{j}\cap g_{k}$
;(2)
 $(d^{2}(d-1))/2$
intersection points
$(d^{2}(d-1))/2$
intersection points
 $q_{ij,k}=h_{ij,k}\cap g_{i}\cap g_{j}=m_{ij,k}\cap m_{ji,k}$
.
$q_{ij,k}=h_{ij,k}\cap g_{i}\cap g_{j}=m_{ij,k}\cap m_{ji,k}$
.
We have
![]() $h_{ij,k}\supset m_{ij,k}\cup m_{ji,k}$
. The disjoint union of the
$h_{ij,k}\supset m_{ij,k}\cup m_{ji,k}$
. The disjoint union of the
![]() $k$
-dimensional stratum is denoted by
$k$
-dimensional stratum is denoted by
![]() $T^{(k)}$
. Then we have
$T^{(k)}$
. Then we have
 $$\begin{eqnarray}\displaystyle T^{(0)} & = & \displaystyle \{{p_{ijk}\}}_{1\leqslant i<j<k\leqslant d}\cup \{{q_{ij,k}\}}_{1\leqslant i<j\leqslant d,1\leqslant k\leqslant d},\nonumber\\ \displaystyle T^{(1)} & = & \displaystyle \{{l_{ij}\}}_{1\leqslant i<j\leqslant d}\cup \{{m_{ij,k}\}}_{1\leqslant i\neq j\leqslant d,1\leqslant k\leqslant d},\nonumber\\ \displaystyle T^{(2)} & = & \displaystyle \{{g_{i}\}}_{1\leqslant i\leqslant d}\cup \{{h_{ij,k}\}}_{1\leqslant i<j\leqslant d,1\leqslant k\leqslant d}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T^{(0)} & = & \displaystyle \{{p_{ijk}\}}_{1\leqslant i<j<k\leqslant d}\cup \{{q_{ij,k}\}}_{1\leqslant i<j\leqslant d,1\leqslant k\leqslant d},\nonumber\\ \displaystyle T^{(1)} & = & \displaystyle \{{l_{ij}\}}_{1\leqslant i<j\leqslant d}\cup \{{m_{ij,k}\}}_{1\leqslant i\neq j\leqslant d,1\leqslant k\leqslant d},\nonumber\\ \displaystyle T^{(2)} & = & \displaystyle \{{g_{i}\}}_{1\leqslant i\leqslant d}\cup \{{h_{ij,k}\}}_{1\leqslant i<j\leqslant d,1\leqslant k\leqslant d}.\nonumber\end{eqnarray}$$
For example, for
![]() $d=4$
, we have
$d=4$
, we have
4.2 The
 $E_{1}$
-term of the monodromy weight spectral sequence
$E_{1}$
-term of the monodromy weight spectral sequence
In this section, we recall the monodromy weight spectral sequence [Reference Peters and SteenbrinkPSt, Section 11.2, p. 259]. We set
![]() $\unicode[STIX]{x1D6E5}^{\ast }=\{t\in \unicode[STIX]{x1D6E5}\mid t\neq 0\}$
. Let
$\unicode[STIX]{x1D6E5}^{\ast }=\{t\in \unicode[STIX]{x1D6E5}\mid t\neq 0\}$
. Let
![]() $\overline{\unicode[STIX]{x1D702}}:H\rightarrow \unicode[STIX]{x1D6E5}^{\ast }$
be the universal covering of
$\overline{\unicode[STIX]{x1D702}}:H\rightarrow \unicode[STIX]{x1D6E5}^{\ast }$
be the universal covering of
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
. We consider the following fiber products:
$\unicode[STIX]{x1D6E5}^{\ast }$
. We consider the following fiber products:
 $$\begin{eqnarray}\begin{array}{@{}ccccc@{}}X_{\overline{\unicode[STIX]{x1D702}}} & \xrightarrow[{}]{k} & X^{\ast } & \xrightarrow[{}]{j} & \widetilde{X}\\ \downarrow & & \downarrow & & \downarrow \\ H & \xrightarrow[{}]{\unicode[STIX]{x1D702}} & \unicode[STIX]{x1D6E5}^{\ast } & \xrightarrow[{}]{} & \unicode[STIX]{x1D6E5}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccccc@{}}X_{\overline{\unicode[STIX]{x1D702}}} & \xrightarrow[{}]{k} & X^{\ast } & \xrightarrow[{}]{j} & \widetilde{X}\\ \downarrow & & \downarrow & & \downarrow \\ H & \xrightarrow[{}]{\unicode[STIX]{x1D702}} & \unicode[STIX]{x1D6E5}^{\ast } & \xrightarrow[{}]{} & \unicode[STIX]{x1D6E5}.\end{array}\end{eqnarray}$$
We set
![]() $\overline{j}=j\circ k$
. We consider the following complex which is quasi-isomorphic to the near by cycle sheaf
$\overline{j}=j\circ k$
. We consider the following complex which is quasi-isomorphic to the near by cycle sheaf
![]() $\mathbf{R}\unicode[STIX]{x1D713}\mathbf{Q}=i^{\ast }\bar{j}_{\ast }~\bar{j}^{\ast }\mathbf{Q}$
.
$\mathbf{R}\unicode[STIX]{x1D713}\mathbf{Q}=i^{\ast }\bar{j}_{\ast }~\bar{j}^{\ast }\mathbf{Q}$
.
We have
![]() $H^{i}(T^{(j)})(-1)=0$
for odd
$H^{i}(T^{(j)})(-1)=0$
for odd
![]() $i$
and
$i$
and
![]() $0\leqslant j\leqslant 2$
. Therefore the
$0\leqslant j\leqslant 2$
. Therefore the
![]() $E_{1}$
-terms of the associate monodromy weight spectral sequence are given as follows:
$E_{1}$
-terms of the associate monodromy weight spectral sequence are given as follows:
 $$\begin{eqnarray}\begin{array}{@{}ccccc@{}}H^{0}(T^{(0)})(-2) & H^{2}(T^{(1)})(-1) & H^{4}(T^{(2)})(0) & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & H^{0}(T^{(1)})(-1) & H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1) & H^{2}(T^{(1)})(0) & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & H^{0}(T^{(2)})(0) & H^{0}(T^{(1)})(0) & H^{0}(T^{(0)})(0).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccccc@{}}H^{0}(T^{(0)})(-2) & H^{2}(T^{(1)})(-1) & H^{4}(T^{(2)})(0) & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & H^{0}(T^{(1)})(-1) & H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1) & H^{2}(T^{(1)})(0) & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & H^{0}(T^{(2)})(0) & H^{0}(T^{(1)})(0) & H^{0}(T^{(0)})(0).\end{array}\end{eqnarray}$$
Therefore
![]() $Gr_{0}^{W}(H^{2}(X_{t_{0}},\mathbf{Q}))$
is isomorphic to the cohomology of
$Gr_{0}^{W}(H^{2}(X_{t_{0}},\mathbf{Q}))$
is isomorphic to the cohomology of
In this section, we consider the
![]() $E_{1}$
-differential for
$E_{1}$
-differential for
![]() $H^{2}(X)$
. We have
$H^{2}(X)$
. We have
 $$\begin{eqnarray}\displaystyle H^{0}(T^{(1)})(-1) & = & \displaystyle \mathop{\bigoplus }_{i,j}\mathbf{Q}1_{l_{ij}}\oplus \mathop{\bigoplus }_{i,j,k}\mathbf{Q}1_{m_{ij,k}},\nonumber\\ \displaystyle H^{2}(T^{(1)})(0) & = & \displaystyle \mathop{\bigoplus }_{i,j}\mathbf{Q}[l_{ij}]\oplus \mathop{\bigoplus }_{i,j,k}\mathbf{Q}[m_{ij,k}],\nonumber\\ \displaystyle H^{0}(T^{(0)})(-1) & = & \displaystyle \mathop{\bigoplus }_{i,j,k}\mathbf{Q}1_{p_{ijk}}\oplus \mathop{\bigoplus }_{i,j,k}\mathbf{Q}1_{q_{ij,k}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{0}(T^{(1)})(-1) & = & \displaystyle \mathop{\bigoplus }_{i,j}\mathbf{Q}1_{l_{ij}}\oplus \mathop{\bigoplus }_{i,j,k}\mathbf{Q}1_{m_{ij,k}},\nonumber\\ \displaystyle H^{2}(T^{(1)})(0) & = & \displaystyle \mathop{\bigoplus }_{i,j}\mathbf{Q}[l_{ij}]\oplus \mathop{\bigoplus }_{i,j,k}\mathbf{Q}[m_{ij,k}],\nonumber\\ \displaystyle H^{0}(T^{(0)})(-1) & = & \displaystyle \mathop{\bigoplus }_{i,j,k}\mathbf{Q}1_{p_{ijk}}\oplus \mathop{\bigoplus }_{i,j,k}\mathbf{Q}1_{q_{ij,k}}.\nonumber\end{eqnarray}$$
The cohomology class of
![]() $[l_{ij}]$
in
$[l_{ij}]$
in
![]() $H^{2}(g_{i})$
is denoted by
$H^{2}(g_{i})$
is denoted by
![]() $[l_{ij}]_{g_{i}}$
, etc. We identify:
$[l_{ij}]_{g_{i}}$
, etc. We identify:
(1)
 $H^{\ast }(l_{12})$
and
$H^{\ast }(l_{12})$
and
 $H^{\ast }(l_{21})$
by
$H^{\ast }(l_{21})$
by
 $[x]_{l_{12}}=-[x]_{l_{21}}$
;
$[x]_{l_{12}}=-[x]_{l_{21}}$
;(2)
 $H^{0}(q_{12,k})(-1)$
and
$H^{0}(q_{12,k})(-1)$
and
 $H^{0}(q_{21,k})(-1)$
by
$H^{0}(q_{21,k})(-1)$
by
 $1_{q_{12,k}}=-1_{q_{21,k}}$
;
$1_{q_{12,k}}=-1_{q_{21,k}}$
;(3)
 $H^{0}(p_{123})(-1)$
and
$H^{0}(p_{123})(-1)$
and
 $H^{0}(p_{213})(-1)$
by
$H^{0}(p_{213})(-1)$
by
 $1_{p_{123}}=-1_{p_{213}}=-1_{p_{132}}$
, etc.;
$1_{p_{123}}=-1_{p_{213}}=-1_{p_{132}}$
, etc.;(4)
 $H^{2}(h_{12,k})(0)$
and
$H^{2}(h_{12,k})(0)$
and
 $H^{2}(h_{21,k})(0)$
by
$H^{2}(h_{21,k})(0)$
by
 $[x]_{h_{12,k}}=-[x]_{h_{21,k}}$
.
$[x]_{h_{12,k}}=-[x]_{h_{21,k}}$
.
We describe the differentials.
The map
![]() $d:H^{0}(T^{(1)})(-1)\rightarrow H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1)$
.
$d:H^{0}(T^{(1)})(-1)\rightarrow H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1)$
.
The differential is given by
The map
![]() $d:H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1)\rightarrow H^{2}(T^{(1)})(0)$
.
$d:H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1)\rightarrow H^{2}(T^{(1)})(0)$
.
The differential is given by
 $$\begin{eqnarray}\displaystyle d([x]_{g_{i}}) & = & \displaystyle \mathop{\sum }_{j\neq i}[l_{ij}](x,l_{ij})_{g_{i}}+\mathop{\sum }_{j\neq i}\mathop{\sum }_{k=1}^{d}[m_{ij,k}](x,m_{ij,k})_{g_{i}},\nonumber\\ \displaystyle d([x]_{h_{ij,l}}) & = & \displaystyle -[m_{ij,l}](x,m_{ij,l})_{h_{ij,l}}+[m_{ji,l}](x,m_{ji,l})_{h_{ij,l}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d([x]_{g_{i}}) & = & \displaystyle \mathop{\sum }_{j\neq i}[l_{ij}](x,l_{ij})_{g_{i}}+\mathop{\sum }_{j\neq i}\mathop{\sum }_{k=1}^{d}[m_{ij,k}](x,m_{ij,k})_{g_{i}},\nonumber\\ \displaystyle d([x]_{h_{ij,l}}) & = & \displaystyle -[m_{ij,l}](x,m_{ij,l})_{h_{ij,l}}+[m_{ji,l}](x,m_{ji,l})_{h_{ij,l}},\nonumber\end{eqnarray}$$
and
Since
![]() $d[x]_{h_{21,k}}=-d[x]_{h_{12,k}}$
, this map is consistent with the rule of suffix. We can check that
$d[x]_{h_{21,k}}=-d[x]_{h_{12,k}}$
, this map is consistent with the rule of suffix. We can check that
![]() $d^{2}=0$
.
$d^{2}=0$
.
4.3 Description of the 1-cocycle associated to
 $\unicode[STIX]{x1D6E4}_{ijk,l}$
$\unicode[STIX]{x1D6E4}_{ijk,l}$
We define a closed element
![]() $\unicode[STIX]{x1D6FE}_{ijk,l}$
in
$\unicode[STIX]{x1D6FE}_{ijk,l}$
in
![]() $H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1)$
by
$H^{2}(T^{(2)})(0)\oplus H^{0}(T^{(0)})(-1)$
by
We prove the following proposition in the next section.
Proposition 4.1. The extension class associated to
![]() $c_{B}^{1,2}(\unicode[STIX]{x1D6E4}_{ijk,l})$
is equal to the image of
$c_{B}^{1,2}(\unicode[STIX]{x1D6E4}_{ijk,l})$
is equal to the image of
![]() $\unicode[STIX]{x1D6FE}_{ijk,l}$
in
$\unicode[STIX]{x1D6FE}_{ijk,l}$
in
![]() $Gr^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
.
$Gr^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
.
5 Extension class and a topological model
In this section, we compute the monodromy on the cohomologies of
![]() $W_{t_{0}}$
. This computation will be used for the computation of
$W_{t_{0}}$
. This computation will be used for the computation of
![]() $c_{B}^{1,2}(\unicode[STIX]{x1D6E4}_{ijk,l})$
.
$c_{B}^{1,2}(\unicode[STIX]{x1D6E4}_{ijk,l})$
.
5.1 Computation of monodromy for the homotopical model
 $W_{t_{0}}$
$W_{t_{0}}$
We define a family of affine varieties
![]() $W$
by
$W$
by
in
![]() $\mathbf{A}^{3}=\{(x,y,z)\mid x,y,z\in \mathbf{C}\}$
. If
$\mathbf{A}^{3}=\{(x,y,z)\mid x,y,z\in \mathbf{C}\}$
. If
![]() $t\neq 0,1/4$
, then it is smooth. Let
$t\neq 0,1/4$
, then it is smooth. Let
![]() $t_{0}$
be a sufficiently small complex number. The fiber at
$t_{0}$
be a sufficiently small complex number. The fiber at
![]() $t_{0}$
is denoted by
$t_{0}$
is denoted by
![]() $W_{t_{0}}$
. We consider the cohomology of
$W_{t_{0}}$
. We consider the cohomology of
![]() $W_{t_{0}}$
in this subsection. Let
$W_{t_{0}}$
in this subsection. Let
![]() $f:W_{t_{0}}\rightarrow \mathbf{A}^{2}$
be a map defined by
$f:W_{t_{0}}\rightarrow \mathbf{A}^{2}$
be a map defined by
![]() $(x,y,z)\rightarrow (y,z)$
. We set
$(x,y,z)\rightarrow (y,z)$
. We set
Let
![]() $\widehat{\mathbf{A}^{2}}$
be the blowing up of
$\widehat{\mathbf{A}^{2}}$
be the blowing up of
![]() $\mathbf{C}^{2}$
at two points
$\mathbf{C}^{2}$
at two points
![]() $p_{1},p_{2}$
. The exceptional divisor at
$p_{1},p_{2}$
. The exceptional divisor at
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
are denoted by
$p_{2}$
are denoted by
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
. Since the defining equation is
$E_{2}$
. Since the defining equation is
![]() $x(yz-t)+t(1-y-z)=0$
, the fiber of
$x(yz-t)+t(1-y-z)=0$
, the fiber of
![]() $f$
at
$f$
at
![]() $p_{1}$
is isomorphic to
$p_{1}$
is isomorphic to
![]() $\mathbf{A}^{1}$
and we have a map
$\mathbf{A}^{1}$
and we have a map
![]() $W_{t_{0}}\rightarrow \widehat{\mathbf{A}^{2}}$
. Let
$W_{t_{0}}\rightarrow \widehat{\mathbf{A}^{2}}$
. Let
![]() $D$
be a curve in
$D$
be a curve in
![]() $\mathbf{A}^{2}$
defined by
$\mathbf{A}^{2}$
defined by
![]() $yz=t_{0}$
and
$yz=t_{0}$
and
![]() $\widehat{D}$
be the proper transform of
$\widehat{D}$
be the proper transform of
![]() $D$
. Then we have
$D$
. Then we have
and a long exact sequence
 $$\begin{eqnarray}\begin{array}{@{}cccccccccc@{}} & H_{\widehat{D}}^{2}(\widehat{\mathbf{A}^{2}}) & \xrightarrow[{}]{\unicode[STIX]{x1D6FC}} & H^{2}(\widehat{\mathbf{A}^{2}}) & \rightarrow & H^{2}(W_{t_{0}}) & \rightarrow & H_{\widehat{D}}^{3}(\widehat{\mathbf{A}^{2}}) & \rightarrow & 0.\\ & \Vert & & \Vert & & & & \Vert & & \\ & \mathbf{Q}[\widehat{D}] & & \mathbf{Q}[E_{1}]\oplus \mathbf{Q}[E_{2}] & & & & H^{1}(\widehat{D})(-1) & & \\ & \Vert & & \Vert & & & & \Vert & & \\ & \mathbf{Q}(-1) & & \mathbf{Q}(-1)\oplus \mathbf{Q}(-1) & & & & \mathbf{Q}(-2) & & \end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cccccccccc@{}} & H_{\widehat{D}}^{2}(\widehat{\mathbf{A}^{2}}) & \xrightarrow[{}]{\unicode[STIX]{x1D6FC}} & H^{2}(\widehat{\mathbf{A}^{2}}) & \rightarrow & H^{2}(W_{t_{0}}) & \rightarrow & H_{\widehat{D}}^{3}(\widehat{\mathbf{A}^{2}}) & \rightarrow & 0.\\ & \Vert & & \Vert & & & & \Vert & & \\ & \mathbf{Q}[\widehat{D}] & & \mathbf{Q}[E_{1}]\oplus \mathbf{Q}[E_{2}] & & & & H^{1}(\widehat{D})(-1) & & \\ & \Vert & & \Vert & & & & \Vert & & \\ & \mathbf{Q}(-1) & & \mathbf{Q}(-1)\oplus \mathbf{Q}(-1) & & & & \mathbf{Q}(-2) & & \end{array}\end{eqnarray}$$
The map
![]() $\unicode[STIX]{x1D6FC}$
is defined by
$\unicode[STIX]{x1D6FC}$
is defined by
![]() $\unicode[STIX]{x1D6FC}(D)=E_{1}+E_{2}$
. As a consequence, we have the following proposition.
$\unicode[STIX]{x1D6FC}(D)=E_{1}+E_{2}$
. As a consequence, we have the following proposition.
Proposition 5.1.
(1) There is a sub Hodge structure
 $V_{2}$
in
$V_{2}$
in
 $H^{2}(W_{t_{0}})$
such that
$H^{2}(W_{t_{0}})$
such that  $$\begin{eqnarray}V_{2}\simeq \mathbf{Q}(-1),\qquad H^{2}(W_{t_{0}})/V_{2}\simeq \mathbf{Q}(-2).\end{eqnarray}$$
$$\begin{eqnarray}V_{2}\simeq \mathbf{Q}(-1),\qquad H^{2}(W_{t_{0}})/V_{2}\simeq \mathbf{Q}(-2).\end{eqnarray}$$
(2) The de Rham part
 $H_{\widehat{D},dR}^{3}(\widehat{\mathbf{A}^{2}})$
is generated by the image of
$H_{\widehat{D},dR}^{3}(\widehat{\mathbf{A}^{2}})$
is generated by the image of  $$\begin{eqnarray}\unicode[STIX]{x1D714}=\frac{dy\,dz}{yz-t}\in H_{dR}^{2}(W_{t_{0}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}=\frac{dy\,dz}{yz-t}\in H_{dR}^{2}(W_{t_{0}}).\end{eqnarray}$$
We set
![]() $V_{4}=H^{2}(W_{t_{0}})/V_{2}$
.
$V_{4}=H^{2}(W_{t_{0}})/V_{2}$
.
Proof. (2) Let
be a differential form on
![]() $\mathbf{A}^{2}-W_{t_{0}}$
. Then the residue
$\mathbf{A}^{2}-W_{t_{0}}$
. Then the residue
![]() $\operatorname{res}_{W_{t_{0}}}(\unicode[STIX]{x1D6FA})$
of
$\operatorname{res}_{W_{t_{0}}}(\unicode[STIX]{x1D6FA})$
of
![]() $\unicode[STIX]{x1D6FA}$
along
$\unicode[STIX]{x1D6FA}$
along
![]() $W_{t_{0}}$
is equal to
$W_{t_{0}}$
is equal to
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() $\mathbf{A}^{2}-D\subset \widehat{A^{2}}-\widehat{D}$
. Therefore
$\mathbf{A}^{2}-D\subset \widehat{A^{2}}-\widehat{D}$
. Therefore
![]() $\unicode[STIX]{x1D714}$
defines a holomorphic two form on
$\unicode[STIX]{x1D714}$
defines a holomorphic two form on
![]() $W_{t_{0}}$
. Since the residue of
$W_{t_{0}}$
. Since the residue of
along
![]() $D$
is equal to
$D$
is equal to
![]() $dz/z$
, the image of
$dz/z$
, the image of
![]() $\unicode[STIX]{x1D714}$
under the map
$\unicode[STIX]{x1D714}$
under the map
![]() $H_{dR}^{2}(W_{t_{0}})\rightarrow H_{dR}^{1}(\widehat{D})(-1)$
is a generator of
$H_{dR}^{2}(W_{t_{0}})\rightarrow H_{dR}^{1}(\widehat{D})(-1)$
is a generator of
![]() $H_{dR}^{1}(\widehat{D})(-1)$
.◻
$H_{dR}^{1}(\widehat{D})(-1)$
.◻
5.2 Relative cycles and extension
We define four affine planes
![]() $L_{1},L_{2},L_{3}$
and
$L_{1},L_{2},L_{3}$
and
![]() $M$
in
$M$
in
![]() $\mathbf{A}^{3}$
by
$\mathbf{A}^{3}$
by
![]() $L_{1}=$
$L_{1}=$
![]() $\{x=0\}$
,
$\{x=0\}$
,
![]() $L_{2}=\{y=0\}$
,
$L_{2}=\{y=0\}$
,
![]() $L_{3}=\{z=0\}$
and
$L_{3}=\{z=0\}$
and
![]() $M=\{1-x-y-z=0\}$
. Then
$M=\{1-x-y-z=0\}$
. Then
![]() $(L_{i}\cap M)_{t_{0}}\subset W_{t_{0}}$
. We set
$(L_{i}\cap M)_{t_{0}}\subset W_{t_{0}}$
. We set
![]() $T=(L_{1}\cap M)\cup (L_{2}\cup M)\cup (L_{3}\cap M)$
. Then we have the following dual exact sequences.
$T=(L_{1}\cap M)\cup (L_{2}\cup M)\cup (L_{3}\cap M)$
. Then we have the following dual exact sequences.
where
![]() $j:W_{t_{0}}-T_{t_{0}}\rightarrow W_{t_{0}}$
is the open immersion. We set
$j:W_{t_{0}}-T_{t_{0}}\rightarrow W_{t_{0}}$
is the open immersion. We set
![]() $\overline{\unicode[STIX]{x1D6FE}}=\overline{\unicode[STIX]{x1D6FE}}_{1}+\overline{\unicode[STIX]{x1D6FE}}_{2}+\overline{\unicode[STIX]{x1D6FE}}_{3}$
, where
$\overline{\unicode[STIX]{x1D6FE}}=\overline{\unicode[STIX]{x1D6FE}}_{1}+\overline{\unicode[STIX]{x1D6FE}}_{2}+\overline{\unicode[STIX]{x1D6FE}}_{3}$
, where
 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6FE}}_{1} & = & \displaystyle \{(x,y,z)=(0,t,1-t)\mid t\in [0,1]\},\nonumber\\ \displaystyle \overline{\unicode[STIX]{x1D6FE}}_{2} & = & \displaystyle \{(x,y,z)=(1-t,0,t)\mid t\in [0,1]\},\nonumber\\ \displaystyle \overline{\unicode[STIX]{x1D6FE}}_{3} & = & \displaystyle \{(x,y,z)=(t,1-t,0)\mid t\in [0,1]\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x1D6FE}}_{1} & = & \displaystyle \{(x,y,z)=(0,t,1-t)\mid t\in [0,1]\},\nonumber\\ \displaystyle \overline{\unicode[STIX]{x1D6FE}}_{2} & = & \displaystyle \{(x,y,z)=(1-t,0,t)\mid t\in [0,1]\},\nonumber\\ \displaystyle \overline{\unicode[STIX]{x1D6FE}}_{3} & = & \displaystyle \{(x,y,z)=(t,1-t,0)\mid t\in [0,1]\}.\nonumber\end{eqnarray}$$
Then
![]() $\overline{\unicode[STIX]{x1D6FE}}$
defines an element in
$\overline{\unicode[STIX]{x1D6FE}}$
defines an element in
![]() $H_{1}(T_{t_{0}},\mathbf{Q})$
, which is also denoted by
$H_{1}(T_{t_{0}},\mathbf{Q})$
, which is also denoted by
![]() $\overline{\unicode[STIX]{x1D6FE}}$
. Let
$\overline{\unicode[STIX]{x1D6FE}}$
. Let
![]() $\unicode[STIX]{x1D6FE}$
be an element in
$\unicode[STIX]{x1D6FE}$
be an element in
![]() $H_{2}(W_{t_{0}},T_{t_{0}},\mathbf{Q})$
such that
$H_{2}(W_{t_{0}},T_{t_{0}},\mathbf{Q})$
such that
![]() $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})$
is equal to
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})$
is equal to
![]() $\overline{\unicode[STIX]{x1D6FE}}$
. Then
$\overline{\unicode[STIX]{x1D6FE}}$
. Then
![]() $\unicode[STIX]{x1D6FE}$
is represented by the relative 2-cycle
$\unicode[STIX]{x1D6FE}$
is represented by the relative 2-cycle
![]() $\unicode[STIX]{x1D6E4}$
defined by
$\unicode[STIX]{x1D6E4}$
defined by
5.3 Pairing given by period integral
We use the coordinate
![]() $(y,z)$
to compute the pairing
$(y,z)$
to compute the pairing
![]() $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})$
. We assume that
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})$
. We assume that
![]() $t\in \mathbf{R}$
and
$t\in \mathbf{R}$
and
![]() $t<0$
. Then we have
$t<0$
. Then we have
It is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\frac{1}{z}\left[\log \left(1-\frac{yz}{t}\right)\right]_{y=0}^{1-z}\,dz=\int _{0}^{1}\frac{dz}{z}\log \left(1-\frac{z}{t}+\frac{z^{2}}{t}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{1}\left\{\log \left(1-\frac{z}{\unicode[STIX]{x1D6FC}(t)}\right)+\log \left(1-\frac{z}{1-\unicode[STIX]{x1D6FC}(t)}\right)\right\}\frac{dz}{z}\nonumber\\ \displaystyle & & \displaystyle \quad =Li_{2}\left(\frac{1}{\unicode[STIX]{x1D6FC}(t)}\right)+Li_{2}\left(\frac{1}{1-\unicode[STIX]{x1D6FC}(t)}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{2}\{\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t))\}^{2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{1}\frac{1}{z}\left[\log \left(1-\frac{yz}{t}\right)\right]_{y=0}^{1-z}\,dz=\int _{0}^{1}\frac{dz}{z}\log \left(1-\frac{z}{t}+\frac{z^{2}}{t}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{1}\left\{\log \left(1-\frac{z}{\unicode[STIX]{x1D6FC}(t)}\right)+\log \left(1-\frac{z}{1-\unicode[STIX]{x1D6FC}(t)}\right)\right\}\frac{dz}{z}\nonumber\\ \displaystyle & & \displaystyle \quad =Li_{2}\left(\frac{1}{\unicode[STIX]{x1D6FC}(t)}\right)+Li_{2}\left(\frac{1}{1-\unicode[STIX]{x1D6FC}(t)}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{1}{2}\{\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t))\}^{2}\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}(t)<0,1-\unicode[STIX]{x1D6FC}(t)>1$
are the solutions of the equation
$\unicode[STIX]{x1D6FC}(t)<0,1-\unicode[STIX]{x1D6FC}(t)>1$
are the solutions of the equation
Then
![]() $\unicode[STIX]{x1D6FC}(t)\rightarrow 0$
for
$\unicode[STIX]{x1D6FC}(t)\rightarrow 0$
for
![]() $t\rightarrow 0$
. As a consequence, we have
$t\rightarrow 0$
. As a consequence, we have
Proposition 5.2.
(1) We have
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})=-{\textstyle \frac{1}{2}}\{\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t))\}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})=-{\textstyle \frac{1}{2}}\{\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t))\}^{2}.\end{eqnarray}$$
(2) Let
 $\unicode[STIX]{x1D70C}_{t}$
be the monodromy action of a small circle around
$\unicode[STIX]{x1D70C}_{t}$
be the monodromy action of a small circle around
 $t=0$
. Then we haveand
$t=0$
. Then we haveand $$\begin{eqnarray}(\unicode[STIX]{x1D70C}_{t}(\unicode[STIX]{x1D6FE}),\unicode[STIX]{x1D714})=-{\textstyle \frac{1}{2}}\{\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t))-2\unicode[STIX]{x1D70B}\mathbf{i}\}^{2},\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70C}_{t}(\unicode[STIX]{x1D6FE}),\unicode[STIX]{x1D714})=-{\textstyle \frac{1}{2}}\{\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t))-2\unicode[STIX]{x1D70B}\mathbf{i}\}^{2},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle ((\unicode[STIX]{x1D70C}_{t}-1)\cdot \unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})=2\unicode[STIX]{x1D70B}\mathbf{i}(\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t)))+2\unicode[STIX]{x1D70B}^{2},\nonumber\\ \displaystyle & & \displaystyle ((\unicode[STIX]{x1D70C}_{t}-1)^{2}\cdot \unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})=4\unicode[STIX]{x1D70B}^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle ((\unicode[STIX]{x1D70C}_{t}-1)\cdot \unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})=2\unicode[STIX]{x1D70B}\mathbf{i}(\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t)))+2\unicode[STIX]{x1D70B}^{2},\nonumber\\ \displaystyle & & \displaystyle ((\unicode[STIX]{x1D70C}_{t}-1)^{2}\cdot \unicode[STIX]{x1D6FE},\unicode[STIX]{x1D714})=4\unicode[STIX]{x1D70B}^{2}.\nonumber\end{eqnarray}$$
5.4 Two topological cycles and the monodromy action on the homology
Definition of
![]() $\unicode[STIX]{x1D6FE}_{1}$
. Let
$\unicode[STIX]{x1D6FE}_{1}$
. Let
![]() $\unicode[STIX]{x1D6FF}$
be a small circle around 0 in
$\unicode[STIX]{x1D6FF}$
be a small circle around 0 in
![]() $z$
-plane and
$z$
-plane and
![]() $\overline{\unicode[STIX]{x1D6FF}}$
be its image in
$\overline{\unicode[STIX]{x1D6FF}}$
be its image in
![]() $\widehat{D}=\{yz=t\}$
. Let
$\widehat{D}=\{yz=t\}$
. Let
![]() $N_{\overline{\unicode[STIX]{x1D6FF}}}$
be its tubular neighborhood in
$N_{\overline{\unicode[STIX]{x1D6FF}}}$
be its tubular neighborhood in
![]() $\widehat{\mathbf{A}^{2}}$
and
$\widehat{\mathbf{A}^{2}}$
and
![]() $\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x2202}N_{\overline{\unicode[STIX]{x1D6FF}}}$
be its boundary. The cycle
$\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x2202}N_{\overline{\unicode[STIX]{x1D6FF}}}$
be its boundary. The cycle
![]() $\unicode[STIX]{x1D6FE}_{1}$
is a
$\unicode[STIX]{x1D6FE}_{1}$
is a
![]() $S^{1}$
bundle over
$S^{1}$
bundle over
![]() $\overline{\unicode[STIX]{x1D6FF}}$
. By Cauchy formula, we have
$\overline{\unicode[STIX]{x1D6FF}}$
. By Cauchy formula, we have
Definition of
![]() $\unicode[STIX]{x1D6FE}_{2}$
. Let
$\unicode[STIX]{x1D6FE}_{2}$
. Let
![]() $l$
be a path connecting
$l$
be a path connecting
![]() $\unicode[STIX]{x1D6FC}(t)$
and
$\unicode[STIX]{x1D6FC}(t)$
and
![]() $1-\unicode[STIX]{x1D6FC}(t)$
in
$1-\unicode[STIX]{x1D6FC}(t)$
in
![]() $\{z\in \mathbf{C}\mid z\neq 0\}$
and
$\{z\in \mathbf{C}\mid z\neq 0\}$
and
![]() $\overline{l}$
be its image in
$\overline{l}$
be its image in
![]() $\widehat{D}=\{yz=t\}$
. We choose a tubular neighborhood
$\widehat{D}=\{yz=t\}$
. We choose a tubular neighborhood
![]() $N_{\overline{l}}$
of
$N_{\overline{l}}$
of
![]() $\overline{l}$
and retraction
$\overline{l}$
and retraction
![]() $r:N_{\overline{l}}\rightarrow \overline{l}$
such that
$r:N_{\overline{l}}\rightarrow \overline{l}$
such that
![]() $r^{-1}(\unicode[STIX]{x1D6FC}(t))\subset E_{1}$
and
$r^{-1}(\unicode[STIX]{x1D6FC}(t))\subset E_{1}$
and
![]() $r^{-1}(1-\unicode[STIX]{x1D6FC}(t))\subset E_{2}$
. Note that the point
$r^{-1}(1-\unicode[STIX]{x1D6FC}(t))\subset E_{2}$
. Note that the point
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
are given by
$p_{2}$
are given by
![]() $(y,z)=(1-\unicode[STIX]{x1D6FC}(t),\unicode[STIX]{x1D6FC}(t))$
and
$(y,z)=(1-\unicode[STIX]{x1D6FC}(t),\unicode[STIX]{x1D6FC}(t))$
and
![]() $(y,z)=(\unicode[STIX]{x1D6FC}(t),1-\unicode[STIX]{x1D6FC}(t))$
. Then
$(y,z)=(\unicode[STIX]{x1D6FC}(t),1-\unicode[STIX]{x1D6FC}(t))$
. Then
![]() $\unicode[STIX]{x2202}(r^{-1}(\unicode[STIX]{x1D6FC}(t)))$
and
$\unicode[STIX]{x2202}(r^{-1}(\unicode[STIX]{x1D6FC}(t)))$
and
![]() $\unicode[STIX]{x2202}(r^{-1}(1-\unicode[STIX]{x1D6FC}(t)))$
are bounded by
$\unicode[STIX]{x2202}(r^{-1}(1-\unicode[STIX]{x1D6FC}(t)))$
are bounded by
![]() $T_{1}$
and
$T_{1}$
and
![]() $T_{2}$
in
$T_{2}$
in
![]() $E_{1}\cap X_{t}$
and
$E_{1}\cap X_{t}$
and
![]() $E_{2}\cap X_{t}$
. Let
$E_{2}\cap X_{t}$
. Let
![]() $z_{0}$
be a point in
$z_{0}$
be a point in
![]() $l$
and
$l$
and
![]() $\overline{z_{0}}$
be the corresponding point in
$\overline{z_{0}}$
be the corresponding point in
![]() $\widehat{D}$
. Then
$\widehat{D}$
. Then
![]() $\unicode[STIX]{x2202}(r^{-1}(\overline{z_{0}}))$
forms an
$\unicode[STIX]{x2202}(r^{-1}(\overline{z_{0}}))$
forms an
![]() $S^{1}$
-bundle
$S^{1}$
-bundle
![]() $S$
over
$S$
over
![]() $\overline{l}$
. We set
$\overline{l}$
. We set
![]() $\unicode[STIX]{x1D6FE}_{2}=S\cup T_{1}\cup T_{2}$
and we have
$\unicode[STIX]{x1D6FE}_{2}=S\cup T_{1}\cup T_{2}$
and we have
It is equal to
![]() $2\unicode[STIX]{x1D70B}\mathbf{i}(\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t)))+2\unicode[STIX]{x1D70B}^{2}$
by choosing a proper choice of
$2\unicode[STIX]{x1D70B}\mathbf{i}(\log (1-\unicode[STIX]{x1D6FC}(t))-\log (-\unicode[STIX]{x1D6FC}(t)))+2\unicode[STIX]{x1D70B}^{2}$
by choosing a proper choice of
![]() $l$
.
$l$
.
Action of the monodromy on the topological cycles. By the previous subsection, we have the following proposition.
Proposition 5.3. Under the above notations, we have
6 Lower bound of the image of cycle map
6.1 Monodromy weight filtration and the element
 $\unicode[STIX]{x1D6FE}_{ijk,l}$
$\unicode[STIX]{x1D6FE}_{ijk,l}$
In this section, we prove Proposition 4.1. We choose an open set
![]() $U_{0}$
of
$U_{0}$
of
![]() $\widetilde{X}_{0}$
such that the pair
$\widetilde{X}_{0}$
such that the pair
![]() $(U_{0},U_{0}\cap M_{l})$
is homeomorphic to
$(U_{0},U_{0}\cap M_{l})$
is homeomorphic to
![]() $(Y_{0},Y_{0}\cap D)$
where
$(Y_{0},Y_{0}\cap D)$
where
![]() $Y_{0}$
and
$Y_{0}$
and
![]() $D_{0}$
is a subvariety of
$D_{0}$
is a subvariety of
![]() $\mathbf{A}_{\mathbf{C}}^{3}$
defined by
$\mathbf{A}_{\mathbf{C}}^{3}$
defined by
![]() $Y_{0}=\{xyz=0\}$
,
$Y_{0}=\{xyz=0\}$
,
![]() $D=\{1-x-y=0\}$
. Let
$D=\{1-x-y=0\}$
. Let
![]() $U$
be a sufficiently small tubular neighborhood of
$U$
be a sufficiently small tubular neighborhood of
![]() $U_{0}$
. Then
$U_{0}$
. Then
![]() $U$
is homeomorphic to
$U$
is homeomorphic to
![]() $\mathbf{A}_{\mathbf{C}}^{3}$
.
$\mathbf{A}_{\mathbf{C}}^{3}$
.
We consider the restriction of the complex (15) to
![]() $U_{0}$
, and the induced filtration
$U_{0}$
, and the induced filtration
![]() $M$
on it. This filtration is also denoted by
$M$
on it. This filtration is also denoted by
![]() $M$
. Let
$M$
. Let
![]() $X\rightarrow \unicode[STIX]{x1D6E5}=\{t\in \mathbf{C}\mid |t|<\unicode[STIX]{x1D716}\}$
be the family of affine varieties defined in (19). We blow up the variety
$X\rightarrow \unicode[STIX]{x1D6E5}=\{t\in \mathbf{C}\mid |t|<\unicode[STIX]{x1D716}\}$
be the family of affine varieties defined in (19). We blow up the variety
![]() $X$
at
$X$
at
![]() $q_{23}=\{(x,y,z,t)=(1,0,0,0)\}$
,
$q_{23}=\{(x,y,z,t)=(1,0,0,0)\}$
,
![]() $q_{31}=\{(x,y,z,t)=(0,1,0,0)\}$
,
$q_{31}=\{(x,y,z,t)=(0,1,0,0)\}$
,
![]() $q_{12}=\{(x,y,z,t)=(0,0,1,0)\}$
, and we have a family
$q_{12}=\{(x,y,z,t)=(0,0,1,0)\}$
, and we have a family
![]() $\widetilde{X}\rightarrow \unicode[STIX]{x1D6E5}$
whose closed fiber is a simple normal crossing variety. Though it is not a proper family of varieties, we consider a filtration similar to the monodromy weight filtration in
$\widetilde{X}\rightarrow \unicode[STIX]{x1D6E5}$
whose closed fiber is a simple normal crossing variety. Though it is not a proper family of varieties, we consider a filtration similar to the monodromy weight filtration in
![]() $i^{\ast }\mathbf{R}\bar{j}_{\ast }\bar{j}^{\ast }\mathbf{Q}$
. The associated spectral sequence will be written as
$i^{\ast }\mathbf{R}\bar{j}_{\ast }\bar{j}^{\ast }\mathbf{Q}$
. The associated spectral sequence will be written as
![]() $E_{U,r}^{p,q}$
.
$E_{U,r}^{p,q}$
.
Proposition 6.1.
(1) The
 $E_{2}$
-terms are given as follows. As a consequence it degenerates at
$E_{2}$
-terms are given as follows. As a consequence it degenerates at $$\begin{eqnarray}E_{U,2}^{-2,4}=\mathbf{Q}(-2),\qquad E_{U,2}^{0,2}=\mathbf{Q}(-1),\qquad E_{U,2}^{2,0}=0.\end{eqnarray}$$
$$\begin{eqnarray}E_{U,2}^{-2,4}=\mathbf{Q}(-2),\qquad E_{U,2}^{0,2}=\mathbf{Q}(-1),\qquad E_{U,2}^{2,0}=0.\end{eqnarray}$$
 $E_{2}$
.
$E_{2}$
.(2) The natural map
 $E_{2}^{p,q}\rightarrow E_{U,2}^{p,q}$
is surjective. As a consequence, the natural map
$E_{2}^{p,q}\rightarrow E_{U,2}^{p,q}$
is surjective. As a consequence, the natural map
 $H^{2}(X_{t_{0}})\rightarrow H^{2}(U_{t_{0}})$
is strictly compatible with respect to the induced filtration.
$H^{2}(X_{t_{0}})\rightarrow H^{2}(U_{t_{0}})$
is strictly compatible with respect to the induced filtration.
Proof. We compute
![]() $E_{2}^{0,2}$
.
$E_{2}^{0,2}$
.
![]() $E_{1}$
-terms are similar as in Section 4.2. The suffix
$E_{1}$
-terms are similar as in Section 4.2. The suffix
![]() $l$
appearing in the symbol
$l$
appearing in the symbol
![]() $m_{ij,l}$
is 1, so we denoted it by
$m_{ij,l}$
is 1, so we denoted it by
![]() $m_{ij}$
. The differentials are given by the same formula.
$m_{ij}$
. The differentials are given by the same formula.
 $$\begin{eqnarray}\displaystyle H^{0}(T_{U}^{(1)})(-1) & \simeq & \displaystyle \langle 1_{l_{ij}}\rangle _{1\leqslant i<j\leqslant 3}\oplus \langle 1_{m_{ij}}\rangle _{1\leqslant i\neq j\leqslant 3},\nonumber\\ \displaystyle H^{0}(T_{U}^{(0)})(-1)\oplus H^{2}(T_{U}^{(2)})(0) & \simeq & \displaystyle \langle [m_{ij}]_{g_{i}}\rangle _{1\leqslant i\neq j\leqslant 3}\oplus \langle [m_{ij}]_{h_{ij}}\rangle _{1\leqslant i\neq j\leqslant 3}\nonumber\\ \displaystyle & & \displaystyle \oplus \,\langle 1_{q_{ij}}\rangle _{1\leqslant i<j\leqslant 3}\oplus \langle 1_{p_{123}}\rangle ,\nonumber\\ \displaystyle H^{2}(T_{U}^{(1)})(0) & \simeq & \displaystyle \langle [m_{ij}]\rangle _{1\leqslant i\neq j\leqslant 3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{0}(T_{U}^{(1)})(-1) & \simeq & \displaystyle \langle 1_{l_{ij}}\rangle _{1\leqslant i<j\leqslant 3}\oplus \langle 1_{m_{ij}}\rangle _{1\leqslant i\neq j\leqslant 3},\nonumber\\ \displaystyle H^{0}(T_{U}^{(0)})(-1)\oplus H^{2}(T_{U}^{(2)})(0) & \simeq & \displaystyle \langle [m_{ij}]_{g_{i}}\rangle _{1\leqslant i\neq j\leqslant 3}\oplus \langle [m_{ij}]_{h_{ij}}\rangle _{1\leqslant i\neq j\leqslant 3}\nonumber\\ \displaystyle & & \displaystyle \oplus \,\langle 1_{q_{ij}}\rangle _{1\leqslant i<j\leqslant 3}\oplus \langle 1_{p_{123}}\rangle ,\nonumber\\ \displaystyle H^{2}(T_{U}^{(1)})(0) & \simeq & \displaystyle \langle [m_{ij}]\rangle _{1\leqslant i\neq j\leqslant 3}.\nonumber\end{eqnarray}$$
The space
![]() $E_{U,2}^{0,2}$
is one dimensional generated by
$E_{U,2}^{0,2}$
is one dimensional generated by
In fact, the linear form
vanishes on the image of
![]() $E_{1}^{-1,2}$
and nonzero on
$E_{1}^{-1,2}$
and nonzero on
![]() $\unicode[STIX]{x1D6FE}_{123}$
. Therefore the restriction
$\unicode[STIX]{x1D6FE}_{123}$
. Therefore the restriction
![]() $E_{2}^{0,2}\rightarrow E_{U,2}^{0.2}$
is surjective.
$E_{2}^{0,2}\rightarrow E_{U,2}^{0.2}$
is surjective.
We can check that
![]() $E_{2}^{-2,4}$
is generated by the class
$E_{2}^{-2,4}$
is generated by the class
![]() $[p_{123}]$
. Since
$[p_{123}]$
. Since
![]() $d\geqslant 4$
, the class
$d\geqslant 4$
, the class
![]() $[p_{123}]-[p_{124}]+[p_{134}]-[p_{234}]$
defines an element in
$[p_{123}]-[p_{124}]+[p_{134}]-[p_{234}]$
defines an element in
![]() $E_{2}^{-2,4}$
, which maps to
$E_{2}^{-2,4}$
, which maps to
![]() $[p_{123}]$
under the natural map
$[p_{123}]$
under the natural map
![]() $E_{2}^{-2,4}\rightarrow E_{U,2}^{-2,4}$
.◻
$E_{2}^{-2,4}\rightarrow E_{U,2}^{-2,4}$
.◻
Let
![]() $\unicode[STIX]{x1D704}:H_{2}(U_{t_{0}},\mathbf{Q})\rightarrow H_{2}(X_{t_{0}},\mathbf{Q})$
be the homomorphism induced by the inclusion. Via this inclusion, the filtration
$\unicode[STIX]{x1D704}:H_{2}(U_{t_{0}},\mathbf{Q})\rightarrow H_{2}(X_{t_{0}},\mathbf{Q})$
be the homomorphism induced by the inclusion. Via this inclusion, the filtration
![]() $M$
induces that on the image of
$M$
induces that on the image of
![]() $\unicode[STIX]{x1D704}$
, which is also denoted
$\unicode[STIX]{x1D704}$
, which is also denoted
![]() $M$
.
$M$
.
Corollary 6.2.
(1) Then the image of
 $Gr_{0}^{M}(\unicode[STIX]{x1D704}):Gr_{0}^{M}(H_{2}(U_{t_{0}},\mathbf{Q}))\rightarrow Gr_{0}^{M}(H_{2}(U_{t_{0}},\mathbf{Q}))$
is equal to
$Gr_{0}^{M}(\unicode[STIX]{x1D704}):Gr_{0}^{M}(H_{2}(U_{t_{0}},\mathbf{Q}))\rightarrow Gr_{0}^{M}(H_{2}(U_{t_{0}},\mathbf{Q}))$
is equal to
 $Gr_{0}^{M}(Im(\unicode[STIX]{x1D704}))$
.
$Gr_{0}^{M}(Im(\unicode[STIX]{x1D704}))$
.(2) The image of
 $Gr_{0}^{M}(\unicode[STIX]{x1D704})$
is equal to the annihilator of the kernel of under the natural pairing
$Gr_{0}^{M}(\unicode[STIX]{x1D704})$
is equal to the annihilator of the kernel of under the natural pairing $$\begin{eqnarray}Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))\rightarrow Gr_{0}^{M}H^{2}(U_{t_{0}},\mathbf{Q}(2))\end{eqnarray}$$
$$\begin{eqnarray}Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))\rightarrow Gr_{0}^{M}H^{2}(U_{t_{0}},\mathbf{Q}(2))\end{eqnarray}$$
 $$\begin{eqnarray}Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))\otimes Gr_{0}^{M}H_{2}(X_{t_{0}},\mathbf{Q})\rightarrow \mathbf{Q}(2).\end{eqnarray}$$
$$\begin{eqnarray}Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))\otimes Gr_{0}^{M}H_{2}(X_{t_{0}},\mathbf{Q})\rightarrow \mathbf{Q}(2).\end{eqnarray}$$
(3) The image
 $Gr_{0}^{M}(\unicode[STIX]{x1D704})$
is generated by
$Gr_{0}^{M}(\unicode[STIX]{x1D704})$
is generated by
 $\unicode[STIX]{x1D6FE}_{ijk,l}$
defined by (18).
$\unicode[STIX]{x1D6FE}_{ijk,l}$
defined by (18).
6.2 The subspace of
 $Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))$
generated by
$Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))$
generated by
 $\unicode[STIX]{x1D6FE}_{ijk,l}$
$\unicode[STIX]{x1D6FE}_{ijk,l}$
In this subsection, we compute the dimension of the subspace of
![]() $Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))$
generated by the image of
$Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))$
generated by the image of
![]() $\unicode[STIX]{x1D6FE}_{ijk,l}$
. Eliminating elements of the form
$\unicode[STIX]{x1D6FE}_{ijk,l}$
. Eliminating elements of the form
![]() $[m_{ij,k}]_{h_{ij,k}}$
using the relation (17), we have an isomorphism
$[m_{ij,k}]_{h_{ij,k}}$
using the relation (17), we have an isomorphism
where
Here
![]() $u_{i}$
is the pull back of the line in
$u_{i}$
is the pull back of the line in
![]() $\overline{g_{i}}$
, and
$\overline{g_{i}}$
, and
![]() $K$
is the space generated by elements of the form (16). By the definition of
$K$
is the space generated by elements of the form (16). By the definition of
![]() $u_{i}$
, we have
$u_{i}$
, we have
Under the isomorphism (20) the class of
![]() $\unicode[STIX]{x1D6FE}_{ijk,l}$
corresponds to
$\unicode[STIX]{x1D6FE}_{ijk,l}$
corresponds to
The projection from
![]() $W$
to
$W$
to
![]() $\langle [u_{i}]_{g_{i}}\rangle _{1\leqslant i\leqslant d}$
(resp.
$\langle [u_{i}]_{g_{i}}\rangle _{1\leqslant i\leqslant d}$
(resp.
![]() $\langle 1_{q_{ij,l}}\rangle _{1\leqslant i<j\leqslant d}$
) with respect to the direct sum (21) is denoted by
$\langle 1_{q_{ij,l}}\rangle _{1\leqslant i<j\leqslant d}$
) with respect to the direct sum (21) is denoted by
![]() $\unicode[STIX]{x1D70B}_{u}$
(resp.
$\unicode[STIX]{x1D70B}_{u}$
(resp.
![]() $\unicode[STIX]{x1D70B}_{q,l}$
).
$\unicode[STIX]{x1D70B}_{q,l}$
).
Lemma 6.3. Suppose that
![]() $v=\sum _{1\leqslant i<j\leqslant d}a_{ij}d(1_{l_{ij}})$
is an element in
$v=\sum _{1\leqslant i<j\leqslant d}a_{ij}d(1_{l_{ij}})$
is an element in
![]() $\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle$
. Then
$\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle$
. Then
![]() $v$
can be uniquely expressed as a linear combination of
$v$
can be uniquely expressed as a linear combination of
![]() $d(1_{l_{1i}}+1_{l_{ij}}+1_{l_{j1}})$
for
$d(1_{l_{1i}}+1_{l_{ij}}+1_{l_{j1}})$
for
![]() $2\leqslant i<j\leqslant d$
.
$2\leqslant i<j\leqslant d$
.
Proof. We set
![]() $A_{ijk}=d(1_{l_{ij}}+1_{l_{jk}}+1_{l_{ki}})$
. We have
$A_{ijk}=d(1_{l_{ij}}+1_{l_{jk}}+1_{l_{ki}})$
. We have
![]() $\unicode[STIX]{x1D70B}_{u}(\unicode[STIX]{x1D6FE}_{ijk,l}^{\ast })=0$
and
$\unicode[STIX]{x1D70B}_{u}(\unicode[STIX]{x1D6FE}_{ijk,l}^{\ast })=0$
and
![]() $\unicode[STIX]{x1D70B}_{u}(d(1_{l_{ij}}))=u_{i}-u_{j}$
. Therefore
$\unicode[STIX]{x1D70B}_{u}(d(1_{l_{ij}}))=u_{i}-u_{j}$
. Therefore
![]() $v$
is a linear combination of
$v$
is a linear combination of
![]() $A_{ijk}$
. Since
$A_{ijk}$
. Since
![]() $A_{1ij}-A_{1ik}+A_{1jk}-A_{ijk}=0$
,
$A_{1ij}-A_{1ik}+A_{1jk}-A_{ijk}=0$
,
![]() $v$
is a linear combination of
$v$
is a linear combination of
![]() $A_{1ij}$
for
$A_{1ij}$
for
![]() $i<j$
. Since
$i<j$
. Since
![]() $A_{1ij}$
(
$A_{1ij}$
(
![]() $1\leqslant i<j\leqslant d$
) are linearly independent by looking the component
$1\leqslant i<j\leqslant d$
) are linearly independent by looking the component
![]() $\langle 1_{q_{ij}}\rangle _{2\leqslant i<j\leqslant d}$
.◻
$\langle 1_{q_{ij}}\rangle _{2\leqslant i<j\leqslant d}$
.◻
For
![]() $1\leqslant i<j<k<m\leqslant d$
and
$1\leqslant i<j<k<m\leqslant d$
and
![]() $1\leqslant l\leqslant d$
, we set
$1\leqslant l\leqslant d$
, we set
Then
![]() $\langle \unicode[STIX]{x1D6FE}_{ijk.l}^{\ast }\rangle$
is generated by
$\langle \unicode[STIX]{x1D6FE}_{ijk.l}^{\ast }\rangle$
is generated by
![]() $\widehat{\unicode[STIX]{x1D6FE}_{1jkm,1}}$
for
$\widehat{\unicode[STIX]{x1D6FE}_{1jkm,1}}$
for
![]() $2\leqslant j<k<m\leqslant d$
and
$2\leqslant j<k<m\leqslant d$
and
![]() $\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast }$
for
$\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast }$
for
![]() $2\leqslant i<j\leqslant d$
,
$2\leqslant i<j\leqslant d$
,
![]() $1\leqslant l\leqslant d$
.
$1\leqslant l\leqslant d$
.
Lemma 6.4.
(1) We have
and $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{q,l}(\unicode[STIX]{x1D6FE}_{1ij,l^{\prime }}^{\ast })=\unicode[STIX]{x1D6FF}_{l,l^{\prime }}(1_{q_{1i,l}}+1_{q_{ij,l}}+1_{q_{j1,l}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{q,l}(\unicode[STIX]{x1D6FE}_{1ij,l^{\prime }}^{\ast })=\unicode[STIX]{x1D6FF}_{l,l^{\prime }}(1_{q_{1i,l}}+1_{q_{ij,l}}+1_{q_{j1,l}})\end{eqnarray}$$
 $\unicode[STIX]{x1D70B}_{q,l}(\widehat{\unicode[STIX]{x1D6FE}_{ijkm,1}})=0$
.
$\unicode[STIX]{x1D70B}_{q,l}(\widehat{\unicode[STIX]{x1D6FE}_{ijkm,1}})=0$
.(2) The set
 $\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast }~(2\leqslant i<j\leqslant d,1\leqslant l\leqslant d)$
are linearly independent in
$\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast }~(2\leqslant i<j\leqslant d,1\leqslant l\leqslant d)$
are linearly independent in
 $\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle /\langle \widehat{\unicode[STIX]{x1D6FE}_{ijkm,l}}\rangle$
. As a consequence, we have
$\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle /\langle \widehat{\unicode[STIX]{x1D6FE}_{ijkm,l}}\rangle$
. As a consequence, we have  $$\begin{eqnarray}\dim (\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle /\langle \widehat{\unicode[STIX]{x1D6FE}_{ijkp,l}}\rangle )=\frac{d(d-1)(d-2)}{2}.\end{eqnarray}$$
$$\begin{eqnarray}\dim (\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle /\langle \widehat{\unicode[STIX]{x1D6FE}_{ijkp,l}}\rangle )=\frac{d(d-1)(d-2)}{2}.\end{eqnarray}$$
(3) Then the set
 $\widehat{\unicode[STIX]{x1D6FE}_{1ijk,1}}$
for
$\widehat{\unicode[STIX]{x1D6FE}_{1ijk,1}}$
for
 $(2\leqslant i<j<k\leqslant d)$
forms a basis of the space
$(2\leqslant i<j<k\leqslant d)$
forms a basis of the space
 $\langle \widehat{\unicode[STIX]{x1D6FE}_{ijkm,l}}\rangle$
. As a consequence, we have
$\langle \widehat{\unicode[STIX]{x1D6FE}_{ijkm,l}}\rangle$
. As a consequence, we have  $$\begin{eqnarray}\dim \langle \widehat{\unicode[STIX]{x1D6FE}_{ijkm,l}}\rangle =\frac{(d-1)(d-2)(d-3)}{6}.\end{eqnarray}$$
$$\begin{eqnarray}\dim \langle \widehat{\unicode[STIX]{x1D6FE}_{ijkm,l}}\rangle =\frac{(d-1)(d-2)(d-3)}{6}.\end{eqnarray}$$
(4) We have
 $$\begin{eqnarray}\dim \langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle =\frac{(d-1)(d-2)(4d-3)}{6}.\end{eqnarray}$$
$$\begin{eqnarray}\dim \langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle =\frac{(d-1)(d-2)(4d-3)}{6}.\end{eqnarray}$$
Proof. The equalities in (1) and (2) are obtained by direct calculations. The argument for linear independence is similar to the previous lemma. The statement (3) is a consequence of (1) and (2). ◻
Proposition 6.5. The set
![]() $\{{A_{1ij}\}}_{1\leqslant i<j\leqslant d}$
forms a basis of
$\{{A_{1ij}\}}_{1\leqslant i<j\leqslant d}$
forms a basis of
![]() $\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle \cap K$
. As a consequence,
$\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle \cap K$
. As a consequence,
![]() $\dim (\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle \cap K)=((d-1)(d-2))/2$
.
$\dim (\langle \unicode[STIX]{x1D6FE}_{ijk,l}^{\ast }\rangle \cap K)=((d-1)(d-2))/2$
.
Proof. Since
![]() $A_{1ij}-\sum _{l=1}^{d}\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast }$
is annihilated by
$A_{1ij}-\sum _{l=1}^{d}\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast }$
is annihilated by
![]() $\unicode[STIX]{x1D70B}_{u}$
and
$\unicode[STIX]{x1D70B}_{u}$
and
![]() $\unicode[STIX]{x1D70B}_{q,l}$
, it is an element in
$\unicode[STIX]{x1D70B}_{q,l}$
, it is an element in
![]() $\langle 1_{p_{ijk}}\rangle$
.
$\langle 1_{p_{ijk}}\rangle$
.
 $$\begin{eqnarray}\displaystyle A_{1ij}-\mathop{\sum }_{l=1}^{d}\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast } & = & \displaystyle (3-d)1_{p_{1ij}}+\mathop{\sum }_{k\neq i,j,k}(1_{p_{1ik}}+1_{p_{ijk}}+1_{p_{j1k}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k\neq i,j,k}(1_{p_{1ik}}+1_{p_{ijk}}+1_{p_{j1k}}-1_{p_{1ij}})\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\sum }_{k\neq i,j,k}\widehat{\unicode[STIX]{x1D6FE}_{1ijk,1}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{1ij}-\mathop{\sum }_{l=1}^{d}\unicode[STIX]{x1D6FE}_{1ij,l}^{\ast } & = & \displaystyle (3-d)1_{p_{1ij}}+\mathop{\sum }_{k\neq i,j,k}(1_{p_{1ik}}+1_{p_{ijk}}+1_{p_{j1k}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k\neq i,j,k}(1_{p_{1ik}}+1_{p_{ijk}}+1_{p_{j1k}}-1_{p_{1ij}})\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\sum }_{k\neq i,j,k}\widehat{\unicode[STIX]{x1D6FE}_{1ijk,1}}.\nonumber\end{eqnarray}$$
As a consequence,
![]() $A_{1ij}$
is an element in
$A_{1ij}$
is an element in
![]() $\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle \cap K$
. Thus we have the proposition.◻
$\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle \cap K$
. Thus we have the proposition.◻
Corollary 6.6. The dimension of the subspace of
![]() $Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))$
generated by
$Gr_{0}^{M}H^{2}(X_{t_{0}},\mathbf{Q}(2))$
generated by
![]() $\unicode[STIX]{x1D6FE}_{ijk,l}$
is equal to
$\unicode[STIX]{x1D6FE}_{ijk,l}$
is equal to
![]() $((d-1)(d-2)(2d-3))/3$
.
$((d-1)(d-2)(2d-3))/3$
.
6.3 The dimension of
 $Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
and the proof of the main theorem
$Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
and the proof of the main theorem
In this subsection, we prove the following proposition.
Proposition 6.7. The dimension of
![]() $Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
is equal to
$Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
is equal to
![]() $((d-1)(d-2)(d-3))/6$
.
$((d-1)(d-2)(d-3))/6$
.
Proof. Since the monodromy weight spectral sequence degenerates at
![]() $E_{2}$
-term, the 0th, 1st and 2nd cohomology of the following complex is isomorphic to
$E_{2}$
-term, the 0th, 1st and 2nd cohomology of the following complex is isomorphic to
![]() $Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
,
$Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
,
![]() $Gr_{-1}^{M}H^{3}(X_{t_{0}},\mathbf{Q})=0$
and
$Gr_{-1}^{M}H^{3}(X_{t_{0}},\mathbf{Q})=0$
and
![]() $Gr_{0}^{M}H^{4}(X_{t_{0}},\mathbf{Q})\simeq \mathbf{Q}(-2)$
. Since
$Gr_{0}^{M}H^{4}(X_{t_{0}},\mathbf{Q})\simeq \mathbf{Q}(-2)$
. Since
![]() $E_{2}$
-term is a cohomology of the complex
$E_{2}$
-term is a cohomology of the complex
and by the expression of strata in Section 4, we have
 $$\begin{eqnarray}\displaystyle \dim (H^{0}(T^{(0)})(-2)) & = & \displaystyle \frac{d(d-1)(d-2)}{6}+d\cdot \frac{d(d-1)}{2},\nonumber\\ \displaystyle \dim (H^{2}(T^{(1)})(-1)) & = & \displaystyle \frac{d(d-1)}{2}+d^{2}(d-1),\nonumber\\ \displaystyle \dim (H^{4}(T^{(2)})(0)) & = & \displaystyle d+d\cdot \frac{d(d-1)}{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim (H^{0}(T^{(0)})(-2)) & = & \displaystyle \frac{d(d-1)(d-2)}{6}+d\cdot \frac{d(d-1)}{2},\nonumber\\ \displaystyle \dim (H^{2}(T^{(1)})(-1)) & = & \displaystyle \frac{d(d-1)}{2}+d^{2}(d-1),\nonumber\\ \displaystyle \dim (H^{4}(T^{(2)})(0)) & = & \displaystyle d+d\cdot \frac{d(d-1)}{2}.\nonumber\end{eqnarray}$$
Therefore we have the dimension of
![]() $Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
.◻
$Gr_{-2}^{M}H^{2}(X_{t_{0}},\mathbf{Q})$
.◻
Proof of Theorem 1.1.
The image of the cycle map
![]() $c_{et}^{2,1}(X)$
contains the image
$c_{et}^{2,1}(X)$
contains the image
Since the monodromy action is strictly compatible with respect to the monodromy weight spectral sequence, the graded piece of the above cokernel is equal to
Now we consider the following homomorphism of vector spaces.
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}} & & W/K\\ & & \bigcup \\ Gr_{-1}^{M}H^{2}(X_{t_{0}}) & \xrightarrow[{}]{N} & Gr_{0}^{M}H^{2}(X_{t_{0}})\\ & & \uparrow \\ & & \langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle .\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}} & & W/K\\ & & \bigcup \\ Gr_{-1}^{M}H^{2}(X_{t_{0}}) & \xrightarrow[{}]{N} & Gr_{0}^{M}H^{2}(X_{t_{0}})\\ & & \uparrow \\ & & \langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle .\end{array}\end{eqnarray}$$
Let
![]() $\overline{\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle }$
be the image of
$\overline{\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle }$
be the image of
![]() $\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle$
in
$\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle$
in
![]() $\operatorname{Coker}(Gr_{-1}^{M}H^{2}(X_{t_{0}})\rightarrow W/K)$
. Then we have
$\operatorname{Coker}(Gr_{-1}^{M}H^{2}(X_{t_{0}})\rightarrow W/K)$
. Then we have
 $$\begin{eqnarray}\displaystyle \dim \overline{\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle } & = & \displaystyle \dim (\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle +Gr_{-1}^{M}H^{2}(X_{t_{0}}))-\dim Gr_{-1}^{M}H^{2}(X_{t_{0}})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim \langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle -\dim Gr_{-1}^{M}H^{2}(X_{t_{0}})\nonumber\\ \displaystyle & = & \displaystyle \frac{(d-1)(d-2)(2d-3)}{3}-\frac{(d-1)(d-2)(d-3)}{6}\nonumber\\ \displaystyle & = & \displaystyle \frac{(d-1)^{2}(d-2)}{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim \overline{\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle } & = & \displaystyle \dim (\langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle +Gr_{-1}^{M}H^{2}(X_{t_{0}}))-\dim Gr_{-1}^{M}H^{2}(X_{t_{0}})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim \langle \unicode[STIX]{x1D6FE}_{ijk,l}\rangle -\dim Gr_{-1}^{M}H^{2}(X_{t_{0}})\nonumber\\ \displaystyle & = & \displaystyle \frac{(d-1)(d-2)(2d-3)}{3}-\frac{(d-1)(d-2)(d-3)}{6}\nonumber\\ \displaystyle & = & \displaystyle \frac{(d-1)^{2}(d-2)}{2}.\nonumber\end{eqnarray}$$
Thus we have the theorem. ◻
Acknowledgments
The author would like to thank S. Saito and M. Asakura for some suggestions on possible alternative arguments to prove the statement of the main theorem. He would also like to thank T. Sasaki for discussions on this topic.