Article contents
CONNECTIVITY AND PURITY FOR LOGARITHMIC MOTIVES
Published online by Cambridge University Press: 14 June 2021
Abstract
The goal of this article is to extend the work of Voevodsky and Morel on the homotopy t-structure on the category of motivic complexes to the context of motives for logarithmic schemes. To do so, we prove an analogue of Morel’s connectivity theorem and show a purity statement for
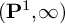 $({\mathbf {P}}^1, \infty )$
-local complexes of sheaves with log transfers. The homotopy t-structure on
$({\mathbf {P}}^1, \infty )$
-local complexes of sheaves with log transfers. The homotopy t-structure on
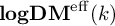 ${\operatorname {\mathbf {logDM}^{eff}}}(k)$
is proved to be compatible with Voevodsky’s t-structure; that is, we show that the comparison functor
${\operatorname {\mathbf {logDM}^{eff}}}(k)$
is proved to be compatible with Voevodsky’s t-structure; that is, we show that the comparison functor
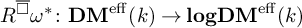 $R^{{\overline {\square }}}\omega ^*\colon {\operatorname {\mathbf {DM}^{eff}}}(k)\to {\operatorname {\mathbf {logDM}^{eff}}}(k)$
is t-exact. The heart of the homotopy t-structure on
$R^{{\overline {\square }}}\omega ^*\colon {\operatorname {\mathbf {DM}^{eff}}}(k)\to {\operatorname {\mathbf {logDM}^{eff}}}(k)$
is t-exact. The heart of the homotopy t-structure on
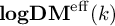 ${\operatorname {\mathbf {logDM}^{eff}}}(k)$
is the Grothendieck abelian category of strictly cube-invariant sheaves with log transfers: we use it to build a new version of the category of reciprocity sheaves in the style of Kahn-Saito-Yamazaki and Rülling.
${\operatorname {\mathbf {logDM}^{eff}}}(k)$
is the Grothendieck abelian category of strictly cube-invariant sheaves with log transfers: we use it to build a new version of the category of reciprocity sheaves in the style of Kahn-Saito-Yamazaki and Rülling.
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 1 , January 2023 , pp. 335 - 381
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
A correction has been issued for this article:
- 2
- Cited by
Linked content
Please note a has been issued for this article.



