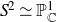1. Introduction
A projective (or equivalently, algebraic) complex K3 surface X is said to be CM (complex multiplication) if the endomorphism field
![]() ${K_{T\left( X \right)}}$
of the Hodge structure on the transcendental lattice
${K_{T\left( X \right)}}$
of the Hodge structure on the transcendental lattice
![]() $T\!\left( X \right) = {\rm{NS}}(X)_\mathbb{Q}^ \bot \subseteq {H^2}\!\left( {X,\mathbb{Q}} \right)$
is a CM field, and
$T\!\left( X \right) = {\rm{NS}}(X)_\mathbb{Q}^ \bot \subseteq {H^2}\!\left( {X,\mathbb{Q}} \right)$
is a CM field, and
![]() ${\rm{di}}{{\rm{m}}_{{K_{T\left( X \right)}}}}T\!\left( X \right) = 1$
. Denote by
${\rm{di}}{{\rm{m}}_{{K_{T\left( X \right)}}}}T\!\left( X \right) = 1$
. Denote by
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
the twistor space of the projective K3 surface X associated with a Kähler class given by an ample class
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
the twistor space of the projective K3 surface X associated with a Kähler class given by an ample class
![]() $\ell = {c_1}\!\left( L \right) \in {H^2}\!\left( {X,\mathbb{Q}} \right)$
(see Section 2·1 for a short description). Despite the transcendental nature of the twistor construction, the fibres
$\ell = {c_1}\!\left( L \right) \in {H^2}\!\left( {X,\mathbb{Q}} \right)$
(see Section 2·1 for a short description). Despite the transcendental nature of the twistor construction, the fibres
![]() ${\mathcal{X}_\zeta }$
that are again algebraic share some arithmetic properties. In particular, all algebraic fibres away from the equator
${\mathcal{X}_\zeta }$
that are again algebraic share some arithmetic properties. In particular, all algebraic fibres away from the equator
![]() $\mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
are CM, and the corresponding CM endomorphism fields share the same totally real maximal subextension [
Reference HuybrechtsHuy20
, theorem 5·3].
$\mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
are CM, and the corresponding CM endomorphism fields share the same totally real maximal subextension [
Reference HuybrechtsHuy20
, theorem 5·3].
In this paper we prove that the CM fields corresponding to fibres at the same altitude of
![]() ${S^2} \simeq \mathbb{P}_\mathbb{C}^1$
coincide (Theorem 6·8). This result will be proven by introducing an action of the topological multiplicative group
${S^2} \simeq \mathbb{P}_\mathbb{C}^1$
coincide (Theorem 6·8). This result will be proven by introducing an action of the topological multiplicative group
![]() $K_{T\left( X \right)}^ \times $
on the Noether–Lefschetz locus of the upper-half sphere.
$K_{T\left( X \right)}^ \times $
on the Noether–Lefschetz locus of the upper-half sphere.

Theorem 1·1.
Consider the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. Assume that
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. Assume that
![]() ${\zeta _1},{\zeta _2} \in \mathbb{P}_\mathbb{C}^1$
are two points of Picard jump at the same altitude and not on the equator. Then
${\zeta _1},{\zeta _2} \in \mathbb{P}_\mathbb{C}^1$
are two points of Picard jump at the same altitude and not on the equator. Then
![]() ${\mathcal{X}_{{\zeta _1}}}$
is algebraic if and only if
${\mathcal{X}_{{\zeta _1}}}$
is algebraic if and only if
![]() ${\mathcal{X}_{{\zeta _2}}}$
is such. If so, then the CM endomorphism fields of these K3 surfaces coincide. Moreover, the set of points of Picard jump at the same altitude of
${\mathcal{X}_{{\zeta _2}}}$
is such. If so, then the CM endomorphism fields of these K3 surfaces coincide. Moreover, the set of points of Picard jump at the same altitude of
![]() ${\zeta _1}$
(and
${\zeta _1}$
(and
![]() ${\zeta _2}$
) is countable and dense in the circle at that altitude.
${\zeta _2}$
) is countable and dense in the circle at that altitude.
The Picard number of a K3 surface is the rank of its Néron–Severi group. Huybrechts proved that, if a fibre
![]() $\mathcal{X}_{\zeta }$
has excessive Picard number (that is, bigger than the original Picard number
$\mathcal{X}_{\zeta }$
has excessive Picard number (that is, bigger than the original Picard number
![]() $\rho \!\left( X \right)$
), then
$\rho \!\left( X \right)$
), then
![]() $\zeta $
lies on the equator of
$\zeta $
lies on the equator of
![]() ${S^2} \simeq \mathbb{P}_\mathbb{C}^1$
[
Reference HuybrechtsHuy20
, proposition 3·2]. We prove, in the CM case, that there is only one admissible excessive Picard value (Theorem 6·3).
${S^2} \simeq \mathbb{P}_\mathbb{C}^1$
[
Reference HuybrechtsHuy20
, proposition 3·2]. We prove, in the CM case, that there is only one admissible excessive Picard value (Theorem 6·3).
Theorem 1·2.
Consider the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. If
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. If
![]() $\zeta $
is a point of Picard jump on the equator, then
$\zeta $
is a point of Picard jump on the equator, then
Moreover, the Noether–Lefschetz locus of the equator is dense in the equator. More precisely, the locus of points on the equator whose fibres are algebraic K3 surfaces is dense in the equator.

Outline. Section 2 contains some basic information about the geometry of the twistor space, Hodge structures of K3 type and CM fields. In Section 3 we describe a family of Hodge structures, parameterised by a sphere, attached to a given Hodge structure of K3 type. This construction is, at the level of Hodge structures, the algebraic equivalent of the twistor space. Afterwards, in Section 4, we prove Proposition 4·4 (algebro-equivalent of Theorem 1·2) and other results characterising points of Picard jump on the equator of the mentioned sphere. Two actions of the topological multiplicative group
![]() $K_{T\left( X \right)}^ \times $
are introduced in Section 5; these will play a key role in the proof of Corollary 5·10 (algebro-equivalent of Theorem 1·1) and related statements. Finally, the translation into geometric terms is exposed in Section 6, and Theorems 1·1 and 1·2 are proven.
$K_{T\left( X \right)}^ \times $
are introduced in Section 5; these will play a key role in the proof of Corollary 5·10 (algebro-equivalent of Theorem 1·1) and related statements. Finally, the translation into geometric terms is exposed in Section 6, and Theorems 1·1 and 1·2 are proven.
2. Preliminaries
We present a short description of the twistor space of a complex K3 surface, and we recall some facts about Hodge structures of K3 type and CM fields.
2·1. The twistor space of a complex K3 surface
A complex K3 surface X admits a sphere of different complex structures. More explicitly, one can attach a set of different complex structures
![]() ${I_\zeta }$
to the underlying differentiable manifold X, so that
${I_\zeta }$
to the underlying differentiable manifold X, so that
![]() $\left( {X,{I_\zeta }} \right)$
is again a K3 surface, and these structures are parameterised by a sphere
$\left( {X,{I_\zeta }} \right)$
is again a K3 surface, and these structures are parameterised by a sphere
![]() $\zeta \in {S^2} \simeq \mathbb{P}_\mathbb{C}^1$
. These K3 surfaces can be patched together into a 3-dimensional complex manifold
$\zeta \in {S^2} \simeq \mathbb{P}_\mathbb{C}^1$
. These K3 surfaces can be patched together into a 3-dimensional complex manifold
![]() $\mathcal{X}$
, called twistor space (see [
Reference Hitchin, Karlhede, Lindström and RočekHKLR87
, section 3·F], [
Reference HitchinHit92
] or [
Reference JoyceJoy00
, chapter 7] for more on the twistor space and the details of its construction).
$\mathcal{X}$
, called twistor space (see [
Reference Hitchin, Karlhede, Lindström and RočekHKLR87
, section 3·F], [
Reference HitchinHit92
] or [
Reference JoyceJoy00
, chapter 7] for more on the twistor space and the details of its construction).
![]() $\mathcal{X}$
comes with a holomorphic map
$\mathcal{X}$
comes with a holomorphic map
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
with the property that, for
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
with the property that, for
![]() $\zeta \in \mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
, the fibre
$\zeta \in \mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
, the fibre
![]() ${\mathcal{X}_\zeta }$
is the K3 surface
${\mathcal{X}_\zeta }$
is the K3 surface
![]() $\left( {X,{I_\zeta }} \right)$
. In fact, this construction is non-canonical, and depends on the choice of a Kähler class of X (any K3 surface is Kähler, [
Reference SiuSiu83
]). The original K3 surface corresponds to one of the poles of
$\left( {X,{I_\zeta }} \right)$
. In fact, this construction is non-canonical, and depends on the choice of a Kähler class of X (any K3 surface is Kähler, [
Reference SiuSiu83
]). The original K3 surface corresponds to one of the poles of
![]() $\mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
.
$\mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
.
Even if the original K3 surface X is algebraic (or equivalently, projective),
![]() $\mathcal{X}$
is no longer algebraic, and has to be thought of as of transcendental nature. The twistor space of a K3 surface plays an important role in several situations. Among all, it provides an example of K3-fibration over a compact base, and it is used in a modern proof of Torelli Theorem (any two K3 surfaces are connected by a finite path of twistor lines, see [
Reference HuybrechtsHuy16
, section 7·3]).
$\mathcal{X}$
is no longer algebraic, and has to be thought of as of transcendental nature. The twistor space of a K3 surface plays an important role in several situations. Among all, it provides an example of K3-fibration over a compact base, and it is used in a modern proof of Torelli Theorem (any two K3 surfaces are connected by a finite path of twistor lines, see [
Reference HuybrechtsHuy16
, section 7·3]).
2·2. Hodge structures of K3 type
By polarised Hodge structure of K3 type we mean the data of a vector space T over
![]() $\mathbb{Q}$
of dimension
$\mathbb{Q}$
of dimension
![]() $r \geq 2$
, endowed with a symmetric bilinear form
$r \geq 2$
, endowed with a symmetric bilinear form
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
of signature
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
of signature
![]() $\left( {2,r - 2} \right)$
, and a decomposition
$\left( {2,r - 2} \right)$
, and a decomposition
such that the
![]() $\mathbb{C}$
-linear extension of
$\mathbb{C}$
-linear extension of
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
satisfies:
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
satisfies:
-
(i) the subspaces
 ${T^{1,1}}$
and
${T^{1,1}}$
and
 ${T^{2,0}} \oplus {T^{0,2}}$
are orthogonal;
${T^{2,0}} \oplus {T^{0,2}}$
are orthogonal; -
(ii)
 $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is positive definite on
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is positive definite on
 ${P_T} = \left( {{T^{2,0}} \oplus {T^{0,2}}} \right) \cap {T_\mathbb{R}}$
and
${P_T} = \left( {{T^{2,0}} \oplus {T^{0,2}}} \right) \cap {T_\mathbb{R}}$
and
 ${T^{2,0}},{T^{0,2}} \subseteq {T_\mathbb{C}}$
are isotropic;
${T^{2,0}},{T^{0,2}} \subseteq {T_\mathbb{C}}$
are isotropic; -
(iii) complex conjugation on
 ${T_\mathbb{C}}$
preserves
${T_\mathbb{C}}$
preserves
 ${T^{1,1}}$
and exchanges
${T^{1,1}}$
and exchanges
 ${T^{2,0}}$
and
${T^{2,0}}$
and
 ${T^{0,2}}$
;
${T^{0,2}}$
; -
(iv)
 ${\rm{di}}{{\rm{m}}_\mathbb{C}}^{2,0} = 1$
.
${\rm{di}}{{\rm{m}}_\mathbb{C}}^{2,0} = 1$
.
We will denote by
![]() $\sigma $
a
$\sigma $
a
![]() $\mathbb{C}$
-generator of
$\mathbb{C}$
-generator of
![]() ${T^{2,0}}$
. Note that
${T^{2,0}}$
. Note that
![]() $\bar \sigma $
generates
$\bar \sigma $
generates
![]() ${T^{0,2}}$
, and the required conditions give
${T^{0,2}}$
, and the required conditions give
![]() $\left( {\sigma .\sigma } \right) = 0$
,
$\left( {\sigma .\sigma } \right) = 0$
,
![]() $\left( {\sigma .\bar \sigma } \right) \gt 0$
,
$\left( {\sigma .\bar \sigma } \right) \gt 0$
,
![]() ${(\Re \!\left( \sigma \right)\!)^2} = {(\Im \!\left( \sigma \right)\!)^2}$
and
${(\Re \!\left( \sigma \right)\!)^2} = {(\Im \!\left( \sigma \right)\!)^2}$
and
![]() $\left( {\Re \!\left( \sigma \right).\Im \!\left( \sigma \right)} \right) = 0$
. The plane
$\left( {\Re \!\left( \sigma \right).\Im \!\left( \sigma \right)} \right) = 0$
. The plane
![]() ${P_T}$
is considered with the orientation given by the basis
${P_T}$
is considered with the orientation given by the basis
![]() $\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right)} \right\}$
. We will also assume that T is irreducible.
$\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right)} \right\}$
. We will also assume that T is irreducible.
Define
![]() ${K_T}$
to be the ring of endomorphism of the Hodge structure T. As T is irreducible,
${K_T}$
to be the ring of endomorphism of the Hodge structure T. As T is irreducible,
![]() ${K_T}$
is a division algebra. It was pointed out by Zarhin [
Reference ZarhinZar83
] that
${K_T}$
is a division algebra. It was pointed out by Zarhin [
Reference ZarhinZar83
] that
![]() ${K_T}$
is indeed a number field, endowed with an embedding
${K_T}$
is indeed a number field, endowed with an embedding
![]() ${K_T} \to \mathbb{C}$
. This embedding is defined in the following way: as
${K_T} \to \mathbb{C}$
. This embedding is defined in the following way: as
![]() $\varphi $
preserves the
$\varphi $
preserves the
![]() $\left( {2,0} \right)$
-part of T,
$\left( {2,0} \right)$
-part of T,
![]() $\varphi \!\left( \sigma \right) = \varphi \cdot \sigma $
, where we identify
$\varphi \!\left( \sigma \right) = \varphi \cdot \sigma $
, where we identify
![]() $\varphi $
with a scalar in
$\varphi $
with a scalar in
![]() $\mathbb{C}$
. Zarhin proved also that
$\mathbb{C}$
. Zarhin proved also that
![]() ${K_T}$
is either totally real or complex multiplication (CM). Notice that T is naturally a
${K_T}$
is either totally real or complex multiplication (CM). Notice that T is naturally a
![]() ${K_T}$
-module and, therefore, it becomes a
${K_T}$
-module and, therefore, it becomes a
![]() ${K_T}$
-vector space.
${K_T}$
-vector space.
Definition 2·1. T is said to be:
-
(i) of totally real type if
 ${{\rm{K}}_{\rm{T}}}$
is totally real;
${{\rm{K}}_{\rm{T}}}$
is totally real; -
(ii) of almost complex multiplication type, or almost CM, if
 ${{\rm{K}}_{\rm{T}}}$
is CM; and
${{\rm{K}}_{\rm{T}}}$
is CM; and -
(iii) of complex multiplication type, or CM, if
 ${{\rm{K}}_{\rm{T}}}$
is CM and
${{\rm{K}}_{\rm{T}}}$
is CM and
 ${\rm{di}}{{\rm{m}}_{{{\rm{K}}_{\rm{T}}}}}{\textit{T}} = 1$
.
${\rm{di}}{{\rm{m}}_{{{\rm{K}}_{\rm{T}}}}}{\textit{T}} = 1$
.
The last condition seems technical, but turns out to be extremely useful in several situations. In fact, one can define the CM type case by requiring the sole condition
![]() ${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
to be satisfied. Indeed, van Geemen [
Reference van GeemenvGe08
, lemma 3·2] proved that, whenever
${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
to be satisfied. Indeed, van Geemen [
Reference van GeemenvGe08
, lemma 3·2] proved that, whenever
![]() ${K_T}$
is totally real,
${K_T}$
is totally real,
![]() ${\rm{di}}{{\rm{m}}_{{K_T}}}T \geq 3$
holds. Of course, the condition
${\rm{di}}{{\rm{m}}_{{K_T}}}T \geq 3$
holds. Of course, the condition
![]() ${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
is equivalent to
${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
is equivalent to
![]() $\left[ {{K_T}\;:\;\mathbb{Q}} \right] = r$
.
$\left[ {{K_T}\;:\;\mathbb{Q}} \right] = r$
.
As the form
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is non-degenerate, we can define the transpose
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is non-degenerate, we can define the transpose
![]() $\varphi '$
of
$\varphi '$
of
![]() $\varphi $
by the condition
$\varphi $
by the condition
for any
![]() $\gamma ,\delta \in T$
.
$\gamma ,\delta \in T$
.
![]() $\varphi '$
is in fact an element of
$\varphi '$
is in fact an element of
![]() ${K_T}$
, and corresponds to the complex conjugate of
${K_T}$
, and corresponds to the complex conjugate of
![]() $\varphi $
via the embedding
$\varphi $
via the embedding
![]() ${K_T} \hookrightarrow \mathbb{C}$
, that is:
${K_T} \hookrightarrow \mathbb{C}$
, that is:
![]() $\varphi '\!\left( \sigma \right) = \bar \varphi \cdot \sigma $
(see [
Reference HuybrechtsHuy20
, remark 2·6] or [
Reference HuybrechtsHuy16
, chapter 3]). In particular, an element
$\varphi '\!\left( \sigma \right) = \bar \varphi \cdot \sigma $
(see [
Reference HuybrechtsHuy20
, remark 2·6] or [
Reference HuybrechtsHuy16
, chapter 3]). In particular, an element
![]() $\varphi \in {K_T}$
is an isometry for
$\varphi \in {K_T}$
is an isometry for
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
if and only if its image in
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
if and only if its image in
![]() $\mathbb{C}$
has unitary norm. We will denote by
$\mathbb{C}$
has unitary norm. We will denote by
![]() $K_T^0 = {K_T} \cap \mathbb{R}$
the real part of
$K_T^0 = {K_T} \cap \mathbb{R}$
the real part of
![]() ${K_T}$
, once seen
${K_T}$
, once seen
![]() ${K_T}$
as a subfield of
${K_T}$
as a subfield of
![]() $\mathbb{C}$
via the prescribed embedding. Notice that
$\mathbb{C}$
via the prescribed embedding. Notice that
![]() $K_T^0$
can be characterised by the subfield of
$K_T^0$
can be characterised by the subfield of
![]() ${K_T}$
of self-transpose endomorphisms.
${K_T}$
of self-transpose endomorphisms.
The period field
![]() ${k_T}$
of T is defined in the following way. Let
${k_T}$
of T is defined in the following way. Let
![]() $\gamma $
vary in T. Among the periods
$\gamma $
vary in T. Among the periods
![]() $\left( {\sigma .\gamma } \right)$
, at least one is not zero, say for
$\left( {\sigma .\gamma } \right)$
, at least one is not zero, say for
![]() $\tilde \gamma $
, since
$\tilde \gamma $
, since
![]() $\sigma \ne 0$
and
$\sigma \ne 0$
and
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is non-degenerate.Footnote 1 The period field is defined to be the subfield of
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is non-degenerate.Footnote 1 The period field is defined to be the subfield of
![]() $\mathbb{C}$
generated over
$\mathbb{C}$
generated over
![]() $\mathbb{Q}$
by the quotients
$\mathbb{Q}$
by the quotients
![]() $\left( {\sigma .\gamma } \right)/\left( {\sigma .\tilde \gamma } \right)$
. Clearly, it is enough to consider these quotients only for
$\left( {\sigma .\gamma } \right)/\left( {\sigma .\tilde \gamma } \right)$
. Clearly, it is enough to consider these quotients only for
![]() $\gamma $
varying in a
$\gamma $
varying in a
![]() $\mathbb{Q}$
-basis of T. For a proof of the following result, see [
Reference HuybrechtsHuy20
, lemma 2·10].
$\mathbb{Q}$
-basis of T. For a proof of the following result, see [
Reference HuybrechtsHuy20
, lemma 2·10].
Lemma 2·2.
Assume that T is a polarised irreducible Hodge structure of K3 type with complex multiplication (i.e.
![]() ${K_T}$
is a CM field and
${K_T}$
is a CM field and
![]() $\rm{dim}_\mathbb{Q}T = \left[ {{K_T}\;:\;\mathbb{Q}} \right]$
). Then:
$\rm{dim}_\mathbb{Q}T = \left[ {{K_T}\;:\;\mathbb{Q}} \right]$
). Then:
-
(i) the endomorphism field
 ${K_T}$
and the period field
${K_T}$
and the period field
 ${k_T}$
coincide (as subfields of
${k_T}$
coincide (as subfields of
 $\mathbb{C}$
);
$\mathbb{C}$
); -
(ii) for any basis
 $\left\{ {{\gamma _i}} \right\}$
of T and any
$\left\{ {{\gamma _i}} \right\}$
of T and any
 $\sigma \in {T^{2,0}}$
,
$\sigma \in {T^{2,0}}$
,
 $\sigma \ne 0$
, the coordinates
$\sigma \ne 0$
, the coordinates
 ${x_i} = \left( {\sigma .{\gamma _i}} \right)$
satisfy
${x_i} = \left( {\sigma .{\gamma _i}} \right)$
satisfy \begin{align*}{K_T} = {k_T} = \mathop {\mathop \oplus \limits_{i = 1} }\limits^r \mathbb{Q} \cdot \left( {{x_i}/{x_1}} \right).\end{align*}
\begin{align*}{K_T} = {k_T} = \mathop {\mathop \oplus \limits_{i = 1} }\limits^r \mathbb{Q} \cdot \left( {{x_i}/{x_1}} \right).\end{align*}
2·3. Useful facts on CM fields
First of all, we recall a result proven by Blanksby and Loxton [ Reference Blanksby and LoxtonBL78 ].
Theorem 2·3.
If
![]() $E \subseteq \mathbb{C}$
is a CM field, then
$E \subseteq \mathbb{C}$
is a CM field, then
![]() $E = \mathbb{Q}\!\left( \alpha \right)$
, for a primitive element
$E = \mathbb{Q}\!\left( \alpha \right)$
, for a primitive element
![]() $\alpha $
satisfying
$\alpha $
satisfying
![]() $\left| \alpha \right| = 1$
.
$\left| \alpha \right| = 1$
.
We now present other elementary properties carried by CM fields.
Lemma 2·4.
Let
![]() $E \subseteq \mathbb{C}$
be a number field given as a subfield of
$E \subseteq \mathbb{C}$
be a number field given as a subfield of
![]() $\mathbb{C}$
, and let
$\mathbb{C}$
, and let
![]() $e \in E$
,
$e \in E$
,
![]() $e \ne 0$
. Then the dimension of the
$e \ne 0$
. Then the dimension of the
![]() $\mathbb{Q}$
-vector space
$\mathbb{Q}$
-vector space
![]() $\left( {\mathbb{R} \cdot e} \right) \cap E$
does not depend on e, and is equal to
$\left( {\mathbb{R} \cdot e} \right) \cap E$
does not depend on e, and is equal to
![]() $\rm{dim}_\mathbb{Q}\!\left( {E \cap \mathbb{R}} \right)$
.
$\rm{dim}_\mathbb{Q}\!\left( {E \cap \mathbb{R}} \right)$
.
Proof. It is enough to notice that
![]() $\left( {\mathbb{R} \cdot e} \right) \cap E = e \cdot \left( {E \cap \mathbb{R}} \right)$
.
$\left( {\mathbb{R} \cdot e} \right) \cap E = e \cdot \left( {E \cap \mathbb{R}} \right)$
.
This Lemma assumes a particular form in the case of a CM field.
Corollary 2·5.
Let
![]() $E \subseteq \mathbb{C}$
be a CM field given as a subfield of
$E \subseteq \mathbb{C}$
be a CM field given as a subfield of
![]() $\mathbb{C}$
, and let
$\mathbb{C}$
, and let
![]() $\alpha $
be a generator of E satisfying
$\alpha $
be a generator of E satisfying
![]() $\left| \alpha \right| = 1$
,
$\left| \alpha \right| = 1$
,
![]() $n = \left[ {E\;:\;\mathbb{Q}} \right]$
. For any
$n = \left[ {E\;:\;\mathbb{Q}} \right]$
. For any
![]() $e \in E$
,
$e \in E$
,
![]() $e \ne 0$
, the dimension of the
$e \ne 0$
, the dimension of the
![]() $\mathbb{Q}$
-vector space
$\mathbb{Q}$
-vector space
![]() $\left( {\mathbb{R} \cdot e} \right) \cap E$
does not depend on e, and is equal to
$\left( {\mathbb{R} \cdot e} \right) \cap E$
does not depend on e, and is equal to
![]() $n/2$
.
$n/2$
.
Proof. The statement follows from Lemma 2·4, together with the fact that
![]() $E \cap \mathbb{R}$
is the maximal totally real subfield of E, satisfying
$E \cap \mathbb{R}$
is the maximal totally real subfield of E, satisfying
![]() ${\rm{di}}{{\rm{m}}_\mathbb{Q}}\!\left( {E \cap \mathbb{R}} \right) = n/2$
.
${\rm{di}}{{\rm{m}}_\mathbb{Q}}\!\left( {E \cap \mathbb{R}} \right) = n/2$
.
Proposition 2·6.
Assume that a number field E is given as a subfield of
![]() $\mathbb{C}$
. Suppose that
$\mathbb{C}$
. Suppose that
![]() $E{\,{\nsubseteq}\,}\mathbb{R}$
and
$E{\,{\nsubseteq}\,}\mathbb{R}$
and
![]() $\bar E = E$
. Then
$\bar E = E$
. Then
![]() $E \cap {S^1}$
is dense in
$E \cap {S^1}$
is dense in
![]() ${S^1}$
.
${S^1}$
.
Proof. It is enough to show that there exist elements
![]() $\alpha \in E$
lying on the circle of arbitrary small non-zero argument (density follows taking powers of these elements). Let
$\alpha \in E$
lying on the circle of arbitrary small non-zero argument (density follows taking powers of these elements). Let
![]() $\delta $
be an element of
$\delta $
be an element of
![]() $E\backslash \mathbb{R}$
. For
$E\backslash \mathbb{R}$
. For
![]() $r \in \mathbb{Q}$
, define
$r \in \mathbb{Q}$
, define
Then
![]() $\left| {{\alpha _r}} \right| = 1$
and
$\left| {{\alpha _r}} \right| = 1$
and
![]() ${\alpha _r}$
has arbitrary small non-zero argument, since
${\alpha _r}$
has arbitrary small non-zero argument, since
![]() ${\rm{li}}{{\rm{m}}_{r \to \infty }}{\alpha _r} = 1$
.
${\rm{li}}{{\rm{m}}_{r \to \infty }}{\alpha _r} = 1$
.
Corollary 2·7.
If E is a CM field given as a subfield of
![]() $\mathbb{C}$
, then
$\mathbb{C}$
, then
![]() $E \cap {S^1}$
is dense in
$E \cap {S^1}$
is dense in
![]() ${S^1}$
.
${S^1}$
.
Proof. A CM field satisfies the hypotheses of Proposition 2·6.
3. Twistor sphere of Hodge structures
Associated with T and an abstract class
![]() $\ell $
of positive square, there exists a sphere of related Hodge structures. Here we outline its construction, following [
Reference HuybrechtsHuy20
, section 3].
$\ell $
of positive square, there exists a sphere of related Hodge structures. Here we outline its construction, following [
Reference HuybrechtsHuy20
, section 3].
If one wishes to keep in mind the geometric picture, they should think of T as the transcendental lattice of a projective complex K3 surface X, of
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
as the restriction of the cup product on
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
as the restriction of the cup product on
![]() ${H^2}\!\left( {X,\mathbb{Q}} \right)$
to T, and of
${H^2}\!\left( {X,\mathbb{Q}} \right)$
to T, and of
![]() $\ell $
as an ample class of X. Altered Hodge structures (or sub-Hodge structures of these) correspond to transcendental lattices of the K3 surfaces constituting the twistor space of X (compare with Remark 6·1).
$\ell $
as an ample class of X. Altered Hodge structures (or sub-Hodge structures of these) correspond to transcendental lattices of the K3 surfaces constituting the twistor space of X (compare with Remark 6·1).
Fix a positive integer
![]() $d \in {\mathbb{Z}_{ \gt 0}}$
. We extend T to the Hodge structure of K3 type
$d \in {\mathbb{Z}_{ \gt 0}}$
. We extend T to the Hodge structure of K3 type
![]() $T \oplus \mathbb{Q}\ell $
, of dimension
$T \oplus \mathbb{Q}\ell $
, of dimension
![]() $r + 1$
and endowed with a form
$r + 1$
and endowed with a form
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
of signature
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
of signature
![]() $\left( {3,r + 1 - 3} \right)$
, by declaring
$\left( {3,r + 1 - 3} \right)$
, by declaring
![]() $\ell $
to be of type
$\ell $
to be of type
![]() $\left( {1,1} \right)$
, orthogonal to T, and to satisfy
$\left( {1,1} \right)$
, orthogonal to T, and to satisfy
![]() $\left( {\ell .\ell } \right) = d$
.
$\left( {\ell .\ell } \right) = d$
.
![]() ${P_T} \oplus \mathbb{R}\ell \subseteq {T_\mathbb{R}} \oplus \mathbb{R}\ell $
is, therefore, a positive 3-space. Notice that
${P_T} \oplus \mathbb{R}\ell \subseteq {T_\mathbb{R}} \oplus \mathbb{R}\ell $
is, therefore, a positive 3-space. Notice that
![]() $T \oplus \mathbb{Q}\ell $
is no longer irreducible. The associated twistor base is the conic
$T \oplus \mathbb{Q}\ell $
is no longer irreducible. The associated twistor base is the conic
Points of the conic
![]() $\mathbb{P}_\ell ^1$
define different Hodge structures on
$\mathbb{P}_\ell ^1$
define different Hodge structures on
![]() $T \oplus \mathbb{Q}\ell $
, in the following sense. Any
$T \oplus \mathbb{Q}\ell $
, in the following sense. Any
![]() $z \in \mathbb{P}_\ell ^1$
defines a Hodge structure of K3 type on
$z \in \mathbb{P}_\ell ^1$
defines a Hodge structure of K3 type on
![]() $T \oplus \mathbb{Q}\ell $
, that we say corresponding to z: its
$T \oplus \mathbb{Q}\ell $
, that we say corresponding to z: its
![]() $\left( {2,0} \right)$
-part is the line corresponding to
$\left( {2,0} \right)$
-part is the line corresponding to
![]() $z = \left[ {\sigma '} \right]$
, i.e. the line
$z = \left[ {\sigma '} \right]$
, i.e. the line
![]() $\mathbb{C}\sigma '$
, its complex conjugate the
$\mathbb{C}\sigma '$
, its complex conjugate the
![]() $\left( {0,2} \right)$
-part, and the
$\left( {0,2} \right)$
-part, and the
![]() $\left( {1,1} \right)$
-part is given as the orthogonal complement of the former two. Notice that
$\left( {1,1} \right)$
-part is given as the orthogonal complement of the former two. Notice that
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is positive definite on
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is positive definite on
![]() $\left( {\mathbb{C}\sigma ' \oplus \mathbb{C}{{\bar \sigma }^{\rm{\prime}}}} \right) \cap \!\left( {{T_\mathbb{R}} \oplus \mathbb{R}\ell } \right) = \mathbb{R}\Re \!\left( {\sigma '} \right) \oplus \mathbb{R}\Im \!\left( {\sigma '} \right)$
; this follows immediately from the fact that
$\left( {\mathbb{C}\sigma ' \oplus \mathbb{C}{{\bar \sigma }^{\rm{\prime}}}} \right) \cap \!\left( {{T_\mathbb{R}} \oplus \mathbb{R}\ell } \right) = \mathbb{R}\Re \!\left( {\sigma '} \right) \oplus \mathbb{R}\Im \!\left( {\sigma '} \right)$
; this follows immediately from the fact that
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is positive definite on
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is positive definite on
![]() ${P_T} \oplus \mathbb{R}\ell $
, which contains
${P_T} \oplus \mathbb{R}\ell $
, which contains
![]() $\mathbb{R}\Re \!\left( {\sigma '} \right) \oplus \mathbb{R}\Im \!\left( {\sigma '} \right)$
.
$\mathbb{R}\Re \!\left( {\sigma '} \right) \oplus \mathbb{R}\Im \!\left( {\sigma '} \right)$
.
Mapping
![]() $z \in \mathbb{P}_\ell ^1$
to the oriented, positive real plane
$z \in \mathbb{P}_\ell ^1$
to the oriented, positive real plane
yields an identification
![]() $\mathbb{P}_\ell ^1 \simeq {\rm{G}}{{\rm{r}}^{{\rm{po}}}}\!\left( {{P_T} \oplus \mathbb{R}\ell } \right)$
with the Grassmannian of oriented, positive planes in
$\mathbb{P}_\ell ^1 \simeq {\rm{G}}{{\rm{r}}^{{\rm{po}}}}\!\left( {{P_T} \oplus \mathbb{R}\ell } \right)$
with the Grassmannian of oriented, positive planes in
![]() ${P_T} \oplus \mathbb{R}\ell $
. The complex conjugate
${P_T} \oplus \mathbb{R}\ell $
. The complex conjugate
![]() $\bar z$
, i.e. the point
$\bar z$
, i.e. the point
![]() $\left[ {{\rm{\;}}\overline {\sigma '} {\rm{\;}}} \right]$
, corresponds to the same plane with reversed orientation:
$\left[ {{\rm{\;}}\overline {\sigma '} {\rm{\;}}} \right]$
, corresponds to the same plane with reversed orientation:
Indeed, the basis given by
![]() $\left\{ {\Re \!\left( z \right), - \Im \!\left( z \right)} \right\}$
induces the same orientation as the basis given by
$\left\{ {\Re \!\left( z \right), - \Im \!\left( z \right)} \right\}$
induces the same orientation as the basis given by
![]() $\left\{ {\Im \!\left( z \right),\Re \!\left( z \right)} \right\}$
.
$\left\{ {\Im \!\left( z \right),\Re \!\left( z \right)} \right\}$
.
We define the period point of T as
![]() $x = \left[ \sigma \right] \in \mathbb{P}\!\left( {{T_\mathbb{C}}} \right)$
. Via the natural inclusion
$x = \left[ \sigma \right] \in \mathbb{P}\!\left( {{T_\mathbb{C}}} \right)$
. Via the natural inclusion
![]() $\mathbb{P}\!\left( {{T_\mathbb{C}}} \right) \subseteq \mathbb{P}\!\left( {{T_\mathbb{C}} \oplus \mathbb{C}\ell } \right)$
, we see that both
$\mathbb{P}\!\left( {{T_\mathbb{C}}} \right) \subseteq \mathbb{P}\!\left( {{T_\mathbb{C}} \oplus \mathbb{C}\ell } \right)$
, we see that both
![]() $x = \left[ \sigma \right]$
and its complex conjugate
$x = \left[ \sigma \right]$
and its complex conjugate
![]() $\bar x = \left[ {\bar \sigma } \right]$
belong to the conic
$\bar x = \left[ {\bar \sigma } \right]$
belong to the conic
![]() $\mathbb{P}_\ell ^1$
, as
$\mathbb{P}_\ell ^1$
, as
![]() $\left( {\sigma .\sigma } \right) = 0$
and
$\left( {\sigma .\sigma } \right) = 0$
and
![]() $\left( {\bar \sigma .\bar \sigma } \right) = 0$
. Thinking of
$\left( {\bar \sigma .\bar \sigma } \right) = 0$
. Thinking of
![]() ${P_z}$
with its orientation being given as the orthogonal complement of a generator
${P_z}$
with its orientation being given as the orthogonal complement of a generator
![]() ${\alpha _z}$
of the line
${\alpha _z}$
of the line
![]() $P_z^ \bot \subseteq {P_T} \oplus \mathbb{R}\ell $
provides a natural identification
$P_z^ \bot \subseteq {P_T} \oplus \mathbb{R}\ell $
provides a natural identification
With this identification, x and
![]() $\bar x$
correspond to the normalisations of
$\bar x$
correspond to the normalisations of
![]() $\ell $
and
$\ell $
and
![]() $ - \ell $
. We think of them as the north and south poles of
$ - \ell $
. We think of them as the north and south poles of
![]() $S_\ell ^2$
. The equator of the twistor base is the circle
$S_\ell ^2$
. The equator of the twistor base is the circle
Indeed, if
![]() $\ell \in {P_z}$
then the line orthogonal to
$\ell \in {P_z}$
then the line orthogonal to
![]() ${P_z}$
in
${P_z}$
in
![]() ${P_T} \oplus \mathbb{R}\ell $
is orthogonal to
${P_T} \oplus \mathbb{R}\ell $
is orthogonal to
![]() $\ell $
, and vice versa.
$\ell $
, and vice versa.
If, for
![]() $z \in \mathbb{P}_\ell ^1$
, we write
$z \in \mathbb{P}_\ell ^1$
, we write
![]() $z = \left[ {\sigma ' = a\sigma + b\bar \sigma + c\ell } \right]$
, for some
$z = \left[ {\sigma ' = a\sigma + b\bar \sigma + c\ell } \right]$
, for some
![]() $a,b,c \in \mathbb{C}$
, then
$a,b,c \in \mathbb{C}$
, then
![]() $z \in \mathbb{P}_\ell ^1$
if and only if
$z \in \mathbb{P}_\ell ^1$
if and only if
![]() $\left( {\sigma '.\sigma '} \right) = 0$
, i.e.
$\left( {\sigma '.\sigma '} \right) = 0$
, i.e.
The only points with
![]() $c = 0$
are the north and the south poles
$c = 0$
are the north and the south poles
![]() $x = \left[ \sigma \right],\bar x = \left[ {\bar \sigma } \right]$
. For all the other points,
$x = \left[ \sigma \right],\bar x = \left[ {\bar \sigma } \right]$
. For all the other points,
![]() $c \ne 0$
and, after rescaling
$c \ne 0$
and, after rescaling
![]() $\sigma '$
, we may assume
$\sigma '$
, we may assume
![]() $c = 1$
. The following result gives the explicit form of the isomorphism
$c = 1$
. The following result gives the explicit form of the isomorphism
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
.
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
.
Lemma 3·1.
Pick an element
![]() $z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right] \in \mathbb{P}_\ell ^1$
corresponding to a point on
$z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right] \in \mathbb{P}_\ell ^1$
corresponding to a point on
![]() $S_\ell ^2$
different from both poles. Then its image in
$S_\ell ^2$
different from both poles. Then its image in
![]() $S_\ell ^2$
is given, in coordinates for the basis
$S_\ell ^2$
is given, in coordinates for the basis
![]() $\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right),\ell } \right\}$
, by the point
$\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right),\ell } \right\}$
, by the point
where
and
![]() $\parallel {\rm{\;}}\parallel $
corresponds to
$\parallel {\rm{\;}}\parallel $
corresponds to
![]() $\sqrt {\!\left( {{\rm{\;}}.{\rm{\;}}} \right)} $
.
$\sqrt {\!\left( {{\rm{\;}}.{\rm{\;}}} \right)} $
.
Remark 3·2. The basis
![]() $\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right),\ell } \right\}$
is orthogonal for
$\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right),\ell } \right\}$
is orthogonal for
![]() $\left( {\;.\;} \right)$
; nonetheless, it is not normalised.
$\left( {\;.\;} \right)$
; nonetheless, it is not normalised.
Remark 3·3. If we assume
![]() $a = \bar b$
, then, if
$a = \bar b$
, then, if
![]() $\sigma ' \ne 0$
,
$\sigma ' \ne 0$
,
as
![]() $\left( {\sigma .\bar \sigma } \right) \gt 0$
. Thus
$\left( {\sigma .\bar \sigma } \right) \gt 0$
. Thus
![]() $z = \left[ {\sigma '} \right] \in \mathbb{P}_\ell ^1$
forces
$z = \left[ {\sigma '} \right] \in \mathbb{P}_\ell ^1$
forces
![]() $a \ne \bar b$
.
$a \ne \bar b$
.
Proof of the Lemma. Consider the plane
![]() ${P_z} = {\langle \Re \!\left( {\sigma '} \right),\Im \!\left( {\sigma '} \right)\rangle _\mathbb{R}}$
. Let
${P_z} = {\langle \Re \!\left( {\sigma '} \right),\Im \!\left( {\sigma '} \right)\rangle _\mathbb{R}}$
. Let
![]() ${\alpha _z}$
be the unique element of
${\alpha _z}$
be the unique element of
![]() ${P_T} \oplus \mathbb{R}\ell $
of norm 1 that is positively orthogonal to
${P_T} \oplus \mathbb{R}\ell $
of norm 1 that is positively orthogonal to
![]() ${P_z}$
. We are proving that
${P_z}$
. We are proving that
![]() $v = v\!\left( {a,b} \right)$
gives the coordinates of a vector in
$v = v\!\left( {a,b} \right)$
gives the coordinates of a vector in
![]() ${P_T} \oplus \mathbb{R}\ell $
that is positively aligned to
${P_T} \oplus \mathbb{R}\ell $
that is positively aligned to
![]() ${\alpha _z}$
, and this will be enough. First of all, we check the orthogonality relations. Note that
${\alpha _z}$
, and this will be enough. First of all, we check the orthogonality relations. Note that
and
Recall that
Then, simple computations give
and
The positive alignment follows from the positivity of the discriminant of the matrix
 \begin{align*}\left[ {\begin{array}{c@{\quad}c@{\quad}c}{\Re \!\left( {b + \bar a} \right)} & {\Im \!\left( {b + \bar a} \right)} & 1\\{\Im \!\left( {a - \bar b} \right)} & {\Re \!\left( {a - \bar b} \right)} & 0\\{\Re \!\left( {b - \bar a} \right)} & {\Im \!\left( {b - \bar a} \right)} & {\!\left( {a\bar a - b\bar b} \right)\frac{{\left( {\sigma .\bar \sigma } \right)}}{{2d}}}\end{array}} \right]\end{align*}
\begin{align*}\left[ {\begin{array}{c@{\quad}c@{\quad}c}{\Re \!\left( {b + \bar a} \right)} & {\Im \!\left( {b + \bar a} \right)} & 1\\{\Im \!\left( {a - \bar b} \right)} & {\Re \!\left( {a - \bar b} \right)} & 0\\{\Re \!\left( {b - \bar a} \right)} & {\Im \!\left( {b - \bar a} \right)} & {\!\left( {a\bar a - b\bar b} \right)\frac{{\left( {\sigma .\bar \sigma } \right)}}{{2d}}}\end{array}} \right]\end{align*}
which is
as
![]() $a \ne \bar b$
, thanks to Remark 3·3.
$a \ne \bar b$
, thanks to Remark 3·3.
Remark 3·4. The equator
![]() $S_\ell ^1$
is defined by the condition
$S_\ell ^1$
is defined by the condition
![]() $\left| a \right| = \left| b \right|$
, or equivalently
$\left| a \right| = \left| b \right|$
, or equivalently
![]() $a\bar a = b\bar b$
, for
$a\bar a = b\bar b$
, for
![]() $z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
.
$z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
.
Lemma 3·5.
Choose a non-zero element
![]() $\ell ' \in T \oplus \mathbb{Q}\ell $
. Then there are exactly two points
$\ell ' \in T \oplus \mathbb{Q}\ell $
. Then there are exactly two points
![]() $z,z' \in \mathbb{P}_\ell ^1$
such that
$z,z' \in \mathbb{P}_\ell ^1$
such that
![]() $\ell '$
is orthogonal to z and
$\ell '$
is orthogonal to z and
![]() $z'$
, i.e.
$z'$
, i.e.
![]() $\ell ' \in P_z^ \bot $
and
$\ell ' \in P_z^ \bot $
and
![]() $\ell ' \in P_{z'}^ \bot $
. Moreover,
$\ell ' \in P_{z'}^ \bot $
. Moreover,
![]() $z' = \bar z$
, and z and
$z' = \bar z$
, and z and
![]() $\bar z$
correspond to antipodal points on
$\bar z$
correspond to antipodal points on
![]() $S_\ell ^2$
via the isomorphism
$S_\ell ^2$
via the isomorphism
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
.
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
.
Proof. The case
![]() $\ell ' = \ell $
has already been discussed; suppose that
$\ell ' = \ell $
has already been discussed; suppose that
![]() $\ell ' \notin \mathbb{Q}\ell $
. The orthogonal complement of
$\ell ' \notin \mathbb{Q}\ell $
. The orthogonal complement of
![]() $\ell '$
in
$\ell '$
in
![]() ${T_\mathbb{C}} \oplus \mathbb{C}\ell $
does not contain the whole
${T_\mathbb{C}} \oplus \mathbb{C}\ell $
does not contain the whole
![]() ${T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell $
(since the form
${T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell $
(since the form
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is non-degenerate on this last vector space). Therefore
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
is non-degenerate on this last vector space). Therefore
![]() ${\ell ^{{\rm{\prime}} \bot }} \cap \!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
is a
${\ell ^{{\rm{\prime}} \bot }} \cap \!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
is a
![]() $\mathbb{C}$
-plane in
$\mathbb{C}$
-plane in
![]() ${T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell $
. Passing to the projective spaces,
${T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell $
. Passing to the projective spaces,
![]() ${\ell ^{{\rm{\prime}} \bot }} \cap \!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
defines a line in
${\ell ^{{\rm{\prime}} \bot }} \cap \!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
defines a line in
![]() $\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
, which cuts the conic
$\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
, which cuts the conic
![]() $\mathbb{P}_\ell ^1$
in two distinct points, or one single point (with double multiplicity). On the other hand, the second case is not admissible: if
$\mathbb{P}_\ell ^1$
in two distinct points, or one single point (with double multiplicity). On the other hand, the second case is not admissible: if
![]() $z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
satisfies conditions (3·1) and (4·1), then
$z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
satisfies conditions (3·1) and (4·1), then
satisfies both equations as well. Besides, as already pointed out in Remark 3·3,
![]() $a \ne \bar b$
, so that
$a \ne \bar b$
, so that
![]() $z \ne \bar z$
. Then
$z \ne \bar z$
. Then
![]() $z,\bar z$
are the required points. Lastly, note that z and
$z,\bar z$
are the required points. Lastly, note that z and
![]() $\bar z$
are antipodal on the sphere
$\bar z$
are antipodal on the sphere
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
; for, compare with the isomorphism of Lemma 3·1.
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
; for, compare with the isomorphism of Lemma 3·1.
4. Picard jump on the equator
We focus our attention on the Noether–Lefschetz locus of the equator
![]() $S_\ell ^1 \subseteq \mathbb{P}_\ell ^1$
, its points of Picard jump and their period fields.
$S_\ell ^1 \subseteq \mathbb{P}_\ell ^1$
, its points of Picard jump and their period fields.
4·1. Excessive Picard jump values
We have already remarked that the original extended Hodge structure of K3 type on
![]() $T \oplus \mathbb{Q}\ell $
is no longer irreducible, being
$T \oplus \mathbb{Q}\ell $
is no longer irreducible, being
![]() $\ell $
a
$\ell $
a
![]() $\left( {1,1} \right)$
-class. Given
$\left( {1,1} \right)$
-class. Given
![]() $z \in \mathbb{P}_\ell ^1$
, we define the Picard number
$z \in \mathbb{P}_\ell ^1$
, we define the Picard number
![]() ${\rho _z}$
of the Hodge structure corresponding to z to be the
${\rho _z}$
of the Hodge structure corresponding to z to be the
![]() $\mathbb{Q}$
-dimension of the space of
$\mathbb{Q}$
-dimension of the space of
![]() $\left( {1,1} \right)$
-classes of
$\left( {1,1} \right)$
-classes of
![]() $T \oplus \mathbb{Q}\ell $
, that is
$T \oplus \mathbb{Q}\ell $
, that is
For instance, as the original T is irreducible, we deduce that
![]() ${\rho _x} = {\rho _{\bar x}} = 1$
.
${\rho _x} = {\rho _{\bar x}} = 1$
.
Definition 4·1. We say that a point
![]() $z \in \mathbb{P}_\ell ^1$
is of Picard jump if
$z \in \mathbb{P}_\ell ^1$
is of Picard jump if
![]() ${\rho _z} \geq 1$
, of excessive Picard jump if
${\rho _z} \geq 1$
, of excessive Picard jump if
![]() ${\rho _z} \gt 1$
. We call Noehter–Lefschetz locus the set of points
${\rho _z} \gt 1$
. We call Noehter–Lefschetz locus the set of points
![]() $z \in \mathbb{P}_\ell ^1$
of Picard jump.
$z \in \mathbb{P}_\ell ^1$
of Picard jump.
We are interested in understanding how points of Picard jump distribute on the sphere
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
, and the possible relative Picard numbers. Huybrechts proved the following result [
Reference HuybrechtsHuy20
, proposition 3·2].
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
, and the possible relative Picard numbers. Huybrechts proved the following result [
Reference HuybrechtsHuy20
, proposition 3·2].
Proposition 4·2.
Assume that T is a polarised irreducible Hodge structure of K3 type. Then, for the twistor base
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
, one has:
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
, one has:
-
(i) the set
 $\{ z \in \mathbb{P}_\ell ^1\;\big|\;{\rho _z} \geq 1\} $
is countable and dense (in the classical topology);
$\{ z \in \mathbb{P}_\ell ^1\;\big|\;{\rho _z} \geq 1\} $
is countable and dense (in the classical topology); -
(ii) the set
 $\left\{ {z \in \mathbb{P}_\ell ^1 \;\big|\; {{\rho _z}} \rangle 1} \right\}$
is at most countable and contained in the equator
$\left\{ {z \in \mathbb{P}_\ell ^1 \;\big|\; {{\rho _z}} \rangle 1} \right\}$
is at most countable and contained in the equator
 $S_\ell ^1$
.
$S_\ell ^1$
.
The fact that the Noether–Lefschetz locus is countable is a particular instance of a more general fact (see [
Reference HuybrechtsHuy16
, chapter 6, proposition 2·9]). However, there is a very simple argument that applies in this case. Assume that z is of Picard jump, and let
![]() $\ell ' \in T \oplus \mathbb{Q}\ell $
be a
$\ell ' \in T \oplus \mathbb{Q}\ell $
be a
![]() $\left( {1,1} \right)$
-class for the Hodge structure induced by z. Then
$\left( {1,1} \right)$
-class for the Hodge structure induced by z. Then
![]() ${\ell ^{{\rm{\prime}} \bot }}$
identifies a line in
${\ell ^{{\rm{\prime}} \bot }}$
identifies a line in
![]() $\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
, that cuts the conic
$\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
, that cuts the conic
![]() $\mathbb{P}_\ell ^1$
in two points: z and
$\mathbb{P}_\ell ^1$
in two points: z and
![]() $\bar z$
. Thus,
$\bar z$
. Thus,
![]() $\ell '$
is a
$\ell '$
is a
![]() $\left( {1,1} \right)$
-class only for finitely many
$\left( {1,1} \right)$
-class only for finitely many
![]() $z \in \mathbb{P}_\ell ^1$
, and therefore the Noether–Lefschetz locus is countable, as
$z \in \mathbb{P}_\ell ^1$
, and therefore the Noether–Lefschetz locus is countable, as
![]() $T \oplus \mathbb{Q}\ell $
is.
$T \oplus \mathbb{Q}\ell $
is.
Assume that
![]() $z = \left[ {a\sigma + b\bar \sigma + c\ell } \right]$
. The condition defining
$z = \left[ {a\sigma + b\bar \sigma + c\ell } \right]$
. The condition defining
![]() ${\ell ^{{\rm{\prime}} \bot }}$
can be translated as
${\ell ^{{\rm{\prime}} \bot }}$
can be translated as
Lemma 4·3.
Assume that
![]() $\ell ' \in T \oplus \mathbb{Q}\ell $
,
$\ell ' \in T \oplus \mathbb{Q}\ell $
,
![]() $\ell ' \notin \mathbb{Q}\ell $
and choose z to be one of the two points orthogonal to
$\ell ' \notin \mathbb{Q}\ell $
and choose z to be one of the two points orthogonal to
![]() $\ell '$
. Then the point z is contained in the equator
$\ell '$
. Then the point z is contained in the equator
![]() $S_\ell ^1$
if and only if
$S_\ell ^1$
if and only if
![]() $\ell ' \in T$
.
$\ell ' \in T$
.

Proof. Write
![]() $z = \left[ {\sigma '} \right]$
. Assume that
$z = \left[ {\sigma '} \right]$
. Assume that
![]() $z \in S_\ell ^1$
, i.e.
$z \in S_\ell ^1$
, i.e.
![]() $\ell \in {P_z} = {\langle \Re \!\left( {\sigma '} \right),\Im \!\left( {\sigma '} \right)\rangle _\mathbb{R}} \subseteq {\langle \sigma ',\overline {\sigma '} \rangle _\mathbb{C}}$
. Then
$\ell \in {P_z} = {\langle \Re \!\left( {\sigma '} \right),\Im \!\left( {\sigma '} \right)\rangle _\mathbb{R}} \subseteq {\langle \sigma ',\overline {\sigma '} \rangle _\mathbb{C}}$
. Then
![]() $\ell = a\sigma ' + b\overline {\sigma '} $
for some
$\ell = a\sigma ' + b\overline {\sigma '} $
for some
![]() $a,b \in \mathbb{C}$
; hence
$a,b \in \mathbb{C}$
; hence
![]() $\left( {\ell .\ell '} \right) = 0$
since
$\left( {\ell .\ell '} \right) = 0$
since
![]() $\left( {\sigma '.\ell '} \right) = 0$
, which means
$\left( {\sigma '.\ell '} \right) = 0$
, which means
![]() $\ell ' \in T$
. Conversely, assume that
$\ell ' \in T$
. Conversely, assume that
![]() $\ell ' \in T$
, i.e.
$\ell ' \in T$
, i.e.
![]() $\left( {\ell .\ell '} \right) = 0$
. Write
$\left( {\ell .\ell '} \right) = 0$
. Write
![]() $\sigma ' = a\sigma + b\bar \sigma + c\ell $
. After rescaling
$\sigma ' = a\sigma + b\bar \sigma + c\ell $
. After rescaling
![]() $\sigma $
, we may assume that
$\sigma $
, we may assume that
![]() $\left( {\sigma .\ell '} \right) = 1$
, so that
$\left( {\sigma .\ell '} \right) = 1$
, so that
![]() $\left( {\bar \sigma .\ell '} \right) = \overline {\!\left( {\sigma .\ell '} \right)} = 1$
as well. The condition
$\left( {\bar \sigma .\ell '} \right) = \overline {\!\left( {\sigma .\ell '} \right)} = 1$
as well. The condition
![]() $\left( {\sigma '.\ell '} \right) = 0$
implies,
$\left( {\sigma '.\ell '} \right) = 0$
implies,
Therefore, the condition (3·1)
implies
![]() $c \ne 0$
(and therefore we may assume
$c \ne 0$
(and therefore we may assume
![]() $c = 1$
) and
$c = 1$
) and
![]() $a \in \mathbb{R}$
(since
$a \in \mathbb{R}$
(since
![]() $d \gt 0$
and
$d \gt 0$
and
![]() $\left( {\sigma .\bar \sigma } \right) \gt 0$
). Therefore
$\left( {\sigma .\bar \sigma } \right) \gt 0$
). Therefore
and
and the proof is concluded, as
![]() $\ell \in {P_z}$
.
$\ell \in {P_z}$
.
If the original Hodge structure T has CM, all points of Picard jump on the equator share the same Picard number.
Proposition 4·4.
Suppose that T is a polarised irreducible Hodge structure of K3 type and CM, and consider its sphere of related Hodge structures. Assume that
![]() $z \in S_\ell ^1$
is a point of Picard jump on the equator. Then
$z \in S_\ell ^1$
is a point of Picard jump on the equator. Then
![]() ${\rho _z} = r/2$
.
${\rho _z} = r/2$
.
Proof. Firstly, note that
![]() $P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right)$
is all contained in T. This follows from Lemma 4·3 applied to any non-zero element
$P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right)$
is all contained in T. This follows from Lemma 4·3 applied to any non-zero element
![]() $\ell ' \in P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right)$
. Hence
$\ell ' \in P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right)$
. Hence
![]() $P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right) = P_z^ \bot \cap T$
. The key remark is that
$P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right) = P_z^ \bot \cap T$
. The key remark is that
![]() $P_z^ \bot \cap T$
admits an action of the real part
$P_z^ \bot \cap T$
admits an action of the real part
![]() $K_T^0 = {K_T} \cap \mathbb{R}$
of the endomorphism field
$K_T^0 = {K_T} \cap \mathbb{R}$
of the endomorphism field
![]() ${K_T}$
. To show this, choose
${K_T}$
. To show this, choose
![]() $\beta \in K_T^0$
and
$\beta \in K_T^0$
and
![]() $\ell ' \in P_z^ \bot \cap T$
. Write
$\ell ' \in P_z^ \bot \cap T$
. Write
![]() $z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
. Then, using that
$z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
. Then, using that
![]() $\ell $
is orthogonal to T, we obtain (
$\ell $
is orthogonal to T, we obtain (
![]() $\beta \in K_T^0$
is
$\beta \in K_T^0$
is

self-adjoint for
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
)
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
)
 \begin{align*}\!\left( {\sigma '.\beta \!\left( {\ell '} \right)} \right) & = \left( {a\sigma + b\bar \sigma + \ell .\beta \!\left( {\ell '} \right)} \right)\\ &= \left( {a\sigma + b\bar \sigma .\beta \!\left( {\ell '} \right)} \right)\\ &= \left( {\beta \!\left( {a\sigma + b\bar \sigma } \right).\ell '} \right)\\ & = a\!\left( {\beta \cdot \sigma .\ell '} \right) + b\!\left( {\beta \cdot \bar \sigma .\ell '} \right)\\ & = \beta \cdot \left( {a\sigma + b\bar \sigma + \ell .\ell '} \right)\\ & = \beta \cdot \left( {\sigma '.\ell '} \right) = 0.\end{align*}
\begin{align*}\!\left( {\sigma '.\beta \!\left( {\ell '} \right)} \right) & = \left( {a\sigma + b\bar \sigma + \ell .\beta \!\left( {\ell '} \right)} \right)\\ &= \left( {a\sigma + b\bar \sigma .\beta \!\left( {\ell '} \right)} \right)\\ &= \left( {\beta \!\left( {a\sigma + b\bar \sigma } \right).\ell '} \right)\\ & = a\!\left( {\beta \cdot \sigma .\ell '} \right) + b\!\left( {\beta \cdot \bar \sigma .\ell '} \right)\\ & = \beta \cdot \left( {a\sigma + b\bar \sigma + \ell .\ell '} \right)\\ & = \beta \cdot \left( {\sigma '.\ell '} \right) = 0.\end{align*}
As a consequence,
![]() $P_z^ \bot \cap T$
is a
$P_z^ \bot \cap T$
is a
![]() $K_T^0$
-vector space. As
$K_T^0$
-vector space. As
![]() $\left[ {K_T^0\;:\;\mathbb{Q}} \right] = r/2$
(we are in the CM case by assumption, so that
$\left[ {K_T^0\;:\;\mathbb{Q}} \right] = r/2$
(we are in the CM case by assumption, so that
![]() $\left[ {{K_T}\;:\;K_T^0} \right] = 2$
and
$\left[ {{K_T}\;:\;K_T^0} \right] = 2$
and
![]() $\left[ {{K_T}\;:\;\mathbb{Q}} \right] = r$
),
$\left[ {{K_T}\;:\;\mathbb{Q}} \right] = r$
),
![]() ${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T$
can only take three different values:
${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T$
can only take three different values:
![]() $0,1,2$
. We immediately exclude the case
$0,1,2$
. We immediately exclude the case
![]() ${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T = 0$
since z is a point of Picard jump. Assume by contradiction that
${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T = 0$
since z is a point of Picard jump. Assume by contradiction that
![]() ${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T = 2$
. In fact, this equality would imply
${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T = 2$
. In fact, this equality would imply
![]() $P_z^ \bot \cap T = T$
. This would force
$P_z^ \bot \cap T = T$
. This would force
![]() $\sigma '$
to belong to
$\sigma '$
to belong to
![]() $\mathbb{C}\ell $
, or equivalently to have zero
$\mathbb{C}\ell $
, or equivalently to have zero
![]() ${T_\mathbb{C}}$
-part (indeed the form
${T_\mathbb{C}}$
-part (indeed the form
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
in non-degenerate on T, and therefore on
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
in non-degenerate on T, and therefore on
![]() ${T_\mathbb{C}}$
). On the other hand, this is a contradiction, since any non-zero
${T_\mathbb{C}}$
). On the other hand, this is a contradiction, since any non-zero
![]() $\sigma ' \in \mathbb{C}\ell $
does not satisfy (3·1). In conclusion,
$\sigma ' \in \mathbb{C}\ell $
does not satisfy (3·1). In conclusion,
![]() ${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T = 1$
, or equivalently
${\rm{di}}{{\rm{m}}_{K_T^0}}P_z^ \bot \cap T = 1$
, or equivalently
![]() ${\rm{di}}{{\rm{m}}_\mathbb{Q}}P_z^ \bot \cap T = \left[ {K_T^0\;:\;\mathbb{Q}} \right] = r/2$
, i.e.
${\rm{di}}{{\rm{m}}_\mathbb{Q}}P_z^ \bot \cap T = \left[ {K_T^0\;:\;\mathbb{Q}} \right] = r/2$
, i.e.
![]() ${\rho _z} = r/2$
.
${\rho _z} = r/2$
.
Remark 4·5. If the original T has CM, the only case where there are no points of excessive Picard jump (i.e.
![]() ${\rho _z} \le 1$
for all
${\rho _z} \le 1$
for all
![]() $z \in \mathbb{P}_\ell ^1$
) is
$z \in \mathbb{P}_\ell ^1$
) is
![]() $r = 2$
.
$r = 2$
.
Remark 4·6. The hypothesis on T of being of CM type plays a fundamental role in order to ensure the validity of the property
![]() ${\rho _z} = r/2$
for all points of jump on the equator. It is not difficult to construct explicit examples of irreducible polarised Hodge structures of K3 type T for which the excessive Picard values are multiple. In addition, not even the sole assumption that
${\rho _z} = r/2$
for all points of jump on the equator. It is not difficult to construct explicit examples of irreducible polarised Hodge structures of K3 type T for which the excessive Picard values are multiple. In addition, not even the sole assumption that
![]() ${K_T}$
is CM, without supposing
${K_T}$
is CM, without supposing
![]() $\textrm{dim}_\mathbb{Q}T = \left[ {{K_T}\;:\;\mathbb{Q}} \right]$
, is enough to guarantee the result.
$\textrm{dim}_\mathbb{Q}T = \left[ {{K_T}\;:\;\mathbb{Q}} \right]$
, is enough to guarantee the result.
Remark 4·7. However, if T is not assumed to be of CM type, one may argue as in the proof of Proposition 4·4 to deduce that
![]() ${\rho _z}$
(for z point of Picard jump on the equator) is divisible by
${\rho _z}$
(for z point of Picard jump on the equator) is divisible by
![]() $\left[ {K_T^0\;:\;\mathbb{Q}} \right]$
and strictly smaller than r.
$\left[ {K_T^0\;:\;\mathbb{Q}} \right]$
and strictly smaller than r.
The following result enriches Proposition 4·2. To prove it, it is not necessary to assume that T has CM, or that
![]() ${K_T}$
is CM. However, in Section 5·2 we will give a better description of the distribution of points of Picard jump on the equator in the CM case.
${K_T}$
is CM. However, in Section 5·2 we will give a better description of the distribution of points of Picard jump on the equator in the CM case.

Proposition 4·8. Assume that T is a polarised irreducible Hodge structure of K3 type, and consider its sphere of related Hodge structures. Then the set of points of Picard jump on the equator is dense in the equator (for the classical topology). In particular, this set is countable (not finite).
Proof. Thanks to Lemma 3·1, a point on the equator
![]() $S_\ell ^1 \subseteq \mathbb{P}_\ell ^1$
corresponds via the isomorphism
$S_\ell ^1 \subseteq \mathbb{P}_\ell ^1$
corresponds via the isomorphism
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
to the normalisation of the vector
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
to the normalisation of the vector
Lemma 3·1 also gives a condition on z to belong to
![]() $S_\ell ^1$
, namely
$S_\ell ^1$
, namely
![]() $\left| a \right| = \left| b \right|$
. Write R to denote these absolute values; then
$\left| a \right| = \left| b \right|$
. Write R to denote these absolute values; then
![]() $a = R{e^{i\theta }},b = R{e^{i\tau }}$
for some
$a = R{e^{i\theta }},b = R{e^{i\tau }}$
for some
![]() $\theta ,\tau \in \mathbb{R}$
. Moreover, (3·1) gives
$\theta ,\tau \in \mathbb{R}$
. Moreover, (3·1) gives
from which we deduce that
![]() $\theta + \tau { \equiv _{2\pi }}\pi $
. Hence,
$\theta + \tau { \equiv _{2\pi }}\pi $
. Hence,
![]() $b = - R{e^{ - i\theta }} = - \bar a$
. Then
$b = - R{e^{ - i\theta }} = - \bar a$
. Then
Therefore, in order to prove the statement, it is enough to show that the set of possible complex arguments assumed by the periods
![]() $\left( {\sigma .\gamma } \right)$
,
$\left( {\sigma .\gamma } \right)$
,
![]() $\gamma \in T$
is dense in the circle
$\gamma \in T$
is dense in the circle
![]() $\{ z \in \mathbb{C}\;|\;\left| z \right| = 1\} $
(the point of Picard jump corresponding to such a
$\{ z \in \mathbb{C}\;|\;\left| z \right| = 1\} $
(the point of Picard jump corresponding to such a
![]() $\gamma $
would be determined by
$\gamma $
would be determined by
![]() $a = R{e^{i\theta }}$
such that
$a = R{e^{i\theta }}$
such that
![]() $\theta $
(or
$\theta $
(or
![]() $\pi + \theta $
) is the opposite of the argument of
$\pi + \theta $
) is the opposite of the argument of
![]() $\left( {\sigma .\gamma } \right)$
). However, the
$\left( {\sigma .\gamma } \right)$
). However, the
![]() $\mathbb{Q}$
-vector space P of the periods
$\mathbb{Q}$
-vector space P of the periods
![]() $\left( {\sigma .\gamma } \right)$
,
$\left( {\sigma .\gamma } \right)$
,
![]() $\gamma \in T$
is not contained in an
$\gamma \in T$
is not contained in an
![]() $\mathbb{R}$
-line of
$\mathbb{R}$
-line of
![]() $\mathbb{C}$
; indeed, if this were the case, then the period field
$\mathbb{C}$
; indeed, if this were the case, then the period field
![]() ${k_T} = \mathbb{Q}\!\left( {\left( {\sigma .{\gamma _i}} \right)/\left( {\sigma .{\gamma _1}} \right)} \right)$
(for a basis
${k_T} = \mathbb{Q}\!\left( {\left( {\sigma .{\gamma _i}} \right)/\left( {\sigma .{\gamma _1}} \right)} \right)$
(for a basis
![]() $\left\{ {{\gamma _i}} \right\}$
of T) would be contained in
$\left\{ {{\gamma _i}} \right\}$
of T) would be contained in
![]() $\mathbb{R}$
, contradiction. As a consequence, P is dense in
$\mathbb{R}$
, contradiction. As a consequence, P is dense in
![]() $\mathbb{C}$
, and then the set of the complex arguments of elements of
$\mathbb{C}$
, and then the set of the complex arguments of elements of
![]() $P\backslash \left\{ 0 \right\}$
is dense in the circle.
$P\backslash \left\{ 0 \right\}$
is dense in the circle.
5. Actions on Noether–Lefschetz loci
In this section, assume that T is a polarised irreducible Hodge structure of K3 type, and consider again the associated twistor base
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
. We define two actions: first, an action of the multiplicative group
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
. We define two actions: first, an action of the multiplicative group
![]() $K_T^ \times $
on the Noether–Lefschetz locus of the upper-half sphere, deprived of the north pole; then, an action of the multiplicative group
$K_T^ \times $
on the Noether–Lefschetz locus of the upper-half sphere, deprived of the north pole; then, an action of the multiplicative group
![]() $K_T^ \times /{(K_T^0)^ \times }$
on the Noether–Lefschetz locus of the equator. We treat in particular the situation arising when we assume that T is of CM type: the jumping loci outside and on the equator are homogeneous under the actions of
$K_T^ \times /{(K_T^0)^ \times }$
on the Noether–Lefschetz locus of the equator. We treat in particular the situation arising when we assume that T is of CM type: the jumping loci outside and on the equator are homogeneous under the actions of
![]() $K_T^ \times $
and
$K_T^ \times $
and
![]() $K_T^ \times /{(K_T^0)^ \times }$
, respectively.
$K_T^ \times /{(K_T^0)^ \times }$
, respectively.
One may define these two actions together as a unique action on the whole
![]() $\mathbb{P}_\ell ^1$
; however, we prefer to keep them separated to analyse the different behaviours on points outside and on the equator
$\mathbb{P}_\ell ^1$
; however, we prefer to keep them separated to analyse the different behaviours on points outside and on the equator
![]() $S_\ell ^1$
.
$S_\ell ^1$
.
5·1. Outside the equator
Denote by
![]() $\mathcal{U}$
the upper-half sphere of
$\mathcal{U}$
the upper-half sphere of
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
(defined by the condition
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
(defined by the condition
![]() $\left| a \right| \gt \left| b \right|$
on
$\left| a \right| \gt \left| b \right|$
on
![]() $z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
, see Lemma 3·1), and by
$z = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
, see Lemma 3·1), and by
![]() $\mathcal{Q}$
the set of points of Picard jump in
$\mathcal{Q}$
the set of points of Picard jump in
![]() $\mathcal{U}$
(that is, the Noether–Lefschetz locus of
$\mathcal{U}$
(that is, the Noether–Lefschetz locus of
![]() $\mathcal{U}$
), deprived of the north pole x. Notice that a point
$\mathcal{U}$
), deprived of the north pole x. Notice that a point
![]() $z \in \mathcal{Q}$
satisfies
$z \in \mathcal{Q}$
satisfies
![]() ${\rho _z} = 1$
, by Proposition 4·2, and hence is orthogonal to a unique (up to a rational scalar) non-zero element
${\rho _z} = 1$
, by Proposition 4·2, and hence is orthogonal to a unique (up to a rational scalar) non-zero element
![]() $\ell ' \in P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right)$
. Denote by
$\ell ' \in P_z^ \bot \cap \!\left( {T \oplus \mathbb{Q}\ell } \right)$
. Denote by
![]() ${\mathcal{Q}^ + }$
the set of
${\mathcal{Q}^ + }$
the set of
![]() $z \in \mathcal{Q}$
for which the corresponding
$z \in \mathcal{Q}$
for which the corresponding
![]() $\ell '$
is such that
$\ell '$
is such that
![]() $\left( {\ell '.\ell '} \right) \gt 0$
.
$\left( {\ell '.\ell '} \right) \gt 0$
.
Remark 5·1. Unless
![]() $r = 2$
, the form
$r = 2$
, the form
![]() $\left( {\;.\;} \right)$
is not positive definite on T. Thus,
$\left( {\;.\;} \right)$
is not positive definite on T. Thus,
![]() ${\mathcal{Q}^ + }{\subsetneq}\mathcal{Q}$
if
${\mathcal{Q}^ + }{\subsetneq}\mathcal{Q}$
if
![]() $r \gt 2$
.
$r \gt 2$
.
For a point
![]() $z \in \mathbb{P}_\ell ^1$
, we define its altitude as the last coordinate of the vector defined by Lemma 3·1, namely the third coordinate of the corresponding point in
$z \in \mathbb{P}_\ell ^1$
, we define its altitude as the last coordinate of the vector defined by Lemma 3·1, namely the third coordinate of the corresponding point in
![]() $S_\ell ^2$
for the basis
$S_\ell ^2$
for the basis
![]() $\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right),\ell } \right\}$
of
$\left\{ {\Re \!\left( \sigma \right),\Im \!\left( \sigma \right),\ell } \right\}$
of
![]() ${P_T} \oplus \mathbb{R}\ell $
.
${P_T} \oplus \mathbb{R}\ell $
.
Recall that
![]() $d = \left( {\ell .\ell } \right) \in {\mathbb{Z}_{ \gt 0}}$
. Choose an element
$d = \left( {\ell .\ell } \right) \in {\mathbb{Z}_{ \gt 0}}$
. Choose an element
![]() $\ell ' = {\gamma _1} + \left( {m/d} \right)\ell \in T \oplus \mathbb{Q}\ell $
,
$\ell ' = {\gamma _1} + \left( {m/d} \right)\ell \in T \oplus \mathbb{Q}\ell $
,
![]() $\ell ' \notin T$
,
$\ell ' \notin T$
,
![]() $\ell ' \notin \mathbb{Q}\ell $
, so that the two corresponding orthogonal points are neither the poles nor on the equator (see Lemma 3·5 and Lemma 4·3). Denote by
$\ell ' \notin \mathbb{Q}\ell $
, so that the two corresponding orthogonal points are neither the poles nor on the equator (see Lemma 3·5 and Lemma 4·3). Denote by
![]() ${z_1} \in \mathcal{Q}$
the only point of Picard jump in the upper-half sphere orthogonal to
${z_1} \in \mathcal{Q}$
the only point of Picard jump in the upper-half sphere orthogonal to
![]() $\ell '$
. Taking a scalar multiple of
$\ell '$
. Taking a scalar multiple of
![]() $\ell '$
identifies the same
$\ell '$
identifies the same
![]() ${z_1}$
; we may assume
${z_1}$
; we may assume
![]() $m = d$
, so that
$m = d$
, so that
![]() $\ell ' = {\gamma _1} + \ell $
. For an element
$\ell ' = {\gamma _1} + \ell $
. For an element
![]() $A \in K_T^ \times $
, we define
$A \in K_T^ \times $
, we define
![]() ${z_2} = A\;{\rm{*}}\;{z_1}$
, where
${z_2} = A\;{\rm{*}}\;{z_1}$
, where
![]() ${z_2} \in \mathcal{Q}$
is the only point of Picard jump in the upper-half sphere orthogonal to
${z_2} \in \mathcal{Q}$
is the only point of Picard jump in the upper-half sphere orthogonal to
![]() $\ell '' = {\gamma _2} + \ell $
, where
$\ell '' = {\gamma _2} + \ell $
, where
![]() ${\gamma _2} = A\!\left( {{\gamma _1}} \right)$
. This association defines an action of
${\gamma _2} = A\!\left( {{\gamma _1}} \right)$
. This association defines an action of
![]() $K_T^ \times $
on
$K_T^ \times $
on
![]() $\mathcal{Q}$
.
$\mathcal{Q}$
.
Proposition 5·2. The action defined above is free. Moreover, if T has CM, the action is transitive.
Proof. If
![]() $A \in K_T^ \times $
is different from the identity morphism,
$A \in K_T^ \times $
is different from the identity morphism,
![]() $\ell '$
and
$\ell '$
and
![]() $\ell ''$
are linearly independent over
$\ell ''$
are linearly independent over
![]() $\mathbb{Q}$
, so that they cannot be orthogonal to the same point in
$\mathbb{Q}$
, so that they cannot be orthogonal to the same point in
![]() $\mathcal{Q}$
(thanks to Proposition 4·2); thus, the action is free. The transitivity of the action in the CM case follows from
$\mathcal{Q}$
(thanks to Proposition 4·2); thus, the action is free. The transitivity of the action in the CM case follows from
![]() ${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
.
${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
.
Remark 5·3. If T does not have CM, the action is not transitive (as
![]() $\textrm{di}{\textrm{m}_{{K_T}}}T \gt 1$
).
$\textrm{di}{\textrm{m}_{{K_T}}}T \gt 1$
).
Proposition 5·4.
Under the same assumptions as above, suppose that
![]() ${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right] \in \mathcal{Q}$
and additionally that
${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right] \in \mathcal{Q}$
and additionally that
![]() $A \in K_T^ \times $
. Then:
$A \in K_T^ \times $
. Then:
-
(i) if
 $\left| A \right| = 1$
, say
$\left| A \right| = 1$
, say
 $A = {e^{i\theta }}$
, then
$A = {e^{i\theta }}$
, then
 ${z_2} = A*{z_1}$
is represented by the element
${z_2} = A*{z_1}$
is represented by the element
 \begin{align*}\sigma '' = aA\!\left( \sigma \right) + bA\!\left( {\bar \sigma } \right) + \ell = aA\sigma + b\bar A\bar \sigma + \ell = a{e^{i\theta }}\sigma + b{e^{ - i\theta }}\bar \sigma + \ell .\end{align*}
\begin{align*}\sigma '' = aA\!\left( \sigma \right) + bA\!\left( {\bar \sigma } \right) + \ell = aA\sigma + b\bar A\bar \sigma + \ell = a{e^{i\theta }}\sigma + b{e^{ - i\theta }}\bar \sigma + \ell .\end{align*}
In particular, A acts on
 $\mathcal{Q}$
by a rotation of angle
$\mathcal{Q}$
by a rotation of angle
 $ - \theta $
along the
$ - \theta $
along the
 $\ell $
-axis, and
$\ell $
-axis, and
 ${z_1}$
and
${z_1}$
and
 ${z_2}$
have the same altitude;
${z_2}$
have the same altitude;
-
(ii) if
 $\left| A \right| \ne 1$
, then
$\left| A \right| \ne 1$
, then
 ${z_1}$
and
${z_1}$
and
 ${z_2} = A*{z_1}$
do not have the same altitude. In particular, if
${z_2} = A*{z_1}$
do not have the same altitude. In particular, if
 $\left| A \right| \lt 1$
the altitude of
$\left| A \right| \lt 1$
the altitude of
 ${z_2}$
is greater than the one of
${z_2}$
is greater than the one of
 ${z_1}$
, and vice versa;
${z_1}$
, and vice versa;
-
(iii) if
 $A \in K_T^0 = {K_T} \cap \mathbb{R}$
, then
$A \in K_T^0 = {K_T} \cap \mathbb{R}$
, then
 ${z_1}$
and
${z_1}$
and
 ${z_2} = A*{z_1}$
lie on the same meridian of
${z_2} = A*{z_1}$
lie on the same meridian of
 $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
.
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
.
Remark 5·5. Recall that the homeomorphism
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
of Lemma 3·1 sends
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
of Lemma 3·1 sends
![]() ${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
to the normalisation of the vector
${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
to the normalisation of the vector
This allows us to deduce that the tangent of the angle between a vector of a point
![]() $S_\ell ^2$
and the plane of zero-altitude is given, up to sign, by
$S_\ell ^2$
and the plane of zero-altitude is given, up to sign, by
Indeed, it is suffices to notice that
since
![]() $ab \in \mathbb{R}$
by (3·1).
$ab \in \mathbb{R}$
by (3·1).
Proof of the Proposition. Firstly, assume that
![]() $\left| A \right| = 1$
. We are showing that
$\left| A \right| = 1$
. We are showing that
![]() ${z_2} = \left[ {\sigma ''} \right]$
actually belongs to the conic
${z_2} = \left[ {\sigma ''} \right]$
actually belongs to the conic
![]() $\mathbb{P}_\ell ^1$
, i.e.
$\mathbb{P}_\ell ^1$
, i.e.
![]() $\left( {\sigma ''.\sigma ''} \right) = 0$
. For, it is enough to observe that the (3·1), that here takes the form
$\left( {\sigma ''.\sigma ''} \right) = 0$
. For, it is enough to observe that the (3·1), that here takes the form
is satisfied since
![]() $\left| A \right| = 1$
and
$\left| A \right| = 1$
and
![]() ${z_1} \in \mathbb{P}_\ell ^1$
. If
${z_1} \in \mathbb{P}_\ell ^1$
. If
![]() $\left| a \right| \gt \left| b \right|$
then
$\left| a \right| \gt \left| b \right|$
then
![]() $\left| {aA} \right| \gt \left| {b\bar A} \right|$
, so that
$\left| {aA} \right| \gt \left| {b\bar A} \right|$
, so that
![]() ${z_2}$
still belongs to the upper-half sphere. To prove the first statement, it suffices to show that
${z_2}$
still belongs to the upper-half sphere. To prove the first statement, it suffices to show that
![]() $\left( {\sigma ''.\ell ''} \right) = 0$
holds true, where
$\left( {\sigma ''.\ell ''} \right) = 0$
holds true, where
![]() $\ell '' = A\!\left( {{\gamma _1}} \right) + \ell $
. Recall that, since
$\ell '' = A\!\left( {{\gamma _1}} \right) + \ell $
. Recall that, since
![]() $\left| A \right| = 1$
, A is an isometry for
$\left| A \right| = 1$
, A is an isometry for
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
; therefore we obtain
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
; therefore we obtain
 \begin{align*}\!\left( {\sigma ''.\ell ''} \right) &= \left( {aA\!\left( \sigma \right) + bA\!\left( {\bar \sigma } \right) + \ell .A\!\left( {{\gamma _1}} \right) + \ell } \right)\\ &= a\!\left( {A\!\left( \sigma \right).A\!\left( {{\gamma _1}} \right)} \right) + b\!\left( {A\!\left( {\bar \sigma } \right).A\!\left( {{\gamma _1}} \right)} \right) + d\\ & = a\!\left( {\sigma .{\gamma _1}} \right) + \left( {\bar \sigma .{\gamma _1}} \right) + d\\ & = \left( {\sigma '.\ell '} \right) = 0.\end{align*}
\begin{align*}\!\left( {\sigma ''.\ell ''} \right) &= \left( {aA\!\left( \sigma \right) + bA\!\left( {\bar \sigma } \right) + \ell .A\!\left( {{\gamma _1}} \right) + \ell } \right)\\ &= a\!\left( {A\!\left( \sigma \right).A\!\left( {{\gamma _1}} \right)} \right) + b\!\left( {A\!\left( {\bar \sigma } \right).A\!\left( {{\gamma _1}} \right)} \right) + d\\ & = a\!\left( {\sigma .{\gamma _1}} \right) + \left( {\bar \sigma .{\gamma _1}} \right) + d\\ & = \left( {\sigma '.\ell '} \right) = 0.\end{align*}
For the statement concerning the action by rotation and the same altitude of
![]() ${z_1}$
and
${z_1}$
and
![]() ${z_2}$
, it is enough to compare the tangents of the angles between the vectors corresponding to
${z_2}$
, it is enough to compare the tangents of the angles between the vectors corresponding to
![]() ${z_1}$
and
${z_1}$
and
![]() ${z_2}$
, as done in Remark 5·5.
${z_2}$
, as done in Remark 5·5.
Remark 5·6. One could expect, for a general
![]() $A \in K_T^ \times $
not necessarily of norm one, the point
$A \in K_T^ \times $
not necessarily of norm one, the point
![]() ${z_2} = A*{z_1}$
to be given by
${z_2} = A*{z_1}$
to be given by
so that
![]() $\left( {\sigma ''.\ell ''} \right) = 0$
by a similar argument. Nonetheless, (3·1) is no longer satisfied and
$\left( {\sigma ''.\ell ''} \right) = 0$
by a similar argument. Nonetheless, (3·1) is no longer satisfied and
![]() ${z_2} \notin \mathbb{P}_l^1$
, so this guess is not true. It is indeed more complicated to deduce an explicit expression for
${z_2} \notin \mathbb{P}_l^1$
, so this guess is not true. It is indeed more complicated to deduce an explicit expression for
![]() ${z_2}$
when A does not have norm one.
${z_2}$
when A does not have norm one.
We continue the proof of Proposition 5·4. Assume now that
![]() $\left| A \right| \ne 1$
. Even without computing explicitly
$\left| A \right| \ne 1$
. Even without computing explicitly
![]() ${z_2}$
we can prove that
${z_2}$
we can prove that
![]() ${z_2}$
has different altitude from
${z_2}$
has different altitude from
![]() ${z_1}$
. Define
${z_1}$
. Define
![]() $B = {\bar A^{ - 1}}$
and consider
$B = {\bar A^{ - 1}}$
and consider
It corresponds to a point in
![]() $\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
orthogonal to
$\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
orthogonal to
![]() $\ell ''$
. Then
$\ell ''$
. Then
![]() $0 = \overline {\!\left( {\sigma ''.\ell ''} \right)} = \left( {\overline {\sigma ''} .\ell ''} \right)$
, where
$0 = \overline {\!\left( {\sigma ''.\ell ''} \right)} = \left( {\overline {\sigma ''} .\ell ''} \right)$
, where
Note that
![]() $\sigma '',\overline {\sigma ''} $
are linearly independent over
$\sigma '',\overline {\sigma ''} $
are linearly independent over
![]() $\mathbb{C}$
since
$\mathbb{C}$
since
![]() $a \ne \bar b$
(see Remark 3·3). Therefore, the line in
$a \ne \bar b$
(see Remark 3·3). Therefore, the line in
![]() $\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
passing through these points is exactly the line of elements orthogonal to
$\mathbb{P}\!\left( {{T^{2,0}} \oplus {T^{0,2}} \oplus \mathbb{C}\ell } \right)$
passing through these points is exactly the line of elements orthogonal to
![]() $\ell ''$
; among these points there are
$\ell ''$
; among these points there are
![]() ${z_2}$
and
${z_2}$
and
![]() $\overline {{z_2}} $
, given by the intersection with the conic
$\overline {{z_2}} $
, given by the intersection with the conic
![]() $\mathbb{P}_\ell ^1$
. The general point of this line has the form
$\mathbb{P}_\ell ^1$
. The general point of this line has the form
![]() $z = \left[ {\lambda \sigma '' + \mu \overline {\sigma ''} } \right]$
. Since
$z = \left[ {\lambda \sigma '' + \mu \overline {\sigma ''} } \right]$
. Since
![]() $\lambda + \mu = 0$
does not give an element of
$\lambda + \mu = 0$
does not give an element of
![]() $\mathbb{P}_\ell ^1$
, we may assume
$\mathbb{P}_\ell ^1$
, we may assume
![]() $\lambda + \mu = 1$
, and
$\lambda + \mu = 1$
, and
![]() $z = \left[ {\lambda \sigma '' + \left( {1 - \lambda } \right)\overline {\sigma ''} } \right]$
.
$z = \left[ {\lambda \sigma '' + \left( {1 - \lambda } \right)\overline {\sigma ''} } \right]$
.

Assume that
![]() $z \in \mathbb{P}_\ell ^1$
. We claim that
$z \in \mathbb{P}_\ell ^1$
. We claim that
![]() $\lambda \in \mathbb{R}$
. Firstly, note that
$\lambda \in \mathbb{R}$
. Firstly, note that
![]() $\lambda \ne 1/2$
, otherwise the
$\lambda \ne 1/2$
, otherwise the
![]() $\sigma $
-coefficient and the
$\sigma $
-coefficient and the
![]() $\bar \sigma $
-coefficient of
$\bar \sigma $
-coefficient of
![]() $\lambda \sigma '' + \left( {1 - \lambda } \right)\overline {\sigma ''} $
would have the same norm, forcing z to be on the equator
$\lambda \sigma '' + \left( {1 - \lambda } \right)\overline {\sigma ''} $
would have the same norm, forcing z to be on the equator
![]() $S_\ell ^1$
, contradiction. Since
$S_\ell ^1$
, contradiction. Since
![]() $z \in \mathbb{P}_\ell ^1$
, then
$z \in \mathbb{P}_\ell ^1$
, then
Note that
![]() $\left( {\sigma ''.\sigma ''} \right) = \left( {\overline {\sigma ''} .\overline {\sigma ''} } \right)$
. Therefore, also the point
$\left( {\sigma ''.\sigma ''} \right) = \left( {\overline {\sigma ''} .\overline {\sigma ''} } \right)$
. Therefore, also the point
![]() $z'$
identified by
$z'$
identified by
is in the intersection of the conic
![]() $\mathbb{P}_\ell ^1$
with the line of elements orthogonal to
$\mathbb{P}_\ell ^1$
with the line of elements orthogonal to
![]() $\ell ''$
. Since
$\ell ''$
. Since
![]() $\lambda \ne 1/2$
, it cannot coincide with z, and thus
$\lambda \ne 1/2$
, it cannot coincide with z, and thus
![]() $z' = \bar z$
, where
$z' = \bar z$
, where
Hence,
![]() $\lambda = \bar \lambda $
.
$\lambda = \bar \lambda $
.
As noticed in Remark 5·5, to discuss the difference of altitude we are interested in the quantity
![]() $\left| {\bar a + b} \right|$
for the new coefficients. We have
$\left| {\bar a + b} \right|$
for the new coefficients. We have
and, using
![]() $\lambda \in \mathbb{R}$
,
$\lambda \in \mathbb{R}$
,
This relation tells us exactly that, for points in the upper-half sphere, acting by an element of
![]() $K_T^ \times $
of norm smaller than one increases the altitude, while the action of elements of
$K_T^ \times $
of norm smaller than one increases the altitude, while the action of elements of
![]() $K_T^ \times $
of norm greater than one decreases the altitude.
$K_T^ \times $
of norm greater than one decreases the altitude.
Finally, we prove the third statement. If
![]() $A \in \mathbb{R}$
then
$A \in \mathbb{R}$
then
![]() $B = {\bar A^{ - 1}} = {A^{ - 1}} \in \mathbb{R}$
, too. Arguing as above, we deduce that
$B = {\bar A^{ - 1}} = {A^{ - 1}} \in \mathbb{R}$
, too. Arguing as above, we deduce that
![]() ${z_2}$
is represented by the element
${z_2}$
is represented by the element
for some
![]() $\lambda \in \mathbb{R}$
. Set
$\lambda \in \mathbb{R}$
. Set
For this element, the quantity
![]() $\tilde{b}-\overline{\tilde{a}}$
is equal to
$\tilde{b}-\overline{\tilde{a}}$
is equal to
As
![]() $\left( {2\lambda - 1} \right)B \in \mathbb{R}$
, the angle determined by
$\left( {2\lambda - 1} \right)B \in \mathbb{R}$
, the angle determined by
![]() $\Re\big(\tilde{b}-\overline{\tilde{a}}\big)$
and
$\Re\big(\tilde{b}-\overline{\tilde{a}}\big)$
and
![]() $\Im\big(\tilde{b}-\overline{\tilde{a}}\big)$
is the same as the angle determined by
$\Im\big(\tilde{b}-\overline{\tilde{a}}\big)$
is the same as the angle determined by
![]() $\Re \!\left( {b - \bar a} \right)$
and
$\Re \!\left( {b - \bar a} \right)$
and
![]() $\Im \!\left( {b - \bar a} \right)$
, so that
$\Im \!\left( {b - \bar a} \right)$
, so that
![]() ${z_2}$
and
${z_2}$
and
![]() ${z_1}$
lie on the same meridian.
${z_1}$
lie on the same meridian.
Remark 5·7. Of course, one can state a similar result for points in the lower-half sphere, as the lower-half may be obtained by conjugating the upper-half sphere.
Huybrechts proved that, for a point
![]() ${z_1} \in {\mathcal{Q}^ + }$
orthogonal to
${z_1} \in {\mathcal{Q}^ + }$
orthogonal to
![]() $\ell '$
, the corresponding polarised irreducible Hodge structure of K3 type, namely
$\ell '$
, the corresponding polarised irreducible Hodge structure of K3 type, namely
![]() $T' = {\ell ^{{\rm{\prime}} \bot }}$
, is of CM type, and the real parts
$T' = {\ell ^{{\rm{\prime}} \bot }}$
, is of CM type, and the real parts
![]() $K_T^0$
and
$K_T^0$
and
![]() $K_{T'}^0$
of
$K_{T'}^0$
of
![]() ${K_T}$
and
${K_T}$
and
![]() ${K_{T'}}$
, respectively, coincide [
Reference HuybrechtsHuy20
, proposition 3·8]. Moreover, he gave an explicit description of
${K_{T'}}$
, respectively, coincide [
Reference HuybrechtsHuy20
, proposition 3·8]. Moreover, he gave an explicit description of
![]() ${K_{T'}}$
[
Reference HuybrechtsHuy20
, corollary 3·10]: it is the quadratic extension of
${K_{T'}}$
[
Reference HuybrechtsHuy20
, corollary 3·10]: it is the quadratic extension of
![]() $K_T^0 = K_{T'}^0$
described by
$K_T^0 = K_{T'}^0$
described by
whereFootnote 2
![]() ${K_T} = \mathbb{Q}\!\left( \alpha \right)$
,
${K_T} = \mathbb{Q}\!\left( \alpha \right)$
,
![]() $d = \left( {\ell .\ell } \right)$
,
$d = \left( {\ell .\ell } \right)$
,
![]() $m = \left( {\ell .\ell '} \right)$
and
$m = \left( {\ell .\ell '} \right)$
and
![]() $\sigma $
is such that
$\sigma $
is such that
![]() $\left( {\sigma .\ell '} \right) = 1$
.
$\left( {\sigma .\ell '} \right) = 1$
.
Proposition 5·8.
Same hypotheses as in Proposition 5·4. Suppose that T has CM. Assume, moreover, that
![]() ${z_1} \in {\mathcal{Q}^ + }$
and that
${z_1} \in {\mathcal{Q}^ + }$
and that
![]() $A \in K_T^ \times $
satisfies
$A \in K_T^ \times $
satisfies
![]() $\left| A \right| = 1$
. Then
$\left| A \right| = 1$
. Then
![]() ${z_2} = A*{z_1} \in {\mathcal{Q}^ + }$
and the polarised irreducible Hodge structures of K3 type corresponding to the points
${z_2} = A*{z_1} \in {\mathcal{Q}^ + }$
and the polarised irreducible Hodge structures of K3 type corresponding to the points
![]() ${z_1}$
and
${z_1}$
and
![]() ${z_2}$
, namely
${z_2}$
, namely
![]() ${\ell ^{\prime \bot }}$
and
${\ell ^{\prime \bot }}$
and
![]() ${\ell ^{\prime\prime \bot }}$
, have the same CM field.
${\ell ^{\prime\prime \bot }}$
, have the same CM field.
Proof. To prove that
![]() ${z_2} \in {\mathcal{Q}^ + }$
, it is enough to notice that
${z_2} \in {\mathcal{Q}^ + }$
, it is enough to notice that
 \begin{align*}\!\left( {\ell ''.\ell ''} \right) &= \left( {A\!\left( {{\gamma _1}} \right) + \ell .A\!\left( {{\gamma _1}} \right) + \ell } \right)\\ &= \left( {A\!\left( {{\gamma _1}} \right).A\!\left( {{\gamma _1}} \right)} \right) + \left( {\ell .\ell } \right)\\ &= \left( {{\gamma _1}.{\gamma _1}} \right) + \left( {\ell .\ell } \right)\\ &= \left( {\ell '.\ell '} \right) \gt 0,\end{align*}
\begin{align*}\!\left( {\ell ''.\ell ''} \right) &= \left( {A\!\left( {{\gamma _1}} \right) + \ell .A\!\left( {{\gamma _1}} \right) + \ell } \right)\\ &= \left( {A\!\left( {{\gamma _1}} \right).A\!\left( {{\gamma _1}} \right)} \right) + \left( {\ell .\ell } \right)\\ &= \left( {{\gamma _1}.{\gamma _1}} \right) + \left( {\ell .\ell } \right)\\ &= \left( {\ell '.\ell '} \right) \gt 0,\end{align*}
as A is an isometry for
![]() $\left( {{\rm{\;}}.{\rm{\;}}} \right)$
and
$\left( {{\rm{\;}}.{\rm{\;}}} \right)$
and
![]() ${z_1} \in {\mathcal{Q}^ + }$
.
${z_1} \in {\mathcal{Q}^ + }$
.
We now prove that the coefficients
![]() $\gamma ,\delta $
are the same for the two points
$\gamma ,\delta $
are the same for the two points
![]() ${z_1},{z_2}$
, so that
${z_1},{z_2}$
, so that
![]() ${K_{T'}} = {K_{T''}}$
. For both points
${K_{T'}} = {K_{T''}}$
. For both points
![]() $m = d$
, since we fixed the
$m = d$
, since we fixed the
![]() $\ell $
-part of
$\ell $
-part of
![]() $\ell ',\ell ''$
; thus
$\ell ',\ell ''$
; thus
![]() $\gamma $
is the same. Note that
$\gamma $
is the same. Note that
![]() $\sigma $
depends on
$\sigma $
depends on
![]() $\ell '$
: it is chosen such that
$\ell '$
: it is chosen such that
![]() $\left( {\sigma .\ell '} \right) = 1$
. On the other hand, if we choose such a
$\left( {\sigma .\ell '} \right) = 1$
. On the other hand, if we choose such a
![]() $\sigma $
for
$\sigma $
for
![]() $\ell '$
, then
$\ell '$
, then
![]() $A\!\left( \sigma \right) = A\sigma $
satisfies
$A\!\left( \sigma \right) = A\sigma $
satisfies
since A is an isometry. Hence, we may choose
![]() $A\!\left( \sigma \right) = A\sigma $
for
$A\!\left( \sigma \right) = A\sigma $
for
![]() $\ell ''$
. Then
$\ell ''$
. Then
so that
![]() $\delta $
is the same as well.
$\delta $
is the same as well.
Remark 5·9. It is possible to construct examples to show that not all the degree-2 CM extensions of
![]() $K_T^0$
are realized as the CM endomorphism fields of some polarised irreducible Hodge structures of K3 type
$K_T^0$
are realized as the CM endomorphism fields of some polarised irreducible Hodge structures of K3 type
![]() $T' = {\ell ^{\prime \bot }}$
. Moreover, the same degree-2 CM extension of
$T' = {\ell ^{\prime \bot }}$
. Moreover, the same degree-2 CM extension of
![]() $K_T^0$
may occur for infinitely many different
$K_T^0$
may occur for infinitely many different
![]() $T' = \ell '$
, even for an Euclidean dense subset of
$T' = \ell '$
, even for an Euclidean dense subset of
![]() ${z_1} \in {\mathcal{Q}^ + }$
(again,
${z_1} \in {\mathcal{Q}^ + }$
(again,
![]() $\ell '$
is chosen orthogonal to
$\ell '$
is chosen orthogonal to
![]() ${z_1} \in {\mathcal{Q}^ + }$
).
${z_1} \in {\mathcal{Q}^ + }$
).
Endow
![]() $K_T^ \times $
with the topology induced as a subspace of
$K_T^ \times $
with the topology induced as a subspace of
![]() ${\mathbb{C}^ \times }$
by the fixed embedding
${\mathbb{C}^ \times }$
by the fixed embedding
![]() ${K_T} \hookrightarrow \mathbb{C}$
. Notice that the proof of Proposition 5·4 also puts in evidence the continuity of the action of
${K_T} \hookrightarrow \mathbb{C}$
. Notice that the proof of Proposition 5·4 also puts in evidence the continuity of the action of
![]() $K_T^ \times $
on
$K_T^ \times $
on
![]() $\mathcal{Q}$
. We summarise all the results in the following corollary.
$\mathcal{Q}$
. We summarise all the results in the following corollary.
Corollary 5·10. Assume that T has CM. Then:
-
(i) the topological group
 $K_T^ \times $
acts freely, transitively and continuously on
$K_T^ \times $
acts freely, transitively and continuously on
 $\mathcal{Q}$
. Having fixed an element
$\mathcal{Q}$
. Having fixed an element
 ${z_1} \in \mathcal{Q}$
, this action induces a homeomorphism between
${z_1} \in \mathcal{Q}$
, this action induces a homeomorphism between
 $K_T^ \times $
and
$K_T^ \times $
and
 $\mathcal{Q}$
, and this homeomorphism induces a homeomorphism between
$\mathcal{Q}$
, and this homeomorphism induces a homeomorphism between
 ${\mathbb{C}^ \times }$
and
${\mathbb{C}^ \times }$
and
 $\mathcal{U}$
, and between
$\mathcal{U}$
, and between
 $\mathbb{C}$
and
$\mathbb{C}$
and
 $\mathcal{U} \cup \left\{ x \right\}$
;
$\mathcal{U} \cup \left\{ x \right\}$
; -
(ii) the subgroup of
 $K_T^ \times $
given by the elements of norm one acts on
$K_T^ \times $
given by the elements of norm one acts on
 $\mathcal{Q}$
by rotation along the
$\mathcal{Q}$
by rotation along the
 $\ell $
-axis;
$\ell $
-axis; -
(iii) all points in
 $\mathcal{Q}$
at the same altitude of
$\mathcal{Q}$
at the same altitude of
 ${z_1}$
are obtained from
${z_1}$
are obtained from
 ${z_1}$
by acting with an element of
${z_1}$
by acting with an element of
 $K_T^ \times $
of norm one. Besides, given a point
$K_T^ \times $
of norm one. Besides, given a point
 ${z_1} \in \mathcal{Q}$
, there exist countably many points at the same altitude, and they are dense in the corresponding circle of
${z_1} \in \mathcal{Q}$
, there exist countably many points at the same altitude, and they are dense in the corresponding circle of
 $\mathcal{U}$
at that altitude;
$\mathcal{U}$
at that altitude; -
(iv) if
 ${z_1} \in {\mathcal{Q}^ + }$
, all the other points of Picard jump at the same altitude are in
${z_1} \in {\mathcal{Q}^ + }$
, all the other points of Picard jump at the same altitude are in
 ${\mathcal{Q}^ + }$
, and the Hodge structures
${\mathcal{Q}^ + }$
, and the Hodge structures
 ${\ell ^{\prime \bot }}$
and
${\ell ^{\prime \bot }}$
and
 ${\ell ^{\prime\prime \bot }}$
corresponding to these points have the same CM;
${\ell ^{\prime\prime \bot }}$
corresponding to these points have the same CM; -
(v) finally,
 ${\mathcal{Q}^ + }$
is dense in
${\mathcal{Q}^ + }$
is dense in
 $\mathcal{U}$
.
$\mathcal{U}$
.
Proof. The only statements left to prove are the ones concerning the density of points of
![]() $\mathcal{Q}$
at the same altitude and the density of points of
$\mathcal{Q}$
at the same altitude and the density of points of
![]() ${\mathcal{Q}^ + }$
. The first assertion follows from the fact that, for a CM field E, the set of points in
${\mathcal{Q}^ + }$
. The first assertion follows from the fact that, for a CM field E, the set of points in
![]() $E \cap {S^1}$
is dense in
$E \cap {S^1}$
is dense in
![]() ${S^1}$
, according to Corollary 2·7. For the second assertion: let
${S^1}$
, according to Corollary 2·7. For the second assertion: let
![]() $\gamma \in T$
such that
$\gamma \in T$
such that
![]() $\left( {\gamma .\gamma } \right) \gt 0$
, so that
$\left( {\gamma .\gamma } \right) \gt 0$
, so that
![]() $\left( {\gamma + \ell .\gamma + \ell } \right) = \left( {\gamma .\gamma } \right) + d \gt 0$
as well. Set
$\left( {\gamma + \ell .\gamma + \ell } \right) = \left( {\gamma .\gamma } \right) + d \gt 0$
as well. Set
![]() $\ell ' = \gamma + \ell $
. Consider an element in
$\ell ' = \gamma + \ell $
. Consider an element in
![]() ${\mathbb{Q}^ \times } \cdot \left( {{S^1} \cap {K_T}} \right) \subseteq K_T^ \times $
, say
${\mathbb{Q}^ \times } \cdot \left( {{S^1} \cap {K_T}} \right) \subseteq K_T^ \times $
, say
![]() $A = \lambda \alpha $
, for
$A = \lambda \alpha $
, for
![]() $\lambda \in {\mathbb{Q}^ \times }$
and
$\lambda \in {\mathbb{Q}^ \times }$
and
![]() $\alpha \in K_T^ \times $
satisfying
$\alpha \in K_T^ \times $
satisfying
![]() $\left| \alpha \right| = 1$
. Then
$\left| \alpha \right| = 1$
. Then
![]() $\ell '' = A\!\left( \gamma \right) + \ell $
satisfies
$\ell '' = A\!\left( \gamma \right) + \ell $
satisfies
The density of
![]() ${\mathcal{Q}^ + }$
in
${\mathcal{Q}^ + }$
in
![]() $\mathcal{U}$
follows, therefore, from the density of
$\mathcal{U}$
follows, therefore, from the density of
![]() ${\mathbb{Q}^ \times } \cdot \left( {{S^1} \cap {K_T}} \right)$
in
${\mathbb{Q}^ \times } \cdot \left( {{S^1} \cap {K_T}} \right)$
in
![]() ${\mathbb{C}^ \times }$
(
${\mathbb{C}^ \times }$
(
![]() ${S^1} \cap {K_T}$
is dense in
${S^1} \cap {K_T}$
is dense in
![]() ${S^1}$
thanks to Proposition 2·6).
${S^1}$
thanks to Proposition 2·6).
5·2. On the equator
Now we focus on the equator
![]() $S_\ell ^1$
. In the case
$S_\ell ^1$
. In the case
![]() $\mathbb{P}_\ell ^1\backslash S_\ell ^1$
we had at our disposal a clean way to choose one of the two points orthogonal to a certain
$\mathbb{P}_\ell ^1\backslash S_\ell ^1$
we had at our disposal a clean way to choose one of the two points orthogonal to a certain
![]() $\ell ' \in T \oplus \mathbb{Q}\ell $
: picking the one in the upper-half sphere (subject to the condition
$\ell ' \in T \oplus \mathbb{Q}\ell $
: picking the one in the upper-half sphere (subject to the condition
![]() $\left| a \right| \gt \left| b \right|$
). Here this choice is not so clear; therefore, we will consider pairs of antipodal points on
$\left| a \right| \gt \left| b \right|$
). Here this choice is not so clear; therefore, we will consider pairs of antipodal points on
![]() $S_\ell ^1$
. Define
$S_\ell ^1$
. Define
![]() $\mathcal{R}$
to be the set of points of Picard jump on the equator modulo the relation
$\mathcal{R}$
to be the set of points of Picard jump on the equator modulo the relation
![]() $\left\{ \pm \right\}$
. Pick an element
$\left\{ \pm \right\}$
. Pick an element
![]() $\ell ' = {\gamma _1} \in T$
,
$\ell ' = {\gamma _1} \in T$
,
![]() ${\gamma _1} \ne 0$
, and consider
${\gamma _1} \ne 0$
, and consider
![]() ${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
on
${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
on
![]() $S_\ell ^1$
which is orthogonal to
$S_\ell ^1$
which is orthogonal to
![]() ${\gamma _1}$
. By our choice of
${\gamma _1}$
. By our choice of
![]() $\mathcal{R}$
, here we mean at the same time
$\mathcal{R}$
, here we mean at the same time
![]() ${z_1}$
and
${z_1}$
and
![]() $\overline {{z_1}} $
. For
$\overline {{z_1}} $
. For
![]() $A \in K_T^ \times $
, we define
$A \in K_T^ \times $
, we define
![]() ${z_2} = A{\rm{*}}{z_1}$
to be the (pair of) point orthogonal to
${z_2} = A{\rm{*}}{z_1}$
to be the (pair of) point orthogonal to
![]() $\ell '' = {\gamma _2} = A\!\left( {{\gamma _1}} \right)$
. This defines an action of
$\ell '' = {\gamma _2} = A\!\left( {{\gamma _1}} \right)$
. This defines an action of
![]() $K_T^ \times $
on
$K_T^ \times $
on
![]() $\mathcal{R}$
. This action is no longer free: indeed, as explained in the proof of Proposition 4·4, two non-zero elements
$\mathcal{R}$
. This action is no longer free: indeed, as explained in the proof of Proposition 4·4, two non-zero elements
![]() $\gamma ,\delta $
in T are orthogonal to the same point if there exists a
$\gamma ,\delta $
in T are orthogonal to the same point if there exists a
![]() $\beta \in {(K_T^0)^ \times } = K_T^ \times \cap \mathbb{R}$
such that
$\beta \in {(K_T^0)^ \times } = K_T^ \times \cap \mathbb{R}$
such that
![]() $\beta \!\left( \gamma \right) = \delta $
. Then,
$\beta \!\left( \gamma \right) = \delta $
. Then,
![]() ${(K_T^0)^ \times }$
is contained in the kernel of this action, or equivalently in the stabiliser of each point. This induces an action of the quotient group
${(K_T^0)^ \times }$
is contained in the kernel of this action, or equivalently in the stabiliser of each point. This induces an action of the quotient group
![]() $K_T^ \times /{(K_T^0)^ \times }$
on
$K_T^ \times /{(K_T^0)^ \times }$
on
![]() $\mathcal{R}$
. If T has CM, the action of the quotient is free, i.e.
$\mathcal{R}$
. If T has CM, the action of the quotient is free, i.e.
![]() ${(K_T^0)^ \times }$
is exactly the stabilizer of each point: this follows from the fact that
${(K_T^0)^ \times }$
is exactly the stabilizer of each point: this follows from the fact that
![]() ${\rho _z} = r/2$
for points of Picard jump on the equator (Proposition 4·4). However, it will be clear later that the action of
${\rho _z} = r/2$
for points of Picard jump on the equator (Proposition 4·4). However, it will be clear later that the action of
![]() $K_T^ \times /{(K_T^0)^ \times }$
is free even if T is not of CM type. Notice that the quotient group is trivial if T is of totally real type. Again, if T has CM then the action is transitive (as
$K_T^ \times /{(K_T^0)^ \times }$
is free even if T is not of CM type. Notice that the quotient group is trivial if T is of totally real type. Again, if T has CM then the action is transitive (as
![]() ${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
).
${\rm{di}}{{\rm{m}}_{{K_T}}}T = 1$
).
We have an explicit way to compute
![]() ${z_2} = A\;{\rm{*}}\;{z_1}$
. Pick
${z_2} = A\;{\rm{*}}\;{z_1}$
. Pick
![]() $\sigma $
satisfying
$\sigma $
satisfying
![]() $\left( {\sigma .\ell '} \right) = 1$
. If
$\left( {\sigma .\ell '} \right) = 1$
. If
![]() ${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
, (4·1) gives
${z_1} = \left[ {\sigma ' = a\sigma + b\bar \sigma + \ell } \right]$
, (4·1) gives
![]() $a + b = 0$
, i.e.
$a + b = 0$
, i.e.
![]() $b = - a$
. On the other hand, we rewrite (3·1) as
$b = - a$
. On the other hand, we rewrite (3·1) as
![]() $ - 2{a^2}\!\left( {\sigma .\bar \sigma } \right) + d = 0$
, which forces
$ - 2{a^2}\!\left( {\sigma .\bar \sigma } \right) + d = 0$
, which forces
![]() $a \in \mathbb{R}$
. Hence,
$a \in \mathbb{R}$
. Hence,
Assume that
![]() $A = R{e^{i\theta }}$
; then
$A = R{e^{i\theta }}$
; then
![]() ${z_2} = \left[ {\sigma ''} \right]$
, where
${z_2} = \left[ {\sigma ''} \right]$
, where
Indeed
![]() ${z_2} \in \mathbb{P}_\ell ^1$
holds since (3·1) is satisfied, and
${z_2} \in \mathbb{P}_\ell ^1$
holds since (3·1) is satisfied, and
 \begin{align*} \!\left( {\sigma ''.A\!\left( {{\gamma _1}} \right)} \right)& = \left( {a{e^{i\theta }}\sigma .A\!\left( {{\gamma _1}} \right)} \right) + \left( { - a{e^{ - i\theta }}\bar \sigma .A\!\left( {{\gamma _1}} \right)} \right)\\ &= a{e^{i\theta }}(\bar A(\sigma).{\gamma _1}) - a{e^{ - i\theta }}\!\left( {\bar A\!\left( {\bar \sigma } \right).{\gamma _1}} \right)\\ & = a{e^{i\theta }}\bar A - a{e^{ - i\theta }}A = 0.\end{align*}
\begin{align*} \!\left( {\sigma ''.A\!\left( {{\gamma _1}} \right)} \right)& = \left( {a{e^{i\theta }}\sigma .A\!\left( {{\gamma _1}} \right)} \right) + \left( { - a{e^{ - i\theta }}\bar \sigma .A\!\left( {{\gamma _1}} \right)} \right)\\ &= a{e^{i\theta }}(\bar A(\sigma).{\gamma _1}) - a{e^{ - i\theta }}\!\left( {\bar A\!\left( {\bar \sigma } \right).{\gamma _1}} \right)\\ & = a{e^{i\theta }}\bar A - a{e^{ - i\theta }}A = 0.\end{align*}
Looking at the isomorphism
![]() $\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
defined in Lemma 3·1, we see that
$\mathbb{P}_\ell ^1 \simeq S_\ell ^2$
defined in Lemma 3·1, we see that
![]() $A = R{e^{i\theta }}$
acts on
$A = R{e^{i\theta }}$
acts on
![]() $\mathcal{R}$
by a rotation of angle
$\mathcal{R}$
by a rotation of angle
![]() $ - \theta $
. Note that if
$ - \theta $
. Note that if
![]() $A \in {(K_T^0)^ \times }$
then
$A \in {(K_T^0)^ \times }$
then
![]() $\theta = 0$
or
$\theta = 0$
or
![]() $\theta = \pi $
, and
$\theta = \pi $
, and
![]() ${z_2} = {z_1}$
(in
${z_2} = {z_1}$
(in
![]() $\mathcal{R}$
), as already mentioned.
$\mathcal{R}$
), as already mentioned.
We add a topological flavour to this discussion. Endow
![]() $K_T^ \times $
with the topology induced by the topology of
$K_T^ \times $
with the topology induced by the topology of
![]() ${\mathbb{C}^ \times }$
under the fixed embedding
${\mathbb{C}^ \times }$
under the fixed embedding
![]() ${K_T} \hookrightarrow \mathbb{C}$
, and
${K_T} \hookrightarrow \mathbb{C}$
, and
![]() ${(K_T^0)^ \times }$
with the subspace topology. Then the topological quotient group
${(K_T^0)^ \times }$
with the subspace topology. Then the topological quotient group
![]() $K_T^ \times /{(K_T^0)^ \times }$
is a subspace of the topological quotient group
$K_T^ \times /{(K_T^0)^ \times }$
is a subspace of the topological quotient group
![]() ${\mathbb{P}^1}\!\left( \mathbb{R} \right) = {\mathbb{C}^ \times }/{\mathbb{R}^ \times }$
. Moreover,
${\mathbb{P}^1}\!\left( \mathbb{R} \right) = {\mathbb{C}^ \times }/{\mathbb{R}^ \times }$
. Moreover,
![]() $\mathcal{R}$
is a subspace of
$\mathcal{R}$
is a subspace of
![]() $S_\ell ^1/\left\{ \pm \right\}$
and the action of
$S_\ell ^1/\left\{ \pm \right\}$
and the action of
![]() $K_T^ \times /{(K_T^0)^ \times }$
on it is given by rotation.
$K_T^ \times /{(K_T^0)^ \times }$
on it is given by rotation.

Remark 5·11. If
![]() ${K_T}$
is a CM field, then
${K_T}$
is a CM field, then
![]() $K_T^ \times /{(K_T^0)^ \times }$
is dense in
$K_T^ \times /{(K_T^0)^ \times }$
is dense in
![]() ${\mathbb{P}^1}\!\left( \mathbb{R} \right)$
. To deduce this, it is enough to show that the elements of norm one inside
${\mathbb{P}^1}\!\left( \mathbb{R} \right)$
. To deduce this, it is enough to show that the elements of norm one inside
![]() ${K_T}$
are dense in the circle: this is the content of Corollary 2·7.
${K_T}$
are dense in the circle: this is the content of Corollary 2·7.
Remark 5·12. We may define the equivalent of
![]() ${\mathcal{Q}^ + }$
also in this setting: let
${\mathcal{Q}^ + }$
also in this setting: let
![]() ${\mathcal{R}^ + }$
be the set of (pair of) points
${\mathcal{R}^ + }$
be the set of (pair of) points
![]() $z \in S_\ell ^1 \subseteq \mathbb{P}_\ell ^1$
that are orthogonal to an element of T of positive self-intersection. If
$z \in S_\ell ^1 \subseteq \mathbb{P}_\ell ^1$
that are orthogonal to an element of T of positive self-intersection. If
![]() ${\gamma _1} \in T$
is of positive self intersection, denote by
${\gamma _1} \in T$
is of positive self intersection, denote by
![]() ${z_1}$
(one of) its orthogonal. For an element
${z_1}$
(one of) its orthogonal. For an element
![]() $A \in K_T^ \times $
,
$A \in K_T^ \times $
,
![]() $\left| A \right| = 1$
implies that
$\left| A \right| = 1$
implies that
![]() ${\gamma _2} = A\!\left( {{\gamma _1}} \right)$
is of positive self-intersection as well. Then, by acting with elements of
${\gamma _2} = A\!\left( {{\gamma _1}} \right)$
is of positive self-intersection as well. Then, by acting with elements of
![]() ${S^1} \cap K_T^ \times $
on
${S^1} \cap K_T^ \times $
on
![]() ${z_1}$
, we see that
${z_1}$
, we see that
![]() ${\mathcal{R}^ + }$
is dense in
${\mathcal{R}^ + }$
is dense in
![]() $S_\ell ^1/\left\{ \pm \right\}$
if
$S_\ell ^1/\left\{ \pm \right\}$
if
![]() ${K_T}$
is a CM field.
${K_T}$
is a CM field.
In retrospect, we have proven the following result.
Proposition 5·13. Assume that T has CM. Then:
-
(i) the topological group
 $K_T^ \times /{(K_T^0)^ \times }$
acts freely, transitively and continuously by rotations on the topological space
$K_T^ \times /{(K_T^0)^ \times }$
acts freely, transitively and continuously by rotations on the topological space
 $\mathcal{R}$
;
$\mathcal{R}$
; -
(ii) having fixed an element
 ${z_1} \in \mathcal{R}$
, this action induces a homeomorphism between
${z_1} \in \mathcal{R}$
, this action induces a homeomorphism between
 $K_T^ \times /{(K_T^0)^ \times }$
and
$K_T^ \times /{(K_T^0)^ \times }$
and
 $\mathcal{R}$
, and this homeomorphism passes to the topological completions, inducing a homeomorphism between
$\mathcal{R}$
, and this homeomorphism passes to the topological completions, inducing a homeomorphism between
 ${\mathbb{P}^1}\!\left( \mathbb{R} \right)$
and
${\mathbb{P}^1}\!\left( \mathbb{R} \right)$
and
 $S_\ell ^1/\left\{ \pm \right\}$
;
$S_\ell ^1/\left\{ \pm \right\}$
; -
(iii)
 $\mathcal{R}$
is dense in
$\mathcal{R}$
is dense in
 $S_\ell ^1/\left\{ \pm \right\}$
, or equivalently: the set of points of Picard jump of the equator is (countable and) dense in the equator;
$S_\ell ^1/\left\{ \pm \right\}$
, or equivalently: the set of points of Picard jump of the equator is (countable and) dense in the equator; -
(iv) finally,
 ${\mathcal{R}^ + }$
is countable and dense in
${\mathcal{R}^ + }$
is countable and dense in
 $S_\ell ^1/\left\{ \pm \right\}$
.
$S_\ell ^1/\left\{ \pm \right\}$
.
6. Geometric interpretation
Suppose that X is a complex projective K3 surface, and let
![]() $\ell = {c_1}\!\left( L \right)$
be the first Chern class of an ample line bundle. We call period field and endomorphism field of X the period field and the endomorphism field, respectively, of the transcendental lattice
$\ell = {c_1}\!\left( L \right)$
be the first Chern class of an ample line bundle. We call period field and endomorphism field of X the period field and the endomorphism field, respectively, of the transcendental lattice
![]() $T\!\left( X \right) \subseteq {H^2}\!\left( {X,\mathbb{Q}} \right)$
, which is a polarised irreducible Hodge structure of K3 type. We say that a complex projective K3 surface X has CM if
$T\!\left( X \right) \subseteq {H^2}\!\left( {X,\mathbb{Q}} \right)$
, which is a polarised irreducible Hodge structure of K3 type. We say that a complex projective K3 surface X has CM if
![]() $T\!\left( X \right)$
has CM, that is: its dimension as a
$T\!\left( X \right)$
has CM, that is: its dimension as a
![]() ${K_{T\left( X \right)}}$
-vector space is 1.
${K_{T\left( X \right)}}$
-vector space is 1.
We can construct the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with
![]() $\left( {X,L} \right)$
, where we put in evidence the considered ample line bundle. The fibre over a point
$\left( {X,L} \right)$
, where we put in evidence the considered ample line bundle. The fibre over a point
![]() $\zeta \in \mathbb{P}_\mathbb{C}^1$
is a K3 surface of complex structure
$\zeta \in \mathbb{P}_\mathbb{C}^1$
is a K3 surface of complex structure
![]() ${x_1}I + {x_2}J + {x_3}K$
, if
${x_1}I + {x_2}J + {x_3}K$
, if
![]() $\zeta $
and
$\zeta $
and
![]() $\left( {{x_1},{x_2},{x_3}} \right)$
correspond one to the other via stereographic projection. One should be careful, for the presence of two spheres:
$\left( {{x_1},{x_2},{x_3}} \right)$
correspond one to the other via stereographic projection. One should be careful, for the presence of two spheres:
![]() $S_\ell ^2 \simeq \mathbb{P}_\ell ^1$
, an element of which corresponds to a class
$S_\ell ^2 \simeq \mathbb{P}_\ell ^1$
, an element of which corresponds to a class
![]() $z = \left[ {\sigma '} \right] \in \mathbb{P}_\ell ^1$
;
$z = \left[ {\sigma '} \right] \in \mathbb{P}_\ell ^1$
;
![]() ${S^2} \simeq \mathbb{P}_\mathbb{C}^1$
, parametrising the complex structures
${S^2} \simeq \mathbb{P}_\mathbb{C}^1$
, parametrising the complex structures
![]() ${x_1}I + {x_2}J + {x_3}K$
of the fibres of the geometric twistor space. We want to underline the relation existing between these spheres. We may give explicitly an isomorphism
${x_1}I + {x_2}J + {x_3}K$
of the fibres of the geometric twistor space. We want to underline the relation existing between these spheres. We may give explicitly an isomorphism
![]() $\mathbb{P}_\ell ^1 \simeq \mathbb{P}_\mathbb{C}^1$
that respects the following property: the Hodge structure determined by
$\mathbb{P}_\ell ^1 \simeq \mathbb{P}_\mathbb{C}^1$
that respects the following property: the Hodge structure determined by
![]() $z = \left[ {\sigma '} \right] \in \mathbb{P}_\ell ^1$
on
$z = \left[ {\sigma '} \right] \in \mathbb{P}_\ell ^1$
on
![]() $T \oplus \mathbb{Q}\ell $
corresponds to the Hodge structure determined by
$T \oplus \mathbb{Q}\ell $
corresponds to the Hodge structure determined by
![]() ${\sigma _\zeta }$
on the same vector space, for
${\sigma _\zeta }$
on the same vector space, for
![]() $\zeta \in \mathbb{P}_\mathbb{C}^1$
corresponding to
$\zeta \in \mathbb{P}_\mathbb{C}^1$
corresponding to
![]() $z \in \mathbb{P}_\ell ^1$
. Equivalently, one may ask
$z \in \mathbb{P}_\ell ^1$
. Equivalently, one may ask
![]() $\sigma '$
and
$\sigma '$
and
![]() ${\sigma _\zeta }$
to differ only by a a complex scalar. The isomorphism
${\sigma _\zeta }$
to differ only by a a complex scalar. The isomorphism
![]() $\mathbb{P}_\mathbb{C}^1 \simeq \mathbb{P}_\ell ^1$
is defined by
$\mathbb{P}_\mathbb{C}^1 \simeq \mathbb{P}_\ell ^1$
is defined by
(sending
![]() $\infty $
to
$\infty $
to
![]() $\left[ {\bar \sigma } \right]$
). This follows from the explicit form of
$\left[ {\bar \sigma } \right]$
). This follows from the explicit form of
![]() ${\sigma _\zeta }$
given in [
Reference HuybrechtsHKLR87
, section 3·F]. It is remarkable that
${\sigma _\zeta }$
given in [
Reference HuybrechtsHKLR87
, section 3·F]. It is remarkable that
![]() ${\sigma _\zeta }$
is a linear combination of
${\sigma _\zeta }$
is a linear combination of
![]() $\sigma ,\bar \sigma $
and
$\sigma ,\bar \sigma $
and
![]() $\ell $
only. Composing these isomorphisms, we get
$\ell $
only. Composing these isomorphisms, we get
We claim that this composition is nothing but the permutation
![]() $\left( {x,y,z} \right) \mapsto \!\left( {{x_1},{x_2},{x_3}} \right) = \left( {z,x,y} \right)$
on the sphere. For, a point
$\left( {x,y,z} \right) \mapsto \!\left( {{x_1},{x_2},{x_3}} \right) = \left( {z,x,y} \right)$
on the sphere. For, a point
![]() $\zeta \in \mathbb{P}_\mathbb{C}^1$
is sent, towards the left, to
$\zeta \in \mathbb{P}_\mathbb{C}^1$
is sent, towards the left, to
![]() $\left[ {\frac{1}{{2\zeta }}\sigma - \frac{\zeta }{2}\bar \sigma + \ell } \right] \in \mathbb{P}_\ell ^1$
. Set
$\left[ {\frac{1}{{2\zeta }}\sigma - \frac{\zeta }{2}\bar \sigma + \ell } \right] \in \mathbb{P}_\ell ^1$
. Set
![]() $a = 1/\left( {2\zeta } \right)$
,
$a = 1/\left( {2\zeta } \right)$
,
![]() $b = - \zeta /2$
. Then
$b = - \zeta /2$
. Then
and
Therefore the vector
that determines the point in
![]() $S_\ell ^2$
(Lemma 3·1), is positively aligned to the vector
$S_\ell ^2$
(Lemma 3·1), is positively aligned to the vector
where we use that
![]() $\left( {\sigma .\bar \sigma } \right) = 2\!\left( {\ell .\ell } \right) = 2d$
, as already noticed. However, the image of
$\left( {\sigma .\bar \sigma } \right) = 2\!\left( {\ell .\ell } \right) = 2d$
, as already noticed. However, the image of
![]() $\zeta $
in
$\zeta $
in
![]() ${S^2}$
via the stereographic projection is positively aligned with
${S^2}$
via the stereographic projection is positively aligned with
and this proves the claim.
Therefore, we may talk about equator and points at the same altitude for
![]() $S_\ell ^2$
and
$S_\ell ^2$
and
![]() ${S^2}$
interchangeably (even if the altitude of
${S^2}$
interchangeably (even if the altitude of
![]() $S_\ell ^2$
corresponds, in fact, to the first coordinate of
$S_\ell ^2$
corresponds, in fact, to the first coordinate of
![]() ${S^2}$
). Points at the same altitude correspond, therefore, to complex structures
${S^2}$
). Points at the same altitude correspond, therefore, to complex structures
![]() ${x_1}I + {x_2}J + {x_3}K$
on X with the same coefficient
${x_1}I + {x_2}J + {x_3}K$
on X with the same coefficient
![]() ${x_1}$
. The equator correspond to complex structures
${x_1}$
. The equator correspond to complex structures
![]() ${x_2}J + {x_3}K$
, for which the I-part is missing.
${x_2}J + {x_3}K$
, for which the I-part is missing.
Remark 6·1. For a point
![]() $\zeta \in \mathbb{P}_\mathbb{C}^1$
, let
$\zeta \in \mathbb{P}_\mathbb{C}^1$
, let
![]() $z \in \mathbb{P}_\ell ^1$
its correspondent under the isomorphism
$z \in \mathbb{P}_\ell ^1$
its correspondent under the isomorphism
![]() $\mathbb{P}_\ell ^1 \simeq \mathbb{P}_\mathbb{C}^1$
. We have the equality
$\mathbb{P}_\ell ^1 \simeq \mathbb{P}_\mathbb{C}^1$
. We have the equality
To prove this, look at the Néron–Severi group of the K3 surface
![]() ${\mathcal{X}_\zeta }$
. For an element
${\mathcal{X}_\zeta }$
. For an element
![]() $\gamma \in {H^2}\!\left( {{\mathcal{X}_\zeta },\mathbb{Q}} \right) = {H^2}\!\left( {X,\mathbb{Q}} \right)$
, being in
$\gamma \in {H^2}\!\left( {{\mathcal{X}_\zeta },\mathbb{Q}} \right) = {H^2}\!\left( {X,\mathbb{Q}} \right)$
, being in
![]() $NS\!\left( {{\mathcal{X}_\zeta }} \right)$
is equivalent to being orthogonal to the
$NS\!\left( {{\mathcal{X}_\zeta }} \right)$
is equivalent to being orthogonal to the
![]() $\left( {2,0} \right)$
-form
$\left( {2,0} \right)$
-form
![]() ${\sigma _\zeta } = \sigma - {\zeta ^2}\bar \sigma + 2\zeta \ell $
. Of course the orthogonal complement of the class
${\sigma _\zeta } = \sigma - {\zeta ^2}\bar \sigma + 2\zeta \ell $
. Of course the orthogonal complement of the class
![]() $\ell $
in the original Néron-Severi group,
$\ell $
in the original Néron-Severi group,
![]() ${\ell ^ \bot } \subseteq NS\!\left( X \right)$
, is always orthogonal to
${\ell ^ \bot } \subseteq NS\!\left( X \right)$
, is always orthogonal to
![]() ${\sigma _\zeta }$
(and this corresponds to the addend
${\sigma _\zeta }$
(and this corresponds to the addend
![]() $\rho \!\left( X \right) - 1$
). The orthogonal complement of this last space in
$\rho \!\left( X \right) - 1$
). The orthogonal complement of this last space in
![]() ${H^2}\!\left( {X,\mathbb{Q}} \right)$
is
${H^2}\!\left( {X,\mathbb{Q}} \right)$
is
![]() $T \oplus \mathbb{Q}\ell $
, and is in direct sum with it. Lying in
$T \oplus \mathbb{Q}\ell $
, and is in direct sum with it. Lying in
![]() $T \oplus \mathbb{Q}\ell $
and, at the same time, being orthogonal to
$T \oplus \mathbb{Q}\ell $
and, at the same time, being orthogonal to
![]() ${\sigma _\zeta }$
means belonging to the space
${\sigma _\zeta }$
means belonging to the space
whose dimension is, by definition,
![]() ${\rho _z}$
. Therefore, the formula above holds.
${\rho _z}$
. Therefore, the formula above holds.
In the following, when talking about the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X, we imply the choice of
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X, we imply the choice of
![]() $\ell = {c_1}\!\left( L \right)$
as Kähler class for the construction of
$\ell = {c_1}\!\left( L \right)$
as Kähler class for the construction of
![]() $\mathcal{X}$
. The analogous of Proposition 4·2, proven by Huybrechts, is the following result.
$\mathcal{X}$
. The analogous of Proposition 4·2, proven by Huybrechts, is the following result.
Corollary 6·2.
Consider the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X. If
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X. If
![]() $\rho \!\left( {{\mathcal{X}_\zeta }} \right) \gt \rho \!\left( X \right)$
, then
$\rho \!\left( {{\mathcal{X}_\zeta }} \right) \gt \rho \!\left( X \right)$
, then
![]() $\zeta $
is contained in the equator
$\zeta $
is contained in the equator
![]() ${S^1} \subseteq {S^2}$
(that is:
${S^1} \subseteq {S^2}$
(that is:
![]() $\zeta $
is mapped to the equator
$\zeta $
is mapped to the equator
![]() ${S^1} \subseteq {S^2}$
under stereographic projection
${S^1} \subseteq {S^2}$
under stereographic projection
![]() $\mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
).
$\mathbb{P}_\mathbb{C}^1 \simeq {S^2}$
).
Proposition 4·4 and Proposition 5·13 yield:
Corollary 6·3.
Consider the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. If
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. If
![]() $\zeta $
is a point of Picard jump on the equator, then
$\zeta $
is a point of Picard jump on the equator, then
Moreover, the Noether–Lefschetz locus of the equator is dense in the equator. More precisely, the locus of points on the equator whose fibres are algebraic K3 surfaces is dense in the equator.

Proof. Only the equation is left to discuss. If
![]() $r = {\rm{di}}{{\rm{m}}_\mathbb{Q}}T$
, then
$r = {\rm{di}}{{\rm{m}}_\mathbb{Q}}T$
, then
![]() $r + \rho \!\left( X \right) = 22$
and
$r + \rho \!\left( X \right) = 22$
and
![]() ${\rho _z} = r/2 = \left( {22 - \rho \!\left( X \right)} \right)/2$
, if z corresponds to
${\rho _z} = r/2 = \left( {22 - \rho \!\left( X \right)} \right)/2$
, if z corresponds to
![]() $\zeta $
via the isomorphism
$\zeta $
via the isomorphism
![]() $\mathbb{P}_\ell ^1 \simeq \mathbb{P}_\mathbb{C}^1$
. Therefore, the formula above follows from Remark 6·1.
$\mathbb{P}_\ell ^1 \simeq \mathbb{P}_\mathbb{C}^1$
. Therefore, the formula above follows from Remark 6·1.
Remark 6·4. The only case where no points of excessive jump appear is under the assumption of maximal Picard number, i.e.
![]() $\rho \!\left( X \right) = 20$
. This answers [
Reference HuybrechtsHuy20
, remark 5·2] in the CM case. Also, it is a generalization of [
Reference HuybrechtsHuy20
, remark 5·5]: not only if
$\rho \!\left( X \right) = 20$
. This answers [
Reference HuybrechtsHuy20
, remark 5·2] in the CM case. Also, it is a generalization of [
Reference HuybrechtsHuy20
, remark 5·5]: not only if
![]() $\rho \!\left( X \right) \lt 20$
there is no fibre such that
$\rho \!\left( X \right) \lt 20$
there is no fibre such that
![]() $\rho \!\left( {{\mathcal{X}_\zeta }} \right) = 20$
, but the set of admissible values of
$\rho \!\left( {{\mathcal{X}_\zeta }} \right) = 20$
, but the set of admissible values of
![]() $\rho \!\left( {{\mathcal{X}_\zeta }} \right)$
is also very constrained.
$\rho \!\left( {{\mathcal{X}_\zeta }} \right)$
is also very constrained.
Remark 6·5. A K3 surface X is projective, or equivalently algebraic, if and only if there exists a line bundle L with
![]() ${L^2} \gt 0$
, where
${L^2} \gt 0$
, where
![]() ${L^2}$
denotes the self-intersection of this line bundle. For a proof, see [
Reference Barth, Hulek, Peters and Van de VenBHPV04
, theorem IV·6·2]. For twistor fibres, we see how the geometric property “being algebraic” agrees with the algebraic requirement
${L^2}$
denotes the self-intersection of this line bundle. For a proof, see [
Reference Barth, Hulek, Peters and Van de VenBHPV04
, theorem IV·6·2]. For twistor fibres, we see how the geometric property “being algebraic” agrees with the algebraic requirement
![]() $\left( {\ell '.\ell '} \right) \gt 0$
.
$\left( {\ell '.\ell '} \right) \gt 0$
.
Remark 6·6. If
![]() $\rho \!\left( X \right) = 20$
, each fibre
$\rho \!\left( X \right) = 20$
, each fibre
![]() ${\mathcal{X}_\zeta }$
corresponding to a point of Picard jump (both on and outside the equator) has Picard number 20 and, therefore, it is automatically algebraic and of CM type. However, when
${\mathcal{X}_\zeta }$
corresponding to a point of Picard jump (both on and outside the equator) has Picard number 20 and, therefore, it is automatically algebraic and of CM type. However, when
![]() $\rho \!\left( X \right) \lt 20$
, thanks to Remark 5·1, there are non-algebraic fibres corresponding to points of Picard jump outside the equator.
$\rho \!\left( X \right) \lt 20$
, thanks to Remark 5·1, there are non-algebraic fibres corresponding to points of Picard jump outside the equator.
Corollary 5·10 yields the following results.
Proposition 6·7.
Consider the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. Then the locus of
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. Then the locus of
![]() $\zeta \in \mathbb{P}_\mathbb{C}^1$
such that
$\zeta \in \mathbb{P}_\mathbb{C}^1$
such that
![]() ${\mathcal{X}_\zeta }$
is algebraic is dense (for the classical topology) in
${\mathcal{X}_\zeta }$
is algebraic is dense (for the classical topology) in
![]() $\mathbb{P}_\mathbb{C}^1$
.
$\mathbb{P}_\mathbb{C}^1$
.
Proof. The density of the locus follows from the density of
![]() ${\mathcal{Q}^ + }$
in
${\mathcal{Q}^ + }$
in
![]() $\mathcal{U}$
.
$\mathcal{U}$
.
Theorem 6·8.
Consider the twistor space
![]() $\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. Assume that
$\mathcal{X} \to \mathbb{P}_\mathbb{C}^1$
associated with a projective complex K3 surface X with complex multiplication. Assume that
![]() ${\zeta _1},{\zeta _2} \in \mathbb{P}_\mathbb{C}^1$
are two points of Picard jump at the same altitude and not on the equator. Then
${\zeta _1},{\zeta _2} \in \mathbb{P}_\mathbb{C}^1$
are two points of Picard jump at the same altitude and not on the equator. Then
![]() ${\mathcal{X}_{{\zeta _1}}}$
is algebraic if and only if
${\mathcal{X}_{{\zeta _1}}}$
is algebraic if and only if
![]() ${\mathcal{X}_{{\zeta _2}}}$
is such. If so, then the CM endomorphism fields of these K3 surfaces coincide. Moreover, the set of points of Picard jump at the same altitude of
${\mathcal{X}_{{\zeta _2}}}$
is such. If so, then the CM endomorphism fields of these K3 surfaces coincide. Moreover, the set of points of Picard jump at the same altitude of
![]() ${\zeta _1}$
(and
${\zeta _1}$
(and
![]() ${\zeta _2}$
) is countable and dense in the circle at that altitude.
${\zeta _2}$
) is countable and dense in the circle at that altitude.

Remark 6·9. For
![]() ${\zeta _1},{\zeta _2} \in \mathbb{P}_\mathbb{C}^1$
, being at the same altitude and outside the equator means corresponding to complex structures on X having the same non-zero I-component.
${\zeta _1},{\zeta _2} \in \mathbb{P}_\mathbb{C}^1$
, being at the same altitude and outside the equator means corresponding to complex structures on X having the same non-zero I-component.
Acknowledgements
FV thanks François Charles for introducing him to the subject, and both François Charles and Daniel Huybrechts for prolific discussions and significant comments. FV is also greatful to Paolo Stellari for his useful remarks in the revision of this paper. FV is currently a PhD student at Imperial College London (and part of the LSGNT, London School of Geometry and Number Theory). FV was funded by the FMJH (Fondation Mathématique Jacques Hadamard) while at the Laboratoire de Mathématiques d’Orsay, Université Paris-Saclay.