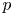1. Introduction
In the present paper we study the following quasilinear problem
where $\Omega$![]() is a smooth bounded domain in $\mathbb {R}^N$
is a smooth bounded domain in $\mathbb {R}^N$![]() , $1< p< N$
, $1< p< N$![]() and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$
and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() is a continuous function fulfilling suitable growth conditions at zero and at infinity.
is a continuous function fulfilling suitable growth conditions at zero and at infinity.
Problem $(P)$![]() appears in connection with the study of non-Newtonian fluids, where $p$
appears in connection with the study of non-Newtonian fluids, where $p$![]() is related to the characteristics of the medium (dilatant for $p>2$
is related to the characteristics of the medium (dilatant for $p>2$![]() , pseudoplastic for $p<2$
, pseudoplastic for $p<2$![]() ). The forcing term $f$
). The forcing term $f$![]() is a convection type term, i.e. it depends on the gradient of the unknown function. The dependence on the gradient in the nonlinearity does not allow to apply in a straightforward way variational methods to find solutions of $(P)$
is a convection type term, i.e. it depends on the gradient of the unknown function. The dependence on the gradient in the nonlinearity does not allow to apply in a straightforward way variational methods to find solutions of $(P)$![]() . However, the existence of constant sign solutions for $(P)$
. However, the existence of constant sign solutions for $(P)$![]() has been obtained by means of topological degree, method of sub-supersolutions, fixed point theory and approximation techniques (see for instance [Reference Amann and Crandall1, Reference Boccardo, Gallouët and Orsina7, Reference De Figueiredo, Girardi and Matzeu12, Reference Pohožaev20, Reference Ruiz21] and the references therein). When the source term does not depend on the gradient, the study of sign changing solutions for semilinear and quasilinear elliptic problems has been addressed in a number of papers. If $p=2$
has been obtained by means of topological degree, method of sub-supersolutions, fixed point theory and approximation techniques (see for instance [Reference Amann and Crandall1, Reference Boccardo, Gallouët and Orsina7, Reference De Figueiredo, Girardi and Matzeu12, Reference Pohožaev20, Reference Ruiz21] and the references therein). When the source term does not depend on the gradient, the study of sign changing solutions for semilinear and quasilinear elliptic problems has been addressed in a number of papers. If $p=2$![]() and $f=f(u)$
and $f=f(u)$![]() is superlinear and subcritical, the existence of a nodal solution (together with a positive and a negative one) has been proved for instance in [Reference Bartsch and Wang6] employing Morse theory and the strong maximum principle, or in [Reference Dancer and Du11] using topological degree technique, assuming also that $f'(0)<\lambda _1$
is superlinear and subcritical, the existence of a nodal solution (together with a positive and a negative one) has been proved for instance in [Reference Bartsch and Wang6] employing Morse theory and the strong maximum principle, or in [Reference Dancer and Du11] using topological degree technique, assuming also that $f'(0)<\lambda _1$![]() (being $\lambda _1$
(being $\lambda _1$![]() the first eigenvalue of the negative Laplacian). In [Reference Dancer and Du11], the sublinear case is also addressed and under the condition $f'(0)>\lambda _2$
the first eigenvalue of the negative Laplacian). In [Reference Dancer and Du11], the sublinear case is also addressed and under the condition $f'(0)>\lambda _2$![]() (being $\lambda _2$
(being $\lambda _2$![]() the second eigenvalue of the negative Laplacian) the existence of the biggest negative solution, the smallest positive solution and of a nontrivial solution in between (thus nodal) is achieved. The theory of invariant sets of descending flow defined by a pseudogradient vector field is deeply investigated in [Reference Liu and Sun19] to localize nodal solutions of a superlinear semilinear problem in different invariant sets. For $p\not =2$
the second eigenvalue of the negative Laplacian) the existence of the biggest negative solution, the smallest positive solution and of a nontrivial solution in between (thus nodal) is achieved. The theory of invariant sets of descending flow defined by a pseudogradient vector field is deeply investigated in [Reference Liu and Sun19] to localize nodal solutions of a superlinear semilinear problem in different invariant sets. For $p\not =2$![]() several contributions extend the quoted results to a nonlinear setting: the existence of nodal solutions is proved in [Reference Bartsch and Liu3–Reference Bartsch, Liu and Weth5, Reference Sun and Sun22, Reference Zhang and Li24] where the theory of invariant sets of descending flow is exploited under various assumptions on $f$
several contributions extend the quoted results to a nonlinear setting: the existence of nodal solutions is proved in [Reference Bartsch and Liu3–Reference Bartsch, Liu and Weth5, Reference Sun and Sun22, Reference Zhang and Li24] where the theory of invariant sets of descending flow is exploited under various assumptions on $f$![]() both in the superlinear and in the sublinear case, or in [Reference Carl and Perera8] by variational and sub–supersolution techniques.
both in the superlinear and in the sublinear case, or in [Reference Carl and Perera8] by variational and sub–supersolution techniques.
The existence of nodal solutions when $f$![]() depends on the gradient is still an almost unexplored issue. Motivated by [Reference Faraci, Motreanu and Puglisi13], where the existence of a positive and a negative solution (actually extremal) for problem $(P)$
depends on the gradient is still an almost unexplored issue. Motivated by [Reference Faraci, Motreanu and Puglisi13], where the existence of a positive and a negative solution (actually extremal) for problem $(P)$![]() has been proved, the following questions arise naturally.
has been proved, the following questions arise naturally.
Question 1.1
1. Does problem $(P)$
 admit a nodal solution for $p>1$
admit a nodal solution for $p>1$ ?
?2. Beside the smallest positive and the biggest negative solution does there exist a non-trivial nodal solution for problem $(P)$
 in between?
in between?
The first question has been partially solved in [Reference Liu, Shi and Wei18] and [Reference Faraci and Puglisi15] where the existence of a nodal solution in the presence of a nonlinearity depending on the gradient has been addressed in the case $p=2$![]() . In [Reference Liu, Shi and Wei18], the authors assume $f$
. In [Reference Liu, Shi and Wei18], the authors assume $f$![]() to be a superlinear function, locally Lipschitz with respect to both the second and the third variable in a neighbourhood of zero, with some further assumptions on the gradient variable. Using the Nehari method, they obtain a sign changing solution as the limit of a sequence of ‘approximated’ nodal functions. In [Reference Faraci and Puglisi15] the sublinear case is studied and the existence of a nodal solution is ensured by suitable growth conditions at zero in the real (second) variable via the theory of invariant sets of descending flow.
to be a superlinear function, locally Lipschitz with respect to both the second and the third variable in a neighbourhood of zero, with some further assumptions on the gradient variable. Using the Nehari method, they obtain a sign changing solution as the limit of a sequence of ‘approximated’ nodal functions. In [Reference Faraci and Puglisi15] the sublinear case is studied and the existence of a nodal solution is ensured by suitable growth conditions at zero in the real (second) variable via the theory of invariant sets of descending flow.
In the present paper, we completely solve the first question above for any $1 < p < \infty$![]() . In the first part of the paper we extend the results of [Reference Faraci and Puglisi15] pointing out some difficulties which arise from the quasilinear setting which prevent a straightforward generalization of the conclusions of [Reference Faraci and Puglisi15]. Combining the gradient flow theory with some essential tools as a gradient regularity result and strong comparison principle for the $p$
. In the first part of the paper we extend the results of [Reference Faraci and Puglisi15] pointing out some difficulties which arise from the quasilinear setting which prevent a straightforward generalization of the conclusions of [Reference Faraci and Puglisi15]. Combining the gradient flow theory with some essential tools as a gradient regularity result and strong comparison principle for the $p$![]() -Laplacian we prove the existence of a nodal solution for a parametrized problem with variational structure. An iteration procedure allows to create a sequence of sign changing solutions converging to a non-trivial nodal solution.
-Laplacian we prove the existence of a nodal solution for a parametrized problem with variational structure. An iteration procedure allows to create a sequence of sign changing solutions converging to a non-trivial nodal solution.
Together with the conclusion of [Reference Faraci, Motreanu and Puglisi13] (see also [Reference Faraci and Puglisi14]), where the existence of the smallest positive solution and of the biggest negative solution for $(P)$![]() was proved via sub-super solution methods and fixed point arguments, we obtain a multiplicity theorem under very natural and verifiable assumptions. It still remains an open question whether the nodal solution lies in between (see remark 5.1). In the last part of the paper we give another contribution to the first question, suggesting a different set of hypotheses to prove the existence of sign changing solutions for an eigenvalue problem.
was proved via sub-super solution methods and fixed point arguments, we obtain a multiplicity theorem under very natural and verifiable assumptions. It still remains an open question whether the nodal solution lies in between (see remark 5.1). In the last part of the paper we give another contribution to the first question, suggesting a different set of hypotheses to prove the existence of sign changing solutions for an eigenvalue problem.
We believe that this work represents the first step in the search of nodal solutions for quasilinear problems depending on the gradient.
Denote by $\|\cdot \|$![]() , the standard norm in $W^{1,p}_0(\Omega )$
, the standard norm in $W^{1,p}_0(\Omega )$![]() , i.e. $\|u\|=(\int _{\Omega } |\nabla u|^p\,{\rm d}x)^{1/p}$
, i.e. $\|u\|=(\int _{\Omega } |\nabla u|^p\,{\rm d}x)^{1/p}$![]() , and by $\|\cdot \|_q$
, and by $\|\cdot \|_q$![]() , $\|\cdot \|_{\infty }$
, $\|\cdot \|_{\infty }$![]() the classical norms in $L^q(\Omega )$
the classical norms in $L^q(\Omega )$![]() and in $L^\infty (\Omega )$
and in $L^\infty (\Omega )$![]() respectively, i.e. $\|u\|_q=(\int _\Omega |u|^q\,{\rm d}x)^{1/q}$
respectively, i.e. $\|u\|_q=(\int _\Omega |u|^q\,{\rm d}x)^{1/q}$![]() and $\|u\|_\infty ={\rm supess}_\Omega |u|$
and $\|u\|_\infty ={\rm supess}_\Omega |u|$![]() . Let $\lambda _1$
. Let $\lambda _1$![]() be the first eigenvalue of the negative $p$
be the first eigenvalue of the negative $p$![]() -Laplacian operator on $W^{1,p}_0(\Omega )$
-Laplacian operator on $W^{1,p}_0(\Omega )$![]() , with first positive eigenfunction $\varphi _1$
, with first positive eigenfunction $\varphi _1$![]() satisfying $\|\varphi _1\|=1$
satisfying $\|\varphi _1\|=1$![]() . The following variational characterization holds
. The following variational characterization holds
It is well known that the cone of nonnegative functions
has a nonempty interior in the Banach space $C^1_0(\overline \Omega )$![]() given by
given by
where $\nu$![]() stands for the outward normal unit vector to $\partial \Omega$
stands for the outward normal unit vector to $\partial \Omega$![]() .
.
Our first set of assumptions is:
(f 1) there exist positive constants $k_0,\theta _0,\theta _1$
 with $\theta _0+\theta _1\lambda _1^{1/p'}<\lambda _1$
with $\theta _0+\theta _1\lambda _1^{1/p'}<\lambda _1$ such that
\[ |f(x,s,\xi)|\leq k_0+\theta_0|s|^{p-1}+\theta_1|\xi|^{p-1} \]for all $x\in \Omega$
such that
\[ |f(x,s,\xi)|\leq k_0+\theta_0|s|^{p-1}+\theta_1|\xi|^{p-1} \]for all $x\in \Omega$
 , $s\in \mathbb {R}$
, $s\in \mathbb {R}$ , and $\xi \in \mathbb {R}^N$
, and $\xi \in \mathbb {R}^N$ ;
;(f 2) for every $M>0$
 there exists a constant $\eta _M>\lambda _1$
there exists a constant $\eta _M>\lambda _1$ such that
\[ \liminf_{s\to 0}\frac{f(x,s,\xi)}{|s|^{p-2}s}\geq \eta_M \]uniformly for all $x\in \Omega$
such that
\[ \liminf_{s\to 0}\frac{f(x,s,\xi)}{|s|^{p-2}s}\geq \eta_M \]uniformly for all $x\in \Omega$
 and all $\xi \in \mathbb {R}^N$
and all $\xi \in \mathbb {R}^N$ with $|\xi |\leq M$
with $|\xi |\leq M$ ;
;(f 3) for every $M>0$
 there exists a constant $\zeta _M>0$
there exists a constant $\zeta _M>0$ such that
\[ \limsup_{s\to 0}\frac{f(x,s,\xi)}{|s|^{p-2}s}\leq \zeta_M \]uniformly for all $x\in \Omega$
such that
\[ \limsup_{s\to 0}\frac{f(x,s,\xi)}{|s|^{p-2}s}\leq \zeta_M \]uniformly for all $x\in \Omega$
 and all $\xi \in \mathbb {R}^N$
and all $\xi \in \mathbb {R}^N$ with $|\xi |\leq M$
with $|\xi |\leq M$ ;
;(f 4) for every $M>0$
 there exists a constant $m_M>0$
there exists a constant $m_M>0$ such that
\[ s\to f(x,s,\xi)+m_M |s|^{p-2}s \]is increasing for all $x\in \Omega$
such that
\[ s\to f(x,s,\xi)+m_M |s|^{p-2}s \]is increasing for all $x\in \Omega$
 and all $\xi \in \mathbb {R}^N$
and all $\xi \in \mathbb {R}^N$ with $|\xi |\leq M$
with $|\xi |\leq M$ .
.
Under such assumptions we prove the following.
Theorem 1.1 Let $\Omega$![]() be a smooth bounded domain in $\mathbb {R}^N$
be a smooth bounded domain in $\mathbb {R}^N$![]() and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$
and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() a continuous function satisfying $(f_1)-(f_4)$
a continuous function satisfying $(f_1)-(f_4)$![]() . Then, problem $(P)$
. Then, problem $(P)$![]() has a nodal solution in $C^1_0(\overline {\Omega })$
has a nodal solution in $C^1_0(\overline {\Omega })$![]() .
.
Combining such conclusion with [Reference Faraci, Motreanu and Puglisi13, Theorem 1.3, Corollary 1.1] we can state the following multiplicity result:
Corollary 1.1 Let $\Omega$![]() be a smooth bounded domain in $\mathbb {R}^N$
be a smooth bounded domain in $\mathbb {R}^N$![]() and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$
and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() a continuous function satisfying $(f_1)-(f_4)$
a continuous function satisfying $(f_1)-(f_4)$![]() . Then, problem $(P)$
. Then, problem $(P)$![]() has the smallest positive solution $u_P \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
has the smallest positive solution $u_P \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() , the biggest negative solution $u_N \in -\mathrm {int}(C^1_0(\overline \Omega )_+)$
, the biggest negative solution $u_N \in -\mathrm {int}(C^1_0(\overline \Omega )_+)$![]() and a nodal solution $\tilde u\in C^1_0(\overline {\Omega })$
and a nodal solution $\tilde u\in C^1_0(\overline {\Omega })$![]() .
.
In the last part of the paper, still exploiting the same iterative approach, we deduce the existence of a nodal solution for the quasilinear elliptic eigenvalue problem
Let us introduce the following assumptions:
$(\tilde f_1)$
 \[ \lim_{(s, \xi)\to \infty}\frac{f(x,s,\xi)}{|s|^{p-1}+|\xi|^{p-1}}=0 \]uniformly for all $x\in \Omega$
\[ \lim_{(s, \xi)\to \infty}\frac{f(x,s,\xi)}{|s|^{p-1}+|\xi|^{p-1}}=0 \]uniformly for all $x\in \Omega$
 ;
;$(\tilde f_2)$
 for every $M>0$
for every $M>0$ ,
\[ \lim_{s\to 0}\frac{f(x,s,\xi)}{|s|^{p-1}}=0 \]uniformly for all $x\in \Omega$
,
\[ \lim_{s\to 0}\frac{f(x,s,\xi)}{|s|^{p-1}}=0 \]uniformly for all $x\in \Omega$
 and all $\xi \in {\mathbb {R}}^N$
and all $\xi \in {\mathbb {R}}^N$ with $|\xi |\leq M$
with $|\xi |\leq M$ ;
;$(\tilde f_3)$
 for every $M>0$
for every $M>0$ ,
\[ \lim_{s\to \infty}\frac{f(x,s,\xi)}{|s|^{p-1}}=0 \]uniformly for all $x\in \Omega$
,
\[ \lim_{s\to \infty}\frac{f(x,s,\xi)}{|s|^{p-1}}=0 \]uniformly for all $x\in \Omega$
 and all $\xi \in {\mathbb {R}}^N$
and all $\xi \in {\mathbb {R}}^N$ with $|\xi |\leq M$
with $|\xi |\leq M$ ;
;$(\tilde f_4)$
 for every $M>0$
for every $M>0$ , there exists $R_M>0$
, there exists $R_M>0$ such that $s f(x,s,\xi )>0$
such that $s f(x,s,\xi )>0$ for all $x\in \Omega$
for all $x\in \Omega$ , $|s|>R_M$
, $|s|>R_M$ and all $\xi \in {\mathbb {R}}^N$
and all $\xi \in {\mathbb {R}}^N$ with $|\xi |\leq M$
with $|\xi |\leq M$ ;
;$(\tilde f_5)$
 there exist $s^-<0< s^+$
there exist $s^-<0< s^+$ such that
\begin{align*} &\inf_{(x, \xi) \in \Omega \times {\mathbb{R}}^N}F(x, s^{{\pm}}, \xi)>0, \\ &\hbox{where}\ F(x,s,\xi) =\int_0^s f(x,t,\xi) dt.\end{align*}
such that
\begin{align*} &\inf_{(x, \xi) \in \Omega \times {\mathbb{R}}^N}F(x, s^{{\pm}}, \xi)>0, \\ &\hbox{where}\ F(x,s,\xi) =\int_0^s f(x,t,\xi) dt.\end{align*}
Our second result states the following.
Theorem 1.2 Let $\Omega$![]() be a smooth bounded domain in $\mathbb {R}^N$
be a smooth bounded domain in $\mathbb {R}^N$![]() and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$
and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() a continuous function satisfying $(\tilde f_1)-(\tilde f_5)$
a continuous function satisfying $(\tilde f_1)-(\tilde f_5)$![]() . Then, there exists $\tilde \lambda$
. Then, there exists $\tilde \lambda$![]() such that for each $\lambda >\tilde \lambda$
such that for each $\lambda >\tilde \lambda$![]() , problem $(P_\lambda )$
, problem $(P_\lambda )$![]() has a nodal solution in $C^1_0(\overline {\Omega })$
has a nodal solution in $C^1_0(\overline {\Omega })$![]() .
.
The plan of the paper is the following: in Section 2 we introduce some common preliminaries. Sections 3 and 4 are devoted to prove our main theorems. Finally, in Section 5 some open questions and final remarks are discussed.
2. Preliminaries
In this section we collect some common preliminaries which will be useful in our study. We introduce the following quasilinear problem
where $\Omega$![]() is a smooth bounded domain in $\mathbb {R}^N$
is a smooth bounded domain in $\mathbb {R}^N$![]() , $1< p< N$
, $1< p< N$![]() , $g:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$
, $g:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() is a continuous function such that $g(x,0,\xi )=0$
is a continuous function such that $g(x,0,\xi )=0$![]() for all $x,\xi$
for all $x,\xi$![]() and
and
($\mathcal {H}$
 ) there exist positive constants $k_0,\theta _0,\theta _1$
) there exist positive constants $k_0,\theta _0,\theta _1$ with $\theta _0+\theta _1\lambda _1^{1/p'}<\lambda _1$
with $\theta _0+\theta _1\lambda _1^{1/p'}<\lambda _1$ such that
\[ |g(x,s,\xi)|\leq k_0+\theta_0|s|^{p-1}+\theta_1|\xi|^{p-1} \]for all $x\in \Omega$
such that
\[ |g(x,s,\xi)|\leq k_0+\theta_0|s|^{p-1}+\theta_1|\xi|^{p-1} \]for all $x\in \Omega$
 , $s\in \mathbb {R}$
, $s\in \mathbb {R}$ , and $\xi \in \mathbb {R}^N$
, and $\xi \in \mathbb {R}^N$ .
.
For every $w\in C^1_0(\overline \Omega )$![]() , let us also consider the parametrized Dirichlet problem
, let us also consider the parametrized Dirichlet problem
Notice that since $w\in C^1_0(\overline \Omega )$![]() , classical regularity results implies that each solution $u$
, classical regularity results implies that each solution $u$![]() of $(P_w)$
of $(P_w)$![]() is in $L^\infty (\Omega )$
is in $L^\infty (\Omega )$![]() , thus in $C^1_0(\overline \Omega )$
, thus in $C^1_0(\overline \Omega )$![]() (see [Reference Ladyzhenskaya and Uraltseva16, Reference Lieberman17]).
(see [Reference Ladyzhenskaya and Uraltseva16, Reference Lieberman17]).
Moreover, from $g(x,0,\xi )=0$![]() for all $x,\xi$
for all $x,\xi$![]() we observe that the zero function is a solution of both $(\tilde P)$
we observe that the zero function is a solution of both $(\tilde P)$![]() and $(\tilde P_w)$
and $(\tilde P_w)$![]() for each $w\in C^1_0(\overline \Omega )$
for each $w\in C^1_0(\overline \Omega )$![]() .
.
Proposition 2.1 below proves an a priori uniform boundedness which will be crucial for our purposes. It makes use of the following gradient regularity result ([Reference Cianchi and Maz'ya9, Theorem 4.3]):
Lemma 2.1 Let $\Omega$![]() be a smooth bounded domain in ${\mathbb {R}}^N$
be a smooth bounded domain in ${\mathbb {R}}^N$![]() , $N\geq 2$
, $N\geq 2$![]() , and let $u\in W^{1,p}_0(\Omega )$
, and let $u\in W^{1,p}_0(\Omega )$![]() , $1< p< N$
, $1< p< N$![]() , be a weak solution of the problem
, be a weak solution of the problem
with $h\in L^q(\Omega )$![]() , $q\geq (p^\ast )'$
, $q\geq (p^\ast )'$![]() .
.
$(i)$
 If $q< N$
If $q< N$ , then
\[ \|\nabla u\|_{q^\ast(p-1)}\leq C\|h\|_{q}^\frac{1}{p-1}. \]
, then
\[ \|\nabla u\|_{q^\ast(p-1)}\leq C\|h\|_{q}^\frac{1}{p-1}. \]
$(ii)$
 If $q=N$
If $q=N$ , then
\[ \|\nabla u\|_{r}\leq C\|h\|_{q}^\frac{1}{p-1} \ \text{for any}\ r<\infty. \]
, then
\[ \|\nabla u\|_{r}\leq C\|h\|_{q}^\frac{1}{p-1} \ \text{for any}\ r<\infty. \]
$(iii)$
 If $q>N$
If $q>N$ , then
\[ \|\nabla u\|_{\infty}\leq C\|h\|_{q}^\frac{1}{p-1}. \]
, then
\[ \|\nabla u\|_{\infty}\leq C\|h\|_{q}^\frac{1}{p-1}. \]
In what stated above, $C$![]() is a constant that depends only on $p,N,q$
is a constant that depends only on $p,N,q$![]() .
.
Proposition 2.1 Assume $(\mathcal {H})$![]() . Then, for every $u_0\in C^1_0(\overline \Omega )$
. Then, for every $u_0\in C^1_0(\overline \Omega )$![]() , there exists $\alpha \in ]0,1[$
, there exists $\alpha \in ]0,1[$![]() and a positive constant $M$
and a positive constant $M$![]() depending on $k_0, \theta _0,\theta _1, \|u_0\|$
depending on $k_0, \theta _0,\theta _1, \|u_0\|$![]() such that if $u_n$
such that if $u_n$![]() is a solution of $(P_{u_{n-1}})$
is a solution of $(P_{u_{n-1}})$![]() one has
one has
Proof. Let us fix $u_0\in C^1_0(\overline \Omega )$![]() . We first prove that if $u_n$
. We first prove that if $u_n$![]() is a solution of $(\tilde P_{u_{n-1}})$
is a solution of $(\tilde P_{u_{n-1}})$![]() , then $\|u_n\|\leq M_0$
, then $\|u_n\|\leq M_0$![]() for some constant $M_0=M_0(\|u_0\|)$
for some constant $M_0=M_0(\|u_0\|)$![]() independent on $n$
independent on $n$![]() . Indeed, acting with $u_n$
. Indeed, acting with $u_n$![]() as test function in $(\tilde P_{u_{n-1}})$
as test function in $(\tilde P_{u_{n-1}})$![]() ,
,

which implies
Denote by

Notice that $\gamma >0$![]() and $0<\delta <1$
and $0<\delta <1$![]() . Thus, using the above notation, we can rewrite
. Thus, using the above notation, we can rewrite
Iterating this inequality, we obtain

which means that there exists a constant $M_0$![]() (depending on $\|u_0\|$
(depending on $\|u_0\|$![]() ) such that
) such that
Denote $h_n(x)=g(x, u_n(x), \nabla u_{n-1}(x))$![]() and fix $q$
and fix $q$![]() with $(p^\ast )'\leq q\leq p'$
with $(p^\ast )'\leq q\leq p'$![]() such that $\frac {N}{q}\notin \mathbb {N}.$
such that $\frac {N}{q}\notin \mathbb {N}.$![]() Using the fact that $|u_n|^{p-1}, |\nabla u_{n-1}|^{p-1}\in L^q(\Omega )$
Using the fact that $|u_n|^{p-1}, |\nabla u_{n-1}|^{p-1}\in L^q(\Omega )$![]() (recall that $u_n\in L^\infty (\Omega )$
(recall that $u_n\in L^\infty (\Omega )$![]() ), and $(\mathcal {H})$
), and $(\mathcal {H})$![]() , we deduce that $h_n\in L^q(\Omega )$
, we deduce that $h_n\in L^q(\Omega )$![]() and its norm $\|h_n\|_q$
and its norm $\|h_n\|_q$![]() can be estimated by a constant which does not depend on $n$
can be estimated by a constant which does not depend on $n$![]() :
:

Hence
We can assume $q\leq N$![]() , otherwise we are done by lemma 2.1 $(iii)$
, otherwise we are done by lemma 2.1 $(iii)$![]() .
.
From lemma 2.1 $(i)-(ii)$![]() we deduce that $|\nabla u_n|\in L^{q^\ast (p-1)}(\Omega )$
we deduce that $|\nabla u_n|\in L^{q^\ast (p-1)}(\Omega )$![]() and that
and that
Since $u_n\in L^\infty (\Omega )$![]() we have that $|u_n|^{p-1}\in L^{q^\ast }(\Omega )$
we have that $|u_n|^{p-1}\in L^{q^\ast }(\Omega )$![]() . Moreover, by the previous inequality we also have $|\nabla u_{n-1}|^{p-1}\in L^{q^\ast }(\Omega )$
. Moreover, by the previous inequality we also have $|\nabla u_{n-1}|^{p-1}\in L^{q^\ast }(\Omega )$![]() , thus $h_n \in L^{q^\ast }(\Omega )$
, thus $h_n \in L^{q^\ast }(\Omega )$![]() and, as above $\|h_n\|_{q^\ast }\leq M'_1$
and, as above $\|h_n\|_{q^\ast }\leq M'_1$![]() .
.
It is easily seen by induction that $(((q^*)^*)^{\cdot \cdot \cdot })^*=q^{\overset {k}{**\cdot \cdot \cdot *}}=\frac {Nq}{N-kq}$![]() provided $k<\frac {N}{q}.$
provided $k<\frac {N}{q}.$![]() We choose then $k=[\frac {N}{q}]$
We choose then $k=[\frac {N}{q}]$![]() (the maximum integer contained in $\frac {N}{q}$
(the maximum integer contained in $\frac {N}{q}$![]() ). Recall that since $\frac {N}{q}\notin \mathbb {N},$
). Recall that since $\frac {N}{q}\notin \mathbb {N},$![]()
Iterating the previous argument $k$![]() times, since $\frac {Nq}{N-kq}>N$
times, since $\frac {Nq}{N-kq}>N$![]() , by lemma 2.1 $(iii)$
, by lemma 2.1 $(iii)$![]()
The uniform boundedness of the gradient of $u_n$![]() in $L^{\infty }(\Omega )$
in $L^{\infty }(\Omega )$![]() , implies the uniform boundedness of $u_n$
, implies the uniform boundedness of $u_n$![]() 's in $L^\infty (\Omega )$
's in $L^\infty (\Omega )$![]() (see [Reference Ladyzhenskaya and Uraltseva16]). Finally, from [Reference Lieberman17, Theorem 1] we obtain the existence of $\alpha \in ]0,1[$
(see [Reference Ladyzhenskaya and Uraltseva16]). Finally, from [Reference Lieberman17, Theorem 1] we obtain the existence of $\alpha \in ]0,1[$![]() and a positive constant $M$
and a positive constant $M$![]() independent on $n$
independent on $n$![]() such that
such that
We introduce now the following abstract setting. Let $X$![]() be a Banach space, $A:X \longrightarrow X$
be a Banach space, $A:X \longrightarrow X$![]() continuous and compact operator, $J:X\to \mathbb {R}$
continuous and compact operator, $J:X\to \mathbb {R}$![]() a functional of class ${C}^1(X, \mathbb {R})$
a functional of class ${C}^1(X, \mathbb {R})$![]() , $p>1$
, $p>1$![]() .
.
Let us introduce the following conditions:
$(J_1)$
 There exist $1< p< 2$
There exist $1< p< 2$ , $d_1, d_2>0$
, $d_1, d_2>0$ such that
\[ \langle J^{\prime}(u), u- A(u) \rangle \geq d_1\|u- A(u)\|^2 (\|u\| + \|A(u)\|)^{p-2} \]and
such that
\[ \langle J^{\prime}(u), u- A(u) \rangle \geq d_1\|u- A(u)\|^2 (\|u\| + \|A(u)\|)^{p-2} \]and \[ \|J^{\prime}(u)\| \leq d_2\|u- A(u)\|^{p-1}, \]for every $u \in X$
\[ \|J^{\prime}(u)\| \leq d_2\|u- A(u)\|^{p-1}, \]for every $u \in X$
 .
.$(J_2)$
 There exist $p\geq 2$
There exist $p\geq 2$ , $d_3, d_4>0$
, $d_3, d_4>0$ such that
\[ \langle J^{\prime}(u), u- A(u) \rangle \geq d_3\|u- A(u)\|^p \]and
such that
\[ \langle J^{\prime}(u), u- A(u) \rangle \geq d_3\|u- A(u)\|^p \]and \[ \|J^{\prime}(u)\| \leq d_4\|u- A(u)\| (\|u\| + \|A(u)\|)^{p-2}, \]for every $u \in X$
\[ \|J^{\prime}(u)\| \leq d_4\|u- A(u)\| (\|u\| + \|A(u)\|)^{p-2}, \]for every $u \in X$
 .
.
Denote by $K$![]() the set of critical points of $J$
the set of critical points of $J$![]() : it is clear that under either $(J_1)$
: it is clear that under either $(J_1)$![]() or $(J_2)$
or $(J_2)$![]() $K$
$K$![]() coincides with the set of fixed points of $A$
coincides with the set of fixed points of $A$![]() .
.
The next lemma allows to replace $A$![]() with a locally Lipschitz operator $B$
with a locally Lipschitz operator $B$![]() which fulfils the same properties as $A$
which fulfils the same properties as $A$![]() .
.
Lemma 2.2 ([Reference Bartsch, Liu and Weth5, Lemma 2.1], [Reference Bartsch and Liu4, Lemma 4.1]) Assume either $(J_1)$![]() or $(J_2)$
or $(J_2)$![]() . Let $D$
. Let $D$![]() be a closed convex subset of $X$
be a closed convex subset of $X$![]() . Then, there exists a locally Lipschitz continuous compact operator $B: X \to X$
. Then, there exists a locally Lipschitz continuous compact operator $B: X \to X$![]() which is a convex combination of $A$
which is a convex combination of $A$![]() such that
such that
$(i)$
 $A(u)=B(u)$
$A(u)=B(u)$ for each $u\in D$
for each $u\in D$ ;
;$(ii)$
 \[ \frac12 \|u-B(u)\| \leq \|u-A(u)\| \leq 2 \|u-B(u)\| \]for all $u \in X$
\[ \frac12 \|u-B(u)\| \leq \|u-A(u)\| \leq 2 \|u-B(u)\| \]for all $u \in X$
 ;
;$(iii)$
 if $1< p< 2$
if $1< p< 2$ then
\[ \langle J^{\prime}(u), u- B(u) \rangle \geq \frac{d_1}{2}\|u- A(u)\|^2 (\|u\| + \|A(u)\|)^{p-2}, \]and if $p\geq 2$
then
\[ \langle J^{\prime}(u), u- B(u) \rangle \geq \frac{d_1}{2}\|u- A(u)\|^2 (\|u\| + \|A(u)\|)^{p-2}, \]and if $p\geq 2$
 then
\[ \langle J^{\prime}(u), u- B(u) \rangle \geq \frac{d_1}{2}\|u- A(u)\|^p \]for all $u \in X$
then
\[ \langle J^{\prime}(u), u- B(u) \rangle \geq \frac{d_1}{2}\|u- A(u)\|^p \]for all $u \in X$
 .
.
Clearly, critical points of $J$![]() turn out to be fixed points of $B$
turn out to be fixed points of $B$![]() .
.
In our setting $X=W^{1,p}_0(\Omega )$![]() endowed with the equivalent norm
endowed with the equivalent norm

for $\mu >0$![]() . For fixed $w\in C^{1}_0(\overline \Omega )$
. For fixed $w\in C^{1}_0(\overline \Omega )$![]() , put $A=A_w^{\mu }:W^{1,p}_0(\Omega ) \longrightarrow W^{1,p}_0(\Omega )$
, put $A=A_w^{\mu }:W^{1,p}_0(\Omega ) \longrightarrow W^{1,p}_0(\Omega )$![]() the operator defined by
the operator defined by
where $h_p(t)=|t|^{p-2}t$![]() for each $t\in {\mathbb {R}}$
for each $t\in {\mathbb {R}}$![]() .
.
Let us note that
Since problem $(\tilde P_w)$![]() has variational form, we can consider the associated energy functional $J_w\in C^1(W^{1,p}_0(\Omega ))$
has variational form, we can consider the associated energy functional $J_w\in C^1(W^{1,p}_0(\Omega ))$![]() , defined by
, defined by
where $G(x, t, \xi ) = \int _0^t g(x, s, \xi )\,{\rm d}s$![]() . Because of $(\mathcal {H})$
. Because of $(\mathcal {H})$![]() , $J_w$
, $J_w$![]() is coercive, thus bounded from below.
is coercive, thus bounded from below.
The following inequalities (see [Reference Damascelli10]) ensure properties $(J_1)$![]() and $(J_2)$
and $(J_2)$![]() above:
above:
Proposition 2.2 There exist positive constants $c_i$![]() , $i=1, \ldots, 4$
, $i=1, \ldots, 4$![]() , such that for all $\xi, \eta \in \mathbb {R}^N$
, such that for all $\xi, \eta \in \mathbb {R}^N$![]()

Thus, lemma 2.2 applies. We will exploit it in the next sections with different choices of $D$![]() , $\mu$
, $\mu$![]() and $g$
and $g$![]() .
.
3. Nodal solution for a quasilinear elliptic problem
In this section we assume conditions $(f_1)-(f_4)$![]() and prove theorem 1.1. Using the theory of invariant sets of descending flow, we will construct first a nodal solution of a parametrized problem and then, following an iterative approach, we will exhibit the existence of a nodal solution for $(P)$
and prove theorem 1.1. Using the theory of invariant sets of descending flow, we will construct first a nodal solution of a parametrized problem and then, following an iterative approach, we will exhibit the existence of a nodal solution for $(P)$![]() .
.
3.1. On a parametrized problem
Throughout the sequel we will take into account the results of Section 2 with $g=f$![]() . Thus, for every $w\in C^1_0(\overline \Omega )$
. Thus, for every $w\in C^1_0(\overline \Omega )$![]() , the parametrized Dirichlet problem reads as follows
, the parametrized Dirichlet problem reads as follows
Recall that each solution $u$![]() of $(P_w)$
of $(P_w)$![]() is in $C^1_0(\overline \Omega )$
is in $C^1_0(\overline \Omega )$![]() . Also, assumptions $(f_2)$
. Also, assumptions $(f_2)$![]() and $(f_3)$
and $(f_3)$![]() imply that $f(x,0,\xi )=0$
imply that $f(x,0,\xi )=0$![]() for all $x,\xi$
for all $x,\xi$![]() , thus the zero function is a solution of $(P)$
, thus the zero function is a solution of $(P)$![]() and $(P_w)$
and $(P_w)$![]() for each $w\in C^1_0(\overline \Omega )$
for each $w\in C^1_0(\overline \Omega )$![]() .
.
In [Reference Faraci, Motreanu and Puglisi13], we have proved the following
Lemma 3.1 ([Reference Faraci, Motreanu and Puglisi13, Lemma 2.2]) Assume $(f_2)$![]() . Then, for every $M>0$
. Then, for every $M>0$![]() and $w \in C^1_0(\overline \Omega )$
and $w \in C^1_0(\overline \Omega )$![]() with $\|w\|_{C^1} \leq M$
with $\|w\|_{C^1} \leq M$![]() , there exists $\delta =\delta (M)>0$
, there exists $\delta =\delta (M)>0$![]() such that if $0<\varepsilon <\delta$
such that if $0<\varepsilon <\delta$![]() , then $\varepsilon \varphi _1$
, then $\varepsilon \varphi _1$![]() and $-\varepsilon \varphi _1$
and $-\varepsilon \varphi _1$![]() are subsolution and supersolution of $(P_w)$
are subsolution and supersolution of $(P_w)$![]() .
.
Theorem 3.1 ([Reference Faraci, Motreanu and Puglisi13, Theorem 2.1]) Assume $(f_1), (f_2), (f_3)$![]() . Then, for every $w \in C^1_0(\overline \Omega )$
. Then, for every $w \in C^1_0(\overline \Omega )$![]() , there exist $u_P^w \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
, there exist $u_P^w \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() and $u_N^w \in - \mathrm {int}(C^1_0(\overline \Omega )_+)$
and $u_N^w \in - \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() the smallest positive solution and the biggest negative solution of $(P_w)$
the smallest positive solution and the biggest negative solution of $(P_w)$![]() respectively.
respectively.
From the proof of [Reference Faraci, Motreanu and Puglisi13, Theorem 2.1] we deduce that
Remark 3.1 $u_P^w \geq \varepsilon \varphi _1$![]() and $u_N^w \leq -\varepsilon \varphi _1$
and $u_N^w \leq -\varepsilon \varphi _1$![]() with $\varepsilon =\varepsilon (M)$
with $\varepsilon =\varepsilon (M)$![]() uniform with respect to $w\in C^1_0(\overline \Omega )$
uniform with respect to $w\in C^1_0(\overline \Omega )$![]() with $\|w\|_{C^1} \leq M$
with $\|w\|_{C^1} \leq M$![]() .
.
We conclude this subsection recalling the strong comparison principle for the $p$![]() -Laplace operator ([Reference Arcoya and Ruiz2]). For $h_1, h_2 \in L^\infty (\Omega )$
-Laplace operator ([Reference Arcoya and Ruiz2]). For $h_1, h_2 \in L^\infty (\Omega )$![]() , we say that $h_1 \prec h_2$
, we say that $h_1 \prec h_2$![]() if for any $\Omega _0 \subseteq \Omega$
if for any $\Omega _0 \subseteq \Omega$![]() compact subset, there exists $\varepsilon >0$
compact subset, there exists $\varepsilon >0$![]() such that $h_1(x) + \varepsilon < h_2(x)$
such that $h_1(x) + \varepsilon < h_2(x)$![]() for almost every $x \in \Omega _0$
for almost every $x \in \Omega _0$![]() . In particular, if $h_1$
. In particular, if $h_1$![]() and $h_2$
and $h_2$![]() are continuous functions such that $h_1(x)< h_2(x)$
are continuous functions such that $h_1(x)< h_2(x)$![]() for all $x\in \Omega$
for all $x\in \Omega$![]() , then $h_1 \prec h_2$
, then $h_1 \prec h_2$![]() .
.
Proposition 3.1 [Reference Arcoya and Ruiz2, Proposition 2.6] For $\lambda \geq 0$![]() and $f, g \in L^\infty (\Omega )$
and $f, g \in L^\infty (\Omega )$![]() , let $v, u$
, let $v, u$![]() be solutions of the problems$:$
be solutions of the problems$:$![]()

If $f \prec g$![]() and $u \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
and $u \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() , then $u-v\in \mathrm {int}(C^1_0(\overline \Omega )_+)$
, then $u-v\in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() .
.
3.2. A pseudogradient vector field
Throughout the sequel, $u_0\in C^1_0(\overline \Omega )$![]() is a fixed function, $M>0$
is a fixed function, $M>0$![]() is given by proposition 2.1 and we choose $m=m_M$
is given by proposition 2.1 and we choose $m=m_M$![]() in assumption $(f_4)$
in assumption $(f_4)$![]() . Thus, following the notation of Section 2 with $g=f$
. Thus, following the notation of Section 2 with $g=f$![]() and $\mu =m$
and $\mu =m$![]() one has
one has

where $F(x, t, \xi ) = \int _0^t f(x, s, \xi )\,{\rm d}s$![]() .
.
Let us introduce the set $\Lambda ^w$![]() which will be crucial in our argument. Let $u_P^w \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
which will be crucial in our argument. Let $u_P^w \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() and $u_N^w \in - \mathrm {int}(C^1_0(\overline \Omega )_+)$
and $u_N^w \in - \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() the smallest positive solution and the biggest negative solution of $(P_w)$
the smallest positive solution and the biggest negative solution of $(P_w)$![]() (see theorem 3.1). Let us denote by $[u_N^w, u_P^w]$
(see theorem 3.1). Let us denote by $[u_N^w, u_P^w]$![]() the set of all $C^1_0$
the set of all $C^1_0$![]() -functions $u$
-functions $u$![]() such that $u_N^w \leq u \leq u_P^w$
such that $u_N^w \leq u \leq u_P^w$![]() .
.
Consider then, the following set
Proposition 3.2
Proof. First, we show that $A_w(\Lambda ^w) \subseteq \Lambda ^w$![]() . Let $u \in \Lambda ^w$
. Let $u \in \Lambda ^w$![]() and $v=A_w(u)$
and $v=A_w(u)$![]() :
:

By proposition 3.1, we conclude that $u_P^w-v \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() . Analogously one obtains that $v- u_N^w \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
. Analogously one obtains that $v- u_N^w \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() . For the other inclusion, let $u \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
. For the other inclusion, let $u \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() and $v=A_w(u)$
and $v=A_w(u)$![]() . Thus,
. Thus,
By the strong maximum principle [Reference Vázquez23], we conclude that $v \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() .
.
Let $B=B_w$![]() be as in lemma 2.2 with $D=\Lambda _w$
be as in lemma 2.2 with $D=\Lambda _w$![]() . Thus, since $B_w$
. Thus, since $B_w$![]() is a convex combination of $A_w$
is a convex combination of $A_w$![]() , one has
, one has
For every $u \in C^1_0(\overline \Omega ) \setminus K_w$![]() (where $K_w$
(where $K_w$![]() is the set of all fixed points of $A_w$
is the set of all fixed points of $A_w$![]() ) consider the following Cauchy problem
) consider the following Cauchy problem

Since $B_w$![]() is locally Lipschitz, the above problem admits a unique solution $\varphi ^t(u)$
is locally Lipschitz, the above problem admits a unique solution $\varphi ^t(u)$![]() in $C^1_0(\overline \Omega )$
in $C^1_0(\overline \Omega )$![]() called descending flow curve with maximal interval of existence $[0, \tau (u)[$
called descending flow curve with maximal interval of existence $[0, \tau (u)[$![]() . Notice that $\tau (u)$
. Notice that $\tau (u)$![]() can be either a positive number or $+\infty$
can be either a positive number or $+\infty$![]() .
.
By lemma 2.2 $(iii)$![]() ,
,

and the inequality is strict since $u \notin K_w$![]() so that it is not a fixed point of $B_w$
so that it is not a fixed point of $B_w$![]() . Thus, $J_w(\varphi ^t(u))$
. Thus, $J_w(\varphi ^t(u))$![]() is strictly decreasing. Recall also that $J_w$
is strictly decreasing. Recall also that $J_w$![]() is coercive, hence bounded from below.
is coercive, hence bounded from below.
Moreover from (3.2), we have
or
By (3.1), one has the following (see [Reference Liu and Sun19, proof of Lemma 3.2]).
Lemma 3.2 If $u \in \Lambda ^w$![]() , then $\varphi ^t(u) \in \Lambda ^w$
, then $\varphi ^t(u) \in \Lambda ^w$![]() and if $u \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
and if $u \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() , then $\varphi ^t(u) \in \mathrm {int}(C^1_0(\overline \Omega )_+)$
, then $\varphi ^t(u) \in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() for all $0< t<\tau (u)$
for all $0< t<\tau (u)$![]() .
.
For $D \subseteq C^1_0(\overline \Omega )$![]() , let us denote by
, let us denote by
We recall that $D$![]() is called an invariant set of descending flow for $J_w$
is called an invariant set of descending flow for $J_w$![]() , if whenever $u\in D\setminus K_w$
, if whenever $u\in D\setminus K_w$![]() , the flow $\{\varphi ^t(u):t\in [0,\tau (u)[\}\subset D$
, the flow $\{\varphi ^t(u):t\in [0,\tau (u)[\}\subset D$![]() . If $D=\mathcal {C}(D)$
. If $D=\mathcal {C}(D)$![]() , then $D$
, then $D$![]() is said complete.
is said complete.
If $D$![]() is invariant then, by the definition above, $\mathcal {C}(D)$
is invariant then, by the definition above, $\mathcal {C}(D)$![]() is invariant. Moreover it is easy to see that $\mathcal {C}(D)$
is invariant. Moreover it is easy to see that $\mathcal {C}(D)$![]() is complete as $\mathcal {C}(\mathcal {C}(D))=\mathcal {C}(D)$
is complete as $\mathcal {C}(\mathcal {C}(D))=\mathcal {C}(D)$![]() . Then $\partial \mathcal {C}(D)$
. Then $\partial \mathcal {C}(D)$![]() is also an invariant set of descending flow [Reference Liu and Sun19, Lemma 2.3]. If $D$
is also an invariant set of descending flow [Reference Liu and Sun19, Lemma 2.3]. If $D$![]() is also open then $\mathcal {C}(D)$
is also open then $\mathcal {C}(D)$![]() is open [Reference Liu and Sun19, Lemma 2.4(i)].
is open [Reference Liu and Sun19, Lemma 2.4(i)].
By lemma 3.2, $\Lambda ^w$![]() and $\mathrm {int}(C^1_0(\overline \Omega )_+)$
and $\mathrm {int}(C^1_0(\overline \Omega )_+)$![]() are invariant sets of descending flow for $J_w$
are invariant sets of descending flow for $J_w$![]() , so $\mathcal {C}(\Lambda ^w)$
, so $\mathcal {C}(\Lambda ^w)$![]() and $\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
and $\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() are invariant, as well as $\partial \mathcal {C}(\Lambda ^w)$
are invariant, as well as $\partial \mathcal {C}(\Lambda ^w)$![]() and $\partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
and $\partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() . Moreover, $\mathcal {C}(\Lambda ^w)$
. Moreover, $\mathcal {C}(\Lambda ^w)$![]() is open in $C^1_0(\overline \Omega )$
is open in $C^1_0(\overline \Omega )$![]() and $\mathcal {C}(\Lambda ^w) \not = C^1_0(\overline \Omega )$
and $\mathcal {C}(\Lambda ^w) \not = C^1_0(\overline \Omega )$![]() (indeed $u^w_P, u^w_N \in K_w\setminus \Lambda ^w$
(indeed $u^w_P, u^w_N \in K_w\setminus \Lambda ^w$![]() , so they cannot lie in $\mathcal {C}(\Lambda ^w)$
, so they cannot lie in $\mathcal {C}(\Lambda ^w)$![]() ). Also, $\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
). Also, $\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() is open in $C^1_0(\overline \Omega )$
is open in $C^1_0(\overline \Omega )$![]() and $\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+)) \not = C^1_0(\overline \Omega )$
and $\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+)) \not = C^1_0(\overline \Omega )$![]() (indeed $0 \in K_w\setminus \mathrm {int}(C^1_0(\overline \Omega )_+)$
(indeed $0 \in K_w\setminus \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() ). Since $C^1_0(\overline {\Omega })_+\subseteq \overline {\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))}$
). Since $C^1_0(\overline {\Omega })_+\subseteq \overline {\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))}$![]() and $\partial \mathcal {C}(\Lambda ^w) \cap C^1_0(\overline {\Omega })_+ \not =\emptyset$
and $\partial \mathcal {C}(\Lambda ^w) \cap C^1_0(\overline {\Omega })_+ \not =\emptyset$![]() , we have $\partial \mathcal {C}(\Lambda ^w) \cap \overline {\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))} \not = \emptyset$
, we have $\partial \mathcal {C}(\Lambda ^w) \cap \overline {\mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))} \not = \emptyset$![]() . Because $\partial \mathcal {C}(\Lambda ^w) \cap (-C^1_0(\overline {\Omega })_+) \not = \emptyset$
. Because $\partial \mathcal {C}(\Lambda ^w) \cap (-C^1_0(\overline {\Omega })_+) \not = \emptyset$![]() , we obtain that $\partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+)) \not = \emptyset$
, we obtain that $\partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+)) \not = \emptyset$![]() . Let us fix
. Let us fix
Lemma 3.3 There exists $u_w \in K_w$![]() and an increasing sequence of positive numbers $(t_n)_n$
and an increasing sequence of positive numbers $(t_n)_n$![]() with $t_n \rightarrow \tau (u^*)$
with $t_n \rightarrow \tau (u^*)$![]() such that $\lim _n \|\varphi ^{t_n}(u^*) -u_w\|_m=0$
such that $\lim _n \|\varphi ^{t_n}(u^*) -u_w\|_m=0$![]() .
.
Proof. Let $0< t_1< t_2<\tau (u^*)$![]() . Then,
. Then,

Assume that $p\geq 2$![]() .
.
Applying Hölder inequality, lemma 2.2 $\it {(iii)}$![]() , the monotonicity of the flow $t\to J_w(\varphi ^{t}(u^*))$
, the monotonicity of the flow $t\to J_w(\varphi ^{t}(u^*))$![]() and the boundedness from below of $J_w$
and the boundedness from below of $J_w$![]() , we obtain
, we obtain

Putting together the above outcomes we get that
Assume now $1< p< 2$![]() . By coercivity of $J_w$
. By coercivity of $J_w$![]() , we deduce that the set $\{u: J_w(u)\leq J_w(\varphi ^0(u^*))=J_w(u^*)\}\subset \overline B(0,b)$
, we deduce that the set $\{u: J_w(u)\leq J_w(\varphi ^0(u^*))=J_w(u^*)\}\subset \overline B(0,b)$![]() for some $b>0$
for some $b>0$![]() where $\overline B(0,b)$
where $\overline B(0,b)$![]() denotes the closed ball in $W^{1,p}_0(\Omega )$
denotes the closed ball in $W^{1,p}_0(\Omega )$![]() centred at zero of radius $b$
centred at zero of radius $b$![]() . By the monotonicity of the flow, $J_w(\varphi ^t(u^*)\leq J_w(u^*)$
. By the monotonicity of the flow, $J_w(\varphi ^t(u^*)\leq J_w(u^*)$![]() , thus there exists a constant $b_1>0$
, thus there exists a constant $b_1>0$![]() , such that $\|\varphi ^t(u^*)\|_m, \|A_w(\varphi ^t(u^*))\|_m\leq b_1$
, such that $\|\varphi ^t(u^*)\|_m, \|A_w(\varphi ^t(u^*))\|_m\leq b_1$![]() for each $t$
for each $t$![]() .
.
Then, by Hölder inequality, lemma 2.2 $(iii)$![]()

Thus, in both cases ($p\geq 2$![]() and $1< p<2$
and $1< p<2$![]() ), if $\tau (u^*)<\infty$
), if $\tau (u^*)<\infty$![]() , there exists $u_w\in W^{1,p}_0(\Omega )$
, there exists $u_w\in W^{1,p}_0(\Omega )$![]() such that
such that
Since the interval $[0,\tau (u^*)[$![]() is maximal it has to be $u_w\in K_w$
is maximal it has to be $u_w\in K_w$![]() .
.
If $\tau (u^*)=\infty$![]() , the boundedness from below of $J_w$
, the boundedness from below of $J_w$![]() allows us to fix an increasing sequence of positive numbers $(t_n)_n$
allows us to fix an increasing sequence of positive numbers $(t_n)_n$![]() , $t_n\to \infty$
, $t_n\to \infty$![]() such that
such that
If $p\geq 2$![]() , one has
, one has

which says that
Now, let us observe that $(\varphi ^{t_n}(u^*))_n$![]() is bounded in $W^{1,p}_0(\Omega )$
is bounded in $W^{1,p}_0(\Omega )$![]() . Indeed, by the monotonicity of the flow, $J_w(\varphi ^{t_n}(u^*)\leq J_w(u^*)$
. Indeed, by the monotonicity of the flow, $J_w(\varphi ^{t_n}(u^*)\leq J_w(u^*)$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() , that means that $\varphi ^{t_n}(u^*)\in J_w^{-1}(]-\infty, J_w(u^*)])$
, that means that $\varphi ^{t_n}(u^*)\in J_w^{-1}(]-\infty, J_w(u^*)])$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() , and the latter is a bounded set because of the coercivity of $J_w$
, and the latter is a bounded set because of the coercivity of $J_w$![]() . Moreover, since $A_w$
. Moreover, since $A_w$![]() is a compact operator, it follows (eventually passing to a subsequence) that there exists $u_w\in W^{1,p}_0(\Omega )$
is a compact operator, it follows (eventually passing to a subsequence) that there exists $u_w\in W^{1,p}_0(\Omega )$![]() such that
such that
In particular, $u_w\in K_w$![]() . Also, for some $b_2>0$
. Also, for some $b_2>0$![]() , one has $\|\varphi ^{t_n}(u^*)\|_m,\|A_w(\varphi ^{t_n}(u^*))\|_m \leq b_2$
, one has $\|\varphi ^{t_n}(u^*)\|_m,\|A_w(\varphi ^{t_n}(u^*))\|_m \leq b_2$![]() .
.
If $1< p<2$![]() ,
,

which says that
and we conclude as above.
In the next lemma we refine the previous result.
Lemma 3.4 With the notation of lemma 3.3, one has that $u_w\in C^1_0(\overline \Omega )$![]() and $\lim _n \|\varphi ^{t_n}(u^*) -u_w\|_{C^1_0}=0$
and $\lim _n \|\varphi ^{t_n}(u^*) -u_w\|_{C^1_0}=0$![]() .
.
Proof. As in the proof of lemma 3.3, we first observe that the set $\{\varphi ^t(u^*) \ : \ t\in [0,\tau (u^*)[\}$![]() is bounded in $W^{1,p}_0(\Omega )$
is bounded in $W^{1,p}_0(\Omega )$![]() . Recalling (3.3),
. Recalling (3.3),
Since $B_w: C^{1}_0(\overline {\Omega }) \to C^{1}_0(\overline {\Omega })$![]() is a compact operator, the set
is a compact operator, the set
is bounded in $C^{1,\alpha }(\overline {\Omega })$![]() , thus relatively compact in $C^1_0(\overline \Omega )$
, thus relatively compact in $C^1_0(\overline \Omega )$![]() . This clearly implies that $\{\varphi ^t(u^*) \ : \ t\in [0,\tau (u^*)[\}$
. This clearly implies that $\{\varphi ^t(u^*) \ : \ t\in [0,\tau (u^*)[\}$![]() is relatively compact in $C^1_0(\overline \Omega )$
is relatively compact in $C^1_0(\overline \Omega )$![]() . The thesis follows from lemma 3.3.
. The thesis follows from lemma 3.3.
We are ready to prove the main result of this subsection.
Theorem 3.2 $u_w$![]() is a nodal solution of $(P_w)$
is a nodal solution of $(P_w)$![]() .
.
Proof. Clearly $u_w$![]() is a solution of $(P_w)$
is a solution of $(P_w)$![]() since it belongs to $K_w$
since it belongs to $K_w$![]() . Since the initial point $u^*$
. Since the initial point $u^*$![]() belongs to $\partial \mathcal {C}(\Lambda ^w)\cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
belongs to $\partial \mathcal {C}(\Lambda ^w)\cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() , and both sets $\partial \mathcal {C}(\Lambda ^w)$
, and both sets $\partial \mathcal {C}(\Lambda ^w)$![]() , $\partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
, $\partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() are invariant sets of descending flow, then $(\varphi ^{t_n}(u^*))_n \subseteq \partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
are invariant sets of descending flow, then $(\varphi ^{t_n}(u^*))_n \subseteq \partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() . Moreover, $\partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
. Moreover, $\partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() is a closed set, so that $u_w \in \partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
is a closed set, so that $u_w \in \partial \mathcal {C}(\Lambda ^w) \cap \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() . Being $u_w \in \partial \mathcal {C}(\Lambda ^w)$
. Being $u_w \in \partial \mathcal {C}(\Lambda ^w)$![]() , we obtain that $u_w \not \in \text {int}_{C^1_0} [u_N^w, u_P^w]$
, we obtain that $u_w \not \in \text {int}_{C^1_0} [u_N^w, u_P^w]$![]() , in particular $u_w \not = 0$
, in particular $u_w \not = 0$![]() . Actually, by remark 3.1, $u_w\not \in \text {int}_{C^1_0} [-\varepsilon \varphi _1, \varepsilon \varphi _1]$
. Actually, by remark 3.1, $u_w\not \in \text {int}_{C^1_0} [-\varepsilon \varphi _1, \varepsilon \varphi _1]$![]() . On the other hand, since $u_w \in \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$
. On the other hand, since $u_w \in \partial \mathcal {C}(\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() , we also have $u_w \not \in \mathrm {int}(C^1_0(\overline \Omega )_+) \cup (-\mathrm {int}(C^1_0(\overline \Omega )_+))$
, we also have $u_w \not \in \mathrm {int}(C^1_0(\overline \Omega )_+) \cup (-\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() . This ensures that $u_w$
. This ensures that $u_w$![]() can not have constant sign. Indeed, if $u_w\geq 0$
can not have constant sign. Indeed, if $u_w\geq 0$![]() , it would be a non negative, non trivial solution of
, it would be a non negative, non trivial solution of
and by assumption $(f_4)$![]() and the strong maximum principle by Vazquez [Reference Vázquez23], we would deduce $u_w\in \mathrm {int}(C^1_0(\overline \Omega )_+)$
and the strong maximum principle by Vazquez [Reference Vázquez23], we would deduce $u_w\in \mathrm {int}(C^1_0(\overline \Omega )_+)$![]() . Thus, $u_w$
. Thus, $u_w$![]() is a nodal solution of $(P_w)$
is a nodal solution of $(P_w)$![]() .
.
3.3. Existence of a nodal solution for $(P)$
In this subsection through an iteration procedure we prove our first main result.
Proof of theorem 1.1. In theorem 3.2 choose $w=u_0$![]() , where $u_0$
, where $u_0$![]() is the function we fixed at the beginning of Section 3.2. Thus, the existence of a nodal solution $u_1$
is the function we fixed at the beginning of Section 3.2. Thus, the existence of a nodal solution $u_1$![]() of $(P_{u_0})$
of $(P_{u_0})$![]() follows. Proceeding in such way, for each $n\in \mathbb {N}$
follows. Proceeding in such way, for each $n\in \mathbb {N}$![]() denote by $u_n$
denote by $u_n$![]() the nodal solution of $(P_{u_{n-1}})$
the nodal solution of $(P_{u_{n-1}})$![]() given by theorem 3.2. Hence, we construct a sequence of functions $u_n\in C^1_0(\overline \Omega )$
given by theorem 3.2. Hence, we construct a sequence of functions $u_n\in C^1_0(\overline \Omega )$![]() such that
such that
By proposition 2.1, $\|u_n\|_{C^{1, \alpha }(\overline {\Omega })} \leq M$![]() , and by the compactness of the embedding ${C^{1, \alpha }}(\overline {\Omega })\hookrightarrow C^1_0(\overline \Omega )$
, and by the compactness of the embedding ${C^{1, \alpha }}(\overline {\Omega })\hookrightarrow C^1_0(\overline \Omega )$![]() , $(u_n)_n$
, $(u_n)_n$![]() is relatively compact in $C^1_0(\overline \Omega )$
is relatively compact in $C^1_0(\overline \Omega )$![]() . Unless to pass to a subsequence, let
. Unless to pass to a subsequence, let
Let us prove that $\tilde u$![]() is the solution of $(P)$
is the solution of $(P)$![]() we are looking for. Since $u_n$
we are looking for. Since $u_n$![]() is a solution of $(P_{u_{n-1}})$
is a solution of $(P_{u_{n-1}})$![]() , for every $\varphi \in W^{1,p}_0({\Omega })$
, for every $\varphi \in W^{1,p}_0({\Omega })$![]() we have
we have
Since $u_n\to \tilde u$![]() in $C^1_0(\overline \Omega )$
in $C^1_0(\overline \Omega )$![]() , we have that $f(x, u_n, \nabla u_{n-1})\rightarrow f(x, \tilde u, \nabla \tilde u)$
, we have that $f(x, u_n, \nabla u_{n-1})\rightarrow f(x, \tilde u, \nabla \tilde u)$![]() in $L^{p'}(\Omega )$
in $L^{p'}(\Omega )$![]() and passing to the limit in the above equality we get
and passing to the limit in the above equality we get
which is our claim. By (3.4) and (3.5), it follows that $\tilde u\not \in \text {int}_{C^1_0} [-\varepsilon \varphi _1, \varepsilon \varphi _1]$![]() and $\tilde u \not \in \mathrm {int}(C^1_0(\overline \Omega )_+) \cup (-\mathrm {int}(C^1_0(\overline \Omega )_+))$
and $\tilde u \not \in \mathrm {int}(C^1_0(\overline \Omega )_+) \cup (-\mathrm {int}(C^1_0(\overline \Omega )_+))$![]() . Thus, $\tilde u \not = 0$
. Thus, $\tilde u \not = 0$![]() , and as in the proof of theorem 3.2, $\tilde u$
, and as in the proof of theorem 3.2, $\tilde u$![]() can not have constant sign.
can not have constant sign.
4. Nodal solution for a quasilinear eigenvalue problem
The goal of the present section is to prove the existence of a nodal solution for $(P_\lambda )$![]() under assumptions $(\tilde f_1) - (\tilde f_5)$
under assumptions $(\tilde f_1) - (\tilde f_5)$![]() . While in theorem 1.1 the construction of the nodal solution was based on the existence of the extremal solutions for the parametrized problem $(P_w)$
. While in theorem 1.1 the construction of the nodal solution was based on the existence of the extremal solutions for the parametrized problem $(P_w)$![]() , here, exploiting the dependence on the parameter $\lambda$
, here, exploiting the dependence on the parameter $\lambda$![]() , we apply an abstract theorem by [Reference Bartsch, Liu and Weth5], which still relies on the theory of invariant sets of descending flow. After deducing the existence of a sign changing solution for the parametrized problem, we conclude as in the previous section.
, we apply an abstract theorem by [Reference Bartsch, Liu and Weth5], which still relies on the theory of invariant sets of descending flow. After deducing the existence of a sign changing solution for the parametrized problem, we conclude as in the previous section.
4.1. On a parametrized problem
Throughout the sequel we will take into account the results of Section 2 with $g=\lambda f$![]() and $\mu = \lambda m$
and $\mu = \lambda m$![]() for some $m$
for some $m$![]() to be chosen later. For every $w\in C^1_0(\overline \Omega )$
to be chosen later. For every $w\in C^1_0(\overline \Omega )$![]() , let us consider the parametrized Dirichlet problem
, let us consider the parametrized Dirichlet problem
From hypothesis $(\tilde f_1)$![]() , it follows that for each $\lambda >0$
, it follows that for each $\lambda >0$![]() we can fix $\varepsilon =\varepsilon (\lambda )>0$
we can fix $\varepsilon =\varepsilon (\lambda )>0$![]() with $\varepsilon (1+\lambda _1^{\frac {1}{p'}})\lambda <\lambda _1$
with $\varepsilon (1+\lambda _1^{\frac {1}{p'}})\lambda <\lambda _1$![]() and $k_0(\lambda ) \in \mathbb {R}$
and $k_0(\lambda ) \in \mathbb {R}$![]() such that
such that
for all $x\in \Omega$![]() , $s\in \mathbb {R}$
, $s\in \mathbb {R}$![]() , and $\xi \in \mathbb {R}^N$
, and $\xi \in \mathbb {R}^N$![]() . This ensures that under the above conditions, the function $g=\lambda f$
. This ensures that under the above conditions, the function $g=\lambda f$![]() fulfils assumption $(\mathcal {H})$
fulfils assumption $(\mathcal {H})$![]() of Section 2 and proposition 2.1 applies, i.e. for every $\lambda >0$
of Section 2 and proposition 2.1 applies, i.e. for every $\lambda >0$![]() and $u_0\in C^1_0(\overline \Omega )$
and $u_0\in C^1_0(\overline \Omega )$![]() , there exists $\alpha \in ]0,1[$
, there exists $\alpha \in ]0,1[$![]() and a positive constant $M$
and a positive constant $M$![]() depending on $\lambda$
depending on $\lambda$![]() and $\|u_0\|$
and $\|u_0\|$![]() such that if $u_n$
such that if $u_n$![]() is a solution of $(P_{\lambda, u_{n-1}})$
is a solution of $(P_{\lambda, u_{n-1}})$![]() , $\|u_n\|_{C^{1,\alpha }(\overline \Omega )}\leq M$
, $\|u_n\|_{C^{1,\alpha }(\overline \Omega )}\leq M$![]() .
.
Remark 4.1 Notice that assumption $(\tilde f_2)$![]() implies that $f(x,0,\xi )=0$
implies that $f(x,0,\xi )=0$![]() for all $x,\xi$
for all $x,\xi$![]() . Thus the zero function is a solution of both $(P_{\lambda, w})$
. Thus the zero function is a solution of both $(P_{\lambda, w})$![]() and $(P_\lambda )$
and $(P_\lambda )$![]() .
.
We will need the following abstract result.
Let $X$![]() be a Banach space, ${D}^\pm$
be a Banach space, ${D}^\pm$![]() closed convex subsets of $X$
closed convex subsets of $X$![]() , $A:X \longrightarrow X$
, $A:X \longrightarrow X$![]() continuous and compact operator and $J:X\to \mathbb {R}$
continuous and compact operator and $J:X\to \mathbb {R}$![]() a functional of class ${C}^1(X, \mathbb {R})$
a functional of class ${C}^1(X, \mathbb {R})$![]() . Introduce the following conditions.
. Introduce the following conditions.
$(D_1)$
 $\mathcal {O}=$
$\mathcal {O}=$ int$({D}^+) \cap \text {int}({D}^-) \not =\emptyset$
int$({D}^+) \cap \text {int}({D}^-) \not =\emptyset$ .
.$(D_2)$
 $A({D}^\pm )\subseteq \hbox {int}({D}^\pm )$
$A({D}^\pm )\subseteq \hbox {int}({D}^\pm )$ .
.$(J_3)$
 For any $b \in \mathbb {R}$
For any $b \in \mathbb {R}$ there exists a constant $a=a(b)>0$
there exists a constant $a=a(b)>0$ such that if $u \in \{u \in X: J(u) \leq b\}$
such that if $u \in \{u \in X: J(u) \leq b\}$ then
\[ \|u\| + \|A(u)\| \leq a (1+ \|u-A(u)\|). \]
then
\[ \|u\| + \|A(u)\| \leq a (1+ \|u-A(u)\|). \]
$(J_4)$
 There exists a path $h:[0,1]\longrightarrow X$
There exists a path $h:[0,1]\longrightarrow X$ such that $h(0) \in \text {int}({D}^+)\setminus {D}^-$
such that $h(0) \in \text {int}({D}^+)\setminus {D}^-$ and $h(1) \in \text {int}({D}^-)\setminus {D}^+$
and $h(1) \in \text {int}({D}^-)\setminus {D}^+$ and
\[ \max_{0\leq t\leq1} J(h(t)) < \alpha_0:=\inf_{{D}^+{\cap} {D}^-}J(u). \]
and
\[ \max_{0\leq t\leq1} J(h(t)) < \alpha_0:=\inf_{{D}^+{\cap} {D}^-}J(u). \]
The next theorem is the abstract tool we will exploit to deduce the existence of a nodal solution for the parametrized problem $(P_{\lambda, w})$![]() , which we state here in a convenient form for our purposes.
, which we state here in a convenient form for our purposes.
Theorem 4.1 [Reference Bartsch, Liu and Weth5, Theorem 2.2] Assume $(D_1)$![]() , $(D_2)$
, $(D_2)$![]() , $(J_3)$
, $(J_3)$![]() , $(J_4)$
, $(J_4)$![]() and either $(J_1)$
and either $(J_1)$![]() or $(J_2)$
or $(J_2)$![]() from Section 2. Then $J$
from Section 2. Then $J$![]() has a critical point in $\partial \mathcal {C}(\mathcal {O}) \setminus ({D}^+ \cup {D}^-)$
has a critical point in $\partial \mathcal {C}(\mathcal {O}) \setminus ({D}^+ \cup {D}^-)$![]() .
.
Following the notation of Section 2, $X=W^{1,p}_0(\Omega )$![]() endowed with the equivalent norm
endowed with the equivalent norm

where $\lambda$![]() and $m$
and $m$![]() will be chosen later in a convenient way,
will be chosen later in a convenient way,
and $B_w^\lambda$![]() as in lemma 2.2. Denote also by $J_w^\lambda : W^{1,p}_0(\Omega ) \longrightarrow {\mathbb {R}}$
as in lemma 2.2. Denote also by $J_w^\lambda : W^{1,p}_0(\Omega ) \longrightarrow {\mathbb {R}}$![]()
and for $\varepsilon >0$![]()
Proposition 4.1 For $\varepsilon >0$![]() small enough,
small enough,
Proof. Let us prove $A_w^\lambda (D_\varepsilon ^+) \subseteq {\rm int} D_\varepsilon ^+$![]() . Notice that by assumptions $(\tilde f_2)-(\tilde f_4)$
. Notice that by assumptions $(\tilde f_2)-(\tilde f_4)$![]() , for any $M\geq \|w\|_{C^1}$
, for any $M\geq \|w\|_{C^1}$![]() there exists $m_M>0$
there exists $m_M>0$![]() such that
such that
In the sequel put $m:=m_M$![]() .
.
By $(\tilde f_2)$![]() and $(\tilde f_3)$
and $(\tilde f_3)$![]() , for each $\varepsilon >0$
, for each $\varepsilon >0$![]() and $q>p$
and $q>p$![]() there exists another constant $c_M>0$
there exists another constant $c_M>0$![]() such that
such that
for each $x\in \Omega, s\neq 0, |\xi |\leq M$![]() .
.
Let $u \in D_\varepsilon ^+$![]() and $v=A_w^\lambda (u)$
and $v=A_w^\lambda (u)$![]() . Thus,
. Thus,
and so testing the above equation with $-v^-$![]() , where $v^-=\max \{-v, \ 0\}$
, where $v^-=\max \{-v, \ 0\}$![]() , we deduce
, we deduce

Hence,
Since $\|u^-\|_p \leq \|u-w\|_p$![]() for all $w \in P$
for all $w \in P$![]() , we get
, we get

Thus,
Thus, since $q>p$![]() , there exists $\varepsilon _0>0$
, there exists $\varepsilon _0>0$![]() such that
such that
and the proof is concluded.
Remark 4.2 From the above construction, $\varepsilon >0$![]() depends on $\lambda$
depends on $\lambda$![]() and $M \geq \|w\|_{C^1}$
and $M \geq \|w\|_{C^1}$![]() . In the sequel, our choice of $M$
. In the sequel, our choice of $M$![]() will be uniform with respect to $w$
will be uniform with respect to $w$![]() (see proposition 2.1).
(see proposition 2.1).
Theorem 4.2 Let $\Omega$![]() be a smooth bounded domain in $\mathbb {R}^N$
be a smooth bounded domain in $\mathbb {R}^N$![]() and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$
and $f:\Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() a continuous function satisfying $(\tilde f_1)-(\tilde f_5)$
a continuous function satisfying $(\tilde f_1)-(\tilde f_5)$![]() . Then, there exists $\tilde \lambda$
. Then, there exists $\tilde \lambda$![]() such that for each $\lambda >\tilde \lambda$
such that for each $\lambda >\tilde \lambda$![]() , and $w\in C^1_0(\overline \Omega )$
, and $w\in C^1_0(\overline \Omega )$![]() , problem $(P_{\lambda,w})$
, problem $(P_{\lambda,w})$![]() has a nodal solution in $C^1_0(\overline {\Omega })$
has a nodal solution in $C^1_0(\overline {\Omega })$![]() .
.
Proof. Fix $w \in C^1_0(\overline \Omega )$![]() . Let us show that all the hypotheses of theorem 4.1 are verified with $A=A_w^\lambda$
. Let us show that all the hypotheses of theorem 4.1 are verified with $A=A_w^\lambda$![]() , $J=J_w^\lambda$
, $J=J_w^\lambda$![]() , $D^+={D}_\varepsilon ^+$
, $D^+={D}_\varepsilon ^+$![]() , $D^-={D}_\varepsilon ^-$
, $D^-={D}_\varepsilon ^-$![]() and $\lambda$
and $\lambda$![]() big enough.
big enough.
Condition $(D_1)$![]() is trivial, $(D_2)$
is trivial, $(D_2)$![]() follows by proposition 4.1 and $(J_1)$
follows by proposition 4.1 and $(J_1)$![]() , $(J_2)$
, $(J_2)$![]() by proposition 2.2. Moreover, the map $A_w^\lambda$
by proposition 2.2. Moreover, the map $A_w^\lambda$![]() is compact (see [Reference Faraci, Motreanu and Puglisi13, Lemma 2.3]) and assumption $(J_3)$
is compact (see [Reference Faraci, Motreanu and Puglisi13, Lemma 2.3]) and assumption $(J_3)$![]() is implied by the coercivity of $J_w^\lambda$
is implied by the coercivity of $J_w^\lambda$![]() . It remains to check the validity of condition $(J_4)$
. It remains to check the validity of condition $(J_4)$![]() . By (4.3), we have that
. By (4.3), we have that
Since $J_w^\lambda$![]() is decreasing over the flow and ${D}_\varepsilon ^+ \cap {D}_\varepsilon ^-$
is decreasing over the flow and ${D}_\varepsilon ^+ \cap {D}_\varepsilon ^-$![]() is an invariant set, it follows that for every $u \in {D}_\varepsilon ^+ \cap {D}_\varepsilon ^-$
is an invariant set, it follows that for every $u \in {D}_\varepsilon ^+ \cap {D}_\varepsilon ^-$![]()
where $u^*=\lim _{t \rightarrow \tau (u)} \varphi _t(u) \in K \cap ({D}_\varepsilon ^+ \cap {D}_\varepsilon ^-)=\{0\}$![]() . Therefore
. Therefore
Let us show that there exists $\tilde \lambda$![]() such that for all $\lambda \geq \tilde \lambda$
such that for all $\lambda \geq \tilde \lambda$![]() $(J_4)$
$(J_4)$![]() holds; we follow the construction of [Reference Bartsch and Liu4, Lemma 3.2]. Let
holds; we follow the construction of [Reference Bartsch and Liu4, Lemma 3.2]. Let
we consider
Thus $\Omega _0=\Omega$![]() and $\Omega _1=\emptyset$
and $\Omega _1=\emptyset$![]() . We define
. We define
Let
(see $(\tilde {f}_5)$![]() ). We can approximate $h^*$
). We can approximate $h^*$![]() by a function $h \in C([0,1], W^{1,p}_0(\Omega )\cap C^1(\overline {\Omega )})$
by a function $h \in C([0,1], W^{1,p}_0(\Omega )\cap C^1(\overline {\Omega )})$![]() such that
such that
We choose $\varepsilon >0$![]() such that $s^- < - \varepsilon <0<\varepsilon < s^+$
such that $s^- < - \varepsilon <0<\varepsilon < s^+$![]() , so that $h(0) \in \text {int}(\mathcal {D}_{\varepsilon }^+) \setminus \mathcal {D}_{\varepsilon }^-$
, so that $h(0) \in \text {int}(\mathcal {D}_{\varepsilon }^+) \setminus \mathcal {D}_{\varepsilon }^-$![]() and $h(1) \in \text {int}(\mathcal {D}_{\varepsilon }^-) \setminus \mathcal {D}_{\varepsilon }^+$
and $h(1) \in \text {int}(\mathcal {D}_{\varepsilon }^-) \setminus \mathcal {D}_{\varepsilon }^+$![]() . Finally
. Finally
Choose $\tilde \lambda =2C/\delta$![]() . Notice that $\tilde \lambda$
. Notice that $\tilde \lambda$![]() does not depend on $w$
does not depend on $w$![]() . The existence of a nodal solution for $(P_{\lambda,w})$
. The existence of a nodal solution for $(P_{\lambda,w})$![]() follows at once by theorem 4.1.
follows at once by theorem 4.1.
4.2. Nodal solution of $(P_\lambda )$
In this subsection we prove theorem 1.2 using an iterative procedure.
Proof of theorem 1.2. Let us choose $\lambda > \tilde \lambda$![]() , where $\tilde \lambda$
, where $\tilde \lambda$![]() is as in theorem 4.2. Fix $u_0$
is as in theorem 4.2. Fix $u_0$![]() and let $M>0$
and let $M>0$![]() , depending on $\lambda$
, depending on $\lambda$![]() and $u_0$
and $u_0$![]() , be as in proposition 2.1. For each $n\in \mathbb {N}^+$
, be as in proposition 2.1. For each $n\in \mathbb {N}^+$![]() denote by $u_n$
denote by $u_n$![]() the nodal solution in $C^1_0(\overline \Omega )$
the nodal solution in $C^1_0(\overline \Omega )$![]() of $(P_{\lambda, u_{n-1}})$
of $(P_{\lambda, u_{n-1}})$![]() given by theorem 4.2. From its proof,
given by theorem 4.2. From its proof,
Let us stress that $\varepsilon$![]() depends on $M$
depends on $M$![]() which is independent on $n$
which is independent on $n$![]() (remark 4.2). Thus the set $\partial \mathcal {C}(\text {int}({D}^+_\varepsilon ) \cap \text {int}({D}^+_\varepsilon ))\setminus (\text {int}({D}^+_\varepsilon ) \cup \text {int}({D}^-_\varepsilon ))$
(remark 4.2). Thus the set $\partial \mathcal {C}(\text {int}({D}^+_\varepsilon ) \cap \text {int}({D}^+_\varepsilon ))\setminus (\text {int}({D}^+_\varepsilon ) \cup \text {int}({D}^-_\varepsilon ))$![]() is a closed invariant set and does not depend on $n$
is a closed invariant set and does not depend on $n$![]() .
.
By proposition 2.1, $\|u_n\|_{C^{1, \alpha }} \leq M$![]() , and by the compactness of the embedding ${C^{1, \alpha }}(\overline {\Omega })\hookrightarrow C^1_0(\overline \Omega )$
, and by the compactness of the embedding ${C^{1, \alpha }}(\overline {\Omega })\hookrightarrow C^1_0(\overline \Omega )$![]() , $(u_n)_n$
, $(u_n)_n$![]() is relatively compact in $C^1_0(\overline \Omega )$
is relatively compact in $C^1_0(\overline \Omega )$![]() . Unless to pass to a subsequence, let
. Unless to pass to a subsequence, let
As in the proof of theorem 1.1, $\tilde u$![]() is a solution of $(P_\lambda )$
is a solution of $(P_\lambda )$![]() . By the closedness of the set $\partial \mathcal {C}(\text {int}({D}^+_\varepsilon ) \cap \text {int}({D}^+_\varepsilon ))\setminus (\text {int}({D}^+_\varepsilon ) \cup \text {int}({D}^-_\varepsilon ))$
. By the closedness of the set $\partial \mathcal {C}(\text {int}({D}^+_\varepsilon ) \cap \text {int}({D}^+_\varepsilon ))\setminus (\text {int}({D}^+_\varepsilon ) \cup \text {int}({D}^-_\varepsilon ))$![]() , it follows from (4.4) that $\tilde u$
, it follows from (4.4) that $\tilde u$![]() is a sign changing function as we claimed.
is a sign changing function as we claimed.
5. Examples and open questions
This section is devoted to some examples of applications of our main theorems and a few open questions.
Example 5.1 Let $k_0,\theta _0,\theta _1$![]() positive numbers with $\theta _0+\theta _1\lambda _1^{1/p'}<\lambda _1$
positive numbers with $\theta _0+\theta _1\lambda _1^{1/p'}<\lambda _1$![]() , $g:\overline \Omega \times \mathbb {R}^N\to \mathbb {R}$
, $g:\overline \Omega \times \mathbb {R}^N\to \mathbb {R}$![]() a continuous, positive function such that $g(x,\xi )\leq k_0+\theta _1|\xi |^{p-1}$
a continuous, positive function such that $g(x,\xi )\leq k_0+\theta _1|\xi |^{p-1}$![]() . Define $f: \overline \Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$
. Define $f: \overline \Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() such that
such that

Then, theorem 1.1 applies.
Example 5.2 Let $r, q, t\geq 1$![]() such that $\max \{ r, q\}< p< t$
such that $\max \{ r, q\}< p< t$![]() , $r+q< p+1$
, $r+q< p+1$![]() , and $g:\overline \Omega \times \mathbb {R}^N\to \mathbb {R}$
, and $g:\overline \Omega \times \mathbb {R}^N\to \mathbb {R}$![]() a continuous function such that $\inf _{\Omega \times \mathbb {R}^N} g(x, \xi )>0$
a continuous function such that $\inf _{\Omega \times \mathbb {R}^N} g(x, \xi )>0$![]() and
and
Define $f: \overline \Omega \times \mathbb {R} \times \mathbb {R}^N\to \mathbb {R}$![]() such that
such that
Then, theorem 1.2 applies.
Question 5.1 Because of the extremality of $u_N$![]() and $u_P$
and $u_P$![]() in corollary 1.1, a non trivial solution of $(P)$
in corollary 1.1, a non trivial solution of $(P)$![]() in between, would be a nodal solution. It still remains an open question whether this situation occurs. We believe that in order to prove that such solution exists, extra assumptions would be needed. Indeed, in [Reference Dancer and Du11] for $p=2$
in between, would be a nodal solution. It still remains an open question whether this situation occurs. We believe that in order to prove that such solution exists, extra assumptions would be needed. Indeed, in [Reference Dancer and Du11] for $p=2$![]() it has been proved that, when $f$
it has been proved that, when $f$![]() does not depend on the gradient, is sublinear, and its derivative at zero is greater than $\lambda _2$
does not depend on the gradient, is sublinear, and its derivative at zero is greater than $\lambda _2$![]() (being $\lambda _2$
(being $\lambda _2$![]() the second eigenvalue of the negative Laplacian), the problem admits the biggest negative and the smallest positive solution which turn out to be also minimizers of the energy functional. The existence of a mountain pass critical point in between follows at once. The variational characterization of $\lambda _2$
the second eigenvalue of the negative Laplacian), the problem admits the biggest negative and the smallest positive solution which turn out to be also minimizers of the energy functional. The existence of a mountain pass critical point in between follows at once. The variational characterization of $\lambda _2$![]() allows finally to prove that such critical value is non zero (see also [Reference Carl and Perera8] for an extension to $p$
allows finally to prove that such critical value is non zero (see also [Reference Carl and Perera8] for an extension to $p$![]() -Laplace equations for $p\neq 2$
-Laplace equations for $p\neq 2$![]() ).
).
Question 5.2 Is it possible to find a positive and a negative solution of $(P_\lambda )$![]() ? We underline that, under our assumption, for fixed $w\in C^1_0(\overline \Omega )$
? We underline that, under our assumption, for fixed $w\in C^1_0(\overline \Omega )$![]() the energy functional $J_{w}^\lambda$
the energy functional $J_{w}^\lambda$![]() has the mountain pass geometry for big $\lambda$
has the mountain pass geometry for big $\lambda$![]() , and a positive /negative solution follows for problem $(P_{\lambda, w})$
, and a positive /negative solution follows for problem $(P_{\lambda, w})$![]() . It should then be proved that the limit of the approximated sequence is not zero.
. It should then be proved that the limit of the approximated sequence is not zero.
Acknowledgements
The authors have been supported by Università degli Studi di Catania, PIACERI 2020-2022, Linea di intervento 2, Progetto ‘MAFANE.’ F. Faraci has been also supported by PRIN 2022BCFHN2 ‘Advanced theoretical aspects in PDEs and their applications’ and she is a member of GNAMPA (INdAM). D. Puglisi is a member of GNSAGA (INdAM).