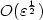Research Article
A Slideing Mesh-Mortar Method for a two Dimensional Currents Model of Electric Engines
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 191-228
-
- Article
- Export citation
On blow-up of solution for Euler equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 229-238
-
- Article
- Export citation
Convergence of finite difference schemes for viscousand inviscid conservation laws with rough coefficients
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 239-269
-
- Article
- Export citation
Approximation of the arch problem by residual-free bubbles
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 271-293
-
- Article
- Export citation
Boundary layer analysis and quasi-neutral limitsin the drift-diffusion equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 295-312
-
- Article
- Export citation
Vorticity dynamics and numerical ResolutionofNavier-Stokes Equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 313-330
-
- Article
- Export citation
Spurious-free approximations of electromagneticeigenproblems by means of Nedelec-type elements
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 331-354
-
- Article
- Export citation
A posteriori error estimates for vertex centered finite volume approximations of convection-diffusion-reaction equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 355-387
-
- Article
- Export citation