§1. I will start with a quick definition of descriptive set theory: It is the study of the structure of definable sets and functions in separable completely metrizable spaces. Such spaces are usually called Polish spaces. Typical examples are ℝn, ℂn, (separable) Hilbert space and more generally all separable Banach spaces, the Cantor space 2ℕ, the Baire space ℕℕ, the infinite symmetric group S∞, the unitary group (of the Hilbert space), the group of measure preserving transformations of the unit interval, etc.
In this theory sets are classified in hierarchies according to the complexity of their definitions and the structure of sets in each level of these hierarchies is systematically analyzed. In the beginning we have the Borel sets in Polish spaces, obtained by starting with the open sets and closing under the operations of complementation and countable unions, and the corresponding Borel hierarchy (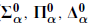 sets). After this come the projective sets, obtained by starting with the Borel sets and closing under the operations of complementation and projection, and the corresponding projective hierarchy (
sets). After this come the projective sets, obtained by starting with the Borel sets and closing under the operations of complementation and projection, and the corresponding projective hierarchy (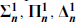 sets).
sets).
There are also transfinite extensions of the projective hierarchy and even much more complex definable sets studied in descriptive set theory, but I will restrict myself here to Borel and projective sets, in fact just those at the first level of the projective hierarchy, i.e., the Borel (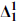 ), analytic (
), analytic (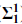 ) and coanalytic (
) and coanalytic (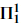 ) sets.
) sets.

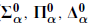 sets). After this come the
sets). After this come the 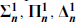 sets).
sets).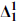 ),
), 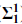 ) and
) and 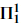 ) sets.
) sets. and
and  which arise from observing restrictions on structural rules on the level of terms as well as propositions. We discuss computational interpretations, based on sharing, at both the propositional and predicate levels.
which arise from observing restrictions on structural rules on the level of terms as well as propositions. We discuss computational interpretations, based on sharing, at both the propositional and predicate levels.