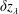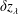1 Introduction
The question of how collisionless plasma turbulence dissipates via kinetic processes has received a great deal of recent interest (Parashar et al. Reference Parashar, Salem, Wicks, Karimabadi, Gary and Matthaeus2015). The heating mechanism(s) that effect this dissipation have dramatic consequences for the basic thermodynamic state of the plasma, controlling the ion-to-electron temperature ratio as well as affecting the temperature anisotropy of the plasma with respect to the local magnetic-field direction. Attempts at solving this problem often fall into one of two camps: (i) studies that invoke the ‘quasilinear premise’ (Klein et al. Reference Klein, Howes, TenBarge, Bale, Chen and Salem2012; Howes, Klein & TenBarge Reference Howes, Klein and TenBarge2014) and propose that turbulent fluctuations damp at the same rate (e.g. the linear Landau damping rate (Landau Reference Landau1946)) as linear plasma waves with similar polarisation properties (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006, Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Howes, Tenbarge & Dorland Reference Howes, Tenbarge and Dorland2011; TenBarge & Howes Reference TenBarge and Howes2013; TenBarge, Howes & Dorland Reference TenBarge, Howes and Dorland2013; Told et al. Reference Told, Jenko, TenBarge, Howes and Hammett2015; Howes, McCubbin & Klein Reference Howes, McCubbin and Klein2018), or, alternatively, (ii) studies that focus on intermittency and the associated ‘coherent structures’ (Matthaeus & Lamkin Reference Matthaeus and Lamkin1986; Burlaga Reference Burlaga1991; Horbury & Balogh Reference Horbury and Balogh1997; Sorriso-Valvo et al. Reference Sorriso-Valvo, Carbone, Veltri, Consolini and Bruno1999; Bruno et al. Reference Bruno, Carbone, Chapman, Hnat, Noullez and Sorriso-Valvo2007; Cho & Lazarian Reference Cho and Lazarian2009; Greco et al. Reference Greco, Matthaeus, Servidio, Chuychai and Dmitruk2009; Parashar et al. Reference Parashar, Shay, Cassak and Matthaeus2009; Salem et al. Reference Salem, Mangeney, Bale and Veltri2009; Servidio et al. Reference Servidio, Matthaeus, Shay, Cassak and Dmitruk2009; Greco et al. Reference Greco, Servidio, Matthaeus and Dmitruk2010; Osman et al. Reference Osman, Matthaeus, Greco and Servidio2011; Servidio et al. Reference Servidio, Dmitruk, Greco, Wan, Donato, Cassak, Shay, Carbone and Matthaeus2011; Greco et al. Reference Greco, Valentini, Servidio and Matthaeus2012; Osman et al. Reference Osman, Matthaeus, Hnat and Chapman2012a ,Reference Osman, Matthaeus, Wan and Rappazzo b ; Perri et al. Reference Perri, Carbone, Vecchio, Bruno, Korth, Zurbuchen and Sorriso-Valvo2012; Karimabadi et al. Reference Karimabadi, Roytershteyn, Wan, Matthaeus, Daughton, Wu, Shay, Loring, Borovsky and Leonardis2013; Wu et al. Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013; Osman et al. Reference Osman, Matthaeus, Gosling, Greco, Servidio, Hnat, Chapman and Phan2014; Chasapis et al. Reference Chasapis, Retinò, Sahraoui, Vaivads, Khotyaintsev, Sundkvist, Greco, Sorriso-Valvo and Canu2015; Bañón Navarro et al. Reference Bañón Navarro, Teaca, Told, Groselj, Crandall and Jenko2016; Lion, Alexandrova & Zaslavsky Reference Lion, Alexandrova and Zaslavsky2016; Perrone et al. Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016; Wan et al. Reference Wan, Matthaeus, Roytershteyn, Parashar, Wu and Karimabadi2016), arguing that these structures dissipate in a fundamentally different way than linear waves. In this Letter, we straddle these two camps by developing a novel modelling framework for the damping of intermittent turbulence. We use this to predict, for the first time, the quantitative dependence (or independence) of different heating mechanisms on the level of intermittency, and the effect (or lack of effect) of these heating mechanisms on the intermittency itself, with several surprising results. These results suggest a simple new observational test, based on the scale-dependent kurtosis near the ion gyroscale, that will allow us to distinguish between different heating mechanisms in collisionless plasma turbulence, for example in the solar wind.
We first show that, in intermittent, critically balanced turbulence, intermittency has no effect upon the total turbulent heating rate resulting from linear Landau damping, and that linear Landau damping has no effect on the level of intermittency. These results only apply when the turbulence is critically balanced: in both weak turbulence and (unphysical) isotropic turbulence, the linear Landau heating rate does depend on the intermittency. Thus, the ‘linear’ nature of Landau damping does not by itself make (as might naïvely be expected) its associated turbulent heating rate independent of intermittency. We then contrast this with the mechanism of stochastic heating (McChesney et al.
Reference McChesney, Stern and Bellan1987; Chen, Lin & White Reference Chen, Lin and White2001; White, Chen & Lin Reference White, Chen and Lin2002; Chaston et al.
Reference Chaston, Bonnell, Carlson, McFadden, Ergun, Strangeway and Lund2004; Voitenko & Goossens Reference Voitenko and Goossens2004; Fiksel et al.
Reference Fiksel, Almagri, Chapman, Mirnov, Ren, Sarff and Terry2009; Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010; Chandran Reference Chandran2010; Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011; Bourouaine & Chandran Reference Bourouaine and Chandran2013; Vech, Klein & Kasper Reference Vech, Klein and Kasper2017); when the turbulence amplitude at the ion gyroscale
![]() $\unicode[STIX]{x1D70C}=v_{\text{th}}/\unicode[STIX]{x1D6FA}_{i}$
(where
$\unicode[STIX]{x1D70C}=v_{\text{th}}/\unicode[STIX]{x1D6FA}_{i}$
(where
![]() $v_{\text{th}}=\sqrt{2T_{i}/m_{i}}$
is the ion thermal speed and
$v_{\text{th}}=\sqrt{2T_{i}/m_{i}}$
is the ion thermal speed and
![]() $\unicode[STIX]{x1D6FA}_{i}=ZeB/m_{i}$
is the ion gyrofrequency) becomes sufficiently large, ion orbits become chaotic, and ions may gain energy by interacting with gyroscale turbulent structures with frequencies much less than
$\unicode[STIX]{x1D6FA}_{i}=ZeB/m_{i}$
is the ion gyrofrequency) becomes sufficiently large, ion orbits become chaotic, and ions may gain energy by interacting with gyroscale turbulent structures with frequencies much less than
![]() $\unicode[STIX]{x1D6FA}_{i}$
. The stochastic damping rate is a highly nonlinear function of turbulent fluctuation amplitude. We show that (i) intermittency dramatically increases the overall stochastic heating rate, and (ii) stochastic heating reduces the scale-dependent kurtosis of the turbulent fluctuations at the scale
$\unicode[STIX]{x1D6FA}_{i}$
. The stochastic damping rate is a highly nonlinear function of turbulent fluctuation amplitude. We show that (i) intermittency dramatically increases the overall stochastic heating rate, and (ii) stochastic heating reduces the scale-dependent kurtosis of the turbulent fluctuations at the scale
![]() $\unicode[STIX]{x1D70C}$
. Finally, we show that because of this strong dependence on intermittency, stochastic heating may remain an important dissipation mechanism in astrophysical situations, where naïvely it would be ignored due to the small overall turbulence amplitude at the gyroscale.
$\unicode[STIX]{x1D70C}$
. Finally, we show that because of this strong dependence on intermittency, stochastic heating may remain an important dissipation mechanism in astrophysical situations, where naïvely it would be ignored due to the small overall turbulence amplitude at the gyroscale.
2 Intermittency model
We restrict our analysis to intermittent Alfvén-wave turbulence and damping mechanisms that are effective at
![]() $k_{\bot }\unicode[STIX]{x1D70C}\lesssim 1$
. We assume that the velocity and magnetic-field fluctuations (in velocity units) are much smaller than the background magnetic field, and that the fluctuations are highly anisotropic with respect to the direction of the background magnetic field, i.e. their parallel wavevectors are much smaller than their perpendicular wavevectors,
$k_{\bot }\unicode[STIX]{x1D70C}\lesssim 1$
. We assume that the velocity and magnetic-field fluctuations (in velocity units) are much smaller than the background magnetic field, and that the fluctuations are highly anisotropic with respect to the direction of the background magnetic field, i.e. their parallel wavevectors are much smaller than their perpendicular wavevectors,
![]() $k_{\Vert }\ll k_{\bot }$
. This allows us to model the turbulence with the equations of reduced magnetohydrodynamics (RMHD) (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1973; Strauss Reference Strauss1976; Montgomery Reference Montgomery1982), compactly written in terms of Elsasser (Reference Elsasser1950) variables
$k_{\Vert }\ll k_{\bot }$
. This allows us to model the turbulence with the equations of reduced magnetohydrodynamics (RMHD) (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1973; Strauss Reference Strauss1976; Montgomery Reference Montgomery1982), compactly written in terms of Elsasser (Reference Elsasser1950) variables
![]() $\boldsymbol{z}_{\bot }^{\pm }=\boldsymbol{u}_{\bot }\pm \boldsymbol{b}_{\bot }$
, where
$\boldsymbol{z}_{\bot }^{\pm }=\boldsymbol{u}_{\bot }\pm \boldsymbol{b}_{\bot }$
, where
![]() $\boldsymbol{u}_{\bot }$
and
$\boldsymbol{u}_{\bot }$
and
![]() $\boldsymbol{b}_{\bot }$
are the perpendicular velocity and magnetic-field (in velocity units) fluctuations respectively. There are a number of different intermittency models (Müller & Biskamp Reference Müller and Biskamp2000; Chandran, Schekochihin & Mallet Reference Chandran, Schekochihin and Mallet2015) available; here, we will use the MS17 (Mallet & Schekochihin Reference Mallet and Schekochihin2017) model, but our results do not depend in detail on this choice.Footnote
1
The Elsasser fluctuation amplitude of a structure with perpendicular scale
$\boldsymbol{b}_{\bot }$
are the perpendicular velocity and magnetic-field (in velocity units) fluctuations respectively. There are a number of different intermittency models (Müller & Biskamp Reference Müller and Biskamp2000; Chandran, Schekochihin & Mallet Reference Chandran, Schekochihin and Mallet2015) available; here, we will use the MS17 (Mallet & Schekochihin Reference Mallet and Schekochihin2017) model, but our results do not depend in detail on this choice.Footnote
1
The Elsasser fluctuation amplitude of a structure with perpendicular scale
![]() $\unicode[STIX]{x1D706}$
is a random variable,
$\unicode[STIX]{x1D706}$
is a random variable,
where
![]() $\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
is the outer scale amplitude, the constant
$\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
is the outer scale amplitude, the constant
![]() $\unicode[STIX]{x1D6E5}=1/\sqrt{2}$
and
$\unicode[STIX]{x1D6E5}=1/\sqrt{2}$
and
![]() $q$
is a Poisson random variableFootnote
2
with mean
$q$
is a Poisson random variableFootnote
2
with mean
![]() $\unicode[STIX]{x1D707}=-\log (\unicode[STIX]{x1D706}/L_{\bot })$
,
$\unicode[STIX]{x1D707}=-\log (\unicode[STIX]{x1D706}/L_{\bot })$
,
![]() $L_{\bot }$
being the outer scale. This distribution has ‘heavy tails’, becoming heavier at smaller scales
$L_{\bot }$
being the outer scale. This distribution has ‘heavy tails’, becoming heavier at smaller scales
![]() $\unicode[STIX]{x1D706}$
, a classic hallmark of intermittency (Frisch Reference Frisch1995). This may be usefully quantified by the scale-dependent kurtosis,
$\unicode[STIX]{x1D706}$
, a classic hallmark of intermittency (Frisch Reference Frisch1995). This may be usefully quantified by the scale-dependent kurtosis,
The nonlinear and linear time scales of each structure are
respectively, where
![]() $v_{\text{A}}=B_{0}/\sqrt{4\unicode[STIX]{x03C0}n_{i}m_{i}}$
is the Alfvén speed,
$v_{\text{A}}=B_{0}/\sqrt{4\unicode[STIX]{x03C0}n_{i}m_{i}}$
is the Alfvén speed,
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}}$
is the ‘alignment angle’ (Boldyrev Reference Boldyrev2006) and
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D706}}$
is the ‘alignment angle’ (Boldyrev Reference Boldyrev2006) and
This model incorporates refined critical balance (Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2015): the linear and nonlinear time scales in each structure are comparable,
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}\equiv \unicode[STIX]{x1D70F}_{\text{A}\unicode[STIX]{x1D706}}/\unicode[STIX]{x1D70F}_{\text{nl}\unicode[STIX]{x1D706}}\sim 1$
.Footnote
3
Thus, either time may be used as the cascade time scale
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D706}}\equiv \unicode[STIX]{x1D70F}_{\text{A}\unicode[STIX]{x1D706}}/\unicode[STIX]{x1D70F}_{\text{nl}\unicode[STIX]{x1D706}}\sim 1$
.Footnote
3
Thus, either time may be used as the cascade time scale
![]() $\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
. The cascade power within the local subvolume of a particular structure is
$\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
. The cascade power within the local subvolume of a particular structure is
Note that
![]() $\langle \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D706}}\rangle =\unicode[STIX]{x1D6FF}z_{L_{\bot }}^{3}/L_{\bot }\equiv \unicode[STIX]{x1D716}$
, the injected power, for
$\langle \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D706}}\rangle =\unicode[STIX]{x1D6FF}z_{L_{\bot }}^{3}/L_{\bot }\equiv \unicode[STIX]{x1D716}$
, the injected power, for
![]() $\unicode[STIX]{x1D706}$
in the inertial range.
$\unicode[STIX]{x1D706}$
in the inertial range.
3 Damping model
In this work, we will assume that the damping mechanisms we study irreversibly dissipate energy that is removed from the Alfvénic cascade.Footnote
4
We can then relate the heating rate
![]() $Q_{\unicode[STIX]{x1D706}}$
to the damping rate
$Q_{\unicode[STIX]{x1D706}}$
to the damping rate
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}$
via
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}$
via
To motivate our model, we begin with the non-intermittent cascade model of Howes et al. (Batchelor Reference Batchelor1953; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008, Reference Howes, Tenbarge and Dorland2011), which in steady state far from the forcing wavenumber leads to
where
![]() $\unicode[STIX]{x1D716}_{k_{\bot }}=(\unicode[STIX]{x1D6FF}z_{k_{\bot }})^{2}/\unicode[STIX]{x1D70F}_{\text{c}k_{\bot }}$
is the cascade power at perpendicular wavenumber
$\unicode[STIX]{x1D716}_{k_{\bot }}=(\unicode[STIX]{x1D6FF}z_{k_{\bot }})^{2}/\unicode[STIX]{x1D70F}_{\text{c}k_{\bot }}$
is the cascade power at perpendicular wavenumber
![]() $k_{\bot }$
,
$k_{\bot }$
,
![]() $\unicode[STIX]{x1D6FF}z_{k_{\bot }}$
is the turbulence amplitude at
$\unicode[STIX]{x1D6FF}z_{k_{\bot }}$
is the turbulence amplitude at
![]() $k_{\bot }$
and
$k_{\bot }$
and
![]() $\unicode[STIX]{x1D6FE}_{k_{\bot }}$
is the damping rate at
$\unicode[STIX]{x1D6FE}_{k_{\bot }}$
is the damping rate at
![]() $k_{\bot }$
. In order to investigate different damping mechanisms analytically, we make the simplifying assumption that the damping is localised to one particular reference scale
$k_{\bot }$
. In order to investigate different damping mechanisms analytically, we make the simplifying assumption that the damping is localised to one particular reference scale
![]() $\unicode[STIX]{x1D70C}$
, i.e.
$\unicode[STIX]{x1D70C}$
, i.e.
![]() $\unicode[STIX]{x1D6FE}_{k_{\bot }}\unicode[STIX]{x1D70F}_{\text{c}k_{\bot }}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6FF}[\log (k_{\bot }\unicode[STIX]{x1D70C})],$
where
$\unicode[STIX]{x1D6FE}_{k_{\bot }}\unicode[STIX]{x1D70F}_{\text{c}k_{\bot }}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6FF}[\log (k_{\bot }\unicode[STIX]{x1D70C})],$
where
![]() $\unicode[STIX]{x1D6FF}[\ldots ]$
denotes the Dirac delta distribution. In practice, various potentially important forms of damping are localised around the ion gyroscale: for example, stochastic heating, and ion Landau damping at high
$\unicode[STIX]{x1D6FF}[\ldots ]$
denotes the Dirac delta distribution. In practice, various potentially important forms of damping are localised around the ion gyroscale: for example, stochastic heating, and ion Landau damping at high
![]() $\unicode[STIX]{x1D6FD}_{i}$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). The cascade power (
$\unicode[STIX]{x1D6FD}_{i}$
(Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). The cascade power (
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}-}$
) and turbulence amplitude (
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}-}$
) and turbulence amplitude (
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}$
) at
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}$
) at
![]() $k_{\bot }\unicode[STIX]{x1D70C}=1+\text{d}$
may then be written in terms of their counterparts
$k_{\bot }\unicode[STIX]{x1D70C}=1+\text{d}$
may then be written in terms of their counterparts
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}$
and
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}$
and
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
at
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
at
![]() $k_{\bot }\unicode[STIX]{x1D70C}=1-\text{d}$
(where
$k_{\bot }\unicode[STIX]{x1D70C}=1-\text{d}$
(where
![]() $\text{d}\ll 1$
),
$\text{d}\ll 1$
),
where to obtain (3.4) we use (2.3), assuming that damping affects the amplitude but not the dynamic alignment.Footnote 5
To generalise this, note that if a turbulent structure has perpendicular scale
![]() $\unicode[STIX]{x1D706}$
and amplitude
$\unicode[STIX]{x1D706}$
and amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
, its fluctuation power
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
, its fluctuation power
![]() $\unicode[STIX]{x1D6FF}z_{k_{\bot }}\sim \unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
peaks at
$\unicode[STIX]{x1D6FF}z_{k_{\bot }}\sim \unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
peaks at
![]() $k_{\bot }\sim 1/\unicode[STIX]{x1D706}$
. We further assume (Kolmogorov Reference Kolmogorov1962) that the local values of random variables in a structure set its dynamical time scales
$k_{\bot }\sim 1/\unicode[STIX]{x1D706}$
. We further assume (Kolmogorov Reference Kolmogorov1962) that the local values of random variables in a structure set its dynamical time scales
![]() $\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
,
$\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
,
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}^{-1}$
, and promote all the variables in (3.3)–(3.4) to configuration-space random variables. We call
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}^{-1}$
, and promote all the variables in (3.3)–(3.4) to configuration-space random variables. We call
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
the damping factor.
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
the damping factor.
We would like to stress that, of course, collisionless damping mechanisms do not appear in RMHD, which models the (undamped) Alfvénic fluctuations at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
(irrespective of collisionality). However, the intermittency at
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
(irrespective of collisionality). However, the intermittency at
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$
, where collisionless damping appears in more complete models, is almost entirely produced by the turbulence in the (assumed to be long,
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$
, where collisionless damping appears in more complete models, is almost entirely produced by the turbulence in the (assumed to be long,
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{i}\gg 1$
) inertial range in which RMHD is a good approximation. Thus, we model the intermittency using RMHD, and then add the dissipation in the simple way described above at the scale at which the RMHD approximation begins to break down.
$L_{\bot }/\unicode[STIX]{x1D70C}_{i}\gg 1$
) inertial range in which RMHD is a good approximation. Thus, we model the intermittency using RMHD, and then add the dissipation in the simple way described above at the scale at which the RMHD approximation begins to break down.
We have made the rather drastic simplification that the damping only occurs over an infinitesimal scale interval. No real damping mechanism is truly this localised in scale. To go beyond this approximation, one would have to simultaneously integrate over scale not only the damping part of the process (as in Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008) but also the random part of the evolution describing the random log-Poisson evolution of the intermittent probability distribution of amplitudes; replacing the algebraic exponents of (3.3) and (3.4) with functional integrals. This makes the model analytically intractable. Moreover, across any particular individual scale, the incremental damping of the fluctuations is well described by (3.3) and (3.4), which means that many of our results will not be qualitatively altered by making this approximation.
Finally, it is worth mentioning that other time scales could potentially enter the problem (Matthaeus et al. Reference Matthaeus, Oughton, Osman, Servidio, Wan, Gary, Shay, Valentini, Roytershteyn and Karimabadi2014); for example, waves could be excited via instability of the particle velocity distribution function. Indeed, Klein et al. Reference Klein, Alterman, Stevens, Vech and Kasper2018 have found that the majority of solar-wind plasma is unstable, although only approximately 10 % appears to be strongly unstable in that the growth time is shorter than their estimate of the cascade time. We have ignored this possibility in our analysis here, and assume that the underlying velocity distribution function is stable.
4 Linear Landau damping
One important and well-studied damping mechanism is linear Landau damping (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006), for which the damping rate may be written (in Fourier space)
where
![]() $F_{k_{\bot }}$
is a function of
$F_{k_{\bot }}$
is a function of
![]() $k_{\bot }$
and plasma parameters, but not
$k_{\bot }$
and plasma parameters, but not
![]() $\unicode[STIX]{x1D6FF}z_{k_{\bot }}$
. Since (refined) critical balance states that (for all structures)
$\unicode[STIX]{x1D6FF}z_{k_{\bot }}$
. Since (refined) critical balance states that (for all structures)
![]() $k_{\Vert }v_{\text{A}}\sim \unicode[STIX]{x1D70F}_{\text{c}k_{\bot }}^{-1}$
, the damping factor is
$k_{\Vert }v_{\text{A}}\sim \unicode[STIX]{x1D70F}_{\text{c}k_{\bot }}^{-1}$
, the damping factor is
where
![]() $F_{\unicode[STIX]{x1D706}}$
is a function of
$F_{\unicode[STIX]{x1D706}}$
is a function of
![]() $\unicode[STIX]{x1D706}$
but not of
$\unicode[STIX]{x1D706}$
but not of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
. This result is true for any intermittency model that incorporates refined critical balance, not solely in the MS17 model (Mallet & Schekochihin Reference Mallet and Schekochihin2017); it is also the case in the CSM15 model (Chandran et al.
Reference Chandran, Schekochihin and Mallet2015). (3.4) yields
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
. This result is true for any intermittency model that incorporates refined critical balance, not solely in the MS17 model (Mallet & Schekochihin Reference Mallet and Schekochihin2017); it is also the case in the CSM15 model (Chandran et al.
Reference Chandran, Schekochihin and Mallet2015). (3.4) yields
Because
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
is independent of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
is independent of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
, the effect of the damping is to shift the whole distribution of log-amplitudes over by the constant
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
, the effect of the damping is to shift the whole distribution of log-amplitudes over by the constant
![]() $(2/3)\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
; i.e. the shape of the distribution is not changed. As a corollary, the kurtosis
$(2/3)\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
; i.e. the shape of the distribution is not changed. As a corollary, the kurtosis
is unchanged. Similarly, the average heating rate per unit volume,
is not affected by the intermittency at all. However, if one looks at the structures in which the heating is happening, the intermittency is relevant: the heating rate random variable for each structure,
follows the (intermittent) distribution of the random variable
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}$
, and damping is concentrated in the higher-amplitude, intermittent structures. Thus, Landau damping certainly does not lead to homogeneous wave damping – a point also made recently by Howes et al. (Reference Howes, McCubbin and Klein2018). These results would also apply generically to any damping mechanism for which the damping factor
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}$
, and damping is concentrated in the higher-amplitude, intermittent structures. Thus, Landau damping certainly does not lead to homogeneous wave damping – a point also made recently by Howes et al. (Reference Howes, McCubbin and Klein2018). These results would also apply generically to any damping mechanism for which the damping factor
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
is independent of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
is independent of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}$
.
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}$
.
It might be naïvely thought that these results (4.4), (4.5) are obvious due to the linear nature of Landau damping. Thinking more carefully, these results only apply if the turbulence is critically balanced in the refined sense. For example, if the turbulence were isotropic (
![]() $l_{\Vert }\sim \unicode[STIX]{x1D706}$
) at the gyroscale,
$l_{\Vert }\sim \unicode[STIX]{x1D706}$
) at the gyroscale,
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}\propto 1/\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}$
. Likewise, if the turbulence were weak (
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}\propto 1/\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}$
. Likewise, if the turbulence were weak (
![]() $l_{\Vert }\sim \text{const.}$
and
$l_{\Vert }\sim \text{const.}$
and
![]() $\unicode[STIX]{x1D70F}_{\text{c}}\sim \unicode[STIX]{x1D706}^{2}v_{\text{A}}/l_{\Vert }\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}^{2}$
),
$\unicode[STIX]{x1D70F}_{\text{c}}\sim \unicode[STIX]{x1D706}^{2}v_{\text{A}}/l_{\Vert }\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}^{2}$
),
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}\propto 1/\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}^{2}$
. In both these non-critically balanced cases, the Landau damping is less important in higher-amplitude structures, i.e. the heating rate is more homogeneous than the distribution of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}\propto 1/\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}^{2}$
. In both these non-critically balanced cases, the Landau damping is less important in higher-amplitude structures, i.e. the heating rate is more homogeneous than the distribution of
![]() $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}$
. This is yet another argument for why critical balance is a crucial organising principle for magnetised plasma turbulence, and for why one cannot neglect either linear or nonlinear physical phenomena when modelling such turbulence.
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}$
. This is yet another argument for why critical balance is a crucial organising principle for magnetised plasma turbulence, and for why one cannot neglect either linear or nonlinear physical phenomena when modelling such turbulence.
5 Stochastic heating
The damping rate of gyroscale fluctuations by stochastic heating may be written (Chandran et al. Reference Chandran, Li, Rogers, Quataert and Germaschewski2010)Footnote 6
We take
![]() $c_{1}=0.75$
and
$c_{1}=0.75$
and
![]() $c_{2}=0.34$
(cf. Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). The exponential suppression depends on the random variable
$c_{2}=0.34$
(cf. Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010). The exponential suppression depends on the random variable
where
![]() $\unicode[STIX]{x1D6FD}_{i}=8\unicode[STIX]{x03C0}n_{i}T_{i}/B_{0}^{2}$
. Using (2.3) and (2.4), the damping factor is
$\unicode[STIX]{x1D6FD}_{i}=8\unicode[STIX]{x03C0}n_{i}T_{i}/B_{0}^{2}$
. Using (2.3) and (2.4), the damping factor is
a (highly nonlinear) function of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
.Footnote
7
In a qualitative sense, our results on the efficiency of intermittent stochastic heating and its effect on intermittency also apply generically to all mechanisms for which
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
.Footnote
7
In a qualitative sense, our results on the efficiency of intermittent stochastic heating and its effect on intermittency also apply generically to all mechanisms for which
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
is an increasing function of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
is an increasing function of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
.
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
.
To illustrate our results, we use a numerically sampled log-Poisson distribution. We take the outer scale amplitudes
![]() $\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
to be distributed as the magnitude of a normal random variable with zero mean and standard deviation
$\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
to be distributed as the magnitude of a normal random variable with zero mean and standard deviation
![]() $\unicode[STIX]{x1D70E}=0.1v_{\text{A}}$
. We multiply
$\unicode[STIX]{x1D70E}=0.1v_{\text{A}}$
. We multiply
![]() $\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
by the log-Poisson factor
$\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
by the log-Poisson factor
![]() $\unicode[STIX]{x1D6E5}^{q}$
(2.1), generating
$\unicode[STIX]{x1D6E5}^{q}$
(2.1), generating
![]() $10^{7}$
samples of the intermittent distribution
$10^{7}$
samples of the intermittent distribution
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
just above the gyroscale
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
just above the gyroscale
![]() $\unicode[STIX]{x1D70C}$
. We then apply damping using (3.4) and (5.3) with various different values of
$\unicode[STIX]{x1D70C}$
. We then apply damping using (3.4) and (5.3) with various different values of
![]() $\unicode[STIX]{x1D6FD}_{i}$
and
$\unicode[STIX]{x1D6FD}_{i}$
and
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
, obtaining the distributions of
$L_{\bot }/\unicode[STIX]{x1D70C}$
, obtaining the distributions of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}$
used in figures 1–3.
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}$
used in figures 1–3.
Figure 1. The distribution of
![]() $\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}/\unicode[STIX]{x1D70E})$
resulting from (nonlinear) stochastic heating at
$\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}/\unicode[STIX]{x1D70E})$
resulting from (nonlinear) stochastic heating at
![]() $\unicode[STIX]{x1D70C}=10^{-4}L_{\bot }$
, for various values of
$\unicode[STIX]{x1D70C}=10^{-4}L_{\bot }$
, for various values of
![]() $\unicode[STIX]{x1D6FD}_{i}=1,0.1,0.01,0.001$
(blue to red). Vertical dotted lines show
$\unicode[STIX]{x1D6FD}_{i}=1,0.1,0.01,0.001$
(blue to red). Vertical dotted lines show
![]() $\unicode[STIX]{x1D6FF}z_{\text{max}}$
for each
$\unicode[STIX]{x1D6FF}z_{\text{max}}$
for each
![]() $\unicode[STIX]{x1D6FD}_{i}$
. The distribution of
$\unicode[STIX]{x1D6FD}_{i}$
. The distribution of
![]() $\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}/\unicode[STIX]{x1D70E})$
is shown in black.
$\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}/\unicode[STIX]{x1D70E})$
is shown in black.
6 Distribution of fluctuation amplitudes
The shape of the distribution of
![]() $\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}/\unicode[STIX]{x1D70E})$
resulting from stochastic heating is shown for
$\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}/\unicode[STIX]{x1D70E})$
resulting from stochastic heating is shown for
![]() $L_{\bot }/\unicode[STIX]{x1D70C}=10^{4}$
(a value similar to that in the solar wind) and various values of
$L_{\bot }/\unicode[STIX]{x1D70C}=10^{4}$
(a value similar to that in the solar wind) and various values of
![]() $\unicode[STIX]{x1D6FD}_{i}$
(i.e. various different overall damping rates) in Figure 1. As the damping becomes more important (i.e. at lower
$\unicode[STIX]{x1D6FD}_{i}$
(i.e. various different overall damping rates) in Figure 1. As the damping becomes more important (i.e. at lower
![]() $\unicode[STIX]{x1D6FD}_{i}$
), the fluctuations with higher amplitude are heavily damped, causing a relatively sharp upper limit on
$\unicode[STIX]{x1D6FD}_{i}$
), the fluctuations with higher amplitude are heavily damped, causing a relatively sharp upper limit on
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}$
. This limit is the amplitude
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}-}$
. This limit is the amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\text{max}}$
for which
$\unicode[STIX]{x1D6FF}z_{\text{max}}$
for which
shown in figure 1 as a vertical dotted line for each
![]() $\unicode[STIX]{x1D6FD}_{i}$
.
$\unicode[STIX]{x1D6FD}_{i}$
.
Because of this modification of the shape, the kurtosis (2.2) is heavily affected by the damping. In the inertial range, the kurtosis increases as
![]() $\unicode[STIX]{x1D706}$
decreases, reaching a value of
$\unicode[STIX]{x1D706}$
decreases, reaching a value of
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}+}=30$
just above
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}+}=30$
just above
![]() $\unicode[STIX]{x1D70C}=10^{-4}L_{\bot }$
. As the stochastic heating becomes more important (with decreasing
$\unicode[STIX]{x1D70C}=10^{-4}L_{\bot }$
. As the stochastic heating becomes more important (with decreasing
![]() $\unicode[STIX]{x1D6FD}_{i}$
), the kurtosis just below
$\unicode[STIX]{x1D6FD}_{i}$
), the kurtosis just below
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}-}^{\text{SH}}$
, decreases significantly – see figure 2(a). Such a decrease in kurtosis is a generic property of nonlinear damping mechanisms for which
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}-}^{\text{SH}}$
, decreases significantly – see figure 2(a). Such a decrease in kurtosis is a generic property of nonlinear damping mechanisms for which
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
is an increasing function of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
is an increasing function of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
.
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
.
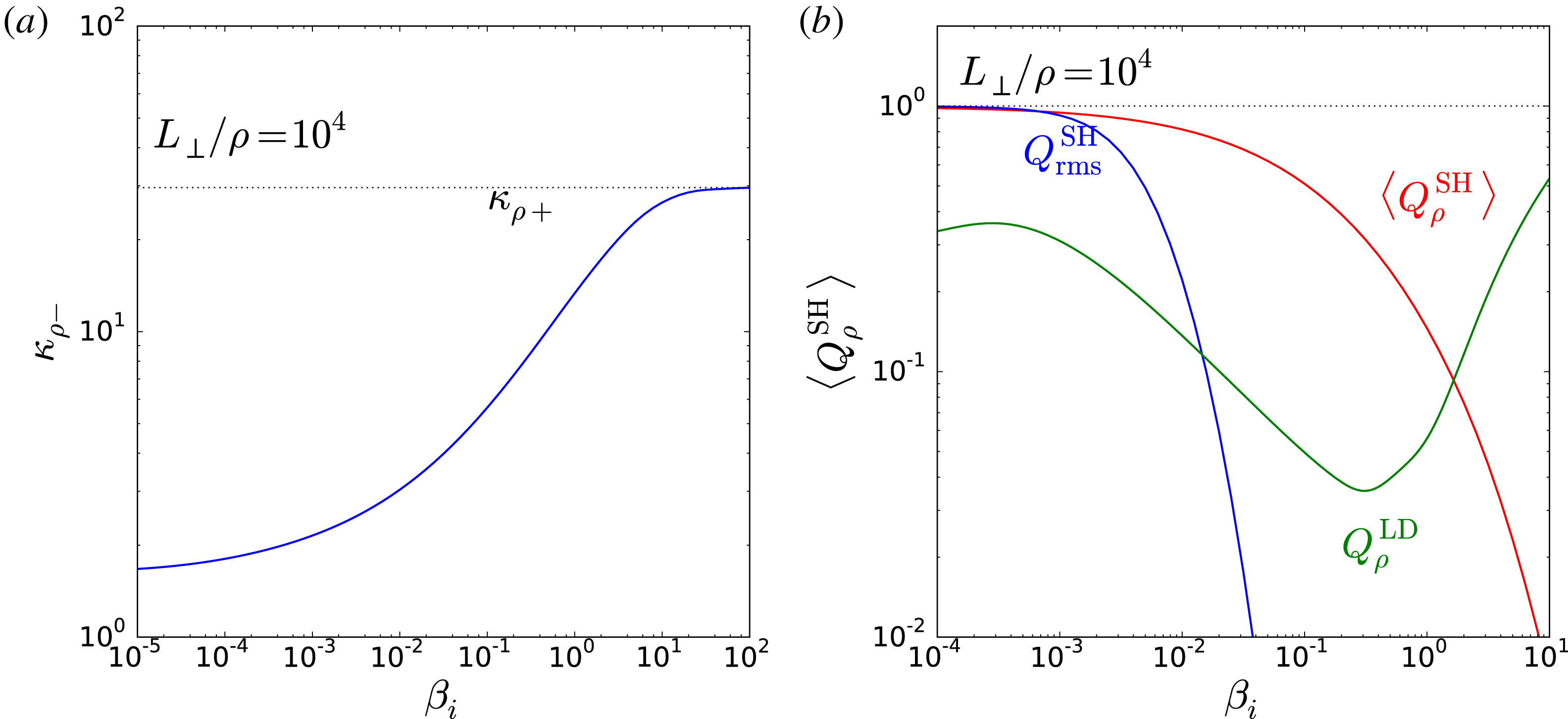
Figure 2. (a) In blue, the kurtosis after damping,
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}-}^{\text{SH}}$
, as a function of
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}-}^{\text{SH}}$
, as a function of
![]() $\unicode[STIX]{x1D6FD}_{i}$
. The black dotted line is the kurtosis without damping
$\unicode[STIX]{x1D6FD}_{i}$
. The black dotted line is the kurtosis without damping
![]() $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}+}$
. (b) The heating rates as functions of
$\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70C}+}$
. (b) The heating rates as functions of
![]() $\unicode[STIX]{x1D6FD}_{i}$
:
$\unicode[STIX]{x1D6FD}_{i}$
:
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
calculated using the intermittent distribution (red),
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
calculated using the intermittent distribution (red),
![]() $Q_{\text{rms}}^{\text{SH}}$
using the root-mean-square (r.m.s.) turbulent amplitude (blue), and
$Q_{\text{rms}}^{\text{SH}}$
using the root-mean-square (r.m.s.) turbulent amplitude (blue), and
![]() $Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}$
, the linear Landau-damping heating rate, normalised to the cascade power
$Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}$
, the linear Landau-damping heating rate, normalised to the cascade power
![]() $\unicode[STIX]{x1D716}$
. In both panels,
$\unicode[STIX]{x1D716}$
. In both panels,
![]() $L_{\bot }/\unicode[STIX]{x1D70C}=10^{4}$
and the outer-scale turbulence amplitude distribution is fixed, parametrised by
$L_{\bot }/\unicode[STIX]{x1D70C}=10^{4}$
and the outer-scale turbulence amplitude distribution is fixed, parametrised by
![]() $\unicode[STIX]{x1D70E}=0.1v_{\text{A}}$
(see text).
$\unicode[STIX]{x1D70E}=0.1v_{\text{A}}$
(see text).
7 Heating
Unlike in the linear case, the average stochastic heating rate
is affected by the intermittency of the turbulence. This heating rate may be compared with
![]() $\langle \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}\rangle =\langle \unicode[STIX]{x1D716}_{L_{\bot }}\rangle =\unicode[STIX]{x1D716}$
, and also with the heating rate that would be obtained without intermittency,
$\langle \unicode[STIX]{x1D716}_{\unicode[STIX]{x1D70C}+}\rangle =\langle \unicode[STIX]{x1D716}_{L_{\bot }}\rangle =\unicode[STIX]{x1D716}$
, and also with the heating rate that would be obtained without intermittency,
![]() $Q_{\text{rms}}^{\text{SH}}$
, using the root-mean-square (r.m.s.) amplitude
$Q_{\text{rms}}^{\text{SH}}$
, using the root-mean-square (r.m.s.) amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\text{rms}\unicode[STIX]{x1D70C}+}\sim \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}/L_{\bot })^{1/4}$
in place of the random variable
$\unicode[STIX]{x1D6FF}z_{\text{rms}\unicode[STIX]{x1D70C}+}\sim \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}/L_{\bot })^{1/4}$
in place of the random variable
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
. These intermittent and r.m.s. heating rates, calculated using (5.3) and normalised to
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}$
. These intermittent and r.m.s. heating rates, calculated using (5.3) and normalised to
![]() $\unicode[STIX]{x1D716}$
, are shown in Figure 2(b), again with
$\unicode[STIX]{x1D716}$
, are shown in Figure 2(b), again with
![]() $L_{\bot }/\unicode[STIX]{x1D70C}=10^{4}$
. The value of
$L_{\bot }/\unicode[STIX]{x1D70C}=10^{4}$
. The value of
![]() $\unicode[STIX]{x1D6FD}_{i}$
at which the damping removes approximately half of the cascade power is significantly higher (by approximately a factor of 20) with intermittency:
$\unicode[STIX]{x1D6FD}_{i}$
at which the damping removes approximately half of the cascade power is significantly higher (by approximately a factor of 20) with intermittency:
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle \gtrsim 0.5$
for
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle \gtrsim 0.5$
for
![]() $\unicode[STIX]{x1D6FD}_{i}\lesssim 0.1$
, while
$\unicode[STIX]{x1D6FD}_{i}\lesssim 0.1$
, while
![]() $Q_{\text{rms}}^{\text{SH}}\gtrsim 0.5$
for
$Q_{\text{rms}}^{\text{SH}}\gtrsim 0.5$
for
![]() $\unicode[STIX]{x1D6FD}_{i}\lesssim 0.005$
.
$\unicode[STIX]{x1D6FD}_{i}\lesssim 0.005$
.
Finally, we calculate the kinetic-Alfvén-wave damping rates
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}$
and real frequencies
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}$
and real frequencies
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}$
for
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}$
for
![]() $k_{\bot }\unicode[STIX]{x1D70C}=1$
and
$k_{\bot }\unicode[STIX]{x1D70C}=1$
and
![]() $k_{\Vert }/k_{\bot }=10^{-3}$
, using the PLUME numerical Vlasov–Maxwell linear dispersion solver (Klein & Howes Reference Klein and Howes2015), thus estimating the average heating rate from linear Landau damping,Footnote
8
$k_{\Vert }/k_{\bot }=10^{-3}$
, using the PLUME numerical Vlasov–Maxwell linear dispersion solver (Klein & Howes Reference Klein and Howes2015), thus estimating the average heating rate from linear Landau damping,Footnote
8
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}\rangle$
(using (4.5) with
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}\rangle$
(using (4.5) with
![]() $F_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}$
), plotted in figure 2(b). At the gyroscale, intermittent stochastic heating is comparable to linear Landau damping even for
$F_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70C}}^{\text{KAW}}$
), plotted in figure 2(b). At the gyroscale, intermittent stochastic heating is comparable to linear Landau damping even for
![]() $\unicode[STIX]{x1D6FD}_{i}=1$
.
$\unicode[STIX]{x1D6FD}_{i}=1$
.
8 Length of the inertial range
The level of intermittency at the gyroscale
![]() $\unicode[STIX]{x1D70C}$
depends on the length of the inertial range
$\unicode[STIX]{x1D70C}$
depends on the length of the inertial range
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
(cf. 2.2).
$L_{\bot }/\unicode[STIX]{x1D70C}$
(cf. 2.2).
![]() $Q_{\text{rms}}^{\text{SH}}$
is a strongly decreasing function of
$Q_{\text{rms}}^{\text{SH}}$
is a strongly decreasing function of
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
, simply because the r.m.s. amplitude
$L_{\bot }/\unicode[STIX]{x1D70C}$
, simply because the r.m.s. amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\text{rms}\unicode[STIX]{x1D70C}+}\sim \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}/L_{\bot })^{1/4}$
. The intermittent stochastic heating rate
$\unicode[STIX]{x1D6FF}z_{\text{rms}\unicode[STIX]{x1D70C}+}\sim \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70C}/L_{\bot })^{1/4}$
. The intermittent stochastic heating rate
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
has a weaker dependence on
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
has a weaker dependence on
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
, because intermittent, high-amplitude fluctuations in the MS17 model resemble discontinuities with (up to) the outer scale amplitude
$L_{\bot }/\unicode[STIX]{x1D70C}$
, because intermittent, high-amplitude fluctuations in the MS17 model resemble discontinuities with (up to) the outer scale amplitude
![]() $\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
.
$\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
.
The dependence of the stochastic heating rates for
![]() $\unicode[STIX]{x1D6FD}_{i}=0.1,1.0$
on
$\unicode[STIX]{x1D6FD}_{i}=0.1,1.0$
on
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
are shown in figure 3, along with
$L_{\bot }/\unicode[STIX]{x1D70C}$
are shown in figure 3, along with
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}\rangle$
. The weak dependence of
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}\rangle$
. The weak dependence of
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
on
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
on
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
means that, for
$L_{\bot }/\unicode[STIX]{x1D70C}$
means that, for
![]() $\unicode[STIX]{x1D6FD}_{i}=0.1$
, stochastic heating still removes approximately 10 % of the overall cascade power at
$\unicode[STIX]{x1D6FD}_{i}=0.1$
, stochastic heating still removes approximately 10 % of the overall cascade power at
![]() $L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{11}$
. Moreover, it remains comparable to
$L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{11}$
. Moreover, it remains comparable to
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}\rangle$
up to
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}\rangle$
up to
![]() $L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{12}$
. Thus, intermittency may have important astrophysical consequences: even at only moderately low
$L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{12}$
. Thus, intermittency may have important astrophysical consequences: even at only moderately low
![]() $\unicode[STIX]{x1D6FD}_{i}$
, stochastic heating may (i) convert a large portion of the total cascade power into ion thermal energy at the gyroscale in solar-wind turbulence, where
$\unicode[STIX]{x1D6FD}_{i}$
, stochastic heating may (i) convert a large portion of the total cascade power into ion thermal energy at the gyroscale in solar-wind turbulence, where
![]() $L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{4}$
, and (ii) be non-negligible (and comparable to linear Landau damping) in the warm interstellar medium (ISM), where
$L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{4}$
, and (ii) be non-negligible (and comparable to linear Landau damping) in the warm interstellar medium (ISM), where
![]() $L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{11}-10^{13}$
(Ferrière Reference Ferrière2001; Cox Reference Cox2005; Beck Reference Beck2007; Haverkorn et al.
Reference Haverkorn, Brown, Gaensler and McClure-Griffiths2008).
$L_{\bot }/\unicode[STIX]{x1D70C}\approx 10^{11}-10^{13}$
(Ferrière Reference Ferrière2001; Cox Reference Cox2005; Beck Reference Beck2007; Haverkorn et al.
Reference Haverkorn, Brown, Gaensler and McClure-Griffiths2008).

Figure 3. Heating rates (normalised to
![]() $\unicode[STIX]{x1D716}$
)
$\unicode[STIX]{x1D716}$
)
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
(red),
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
(red),
![]() $Q_{\text{rms}}^{\text{SH}}$
(blue), and
$Q_{\text{rms}}^{\text{SH}}$
(blue), and
![]() $Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}$
(green), all at
$Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}$
(green), all at
![]() $\unicode[STIX]{x1D6FD}_{i}=0.1$
(solid lines) and
$\unicode[STIX]{x1D6FD}_{i}=0.1$
(solid lines) and
![]() $\unicode[STIX]{x1D6FD}_{i}=1$
(dotted lines) as a function of
$\unicode[STIX]{x1D6FD}_{i}=1$
(dotted lines) as a function of
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
. The two curves for
$L_{\bot }/\unicode[STIX]{x1D70C}$
. The two curves for
![]() $Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}$
are nearly identical (and thus indistinguishable here – see figure 2(b)). Approximate ranges of
$Q_{\unicode[STIX]{x1D70C}}^{\text{LD}}$
are nearly identical (and thus indistinguishable here – see figure 2(b)). Approximate ranges of
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
in the solar wind and in the warm ISM are labelled as SW (dotted line) and ISM (grey box).
$L_{\bot }/\unicode[STIX]{x1D70C}$
in the solar wind and in the warm ISM are labelled as SW (dotted line) and ISM (grey box).
![]() $Q_{\unicode[STIX]{x1D70C}}^{\ast }$
multiplied by a factor (
$Q_{\unicode[STIX]{x1D70C}}^{\ast }$
multiplied by a factor (
![]() $4$
for
$4$
for
![]() $\unicode[STIX]{x1D6FD}_{i}=0.1$
and
$\unicode[STIX]{x1D6FD}_{i}=0.1$
and
![]() $6.5$
for
$6.5$
for
![]() $\unicode[STIX]{x1D6FD}_{i}=1$
) is also shown (black dashed lines).
$\unicode[STIX]{x1D6FD}_{i}=1$
) is also shown (black dashed lines).
To explain the shallow dependence of
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
on
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
on
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
, we calculate the minimum amplitude
$L_{\bot }/\unicode[STIX]{x1D70C}$
, we calculate the minimum amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
for which fluctuations are strongly damped. Setting
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
for which fluctuations are strongly damped. Setting
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}=1$
in (5.3), we obtain
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}=1$
in (5.3), we obtain
where
![]() $W$
is the Lambert W function. This analytic expression for
$W$
is the Lambert W function. This analytic expression for
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
approximates
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
approximates
![]() $\unicode[STIX]{x1D6FF}z_{\text{max}}$
in (6.1). If
$\unicode[STIX]{x1D6FF}z_{\text{max}}$
in (6.1). If
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
were determined by simply setting the exponent in (5.3) equal to some constant threshold value, then
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
were determined by simply setting the exponent in (5.3) equal to some constant threshold value, then
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
would be independent of
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
would be independent of
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
. However, as
$L_{\bot }/\unicode[STIX]{x1D70C}$
. However, as
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
increases, the fluctuations are increasingly highly aligned (see (2.4)) at the gyroscale, which increases
$L_{\bot }/\unicode[STIX]{x1D70C}$
increases, the fluctuations are increasingly highly aligned (see (2.4)) at the gyroscale, which increases
![]() $\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
but not
$\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
but not
![]() $\unicode[STIX]{x1D6FE}^{-1}$
. This introduces the factor
$\unicode[STIX]{x1D6FE}^{-1}$
. This introduces the factor
![]() $(L_{\bot }/\unicode[STIX]{x1D70C})^{1/2}$
in (5.3), causing
$(L_{\bot }/\unicode[STIX]{x1D70C})^{1/2}$
in (5.3), causing
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
to decrease with increasing
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
to decrease with increasing
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
.
$L_{\bot }/\unicode[STIX]{x1D70C}$
.
The corresponding heating rate from the damping of the structures with this amplitude is
where
![]() $q^{\ast }=\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }/\unicode[STIX]{x1D6FF}z_{L_{\bot }})/\log \unicode[STIX]{x1D6E5}$
(cf. (2.1)), and we have used Stirling’s formula to approximate the factorial in the Poisson probability mass function.
$q^{\ast }=\log (\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }/\unicode[STIX]{x1D6FF}z_{L_{\bot }})/\log \unicode[STIX]{x1D6E5}$
(cf. (2.1)), and we have used Stirling’s formula to approximate the factorial in the Poisson probability mass function.
![]() $Q_{\unicode[STIX]{x1D70C}}^{\ast }$
is a reasonable analytic estimate for the scaling dependence of
$Q_{\unicode[STIX]{x1D70C}}^{\ast }$
is a reasonable analytic estimate for the scaling dependence of
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
on
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
on
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
for
$L_{\bot }/\unicode[STIX]{x1D70C}$
for
![]() $\log (L_{\bot }/\unicode[STIX]{x1D70C})\gg 1$
; however, it is an underestimate (by a factor approximately independent of
$\log (L_{\bot }/\unicode[STIX]{x1D70C})\gg 1$
; however, it is an underestimate (by a factor approximately independent of
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
), due to (i)
$L_{\bot }/\unicode[STIX]{x1D70C}$
), due to (i)
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
being an overestimate of the true cutoff,
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
being an overestimate of the true cutoff,
![]() $\unicode[STIX]{x1D6FF}z_{\text{max}}$
, (ii) the neglect of the cascade power damped in structures with higher amplitudes
$\unicode[STIX]{x1D6FF}z_{\text{max}}$
, (ii) the neglect of the cascade power damped in structures with higher amplitudes
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }<\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}<\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
, (iii) the neglect of the width of the outer scale (normal) distribution of fluctuation amplitudes. For each
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }<\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}<\unicode[STIX]{x1D6FF}z_{L_{\bot }}$
, (iii) the neglect of the width of the outer scale (normal) distribution of fluctuation amplitudes. For each
![]() $\unicode[STIX]{x1D6FD}_{i}$
,
$\unicode[STIX]{x1D6FD}_{i}$
,
![]() $Q_{\unicode[STIX]{x1D70C}}^{\ast }$
multiplied by an empirical correction factor is plotted in figure 3. The analytic expressions for
$Q_{\unicode[STIX]{x1D70C}}^{\ast }$
multiplied by an empirical correction factor is plotted in figure 3. The analytic expressions for
![]() $Q_{\unicode[STIX]{x1D70C}}^{\ast }$
and
$Q_{\unicode[STIX]{x1D70C}}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
make clear that the slowly decreasing nature of
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
make clear that the slowly decreasing nature of
![]() $\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
with
$\langle Q_{\unicode[STIX]{x1D70C}}^{\text{SH}}\rangle$
with
![]() $L_{\bot }/\unicode[STIX]{x1D70C}$
arises due to a competition between the decreasing volume-filling fraction of structures above any particular amplitude and the decreasing cutoff amplitude
$L_{\bot }/\unicode[STIX]{x1D70C}$
arises due to a competition between the decreasing volume-filling fraction of structures above any particular amplitude and the decreasing cutoff amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\text{max}}$
(
$\unicode[STIX]{x1D6FF}z_{\text{max}}$
(
![]() ${\approx}\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
).
${\approx}\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}+}^{\ast }$
).
In many astrophysical plasmas,
![]() $\unicode[STIX]{x1D6FF}z_{L_{0}}\sim v_{\text{A}}$
at an outer scale
$\unicode[STIX]{x1D6FF}z_{L_{0}}\sim v_{\text{A}}$
at an outer scale
![]() $L_{0}$
that is beyond the RMHD regime. We can apply our model in such cases on scales
$L_{0}$
that is beyond the RMHD regime. We can apply our model in such cases on scales
![]() $\unicode[STIX]{x1D706}$
smaller than an effective outer scale
$\unicode[STIX]{x1D706}$
smaller than an effective outer scale
![]() $L_{\bot }\ll L_{0}$
, where
$L_{\bot }\ll L_{0}$
, where
![]() $\unicode[STIX]{x1D6FF}z_{\text{rms}L_{\bot }}\approx 0.1v_{\text{A}}$
. For example, if
$\unicode[STIX]{x1D6FF}z_{\text{rms}L_{\bot }}\approx 0.1v_{\text{A}}$
. For example, if
![]() $\unicode[STIX]{x1D6FF}z_{\text{rms}\unicode[STIX]{x1D706}}\propto \unicode[STIX]{x1D706}^{1/4}$
at
$\unicode[STIX]{x1D6FF}z_{\text{rms}\unicode[STIX]{x1D706}}\propto \unicode[STIX]{x1D706}^{1/4}$
at
![]() $L_{\bot }<\unicode[STIX]{x1D706}<L_{0}$
, then
$L_{\bot }<\unicode[STIX]{x1D706}<L_{0}$
, then
![]() $L_{\bot }=10^{-4}L_{0}$
. The stochastic heating rate when the outer scale amplitude
$L_{\bot }=10^{-4}L_{0}$
. The stochastic heating rate when the outer scale amplitude
![]() $\unicode[STIX]{x1D6FF}z_{L_{0}}\sim v_{\text{A}}$
is then much larger than our numerical example, where
$\unicode[STIX]{x1D6FF}z_{L_{0}}\sim v_{\text{A}}$
is then much larger than our numerical example, where
![]() $\unicode[STIX]{x1D6FF}z_{L_{0}}\sim 0.1v_{\text{A}}$
, because the gyroscale fluctuation amplitudes are much larger. Our figures thus provide a highly conservative lower limit on the stochastic heating rate in plasmas in which
$\unicode[STIX]{x1D6FF}z_{L_{0}}\sim 0.1v_{\text{A}}$
, because the gyroscale fluctuation amplitudes are much larger. Our figures thus provide a highly conservative lower limit on the stochastic heating rate in plasmas in which
![]() $\unicode[STIX]{x1D6FF}z_{L_{0}}\sim v_{\text{A}}$
.
$\unicode[STIX]{x1D6FF}z_{L_{0}}\sim v_{\text{A}}$
.
9 Conclusions
In this study, we consider the collisionless damping of critically balanced, intermittent plasma turbulence by two mechanisms. We develop a new general modelling framework for studying the effects of intermittency on dissipation (and vice versa), and use it to make specific predictions for the efficiency of two different mechanisms. First, for linear Landau damping (Landau Reference Landau1946; Howes et al.
Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006, Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008, Reference Howes, Tenbarge and Dorland2011),
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
is independent of the turbulent amplitude
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
is independent of the turbulent amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
. In this case, (i) damping affects neither the shape of the distribution of log-fluctuation amplitudes, nor the kurtosis of the distribution of fluctuation amplitudes, and (ii) the overall efficiency of damping is not enhanced by the presence of intermittency. However, (iii) locally, damping is still concentrated near coherent structures (TenBarge & Howes Reference TenBarge and Howes2013; Howes et al.
Reference Howes, McCubbin and Klein2018). Importantly, these results are not an inevitable consequence of the ‘linear’ nature of linear Landau damping: the efficiency would be strongly affected by intermittency if the turbulence did not obey the refined critical balance (Mallet et al.
Reference Mallet, Schekochihin and Chandran2015).
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
. In this case, (i) damping affects neither the shape of the distribution of log-fluctuation amplitudes, nor the kurtosis of the distribution of fluctuation amplitudes, and (ii) the overall efficiency of damping is not enhanced by the presence of intermittency. However, (iii) locally, damping is still concentrated near coherent structures (TenBarge & Howes Reference TenBarge and Howes2013; Howes et al.
Reference Howes, McCubbin and Klein2018). Importantly, these results are not an inevitable consequence of the ‘linear’ nature of linear Landau damping: the efficiency would be strongly affected by intermittency if the turbulence did not obey the refined critical balance (Mallet et al.
Reference Mallet, Schekochihin and Chandran2015).
On the other hand, for stochastic heating (Chandran et al.
Reference Chandran, Li, Rogers, Quataert and Germaschewski2010),
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
depends on
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
depends on
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
, leading to damping that (i) strongly affects the shape of the distribution of log-fluctuation amplitudes and the kurtosis of the distribution of fluctuation amplitudes. In addition, stochastic heating is (ii) much more efficient if one accounts for intermittency and (iii) even more concentrated near coherent structures than heating by linear Landau damping. Our results suggest that, once intermittency is incorporated, stochastic heating may be an important damping mechanism for solar-wind turbulence, and perhaps also for some regimes of interstellar turbulence, even when
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
, leading to damping that (i) strongly affects the shape of the distribution of log-fluctuation amplitudes and the kurtosis of the distribution of fluctuation amplitudes. In addition, stochastic heating is (ii) much more efficient if one accounts for intermittency and (iii) even more concentrated near coherent structures than heating by linear Landau damping. Our results suggest that, once intermittency is incorporated, stochastic heating may be an important damping mechanism for solar-wind turbulence, and perhaps also for some regimes of interstellar turbulence, even when
![]() $\unicode[STIX]{x1D709}\sim \unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}\text{rms}}/v_{\text{th}}\ll 1$
(in which case one would be justified in ignoring stochastic heating if the turbulence were not intermittent).
$\unicode[STIX]{x1D709}\sim \unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}\text{rms}}/v_{\text{th}}\ll 1$
(in which case one would be justified in ignoring stochastic heating if the turbulence were not intermittent).
Our results can be easily extended to other dissipation mechanisms, which may be divided into different classes based on the (in)dependence of
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
on
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
on
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
. This will allow us to quantitatively distinguish between different dissipation mechanisms in observations and simulations of collisionless plasma turbulence. We predict that a nonlinear heating mechanism (for which
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
. This will allow us to quantitatively distinguish between different dissipation mechanisms in observations and simulations of collisionless plasma turbulence. We predict that a nonlinear heating mechanism (for which
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
is an increasing function of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D706}}$
is an increasing function of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
) decreases the scale-dependent kurtosis just below the dissipation scale. This leads to a simple observational test to establish the presence of a nonlinear mechanism. Indeed, there are numerous observations of decreases in or flattening of the scale-dependent kurtosis at around the ion scale in both numerical and solar-wind turbulence (Sundkvist et al.
Reference Sundkvist, Retinò, Vaivads and Bale2007; Alexandrova et al.
Reference Alexandrova, Carbone, Veltri and Sorriso- Valvo2008; Wan et al.
Reference Wan, Osman, Matthaeus and Oughton2012; Wu et al.
Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013; Leonardis et al.
Reference Leonardis, Sorriso-Valvo, Valentini, Servidio, Carbone and Veltri2016); our model provides a natural explanation for this phenomenon (however, we cannot explain why the scale-dependent kurtosis remains rather constant in the range of scales between the ion and electron gyroradii, as in the results of Wu et al. (Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013) and Chen et al. (Reference Chen, Sorriso-Valvo, Šafránková and Němeček2014)). Moreover, there is direct evidence for a nonlinear ion heating mechanism, whose efficiency depends on
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D706}}$
) decreases the scale-dependent kurtosis just below the dissipation scale. This leads to a simple observational test to establish the presence of a nonlinear mechanism. Indeed, there are numerous observations of decreases in or flattening of the scale-dependent kurtosis at around the ion scale in both numerical and solar-wind turbulence (Sundkvist et al.
Reference Sundkvist, Retinò, Vaivads and Bale2007; Alexandrova et al.
Reference Alexandrova, Carbone, Veltri and Sorriso- Valvo2008; Wan et al.
Reference Wan, Osman, Matthaeus and Oughton2012; Wu et al.
Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013; Leonardis et al.
Reference Leonardis, Sorriso-Valvo, Valentini, Servidio, Carbone and Veltri2016); our model provides a natural explanation for this phenomenon (however, we cannot explain why the scale-dependent kurtosis remains rather constant in the range of scales between the ion and electron gyroradii, as in the results of Wu et al. (Reference Wu, Perri, Osman, Wan, Matthaeus, Shay, Goldstein, Karimabadi and Chapman2013) and Chen et al. (Reference Chen, Sorriso-Valvo, Šafránková and Němeček2014)). Moreover, there is direct evidence for a nonlinear ion heating mechanism, whose efficiency depends on
![]() $\unicode[STIX]{x1D709}$
(suggestive of stochastic heating, cf. (5.2)), in some numerical simulations (Matthaeus et al.
Reference Matthaeus, Parashar, Wan and Wu2016; Grošelj et al.
Reference Grošelj, Cerri, Bañón Navarro, Willmott, Told, Loureiro, Califano and Jenko2017; Shay et al.
Reference Shay, Haggerty, Matthaeus, Parashar, Wan and Wu2018), while electron heating appears to have
$\unicode[STIX]{x1D709}$
(suggestive of stochastic heating, cf. (5.2)), in some numerical simulations (Matthaeus et al.
Reference Matthaeus, Parashar, Wan and Wu2016; Grošelj et al.
Reference Grošelj, Cerri, Bañón Navarro, Willmott, Told, Loureiro, Califano and Jenko2017; Shay et al.
Reference Shay, Haggerty, Matthaeus, Parashar, Wan and Wu2018), while electron heating appears to have
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
independent of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D70F}_{\text{c}\unicode[STIX]{x1D70C}}$
independent of
![]() $\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}$
(suggestive of linear Landau damping; see also Bañón Navarro et al. (Reference Bañón Navarro, Teaca, Told, Groselj, Crandall and Jenko2016) and Chen, Klein & Howes (Reference Chen, Klein and Howes2019)). Our new modelling framework provides a useful way to interpret these simulation results.
$\unicode[STIX]{x1D6FF}z_{\unicode[STIX]{x1D70C}}$
(suggestive of linear Landau damping; see also Bañón Navarro et al. (Reference Bañón Navarro, Teaca, Told, Groselj, Crandall and Jenko2016) and Chen, Klein & Howes (Reference Chen, Klein and Howes2019)). Our new modelling framework provides a useful way to interpret these simulation results.
Our results clarify the role of intermittency in heating by collisionless plasma turbulence: since heating rates for nonlinear mechanisms (e.g. stochastic heating) are dramatically enhanced by intermittency, an understanding of the intermittency is essential for determining relative heating rates of different mechanisms, and thus for explaining the eventual thermodynamic state of a turbulent collisionless plasma.
Acknowledgements
We thank A. A. Schekochihin and R. Meyrand for useful discussions. A.M. was supported by NSF grant AGS-1624501. K.G.K. was supported by NASA grant NNX16AM23G. C.S.S. was supported by NASA grant NNX16AI59G and NSF SHINE 1622498. Work at Berkeley is also supported by NASA grants NNX14AJ70G and NNX16AP95G. B.D.G. Chandran was supported by NASA grants NNX15AI80, NNX16AG81G, NNN06AA01C and NNX17AI18G, and NSF grant PHY-1500041.