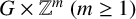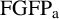A NOTE ON THE FINITELY GENERATED FIXED SUBGROUP PROPERTY

Abstract

We investigate when a group of the form $G\times \mathbb {Z}^m\ (m\geq 1)$ has the finitely generated fixed subgroup property of automorphisms ($\mathrm {FGFP_a}$), by using the BNS-invariant, and provide some partial answers and nontrivial examples.

1 Introduction

For a group G, the rank of G, denoted $\mathrm {rk}(G)$ , is the minimal number of generators of G and $\mathrm {Aut}(G)$ denotes the group of all automorphisms of G. For an endomorphism $\phi $ of G, the fixed subgroup of $\phi $ is

$$ \begin{align*}\mathrm{Fix}\phi :=\{g\in G \mid \phi(g)=g\}.\end{align*} $$

The study of fixed subgroups goes back to Dyer and Scott in 1975. In [7], they proved that for a finite order automorphism $\phi $ of a free group $F_n$ of rank n, the rank of $\mathrm {Fix}\phi $ is not greater than n. Moreover, Scott conjectured that $\mathrm {rk}(\mathrm {Fix}\phi )\leq n$ for any $\phi \in \mathrm {Aut}(F_n)$ . Scott’s conjecture was resolved by Bestvina and Handel [2] in 1988, and extended to all endomorphisms by Imrich and Turner [11] almost simultaneously. For every endomorphism $\phi $ of a surface group G (that is, the fundamental group of a closed surface), the same bound $\mathrm {rk}(\mathrm {Fix}\phi )\leq \mathrm {rk}(G)$ also holds [13]. The study of fixed subgroups of various groups and related topics, such as the Nielsen fixed point theory, has produced many interesting results (see [6, 12, 23, 29–31]).

More generally, we say that a group G has the finitely generated fixed subgroup property of automorphisms ( $\mathrm {FGFP_a}$ ), if the fixed subgroup $\mathrm {Fix}\phi $ is finitely generated for every automorphism $\phi \in \mathrm {Aut}(G)$ . Note that if a group G has $\mathrm {FGFP_a}$ , it must itself be finitely generated. In addition to free groups and surface groups mentioned above, many types of groups had been proven to have $\mathrm {FGFP_a}$ , such as Gromov hyperbolic groups [20, 21, 24] and limit groups [18]. The $\mathrm {FGFP_a}$ property is preserved under taking free products [15], but not under taking direct products [28]. For example, the free group $F_2$ and $\mathbb Z$ both have $\mathrm {FGFP_a}$ , but their direct product $F_2\times \mathbb Z$ does not.

Example 1.1. Let $\phi $ be the automorphism of $F_2\times \mathbb Z=\langle a, b\rangle \times \langle t \rangle $ defined by $\phi (a)=at$ , $\phi (b)=b$ and $\phi (t)=t$ . An element u is in $\mathrm {Fix}\phi $ if and only if the total a exponent in u is zero. Then the fixed subgroup $\mathrm {Fix}\phi \cong F_{\aleph _{0}}\times \mathbb Z$ is not finitely generated (it is generated by the set $\{ t, a^iba^{-i}\mid i\in \mathbb Z\}$ ).

In this note, we will investigate the following question.

Question 1.2. For a group G, when does $G\times \mathbb {Z}^m\ (m\geq 1)$ have $\mathrm {FGFP_a}$ ?

We provide some partial answers (see Theorems 3.1, 3.7 and 3.11) by using the BNS-invariant.

2 Preliminaries

2.1 BNS-invariant

The BNS-invariant, introduced in 1987 by Bieri et al. [3], is a geometric invariant of finitely generated groups inspired by the work of Thurston [27]. It determines whether the kernel of a homomorphism from a group to an abelian group is finitely generated or not. Generally, the BNS-invariant is hard to compute. It was described for some families of groups like RAAGs [17], limit groups [14] and some other groups. Bieri and Renz [4] introduced the higher dimension BNS-invariant to get more information on the kernel.

Definition 2.1. Let G be a finitely generated group with a finite generating set $X\subset G$ , $n=\mathrm {rk}(H^1(G; \mathbb Z))$ the torsion-free rank of the abelianisation of G, and $S(G)=(\mathrm {Hom}(G,\mathbb {R})-{0})/\mathbb {R}_{+}$ the character sphere which is an $(n-1)$ -sphere. Note that an element of $S(G)$ is an equivalence class $[\chi ]=\{r\chi \mid r\in \mathbb {R}_+\}$ . Denote by $\Gamma =\Gamma (G,X)$ the Cayley graph of G with respect to X. The first $\Sigma $ -invariant (or $BNS$ -invariant) of G is

$$ \begin{align*}\Sigma^1(G):=\{[\chi]\in S(G) \mid \Gamma_{\chi} ~\text{is ~connected}\},\end{align*} $$

where $\Gamma _{\chi }$ is the subgraph of $\Gamma $ whose vertices are the elements $g\in G$ with $\chi (g)\geq 0$ and whose edges are the edges of $\Gamma $ which connect two such vertices.

A nontrivial homomorphism $\chi : G \to \mathbb R$ with discrete (and hence infinite cyclic) image is said to be a discrete or rank one homomorphism. It represents a rational point of $S(G)$ . The set of rational points,

$$ \begin{align*}S\mathbb Q(G):=\{[\chi] \in S(G) \mid \chi ~\text{is ~discrete}\},\end{align*} $$

is dense in $S(G$ ).

For later use, we present the main results of the paper [3].

Theorem 2.2 (Bieri, Neumann and Strebel).

Let G be a finitely generated group.

1. (1) Let N be a normal subgroup of G with $G/N$ abelian. Then N is finitely generated if and only if $S(G, N):=\{[\chi ]\in S(G) \mid \chi (N)=0\}\subset \Sigma ^1(G)$ . In particular, $\Sigma ^1(G)=S(G)$ if and only if the derived subgroup $[G,G]$ is finitely generated.

2. (2) Let $\phi : G \rightarrow \mathbb {Z}$ be a nontrivial homomorphism. Then $\ker \phi $ is finitely generated if and only if $\{\phi , -\phi \} \subset \Sigma ^1(G)$ . In particular, $S\mathbb Q(G)\subset \Sigma ^1(G)$ if and only if $\ker \phi $ is finitely generated for every homomorphism $\phi : G \rightarrow \mathbb {Z}$ .

2.2 Automorphism

A centreless group G is one in which the centre $C(G)$ is trivial.

Proposition 2.3. If G is a centreless group, then every automorphism $\phi : G\times \mathbb Z^m\rightarrow G\times \mathbb Z^m\ (m\geq 1)$ has the form:

$$ \begin{align*} \phi(g,v)=(\psi(g), \alpha(g)+\mathcal Lv), \quad (g, v)\in G\times \mathbb Z^m, \end{align*} $$

where $\psi :G\rightarrow G$ and $\mathcal L: \mathbb Z^m\to \mathbb Z^m$ are automorphisms and $\alpha :G\rightarrow \mathbb Z^m$ is a homomorphism.

Proof. Since G is a centreless group, the centre

$$ \begin{align*}C(G\times \mathbb Z^m)=C(G)\times C(\mathbb Z^m)=1\times \mathbb Z^m.\end{align*} $$

Note that an automorphism preserves the centre, so $\phi (1\times \mathbb Z^m)=1\times \mathbb Z^m$ and $\phi (1,v)=(1, \mathcal {L}v)$ for $\mathcal {L}$ an invertible matrix. Therefore, we can suppose

$$ \begin{align*} \phi(g,v)=(\psi(g), \alpha(g)+\mathcal Lv), \quad(g, v)\in G\times \mathbb Z^m. \end{align*} $$

The endomorphism $\psi :G\rightarrow G$ is clearly surjective, so it remains to show that it is also injective. Indeed, for any $g\in \ker \psi $ ,

$$ \begin{align*}\phi(g,0)=(1, \alpha(g))\in 1\times \mathbb Z^m=C(G\times \mathbb Z^m).\end{align*} $$

Now $(g,0)\in 1 \times \mathbb Z^m$ implies $g=1$ and hence $\psi :G\rightarrow G$ is an automorphism.

3 Main results

In this section, we study the necessary and sufficient conditions for Question 1.2 to have a positive answer.

3.1 Necessary condition

Theorem 3.1. For a group G:

1. (1) if $G\times \mathbb {Z}$ has $\mathrm {FGFP_a}$ , then G has $\mathrm {FGFP_a}$ and $S\mathbb Q(G)\subset \Sigma ^1(G)$ , or equivalently, every homomorphism $\alpha : G\to \mathbb Z$ has finitely generated kernel;

2. (2) if $G\times \mathbb {Z}^m$ has $\mathrm {FGFP_a}$ for some $m\geq \mathrm {rk}(H^1(G;\mathbb Z))$ , then $G\times \mathbb {Z}^n$ has $\mathrm {FGFP_a}$ for every n with $0\leq n\leq m$ , and $\Sigma ^1(G)=S(G)$ , or equivalently, its derived subgroup $[G,G]$ is finitely generated.

Proof. (1) First, we assume that G does not have $\mathrm {FGFP_a}$ , that is, there is an automorphism $\psi $ of G, such that $\mathrm {Fix}\psi $ is not finitely generated. Consider the automorphism $\phi :G\times \mathbb Z \to G\times \mathbb Z$ given by

$$ \begin{align*}\phi(g, n)=(\psi(g), n).\end{align*} $$

Its fixed subgroup, $\mathrm {Fix}\phi =\mathrm {Fix}\psi \times \mathbb Z$ , is not finitely generated, contradicting the hypothesis that $G\times \mathbb Z$ has $\mathrm {FGFP_a}$ .

Now we assume $S\mathbb Q(G)\not \subset \Sigma ^1(G)$ , or equivalently by Theorem 2.2, there is a nontrivial homomorphism $\alpha : G\to \mathbb Z$ such that $\ker \alpha $ is not finitely generated. Let $\phi :G\times \mathbb Z \to G\times \mathbb Z$ be given by

$$ \begin{align*}\phi(g,n)=(g, ~\alpha(g)+n).\end{align*} $$

Then $\phi $ is an automorphism whose inverse is $\phi ^{-1}(g,n)=(g, n-\alpha (g))$ . It is easy to see that $\mathrm {Fix}\phi =\ker \alpha \times \mathbb {Z}$ is not finitely generated, also contradicting the hypothesis that $G\times \mathbb Z$ has $\mathrm {FGFP_a}$ .

(2) If $G\times \mathbb {Z}^m$ has $\mathrm {FGFP_a}$ for some $m\geq \mathrm {rk}(H^1(G;\mathbb Z))$ , then $G\times \mathbb {Z}^n$ has $\mathrm {FGFP_a}$ for every n with $0\leq n\leq m$ . This follows directly from proof (1) because $G\times \mathbb Z^m=(G\times \mathbb Z^{m-1})\times \mathbb Z$ .

Now we assume that $[G,G]$ is not finitely generated. Then Theorem 2.2 implies $\Sigma ^1(G)\neq S(G)$ and there is a nontrivial homomorphism $\alpha : G\to \mathbb R$ such that $\ker \alpha $ is not finitely generated. Note that the image of $\alpha $ is an abelian group $\mathbb Z^n$ with $n\leq \mathrm {rk}(H^1(G;\mathbb Z))$ . So $\alpha $ can be viewed as a homomorphism $\alpha : G\to \mathbb Z^n$ , and the automorphism

$$ \begin{align*}\phi:G\times \mathbb Z^n \to G\times \mathbb Z^n, \quad \phi(g,v)=(g, ~\alpha(g)+v),\end{align*} $$

has fixed subgroup $\mathrm {Fix}\phi =\ker \alpha \times \mathbb {Z}^n$ which is not finitely generated, contradicting the hypothesis that $G\times \mathbb Z^n$ has $\mathrm {FGFP_a}$ .

Remark 3.2. Spahn and Zaremsky [26] showed that every kernel of a map from the group $F_{2,3}$ to $\mathbb Z$ is finitely generated, but there exist maps from $F_{2,3}$ to $\mathbb Z^2$ whose kernels are not finitely generated. For the definition of $F_{2,3}$ and more details, see [26].

Example 3.3. Let G be a nonabelian limit group. Then $G\times \mathbb {Z}$ (and hence $G\times \mathbb Z^m\ (m\geq 1)$ ) does not have $\mathrm {FGFP_a}$ . Indeed, Kochloukova [14] proved that the BNS-invariant of a nonabelian limit group is the empty set. Note that the sphere $S(G)$ is not empty, so $S\mathbb Q(G)\not \subset \Sigma ^1(G)$ . By Theorem 3.1, $G\times \mathbb {Z}$ does not have $\mathrm {FGFP_a}$ .

3.2 Sufficient condition

To give sufficient conditions for Question 1.2 to have a positive answer, we need to introduce the Howson and weakly Howson properties.

Definition 3.4. A group G is said to have the Howson property if the intersection $H\cap K$ of any two finitely generated subgroups $H, K<G$ is again finitely generated; G is said to have the weakly Howson property, if in addition, one of H and K is normal in G.

Note that a group with the Howson property necessarily has the weakly Howson property and simple groups clearly have the weakly Howson property. Free groups and surface groups both have the Howson property [10]. More concretely, for a free or surface group G,

$$ \begin{align*}\mathrm{rk}(H\cap K)-1\leq (\mathrm{rk}(H)-1)(\mathrm{rk}(K)-1),\end{align*} $$

which was conjectured by Hanna Neumann in 1957, and proved independently by Friedman [8] and Mineyev [19] in 2011 for free groups and by Antolín and Jaikin-Zapirain [1] in 2022 for surface groups.

Lemma 3.5. (Some basic properties of the weakly Howson property).

1. (1) $F_2\times \mathbb Z$ does not have the weakly Howson property, and hence does not have the Howson property;

2. (2) the Howson property is heritable (that is, if a group has the Howson property, then each subgroup of it does), and hence any group containing a subgroup isomorphic to $F_2\times \mathbb Z$ does not have the Howson property;

3. (3) Thompson’s group V has the weakly Howson property but does not have the Howson property;

4. (4) the weakly Howson property is not heritable.

Proof. (1) Let $F_2\times \mathbb Z=\langle a, b\rangle \times \langle t \rangle $ and let $K=\langle a, bt\rangle $ be a finitely generated subgroup. Then $F_2=\langle a, b\rangle $ is normal in $F_2\times \mathbb Z$ , and $F_2\cap K=\langle b^nab^{-n}\mid n\in \mathbb Z\rangle $ is the normal closure of a in $F_2$ and hence not finitely generated. Therefore, $F_2\times \mathbb Z$ does not have the weakly Howson property (and hence does not have the Howson property).

(2) The Howson property is clearly heritable. So any group with a subgroup isomorphic to $F_2\times \mathbb Z$ does not have the Howson property. For example, the special linear group $\mbox {SL}(n, \mathbb Z) ~( n\geq 4)$ contains a subgroup isomorphic to $F_2\times \mathbb Z$ and does not have the Howson property. Moreover, by the virtually fibred theorem of 3-manifolds, every hyperbolic 3-manifold of finite volume is finitely covered by a surface bundle over the circle. So the fundamental group of every hyperbolic 3-manifold of finite volume does not have the Howson property [25].

(3) Note that Thompson’s group V is a finitely presented infinite simple group, so it has the weakly Howson property. Moreover, Thompson’s group V contains a remarkable variety of subgroups, such as finitely generated free groups, finitely generated abelian groups and Houghton’s groups. The class of subgroups of V is closed under direct products and restricted wreath products with finite or infinite cyclic top group [9]. In particular, V contains $F_2\times \mathbb Z$ as a subgroup and hence V does not have the Howson property.

(4) This clearly follows from item (3).

Lemma 3.6. Let G be a finitely generated group, $H<G$ a finite index subgroup and $K<G$ a finitely generated subgroup. Then $H\cap K$ is finitely generated.

Proof. It is easy to see that $H\cap K$ has finite index in K. Since K is finitely generated, $H\cap K$ is also finitely generated.

Theorem 3.7. Let G be a centreless group with the weakly Howson property. Then:

1. (1) $G\times \mathbb {Z}$ has $\mathrm {FGFP_a}$ if and only if G has $\mathrm {FGFP_a}$ and $S\mathbb Q(G)\subset \Sigma ^1(G)$ , or equivalently, every homomorphism $\alpha : G\to \mathbb Z$ has finitely generated kernel;

2. (2) $G\times \mathbb {Z}^m$ has $\mathrm {FGFP_a}$ for every $m\geq 1$ if and only if G has $\mathrm {FGFP_a}$ and $\Sigma ^1(G)=S(G)$ , or equivalently, the derived subgroup $[G,G]$ is finitely generated.

Proof. The ‘only if’ part clearly follows from Theorem 3.1. For the ‘if’ part, note that G is centreless, so by Proposition 2.3, every automorphism $\phi $ of $G\times \mathbb {Z}^m\ (m\geq 1)$ has the form

$$ \begin{align*}\phi(g,v)=(\psi(g),\alpha(g)+\mathcal{L}v),\end{align*} $$

where $\psi \in \mathrm {Aut}(G)$ , $\alpha \in \mathrm {Hom}(G,\mathbb {Z}^m)$ and $\mathcal {L}\in \mathrm {Aut}(\mathbb Z^m).$ This gives the fixed subgroup

(3.1) $$ \begin{align} \mathrm{Fix}\phi=\{(g, v)\in G\times \mathbb Z^m\mid \psi(g)=g, ~\alpha(g)+\mathcal{L}v=v\}. \end{align} $$

We now prove the ‘if’ part for the two statements in the theorem.

(1) In this case, $m=1$ and $\mathcal {L}=\pm \mathrm {Id}$ . Since G has $\mathrm {FGFP_a}$ and $S\mathbb Q(G)\subset \Sigma ^1(G)$ , $\mathrm {Fix}\psi $ and $\ker \alpha $ are both finitely generated for every homomorphism $\alpha : G\to \mathbb Z$ by Theorem 2.2. When $\mathcal {L}=\mathrm {Id}$ ,

$$ \begin{align*}\mathrm{Fix}\phi=\{(g, n)\mid \psi(g)=g, ~\alpha(g)+n=n\}=(\mathrm{Fix}\psi\cap\ker\alpha)\times\mathbb{Z}\end{align*} $$

and $\mathrm {Fix}\phi $ is finitely generated by the weakly Howson property of G. When $\mathcal {L}=-\mathrm {Id}$ , the fixed subgroup is

$$ \begin{align*} \mathrm{Fix}\phi&=\{(g, n)\mid \psi(g)=g, ~\alpha(g)-n=n\}\nonumber\\ &=\{(g, n)\mid g\in \mathrm{Fix}\psi\cap\alpha^{-1}(2\mathbb{Z}), ~n=\alpha(g)/2\}\nonumber\\ &\cong\mathrm{Fix}\psi\cap \alpha^{-1}(2\mathbb{Z}).\nonumber \end{align*} $$

Actually, the weakly Howson property adds nothing in this case, because $\alpha ^{-1}(2\mathbb {Z})<G$ is a subgroup of index $\leq 2$ and $\mathrm {Fix}\phi $ is finitely generated by Lemma 3.6. In both cases, $G\times \mathbb Z$ has $\mathrm {FGFP_a}$ and item (1) holds.

(2) To prove $ G\times \mathbb Z^m$ has $\mathrm {FGFP_a}$ for every $m\geq 1$ , let us consider the projection

$$ \begin{align*}p: G\times \mathbb Z^m\to G, \quad p(g, v)=g.\end{align*} $$

Then, by (3.1), we have the natural short exact sequence

$$ \begin{align*}0\to \mathrm{Fix}\phi\cap\ker p\hookrightarrow\mathrm{Fix}\phi \xrightarrow{p} p(\mathrm{Fix}\phi)\to 1,\end{align*} $$

where

$$ \begin{align*}\mathrm{Fix}\phi\cap\ker p=\{(1, v)\in G\times \mathbb Z^m\mid \mathcal{L}v=v\}\cong \mathbb Z^s\end{align*} $$

for some $s\leq m$ , and

(3.2) $$ \begin{align} p(\mathrm{Fix}\phi)=\{g\in \mathrm{Fix}\psi \mid \mbox{there is } v=\alpha(g)+\mathcal{L}v\in \mathbb Z^m \} =\mathrm{Fix}\psi\cap\alpha^{-1}((\mathrm{Id}-\mathcal{L})\mathbb{Z}^m) \end{align} $$

is a normal subgroup of $\mathrm {Fix}\psi $ .

By the above exact sequence, to prove that $\mathrm {Fix}\phi $ is finitely generated, it suffices to prove that $p(\mathrm {Fix}\phi )$ is finitely generated. Indeed, note that $\Sigma ^1(G)=S(G)$ , and $G/\alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$ is a quotient of $\alpha (G)$ and hence abelian. So by Theorem 2.2, $\alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$ is a finitely generated normal subgroup of G. Moreover, since G has $\mathrm {FGFP_a}$ , both G and $\mathrm {Fix}\psi $ are finitely generated. By the weakly Howson property of G, $p(\mathrm {Fix}\phi )$ is again finitely generated.

Therefore, $\mathrm {Fix}\phi $ is finitely generated and hence $G\times \mathbb {Z}^m\ (m\geq 1)$ has $\mathrm {FGFP_a}$ .

For an arbitrary group G, it seems too difficult to guarantee that G has both the (weakly) Howson and $\mathrm {FGFP_a}$ properties and that $[G, G]$ is finitely generated, unless G is slender, that is, every subgroup of G is finitely generated. For example, all finite groups and all finitely generated nilpotent groups are slender. Note that nilpotent groups have nontrivial centres.

Hyperbolic groups have $\mathrm {FGFP_a}$ and nonelementary hyperbolic groups are centreless. However, for a hyperbolic group G, we do not necessarily have the Howson property and $[G,G]$ finitely generated. For example, every nonsolvable surface group is hyperbolic and has the Howson property, but its derived subgroup is not finitely generated.

Every finitely generated nonabelian simple group G (for example, Thompson’s group V) is centreless, with $[G, G]$ finitely generated and satisfies the weakly Howson property, but currently, little is known about the fixed subgroups.

Question 3.8. Is there a centreless, infinite group G with $[G, G]$ finitely generated and satisfying the (weakly) Howson and $\mathrm {FGFP_a}$ properties?

3.3 Nontrivial example

For a hyperbolic 3-manifold M, Soma [25] showed that the fundamental group $\pi _1(M)$ has the Howson property if and only if M has infinite volume. Although the fundamental group $G=\pi _1(M)$ of a hyperbolic 3-manifold M with infinite volume has the Howson property, it never has a finitely generated derived subgroup $[G, G]$ unless G is nilpotent. In fact, assume there is a hyperbolic 3-manifold M with infinite volume and with fundamental group having finitely generated derived subgroup $[G, G]$ . Moreover, assume that M is not the solid torus and not homotopic to a closed surface. For such a hyperbolic 3-manifold M, we know one component of $\partial M$ has genus at least two, so the first homology group of M is infinite. Let N be the infinite regular cover of M with fundamental group $\pi _1(N)=[G, G]$ . We may deform the hyperbolic structure on M so that it is geometrically finite and has no cusps. By Thurston’s theorem [5], the hyperbolic structure on N is also geometrically finite. Since $[G, G]$ is a normal subgroup of G, the groups have the same limit set. Let C be the convex hull of the limit set. Then the convex core of N is $C/[G, G]$ and the convex core of M is $C/G$ . Both have nonzero finite volume since N and M are geometrically finite. However, $C/[G, G]$ is an infinite cover of $C/G$ , which is a contradiction.

In the case of M having finite volume, Lin and Wang [16] studied the fixed subgroups of automorphisms of $\pi _1(M)$ and obtained the following result.

Theorem 3.9 [16, Theorem 1.6].

Suppose $G=\pi _1(M)$ , where M is an orientable hyperbolic $3$ -manifold with finite volume and $\phi $ is an automorphism of G. Then $\mathrm {Fix}\phi $ is either the whole group G, or the trivial group 1, or $\mathbb {Z}$ , or $\mathbb {Z}\times \mathbb {Z}$ , or a surface group $\pi _1(S)$ , where S can be orientable or not and closed or not. More precisely:

1. (1) if $\phi $ is induced by an orientation-preserving isometry, then:

   1. (a) $\mathrm {Fix}\phi $ is either $\mathbb {Z}$ or $\mathbb {Z}\times \mathbb {Z}$ or G or 1;

   2. (b) moreover, if M is closed, then $\mathrm {Fix}\phi $ is either $\mathbb {Z}$ or G;

2. (2) if $\phi $ is induced by an orientation-reversing isometry f, then:

   1. (a) if $\phi ^2\neq \mathrm {id}$ , $\mathrm {Fix}\phi $ is either $\mathbb {Z}$ or 1;

   2. (b) if $\phi ^2= \mathrm {id}$ , $\mathrm {Fix}\phi $ is either 1 or the surface group $\pi _1(S)$ , where S is an embedded surface in M that is pointwise fixed by f.

Note that in [16], a 3-manifold M is hyperbolic if M is orientable, compact and the interior of M admits a complete hyperbolic structure of finite volume (so that M is either closed or has a boundary consisting of a union of tori).

Proposition 3.10. Let $G=\pi _1(M)$ for M an orientable hyperbolic $3$ -manifold with finite volume and without an involution. Then for any automorphism $\phi $ of G, the fixed subgroup $\mathrm {Fix}\phi $ is inert in G, that is, $\mathrm {rk}(H\cap \mathrm {Fix}\phi )\leq \mathrm {rk}(H)$ for any finitely generated subgroup $H<G$ .

Proof. Since M has no involution, we have $\phi ^2\neq \mathrm {id}$ for any automorphism $\phi $ of ${G=\pi _1(M)}$ , by Mostow’s rigidity theorem. Then by Theorem 3.9, the fixed subgroup $\mathrm {Fix}\phi $ is either 1, $\mathbb Z$ , $\mathbb {Z}\times \mathbb {Z}$ or the whole group G, and the proposition follows.

To get nontrivial examples, we remove the weakly Howson property from the conditions in Theorem 3.7.

Theorem 3.11. The group $G\times \mathbb {Z}^m$ has $\mathrm {FGFP_a}$ for every $m\geq 1$ if G is one of the following types:

1. (1) a slender group (for example, a finite group or a finitely generated nilpotent group);

2. (2) $G=\pi _1(M)$ where M is a closed orientable hyperbolic 3-manifold with finite first homology group $H_1(M)$ and with the isometry group $\mathrm {Isom}(M)$ of odd order.

Proof. (1) Let G be a slender group, that is, every subgroup of G is finitely generated. Then $G\times \mathbb Z^m$ is again slender, and hence it has $\mathrm {FGFP_a}$ . Indeed, for any subgroup $H<G\times \mathbb Z^m$ , we have a short exact sequence

$$ \begin{align*}1\to H\cap\ker(p)\to H\to p(H)<\mathbb Z^m,\end{align*} $$

where p is the natural projection $G\times \mathbb Z^m\to \mathbb Z^m$ with $\ker (p)=G$ . Then, $H\cap \ker (p)$ is a subgroup of the slender group G and hence it is finitely generated. So H is also finitely generated.

(2) Since M is a closed orientable hyperbolic 3-manifold, $G=\pi _1(M)$ is a centreless, finitely generated Gromov hyperbolic group, and hence, G has $\mathrm {FGFP_a}$ . Moreover, $H_1(M)$ finite implies that the derived subgroup $[G, G]$ is of finite index in the finitely generated group G and hence it is again finitely generated. Note that the weakly Howson property in the proof of Theorem 3.7(2) is only used to ensure that

$$ \begin{align*}\mathrm{Fix}\psi\cap\alpha^{-1}((\mathrm{Id}-\mathcal{L})\mathbb{Z}^m)\end{align*} $$

in (3.2) is finitely generated. However, now, since $\mathrm {Isom}(M)$ is of odd order, M has no involution. By Proposition 3.10, the fixed subgroup $\mathrm {Fix}\psi $ is inert in G for every automorphism $\psi :G\to G$ . So

$$ \begin{align*}\mathrm{rk}(\mathrm{Fix}\psi\cap\alpha^{-1}((\mathrm{Id}-\mathcal{L})\mathbb{Z}^m))\leq\mathrm{rk}(\alpha^{-1}((\mathrm{Id}-\mathcal{L})\mathbb{Z}^m))<\infty,\end{align*} $$

that is, $\mathrm {Fix}\psi \cap \alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$ is finitely generated.

In conclusion, we can show that $G\times \mathbb {Z}^m$ has $\mathrm {FGFP_a}$ , by the same argument as in the proof of Theorem 3.7(2), without using the weakly Howson property.

There are many closed hyperbolic 3-manifolds such that their fundamental groups satisfy condition (2) of Theorem 3.11.

Example 3.12. Let M be the 3-manifold $\mathbb {S}^3-9_{32}$ and $M_{p,q}$ be the Dehn filling from M along the slope $p \mathcal {M}+q\mathcal {L}$ . Here, $9_{32}$ is the knot in Rolfsen’s list [22], and $(\mathcal {M},\mathcal {L})$ is the canonical meridian-longitude system of the cusp of M. So $H_{1}(M)= \mathbb {Z}_{p}$ . From Snappy, we know that $\mathbb {S}^3-9_{32}$ is hyperbolic with trivial isometry group. When p, q are large enough, $M_{p,q}$ is a closed hyperbolic 3-manifold by Thurston’s hyperbolic Dehn surgery theorem. The proof of Thurston’s hyperbolic Dehn surgery theorem also implies the Dehn filling has a very short geodesic core when p, q are large. So any isometry of $M_{p,q}$ will preserve the core of the Dehn filling, and hence will preserve M, that is, it will be isotopic to the identity. In summary, when p, q are large enough, $M_{p,q}$ is a closed hyperbolic 3-manifold with trivial isometry group and finite first homology group. So its fundamental group satisfies condition (2) of Theorem 3.11.

Finally, inspired by Theorem 3.11, we may wonder whether the assumption ‘centreless and with the weakly Howson property’ in Theorem 3.7 can be removed or not.

Question 3.13. Does $G\times \mathbb Z$ have $\mathrm {FGFP_a}$ if the group G has $\mathrm {FGFP_a}$ and the derived subgroup $[G, G]$ is finitely generated?