We introduce a tool for analysing models of $\text {CT}^-$ , the compositional truth theory over Peano Arithmetic. We present a new proof of Lachlan’s theorem that the arithmetical part of models of $\text {CT}^-$ are recursively saturated. We also use this tool to provide a new proof of theorem from [8] that all models of $\text {CT}^-$ carry a partial inductive truth predicate. Finally, we construct a partial truth predicate defined for a set of formulae whose syntactic depth forms a nonstandard cut which cannot be extended to a full truth predicate satisfying $\text {CT}^-$ .

A set of reals is universally Baire if all of its continuous preimages in topological spaces have the Baire property. ${\sf Sealing}$ is a type of generic absoluteness condition introduced by Woodin that asserts in strong terms that the theory of the universally Baire sets cannot be changed by set forcings. The ${\sf Largest\ Suslin\ Axiom}$ ( ${\sf LSA}$ ) is a determinacy axiom isolated by Woodin. It asserts that the largest Suslin cardinal is inaccessible for ordinal definable surjections. Let ${\sf LSA}$ - ${\sf over}$ - ${\sf uB}$ be the statement that in all (set) generic extensions there is a model of $\sf {LSA}$ whose Suslin, co-Suslin sets are the universally Baire sets. 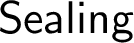We outline the proof that over some mild large cardinal theory, $\sf {Sealing}$ is equiconsistent with $\sf {LSA}$ - $\sf {over}$ - $\sf {uB}$ . In fact, we isolate an exact theory (in the hierarchy of strategy mice) that is equiconsistent with both (see Definition 3.1). 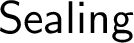As a consequence, we obtain that $\sf {Sealing}$ is weaker than the theory “ $\sf {ZFC}$ + there is a Woodin cardinal which is a limit of Woodin cardinals.” This significantly improves upon the earlier consistency proof of 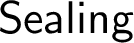$\sf {Sealing}$ by Woodin. A variation of $\sf {Sealing}$ , called 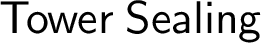$\sf {Tower \ Sealing}$ , is also shown to be equiconsistent with $\sf {Sealing}$ over the same large cardinal theory. We also outline the proof that if V has a proper class of Woodin cardinals, a strong cardinal, and a generically universally Baire iteration strategy, then $\sf {Sealing}$ holds after collapsing the successor of the least strong cardinal to be countable. 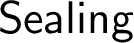This result is complementary to the aforementioned equiconsistency result, where it is shown that $\sf {Sealing}$ holds in a generic extension of a certain minimal universe. This theorem is more general in that no minimal assumption is needed. A corollary of this is that $\sf {LSA}$ - $\sf {over}$ - $\sf {uB}$ is not equivalent to $\sf {Sealing}$ .

This paper presents hitherto unpublished writings of Kurt Gödel concerning logical, epistemological, theological, and physical antinomies, which he generally considered as “the most interesting facts in modern logic,” and which he used as a basis for his famous metamathematical results. After investigating different perspectives on the notion of the logical structure of the antinomies and presenting two “antinomies of the intensional,” a new kind of paradox closely related to Gödel’s ontological proof for the existence of God is introduced and completed by a compilation of further theological antinomies. Finally, after a presentation of unpublished general philosophical remarks concerning the antinomies, Gödel’s type-theoretic variant of Leibniz’ Monadology, discovered in his notes on the foundations of quantum mechanics, is examined. Most of the material presented here has been transcribed from the Gabelsberger shorthand system for the first time.