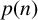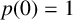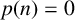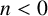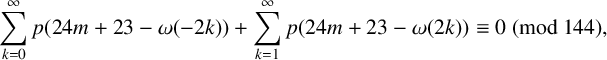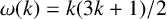1 Introduction
A partition
![]() $\lambda =(\lambda _1, \lambda _2, \ldots , \lambda _k)$
of a positive integer n is a nonincreasing sequence of positive integers that sum to n, that is,
$\lambda =(\lambda _1, \lambda _2, \ldots , \lambda _k)$
of a positive integer n is a nonincreasing sequence of positive integers that sum to n, that is,
![]() $\lambda _1+\lambda _2+\cdots +\lambda _k=n$
. The numbers
$\lambda _1+\lambda _2+\cdots +\lambda _k=n$
. The numbers
![]() $\lambda _j$
are known as the parts of
$\lambda _j$
are known as the parts of
![]() $\lambda $
. The partition function
$\lambda $
. The partition function
![]() $p(n)$
enumerates the partitions of n. For example,
$p(n)$
enumerates the partitions of n. For example,
![]() $p(4)=5$
, since there are 5 partitions of 4, namely,
$p(4)=5$
, since there are 5 partitions of 4, namely,
By convention, we take
![]() $p(0)=1$
and
$p(0)=1$
and
![]() $p(n)=0$
if n is not a nonnegative integer.
$p(n)=0$
if n is not a nonnegative integer.
The generating function of
![]() $p(n)$
, found by Euler, is given by
$p(n)$
, found by Euler, is given by
 $$ \begin{align} \sum_{n=0}^\infty p(n)q^n= \dfrac{1}{(q;q)_\infty} \end{align} $$
$$ \begin{align} \sum_{n=0}^\infty p(n)q^n= \dfrac{1}{(q;q)_\infty} \end{align} $$
(see [Reference Andrews3]), where for complex numbers a and q with
![]() $|q|<1$
, the standard q-product
$|q|<1$
, the standard q-product
![]() $(a;q)_\infty $
is defined by
$(a;q)_\infty $
is defined by
 $$ \begin{align*} (a;q)_\infty:=\prod_{j=0}^{\infty}(1-a q^j). \end{align*} $$
$$ \begin{align*} (a;q)_\infty:=\prod_{j=0}^{\infty}(1-a q^j). \end{align*} $$
Work on the arithmetic properties of
![]() $p(n)$
started when Ramanujan [Reference Ramanujan20], [Reference Ramanujan21, pages 210–213] discovered his famous congruences for
$p(n)$
started when Ramanujan [Reference Ramanujan20], [Reference Ramanujan21, pages 210–213] discovered his famous congruences for
![]() $p(n)$
: for every nonnegative integer n,
$p(n)$
: for every nonnegative integer n,
 $$ \begin{align*} p(5n + 4) &\equiv 0~ (\text{mod}~ 5),\\ p(7n + 5) &\equiv 0~ (\text{mod}~ 7),\\ p(11n + 6) &\equiv 0~ (\text{mod}~ 11). \end{align*} $$
$$ \begin{align*} p(5n + 4) &\equiv 0~ (\text{mod}~ 5),\\ p(7n + 5) &\equiv 0~ (\text{mod}~ 7),\\ p(11n + 6) &\equiv 0~ (\text{mod}~ 11). \end{align*} $$
Since then, these congruences have been studied and generalised extensively in many directions. Ono [Reference Ono18] proved that for every prime
![]() $M \geq 5$
there exist infinitely many nonnested arithmetic progressions
$M \geq 5$
there exist infinitely many nonnested arithmetic progressions
![]() $An+B$
such that
$An+B$
such that
Ahlgren [Reference Ahlgren1] extended this result for arbitrary integers M with
![]() $\text {gcd}(6,M)=1$
. However, for the primes
$\text {gcd}(6,M)=1$
. However, for the primes
![]() $2$
and
$2$
and
![]() $3$
, we have different results on the divisibility of the partition function. Subbarao [Reference Subbarao24] conjectured that every arithmetic progression contains infinitely many integers n for which
$3$
, we have different results on the divisibility of the partition function. Subbarao [Reference Subbarao24] conjectured that every arithmetic progression contains infinitely many integers n for which
![]() $p(n)$
is odd as well as infinitely many integers m for which
$p(n)$
is odd as well as infinitely many integers m for which
![]() $p(m)$
is even. The conjecture has been settled by Ono [Reference Ono17] and Radu [Reference Radu19]. Suppose that A and B are integers with
$p(m)$
is even. The conjecture has been settled by Ono [Reference Ono17] and Radu [Reference Radu19]. Suppose that A and B are integers with
![]() $A>B\geq 0$
. If
$A>B\geq 0$
. If
![]() $\nu =2$
or
$\nu =2$
or
![]() $3$
, then Radu [Reference Radu19] proved that there are infinitely many integers n such that
$3$
, then Radu [Reference Radu19] proved that there are infinitely many integers n such that
Recently, Ballantine and Merca [Reference Ballantine and Merca5] explored the parity of sums of partition numbers at certain places in arithmetic progressions. In particular, they proved that if
then
 $$ \begin{align*} \sum_{ak+1\,\text{square}} p(n-k) \equiv 1~ (\text{mod}~2) \quad\text{if~and~only~if}\ bn + 1 ~\text{is~a~square} \end{align*} $$
$$ \begin{align*} \sum_{ak+1\,\text{square}} p(n-k) \equiv 1~ (\text{mod}~2) \quad\text{if~and~only~if}\ bn + 1 ~\text{is~a~square} \end{align*} $$
(see [Reference Hong and Zhang12, Reference Hu, Yao and Zhao13] for further results of this type).
In this paper, we show that certain sums of partition numbers are divisible by multiples of 2 and 3. Unlike the results of Ballantine and Merca [Reference Ballantine and Merca5], our results do not depend on the squares in arithmetic progressions. To state the main results in the next section, we now recall some more partition functions in the remainder of this section.
An overpartition of a positive integer n is a nonincreasing sequence of positive integers that sum to n, where the first occurrence of parts of each size may be overlined (see [Reference Corteel and Lovejoy10]). The overpartition function
![]() $\overline {p}(n)$
counts the overpartitions of n. For example,
$\overline {p}(n)$
counts the overpartitions of n. For example,
![]() $\overline {p}(4)=14$
and the overpartitions of
$\overline {p}(4)=14$
and the overpartitions of
![]() $4$
are
$4$
are
 $$ \begin{align*}& \quad 4, \ \overline{4}, \ 3+1, \ \overline{3}+1, \ 3+\overline{1}, \ \overline{3}+\overline{1}, \ 2+2, \ \overline{2}+2, \ 2+1+1, \notag\\& \overline{2}+1+1, \ 2+\overline{1}+1, \ \overline{2}+\overline{1}+1, \ 1+1+1+1, \ \overline{1}+1+1+1. \end{align*} $$
$$ \begin{align*}& \quad 4, \ \overline{4}, \ 3+1, \ \overline{3}+1, \ 3+\overline{1}, \ \overline{3}+\overline{1}, \ 2+2, \ \overline{2}+2, \ 2+1+1, \notag\\& \overline{2}+1+1, \ 2+\overline{1}+1, \ \overline{2}+\overline{1}+1, \ 1+1+1+1, \ \overline{1}+1+1+1. \end{align*} $$
Since the overlined parts form a partition into unequal parts and the nonoverlined parts form an ordinary partition, the generating function of
![]() $\overline {p}(n)$
, as noted by Corteel and Lovejoy [Reference Corteel and Lovejoy10], is given by
$\overline {p}(n)$
, as noted by Corteel and Lovejoy [Reference Corteel and Lovejoy10], is given by
 $$ \begin{align} \sum_{n=0}^\infty \overline{p}(n)q^n= \dfrac{(-q;q)_\infty}{(q;q)_\infty}. \end{align} $$
$$ \begin{align} \sum_{n=0}^\infty \overline{p}(n)q^n= \dfrac{(-q;q)_\infty}{(q;q)_\infty}. \end{align} $$
In 2003, Lovejoy [Reference Lovejoy15] considered the function
![]() $\overline {A}_\ell (n)$
, known as the
$\overline {A}_\ell (n)$
, known as the
![]() $\ell $
-regular overpartition function [Reference Shen22], that enumerates the overpartitions of n, which have no parts being a multiple of
$\ell $
-regular overpartition function [Reference Shen22], that enumerates the overpartitions of n, which have no parts being a multiple of
![]() $\ell $
. For example,
$\ell $
. For example,
![]() $\overline {A}_3(4)=10$
and the 3-regular overpartitions of
$\overline {A}_3(4)=10$
and the 3-regular overpartitions of
![]() $4$
are given by
$4$
are given by
 $$ \begin{align*} &4,\ \overline{4}, \ 2+2, \ \overline{2}+2, \ 2+1+1, \ \overline{2}+1+1, \ 2+\overline{1}+1, \notag\\& \qquad \overline{2}+\overline{1}+1, \ 1+1+1+1, \ \overline{1}+1+1+1. \end{align*} $$
$$ \begin{align*} &4,\ \overline{4}, \ 2+2, \ \overline{2}+2, \ 2+1+1, \ \overline{2}+1+1, \ 2+\overline{1}+1, \notag\\& \qquad \overline{2}+\overline{1}+1, \ 1+1+1+1, \ \overline{1}+1+1+1. \end{align*} $$
Andrews [Reference Andrews4] extended the idea of
![]() $\ell $
-regular overpartitions by considering the enumeration
$\ell $
-regular overpartitions by considering the enumeration
![]() $\overline {C}_{k,i}(n)$
of so-called singular overpartitions of n that correspond to
$\overline {C}_{k,i}(n)$
of so-called singular overpartitions of n that correspond to
![]() $\ell $
-regular overpartitions of n in which only parts
$\ell $
-regular overpartitions of n in which only parts
![]() $\equiv \pm i~(\text {mod}~k)$
may be overlined. Clearly,
$\equiv \pm i~(\text {mod}~k)$
may be overlined. Clearly,
![]() $\overline {A}_3(n)=\overline {C}_{3,1}(n)$
for all
$\overline {A}_3(n)=\overline {C}_{3,1}(n)$
for all
![]() $n\geq 1$
.
$n\geq 1$
.
Since the multiples of
![]() $\ell $
cannot appear in an
$\ell $
cannot appear in an
![]() $\ell $
-regular overpartition, it follows from (1.2) that the generating function of
$\ell $
-regular overpartition, it follows from (1.2) that the generating function of
![]() $\overline {A}_\ell (n)$
is given by
$\overline {A}_\ell (n)$
is given by
 $$ \begin{align} \sum_{n=0}^\infty \overline{A}_\ell(n)q^n= \dfrac{(-q;q)_\infty/(q;q)_\infty}{(-q^\ell;q^\ell)_\infty/(q^\ell;q^\ell)_\infty}=\dfrac{(-q;q)_\infty(q^\ell;q^\ell)_\infty}{(q;q)_\infty(-q^\ell;q^\ell)_\infty}. \end{align} $$
$$ \begin{align} \sum_{n=0}^\infty \overline{A}_\ell(n)q^n= \dfrac{(-q;q)_\infty/(q;q)_\infty}{(-q^\ell;q^\ell)_\infty/(q^\ell;q^\ell)_\infty}=\dfrac{(-q;q)_\infty(q^\ell;q^\ell)_\infty}{(q;q)_\infty(-q^\ell;q^\ell)_\infty}. \end{align} $$
2 Main results
Euler’s famous recurrence relation for
![]() $p(n)$
is given by
$p(n)$
is given by
 $$ \begin{align} \sum_{k=-\infty}^{\infty}(-1)^kp(n-\omega(k))=\delta_{0,n}, \end{align} $$
$$ \begin{align} \sum_{k=-\infty}^{\infty}(-1)^kp(n-\omega(k))=\delta_{0,n}, \end{align} $$
where
![]() $\omega (k)=k(3k+1)/2$
, for integers k, are the generalised pentagonal numbers and
$\omega (k)=k(3k+1)/2$
, for integers k, are the generalised pentagonal numbers and
![]() $\delta _{i,j}$
is the Kronecker delta. For integers
$\delta _{i,j}$
is the Kronecker delta. For integers
![]() $n\geq 1$
, it easily follows from (2.1) that
$n\geq 1$
, it easily follows from (2.1) that
 $$ \begin{align} &\sum_{k=0}^{\infty}p(n-\omega(-2k)) +\sum_{k=1}^{\infty}p(n-\omega(2k)) \notag \\ &\quad =\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1)). \end{align} $$
$$ \begin{align} &\sum_{k=0}^{\infty}p(n-\omega(-2k)) +\sum_{k=1}^{\infty}p(n-\omega(2k)) \notag \\ &\quad =\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1)). \end{align} $$
In this paper, we show divisibility of the above sums of partition numbers by multiples of 2 and 3. The following main result arises from (2.2) and Jacobi’s triple product identity [Reference Andrews3, page 21, Theorem 2.8].
Theorem 2.1. Let
![]() $\overline {A}_3(n)$
denote the number of 3-regular overpartitions of n, which is also equal to Andrews’ singular overpartition function
$\overline {A}_3(n)$
denote the number of 3-regular overpartitions of n, which is also equal to Andrews’ singular overpartition function
![]() $\overline {C}_{3,1}(n)$
. Then, for all integers
$\overline {C}_{3,1}(n)$
. Then, for all integers
![]() $n\geq 1$
,
$n\geq 1$
,
 $$ \begin{align} &\sum_{k=0}^{\infty}p(n-\omega(-2k)) +\sum_{k=1}^{\infty}p(n-\omega(2k))\notag\\ &\quad=\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1))=\dfrac{\overline{A}_3(n)}{2}. \end{align} $$
$$ \begin{align} &\sum_{k=0}^{\infty}p(n-\omega(-2k)) +\sum_{k=1}^{\infty}p(n-\omega(2k))\notag\\ &\quad=\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1))=\dfrac{\overline{A}_3(n)}{2}. \end{align} $$
There are several recent papers that studied the arithmetical properties of
![]() $\overline {A}_\ell (n)$
and
$\overline {A}_\ell (n)$
and
![]() $\overline {C}_{k,i}(n)$
. For results on
$\overline {C}_{k,i}(n)$
. For results on
![]() $\overline {A}_3(n)$
and
$\overline {A}_3(n)$
and
![]() $\overline {C}_{3,1}(n)$
, see [Reference Ahmed and Baruah2, Reference Andrews4, Reference Barman and Ray6–Reference Chern9, Reference Hao and Shen11, Reference Li and Yao14, Reference Mahadeva Naika and Gireesh16, Reference Shen22, Reference Shen23, Reference Yao26]. Employing Theorem 2.1 and congruences for
$\overline {C}_{3,1}(n)$
, see [Reference Ahmed and Baruah2, Reference Andrews4, Reference Barman and Ray6–Reference Chern9, Reference Hao and Shen11, Reference Li and Yao14, Reference Mahadeva Naika and Gireesh16, Reference Shen22, Reference Shen23, Reference Yao26]. Employing Theorem 2.1 and congruences for
![]() $\overline {A}_3(n)$
, that is, for
$\overline {A}_3(n)$
, that is, for
![]() $\overline {C}_{3,1}(n)$
, one can easily deduce divisibility properties of the sums of the partition numbers in (2.2). For example, Barman and Ray [Reference Barman and Ray7, Theorems 1.1–1.3] proved that for a fixed positive integer k,
$\overline {C}_{3,1}(n)$
, one can easily deduce divisibility properties of the sums of the partition numbers in (2.2). For example, Barman and Ray [Reference Barman and Ray7, Theorems 1.1–1.3] proved that for a fixed positive integer k,
![]() $\overline {C}_{3,1}(n)$
is divisible by
$\overline {C}_{3,1}(n)$
is divisible by
![]() $2^k$
and
$2^k$
and
![]() $2\cdot 3^k$
for almost all n. Therefore, it follows that the above sums of partition numbers are divisible by
$2\cdot 3^k$
for almost all n. Therefore, it follows that the above sums of partition numbers are divisible by
![]() $3^k$
for almost all n. In the following corollary, we present selected congruences for the sums in nondecreasing order of the moduli that arise from the congruences for
$3^k$
for almost all n. In the following corollary, we present selected congruences for the sums in nondecreasing order of the moduli that arise from the congruences for
![]() $\overline {A}_3(n)$
or
$\overline {A}_3(n)$
or
![]() $\overline {C}_{3,1}(n)$
, which either appeared in [Reference Ahmed and Baruah2, Reference Andrews4, Reference Barman and Ray6, Reference Chen, Hirschhorn and Sellers8, Reference Chern9, Reference Hao and Shen11, Reference Li and Yao14, Reference Mahadeva Naika and Gireesh16, Reference Shen22, Reference Shen23, Reference Yao26] or are easily deduced from these results.
$\overline {C}_{3,1}(n)$
, which either appeared in [Reference Ahmed and Baruah2, Reference Andrews4, Reference Barman and Ray6, Reference Chen, Hirschhorn and Sellers8, Reference Chern9, Reference Hao and Shen11, Reference Li and Yao14, Reference Mahadeva Naika and Gireesh16, Reference Shen22, Reference Shen23, Reference Yao26] or are easily deduced from these results.
Corollary 2.2. For brevity, set
 $$ \begin{align*} S(n):&=\sum_{k=0}^{\infty}p(n-\omega(-2k))+\sum_{k=1}^{\infty}p(n-\omega(2k))\notag\\&=\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1)). \end{align*} $$
$$ \begin{align*} S(n):&=\sum_{k=0}^{\infty}p(n-\omega(-2k))+\sum_{k=1}^{\infty}p(n-\omega(2k))\notag\\&=\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1)). \end{align*} $$
For any nonnegative integers k and n,
 $$ \begin{align*} S(3n+2)&\equiv 0~(\mathrm{mod}~2),\\S(4n+2)&\equiv 0~(\mathrm{mod}~2),\\S(2^k(4n+3))&\equiv 0~(\mathrm{mod}~3),\\S(9n+3)&\equiv 0~(\mathrm{mod}~3),\\S(2^{k+1}(6n+5))&\equiv 0~(\mathrm{mod}~4),\\S(4^k(16n+6))&\equiv 0~(\mathrm{mod}~4),\\ S(4^k(16n+10))&\equiv 0~(\mathrm{mod}~4),\\ S(4^k(16n+14))&\equiv 0~(\mathrm{mod}~4),\\ S(8n+7)&\equiv 0~(\mathrm{mod}~6),\\ S(36n+21)&\equiv 0~(\mathrm{mod}~6),\\ S(6n+5)&\equiv 0~(\mathrm{mod}~8),\\ S(4^k(72n+42))&\equiv 0~(\mathrm{mod}~8),\\ S(4^k(144n+78))&\equiv 0~(\mathrm{mod}~8),\\ S(48n+12)&\equiv 0~(\mathrm{mod}~9),\\ S(8n+6)&\equiv 0~(\mathrm{mod}~12),\\ S(9n+6)&\equiv 0~(\mathrm{mod}~12),\\ S(36n+30)&\equiv 0~(\mathrm{mod}~12),\\ S(24n+17)&\equiv 0~(\mathrm{mod}~16),\\ S(4^k(72n+60))&\equiv 0~(\mathrm{mod}~16),\\ S(2^k(12n+7))&\equiv 0~(\mathrm{mod}~18),\\ S(144n+102)&\equiv 0~(\mathrm{mod}~24),\\ S(9^k(48n+28))&\equiv 0~(\mathrm{mod}~27),\\ S(9^k(48n+44))&\equiv 0~(\mathrm{mod}~27),\\ S(72n+51)&\equiv 0~(\mathrm{mod}~32),\\ S(72n+69)&\equiv 0~(\mathrm{mod}~32),\\ S(2^{k+1}(12n+11))&\equiv 0~(\mathrm{mod}~36),\\ S(24n+14)&\equiv 0~(\mathrm{mod}~36),\\ S(18n+15)&\equiv 0~(\mathrm{mod}~48),\\ S(12n+11)&\equiv 0~(\mathrm{mod}~72),\\ S(24n+23)&\equiv 0~(\mathrm{mod}~144). \end{align*} $$
$$ \begin{align*} S(3n+2)&\equiv 0~(\mathrm{mod}~2),\\S(4n+2)&\equiv 0~(\mathrm{mod}~2),\\S(2^k(4n+3))&\equiv 0~(\mathrm{mod}~3),\\S(9n+3)&\equiv 0~(\mathrm{mod}~3),\\S(2^{k+1}(6n+5))&\equiv 0~(\mathrm{mod}~4),\\S(4^k(16n+6))&\equiv 0~(\mathrm{mod}~4),\\ S(4^k(16n+10))&\equiv 0~(\mathrm{mod}~4),\\ S(4^k(16n+14))&\equiv 0~(\mathrm{mod}~4),\\ S(8n+7)&\equiv 0~(\mathrm{mod}~6),\\ S(36n+21)&\equiv 0~(\mathrm{mod}~6),\\ S(6n+5)&\equiv 0~(\mathrm{mod}~8),\\ S(4^k(72n+42))&\equiv 0~(\mathrm{mod}~8),\\ S(4^k(144n+78))&\equiv 0~(\mathrm{mod}~8),\\ S(48n+12)&\equiv 0~(\mathrm{mod}~9),\\ S(8n+6)&\equiv 0~(\mathrm{mod}~12),\\ S(9n+6)&\equiv 0~(\mathrm{mod}~12),\\ S(36n+30)&\equiv 0~(\mathrm{mod}~12),\\ S(24n+17)&\equiv 0~(\mathrm{mod}~16),\\ S(4^k(72n+60))&\equiv 0~(\mathrm{mod}~16),\\ S(2^k(12n+7))&\equiv 0~(\mathrm{mod}~18),\\ S(144n+102)&\equiv 0~(\mathrm{mod}~24),\\ S(9^k(48n+28))&\equiv 0~(\mathrm{mod}~27),\\ S(9^k(48n+44))&\equiv 0~(\mathrm{mod}~27),\\ S(72n+51)&\equiv 0~(\mathrm{mod}~32),\\ S(72n+69)&\equiv 0~(\mathrm{mod}~32),\\ S(2^{k+1}(12n+11))&\equiv 0~(\mathrm{mod}~36),\\ S(24n+14)&\equiv 0~(\mathrm{mod}~36),\\ S(18n+15)&\equiv 0~(\mathrm{mod}~48),\\ S(12n+11)&\equiv 0~(\mathrm{mod}~72),\\ S(24n+23)&\equiv 0~(\mathrm{mod}~144). \end{align*} $$
Note that the last congruence is equivalent to the example stated in the abstract.
The powers of 2 and 3 in the modulus in each of the above congruences are sharp. However, there might be sub-progressions of the given arithmetic progression along which the powers of 2 and 3 in the modulus may be higher. Furthermore, combining two congruences may also give congruences for higher modulus.
There are congruences for
![]() $\overline {A}_3(n)$
or
$\overline {A}_3(n)$
or
![]() $\overline {C}_{3,1}(n)$
that depend on specific properties of the integer n. For example, Li and Yao [Reference Li and Yao14] show that if
$\overline {C}_{3,1}(n)$
that depend on specific properties of the integer n. For example, Li and Yao [Reference Li and Yao14] show that if
![]() $p\equiv 3~(\text {mod}~4)$
and
$p\equiv 3~(\text {mod}~4)$
and
![]() $p\not \mid ~ n$
, then for any
$p\not \mid ~ n$
, then for any
![]() $k\geq 0$
,
$k\geq 0$
,
Noting also that
![]() $\overline {A}_3(n)\equiv 0~(\text {mod}~2)$
for all integers
$\overline {A}_3(n)\equiv 0~(\text {mod}~2)$
for all integers
![]() $n\geq 1$
(see [Reference Chen, Hirschhorn and Sellers8, Theorem 2.9]), it readily follows from (2.4) that
$n\geq 1$
(see [Reference Chen, Hirschhorn and Sellers8, Theorem 2.9]), it readily follows from (2.4) that
There are several other results like (2.4), which can be derived from results in [Reference Chen, Hirschhorn and Sellers8, Reference Chern9, Reference Li and Yao14, Reference Mahadeva Naika and Gireesh16, Reference Shen23, Reference Sumanth Bharadwaj, Hemanthkumar and Mahadeva Naika25, Reference Yao26].
We prove Theorem 2.1 and Corollary 2.2 in the next two sections.
3 Proof of Theorem 2.1
We use Jacobi’s triple product identity and (2.1) to prove Theorem 2.1.
Jacobi’s triple product identity [Reference Andrews3, page 21, Theorem 2.8] can be stated as follows. For
![]() $z\neq 0$
and
$z\neq 0$
and
![]() $|q|<1$
,
$|q|<1$
,
 $$ \begin{align*} \sum_{k=-\infty}^\infty z^kq^{k^2}=(-zq;q^2)_\infty(-q/z;q^2)_\infty(q^2;q^2)_\infty.\end{align*} $$
$$ \begin{align*} \sum_{k=-\infty}^\infty z^kq^{k^2}=(-zq;q^2)_\infty(-q/z;q^2)_\infty(q^2;q^2)_\infty.\end{align*} $$
Replacing q by
![]() $q^{3/2}$
and z by
$q^{3/2}$
and z by
![]() $\sqrt {q}$
and then manipulating the q-products,
$\sqrt {q}$
and then manipulating the q-products,
 $$ \begin{align*} \sum_{k=-\infty}^\infty q^{k(3k+1)/2}&=(-q^2;q^3)_\infty(-q;q^3)_\infty(q^3;q^3)_\infty\notag\\ &=\dfrac{(-q;q)_\infty(q^3;q^3)_\infty}{(-q^3;q^3)_\infty}\notag\\ &=\dfrac{(-q;q)_\infty(q^3;q^3)_\infty}{(q;q)_\infty(-q^3;q^3)_\infty}\cdot (q;q)_\infty. \end{align*} $$
$$ \begin{align*} \sum_{k=-\infty}^\infty q^{k(3k+1)/2}&=(-q^2;q^3)_\infty(-q;q^3)_\infty(q^3;q^3)_\infty\notag\\ &=\dfrac{(-q;q)_\infty(q^3;q^3)_\infty}{(-q^3;q^3)_\infty}\notag\\ &=\dfrac{(-q;q)_\infty(q^3;q^3)_\infty}{(q;q)_\infty(-q^3;q^3)_\infty}\cdot (q;q)_\infty. \end{align*} $$
It follows that
 $$ \begin{align*} \dfrac{1}{(q;q)_\infty}\sum_{k=-\infty}^\infty q^{k(3k+1)/2}&=\dfrac{(-q;q)_\infty(q^3;q^3)_\infty}{(q;q)_\infty(-q^3;q^3)_\infty}, \end{align*} $$
$$ \begin{align*} \dfrac{1}{(q;q)_\infty}\sum_{k=-\infty}^\infty q^{k(3k+1)/2}&=\dfrac{(-q;q)_\infty(q^3;q^3)_\infty}{(q;q)_\infty(-q^3;q^3)_\infty}, \end{align*} $$
which, with the aid of (1.1) and (1.3), may be rewritten as
 $$ \begin{align*} \bigg(\sum_{n=0}^\infty p(n)q^n\bigg)\bigg(\sum_{k=-\infty}^\infty q^{k(3k+1)/2}\bigg)&=\sum_{n=0}^\infty \overline{A}_3(n)q^n. \end{align*} $$
$$ \begin{align*} \bigg(\sum_{n=0}^\infty p(n)q^n\bigg)\bigg(\sum_{k=-\infty}^\infty q^{k(3k+1)/2}\bigg)&=\sum_{n=0}^\infty \overline{A}_3(n)q^n. \end{align*} $$
Equating the coefficients of
![]() $q^n$
on both sides of this equation yields
$q^n$
on both sides of this equation yields
 $$ \begin{align*} \sum_{k=-\infty}^{\infty}p(n-\omega(k))=\overline{A}_3(n), \end{align*} $$
$$ \begin{align*} \sum_{k=-\infty}^{\infty}p(n-\omega(k))=\overline{A}_3(n), \end{align*} $$
which may be rewritten as
 $$ \begin{align} \sum_{k=0}^{\infty}p(n-\omega(-2k))+\sum_{k=1}^{\infty}p(n-\omega(2k)) & +\sum_{k=1}^{\infty}p(n-\omega(-2k+1)) \notag\\ &+\sum_{k=1}^{\infty}p(n-\omega(2k-1)) =\overline{A}_3(n). \end{align} $$
$$ \begin{align} \sum_{k=0}^{\infty}p(n-\omega(-2k))+\sum_{k=1}^{\infty}p(n-\omega(2k)) & +\sum_{k=1}^{\infty}p(n-\omega(-2k+1)) \notag\\ &+\sum_{k=1}^{\infty}p(n-\omega(2k-1)) =\overline{A}_3(n). \end{align} $$
From (2.2) and (3.1) it readily follows that
 $$ \begin{align*}&2\bigg(\sum_{k=0}^{\infty}p(n-\omega(-2k))+\sum_{k=1}^{\infty}p(n-\omega(2k))\bigg)=\overline{A}_3(n)\notag\end{align*} $$
$$ \begin{align*}&2\bigg(\sum_{k=0}^{\infty}p(n-\omega(-2k))+\sum_{k=1}^{\infty}p(n-\omega(2k))\bigg)=\overline{A}_3(n)\notag\end{align*} $$
and
 $$ \begin{align*} &2\bigg(\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1))\bigg)=\overline{A}_3(n); \end{align*} $$
$$ \begin{align*} &2\bigg(\sum_{k=1}^{\infty}p(n-\omega(-2k+1))+\sum_{k=1}^{\infty}p(n-\omega(2k-1))\bigg)=\overline{A}_3(n); \end{align*} $$
which is equivalent to (2.3). This completes the proof of Theorem 2.1.
4 Proof of Corollary 2.2
Most of the congruences follow easily from the corresponding congruences and generating function representations of
![]() $\overline {A}_3(n)$
or
$\overline {A}_3(n)$
or
![]() $\overline {C}_{3,1}(n)$
in [Reference Ahmed and Baruah2, Reference Andrews4, Reference Barman and Ray6, Reference Chen, Hirschhorn and Sellers8, Reference Chern9, Reference Hao and Shen11, Reference Li and Yao14, Reference Mahadeva Naika and Gireesh16, Reference Shen22, Reference Shen23, Reference Yao26] and Theorem 2.1. Therefore, we only prove the last three congruences in Corollary 2.2, that is,
$\overline {C}_{3,1}(n)$
in [Reference Ahmed and Baruah2, Reference Andrews4, Reference Barman and Ray6, Reference Chen, Hirschhorn and Sellers8, Reference Chern9, Reference Hao and Shen11, Reference Li and Yao14, Reference Mahadeva Naika and Gireesh16, Reference Shen22, Reference Shen23, Reference Yao26] and Theorem 2.1. Therefore, we only prove the last three congruences in Corollary 2.2, that is,
and
Andrews [Reference Andrews4, Theorem 2] and Yao [Reference Yao26, Theorem 1.1, (1.8)] proved that
from which it follows that
Now (4.1) is apparent from Theorem 2.1 and the above congruence.
Next, Barman and Ray [Reference Barman and Ray6, Section 3] showed that
 $$ \begin{align} \sum_{n=0}^\infty \overline{A}_3(12n+11)q^n =144 \dfrac{(q^2;q^2)_\infty^{13}(q^3;q^3)_\infty^{12}}{(q;q)_\infty^{22}(q^6;q^6)_\infty^{3}}+576q\dfrac{(q^2;q^2)_\infty^{10}(q^3;q^3)_\infty^{3}(q^6;q^6)_\infty^{6}}{(q;q)_\infty^{19}}. \end{align} $$
$$ \begin{align} \sum_{n=0}^\infty \overline{A}_3(12n+11)q^n =144 \dfrac{(q^2;q^2)_\infty^{13}(q^3;q^3)_\infty^{12}}{(q;q)_\infty^{22}(q^6;q^6)_\infty^{3}}+576q\dfrac{(q^2;q^2)_\infty^{10}(q^3;q^3)_\infty^{3}(q^6;q^6)_\infty^{6}}{(q;q)_\infty^{19}}. \end{align} $$
Therefore,
which, by Theorem 2.1, readily implies (4.2).
It also follows from (4.4) that
 $$ \begin{align} \sum_{n=0}^\infty \overline{A}_3(12n+11)q^n&\equiv144 \dfrac{(q^2;q^2)_\infty^{13}(q^3;q^3)_\infty^{12}}{(q;q)_\infty^{22}(q^6;q^6)_\infty^{3}}~(\text{mod}~288). \end{align} $$
$$ \begin{align} \sum_{n=0}^\infty \overline{A}_3(12n+11)q^n&\equiv144 \dfrac{(q^2;q^2)_\infty^{13}(q^3;q^3)_\infty^{12}}{(q;q)_\infty^{22}(q^6;q^6)_\infty^{3}}~(\text{mod}~288). \end{align} $$
But, by the binomial theorem,
![]() $(q^j;q^j)_\infty ^2\equiv (q^{2j};q^{2j})_\infty ~(\text {mod}~2)$
for any integer
$(q^j;q^j)_\infty ^2\equiv (q^{2j};q^{2j})_\infty ~(\text {mod}~2)$
for any integer
![]() $j\geq 1$
. Therefore, it follows from (4.5) that
$j\geq 1$
. Therefore, it follows from (4.5) that
 $$ \begin{align*} \sum_{n=0}^\infty \overline{A}_3(12n+11)q^n&\equiv144 f_4f_6^{3}~(\text{mod}~288). \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty \overline{A}_3(12n+11)q^n&\equiv144 f_4f_6^{3}~(\text{mod}~288). \end{align*} $$
Equating the coefficients of
![]() $q^{2n+1}$
on both sides of this congruence yields
$q^{2n+1}$
on both sides of this congruence yields