1. Introduction
Computational fluid dynamics for simulating of a flow past complicated time-varying geometries is still a challenging issue and requires advanced numerical techniques. In a computational procedure the no-slip boundary condition is enforced on the surface of a bluff body and in, e.g. the vortex particle method, the boundary element method is employed to satisfy the no-slip condition (see Koumoutsakos, Leonard & Pépin Reference Koumoutsakos, Leonard and Pépin1994; Koumoutsakos & Leonard Reference Koumoutsakos and Leonard1995). To overcome the difficulty of enforcing the no-slip condition, the Brinkman penalization strategy has been introduced together with grid-based numerical methods such as the volume penalization method (see, e.g. Schneider & Farge Reference Schneider and Farge2002; Kadoch et al. Reference Kadoch, Kolomenskiy, Angot and Schneider2013; Engels et al. Reference Engels, Kolomenskiy, Schneider and Sesterhenn2015; Uchiyama et al. Reference Uchiyama, Gu, Degawa, Iio, Ikeda and Tamura2020) and the vortex penalization method (see, e.g. Gazzola et al. Reference Gazzola, Chatelain, van Rees and Koumoutsakos2011; Rasmussen, Cottet & Walther Reference Rasmussen, Cottet and Walther2011; Hejlesen et al. Reference Hejlesen, Koumoutsakos, Leonard and Walther2015). In these studies, the penalization methods are shown to be a fruitful technique for the simulation of a complicated geometry.
As cited in our previous study (see Ueda & Kida Reference Ueda and Kida2021), the convergence analysis of the penalization methods for the Navier–Stokes flow is given by Angot, Bruneau & Fabrie (Reference Angot, Bruneau and Fabrie1999), and the error is estimated to be of the order of ![]() $1 / \lambda ^{1/4}$, where
$1 / \lambda ^{1/4}$, where ![]() $\lambda$ is the penalization parameter. In their paper, the numerical and theoretical results are given for the two-dimensional flow past a square cylinder in a channel. Also, Angot (Reference Angot2011) proposed a well-posed model for the Stokes flow with jump boundary conditions. Bost, Cottet & Maitre (Reference Bost, Cottet and Maitre2010) showed the convergence analysis, extending the analysis of Angot et al. (Reference Angot, Bruneau and Fabrie1999). Feireisl, Neustupa & Stebel (Reference Feireisl, Neustupa and Stebel2011) showed the convergence for compressible flows. Kadoch et al. (Reference Kadoch, Kolomenskiy, Angot and Schneider2013) analysed a one-dimensional diffusion equation, and the error of the
$\lambda$ is the penalization parameter. In their paper, the numerical and theoretical results are given for the two-dimensional flow past a square cylinder in a channel. Also, Angot (Reference Angot2011) proposed a well-posed model for the Stokes flow with jump boundary conditions. Bost, Cottet & Maitre (Reference Bost, Cottet and Maitre2010) showed the convergence analysis, extending the analysis of Angot et al. (Reference Angot, Bruneau and Fabrie1999). Feireisl, Neustupa & Stebel (Reference Feireisl, Neustupa and Stebel2011) showed the convergence for compressible flows. Kadoch et al. (Reference Kadoch, Kolomenskiy, Angot and Schneider2013) analysed a one-dimensional diffusion equation, and the error of the ![]() $L^2$-norm is shown to be
$L^2$-norm is shown to be ![]() $O ( 1 / \sqrt {\lambda } )$ in a fluid domain and
$O ( 1 / \sqrt {\lambda } )$ in a fluid domain and ![]() $O ( 1 / \lambda ^{1/4} )$ in a solid domain. Furthermore, they verified the computed flows around moving circular cylinders. Carbou & Fabrie (Reference Carbou and Fabrie2003) analysed the penalization model of the viscous incompressible Navier–Stokes equations for a small parameter of
$O ( 1 / \lambda ^{1/4} )$ in a solid domain. Furthermore, they verified the computed flows around moving circular cylinders. Carbou & Fabrie (Reference Carbou and Fabrie2003) analysed the penalization model of the viscous incompressible Navier–Stokes equations for a small parameter of ![]() $\epsilon = 1 / \sqrt {\lambda }$ using the Wentzel–Kramers–Brillouin method, and the error estimation in a fluid domain is shown to be of the order of
$\epsilon = 1 / \sqrt {\lambda }$ using the Wentzel–Kramers–Brillouin method, and the error estimation in a fluid domain is shown to be of the order of ![]() $\epsilon$ unlike Angot et al. (Reference Angot, Bruneau and Fabrie1999). Carbou (Reference Carbou2004) studied the porous thin layer model for the interface of a solid boundary on the penalized Navier–Stokes equations and the error is shown to be of the order of
$\epsilon$ unlike Angot et al. (Reference Angot, Bruneau and Fabrie1999). Carbou (Reference Carbou2004) studied the porous thin layer model for the interface of a solid boundary on the penalized Navier–Stokes equations and the error is shown to be of the order of ![]() $\epsilon$ in a fluid domain. Furthermore, Carbou studied the double penalization model in which one adds the penalization term to the thin porous layer, and showed that the error is
$\epsilon$ in a fluid domain. Furthermore, Carbou studied the double penalization model in which one adds the penalization term to the thin porous layer, and showed that the error is ![]() $\epsilon$ in a fluid domain. Nguyen van yen, Kolomenskiy & Schneider (Reference Nguyen van yen, Kolomenskiy and Schneider2014) analysed the Laplace and Stokes operators with Dirichlet boundary conditions of the volume penalization using a spectral approach and carried out the dipole–wall collision numerically (see Nguyen van yen & Farge Reference Nguyen van yen and Farge2011). In their studies, they derived the Navier boundary condition for the tangential velocity.
$\epsilon$ in a fluid domain. Nguyen van yen, Kolomenskiy & Schneider (Reference Nguyen van yen, Kolomenskiy and Schneider2014) analysed the Laplace and Stokes operators with Dirichlet boundary conditions of the volume penalization using a spectral approach and carried out the dipole–wall collision numerically (see Nguyen van yen & Farge Reference Nguyen van yen and Farge2011). In their studies, they derived the Navier boundary condition for the tangential velocity.
In the numerical studies of the volume and vortex penalization methods, the initial flow past an impulsively started circular cylinder is often selected as a benchmark target (see, e.g. Schneider & Farge Reference Schneider and Farge2002; Rasmussen et al. Reference Rasmussen, Cottet and Walther2011; Hejlesen et al. Reference Hejlesen, Koumoutsakos, Leonard and Walther2015; Rossinelli et al. Reference Rossinelli, Bergdorf, Cottet and Koumoutsakos2010; Verma et al. Reference Verma, Abbati, Novati and Koumoutsakos2017; Mimeau, Cottet & Mortazavi Reference Mimeau, Cottet and Mortazavi2015). This flow is solved analytically by Bar-Lev & Yang (Reference Bar-Lev and Yang1975) using the method of matched asymptotic expansions based on the conventional Navier–Stokes equations. Also, Collins & Dennis (Reference Collins and Dennis1973) investigated the flow that is valid for time beyond the first separation. In their analysis, the Fourier series, employed with respect to two space variables and time, was truncated to a finite number of terms. The initial stage of a flow caused by an impulsively started rotating and translating circular cylinder was solved by Badr & Dennis (Reference Badr and Dennis1985) along the lines of the methodology of Collins & Dennis (Reference Collins and Dennis1973). In unsteady flow past an impulsively started rotating and translating circular cylinder, we also obtained the asymptotic solutions at a low Reynolds number (see Ueda et al. Reference Ueda, Kida, Nakanishi and Sellier2001; Ueda & Kida Reference Ueda and Kida2002a) and high Reynolds number but at the early stage of motion (see Ueda & Kida Reference Ueda and Kida2002b). Chang & Chern (Reference Chang and Chern1991) computed the vortex shedding from the cylinder that is impulsively started with translating and rotating velocities, employing the hybrid vortex method. The flow around a rotating cylinder was studied by Mittal & Kumar (Reference Mittal and Kumar2003). Al-Mdallal (Reference Al-Mdallal2012) and Mittal, Ray & Al-Mdallal (Reference Mittal, Ray and Al-Mdallal2017) treated the initial stage of a circular cylinder impulsively started with rotational oscillation. Rotational oscillating flow around a circular cylinder was studied by Lu & Sato (Reference Lu and Sato1996) numerically. Dennis, Nguyen & Kocabiyik (Reference Dennis, Nguyen and Kocabiyik2000) also studied the flow caused by a rotationally oscillating and translating circular cylinder using the same approach as Collins & Dennis (Reference Collins and Dennis1973).
The present study investigates the initial flow past an impulsively started rotating and translating circular cylinder from rest, employing the same approach as our previous study (see Ueda & Kida Reference Ueda and Kida2021), i.e. the method of matched asymptotic expansions for the Brinkman penalization model of the full Navier–Stokes equations. A particular finding of our previous study is the fact that the drag coefficient obtained from the integration of the penalization term exhibits the half of the results of Bar-Lev & Yang (Reference Bar-Lev and Yang1975) as the penalization parameter ![]() $\lambda \to \infty$. Also, this variance was deduced to arise from the discontinuity of the gradient of vorticity on the cylinder surface. This study aims to elucidate the reason of the variance. The gradient of vorticity on the cylinder surface is known to be related to the pressure force on the cylinder and, furthermore, the pressure force is independent of the moment. Therefore, this study first considers the problem that a circular cylinder impulsively rotates from rest. The second problem of an impulsively started rotating and translating circular cylinder from rest is then investigated. In this analysis, the drag and lift forces are obtained for
$\lambda \to \infty$. Also, this variance was deduced to arise from the discontinuity of the gradient of vorticity on the cylinder surface. This study aims to elucidate the reason of the variance. The gradient of vorticity on the cylinder surface is known to be related to the pressure force on the cylinder and, furthermore, the pressure force is independent of the moment. Therefore, this study first considers the problem that a circular cylinder impulsively rotates from rest. The second problem of an impulsively started rotating and translating circular cylinder from rest is then investigated. In this analysis, the drag and lift forces are obtained for ![]() $\lambda \to \infty$ and
$\lambda \to \infty$ and ![]() $t \ll 1$. On the basis of the analytical results, the above-mentioned variance will be discussed.
$t \ll 1$. On the basis of the analytical results, the above-mentioned variance will be discussed.
This paper organizes as follows. In § 2 we briefly address the governing equations of the Brinkman penalization method. In this study the relative coordinate system fixed with the cylinder is taken for the translating movement of the cylinder along the lines with our previous study and Bar-Lev & Yang (Reference Bar-Lev and Yang1975). The problem of an impulsively started translating and rotating cylinder can therefore be replaced by the problem that the cylinder is impulsively immersed in a uniform flow and impulsively rotates with a constant angular velocity. The asymptotic solutions are obtained using the Laplace transform to the governing penalization equation of motion in § 3. In § 3.2 the impulsive rotation problem is analysed, and the moment due to the force on the cylinder is obtained: (I) from the time derivative of the tangential component of the momentum of the entire fluid, (II) from the shear stress on the cylinder surface, (III) by integrating the penalization layer. The results of the moment obtained by these three approaches are shown to be the same, and it can therefore be found that the pressure field plays a key role to the variance on the drag force against the result obtained by integrating the penalization layer. The second problem of an impulsively rotating and translating circular cylinder is then investigated using the method of the matched asymptotic expansion in § 3.3. In § 3.4 the drag and lift forces are obtained for ![]() $\lambda \gg 1$ and
$\lambda \gg 1$ and ![]() $t \ll 1$ by the following: (i) the momentum of the whole fluid domain and the pressure sufficiently far from the cylinder, (ii) the integration of the penalization layer. Although the unsteady pressure force of the fluid domain is found to cause the variance for the drag force in § 3.4, the variance between the two approaches still exists and the difference is not so small. To resolve the variance, the alternative formula to calculate the fluid force for a solid cylindrical body with the continuous boundary is derived based on the fact that there is the pressure jump on the cylinder surface. The accuracy for the impulsively started translating and rotating case is verified asymptotically in § 3.5. Taking into account the pressure jump, the variance can be reduced to a sufficiently small quantity. In § 4 we summarize our conclusions.
$t \ll 1$ by the following: (i) the momentum of the whole fluid domain and the pressure sufficiently far from the cylinder, (ii) the integration of the penalization layer. Although the unsteady pressure force of the fluid domain is found to cause the variance for the drag force in § 3.4, the variance between the two approaches still exists and the difference is not so small. To resolve the variance, the alternative formula to calculate the fluid force for a solid cylindrical body with the continuous boundary is derived based on the fact that there is the pressure jump on the cylinder surface. The accuracy for the impulsively started translating and rotating case is verified asymptotically in § 3.5. Taking into account the pressure jump, the variance can be reduced to a sufficiently small quantity. In § 4 we summarize our conclusions.
2. Governing equations based on the Brinkman penalization
We consider an unsteady incompressible viscous flow that is governed by the Navier–Stokes equation. In the Brinkman penalization model the governing equation based on the Navier–Stokes equation is written as
where ![]() ${\boldsymbol {u}}$ is the velocity that fulfils the divergence-free condition of
${\boldsymbol {u}}$ is the velocity that fulfils the divergence-free condition of ![]() ${\boldsymbol {\nabla }}\boldsymbol{\cdot}{\boldsymbol {u}} = 0$,
${\boldsymbol {\nabla }}\boldsymbol{\cdot}{\boldsymbol {u}} = 0$, ![]() $p$ is the pressure,
$p$ is the pressure, ![]() $\rho$ is the fluid density that is assumed to be constant and
$\rho$ is the fluid density that is assumed to be constant and ![]() $\nu$ is the kinematic viscosity. In addition,
$\nu$ is the kinematic viscosity. In addition, ![]() ${\boldsymbol {u}}_S$ denotes the velocity of a solid body. The present study adopts the relative coordinate system fixed with the centre of a body that moves with a translating velocity. We can therefore replace it by the problem that the body rotates with respect to the centre of the body without the translating motion, i.e.
${\boldsymbol {u}}_S$ denotes the velocity of a solid body. The present study adopts the relative coordinate system fixed with the centre of a body that moves with a translating velocity. We can therefore replace it by the problem that the body rotates with respect to the centre of the body without the translating motion, i.e. ![]() ${\boldsymbol {u}}_S =\varOmega {\boldsymbol {e}}_z \times {\boldsymbol {x}}$. Here, the third term on the right-hand side of (2.1) accounts for the penalization term to enforce the no-slip boundary condition. The characteristic function,
${\boldsymbol {u}}_S =\varOmega {\boldsymbol {e}}_z \times {\boldsymbol {x}}$. Here, the third term on the right-hand side of (2.1) accounts for the penalization term to enforce the no-slip boundary condition. The characteristic function, ![]() $\chi$, defines the domain of active penalization, i.e.
$\chi$, defines the domain of active penalization, i.e.
in which ![]() ${\mathscr {S}}$ denotes the domain occupied by the solid body and
${\mathscr {S}}$ denotes the domain occupied by the solid body and ![]() ${\mathscr {F}}$ is the domain occupied by the fluid. In addition,
${\mathscr {F}}$ is the domain occupied by the fluid. In addition, ![]() $\lambda$ is the penalization parameter. The conventional Navier–Stokes equations are found to be recovered in the fluid domain. The penalization approach regards a solid body as a porous media with the permeability being vanishingly small. This results in the fluid velocity being zero at a solid/fluid interface so that the penalization parameter can be required to be a sufficiently large value. The present two-dimensional flow is considered on the orthogonal
$\lambda$ is the penalization parameter. The conventional Navier–Stokes equations are found to be recovered in the fluid domain. The penalization approach regards a solid body as a porous media with the permeability being vanishingly small. This results in the fluid velocity being zero at a solid/fluid interface so that the penalization parameter can be required to be a sufficiently large value. The present two-dimensional flow is considered on the orthogonal ![]() $( x, y )$ plane, and the normal unit vector
$( x, y )$ plane, and the normal unit vector ![]() ${\boldsymbol {e}}_z$ is the
${\boldsymbol {e}}_z$ is the ![]() $z$ direction perpendicular to the
$z$ direction perpendicular to the ![]() $( x, y )$ plane.
$( x, y )$ plane.
In the penalization method the total hydrodynamic force ![]() ${\boldsymbol {F}}$ is calculated by the integration of the penalization term (e.g. Angot et al. Reference Angot, Bruneau and Fabrie1999; Hejlesen et al. Reference Hejlesen, Koumoutsakos, Leonard and Walther2015)
${\boldsymbol {F}}$ is calculated by the integration of the penalization term (e.g. Angot et al. Reference Angot, Bruneau and Fabrie1999; Hejlesen et al. Reference Hejlesen, Koumoutsakos, Leonard and Walther2015)
where the domain ![]() ${\mathscr {D}}$ indicates
${\mathscr {D}}$ indicates ![]() ${\mathscr {D}} = {\mathscr {S}} \cup {\mathscr {F}}$. The moving velocity
${\mathscr {D}} = {\mathscr {S}} \cup {\mathscr {F}}$. The moving velocity ![]() ${\boldsymbol {u}}_S$ of the solid body is obtained as the average velocity inside the domain
${\boldsymbol {u}}_S$ of the solid body is obtained as the average velocity inside the domain ![]() ${\mathscr {S}}$, i.e.
${\mathscr {S}}$, i.e.
where ![]() $M$ is the mass of the solid body. As shown in the previous work (see Ueda & Kida Reference Ueda and Kida2021) that investigates an impulsively started translating circular cylinder without rotation, the drag coefficient calculated by (2.3) exhibits a half-value of the result obtained by Bar-Lev & Yang (Reference Bar-Lev and Yang1975). It is found that a special notice, whether (2.3) is available or not, is required. This study therefore aims to elucidate this variance. To do so, we set the assumption that the velocity and the vorticity are continuous at the interface between
$M$ is the mass of the solid body. As shown in the previous work (see Ueda & Kida Reference Ueda and Kida2021) that investigates an impulsively started translating circular cylinder without rotation, the drag coefficient calculated by (2.3) exhibits a half-value of the result obtained by Bar-Lev & Yang (Reference Bar-Lev and Yang1975). It is found that a special notice, whether (2.3) is available or not, is required. This study therefore aims to elucidate this variance. To do so, we set the assumption that the velocity and the vorticity are continuous at the interface between ![]() ${\mathscr {S}}$ and
${\mathscr {S}}$ and ![]() ${\mathscr {F}}$. As will be shown in § 3.5 later, we will require the terms in addition to (2.3) due to the pressure jump between the outside and the inside of the cylinder.
${\mathscr {F}}$. As will be shown in § 3.5 later, we will require the terms in addition to (2.3) due to the pressure jump between the outside and the inside of the cylinder.
3. Asymptotic analysis of an initial flow
3.1. Problem settings and statement
This section addresses the problem settings and the asymptotic analysis for the present target situations, i.e. initial flows around (1) an impulsively started rotating circular cylinder, and (2) an impulsively started rotating and translating circular cylinder. The governing equation for both problems is written by the nonlinear penalization equation of motion (2.1) with respect to time.
Similar to our previous study (see Ueda & Kida Reference Ueda and Kida2021), a small parameter, ![]() $\epsilon = U_t T_o / l_o$, is introduced in the present analysis, where
$\epsilon = U_t T_o / l_o$, is introduced in the present analysis, where ![]() $l_o$,
$l_o$, ![]() $T_o$ and
$T_o$ and ![]() $U_t$ are the reference length, time and velocity, respectively. The angular velocity,
$U_t$ are the reference length, time and velocity, respectively. The angular velocity, ![]() $\varOmega l_o$, is selected as the reference velocity
$\varOmega l_o$, is selected as the reference velocity ![]() $U_t$ for the first problem (pure rotating motion of a circular cylinder). The translating velocity
$U_t$ for the first problem (pure rotating motion of a circular cylinder). The translating velocity ![]() $U_o$ is also selected for the second problem (an impulsively started rotating and translating circular cylinder). In this study the radius of a cylinder is selected as the reference length
$U_o$ is also selected for the second problem (an impulsively started rotating and translating circular cylinder). In this study the radius of a cylinder is selected as the reference length ![]() $l_o$. Then, the actual time
$l_o$. Then, the actual time ![]() $t^*$ is non-dimensionalized as
$t^*$ is non-dimensionalized as ![]() $t = ( U_t / l_o ) t^*$ with respect to
$t = ( U_t / l_o ) t^*$ with respect to ![]() $l_o$ and
$l_o$ and ![]() $U_t$.
$U_t$.
This study considers an initial flow past an impulsively started rotating and translating circular cylinder from a quiescent state. On the relative coordinate system fixed with the centre of the cylinder, this flow is replaced by the situation that the circular cylinder is impulsively immersed in the uniform flow ![]() $U_o H ( t )$ with a constant angular velocity
$U_o H ( t )$ with a constant angular velocity ![]() $\varOmega H ( t )$ at
$\varOmega H ( t )$ at ![]() $t = 0$. Here, the Heaviside step function
$t = 0$. Here, the Heaviside step function ![]() $H (t )$ is defined as
$H (t )$ is defined as ![]() $H ( t ) = 0$ for
$H ( t ) = 0$ for ![]() $t \leq 0$ and
$t \leq 0$ and ![]() $H ( t ) = 1$ for
$H ( t ) = 1$ for ![]() $t > 0$. The problem setting is then illustrated as figure 1, where
$t > 0$. The problem setting is then illustrated as figure 1, where ![]() $( x, y )$ denotes the orthogonal coordinate system and
$( x, y )$ denotes the orthogonal coordinate system and ![]() $( r, \theta )$ denotes the polar coordinate system.
$( r, \theta )$ denotes the polar coordinate system.

Figure 1. Notations for a circular cylinder impulsively immersed in a constant uniform stream ![]() $U_o$ with a constant angular velocity
$U_o$ with a constant angular velocity ![]() $\varOmega H ( t )$.
$\varOmega H ( t )$.
The present target problem mentioned in § 2 is formulated within a singular perturbation framework with respect to a perturbation parameter ![]() $\epsilon$ for the penalized Navier–Stokes equation (2.1). The time
$\epsilon$ for the penalized Navier–Stokes equation (2.1). The time ![]() $t$ is then stretched as
$t$ is then stretched as ![]() $T = t / \epsilon$ (see Bar-Lev & Yang Reference Bar-Lev and Yang1975). Because the penalization parameter
$T = t / \epsilon$ (see Bar-Lev & Yang Reference Bar-Lev and Yang1975). Because the penalization parameter ![]() $\lambda$ is taken to be proportional to the inverse of the time increment
$\lambda$ is taken to be proportional to the inverse of the time increment ![]() $\delta t$ (i.e.
$\delta t$ (i.e. ![]() $\lambda = \alpha / \delta t$ with the relaxation coefficient
$\lambda = \alpha / \delta t$ with the relaxation coefficient ![]() $\alpha$ in Hejlesen et al. Reference Hejlesen, Koumoutsakos, Leonard and Walther2015), it is set as
$\alpha$ in Hejlesen et al. Reference Hejlesen, Koumoutsakos, Leonard and Walther2015), it is set as ![]() $\lambda = \lambda _o / \epsilon$ with
$\lambda = \lambda _o / \epsilon$ with ![]() $\lambda _o = O ( 1 )$. To compare with the analytical results of Bar-Lev & Yang (Reference Bar-Lev and Yang1975), the Reynolds number
$\lambda _o = O ( 1 )$. To compare with the analytical results of Bar-Lev & Yang (Reference Bar-Lev and Yang1975), the Reynolds number ![]() $\textit {Re}$ is taken as a sufficiently large value so that the kinematic viscosity
$\textit {Re}$ is taken as a sufficiently large value so that the kinematic viscosity ![]() $\nu$ can be set as
$\nu$ can be set as ![]() $\nu = \epsilon \nu _o$ with
$\nu = \epsilon \nu _o$ with ![]() $\nu _o = O ( 1 )$. The penalized governing equation (2.1) is then written as, on the polar coordinate system,
$\nu _o = O ( 1 )$. The penalized governing equation (2.1) is then written as, on the polar coordinate system,
 \begin{align} \frac{\partial u_r}{\partial T} + \epsilon \biggl( u_r \frac{\partial u_r}{\partial r} + u_\theta \frac{\partial u_r}{r \partial \theta} - \frac{u_\theta^2}{r} \biggr) & =- \frac{\epsilon}{\rho} \frac{\partial p}{\partial r} + \lambda_o \chi ( u_{sr} - u_r )\nonumber\\ &\quad + \epsilon^2 \nu_o \left( \nabla^2 u_r - \frac{u_r}{r^2} - \frac{2}{r^2} \frac{\partial u_\theta}{\partial \theta} \right), \end{align}
\begin{align} \frac{\partial u_r}{\partial T} + \epsilon \biggl( u_r \frac{\partial u_r}{\partial r} + u_\theta \frac{\partial u_r}{r \partial \theta} - \frac{u_\theta^2}{r} \biggr) & =- \frac{\epsilon}{\rho} \frac{\partial p}{\partial r} + \lambda_o \chi ( u_{sr} - u_r )\nonumber\\ &\quad + \epsilon^2 \nu_o \left( \nabla^2 u_r - \frac{u_r}{r^2} - \frac{2}{r^2} \frac{\partial u_\theta}{\partial \theta} \right), \end{align} \begin{align} \frac{\partial u_\theta}{\partial T} + \epsilon \left( u_r \frac{\partial u_\theta}{\partial r} + u_\theta \frac{\partial u_\theta}{r \partial \theta} + \frac{u_r u_\theta}{r} \right) & =- \frac{\epsilon}{\rho} \frac{\partial p}{r \partial \theta} + \lambda_o \chi ( u_{s \theta} - u_\theta )\nonumber\\ &\quad+ \epsilon^2 \nu_o \left( \nabla^2 u_\theta - \frac{u_\theta}{r^2} + \frac{2}{r^2} \frac{\partial u_r}{\partial \theta} \right), \end{align}
\begin{align} \frac{\partial u_\theta}{\partial T} + \epsilon \left( u_r \frac{\partial u_\theta}{\partial r} + u_\theta \frac{\partial u_\theta}{r \partial \theta} + \frac{u_r u_\theta}{r} \right) & =- \frac{\epsilon}{\rho} \frac{\partial p}{r \partial \theta} + \lambda_o \chi ( u_{s \theta} - u_\theta )\nonumber\\ &\quad+ \epsilon^2 \nu_o \left( \nabla^2 u_\theta - \frac{u_\theta}{r^2} + \frac{2}{r^2} \frac{\partial u_r}{\partial \theta} \right), \end{align}
where ![]() $\nabla ^2$ is given by
$\nabla ^2$ is given by
In addition, the equation of continuity is written as
Note that (3.1a)–(3.3) are written as the dimensionless form with respect to ![]() $U_t$ and
$U_t$ and ![]() $l_o$ and, therefore,
$l_o$ and, therefore, ![]() $\nu _o$ is found to be the dimensionless kinematic viscosity. Furthermore, the velocity of the solid body is written as
$\nu _o$ is found to be the dimensionless kinematic viscosity. Furthermore, the velocity of the solid body is written as ![]() ${\boldsymbol {u}}_S = r \varOmega {\boldsymbol {e}}_{\theta } H ( T )$ on the relative coordinate system fixed with the centre of the cylinder, where
${\boldsymbol {u}}_S = r \varOmega {\boldsymbol {e}}_{\theta } H ( T )$ on the relative coordinate system fixed with the centre of the cylinder, where ![]() ${\boldsymbol {e}}_\theta$ denotes the unit vector in the
${\boldsymbol {e}}_\theta$ denotes the unit vector in the ![]() $\theta$ direction.
$\theta$ direction.
3.2. First problem: an impulsively rotating circular cylinder
In this subsection we first consider the problem that a circular cylinder impulsively rotates with a constant angular velocity ![]() $\varOmega$ without translating motion. In this problem, the moment exerted by the cylinder can be obtained from the tangential force acting on the cylinder surface, i.e. the force due to the pressure is independent of the moment. This problem makes it possible to investigate the contribution from the velocity field on the hydrodynamic force acting on the cylinder because it is free from the pressure contribution.
$\varOmega$ without translating motion. In this problem, the moment exerted by the cylinder can be obtained from the tangential force acting on the cylinder surface, i.e. the force due to the pressure is independent of the moment. This problem makes it possible to investigate the contribution from the velocity field on the hydrodynamic force acting on the cylinder because it is free from the pressure contribution.
3.2.1. Outer solutions
We attempt to obtain the outer solutions ![]() ${\boldsymbol {u}}^o$, denoted by the superscript ‘
${\boldsymbol {u}}^o$, denoted by the superscript ‘![]() $o$’, of the governing equations (3.1a)–(3.3). The outer domain is defined as the outside or the inside of the cylinder with respect to
$o$’, of the governing equations (3.1a)–(3.3). The outer domain is defined as the outside or the inside of the cylinder with respect to ![]() $\epsilon$, i.e.
$\epsilon$, i.e. ![]() $r - 1 = O ( 1 )$. The outer solutions cannot satisfy the boundary condition on the solid–fluid boundary, as mentioned below. The inner solution near the boundary is therefore defined as
$r - 1 = O ( 1 )$. The outer solutions cannot satisfy the boundary condition on the solid–fluid boundary, as mentioned below. The inner solution near the boundary is therefore defined as ![]() $r - 1 = O ( \epsilon )$ in the subsequent § 3.2.2.
$r - 1 = O ( \epsilon )$ in the subsequent § 3.2.2.
Following our previous study (see Ueda & Kida Reference Ueda and Kida2021), the velocities, ![]() $u_r^o$ and
$u_r^o$ and ![]() $u_\theta ^o$, in the radial (
$u_\theta ^o$, in the radial (![]() $r$) and tangential (
$r$) and tangential (![]() $\theta$) directions are asymptotically represented by
$\theta$) directions are asymptotically represented by
 \begin{equation} u_{r}^o =\sum_{n = 0}^\infty \epsilon^n u_{r,n}^o, \quad u_{\theta}^o = \sum_{n = 0}^\infty \epsilon^n u_{\theta,n}^o. \end{equation}
\begin{equation} u_{r}^o =\sum_{n = 0}^\infty \epsilon^n u_{r,n}^o, \quad u_{\theta}^o = \sum_{n = 0}^\infty \epsilon^n u_{\theta,n}^o. \end{equation}
Also, the pressure ![]() $p^o$ is asymptotically written as
$p^o$ is asymptotically written as
 \begin{equation} p^o = \sum_{n = 0}^\infty \epsilon^n p_{n}^o. \end{equation}
\begin{equation} p^o = \sum_{n = 0}^\infty \epsilon^n p_{n}^o. \end{equation}
Then, (3.1a) and (3.1b) reduce to the following for the first two lowest-order solutions in the ![]() $r$ and
$r$ and ![]() $\theta$ directions, respectively;
$\theta$ directions, respectively;
In the fluid domain, we have ![]() $\partial u_{r,0}^o / \partial T = \partial u_{\theta,0}^o / \partial T = 0$, because of
$\partial u_{r,0}^o / \partial T = \partial u_{\theta,0}^o / \partial T = 0$, because of ![]() $\chi = 0$. This gives
$\chi = 0$. This gives ![]() $u_{r,0}^o = u_{\theta,0}^0 = 0$ because
$u_{r,0}^o = u_{\theta,0}^0 = 0$ because ![]() $u_{r,0}^o$ and
$u_{r,0}^o$ and ![]() $u_{\theta,0}^o$ are zero at
$u_{\theta,0}^o$ are zero at ![]() $T = 0$. We can obtain the outer solutions in the fluid domain by the recursive calculations for the higher-order approximation of (3.1a) and (3.1b) such as
$T = 0$. We can obtain the outer solutions in the fluid domain by the recursive calculations for the higher-order approximation of (3.1a) and (3.1b) such as
Assuming that the pressure sufficiently far from the cylinder is zero, we have also
In contrast, since ![]() $\chi = 1$ in the body domain
$\chi = 1$ in the body domain ![]() ${\mathscr {S}}$, we have
${\mathscr {S}}$, we have ![]() $u_{r,i}^o = 0$ and
$u_{r,i}^o = 0$ and ![]() $u_{\theta, i}^o = \varOmega r H ( T ) \delta _{i 0}$ for
$u_{\theta, i}^o = \varOmega r H ( T ) \delta _{i 0}$ for ![]() $i = 0, 1, 2, \ldots$. This relation gives, in the body domain,
$i = 0, 1, 2, \ldots$. This relation gives, in the body domain,
where ![]() $C$ is an integral constant.
$C$ is an integral constant.
3.2.2. Inner solutions
The outer flow described by (3.7) and (3.9a–c) causes the slip velocity on the surface of the cylinder (at ![]() $r = 1$) so that a non-uniform domain can exist near the cylinder surface. To remedy this, the radial coordinate
$r = 1$) so that a non-uniform domain can exist near the cylinder surface. To remedy this, the radial coordinate ![]() $r$ is stretched as
$r$ is stretched as ![]() $R = ( r - 1 ) / \epsilon$ where the solution in the stretched domain is called the inner solution that is denoted by the superscript ‘
$R = ( r - 1 ) / \epsilon$ where the solution in the stretched domain is called the inner solution that is denoted by the superscript ‘![]() $i$’. The governing equations and the continuity equation of (3.1a)–(3.3) are then described as, in the inner domain,
$i$’. The governing equations and the continuity equation of (3.1a)–(3.3) are then described as, in the inner domain,
 \begin{align} & \frac{\partial u_r^i}{\partial T} + u_r^i \frac{\partial u_r^i}{\partial R} + \frac{\epsilon}{1 + \epsilon R} u_\theta^i \frac{\partial u_r^i}{\partial \theta} - \epsilon \frac{u_\theta^{i2}}{1 + \epsilon R} =- \frac{1}{\rho} \frac{\partial p^i}{\partial R} - \lambda_o \chi u_r^i \nonumber\\ & \quad + \nu_o \Bigg[ \bigg( \frac{\partial^2}{\partial R^2} + \frac{\epsilon}{1 + \epsilon R} \frac{\partial}{\partial R} + \frac{\epsilon^2}{( 1 + \epsilon R )^2} \frac{\partial^2}{\partial \theta^2} \bigg) u_r^i - \frac{\epsilon^2}{( 1 + \epsilon R )^2} \Bigg( u_r^i + 2 \frac{\partial u_\theta^i}{\partial \theta} \Bigg)\Bigg], \end{align}
\begin{align} & \frac{\partial u_r^i}{\partial T} + u_r^i \frac{\partial u_r^i}{\partial R} + \frac{\epsilon}{1 + \epsilon R} u_\theta^i \frac{\partial u_r^i}{\partial \theta} - \epsilon \frac{u_\theta^{i2}}{1 + \epsilon R} =- \frac{1}{\rho} \frac{\partial p^i}{\partial R} - \lambda_o \chi u_r^i \nonumber\\ & \quad + \nu_o \Bigg[ \bigg( \frac{\partial^2}{\partial R^2} + \frac{\epsilon}{1 + \epsilon R} \frac{\partial}{\partial R} + \frac{\epsilon^2}{( 1 + \epsilon R )^2} \frac{\partial^2}{\partial \theta^2} \bigg) u_r^i - \frac{\epsilon^2}{( 1 + \epsilon R )^2} \Bigg( u_r^i + 2 \frac{\partial u_\theta^i}{\partial \theta} \Bigg)\Bigg], \end{align} \begin{align} & \frac{\partial u_\theta^i}{\partial T} + u_r^i \frac{\partial u_\theta^i}{\partial R} + \frac{\epsilon}{1 + \epsilon R} u_\theta^i \frac{\partial u_\theta^i}{\partial \theta} + \epsilon \frac{u_r^i u_\theta^i}{1 + \epsilon R} \nonumber\\ &\quad =- \frac{1}{\rho} \frac{\epsilon}{1 + \epsilon R} \frac{\partial p^i}{\partial \theta} + \lambda_o \chi [ ( 1 + \epsilon R ) \varOmega H ( T ) - u_\theta^i ]\nonumber\\ & \qquad + \nu_o \left[ \left( \frac{\partial^2}{\partial R^2} + \frac{\epsilon}{1 + \epsilon R} \frac{\partial}{\partial R} + \frac{\epsilon^2}{( 1 + \epsilon R )^2} \frac{\partial^2}{\partial \theta^2} \right) u_\theta^i - \frac{\epsilon^2}{( 1 + \epsilon R )^2} \left( u_\theta^i - 2 \frac{\partial u_r^i}{\partial \theta} \right) \right], \end{align}
\begin{align} & \frac{\partial u_\theta^i}{\partial T} + u_r^i \frac{\partial u_\theta^i}{\partial R} + \frac{\epsilon}{1 + \epsilon R} u_\theta^i \frac{\partial u_\theta^i}{\partial \theta} + \epsilon \frac{u_r^i u_\theta^i}{1 + \epsilon R} \nonumber\\ &\quad =- \frac{1}{\rho} \frac{\epsilon}{1 + \epsilon R} \frac{\partial p^i}{\partial \theta} + \lambda_o \chi [ ( 1 + \epsilon R ) \varOmega H ( T ) - u_\theta^i ]\nonumber\\ & \qquad + \nu_o \left[ \left( \frac{\partial^2}{\partial R^2} + \frac{\epsilon}{1 + \epsilon R} \frac{\partial}{\partial R} + \frac{\epsilon^2}{( 1 + \epsilon R )^2} \frac{\partial^2}{\partial \theta^2} \right) u_\theta^i - \frac{\epsilon^2}{( 1 + \epsilon R )^2} \left( u_\theta^i - 2 \frac{\partial u_r^i}{\partial \theta} \right) \right], \end{align}
in which ![]() $u_r^i$,
$u_r^i$, ![]() $u_\theta ^i$ and
$u_\theta ^i$ and ![]() $p^i$ are assumed to be asymptotically represented as
$p^i$ are assumed to be asymptotically represented as
 \begin{equation} u_r^i = \sum_{n = 0}^\infty \epsilon^n u_{r n}^i, \quad u_\theta^i = \sum_{n = 0}^\infty \epsilon^n u_{\theta n}^i, \quad p^i = \sum_{n = 0}^\infty \epsilon^n p_n^i. \end{equation}
\begin{equation} u_r^i = \sum_{n = 0}^\infty \epsilon^n u_{r n}^i, \quad u_\theta^i = \sum_{n = 0}^\infty \epsilon^n u_{\theta n}^i, \quad p^i = \sum_{n = 0}^\infty \epsilon^n p_n^i. \end{equation}
From (3.10c), we have ![]() $\partial u_{r0}^i / \partial R = 0$ and, therefore, the first-order solution of
$\partial u_{r0}^i / \partial R = 0$ and, therefore, the first-order solution of ![]() $u_r^i$ is found to be independent of
$u_r^i$ is found to be independent of ![]() $R$. The matching procedure to the outer solution inside the body domain (i.e.
$R$. The matching procedure to the outer solution inside the body domain (i.e. ![]() $u_r^{io} = u_r^{oi} = 0$) yields
$u_r^{io} = u_r^{oi} = 0$) yields
Equation (3.12) is found to fulfil the matching condition to the outer solution of the fluid domain. The first approximations of (3.10a) and (3.10b) are written as
From (3.13a), ![]() $p_0^i$ is found to be independent of
$p_0^i$ is found to be independent of ![]() $R$. Furthermore, from the matching procedure to
$R$. Furthermore, from the matching procedure to ![]() $p_i^o$ of (3.8) in the flow domain (i.e.
$p_i^o$ of (3.8) in the flow domain (i.e. ![]() $p^{io} = p_0^i + O ( \epsilon ) = p^{o i} = 0$), we have
$p^{io} = p_0^i + O ( \epsilon ) = p^{o i} = 0$), we have ![]() $p_0^i = 0$ for
$p_0^i = 0$ for ![]() $R \geq 0$. For
$R \geq 0$. For ![]() $R < 0$, (3.9a–c) becomes
$R < 0$, (3.9a–c) becomes ![]() $p^{o i} = ( \rho / 2 ) \varOmega ^2 H ( T ) + C$ and we have
$p^{o i} = ( \rho / 2 ) \varOmega ^2 H ( T ) + C$ and we have
 \begin{equation} p_0^i = \left\{ \begin{array}{@{}ll} 0 & \text{for} \ R \geq 0,\\ \displaystyle\dfrac{\rho}{2} \varOmega^2 H ( T ) + C & \text{for}\ R < 0. \end{array} \right.\end{equation}
\begin{equation} p_0^i = \left\{ \begin{array}{@{}ll} 0 & \text{for} \ R \geq 0,\\ \displaystyle\dfrac{\rho}{2} \varOmega^2 H ( T ) + C & \text{for}\ R < 0. \end{array} \right.\end{equation} For ![]() $R \geq 0$, the governing equation of (3.13b) with respect to
$R \geq 0$, the governing equation of (3.13b) with respect to ![]() $u_{\theta 0}^i$ is written as
$u_{\theta 0}^i$ is written as
The matching condition to the fluid domain gives the following boundary condition:
To solve (3.15) with (3.16), we employ the Laplace transform, ![]() $U_{\theta 0} = {\mathcal {L}} ( u_{\theta 0}^i ) = \int _0^\infty {\rm e}^{- s T} u_{\theta 0}^i ( R, \theta ; T) \,{\rm d} T$, similar to our previous study (see Ueda & Kida Reference Ueda and Kida2021). Then, the solution to (3.15) is easily derived as
$U_{\theta 0} = {\mathcal {L}} ( u_{\theta 0}^i ) = \int _0^\infty {\rm e}^{- s T} u_{\theta 0}^i ( R, \theta ; T) \,{\rm d} T$, similar to our previous study (see Ueda & Kida Reference Ueda and Kida2021). Then, the solution to (3.15) is easily derived as
where ![]() $A$ is an integral constant that is a function of
$A$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$.
$\theta$.
For ![]() $R < 0$, the governing equation of (3.13b) is also written as
$R < 0$, the governing equation of (3.13b) is also written as
Taking into account the initial condition of ![]() $u_{\theta 0}^i = \varOmega$, the Laplace transform to (3.18) is written as
$u_{\theta 0}^i = \varOmega$, the Laplace transform to (3.18) is written as
The boundary condition as ![]() $R \to - \infty$ is obtained from the matching condition to the outer solution inside the body domain, i.e.
$R \to - \infty$ is obtained from the matching condition to the outer solution inside the body domain, i.e. ![]() $u_{\theta 0}^i \to \varOmega H ( T )$. Then, the solution to (3.19) is written as
$u_{\theta 0}^i \to \varOmega H ( T )$. Then, the solution to (3.19) is written as
where ![]() $B$ is an integral constant that is a function of
$B$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$. The integral constants,
$\theta$. The integral constants, ![]() $A$ and
$A$ and ![]() $B$, can be determined as
$B$, can be determined as ![]() $A = B + \varOmega / s$ and
$A = B + \varOmega / s$ and ![]() $- a A = \bar {a} B$ by the enforcements of the continuity of the velocity and its gradient with respect to
$- a A = \bar {a} B$ by the enforcements of the continuity of the velocity and its gradient with respect to ![]() $R$ at
$R$ at ![]() $R = 0$. Therefore, we have, for (3.17) and (3.20),
$R = 0$. Therefore, we have, for (3.17) and (3.20),
 \begin{equation} U_{\theta 0} = \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{\bar{a}}{a + \bar{a}} \dfrac{\varOmega}{s} {\rm e}^{- a R} & \text{for}\ R \geq 0,\\[9pt] \displaystyle - \dfrac{{a}}{a + \bar{a}} \dfrac{\varOmega}{s} {\rm e}^{\bar{a} R} + \dfrac{\varOmega}{s} & \text{for}\ R < 0. \end{array} \right. \end{equation}
\begin{equation} U_{\theta 0} = \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{\bar{a}}{a + \bar{a}} \dfrac{\varOmega}{s} {\rm e}^{- a R} & \text{for}\ R \geq 0,\\[9pt] \displaystyle - \dfrac{{a}}{a + \bar{a}} \dfrac{\varOmega}{s} {\rm e}^{\bar{a} R} + \dfrac{\varOmega}{s} & \text{for}\ R < 0. \end{array} \right. \end{equation}
Using the relations of (A1) and (A2) in Appendix A, (3.21) becomes, for ![]() $R \geq 0$,
$R \geq 0$,
 \begin{align} u_{\theta 0}^i&= \varOmega
\Biggl\{ \text{erfc} \left( \frac{R}{2 \sqrt{\nu_o T}}
\right) - \frac{R}{4 \sqrt{{\rm \pi} \nu_o}} \int_0^T
\frac{\exp\left({- \dfrac{\lambda_o}{2} \xi}\right)}{( T -
\xi )^{3 / 2}} \left[ {\rm I}_1 ( \lambda_o \xi / 2 ) +
{\rm I}_0 ( \lambda_o \xi / 2 ) \right]\nonumber\\
&\quad \vphantom{\frac{\exp\left({-
\dfrac{\lambda_o}{2} \xi}\right)}{( T - \xi )^{3 /
2}}}\times \exp\left({ - \frac{R^2}{4 \nu_o ( T - \xi
)}}\right) {\rm d} \xi \Biggr\},
\end{align}
\begin{align} u_{\theta 0}^i&= \varOmega
\Biggl\{ \text{erfc} \left( \frac{R}{2 \sqrt{\nu_o T}}
\right) - \frac{R}{4 \sqrt{{\rm \pi} \nu_o}} \int_0^T
\frac{\exp\left({- \dfrac{\lambda_o}{2} \xi}\right)}{( T -
\xi )^{3 / 2}} \left[ {\rm I}_1 ( \lambda_o \xi / 2 ) +
{\rm I}_0 ( \lambda_o \xi / 2 ) \right]\nonumber\\
&\quad \vphantom{\frac{\exp\left({-
\dfrac{\lambda_o}{2} \xi}\right)}{( T - \xi )^{3 /
2}}}\times \exp\left({ - \frac{R^2}{4 \nu_o ( T - \xi
)}}\right) {\rm d} \xi \Biggr\},
\end{align}
for ![]() $R < 0$,
$R < 0$,
 \begin{align} u_{\theta 0}^i &= \varOmega \left\{ 1 - \frac{| R |}{4 \sqrt{{\rm \pi} \nu_o}} \int_0^T \frac{\exp({- \lambda_o ( T - \xi / 2 )})}{( T - \xi )^{3 / 2}} \left[ {\rm I}_1 ( \lambda_o \xi / 2 ) + {\rm I}_0 ( \lambda_o \xi / 2 ) \right] \right.\nonumber\\ &\quad\times\exp\left.\left({- \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \right\}. \end{align}
\begin{align} u_{\theta 0}^i &= \varOmega \left\{ 1 - \frac{| R |}{4 \sqrt{{\rm \pi} \nu_o}} \int_0^T \frac{\exp({- \lambda_o ( T - \xi / 2 )})}{( T - \xi )^{3 / 2}} \left[ {\rm I}_1 ( \lambda_o \xi / 2 ) + {\rm I}_0 ( \lambda_o \xi / 2 ) \right] \right.\nonumber\\ &\quad\times\exp\left.\left({- \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \right\}. \end{align}
Here, ![]() ${\rm I}_0 ( z )$ and
${\rm I}_0 ( z )$ and ![]() ${\rm I}_1 ( z )$ are the zeroth- and the first-order modified Bessel functions of the first kind, respectively.
${\rm I}_1 ( z )$ are the zeroth- and the first-order modified Bessel functions of the first kind, respectively.
Let us carry out further analysis to the second approximation for seeking the solutions of ![]() $u_{r1}^i$ and
$u_{r1}^i$ and ![]() $u_{\theta 1}^i$. Taking into account (3.12) and (3.22)–(3.23), (3.10c) is written as
$u_{\theta 1}^i$. Taking into account (3.12) and (3.22)–(3.23), (3.10c) is written as
Hence, we find that
where ![]() $C$ is an integral constant that is a function of
$C$ is an integral constant that is a function of ![]() $T$ and
$T$ and ![]() $\theta$. The matching to the outer solution and the enforcement of the continuity of
$\theta$. The matching to the outer solution and the enforcement of the continuity of ![]() $u_{r1}^i$ at
$u_{r1}^i$ at ![]() $R = 0$ determine the integral constant of (3.25) as
$R = 0$ determine the integral constant of (3.25) as
The second approximations of the governing equations (3.10a) and (3.10b) are written as, taking into account (3.12) and (3.14),
 $$\begin{gather}\frac{\partial u_{\theta 1}^i}{\partial T} = \lambda_o \chi ( R \varOmega H ( T ) - u_{\theta 1}^i ) + \nu_o \Bigg( \frac{\partial^2 u_{\theta 1}^i}{\partial R^2} + \frac{\partial u_{\theta 0}^i}{\partial R} \Bigg). \end{gather}$$
$$\begin{gather}\frac{\partial u_{\theta 1}^i}{\partial T} = \lambda_o \chi ( R \varOmega H ( T ) - u_{\theta 1}^i ) + \nu_o \Bigg( \frac{\partial^2 u_{\theta 1}^i}{\partial R^2} + \frac{\partial u_{\theta 0}^i}{\partial R} \Bigg). \end{gather}$$
The matching conditions to the outer solutions in the fluid and the solid domains give ![]() $p_1^i \to 0$ as
$p_1^i \to 0$ as ![]() $R \to \infty$, and
$R \to \infty$, and ![]() $p_1^i \to \rho R \varOmega ^2 H(T)$ and
$p_1^i \to \rho R \varOmega ^2 H(T)$ and ![]() $u_{\theta 0}^i \to \varOmega H(T)$ as
$u_{\theta 0}^i \to \varOmega H(T)$ as ![]() $R \to - \infty$. From (3.27a), the pressure
$R \to - \infty$. From (3.27a), the pressure ![]() $p_1^i$ is then described as
$p_1^i$ is then described as
 \begin{equation} p_1^i = \left\{ \begin{array}{@{}ll} \displaystyle - \rho \int_R^\infty u_{\theta 0}^{i 2} \,{\rm d} R & \text{for} \ R \geq 0,\\[10pt] \displaystyle \rho \int_{- \infty}^R [ u_{\theta 0}^{i 2} - \varOmega^2 H(T) ] \,{\rm d} R + \rho \varOmega^2 R H ( T ) & \text{for}\ R < 0. \end{array}\right. \end{equation}
\begin{equation} p_1^i = \left\{ \begin{array}{@{}ll} \displaystyle - \rho \int_R^\infty u_{\theta 0}^{i 2} \,{\rm d} R & \text{for} \ R \geq 0,\\[10pt] \displaystyle \rho \int_{- \infty}^R [ u_{\theta 0}^{i 2} - \varOmega^2 H(T) ] \,{\rm d} R + \rho \varOmega^2 R H ( T ) & \text{for}\ R < 0. \end{array}\right. \end{equation}
Here, we introduce ![]() $\hat {u}_{\theta 1}^i$ as
$\hat {u}_{\theta 1}^i$ as
 \begin{equation} u_{\theta 1}^i =
\left\{ \begin{array}{@{}ll} - \dfrac{1}{2} R u_{\theta
0}^i + \hat{u}_{\theta 1}^i & \text{for} \ R \geq 0,\\
- \dfrac{1}{2} R \left[ u_{\theta 0}^i - \varOmega H ( T )
\right] + R \varOmega H ( T ) + \hat{u}_{\theta 1}^i &
\text{for}\ R < 0. \end{array} \right.
\end{equation}
\begin{equation} u_{\theta 1}^i =
\left\{ \begin{array}{@{}ll} - \dfrac{1}{2} R u_{\theta
0}^i + \hat{u}_{\theta 1}^i & \text{for} \ R \geq 0,\\
- \dfrac{1}{2} R \left[ u_{\theta 0}^i - \varOmega H ( T )
\right] + R \varOmega H ( T ) + \hat{u}_{\theta 1}^i &
\text{for}\ R < 0. \end{array} \right.
\end{equation}Then, (3.27b) reduces to
 \begin{equation} \frac{\partial \hat{u}_{\theta 1}^i}{\partial T} = \left\{ \begin{array}{@{}ll} \displaystyle \nu_o \dfrac{\partial^2 \hat{u}_{\theta 1}^i}{\partial R^2} & \text{for} \ R \geq 0,\\[10pt] \displaystyle \nu_o \dfrac{\partial^2 \hat{u}_{\theta 1}^i}{\partial R^2} - \lambda_o \hat{u}_{\theta 1}^i & \text{for} \ R < 0. \end{array} \right.\end{equation}
\begin{equation} \frac{\partial \hat{u}_{\theta 1}^i}{\partial T} = \left\{ \begin{array}{@{}ll} \displaystyle \nu_o \dfrac{\partial^2 \hat{u}_{\theta 1}^i}{\partial R^2} & \text{for} \ R \geq 0,\\[10pt] \displaystyle \nu_o \dfrac{\partial^2 \hat{u}_{\theta 1}^i}{\partial R^2} - \lambda_o \hat{u}_{\theta 1}^i & \text{for} \ R < 0. \end{array} \right.\end{equation}Employing the Laplace transform, the solution to (3.30) is obtained as
where ![]() $A_1$ and
$A_1$ and ![]() $B_1$ are respectively integral constants that are functions of
$B_1$ are respectively integral constants that are functions of ![]() $s$ and
$s$ and ![]() $\theta$. Here, for obtaining (3.31), the matching condition to the outer solution, i.e.
$\theta$. Here, for obtaining (3.31), the matching condition to the outer solution, i.e. ![]() $\hat {u}_{\theta 1}^i \to 0$ as
$\hat {u}_{\theta 1}^i \to 0$ as ![]() $R \to \pm \infty$, is used. Equation (3.29) is therefore written as
$R \to \pm \infty$, is used. Equation (3.29) is therefore written as
 \begin{equation} u_{\theta 1}^i = \left\{ \begin{array}{@{}ll} - \dfrac{1}{2} R u_{\theta 0}^i + {\mathcal{L}}^{-1} ( A_1( s, \theta ) {\rm e}^{- a R} ) & \text{for} \ R \geq 0,\\ - \dfrac{1}{2} R [ u_{\theta 0}^i - \varOmega H ( T ) ] + R \varOmega H ( T ) + {\mathcal{L}}^{-1} ( B_1 ( s, \theta ) {\rm e}^{\bar{a} R} ) & \text{for}\ R < 0. \end{array} \right.\end{equation}
\begin{equation} u_{\theta 1}^i = \left\{ \begin{array}{@{}ll} - \dfrac{1}{2} R u_{\theta 0}^i + {\mathcal{L}}^{-1} ( A_1( s, \theta ) {\rm e}^{- a R} ) & \text{for} \ R \geq 0,\\ - \dfrac{1}{2} R [ u_{\theta 0}^i - \varOmega H ( T ) ] + R \varOmega H ( T ) + {\mathcal{L}}^{-1} ( B_1 ( s, \theta ) {\rm e}^{\bar{a} R} ) & \text{for}\ R < 0. \end{array} \right.\end{equation}
Here, the enforcements of the continuity of the velocity and its radial derivative at ![]() $R = 0$ determine the values of the integral constants
$R = 0$ determine the values of the integral constants ![]() $A_1$ and
$A_1$ and ![]() $B_1$ as follows:
$B_1$ as follows:
Using the relations of
and (A3) and (A4) in Appendix A, we finally obtain
 \begin{align} u_{\theta 1}^i & =- \frac{1}{2} R u_{\theta 0}^i - \frac{3 R \varOmega}{4 \lambda_o {\rm \pi}} \int_0^T \frac{\exp({- \lambda_o \xi}) - 1}{\sqrt{\xi ( T - \xi )^3}} \exp\left({- \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \nonumber\\ &\quad - \frac{3 R \varOmega}{4 \sqrt{{\rm \pi} \lambda_o}} \int_0^T \frac{ \exp\left({- \dfrac{R^2}{4 \nu_o ( T - \xi )}}\right)}{( T - \xi )^{3/2}} \text{erf} ( \sqrt{\lambda_o \xi} ) \,{\rm d} \xi \quad\text{for} \ R \geq 0, \end{align}
\begin{align} u_{\theta 1}^i & =- \frac{1}{2} R u_{\theta 0}^i - \frac{3 R \varOmega}{4 \lambda_o {\rm \pi}} \int_0^T \frac{\exp({- \lambda_o \xi}) - 1}{\sqrt{\xi ( T - \xi )^3}} \exp\left({- \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \nonumber\\ &\quad - \frac{3 R \varOmega}{4 \sqrt{{\rm \pi} \lambda_o}} \int_0^T \frac{ \exp\left({- \dfrac{R^2}{4 \nu_o ( T - \xi )}}\right)}{( T - \xi )^{3/2}} \text{erf} ( \sqrt{\lambda_o \xi} ) \,{\rm d} \xi \quad\text{for} \ R \geq 0, \end{align} \begin{align} u_{\theta 1}^i & =- \frac{1}{2} R \left( u_{\theta 0}^i - \varOmega H ( T ) \right) + R \varOmega H ( T ) \nonumber\\ &\quad - \frac{3 | R | \varOmega}{4 \lambda_o {\rm \pi}} \int_0^T \frac{\exp({- \lambda_o \xi}) - 1}{\sqrt{\xi ( T - \xi )^3}} \exp\left({- \lambda_o ( T - \xi ) - \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \nonumber\\ & \quad - \frac{3 | R | \varOmega}{4 \sqrt{{\rm \pi} \lambda_o}} \int_0^T \frac{\exp\left({- \lambda_o ( T - \xi ) - \dfrac{R^2}{4 \nu_o ( T - \xi )}}\right)}{( T - \xi )^{3/2}} \text{erf} ( \sqrt{\lambda_o \xi} ) \,{\rm d} \xi \quad \text{for} \ R < 0. \end{align}
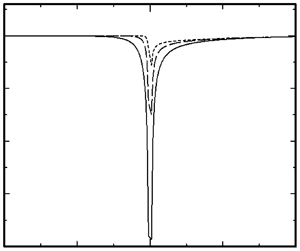
\begin{align} u_{\theta 1}^i & =- \frac{1}{2} R \left( u_{\theta 0}^i - \varOmega H ( T ) \right) + R \varOmega H ( T ) \nonumber\\ &\quad - \frac{3 | R | \varOmega}{4 \lambda_o {\rm \pi}} \int_0^T \frac{\exp({- \lambda_o \xi}) - 1}{\sqrt{\xi ( T - \xi )^3}} \exp\left({- \lambda_o ( T - \xi ) - \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \nonumber\\ & \quad - \frac{3 | R | \varOmega}{4 \sqrt{{\rm \pi} \lambda_o}} \int_0^T \frac{\exp\left({- \lambda_o ( T - \xi ) - \dfrac{R^2}{4 \nu_o ( T - \xi )}}\right)}{( T - \xi )^{3/2}} \text{erf} ( \sqrt{\lambda_o \xi} ) \,{\rm d} \xi \quad \text{for} \ R < 0. \end{align} Figure 2 shows the comparison of ![]() $u_{\theta 0}^i / \varOmega$ (first-order solution) and
$u_{\theta 0}^i / \varOmega$ (first-order solution) and ![]() $u_{\theta 1}^i / ( R \varOmega )$ (second-order solution) among three values of
$u_{\theta 1}^i / ( R \varOmega )$ (second-order solution) among three values of ![]() $\lambda$ with respect to
$\lambda$ with respect to ![]() $\eta = R / ( 2 \sqrt {\nu _o T} )$. To plot the data of figure 2, the numerical calculation of the following integral that is shown in (3.36) is needed. To do so, the integral variable
$\eta = R / ( 2 \sqrt {\nu _o T} )$. To plot the data of figure 2, the numerical calculation of the following integral that is shown in (3.36) is needed. To do so, the integral variable ![]() $\xi$ is changed by
$\xi$ is changed by ![]() $\xi = T x$ and, then, the variable
$\xi = T x$ and, then, the variable ![]() $x$ is changed to
$x$ is changed to ![]() $y$ by
$y$ by ![]() $x = 1 - \eta ^2 / [ (\kern0.7pt y + \eta )^2 ]$;
$x = 1 - \eta ^2 / [ (\kern0.7pt y + \eta )^2 ]$;
 \begin{align} &\int_0^T \frac{f ( \xi )}{( T - \xi )^{3 / 2}} \exp\left({- \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \nonumber\\ &\quad = 2 \frac{\exp({- \eta^2})}{\eta} \int_0^\infty \exp({- y^2 - 2 y \eta}) f \left( 1 - \frac{\eta^2}{(\kern0.7pt y + \eta )^2} \right) {\rm d} y. \end{align}
\begin{align} &\int_0^T \frac{f ( \xi )}{( T - \xi )^{3 / 2}} \exp\left({- \frac{R^2}{4 \nu_o ( T - \xi )}}\right) {\rm d} \xi \nonumber\\ &\quad = 2 \frac{\exp({- \eta^2})}{\eta} \int_0^\infty \exp({- y^2 - 2 y \eta}) f \left( 1 - \frac{\eta^2}{(\kern0.7pt y + \eta )^2} \right) {\rm d} y. \end{align}
In the numerical calculation of figure 2, the Hermite quadrature formula of ![]() $n = 9$ (see table 25.10 in Abramowitz & Stegun Reference Abramowitz and Stegun1954) is used for the quadrature of the integral on the right-hand side of (3.36).
$n = 9$ (see table 25.10 in Abramowitz & Stegun Reference Abramowitz and Stegun1954) is used for the quadrature of the integral on the right-hand side of (3.36).

Figure 2. Comparison of the tangential velocities ![]() $u_{\theta 0}^i$ (first-order solution) and
$u_{\theta 0}^i$ (first-order solution) and ![]() $u_{\theta 1}^i$ (second-order solution) among three values of
$u_{\theta 1}^i$ (second-order solution) among three values of ![]() $\lambda$ with respect to
$\lambda$ with respect to ![]() $\eta = R / ( 2 \sqrt {\nu _o T} )$.
$\eta = R / ( 2 \sqrt {\nu _o T} )$.
3.2.3. Moment exerted by a cylinder
In this subsection we attempt to obtain the moment exerted by the circular cylinder, using three kinds of approaches. Each approach is calculated (I) by the time derivative of the tangential component of the momentum of the entire fluid, (II) by the integration of the shear stress on the cylinder surface, and (III) by the integration of the penalization layer based on (2.3).
In approach (I) we consider the control surface that surrounds a circular domain having a radius of ![]() $r_\infty \gg 1$. Then, we can define the fluid domain as
$r_\infty \gg 1$. Then, we can define the fluid domain as ![]() ${\mathscr {F}} = [ ( r, \theta ) | 1 \leq r \leq r_\infty, 0 \leq \theta < 2 {\rm \pi}]$. The small fluid element
${\mathscr {F}} = [ ( r, \theta ) | 1 \leq r \leq r_\infty, 0 \leq \theta < 2 {\rm \pi}]$. The small fluid element ![]() ${\rm d}\kern0.06em x\ {\rm d} y$ has the momentum
${\rm d}\kern0.06em x\ {\rm d} y$ has the momentum ![]() $\rho u_{\theta } \,{\rm d}\kern0.06em x \,{\rm d} y$ in the tangential direction. The moment induced by the fluid element is therefore described as
$\rho u_{\theta } \,{\rm d}\kern0.06em x \,{\rm d} y$ in the tangential direction. The moment induced by the fluid element is therefore described as ![]() $| {\boldsymbol x} | \rho [ ( {\rm d} / {\rm d} t ) u_{\theta } ] \,{\rm d}\kern0.06em x \,{\rm d} y$. The moment
$| {\boldsymbol x} | \rho [ ( {\rm d} / {\rm d} t ) u_{\theta } ] \,{\rm d}\kern0.06em x \,{\rm d} y$. The moment ![]() $M_1$ of the flow exerted by the cylinder rotation is found to be calculated by, noting that the pressure on the control surface does not affect the moment,
$M_1$ of the flow exerted by the cylinder rotation is found to be calculated by, noting that the pressure on the control surface does not affect the moment,
To obtain ![]() $M_1$, we employ the Laplace transform to (3.37) and take the limit of
$M_1$, we employ the Laplace transform to (3.37) and take the limit of ![]() $r_\infty \to \infty$. Then, we have, taking into account that the outer solution is described as
$r_\infty \to \infty$. Then, we have, taking into account that the outer solution is described as ![]() $u_{\theta }^o = 0$ and
$u_{\theta }^o = 0$ and ![]() $u_{\theta }^i$ is independent of
$u_{\theta }^i$ is independent of ![]() $\theta$,
$\theta$,
where ![]() $U_{\theta 1} = {\mathcal {L}} ( u_{\theta 1}^i )$. Using (3.21) and the first equation of (3.32),
$U_{\theta 1} = {\mathcal {L}} ( u_{\theta 1}^i )$. Using (3.21) and the first equation of (3.32), ![]() $M_1$ can be obtained as
$M_1$ can be obtained as
In approach (II) the moment ![]() $M_2$ on the fluid is calculated by the integration of the shear stress on the cylinder surface
$M_2$ on the fluid is calculated by the integration of the shear stress on the cylinder surface
 \begin{equation} M_2 = \int_0^{2 {\rm \pi}} 1 \times \tau_{r \theta} \,{\rm d} \theta = \rho \nu \int_0^{2 {\rm \pi}} \left( \frac{\partial u_\theta}{\partial r} - u_\theta + \frac{\partial u_r}{\partial \theta} \right)_{r = 1 + 0} \,{\rm d} \theta. \end{equation}
\begin{equation} M_2 = \int_0^{2 {\rm \pi}} 1 \times \tau_{r \theta} \,{\rm d} \theta = \rho \nu \int_0^{2 {\rm \pi}} \left( \frac{\partial u_\theta}{\partial r} - u_\theta + \frac{\partial u_r}{\partial \theta} \right)_{r = 1 + 0} \,{\rm d} \theta. \end{equation}
The Laplace transform to (3.40) becomes, using the relations of ![]() $U_{r0} = U_{r1} = 0$,
$U_{r0} = U_{r1} = 0$,
Substituting (3.21) and the first equation of (3.32) into (3.41), we have
Comparing the results between (3.39) and (3.42), it is found that ![]() $M_1$ is identical with
$M_1$ is identical with ![]() $M_2$ within the order of
$M_2$ within the order of ![]() $\epsilon$, i.e. the moment calculated from the entire fluid domain is the same as that calculated from the tangential force on the cylinder surface. Making use of the inverse Laplace transform, the moment
$\epsilon$, i.e. the moment calculated from the entire fluid domain is the same as that calculated from the tangential force on the cylinder surface. Making use of the inverse Laplace transform, the moment ![]() $M_1$ (or
$M_1$ (or ![]() $M_2$) is obtained as
$M_2$) is obtained as
 \begin{align} M_1= M_2 & =- 2{\rm \pi} \rho
\varOmega \left\{ \sqrt{\frac{\nu_o}{{\rm \pi} T}} + \frac{1}{2}
\sqrt{\frac{\nu_o}{{\rm \pi} T^3}} \frac{1 - {\rm e}^{-
\lambda_o T}}{\lambda_o}\right.\nonumber\\ &\quad\left.+\,
\frac{3}{2} \epsilon \nu_o [ H ( T ) - {\rm e}^{-
\lambda_o T / 2} \left( {\rm I}_0 ( \lambda_o T / 2 ) +
{\rm I}_1 ( \lambda_o T / 2 ) \right)] + O (
\epsilon^2 ) \right\}.
\end{align}
\begin{align} M_1= M_2 & =- 2{\rm \pi} \rho
\varOmega \left\{ \sqrt{\frac{\nu_o}{{\rm \pi} T}} + \frac{1}{2}
\sqrt{\frac{\nu_o}{{\rm \pi} T^3}} \frac{1 - {\rm e}^{-
\lambda_o T}}{\lambda_o}\right.\nonumber\\ &\quad\left.+\,
\frac{3}{2} \epsilon \nu_o [ H ( T ) - {\rm e}^{-
\lambda_o T / 2} \left( {\rm I}_0 ( \lambda_o T / 2 ) +
{\rm I}_1 ( \lambda_o T / 2 ) \right)] + O (
\epsilon^2 ) \right\}.
\end{align} In approach (III) the moment ![]() $M_3$ on the fluid is calculated by the integration of the penalization layer, based on (2.3),
$M_3$ on the fluid is calculated by the integration of the penalization layer, based on (2.3),
 \begin{align} M_3& =- \rho \lambda
\int_0^{2 {\rm \pi}} \!\! \int_0^1 r ( r \varOmega - u_\theta )
r \, {\rm d} r\, {\rm d} \theta\nonumber\\ & =- \rho
\lambda \epsilon \int_0^{2 {\rm \pi}} \!\! \int_{- \infty}^0
[ ( 1 + \epsilon R ) \varOmega - u_\theta^i ] (
1 + \epsilon R )^2 \,{\rm d} R\, {\rm d} \theta.
\end{align}
\begin{align} M_3& =- \rho \lambda
\int_0^{2 {\rm \pi}} \!\! \int_0^1 r ( r \varOmega - u_\theta )
r \, {\rm d} r\, {\rm d} \theta\nonumber\\ & =- \rho
\lambda \epsilon \int_0^{2 {\rm \pi}} \!\! \int_{- \infty}^0
[ ( 1 + \epsilon R ) \varOmega - u_\theta^i ] (
1 + \epsilon R )^2 \,{\rm d} R\, {\rm d} \theta.
\end{align} Similar to the calculation of ![]() $M_1$ or
$M_1$ or ![]() $M_2$, the Laplace transform to
$M_2$, the Laplace transform to ![]() $M_3$ is written as, using (3.21) and the second equation of (3.32),
$M_3$ is written as, using (3.21) and the second equation of (3.32),
The inverse Laplace transform to (3.45) yields
From the results of (3.43) and (3.46), each moment is found to behave like, as ![]() $\lambda _o \to \infty$,
$\lambda _o \to \infty$,
It can therefore be found that the moment ![]() $M_3$ obtained by the integration of the penalization layer is identical to
$M_3$ obtained by the integration of the penalization layer is identical to ![]() $M_1$ and
$M_1$ and ![]() $M_2$ as
$M_2$ as ![]() $\lambda _o \to \infty$. Because the pressure is independent of the moment in this pure rotation problem, the pressure is found to play an important role to the variance of the drag force, which is demonstrated in our previous study (see Ueda & Kida Reference Ueda and Kida2021). Note that (3.47a–c) is the same as the result of Badr & Dennis (Reference Badr and Dennis1985). Figure 3 shows the comparisons of the values between
$\lambda _o \to \infty$. Because the pressure is independent of the moment in this pure rotation problem, the pressure is found to play an important role to the variance of the drag force, which is demonstrated in our previous study (see Ueda & Kida Reference Ueda and Kida2021). Note that (3.47a–c) is the same as the result of Badr & Dennis (Reference Badr and Dennis1985). Figure 3 shows the comparisons of the values between ![]() $M_1$ and
$M_1$ and ![]() $M_3$ with respect to
$M_3$ with respect to ![]() $t$ among the three values of
$t$ among the three values of ![]() $\lambda$ at
$\lambda$ at ![]() $Re = 100$ (i.e.
$Re = 100$ (i.e. ![]() $\nu = 1 / 100$). It seems that the variance between
$\nu = 1 / 100$). It seems that the variance between ![]() $M_1$ (or
$M_1$ (or ![]() $M_2$) and
$M_2$) and ![]() $M_3$ decreases exponentially with an increase in the value of
$M_3$ decreases exponentially with an increase in the value of ![]() $\lambda$.
$\lambda$.

Figure 3. Initial behaviours of the moments ![]() $M_1$ and
$M_1$ and ![]() $M_3$ with respect to
$M_3$ with respect to ![]() $t$ among the different values of
$t$ among the different values of ![]() $\lambda$ at
$\lambda$ at ![]() $\nu = 1 / 100$.
$\nu = 1 / 100$.
3.3. Second problem: an impulsively rotating and translating circular cylinder
In this subsection we consider the problem that a circular cylinder impulsively starts with the angular velocity ![]() $\varOmega$ and the translating velocity
$\varOmega$ and the translating velocity ![]() $U_o$. The velocity is normalized with
$U_o$. The velocity is normalized with ![]() $U_o$ and, then, the translating velocity and the rotational angular velocity of the cylinder are non-dimensionalized as
$U_o$ and, then, the translating velocity and the rotational angular velocity of the cylinder are non-dimensionalized as ![]() $1$ and
$1$ and ![]() $\varOmega$, respectively. Similar to the analysis in § 3.2, the governing equations (3.1a)–(3.3) are adopted in this problem.
$\varOmega$, respectively. Similar to the analysis in § 3.2, the governing equations (3.1a)–(3.3) are adopted in this problem.
3.3.1. Outer solutions
The outer solutions in the fluid domain are described by (3.6a)–(3.6d) in the same manner as § 3.2.1, and the first approximation reduces to
The velocities ![]() $u_{r0}^0$ and
$u_{r0}^0$ and ![]() $u_{\theta 0}^o$ are then found to be independent of
$u_{\theta 0}^o$ are then found to be independent of ![]() $T$. The first-order outer solution in the fluid domain is known to exhibit a potential flow (i.e. inviscid solution). This fact can be confirmed by performing the recursive calculation. Based on this fact and the initial condition of the fluid velocity that
$T$. The first-order outer solution in the fluid domain is known to exhibit a potential flow (i.e. inviscid solution). This fact can be confirmed by performing the recursive calculation. Based on this fact and the initial condition of the fluid velocity that ![]() $u_{r}^o = \cos {\theta } H ( T )$ and
$u_{r}^o = \cos {\theta } H ( T )$ and ![]() $u_{\theta }^0 = - \sin {\theta } H ( T )$ for
$u_{\theta }^0 = - \sin {\theta } H ( T )$ for ![]() $r \geq 1$, the outer streamfunction
$r \geq 1$, the outer streamfunction ![]() $\psi ^o$ can be described as
$\psi ^o$ can be described as
 \begin{equation} \psi^o = r \sin{\theta} H ( T ) + \sum_{n = 1}^\infty \frac{1}{r^n} ( a_n^c \cos{n \theta} + a_n^s \sin{n \theta} ), \end{equation}
\begin{equation} \psi^o = r \sin{\theta} H ( T ) + \sum_{n = 1}^\infty \frac{1}{r^n} ( a_n^c \cos{n \theta} + a_n^s \sin{n \theta} ), \end{equation}
where ![]() $a_n^c$ and
$a_n^c$ and ![]() $a_n^s$ are functions of
$a_n^s$ are functions of ![]() $T$ and
$T$ and ![]() $\epsilon$, respectively.
$\epsilon$, respectively.
The outer solutions inside the body domain are also described by (3.6a)–(3.6d). Taking into account that the initial condition is given by ![]() $u_r^o = 0$ and
$u_r^o = 0$ and ![]() $u_{\theta }^o = r \varOmega H ( T )$, we readily have
$u_{\theta }^o = r \varOmega H ( T )$, we readily have
where ![]() $C$ is an integral constant that is a function of
$C$ is an integral constant that is a function of ![]() $T$.
$T$.
3.3.2. Inner solutions
The inner solutions are described by the same governing equations as (3.10a)–(3.10c). The continuity equation (3.10c) gives
in which ![]() $u_{r 0}^i$ is found to be independent of
$u_{r 0}^i$ is found to be independent of ![]() $R$ (i.e. a function of
$R$ (i.e. a function of ![]() $T$ and
$T$ and ![]() $\theta$). Because the outer solutions inside the body domain were
$\theta$). Because the outer solutions inside the body domain were ![]() $u_r^o = 0$ and
$u_r^o = 0$ and ![]() $u_\theta ^o = r \varOmega H ( T )$ as obtained in (3.50a–c), we have the following first-order inner solution, for
$u_\theta ^o = r \varOmega H ( T )$ as obtained in (3.50a–c), we have the following first-order inner solution, for ![]() $R \geq 0$ and
$R \geq 0$ and ![]() $R < 0$, taking into account the matching condition to the outer solutions:
$R < 0$, taking into account the matching condition to the outer solutions:
The first-order outer solution in the fluid domain described by (3.49) can be determined from the matching procedure to the inner solution of (3.52) and, therefore, we have ![]() $u_{r 0}^{o i} = u_{r 0}^{i o} = 0$. Here, the inner (or outer) expansion of the outer (or inner) solution is denoted by the superscript ‘
$u_{r 0}^{o i} = u_{r 0}^{i o} = 0$. Here, the inner (or outer) expansion of the outer (or inner) solution is denoted by the superscript ‘![]() $oi$’ (or ‘
$oi$’ (or ‘![]() $io$’). Taking into account that the outer solution of
$io$’). Taking into account that the outer solution of ![]() $\psi ^o$ is written by (3.49), the above-mentioned matching condition (i.e.
$\psi ^o$ is written by (3.49), the above-mentioned matching condition (i.e. ![]() $u_{r 0}^{o i} = u_{r 0}^{i o} = 0$) yields the first-order streamfunction in the outer fluid domain as
$u_{r 0}^{o i} = u_{r 0}^{i o} = 0$) yields the first-order streamfunction in the outer fluid domain as
which is known to be the solution of an inviscid uniform flow past a circular cylinder. The governing equations that describe the first-order solutions in the inner fluid domain are the same as (3.13a) and (3.13b), i.e.
Here, let us consider ![]() $u_{\theta 0}^i$ of (3.54b). From (3.53), the inner expansion of
$u_{\theta 0}^i$ of (3.54b). From (3.53), the inner expansion of ![]() $u_{\theta 0}^o$ in the fluid domain is written as
$u_{\theta 0}^o$ in the fluid domain is written as ![]() $u_{\theta 0}^{o i} = - 2 \sin {\theta } H ( T )$ and, therefore, we can write
$u_{\theta 0}^{o i} = - 2 \sin {\theta } H ( T )$ and, therefore, we can write
In contrast, since ![]() $u_{\theta 0}^o = r \varOmega H ( T )$ inside the body domain, we can write
$u_{\theta 0}^o = r \varOmega H ( T )$ inside the body domain, we can write
The Laplace transform to (3.54b) for ![]() $R \geq 0$ is written as, taking into account the initial condition of
$R \geq 0$ is written as, taking into account the initial condition of ![]() $u_{\theta 0}^i = - 2 \sin {\theta }$,
$u_{\theta 0}^i = - 2 \sin {\theta }$,
where ![]() $U_{\theta 0} = {\mathcal {L}} ( u_{\theta 0}^i )$. The solution to (3.55) can be then obtained as (see Appendix B for the detailed derivation)
$U_{\theta 0} = {\mathcal {L}} ( u_{\theta 0}^i )$. The solution to (3.55) can be then obtained as (see Appendix B for the detailed derivation)
where ![]() $A_0$ is an integral constant that is a function of
$A_0$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$. For
$\theta$. For ![]() $R < 0$, the governing equation is given in (3.54b) as
$R < 0$, the governing equation is given in (3.54b) as ![]() $\chi = 1$, and the initial condition is written as
$\chi = 1$, and the initial condition is written as ![]() $u_{\theta 0}^i = \varOmega$. Therefore, the Laplace transform to the governing equation yields, for
$u_{\theta 0}^i = \varOmega$. Therefore, the Laplace transform to the governing equation yields, for ![]() $R < 0$,
$R < 0$,
The solution to (3.59) is obtained as, taking into account (3.56) (see Appendix B),
where ![]() $B_0$ is an integral constant that is a function of
$B_0$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$. The indeterminate functions,
$\theta$. The indeterminate functions, ![]() $A_0$ and
$A_0$ and ![]() $B_0$, are determined by the enforcements of the continuity of the velocity and its derivative with respect to
$B_0$, are determined by the enforcements of the continuity of the velocity and its derivative with respect to ![]() $R$ at
$R$ at ![]() $R = 0$. Therefore, we can finally obtain
$R = 0$. Therefore, we can finally obtain
 \begin{equation} U_{\theta 0} = \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{\bar{a}}{a + \bar{a}} \dfrac{\varOmega + 2 \sin{\theta}}{s} {\rm e}^{- a R} - \dfrac{2}{s} \sin{\theta} & \text{for} \ R \geq 0,\\[10pt] \displaystyle - \dfrac{{a}}{a + \bar{a}} \dfrac{\varOmega + 2 \sin{\theta}}{s} {\rm e}^{\bar{a} R} + \dfrac{\varOmega}{s} & \text{for} \ R < 0. \end{array} \right. \end{equation}
\begin{equation} U_{\theta 0} = \left\{ \begin{array}{@{}ll} \displaystyle \dfrac{\bar{a}}{a + \bar{a}} \dfrac{\varOmega + 2 \sin{\theta}}{s} {\rm e}^{- a R} - \dfrac{2}{s} \sin{\theta} & \text{for} \ R \geq 0,\\[10pt] \displaystyle - \dfrac{{a}}{a + \bar{a}} \dfrac{\varOmega + 2 \sin{\theta}}{s} {\rm e}^{\bar{a} R} + \dfrac{\varOmega}{s} & \text{for} \ R < 0. \end{array} \right. \end{equation}
By virtue of the form of (3.61) in the Laplace space, the solution ![]() $u_{\theta 0}^i$ in the real space is found to be written as
$u_{\theta 0}^i$ in the real space is found to be written as
Here, ![]() $\hat {u}_{\theta 0}^0$ is the same as (3.22) and (3.23) that are the solutions for the pure rotation problem analysed in § 3.2. In addition,
$\hat {u}_{\theta 0}^0$ is the same as (3.22) and (3.23) that are the solutions for the pure rotation problem analysed in § 3.2. In addition, ![]() $\hat {u}_{\theta 0}^s$ is the same as the solution for the pure translating motion that was derived in our previous study (see Ueda & Kida Reference Ueda and Kida2021).
$\hat {u}_{\theta 0}^s$ is the same as the solution for the pure translating motion that was derived in our previous study (see Ueda & Kida Reference Ueda and Kida2021).
For the second approximation, ![]() $u_{r1}^i$ is described by (3.10c), and it reduces to
$u_{r1}^i$ is described by (3.10c), and it reduces to
Using the matching condition to the outer solution inside the body domain (![]() $u_{r 1}^i \to 0$ as
$u_{r 1}^i \to 0$ as ![]() $R \to - \infty$), (3.63) becomes
$R \to - \infty$), (3.63) becomes
Making use of the Laplace transform and the first-order solution of (3.61) in the Laplace space, (3.64) can be written as, for ![]() $R < 0$,
$R < 0$,
where ![]() $U_{r 1} = {\mathcal {L}} ( u_{r 1}^i )$. For
$U_{r 1} = {\mathcal {L}} ( u_{r 1}^i )$. For ![]() $R \geq 0$, the function
$R \geq 0$, the function ![]() $U_{r 1}$ is continuous at
$U_{r 1}$ is continuous at ![]() $R = 0$ and, therefore, (3.64) can be written as
$R = 0$ and, therefore, (3.64) can be written as
 \begin{align} U_{r 1}& =-
\frac{\partial}{\partial \theta} \Bigg( \int_{- \infty}^0
U_{\theta 0} \,{\rm d} R + \int_0^R U_{\theta 0} \,{\rm d}
R \Bigg)\nonumber\\ & = 2 \frac{a}{\bar{a} ( a + \bar{a}
)} \frac{1}{s} \cos{\theta} - 2 \frac{\bar{a}}{a ( a +
\bar{a} )} \frac{1 - {\rm e}^{- a R}}{s} \cos{\theta} +
\frac{2}{s} R \cos{\theta}.
\end{align}
\begin{align} U_{r 1}& =-
\frac{\partial}{\partial \theta} \Bigg( \int_{- \infty}^0
U_{\theta 0} \,{\rm d} R + \int_0^R U_{\theta 0} \,{\rm d}
R \Bigg)\nonumber\\ & = 2 \frac{a}{\bar{a} ( a + \bar{a}
)} \frac{1}{s} \cos{\theta} - 2 \frac{\bar{a}}{a ( a +
\bar{a} )} \frac{1 - {\rm e}^{- a R}}{s} \cos{\theta} +
\frac{2}{s} R \cos{\theta}.
\end{align}
By virtue of (3.65) and (3.66), the function ![]() $u_{r 1}^i$ is found to be expressed as the form of
$u_{r 1}^i$ is found to be expressed as the form of
Here, we consider the matching to the outer solution. Equation (3.66) tends to, as ![]() $R \to \infty$,
$R \to \infty$,
Taking into account that the outer streamfunction is asymptotically represented as ![]() $\psi ^o = \psi _0^o + \epsilon \psi _1^o + O ( \epsilon ^2 )$, i.e.
$\psi ^o = \psi _0^o + \epsilon \psi _1^o + O ( \epsilon ^2 )$, i.e.
 \begin{equation} \psi^o = \left( r - \frac{1}{r} \right) H ( T ) \sin{\theta} + \epsilon \sum_{n = 1}^\infty \frac{1}{r^n} ( a_n^c \cos{n \theta} + a_n^s \sin{n \theta} ) + O ( \epsilon^2 ), \end{equation}
\begin{equation} \psi^o = \left( r - \frac{1}{r} \right) H ( T ) \sin{\theta} + \epsilon \sum_{n = 1}^\infty \frac{1}{r^n} ( a_n^c \cos{n \theta} + a_n^s \sin{n \theta} ) + O ( \epsilon^2 ), \end{equation}the matching procedure between (3.68) and (3.69) determines the values of the coefficients as
The streamfunction in the outer fluid domain is therefore written as
where ![]() $A$ is defined by
$A$ is defined by
The inner expansion of the outer solution (3.71) is calculated as, in the Laplace space,
The matching to (3.73) (i.e. ![]() ${\mathcal {L}} ( u_\theta ^{o i} ) = {\mathcal {L}} ( u_\theta ^{i o} )$) gives the following boundary condition of
${\mathcal {L}} ( u_\theta ^{o i} ) = {\mathcal {L}} ( u_\theta ^{i o} )$) gives the following boundary condition of ![]() $u_{\theta 1}^i$ as
$u_{\theta 1}^i$ as ![]() $R \to \infty$:
$R \to \infty$:
Similarly, since ![]() $u_\theta ^o = r \varOmega H ( T )$ inside the body domain, we have
$u_\theta ^o = r \varOmega H ( T )$ inside the body domain, we have
The second approximation of (3.10a) and (3.10b) are written as
 $$\begin{gather}\frac{\partial u_{\theta 1}^i}{\partial T} + u_{r 1}^i \frac{\partial u_{\theta 0}^i}{\partial R} + u_{\theta 0}^i \frac{\partial u_{\theta 0}^i}{\partial \theta} =- \frac{1}{\rho} \frac{\partial p_0^i}{\partial \theta} + \lambda_o \chi ( R \varOmega H ( T ) - u_{\theta 1}^i) + \nu_o \Bigg( \frac{\partial^2 u_{\theta 1}^i}{\partial R^2} + \frac{\partial u_{\theta 0}^i}{\partial R} \Bigg). \end{gather}$$
$$\begin{gather}\frac{\partial u_{\theta 1}^i}{\partial T} + u_{r 1}^i \frac{\partial u_{\theta 0}^i}{\partial R} + u_{\theta 0}^i \frac{\partial u_{\theta 0}^i}{\partial \theta} =- \frac{1}{\rho} \frac{\partial p_0^i}{\partial \theta} + \lambda_o \chi ( R \varOmega H ( T ) - u_{\theta 1}^i) + \nu_o \Bigg( \frac{\partial^2 u_{\theta 1}^i}{\partial R^2} + \frac{\partial u_{\theta 0}^i}{\partial R} \Bigg). \end{gather}$$
The pressure ![]() $p_0^i$ is found to be independent of
$p_0^i$ is found to be independent of ![]() $R$ from (3.54a), and
$R$ from (3.54a), and ![]() $p^o$ is given by (3.50a–c) in the outer domain inside the body. In the fluid domain, since the outer solution is described by a potential flow (inviscid solution), the following unsteady Bernoulli's equation is valid:
$p^o$ is given by (3.50a–c) in the outer domain inside the body. In the fluid domain, since the outer solution is described by a potential flow (inviscid solution), the following unsteady Bernoulli's equation is valid:
Here, ![]() $\phi ^o$ is the velocity potential in the outer fluid domain, and it is given from (3.71), as
$\phi ^o$ is the velocity potential in the outer fluid domain, and it is given from (3.71), as
Substituting (3.78) into (3.77) yields
Setting ![]() $r = 1 + \epsilon R$, we have
$r = 1 + \epsilon R$, we have
Since ![]() $p_0^{o i} = C + ( \rho / 2 ) \varOmega ^2 H ( T ) + O ( \epsilon )$ for
$p_0^{o i} = C + ( \rho / 2 ) \varOmega ^2 H ( T ) + O ( \epsilon )$ for ![]() $R < 0$ from (3.50a–c), the function
$R < 0$ from (3.50a–c), the function ![]() $p_0^i$ is written as, taking into account (3.54a),
$p_0^i$ is written as, taking into account (3.54a),
 \begin{equation} \frac{p_0^i}{\rho} = \left\{ \begin{array}{@{}ll} \displaystyle 2 \dfrac{{\rm d} A}{{\rm d} T} \cos{\theta} - 2 H ( T ) \sin^2{\theta} + \dfrac{1}{2} H ( T ) & \text{for} \ R \geq 0,\\[10pt] \displaystyle \dfrac{C}{\rho} + \dfrac{1}{2} \varOmega^2 H ( T ) & \text{for} \ R < 0. \end{array} \right.\end{equation}
\begin{equation} \frac{p_0^i}{\rho} = \left\{ \begin{array}{@{}ll} \displaystyle 2 \dfrac{{\rm d} A}{{\rm d} T} \cos{\theta} - 2 H ( T ) \sin^2{\theta} + \dfrac{1}{2} H ( T ) & \text{for} \ R \geq 0,\\[10pt] \displaystyle \dfrac{C}{\rho} + \dfrac{1}{2} \varOmega^2 H ( T ) & \text{for} \ R < 0. \end{array} \right.\end{equation}Equation (3.76b) can then be rewritten as
 \begin{align} \frac{\partial u_{\theta 1}^i}{\partial T} - \nu_o \frac{\partial^2 u_{\theta 1}^i}{\partial R^2} + \lambda_o \chi u_{\theta 1}^i & = \left\{\begin{array}{ll} \displaystyle 2\dfrac{{\rm d} A}{{\rm d} T} \sin{\theta} + 4 H ( T ) \sin{\theta} \cos{\theta} & \text{for}\ R \geq 0 \\[10pt] \displaystyle 0 & \text{for}\ R < 0 \end{array}\right\} - u_{r 1}^i \frac{\partial u_{\theta 0}^i}{\partial R} \nonumber\\ &\quad - u_{\theta 0}^i \frac{\partial u_{\theta 0}^i}{\partial \theta} + \nu_o \frac{\partial u_{\theta 0}^i}{\partial R} + \lambda_o \chi ( \varOmega R H ( T ) ). \end{align}
\begin{align} \frac{\partial u_{\theta 1}^i}{\partial T} - \nu_o \frac{\partial^2 u_{\theta 1}^i}{\partial R^2} + \lambda_o \chi u_{\theta 1}^i & = \left\{\begin{array}{ll} \displaystyle 2\dfrac{{\rm d} A}{{\rm d} T} \sin{\theta} + 4 H ( T ) \sin{\theta} \cos{\theta} & \text{for}\ R \geq 0 \\[10pt] \displaystyle 0 & \text{for}\ R < 0 \end{array}\right\} - u_{r 1}^i \frac{\partial u_{\theta 0}^i}{\partial R} \nonumber\\ &\quad - u_{\theta 0}^i \frac{\partial u_{\theta 0}^i}{\partial \theta} + \nu_o \frac{\partial u_{\theta 0}^i}{\partial R} + \lambda_o \chi ( \varOmega R H ( T ) ). \end{align}
The second-order solution ![]() $u_{\theta 1}^i$ is therefore found to be expressed as, with respect to
$u_{\theta 1}^i$ is therefore found to be expressed as, with respect to ![]() $\theta$,
$\theta$,
Substituting (3.83) into (3.82), we can write (3.82) separately:
 $$\begin{gather}\frac{\partial \hat{u}_{\theta 1}^s}{\partial T} - \nu_o \frac{\partial^2 \hat{u}_{\theta 1}^s}{\partial R^2} + \lambda_o \chi \hat{u}_{\theta 1}^s = \nu_o \frac{\partial \hat{u}_{\theta 0}^s}{\partial R} + \left\{\begin{array}{@{}ll@{}} \displaystyle2 \dfrac{{\rm d} A}{{\rm d} T} & \text{for} \ R \geq 0\\[9pt] \displaystyle 0 & \text{for}\ R < 0 \end{array} \right\}, \end{gather}$$
$$\begin{gather}\frac{\partial \hat{u}_{\theta 1}^s}{\partial T} - \nu_o \frac{\partial^2 \hat{u}_{\theta 1}^s}{\partial R^2} + \lambda_o \chi \hat{u}_{\theta 1}^s = \nu_o \frac{\partial \hat{u}_{\theta 0}^s}{\partial R} + \left\{\begin{array}{@{}ll@{}} \displaystyle2 \dfrac{{\rm d} A}{{\rm d} T} & \text{for} \ R \geq 0\\[9pt] \displaystyle 0 & \text{for}\ R < 0 \end{array} \right\}, \end{gather}$$
The boundary condition are written as, ![]() $R \to \infty$,
$R \to \infty$,
As ![]() $R \to -\infty$, the boundary conditions are also written as
$R \to -\infty$, the boundary conditions are also written as
Using the Laplace transformation and the similar procedure for the derivation of the first approximations, we finally obtain the following solutions (the detailed derivation is described in Appendix C):
 \begin{equation} U_{\theta 1}^0 = \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2} \dfrac{\varOmega}{s ( a + \bar{a} )} \left( \bar{a} R - 3 \right) {\rm e}^{- a R} & \text{for} \ R \geq 0,\\[10pt] \displaystyle \dfrac{1}{2} \dfrac{\varOmega}{s ( a + \bar{a} )} \left( a R - 3 \right) {\rm e}^{\bar{a} R} + \dfrac{\varOmega}{s} R & \text{for} \ R < 0. \end{array} \right.\end{equation}
\begin{equation} U_{\theta 1}^0 = \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2} \dfrac{\varOmega}{s ( a + \bar{a} )} \left( \bar{a} R - 3 \right) {\rm e}^{- a R} & \text{for} \ R \geq 0,\\[10pt] \displaystyle \dfrac{1}{2} \dfrac{\varOmega}{s ( a + \bar{a} )} \left( a R - 3 \right) {\rm e}^{\bar{a} R} + \dfrac{\varOmega}{s} R & \text{for} \ R < 0. \end{array} \right.\end{equation}
The velocity, ![]() $\hat {u}_{\theta 1}^0$, is then found to be the same as the solution to the pure rotation problem obtained in (3.32).
$\hat {u}_{\theta 1}^0$, is then found to be the same as the solution to the pure rotation problem obtained in (3.32).
For ![]() $u_{\theta 1}^s$, we have
$u_{\theta 1}^s$, we have
 \begin{equation}
U_{\theta 1}^s =
\left\{ \begin{array}{@{}ll} \displaystyle 2 \dfrac{R}{s} +
2 \dfrac{a - \bar{a}}{s a \bar{a}} - \dfrac{\bar{a}}{s ( a
+ \bar{a} )} R {\rm e}^{- a R} + D_s {\rm e}^{- a R} &
\text{for} \ R \geq 0,\\[10pt] \displaystyle \dfrac{a}{s (
a + \bar{a} )} R {\rm e}^{\bar{a} R} + E_s {\rm e}^{\bar{a}
R} & \text{for} \ R < 0, \end{array}
\right.
\end{equation}
\begin{equation}
U_{\theta 1}^s =
\left\{ \begin{array}{@{}ll} \displaystyle 2 \dfrac{R}{s} +
2 \dfrac{a - \bar{a}}{s a \bar{a}} - \dfrac{\bar{a}}{s ( a
+ \bar{a} )} R {\rm e}^{- a R} + D_s {\rm e}^{- a R} &
\text{for} \ R \geq 0,\\[10pt] \displaystyle \dfrac{a}{s (
a + \bar{a} )} R {\rm e}^{\bar{a} R} + E_s {\rm e}^{\bar{a}
R} & \text{for} \ R < 0, \end{array}
\right.
\end{equation}where
It is then found that the velocity ![]() $\hat {u}_{\theta 1}^s$ is the same as the solution to the pure translation problem analysed in our previous paper (see Ueda & Kida Reference Ueda and Kida2021).
$\hat {u}_{\theta 1}^s$ is the same as the solution to the pure translation problem analysed in our previous paper (see Ueda & Kida Reference Ueda and Kida2021).
We define the following relations that are written as
 \begin{equation} U_{\theta 1}^c = {\mathcal{L}} ( \hat{u}_{\theta 1}^c ) \quad \text{and} \quad F^c = {\mathcal{L}} \Bigg( \hat{u}_{r 1} \frac{\partial \hat{u}_{\theta 0}^0}{\partial R} + \hat{u}_{\theta 0}^0 \hat{u}_{\theta 0}^s \Bigg). \end{equation}
\begin{equation} U_{\theta 1}^c = {\mathcal{L}} ( \hat{u}_{\theta 1}^c ) \quad \text{and} \quad F^c = {\mathcal{L}} \Bigg( \hat{u}_{r 1} \frac{\partial \hat{u}_{\theta 0}^0}{\partial R} + \hat{u}_{\theta 0}^0 \hat{u}_{\theta 0}^s \Bigg). \end{equation}Then, we can have the following relations:
 \begin{equation} U_{\theta 1}^c = \left\{\begin{array}{@{}ll} - \displaystyle\dfrac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^c {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^c {\rm e}^{a R} \,{\rm d} R \right) + D_c {\rm e}^{- a R}, & R\geq 0, \\[10pt] \displaystyle- \dfrac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^c {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^c {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_c {\rm e}^{\bar{a} R}, & R<0, \end{array} \right. \end{equation}
\begin{equation} U_{\theta 1}^c = \left\{\begin{array}{@{}ll} - \displaystyle\dfrac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^c {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^c {\rm e}^{a R} \,{\rm d} R \right) + D_c {\rm e}^{- a R}, & R\geq 0, \\[10pt] \displaystyle- \dfrac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^c {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^c {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_c {\rm e}^{\bar{a} R}, & R<0, \end{array} \right. \end{equation}
where ![]() $D_c$ and
$D_c$ and ![]() $E_c$ are respectively given by
$E_c$ are respectively given by
We also define ![]() $\hat {U}_{\theta 1}^{c s}$ and
$\hat {U}_{\theta 1}^{c s}$ and ![]() $F^{c s}$ as
$F^{c s}$ as
Then, we can obtain
 \begin{align} U_{\theta 1}^{c s} = \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^{c s} {\rm e}^{a R} \,{\rm d} R \right) + D_{c s} {\rm e}^{- a R} & \text{for} \ R \geq 0,\\[10pt] \displaystyle - \dfrac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^{c s} {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_{c s} {\rm e}^{\bar{a} R} & \text{for}\ R < 0, \end{array} \right. \end{align}
\begin{align} U_{\theta 1}^{c s} = \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^{c s} {\rm e}^{a R} \,{\rm d} R \right) + D_{c s} {\rm e}^{- a R} & \text{for} \ R \geq 0,\\[10pt] \displaystyle - \dfrac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^{c s} {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_{c s} {\rm e}^{\bar{a} R} & \text{for}\ R < 0, \end{array} \right. \end{align}
in which the constants ![]() $D_{c s}$ and
$D_{c s}$ and ![]() $E_{c s}$ are respectively given by
$E_{c s}$ are respectively given by
Based on the solutions obtained, each velocity component is found to asymptotically behave like, for ![]() $\lambda _o \gg 1$,
$\lambda _o \gg 1$,
 \begin{gather} \hat{u}_{\theta 0}^0 \sim \left\{ \begin{array}{@{}ll} \displaystyle \varOmega \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right): & R \geq 0,\\[10pt] \displaystyle \varOmega H ( T ) : & R < 0. \end{array}\right.\end{gather}
\begin{gather} \hat{u}_{\theta 0}^0 \sim \left\{ \begin{array}{@{}ll} \displaystyle \varOmega \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right): & R \geq 0,\\[10pt] \displaystyle \varOmega H ( T ) : & R < 0. \end{array}\right.\end{gather} \begin{gather} \hat{u}_{\theta 0}^s \sim \left\{ \begin{array}{@{}ll} \displaystyle 2 \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right)- 2 H ( T ) : & R \geq 0,\\ \displaystyle 0 : & R < 0. \end{array} \right.\end{gather}
\begin{gather} \hat{u}_{\theta 0}^s \sim \left\{ \begin{array}{@{}ll} \displaystyle 2 \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right)- 2 H ( T ) : & R \geq 0,\\ \displaystyle 0 : & R < 0. \end{array} \right.\end{gather} \begin{gather} \hat{u}_{r1} \sim \left\{ \begin{array}{@{}ll} \displaystyle 2 R H ( T ) - 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} + 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} \exp\left({- \dfrac{R^2}{4 \nu_o T}}\right) - 2 R \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right) : & R \geq 0,\\ \displaystyle 0 : & R < 0. \end{array} \right.\end{gather}
\begin{gather} \hat{u}_{r1} \sim \left\{ \begin{array}{@{}ll} \displaystyle 2 R H ( T ) - 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} + 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} \exp\left({- \dfrac{R^2}{4 \nu_o T}}\right) - 2 R \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right) : & R \geq 0,\\ \displaystyle 0 : & R < 0. \end{array} \right.\end{gather} \begin{gather} \hat{u}_{\theta 1}^0 \sim \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2} \varOmega R \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right) : & R \geq 0,\\ \displaystyle \varOmega R H ( T ) : & R < 0. \end{array} \right. \end{gather}
\begin{gather} \hat{u}_{\theta 1}^0 \sim \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2} \varOmega R \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right) : & R \geq 0,\\ \displaystyle \varOmega R H ( T ) : & R < 0. \end{array} \right. \end{gather} \begin{gather} \hat{u}_{\theta 1}^s \sim \left\{ \begin{array}{@{}ll} \displaystyle 2 R H ( T ) - 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} + 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} \exp\left({- \dfrac{R^2}{4 \nu_o T}}\right) - 3 R \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right) : & R \geq 0,\\ \displaystyle 0 : & R < 0. \end{array} \right. \end{gather}
\begin{gather} \hat{u}_{\theta 1}^s \sim \left\{ \begin{array}{@{}ll} \displaystyle 2 R H ( T ) - 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} + 4 \sqrt{\dfrac{\nu_o T}{\rm \pi}} \exp\left({- \dfrac{R^2}{4 \nu_o T}}\right) - 3 R \, \text{erfc} \left( \dfrac{R}{2 \sqrt{\nu_o T}} \right) : & R \geq 0,\\ \displaystyle 0 : & R < 0. \end{array} \right. \end{gather} \begin{gather} \hat{u}_{\theta 1}^c \sim \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2\sqrt{{\rm \pi} \nu_o}} \int_0^\infty \,{\rm d} R' \,\int_0^T \dfrac{f^c ( \xi, R' )}{\sqrt{T - \xi}}\left[ \exp\left({- \dfrac{( R - R' )^2}{4 \nu_o ( T - \xi )}}\right) \right. & \\[10pt] \quad -\left. \exp\left({- \dfrac{( R + R' )^2}{4 \nu_o ( T - \xi )}}\right) \right] {\rm d} \xi : & R \geq 0,\\[10pt] \displaystyle 0 : & R < 0. \end{array} \right.\end{gather}
\begin{gather} \hat{u}_{\theta 1}^c \sim \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2\sqrt{{\rm \pi} \nu_o}} \int_0^\infty \,{\rm d} R' \,\int_0^T \dfrac{f^c ( \xi, R' )}{\sqrt{T - \xi}}\left[ \exp\left({- \dfrac{( R - R' )^2}{4 \nu_o ( T - \xi )}}\right) \right. & \\[10pt] \quad -\left. \exp\left({- \dfrac{( R + R' )^2}{4 \nu_o ( T - \xi )}}\right) \right] {\rm d} \xi : & R \geq 0,\\[10pt] \displaystyle 0 : & R < 0. \end{array} \right.\end{gather} \begin{gather} \hat{u}_{\theta 1}^{c s} \sim \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2\sqrt{{\rm \pi} \nu_o}} \int_0^\infty \, {\rm d} R' \,\int_0^T \,\dfrac{f^{c s} ( \xi, R' )}{\sqrt{T - \xi}} \left[ \exp\left({- \dfrac{( R - R' )^2}{4 \nu_o ( T - \xi )}}\right)\right. & \\[10pt] \quad - \left.\exp\left({- \dfrac{( R +R' )^2}{4 \nu_o ( T - \xi )}}\right) \right] {\rm d} \xi : & R \geq 0,\\[10pt] \displaystyle 0 : & R < 0. \end{array} \right. \end{gather}
\begin{gather} \hat{u}_{\theta 1}^{c s} \sim \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2\sqrt{{\rm \pi} \nu_o}} \int_0^\infty \, {\rm d} R' \,\int_0^T \,\dfrac{f^{c s} ( \xi, R' )}{\sqrt{T - \xi}} \left[ \exp\left({- \dfrac{( R - R' )^2}{4 \nu_o ( T - \xi )}}\right)\right. & \\[10pt] \quad - \left.\exp\left({- \dfrac{( R +R' )^2}{4 \nu_o ( T - \xi )}}\right) \right] {\rm d} \xi : & R \geq 0,\\[10pt] \displaystyle 0 : & R < 0. \end{array} \right. \end{gather} Figure 4(a) shows the velocity distribution of ![]() $u_x$ on the
$u_x$ on the ![]() $y$ axis as
$y$ axis as ![]() $\lambda _o \to \infty$ in the case of
$\lambda _o \to \infty$ in the case of ![]() $\nu = 1 / 500$ and
$\nu = 1 / 500$ and ![]() $\varOmega = 0.5$. Note here that the definition of the Reynolds number accounts for the fact that the quantity
$\varOmega = 0.5$. Note here that the definition of the Reynolds number accounts for the fact that the quantity ![]() $1 / \nu$ is replaced by
$1 / \nu$ is replaced by ![]() $2 / \nu$ for the Reynolds number used in Badr & Dennis (Reference Badr and Dennis1985). Since the velocity
$2 / \nu$ for the Reynolds number used in Badr & Dennis (Reference Badr and Dennis1985). Since the velocity ![]() $u_x$ on the y axis is equal to
$u_x$ on the y axis is equal to ![]() $u_\theta$ at
$u_\theta$ at ![]() $\theta = {\rm \pi}/ 2$, it can be obtained as the composite velocity,
$\theta = {\rm \pi}/ 2$, it can be obtained as the composite velocity, ![]() $u_{\theta }^i + u_\theta ^o - u_\theta ^{o i}$ at
$u_{\theta }^i + u_\theta ^o - u_\theta ^{o i}$ at ![]() $\theta = {\rm \pi}/2$, i.e.
$\theta = {\rm \pi}/2$, i.e.
The vorticity distribution on the cylinder surface is shown on figure 4(b). The solid line denotes the present results and the dotted line is the result of Badr & Dennis (Reference Badr and Dennis1985) that is written as
Since the vorticity distribution is then obtained from the inner solutions, i.e.
we have
in which the coefficients ![]() $c_1$ and
$c_1$ and ![]() $c_2$ are given as
$c_2$ are given as ![]() $c_1 = 0.0452900$ and
$c_1 = 0.0452900$ and ![]() $c_2 = - 1.34657$. We find that the leading term of the vorticity distribution is equal to the results of Badr & Dennis (Reference Badr and Dennis1985).
$c_2 = - 1.34657$. We find that the leading term of the vorticity distribution is equal to the results of Badr & Dennis (Reference Badr and Dennis1985).

Figure 4. Velocity distribution of ![]() $u_x$ on the
$u_x$ on the ![]() $y$ axis (a) and the vorticity distribution on the cylinder surface (b) in the case of
$y$ axis (a) and the vorticity distribution on the cylinder surface (b) in the case of ![]() $\nu = 1 / 500$ and
$\nu = 1 / 500$ and ![]() $\varOmega = 0.5$.
$\varOmega = 0.5$.
We obtain the second-order solution of the pressure ![]() $p_1^i$ that is governed by
$p_1^i$ that is governed by
Inside the body domain (i.e. ![]() $R < 0$), the inner expansion of the outer solution of the pressure is readily found to be written as
$R < 0$), the inner expansion of the outer solution of the pressure is readily found to be written as
Furthermore, because of ![]() $u_{\theta 0}^{i o} = \varOmega H(T)$ and
$u_{\theta 0}^{i o} = \varOmega H(T)$ and ![]() $u_{r 1}^{i o} = 0$, (3.103) is rewritten as
$u_{r 1}^{i o} = 0$, (3.103) is rewritten as
 \begin{align} \frac{p_1^i}{\rho}& =- \frac{\partial}{\partial T} \int_{- \infty}^R u_{r 1}^i \,{\rm d} R - \lambda_o \int_{- \infty}^R u_{r 1}^i \,{\rm d} R + \nu_o \frac{\partial u_{r 1}^i}{\partial R} \nonumber\\ &\quad + \int_{- \infty}^R ( u_{\theta 0}^{i 2} - \varOmega^2 H(T) ) \,{\rm d} R + \varOmega^2 R H ( T ). \end{align}
\begin{align} \frac{p_1^i}{\rho}& =- \frac{\partial}{\partial T} \int_{- \infty}^R u_{r 1}^i \,{\rm d} R - \lambda_o \int_{- \infty}^R u_{r 1}^i \,{\rm d} R + \nu_o \frac{\partial u_{r 1}^i}{\partial R} \nonumber\\ &\quad + \int_{- \infty}^R ( u_{\theta 0}^{i 2} - \varOmega^2 H(T) ) \,{\rm d} R + \varOmega^2 R H ( T ). \end{align}
For ![]() $R < 0$, the functions
$R < 0$, the functions ![]() $u_{r 1}$ and
$u_{r 1}$ and ![]() $u_{\theta 0}$ are given by (3.96a)–(3.96c) for
$u_{\theta 0}$ are given by (3.96a)–(3.96c) for ![]() $\lambda _o \gg 1$. Therefore, (3.105) can be calculated as
$\lambda _o \gg 1$. Therefore, (3.105) can be calculated as
For ![]() $R > 0$, we find that
$R > 0$, we find that ![]() $u_{r 1}^i \sim 2 ( A + RH(T) ) \cos {\theta }$ and
$u_{r 1}^i \sim 2 ( A + RH(T) ) \cos {\theta }$ and ![]() $u_{\theta 0}^i \sim - 2 \sin {\theta }H(T)$ as
$u_{\theta 0}^i \sim - 2 \sin {\theta }H(T)$ as ![]() $R \to \infty$ from (3.61)–(3.68). Therefore, (3.103) is rewritten as
$R \to \infty$ from (3.61)–(3.68). Therefore, (3.103) is rewritten as
 \begin{align} \frac{1}{\rho} \frac{\partial p_1^i}{\partial R} & =- \frac{\partial}{\partial T} [ u_{r 1}^i - ( 2 A +2 R H ( T ) ) \cos{\theta}] + ( u_{\theta 0}^{i 2} - 4 H ( T ) \sin^2{\theta} ) \nonumber\\ &\quad + \nu_o \frac{\partial^2 u_{r 1}^i}{\partial R^2} - 2 \frac{{\rm d} A}{{\rm d} T} \cos{\theta} + 4 H ( T ) \sin^2{\theta}. \end{align}
\begin{align} \frac{1}{\rho} \frac{\partial p_1^i}{\partial R} & =- \frac{\partial}{\partial T} [ u_{r 1}^i - ( 2 A +2 R H ( T ) ) \cos{\theta}] + ( u_{\theta 0}^{i 2} - 4 H ( T ) \sin^2{\theta} ) \nonumber\\ &\quad + \nu_o \frac{\partial^2 u_{r 1}^i}{\partial R^2} - 2 \frac{{\rm d} A}{{\rm d} T} \cos{\theta} + 4 H ( T ) \sin^2{\theta}. \end{align}
Integrating (3.107) with respect to ![]() $R$, we have
$R$, we have
 \begin{align} \frac{p_1^i}{\rho} & = \frac{\partial}{\partial T} \int_R^\infty [ u_{r 1}^i - ( 2 A + 2R H ( T ) ) \cos{\theta}] {\rm d} R - \int_R^\infty [ u_{\theta 0}^{i 2} - 4 H ( T ) \sin^2{\theta}] {\rm d} R\nonumber\\ &\quad + \nu_o \frac{\partial u_{r 1}^i}{\partial R} - 2 \frac{{\rm d} A}{{\rm d} T} R \cos{\theta} + 4 R H ( T ) \sin^2{\theta} + C_1 ( \theta, T ), \end{align}
\begin{align} \frac{p_1^i}{\rho} & = \frac{\partial}{\partial T} \int_R^\infty [ u_{r 1}^i - ( 2 A + 2R H ( T ) ) \cos{\theta}] {\rm d} R - \int_R^\infty [ u_{\theta 0}^{i 2} - 4 H ( T ) \sin^2{\theta}] {\rm d} R\nonumber\\ &\quad + \nu_o \frac{\partial u_{r 1}^i}{\partial R} - 2 \frac{{\rm d} A}{{\rm d} T} R \cos{\theta} + 4 R H ( T ) \sin^2{\theta} + C_1 ( \theta, T ), \end{align}
where ![]() $C_1$ is an integral constant that can be determined from the matching procedure to the inner expansion of the outer pressure
$C_1$ is an integral constant that can be determined from the matching procedure to the inner expansion of the outer pressure ![]() $p^{oi}$. The derivations of the pressure
$p^{oi}$. The derivations of the pressure ![]() $p_1^o$ and
$p_1^o$ and ![]() $p^{oi}$ are described in Appendix D. Therefore, we have
$p^{oi}$ are described in Appendix D. Therefore, we have
where ![]() $a_1^{c}$,
$a_1^{c}$, ![]() $a_1^{s}$ and
$a_1^{s}$ and ![]() $a_2^c$ are given in Appendix D. Using (3.105) and (3.108), we have the pressure jump of
$a_2^c$ are given in Appendix D. Using (3.105) and (3.108), we have the pressure jump of ![]() $\Delta p_1 = p_1^i |_{r = 1 + 0} - p_1^i |_{r = 1 - 0}$ as
$\Delta p_1 = p_1^i |_{r = 1 + 0} - p_1^i |_{r = 1 - 0}$ as
where the symbol ![]() $\text {pf}$ denotes the integration in the finite part sense of Hadamard (see Hadamard Reference Hadamard1932).
$\text {pf}$ denotes the integration in the finite part sense of Hadamard (see Hadamard Reference Hadamard1932).
Figure 5 shows the pressure distribution on the cylinder surface. The present result is given by
 \begin{align} \frac{p - p_\infty}{\rho}
& \approx- 2 \sqrt{\frac{\nu}{{\rm \pi} t}} \cos{\theta} +
\frac{1}{2} - 2 \sin^2{\theta}\nonumber\\ &\quad - 16
\sqrt{\frac{\nu t}{\rm \pi}} ( \varOmega + \sin{\theta})
\left[ \varOmega \left( 1 - \frac{1}{\sqrt{2}} \right) -
\frac{1}{\sqrt{2}} \sin{\theta} \right]\nonumber\\ &\quad -
\nu \cos{\theta} - 8 \sqrt{\frac{\nu t}{\rm \pi}}
\sin^2{\theta} + \Bigg[ 4 \varOmega \sqrt{\frac{\nu
t}{\rm \pi}} f_m^c - 4 \varOmega \sqrt{\frac{\nu t}{\rm \pi}} ( 3
- 2 \sqrt{2} ) \Bigg] \sin{\theta}\nonumber\\ &\quad+
\Bigg[ 2 \sqrt{\frac{\nu t}{\rm \pi}} f_m^{c s} - 8
\sqrt{\frac{\nu t}{\rm \pi}} ( 3 - 2 \sqrt{2}) \Bigg] \cos{2
\theta}.
\end{align}
\begin{align} \frac{p - p_\infty}{\rho}
& \approx- 2 \sqrt{\frac{\nu}{{\rm \pi} t}} \cos{\theta} +
\frac{1}{2} - 2 \sin^2{\theta}\nonumber\\ &\quad - 16
\sqrt{\frac{\nu t}{\rm \pi}} ( \varOmega + \sin{\theta})
\left[ \varOmega \left( 1 - \frac{1}{\sqrt{2}} \right) -
\frac{1}{\sqrt{2}} \sin{\theta} \right]\nonumber\\ &\quad -
\nu \cos{\theta} - 8 \sqrt{\frac{\nu t}{\rm \pi}}
\sin^2{\theta} + \Bigg[ 4 \varOmega \sqrt{\frac{\nu
t}{\rm \pi}} f_m^c - 4 \varOmega \sqrt{\frac{\nu t}{\rm \pi}} ( 3
- 2 \sqrt{2} ) \Bigg] \sin{\theta}\nonumber\\ &\quad+
\Bigg[ 2 \sqrt{\frac{\nu t}{\rm \pi}} f_m^{c s} - 8
\sqrt{\frac{\nu t}{\rm \pi}} ( 3 - 2 \sqrt{2}) \Bigg] \cos{2
\theta}.
\end{align}Thus, we have the alternative expression to compare with the result of Badr & Dennis (Reference Badr and Dennis1985):
 \begin{align} \Delta C_p & = \frac{p (
\theta )- p ( {\rm \pi})}{\rho} \approx- 2
\sqrt{\frac{\nu}{{\rm \pi} t}} ( 1 + \cos{\theta} ) - 2
\sin^2{\theta} - 16 \varOmega \sqrt{\frac{\nu t}{\rm \pi}} ( 1
- \sqrt{2} ) \sin{\theta}\nonumber\\ &\quad - 8
\sqrt{\frac{\nu t}{\rm \pi}} \sin^2{\theta} + \nu (
\cos{\theta} - 1 ) + \sqrt{\frac{\nu t}{\rm \pi}} [ 4
\varOmega f_m^c - 4 \varOmega ( 3 - 2 \sqrt{2} )]
\sin{\theta}\nonumber\\ &\quad + \sqrt{\frac{\nu t}{\rm \pi}}
[ 2 f_m^{c s} - 8 ( 1 - 2 \sqrt{2})] ( \cos{2
\theta} - 1 ).
\end{align}
\begin{align} \Delta C_p & = \frac{p (
\theta )- p ( {\rm \pi})}{\rho} \approx- 2
\sqrt{\frac{\nu}{{\rm \pi} t}} ( 1 + \cos{\theta} ) - 2
\sin^2{\theta} - 16 \varOmega \sqrt{\frac{\nu t}{\rm \pi}} ( 1
- \sqrt{2} ) \sin{\theta}\nonumber\\ &\quad - 8
\sqrt{\frac{\nu t}{\rm \pi}} \sin^2{\theta} + \nu (
\cos{\theta} - 1 ) + \sqrt{\frac{\nu t}{\rm \pi}} [ 4
\varOmega f_m^c - 4 \varOmega ( 3 - 2 \sqrt{2} )]
\sin{\theta}\nonumber\\ &\quad + \sqrt{\frac{\nu t}{\rm \pi}}
[ 2 f_m^{c s} - 8 ( 1 - 2 \sqrt{2})] ( \cos{2
\theta} - 1 ).
\end{align}
Here ![]() $f_m^c = 0.21483$ and
$f_m^c = 0.21483$ and ![]() $f_m^{c s} = -2.69143$. In contrast, the result of Badr & Dennis (Reference Badr and Dennis1985) is given by
$f_m^{c s} = -2.69143$. In contrast, the result of Badr & Dennis (Reference Badr and Dennis1985) is given by
in which the coefficients ![]() $q_1$ and
$q_1$ and ![]() $q_2$ are written as
$q_2$ are written as ![]() $q_1 = 5.79901$ and
$q_1 = 5.79901$ and ![]() $q_2 = 14.3122$. Note here that the leading term is found to be the same between both results.
$q_2 = 14.3122$. Note here that the leading term is found to be the same between both results.

Figure 5. Comparison of the pressure distribution ![]() $\Delta C_p = (\kern0.7pt p( \theta ) - p ( {\rm \pi}) ) / \rho$ on the cylinder surface between the present results and Badr & Dennis (Reference Badr and Dennis1985) in the case of
$\Delta C_p = (\kern0.7pt p( \theta ) - p ( {\rm \pi}) ) / \rho$ on the cylinder surface between the present results and Badr & Dennis (Reference Badr and Dennis1985) in the case of ![]() $\nu = 1 / 500$ and
$\nu = 1 / 500$ and ![]() $\varOmega = 0.5$.
$\varOmega = 0.5$.
3.4. Hydrodynamic forces
This section attempts to investigate the variance of the drag force against the results of Bar-Lev & Yang (Reference Bar-Lev and Yang1975), which is demonstrated in our previous paper (see Ueda & Kida Reference Ueda and Kida2021). We calculate the hydrodynamic force ![]() ${\boldsymbol {F}} = ( F_x, F_y )$ by the following two approaches: (i) by the time derivative of the momentum of the fluid flow and the pressure on the control surface, and (ii) by the integration of the penalization layer given by (2.3). In this section we intend to first investigate the drag force
${\boldsymbol {F}} = ( F_x, F_y )$ by the following two approaches: (i) by the time derivative of the momentum of the fluid flow and the pressure on the control surface, and (ii) by the integration of the penalization layer given by (2.3). In this section we intend to first investigate the drag force ![]() $F_x$ and, then, the lift force
$F_x$ and, then, the lift force ![]() $F_y$. In the subsequent § 3.5 the relation between approaches (i) and (ii) will be presented for the solid cylindrical body having a continuous contour.
$F_y$. In the subsequent § 3.5 the relation between approaches (i) and (ii) will be presented for the solid cylindrical body having a continuous contour.
In approach (i) we set the circular control surface around the circular cylinder, of which the centre is set at the origin, with a large radius of ![]() $r_\infty$. The fluid domain is then defined as
$r_\infty$. The fluid domain is then defined as ![]() ${\mathscr {F}} = [ ( r, \theta ) | 1 \leq r \leq r_\infty, 0 \leq \theta < 2 {\rm \pi}]$. The small fluid element
${\mathscr {F}} = [ ( r, \theta ) | 1 \leq r \leq r_\infty, 0 \leq \theta < 2 {\rm \pi}]$. The small fluid element ![]() ${\rm d} m = r \,{\rm d} r \,{\rm d} \theta$ in the fluid domain
${\rm d} m = r \,{\rm d} r \,{\rm d} \theta$ in the fluid domain ![]() ${\mathscr {F}}$ has the momentum
${\mathscr {F}}$ has the momentum ![]() $\rho {\boldsymbol {u}} \,{\rm d} m$ and, therefore, the force of
$\rho {\boldsymbol {u}} \,{\rm d} m$ and, therefore, the force of ![]() $- ( {\rm d} / {\rm d} t ) \int _1^{r_\infty } \rho {\boldsymbol {u}} r \,{\rm d} r \,{\rm d} \theta$ affects the fluid in
$- ( {\rm d} / {\rm d} t ) \int _1^{r_\infty } \rho {\boldsymbol {u}} r \,{\rm d} r \,{\rm d} \theta$ affects the fluid in ![]() ${\mathscr {F}}$. Furthermore, the fluid experiences the force exerted by the pressure on the control surface having the radius of
${\mathscr {F}}$. Furthermore, the fluid experiences the force exerted by the pressure on the control surface having the radius of ![]() $r_\infty$, i.e.
$r_\infty$, i.e. ![]() $- \int _0^{2 {\rm \pi}} p ( \cos {\theta }, \sin {\theta } ) r_\infty \,{\rm d} \theta$. Therefore, the hydrodynamic force
$- \int _0^{2 {\rm \pi}} p ( \cos {\theta }, \sin {\theta } ) r_\infty \,{\rm d} \theta$. Therefore, the hydrodynamic force ![]() ${\boldsymbol {F}}$ can be written as
${\boldsymbol {F}}$ can be written as
where ![]() ${\boldsymbol {u}} = ( u, v )$ is the velocity defined on the
${\boldsymbol {u}} = ( u, v )$ is the velocity defined on the ![]() $( x, y )$ plane.
$( x, y )$ plane.
In the outer fluid domain for ![]() $r > 1$, we have, from (D11),
$r > 1$, we have, from (D11),
Here, the ![]() $r$ and
$r$ and ![]() $\theta$ components of the velocity (i.e.
$\theta$ components of the velocity (i.e. ![]() $u_r^o$ and
$u_r^o$ and ![]() $u_\theta ^o$) in the outer fluid domain (for
$u_\theta ^o$) in the outer fluid domain (for ![]() $r > 1$) are obtained by (D12a) and (D12b). Therefore, we find that
$r > 1$) are obtained by (D12a) and (D12b). Therefore, we find that ![]() $| {\boldsymbol {u}} |^2 = 1 + O ( 1 / r^2 ) + O ( \epsilon ^2 )$. Using (3.115) with (3.72), the Laplace transform to unsteady Bernoulli's equation yields the pressure for
$| {\boldsymbol {u}} |^2 = 1 + O ( 1 / r^2 ) + O ( \epsilon ^2 )$. Using (3.115) with (3.72), the Laplace transform to unsteady Bernoulli's equation yields the pressure for ![]() $r \gg 1$:
$r \gg 1$:
The drag force ![]() $F_x$ of (3.114) is calculated as, taking the limit of
$F_x$ of (3.114) is calculated as, taking the limit of ![]() $r_\infty \gg 1$,
$r_\infty \gg 1$,
 \begin{align} F_x & =- \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} \int_1^\infty \rho u r \,{\rm d} r \,{\rm d} \theta - 2 \rho\sqrt{\frac{\nu_o {\rm \pi}}{T}} \left( {\rm e}^{- \lambda_o T} - 1 \right)\nonumber\\ &\quad + {\rm \pi}\rho\nu_o \epsilon [ ( 1 + {\rm e}^{- \lambda_o T} ) H ( T ) - 2 {\rm e}^{- \lambda_o T / 2} {\rm I}_0 ( \lambda_o T / 2 )] + O ( \epsilon^2 ). \end{align}
\begin{align} F_x & =- \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} \int_1^\infty \rho u r \,{\rm d} r \,{\rm d} \theta - 2 \rho\sqrt{\frac{\nu_o {\rm \pi}}{T}} \left( {\rm e}^{- \lambda_o T} - 1 \right)\nonumber\\ &\quad + {\rm \pi}\rho\nu_o \epsilon [ ( 1 + {\rm e}^{- \lambda_o T} ) H ( T ) - 2 {\rm e}^{- \lambda_o T / 2} {\rm I}_0 ( \lambda_o T / 2 )] + O ( \epsilon^2 ). \end{align}
Note that ![]() $s {\mathcal {L}} ( a_1^c ) = \nu _o [ 1 / s + 1 / ( s + \lambda _o ) - 2 / \sqrt {s ( s + \lambda _o )} ]$ from (D9a). The first term on the right-hand side of (3.117), which is denoted by
$s {\mathcal {L}} ( a_1^c ) = \nu _o [ 1 / s + 1 / ( s + \lambda _o ) - 2 / \sqrt {s ( s + \lambda _o )} ]$ from (D9a). The first term on the right-hand side of (3.117), which is denoted by ![]() $F_{x 1}$, is calculated as
$F_{x 1}$, is calculated as
 \begin{align} F_{x 1}& =- \rho
\frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} \int_1^\infty (
u_r \cos{\theta} - u_\theta \sin{\theta} ) r \,{\rm d} r
\,{\rm d} \theta\nonumber\\ & =- \rho \frac{{\rm d}}{{\rm
d} t} \int_0^{2 {\rm \pi}} \int_1^\infty ( u_r^o \cos{\theta} -
u_\theta^o \sin{\theta} ) r \,{\rm d} r \,{\rm d}
\theta\nonumber\\ &\quad- \rho \frac{{\rm d}}{{\rm d} T}
\int_0^{2 {\rm \pi}} \int_0^\infty [ ( u_r^i - u_r^{i o} )
\cos{\theta} - ( u_\theta^i - u_\theta^{i o}) \sin{\theta}] ( 1 + \epsilon R ) \,{\rm d} R \,{\rm d} \theta.
\end{align}
\begin{align} F_{x 1}& =- \rho
\frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} \int_1^\infty (
u_r \cos{\theta} - u_\theta \sin{\theta} ) r \,{\rm d} r
\,{\rm d} \theta\nonumber\\ & =- \rho \frac{{\rm d}}{{\rm
d} t} \int_0^{2 {\rm \pi}} \int_1^\infty ( u_r^o \cos{\theta} -
u_\theta^o \sin{\theta} ) r \,{\rm d} r \,{\rm d}
\theta\nonumber\\ &\quad- \rho \frac{{\rm d}}{{\rm d} T}
\int_0^{2 {\rm \pi}} \int_0^\infty [ ( u_r^i - u_r^{i o} )
\cos{\theta} - ( u_\theta^i - u_\theta^{i o}) \sin{\theta}] ( 1 + \epsilon R ) \,{\rm d} R \,{\rm d} \theta.
\end{align}
The first term on the right-hand side of (3.118) is calculated from the outer solution of the velocity ![]() $u_r^o$ and
$u_r^o$ and ![]() $u_\theta ^o$:
$u_\theta ^o$:
It can be found that the outer solutions do not affect ![]() $F_{x 1}$ within the order of
$F_{x 1}$ within the order of ![]() $\epsilon$. Therefore,
$\epsilon$. Therefore, ![]() $F_{x 1}$ is calculated as, using the Laplace transform,
$F_{x 1}$ is calculated as, using the Laplace transform,
 \begin{align} {\mathcal{L}} ( F_{x 1} ) & =- {\rm \pi}\rho s \int_0^\infty \{ - U_{\theta 0}^s + U_{\theta 0}^{s i o} + \epsilon [ U_{r 1} - U_{r 1}^{i o} - U_{\theta 1}^s + U_{\theta 1}^{s i o} - R ( U_{\theta 0}^s - U_{\theta 0}^{s i o} ) ]\} {\rm d} R\nonumber\\ &\quad + O ( \epsilon^2 ). \end{align}
\begin{align} {\mathcal{L}} ( F_{x 1} ) & =- {\rm \pi}\rho s \int_0^\infty \{ - U_{\theta 0}^s + U_{\theta 0}^{s i o} + \epsilon [ U_{r 1} - U_{r 1}^{i o} - U_{\theta 1}^s + U_{\theta 1}^{s i o} - R ( U_{\theta 0}^s - U_{\theta 0}^{s i o} ) ]\} {\rm d} R\nonumber\\ &\quad + O ( \epsilon^2 ). \end{align}Here, the following relations are obtained from the inner solutions:
 \begin{equation} \left.\begin{gathered} \int_0^\infty ( U_{\theta 0}^s - U_{\theta 0}^{s i o} ) \,{\rm d} R = \int_0^\infty \frac{2 \bar{a}}{s ( a + \bar{a} )} {\rm e}^{- a R} \,{\rm d} R = \frac{2 \bar{a}}{s a ( a + \bar{a} )},\\ \int_0^\infty R ( U_{\theta 0}^s - U_{\theta 0}^{s i o} ) \,{\rm d} R = \int_0^\infty \frac{2 \bar{a}}{s ( a + \bar{a} )} R {\rm e}^{- a R} \,{\rm d} R = \frac{2 \bar{a}}{s a^2 ( a + \bar{a} )},\\ \int_0^\infty ( U_{r 1} - U_{r 1}^{i o} ) \,{\rm d} R = \int_0^\infty \frac{2 \bar{a}}{s a ( a + \bar{a} )} {\rm e}^{- a R} \,{\rm d} R = \frac{2 \bar{a}}{s a^2 ( a + \bar{a} )},\\ \int_0^\infty ( U_{\theta 1}^s - U_{\theta 1}^{s i o} ) \,{\rm d} R = \frac{\bar{a}}{s a^2 ( a + \bar{a} )} + \frac{D_s}{a}. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \int_0^\infty ( U_{\theta 0}^s - U_{\theta 0}^{s i o} ) \,{\rm d} R = \int_0^\infty \frac{2 \bar{a}}{s ( a + \bar{a} )} {\rm e}^{- a R} \,{\rm d} R = \frac{2 \bar{a}}{s a ( a + \bar{a} )},\\ \int_0^\infty R ( U_{\theta 0}^s - U_{\theta 0}^{s i o} ) \,{\rm d} R = \int_0^\infty \frac{2 \bar{a}}{s ( a + \bar{a} )} R {\rm e}^{- a R} \,{\rm d} R = \frac{2 \bar{a}}{s a^2 ( a + \bar{a} )},\\ \int_0^\infty ( U_{r 1} - U_{r 1}^{i o} ) \,{\rm d} R = \int_0^\infty \frac{2 \bar{a}}{s a ( a + \bar{a} )} {\rm e}^{- a R} \,{\rm d} R = \frac{2 \bar{a}}{s a^2 ( a + \bar{a} )},\\ \int_0^\infty ( U_{\theta 1}^s - U_{\theta 1}^{s i o} ) \,{\rm d} R = \frac{\bar{a}}{s a^2 ( a + \bar{a} )} + \frac{D_s}{a}. \end{gathered}\right\} \end{equation}Taking the inverse Laplace transform to (3.120), we obtain
 \begin{align} F_{x 1}& = {\rm \pi}\rho \left\{ 2 \sqrt{\frac{\nu_o}{{\rm \pi} T}} - \sqrt{\frac{\nu_o}{{\rm \pi} T^3}} \frac{1 - {\rm e}^{- \lambda_o T}}{\lambda_o}\right.\nonumber\\ &\quad \left.+ \,\epsilon \nu_o [ 3 H ( T ) - 2 {\rm e}^{- \lambda_o T / 2} ( {\rm I}_0 ( \lambda_o T / 2 ) + {\rm I}_1 ( \lambda_o T / 2 ) )] \vphantom{\sqrt{\frac{\nu_o}{{\rm \pi} T}} - \sqrt{\frac{\nu_o}{{\rm \pi} T^3}}}\right\} + O ( \epsilon^2 ). \end{align}
\begin{align} F_{x 1}& = {\rm \pi}\rho \left\{ 2 \sqrt{\frac{\nu_o}{{\rm \pi} T}} - \sqrt{\frac{\nu_o}{{\rm \pi} T^3}} \frac{1 - {\rm e}^{- \lambda_o T}}{\lambda_o}\right.\nonumber\\ &\quad \left.+ \,\epsilon \nu_o [ 3 H ( T ) - 2 {\rm e}^{- \lambda_o T / 2} ( {\rm I}_0 ( \lambda_o T / 2 ) + {\rm I}_1 ( \lambda_o T / 2 ) )] \vphantom{\sqrt{\frac{\nu_o}{{\rm \pi} T}} - \sqrt{\frac{\nu_o}{{\rm \pi} T^3}}}\right\} + O ( \epsilon^2 ). \end{align}
Substituting (3.122) into (3.117), we find that ![]() $F_x$ behaves like
$F_x$ behaves like
The result of (3.123) is found to be the same as that obtained by Bar-Lev & Yang (Reference Bar-Lev and Yang1975) and our previous study (see Ueda & Kida Reference Ueda and Kida2021) for an impulsively started translating circular cylinder without rotating motion. As found by the above analysis, the force exerted by the pressure far from the body plays an important role for the calculation of the hydrodynamic force. Figure 6 shows the comparison of the drag coefficient ![]() $C_D$, which is calculated by
$C_D$, which is calculated by ![]() $C_D = F_x / \rho$ in the present paper, between the result of Badr & Dennis (Reference Badr and Dennis1985) (i.e.
$C_D = F_x / \rho$ in the present paper, between the result of Badr & Dennis (Reference Badr and Dennis1985) (i.e. ![]() $C_D = 4 \sqrt {{\rm \pi} \nu / t} + {\rm \pi}\nu$) and the leading term of the present result as
$C_D = 4 \sqrt {{\rm \pi} \nu / t} + {\rm \pi}\nu$) and the leading term of the present result as ![]() $\lambda _o \to \infty$. In the previous study (see Ueda & Kida Reference Ueda and Kida2021), the drag force
$\lambda _o \to \infty$. In the previous study (see Ueda & Kida Reference Ueda and Kida2021), the drag force ![]() $F_x$ was obtained by the following two equations:
$F_x$ was obtained by the following two equations:
These relations are derived by imposing the no-slip condition on the cylinder surface. In the penalization method the no-slip condition is not imposed. Therefore, these formulae are not directly available for the penalization method. In Appendix F we note an additional term to the above relations in the penalization method, i.e.

Figure 6. Comparison of the drag coefficient ![]() $C_D$ with the result of Badr & Dennis (Reference Badr and Dennis1985) in the case of
$C_D$ with the result of Badr & Dennis (Reference Badr and Dennis1985) in the case of ![]() $\nu =1/500$ and
$\nu =1/500$ and ![]() $\varOmega =0.5$.
$\varOmega =0.5$.
Here, let us calculate the hydrodynamic force by approach (ii). The ![]() $x$ component of the hydrodynamic force is denoted by
$x$ component of the hydrodynamic force is denoted by ![]() $F_{p x}$ and, then, it is written as, from (2.3),
$F_{p x}$ and, then, it is written as, from (2.3),
The outer solution inside the body domain is governed by the rotational motion of the cylinder alone so that it cannot affect the ![]() $x$ component of the force. Using the result of the Laplace transform to (3.127), which is written as
$x$ component of the force. Using the result of the Laplace transform to (3.127), which is written as
we have
Also, ![]() $F_{p x}$ behaves like
$F_{p x}$ behaves like
It can be found that the result of (3.130) exhibits the half-value of ![]() $F_x$, and this finding is the same as our previous study (see Ueda & Kida Reference Ueda and Kida2021).
$F_x$, and this finding is the same as our previous study (see Ueda & Kida Reference Ueda and Kida2021).
Let us calculate the lift force ![]() $F_y$ by approach (i) that uses the force
$F_y$ by approach (i) that uses the force ![]() $F_{m y}$ exerted by the momentum of the fluid flow and the force
$F_{m y}$ exerted by the momentum of the fluid flow and the force ![]() $F_{y 1}$ exerted by the pressure on the circular control surface at
$F_{y 1}$ exerted by the pressure on the circular control surface at ![]() $r = r_\infty$. The lift force
$r = r_\infty$. The lift force ![]() $F_{m y}$ exerted by the momentum of the fluid flow is written as
$F_{m y}$ exerted by the momentum of the fluid flow is written as
 \begin{align} F_{m y} & =- \rho \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} \!\! \int_1^\infty ( u_r \sin{\theta} + u_\theta \cos{\theta} ) r \,{\rm d} r \,{\rm d} \theta\nonumber\\ & =- \rho {\rm \pi}\frac{{\rm d}}{{\rm d} T} \int_0^\infty [ \epsilon ( \hat{u}_{\theta 1}^c - \hat{u}_{\theta 1}^{c i o} ) + O ( \epsilon^2 )] {\rm d} R. \end{align}
\begin{align} F_{m y} & =- \rho \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} \!\! \int_1^\infty ( u_r \sin{\theta} + u_\theta \cos{\theta} ) r \,{\rm d} r \,{\rm d} \theta\nonumber\\ & =- \rho {\rm \pi}\frac{{\rm d}}{{\rm d} T} \int_0^\infty [ \epsilon ( \hat{u}_{\theta 1}^c - \hat{u}_{\theta 1}^{c i o} ) + O ( \epsilon^2 )] {\rm d} R. \end{align}Making use of the Laplace transform to (3.131) and the integration by parts, we have
 \begin{align} {\mathcal{L}} ( F_{m y} )
&=- \rho {\rm \pi}\epsilon s \left[ - \frac{1}{2 a \nu_o}
\int_0^\infty {\rm e}^{a R} \left( \int_R^\infty F^c {\rm
e}^{- a R'} {\rm d} R' \right) {\rm d} R\right.\nonumber\\
&\quad\left. -\, \frac{1}{2 a \nu_o} \int_0^\infty {\rm
e}^{- a R} \left( \int_0^R F^c {\rm e}^{a R'} \,{\rm d} R'
\right) {\rm d} R + \frac{D_c}{a} \right] + O ( \epsilon^2
)\nonumber\\ &=- \rho {\rm \pi}\epsilon \biggl[ \frac{\bar{a}}{a
+ \bar{a}} \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R -
\int_0^\infty F^c \,{\rm d} R - \frac{a}{a + \bar{a}}
\int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm d} R \biggr] + O ( \epsilon^2 ).
\end{align}
\begin{align} {\mathcal{L}} ( F_{m y} )
&=- \rho {\rm \pi}\epsilon s \left[ - \frac{1}{2 a \nu_o}
\int_0^\infty {\rm e}^{a R} \left( \int_R^\infty F^c {\rm
e}^{- a R'} {\rm d} R' \right) {\rm d} R\right.\nonumber\\
&\quad\left. -\, \frac{1}{2 a \nu_o} \int_0^\infty {\rm
e}^{- a R} \left( \int_0^R F^c {\rm e}^{a R'} \,{\rm d} R'
\right) {\rm d} R + \frac{D_c}{a} \right] + O ( \epsilon^2
)\nonumber\\ &=- \rho {\rm \pi}\epsilon \biggl[ \frac{\bar{a}}{a
+ \bar{a}} \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R -
\int_0^\infty F^c \,{\rm d} R - \frac{a}{a + \bar{a}}
\int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm d} R \biggr] + O ( \epsilon^2 ).
\end{align}
The lift force ![]() $F_{y 1}$ exerted by the pressure on the circular control surface at
$F_{y 1}$ exerted by the pressure on the circular control surface at ![]() $r = r_\infty$ is calculated as, by the use of (3.116),
$r = r_\infty$ is calculated as, by the use of (3.116),
 \begin{align} \frac{1}{\rho}
{\mathcal{L}} ( F_{y 1} ) & =- \frac{1}{\rho} \int_0^{2
{\rm \pi}} {\mathcal{L}} (\kern0.7pt p ) |_{r = r_\infty}
r_\infty \sin{\theta} \,{\rm d} \theta = {\rm \pi}\epsilon s
{\mathcal{L}} ( a_1^s ) + O ( \epsilon^2 )\nonumber\\ & =
{\rm \pi} \epsilon s \biggl[ - \frac{1}{\nu_o ( a + \bar{a} )}
\left( \frac{1}{\bar{a}} + \frac{\bar{a}}{a^2} \right)
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R + \frac{1}{s}
\int_0^\infty F^c \,{\rm d} R\nonumber\\ &\quad
+\, \frac{1}{\nu_o ( a + \bar{a} )} \left(
\frac{1}{a} - \frac{1}{\bar{a}} \right) \int_{- \infty}^0
F^c {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{s +
\lambda_o} \int_{- \infty}^0 F^c \,{\rm d} R
\vphantom{\frac{1}{\nu_o ( a + \bar{a} )}}\biggr].
\end{align}
\begin{align} \frac{1}{\rho}
{\mathcal{L}} ( F_{y 1} ) & =- \frac{1}{\rho} \int_0^{2
{\rm \pi}} {\mathcal{L}} (\kern0.7pt p ) |_{r = r_\infty}
r_\infty \sin{\theta} \,{\rm d} \theta = {\rm \pi}\epsilon s
{\mathcal{L}} ( a_1^s ) + O ( \epsilon^2 )\nonumber\\ & =
{\rm \pi} \epsilon s \biggl[ - \frac{1}{\nu_o ( a + \bar{a} )}
\left( \frac{1}{\bar{a}} + \frac{\bar{a}}{a^2} \right)
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R + \frac{1}{s}
\int_0^\infty F^c \,{\rm d} R\nonumber\\ &\quad
+\, \frac{1}{\nu_o ( a + \bar{a} )} \left(
\frac{1}{a} - \frac{1}{\bar{a}} \right) \int_{- \infty}^0
F^c {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{s +
\lambda_o} \int_{- \infty}^0 F^c \,{\rm d} R
\vphantom{\frac{1}{\nu_o ( a + \bar{a} )}}\biggr].
\end{align}
Therefore, we have, for ![]() $\lambda _o \gg 1$,
$\lambda _o \gg 1$,
 \begin{align} \frac{F_{m y}}{\rho} &
\sim \frac{F_{y 1}}{\rho} \sim {\rm \pi}\epsilon
{\mathcal{L}}^{- 1} \left( \int_0^\infty F^c \,{\rm d} R -
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R
\right)\nonumber\\ & \sim {\rm \pi}\epsilon \begin{pmatrix}
\displaystyle\int_0^\infty f^c ( T, R ) \,{\rm d} R - \frac{1}{2
\sqrt{{\rm \pi} \nu_o}} \int_0^\infty R \,{\rm d} R \int_0^T f^c
( T - \xi, R ) \frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}} \,{\rm d} \xi \end{pmatrix},
\end{align}
\begin{align} \frac{F_{m y}}{\rho} &
\sim \frac{F_{y 1}}{\rho} \sim {\rm \pi}\epsilon
{\mathcal{L}}^{- 1} \left( \int_0^\infty F^c \,{\rm d} R -
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R
\right)\nonumber\\ & \sim {\rm \pi}\epsilon \begin{pmatrix}
\displaystyle\int_0^\infty f^c ( T, R ) \,{\rm d} R - \frac{1}{2
\sqrt{{\rm \pi} \nu_o}} \int_0^\infty R \,{\rm d} R \int_0^T f^c
( T - \xi, R ) \frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}} \,{\rm d} \xi \end{pmatrix},
\end{align}
where ![]() $f^c = {\mathcal {L}}^{-1} ( F^c )$.
$f^c = {\mathcal {L}}^{-1} ( F^c )$.
Let us calculate the lift force ![]() $F_{p y}$ by approach (ii) that uses the integration of the penalization layer, as shown in (2.3). Then, the Laplace transform of
$F_{p y}$ by approach (ii) that uses the integration of the penalization layer, as shown in (2.3). Then, the Laplace transform of ![]() $F_{p y}$ is written as
$F_{p y}$ is written as
 \begin{align} {\mathcal{L}} ( F_{p y} )
& = \rho {\rm \pi}\epsilon \lambda_o \int_{- \infty}^0
U_{\theta 1}^c \,{\rm d} R + O ( \epsilon^2 )\nonumber\\ &
= \rho {\rm \pi}\epsilon \lambda_o \Bigg( \frac{1}{2 \nu_o
\bar{a}^2} \int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm
d} R - \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^c
\,{\rm d} R + \frac{E_c}{\bar{a}} \Bigg) + O ( \epsilon^2
)\nonumber\\ & = \rho {\rm \pi}\epsilon \lambda_o \Bigg(
\frac{a}{\nu_o \bar{a}^2 ( a + \bar{a} )} \int_{- \infty}^0
F^c {\rm e}^{\bar{a} R} \,{\rm d} R\nonumber\\ &
\quad - \,\frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0
F^c \,{\rm d} R - \frac{1}{\nu_o \bar{a} ( a + \bar{a} )}
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R \Bigg) + O (
\epsilon^2 ).
\end{align}
\begin{align} {\mathcal{L}} ( F_{p y} )
& = \rho {\rm \pi}\epsilon \lambda_o \int_{- \infty}^0
U_{\theta 1}^c \,{\rm d} R + O ( \epsilon^2 )\nonumber\\ &
= \rho {\rm \pi}\epsilon \lambda_o \Bigg( \frac{1}{2 \nu_o
\bar{a}^2} \int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm
d} R - \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^c
\,{\rm d} R + \frac{E_c}{\bar{a}} \Bigg) + O ( \epsilon^2
)\nonumber\\ & = \rho {\rm \pi}\epsilon \lambda_o \Bigg(
\frac{a}{\nu_o \bar{a}^2 ( a + \bar{a} )} \int_{- \infty}^0
F^c {\rm e}^{\bar{a} R} \,{\rm d} R\nonumber\\ &
\quad - \,\frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0
F^c \,{\rm d} R - \frac{1}{\nu_o \bar{a} ( a + \bar{a} )}
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R \Bigg) + O (
\epsilon^2 ).
\end{align}
For ![]() $\lambda _o \gg 1$, we have
$\lambda _o \gg 1$, we have
 \begin{equation} {\mathcal{L}} ( F_{p y} ) \sim- \rho {\rm \pi}\epsilon \Bigg( \int_{- \infty}^0 F^c \,{\rm d} R + \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R \Bigg). \end{equation}
\begin{equation} {\mathcal{L}} ( F_{p y} ) \sim- \rho {\rm \pi}\epsilon \Bigg( \int_{- \infty}^0 F^c \,{\rm d} R + \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R \Bigg). \end{equation}
From (3.134) (note that ![]() $F_y = F_{m y} + F_{y 1}$) and the inverse Laplace transform to (3.136), we have, for
$F_y = F_{m y} + F_{y 1}$) and the inverse Laplace transform to (3.136), we have, for ![]() $\lambda _o \gg 1$,
$\lambda _o \gg 1$,
 \begin{align} F_y \sim 2 \rho {\rm \pi}
\epsilon \begin{pmatrix}\vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\displaystyle\int_0^\infty f^c ( T,
R ) \,{\rm d} R - \frac{1}{2 \sqrt{\nu_o {\rm \pi}}}
\int_0^\infty R \,{\rm d} R \int_0^T f^c ( T - \xi, R )
\dfrac{\exp\left({- \dfrac{R^2}{4 \nu_o \xi}}\right)}{\xi^{3
/ 2}} \,{\rm d} \xi \vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\end{pmatrix},
\end{align}
\begin{align} F_y \sim 2 \rho {\rm \pi}
\epsilon \begin{pmatrix}\vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\displaystyle\int_0^\infty f^c ( T,
R ) \,{\rm d} R - \frac{1}{2 \sqrt{\nu_o {\rm \pi}}}
\int_0^\infty R \,{\rm d} R \int_0^T f^c ( T - \xi, R )
\dfrac{\exp\left({- \dfrac{R^2}{4 \nu_o \xi}}\right)}{\xi^{3
/ 2}} \,{\rm d} \xi \vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\end{pmatrix},
\end{align} \begin{align}F_{p y} \sim- \rho {\rm \pi}
\epsilon \begin{pmatrix}\vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\displaystyle\int_{- \infty}^0 f^c
( T, R ) \,{\rm d} R + \frac{1}{2 \sqrt{\nu_o {\rm \pi}}}
\int_0^\infty R \,{\rm d} R \int_0^T f^c ( T - \xi, R )
\dfrac{\exp\left({- \dfrac{R^2}{4 \nu_o \xi}}\right)}{\xi^{3
/ 2}}\,{\rm d} \xi \vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\end{pmatrix}.
\end{align}
\begin{align}F_{p y} \sim- \rho {\rm \pi}
\epsilon \begin{pmatrix}\vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\displaystyle\int_{- \infty}^0 f^c
( T, R ) \,{\rm d} R + \frac{1}{2 \sqrt{\nu_o {\rm \pi}}}
\int_0^\infty R \,{\rm d} R \int_0^T f^c ( T - \xi, R )
\dfrac{\exp\left({- \dfrac{R^2}{4 \nu_o \xi}}\right)}{\xi^{3
/ 2}}\,{\rm d} \xi \vphantom{\frac{\exp\left({- \dfrac{R^2}{4 \nu_o
\xi}}\right)}{\xi^{3 / 2}}}\end{pmatrix}.
\end{align}
Note that the asymptotic behaviours, for ![]() $\lambda _o \gg 1$, of (3.137a)–(3.137b) are obtained by using the result of Appendix E.
$\lambda _o \gg 1$, of (3.137a)–(3.137b) are obtained by using the result of Appendix E.
Here, let us consider the behaviour of ![]() $F_y$ for
$F_y$ for ![]() $\lambda _o \gg 1$ and
$\lambda _o \gg 1$ and ![]() $T \ll 1$ to describe
$T \ll 1$ to describe ![]() $F_y$ explicitly. To calculate (3.137a)–(3.137b), we need to obtain the function
$F_y$ explicitly. To calculate (3.137a)–(3.137b), we need to obtain the function ![]() $f^c$ to which the Laplace transform is given by (C11a,b). Using (3.96a)–(3.96g),
$f^c$ to which the Laplace transform is given by (C11a,b). Using (3.96a)–(3.96g), ![]() $f^c$ (
$f^c$ (![]() $=\hat {u}_{r1} ( \partial \hat {u}_{\theta 0}^0 / \partial R ) + \hat {u}_{\theta 0}^0 \hat {u}_{\theta 0}^s$) is written as
$=\hat {u}_{r1} ( \partial \hat {u}_{\theta 0}^0 / \partial R ) + \hat {u}_{\theta 0}^0 \hat {u}_{\theta 0}^s$) is written as
 \begin{equation} f^c ( T, R ) = \left\{\begin{array}{@{}ll} \displaystyle - \dfrac{4 \varOmega}{\sqrt{\rm \pi}} {\rm e}^{- \eta^2} \Bigg( \eta \, \text{erf} ( \eta ) + \dfrac{{\rm e}^{- \eta^2} - 1}{\sqrt{\rm \pi}} \Bigg) & {}\\ \quad - 2 \varOmega \, \text{erf} (\eta ) ( 1 - \, \text{erf} ( \eta ) ) + O ( 1 / \sqrt{\lambda_o} ) & \text{for}\ R \geq 0,\\[10pt] \displaystyle O ( 1 / \sqrt{\lambda_o} ) & \text{for} \ R < 0, \end{array} \right.\end{equation}
\begin{equation} f^c ( T, R ) = \left\{\begin{array}{@{}ll} \displaystyle - \dfrac{4 \varOmega}{\sqrt{\rm \pi}} {\rm e}^{- \eta^2} \Bigg( \eta \, \text{erf} ( \eta ) + \dfrac{{\rm e}^{- \eta^2} - 1}{\sqrt{\rm \pi}} \Bigg) & {}\\ \quad - 2 \varOmega \, \text{erf} (\eta ) ( 1 - \, \text{erf} ( \eta ) ) + O ( 1 / \sqrt{\lambda_o} ) & \text{for}\ R \geq 0,\\[10pt] \displaystyle O ( 1 / \sqrt{\lambda_o} ) & \text{for} \ R < 0, \end{array} \right.\end{equation}
where ![]() $\eta = R / ( 2\sqrt {\nu _o T} )$. To calculate (3.137a)–(3.137b), we define the functions
$\eta = R / ( 2\sqrt {\nu _o T} )$. To calculate (3.137a)–(3.137b), we define the functions ![]() $S_1$ and
$S_1$ and ![]() $S_2$ as
$S_2$ as
 $$\begin{gather}S_2 = \frac{1}{2 \sqrt{{\rm \pi} \nu_o}} \int_0^\infty \int_0^T f^c ( T - \xi, R ) \frac{\exp\left({- \dfrac{R^2}{4 \nu_o \xi}}\right)}{\xi^{3 / 2}} R \,{\rm d} R \,{\rm d} \xi. \end{gather}$$
$$\begin{gather}S_2 = \frac{1}{2 \sqrt{{\rm \pi} \nu_o}} \int_0^\infty \int_0^T f^c ( T - \xi, R ) \frac{\exp\left({- \dfrac{R^2}{4 \nu_o \xi}}\right)}{\xi^{3 / 2}} R \,{\rm d} R \,{\rm d} \xi. \end{gather}$$
Substituting (3.138) into (3.139a), ![]() $S_1$ is written as
$S_1$ is written as
 \begin{align} S_1&=- 4 \varOmega
\sqrt{\nu_o T} \int_0^\infty \Big\{ \frac{2}{\sqrt{\rm \pi}}
{\rm e}^{- \eta^2} \Big( \eta \, \text{erf} ( \eta ) +
\frac{{\rm e}^{- \eta^2} - 1}{\sqrt{\rm \pi}} \Big) +
\text{erf} ( \eta ) [ 1 - \text{erf} ( \eta ) ] \Big\}
{\rm d} \eta\nonumber\\ & \quad + O ( 1 / \sqrt{\lambda_o}
).
\end{align}
\begin{align} S_1&=- 4 \varOmega
\sqrt{\nu_o T} \int_0^\infty \Big\{ \frac{2}{\sqrt{\rm \pi}}
{\rm e}^{- \eta^2} \Big( \eta \, \text{erf} ( \eta ) +
\frac{{\rm e}^{- \eta^2} - 1}{\sqrt{\rm \pi}} \Big) +
\text{erf} ( \eta ) [ 1 - \text{erf} ( \eta ) ] \Big\}
{\rm d} \eta\nonumber\\ & \quad + O ( 1 / \sqrt{\lambda_o}
).
\end{align}Using the relations, which are calculated by integration by parts,
the function ![]() $S_1$ can be obtained as
$S_1$ can be obtained as
Similarly, the function ![]() $S_2$ is written as, substituting (3.138) into (3.139b) and taking into account
$S_2$ is written as, substituting (3.138) into (3.139b) and taking into account ![]() $f^c ( T - \xi, 0 ) = 0$,
$f^c ( T - \xi, 0 ) = 0$,
 \begin{align} S_2 & = \sqrt{\frac{\nu_o}{\rm \pi}} \int_0^T \frac{{\rm d} \xi}{\sqrt{\xi}} \int_0^\infty \frac{\partial f^c ( T - \xi, R )}{\partial R} \exp\left({- \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} R + O ( 1 / \sqrt{\lambda_o} ) \nonumber\\ & =\frac{1}{2 \sqrt{\rm \pi}} \int_0^T \frac{{\rm d} \xi}{\sqrt{\xi ( T - \xi )}} \int_0^\infty \frac{\partial f^c ( \eta' )}{\partial \eta'} \exp\left({- \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} R + O ( 1 / \sqrt{\lambda_o} ), \end{align}
\begin{align} S_2 & = \sqrt{\frac{\nu_o}{\rm \pi}} \int_0^T \frac{{\rm d} \xi}{\sqrt{\xi}} \int_0^\infty \frac{\partial f^c ( T - \xi, R )}{\partial R} \exp\left({- \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} R + O ( 1 / \sqrt{\lambda_o} ) \nonumber\\ & =\frac{1}{2 \sqrt{\rm \pi}} \int_0^T \frac{{\rm d} \xi}{\sqrt{\xi ( T - \xi )}} \int_0^\infty \frac{\partial f^c ( \eta' )}{\partial \eta'} \exp\left({- \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} R + O ( 1 / \sqrt{\lambda_o} ), \end{align}
where ![]() $\eta ' = \eta \sqrt {T / ( T - \xi )}$. Note that the first integral in (3.143) is calculated by integration by parts. Changing the integral variable
$\eta ' = \eta \sqrt {T / ( T - \xi )}$. Note that the first integral in (3.143) is calculated by integration by parts. Changing the integral variable ![]() $\xi$ to
$\xi$ to ![]() $x$ by
$x$ by ![]() $x = \xi / T$, the function
$x = \xi / T$, the function ![]() $S_2$ is rewritten as
$S_2$ is rewritten as
Using the relation, which is calculated by changing the variable ![]() $x$ to
$x$ to ![]() $y$ by
$y$ by ![]() $x = \eta ^2 / y^2$,
$x = \eta ^2 / y^2$,
 \begin{equation} \int_0^1 \frac{1}{\sqrt{x}} {\rm e}^{- {\eta^2}/{x}} \,{\rm d}\kern0.06em x = 2 \eta \int_\eta^\infty \frac{{\rm e}^{- y^2}}{y^2} \,{\rm d} y = 2 {\rm e}^{- \eta^2} - 2 \sqrt{\rm \pi} \eta [ 1 - \text{erf} ( \eta ) ], \end{equation}
\begin{equation} \int_0^1 \frac{1}{\sqrt{x}} {\rm e}^{- {\eta^2}/{x}} \,{\rm d}\kern0.06em x = 2 \eta \int_\eta^\infty \frac{{\rm e}^{- y^2}}{y^2} \,{\rm d} y = 2 {\rm e}^{- \eta^2} - 2 \sqrt{\rm \pi} \eta [ 1 - \text{erf} ( \eta ) ], \end{equation}
the function ![]() $S_2$ reduces to
$S_2$ reduces to
where
The value of the integral included in (3.146) can be estimated numerically by the Hermite quadrature formula of ![]() $n = 9$:
$n = 9$:
The lift forces ![]() $F_y$ and
$F_y$ and ![]() $F_{p y}$ are therefore found to asymptotically behave like
$F_{p y}$ are therefore found to asymptotically behave like
Figure 7 shows the comparison of the asymptotic behaviours of ![]() $F_y / ( \rho \varOmega )$ and
$F_y / ( \rho \varOmega )$ and ![]() $F_{p y} / ( \rho \varOmega )$ given by (3.149a) and (3.149b) against the asymptotic solution obtained by Badr & Dennis (Reference Badr and Dennis1985):
$F_{p y} / ( \rho \varOmega )$ given by (3.149a) and (3.149b) against the asymptotic solution obtained by Badr & Dennis (Reference Badr and Dennis1985): ![]() $F_y / ( \rho \varOmega ) \sim - 2 \sqrt {\nu t} [ 1.4499 {\rm \pi}- 4 / ( 3 \sqrt {{\rm \pi} } ) + 2.0 \times 0.6961 {\rm \pi}\sqrt {\nu t} ]$. It seems that the result of approach (ii) (by the integration of the penalization layer) is completely different from the result of approach (i) (by the time derivative of the momentum of the fluid flow and the pressure on the control surface) that is similar to the asymptotic solution of Badr & Dennis (Reference Badr and Dennis1985). In figure 7 the lift coefficient
$F_y / ( \rho \varOmega ) \sim - 2 \sqrt {\nu t} [ 1.4499 {\rm \pi}- 4 / ( 3 \sqrt {{\rm \pi} } ) + 2.0 \times 0.6961 {\rm \pi}\sqrt {\nu t} ]$. It seems that the result of approach (ii) (by the integration of the penalization layer) is completely different from the result of approach (i) (by the time derivative of the momentum of the fluid flow and the pressure on the control surface) that is similar to the asymptotic solution of Badr & Dennis (Reference Badr and Dennis1985). In figure 7 the lift coefficient ![]() $C_L$, which is calculated by
$C_L$, which is calculated by ![]() $C_L = F_y / \rho$ in the present paper, is also shown together with the result of Badr & Dennis (Reference Badr and Dennis1985):
$C_L = F_y / \rho$ in the present paper, is also shown together with the result of Badr & Dennis (Reference Badr and Dennis1985): ![]() $C_L = - 8 \varOmega \sqrt {{\rm \pi} \nu t} [ 2 ( \sqrt {2} - 1 ) - 0.21578 ]$.
$C_L = - 8 \varOmega \sqrt {{\rm \pi} \nu t} [ 2 ( \sqrt {2} - 1 ) - 0.21578 ]$.

Figure 7. (a) Comparison of the lift force between ![]() $F_y$ (by approach (i)) and
$F_y$ (by approach (i)) and ![]() $F_{p y}$ (by approach (ii)) against the asymptotic solution of Badr & Dennis (Reference Badr and Dennis1985) at
$F_{p y}$ (by approach (ii)) against the asymptotic solution of Badr & Dennis (Reference Badr and Dennis1985) at ![]() $Re = 100$ for
$Re = 100$ for ![]() $\lambda _o \gg 1$ and
$\lambda _o \gg 1$ and ![]() $t \ll 1$. (b) Comparison of the lift coefficient
$t \ll 1$. (b) Comparison of the lift coefficient ![]() $C_L$ with the result of Badr & Dennis (Reference Badr and Dennis1985) in the case of
$C_L$ with the result of Badr & Dennis (Reference Badr and Dennis1985) in the case of ![]() $\nu = 1 / 500$ and
$\nu = 1 / 500$ and ![]() $\varOmega = 0.5$.
$\varOmega = 0.5$.
3.5. Alternative formula of hydrodynamic force
As seen in the preceding subsection § 3.4, the lift force calculated by approach (ii) yields a completely different value from the result of approach (i). In particular, the result of approach (ii) exhibits the opposite sign against the result of approach (i) and the asymptotic solution of Badr & Dennis (Reference Badr and Dennis1985) (see figure 7). To resolve the variance, we attempt to derive an alternative formula to calculate the hydrodynamic forces.
In general, let us consider a two-dimensional domain ![]() ${\mathscr {D}}$ that consists of two closed boundaries
${\mathscr {D}}$ that consists of two closed boundaries ![]() ${\mathscr {C}}_o$ and
${\mathscr {C}}_o$ and ![]() ${\mathscr {C}}_i$ such that
${\mathscr {C}}_i$ such that ![]() ${\mathscr {C}}_i \subset {\mathscr {C}}_o$. The hydrodynamic force due to the momentum of the fluid flow in the domain
${\mathscr {C}}_i \subset {\mathscr {C}}_o$. The hydrodynamic force due to the momentum of the fluid flow in the domain ![]() ${\mathscr {D}}$ is defined as
${\mathscr {D}}$ is defined as ![]() $( F_x, F_y )_{\mathscr {D}}$ and, then, it is written as
$( F_x, F_y )_{\mathscr {D}}$ and, then, it is written as
Substituting (2.1) into (3.150), we have
Using Green's theorem, we have the following relations with respect to the first and third terms on the right-hand side of (3.151):
Here ![]() $\omega$ is the vorticity.
$\omega$ is the vorticity.
Here, in general, we look at a closed contour ![]() ${\mathscr {C}}$ that surrounds a two-dimensional fluid domain
${\mathscr {C}}$ that surrounds a two-dimensional fluid domain ![]() ${\mathscr {D}}'$, and we consider the hydrodynamic force
${\mathscr {D}}'$, and we consider the hydrodynamic force ![]() $( F_{b x}, F_{b y} )$ on the fluid in
$( F_{b x}, F_{b y} )$ on the fluid in ![]() ${\mathscr {D}}'$ exerted by the outer domain of
${\mathscr {D}}'$ exerted by the outer domain of ![]() ${\mathscr {C}}$. The small element
${\mathscr {C}}$. The small element ![]() ${\rm d} s$ on
${\rm d} s$ on ![]() ${\mathscr {C}}$ is acted on by normal and tangential stresses and outflow momentum from
${\mathscr {C}}$ is acted on by normal and tangential stresses and outflow momentum from ![]() ${\mathscr {C}}$. Note that the outflow momentum is written as
${\mathscr {C}}$. Note that the outflow momentum is written as ![]() $- \rho u_n ( u, v ) \,{\rm d} s$, where the subscript
$- \rho u_n ( u, v ) \,{\rm d} s$, where the subscript ![]() $n$ indicates the outward normal direction of the contour
$n$ indicates the outward normal direction of the contour ![]() ${\mathscr {C}}$. Then, the hydrodynamic force
${\mathscr {C}}$. Then, the hydrodynamic force ![]() $( F_{b x}, F_{b y} )$ is described as
$( F_{b x}, F_{b y} )$ is described as
We apply (3.153a) and (3.153b) to the contours ![]() ${\mathscr {C}}_o$ and
${\mathscr {C}}_o$ and ![]() ${\mathscr {C}}_i$. Taking into account (3.152a)–(3.152b), (3.151) can be then described as
${\mathscr {C}}_i$. Taking into account (3.152a)–(3.152b), (3.151) can be then described as
Now, let us apply (3.154) to the fluid domain ![]() ${\mathscr {D}}_f$ that is surrounded by the control surface
${\mathscr {D}}_f$ that is surrounded by the control surface ![]() ${\mathscr {C}}_\infty$ and the body surface
${\mathscr {C}}_\infty$ and the body surface ![]() ${\mathscr {C}}_+$. Then, because of
${\mathscr {C}}_+$. Then, because of ![]() $\chi = 0$, (3.154) is rewritten as
$\chi = 0$, (3.154) is rewritten as
 \begin{equation} \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_f} =- \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} - \int_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} u_n ( u, v ) \,{\rm d} s. \end{equation}
\begin{equation} \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_f} =- \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} - \int_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} u_n ( u, v ) \,{\rm d} s. \end{equation}
Therefore, the hydrodynamic force on the cylinder, ![]() $( F_{b x}, F_{b y} )$, which is exerted from the fluid domain, is obtained as
$( F_{b x}, F_{b y} )$, which is exerted from the fluid domain, is obtained as
 \begin{equation} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} = \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_f} + \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_\infty} + \int_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} u_n ( u, v ) \,{\rm d} s. \end{equation}
\begin{equation} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} = \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_f} + \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_\infty} + \int_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} u_n ( u, v ) \,{\rm d} s. \end{equation}
Because of ![]() $\omega \approx 0$ and
$\omega \approx 0$ and ![]() $( u, v ) = ( 1 + O ( 1 / r^2 ), O ( 1 / r^2) )$ in the neighbourhood of the control surface
$( u, v ) = ( 1 + O ( 1 / r^2 ), O ( 1 / r^2) )$ in the neighbourhood of the control surface ![]() ${\mathscr {C}}_\infty$, the pressure solely affects the second term on the right-hand side of (3.156), and the momentum of the fluid flow affects the first term (see § 3.4).
${\mathscr {C}}_\infty$, the pressure solely affects the second term on the right-hand side of (3.156), and the momentum of the fluid flow affects the first term (see § 3.4).
For the domain ![]() ${\mathscr {D}}_s$ inside the body whose surface is defined as
${\mathscr {D}}_s$ inside the body whose surface is defined as ![]() ${{\mathscr {C}}_-}$, (3.154) is written as
${{\mathscr {C}}_-}$, (3.154) is written as
From (3.155) and (3.157), we have
 \begin{align} \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_f + {\mathscr{D}}_s} & =- \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_\infty} + \left( \frac{F_{v x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+- {\mathscr{C}}_-}\nonumber\\ &\quad - \int_{{\mathscr{C}}_\infty} u_n ( u, v ) \,{\rm d} s - \lambda \int_{{\mathscr{D}}_s} ( {\boldsymbol{u}}_s - {\boldsymbol{u}} ) \,{\rm d}\kern0.06em x \,{\rm d} y. \end{align}
\begin{align} \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_f + {\mathscr{D}}_s} & =- \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_\infty} + \left( \frac{F_{v x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+- {\mathscr{C}}_-}\nonumber\\ &\quad - \int_{{\mathscr{C}}_\infty} u_n ( u, v ) \,{\rm d} s - \lambda \int_{{\mathscr{D}}_s} ( {\boldsymbol{u}}_s - {\boldsymbol{u}} ) \,{\rm d}\kern0.06em x \,{\rm d} y. \end{align} As shown in § 3.3.2, there is the pressure difference ![]() $\Delta p$ (i.e.
$\Delta p$ (i.e. ![]() $\Delta p \neq 0$) between the inside and the outside of the cylinder surface
$\Delta p \neq 0$) between the inside and the outside of the cylinder surface ![]() ${\mathscr {C}}$ and, therefore, we can write
${\mathscr {C}}$ and, therefore, we can write
 \begin{equation} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} = \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_-} - \int_{\mathscr{C}} \left( \frac{\Delta p}{\rho} {\rm d} y, - \frac{\Delta p}{\rho} \,{\rm d}\kern0.06em x \right), \end{equation}
\begin{equation} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} = \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_-} - \int_{\mathscr{C}} \left( \frac{\Delta p}{\rho} {\rm d} y, - \frac{\Delta p}{\rho} \,{\rm d}\kern0.06em x \right), \end{equation}
where ![]() ${\mathscr {C}}_\pm$ denotes the contour of the cylinder surface on the side of
${\mathscr {C}}_\pm$ denotes the contour of the cylinder surface on the side of ![]() ${\mathscr {D}}_f$ and
${\mathscr {D}}_f$ and ![]() ${\mathscr {D}}_s$, respectively. Taking into account (3.157), (3.159) is written as
${\mathscr {D}}_s$, respectively. Taking into account (3.157), (3.159) is written as
 \begin{align} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} &=- \left( \frac{F_{x}}{\rho}, \frac{F_{y}}{\rho} \right)_{{\mathscr{D}}_s} - \int_{\mathscr{C}} u_n ( u, v ) \,{\rm d} s\nonumber\\ &\quad - \lambda \int_{{\mathscr{D}}_s} ( {\boldsymbol{u}}_s - {\boldsymbol{u}} ) \,{\rm d}\kern0.06em x \,{\rm d} y - \int_{\mathscr{C}} \left( \frac{\Delta p}{\rho} \,{\rm d} y, \frac{\Delta p}{\rho} \,{\rm d}\kern0.06em x \right). \end{align}
\begin{align} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} &=- \left( \frac{F_{x}}{\rho}, \frac{F_{y}}{\rho} \right)_{{\mathscr{D}}_s} - \int_{\mathscr{C}} u_n ( u, v ) \,{\rm d} s\nonumber\\ &\quad - \lambda \int_{{\mathscr{D}}_s} ( {\boldsymbol{u}}_s - {\boldsymbol{u}} ) \,{\rm d}\kern0.06em x \,{\rm d} y - \int_{\mathscr{C}} \left( \frac{\Delta p}{\rho} \,{\rm d} y, \frac{\Delta p}{\rho} \,{\rm d}\kern0.06em x \right). \end{align}Approach (i) in the preceding § 3.4 is
 \begin{align} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{\text{(i)}} &= \left( \frac{F_{x}}{\rho}, \frac{F_{y}}{\rho} \right)_{{\mathscr{D}}_f} + \left( \frac{F_{b x}}{\rho}, \frac{F_{by}}{\rho} \right)_{{\mathscr{C}}_\infty} \nonumber\\ &= \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} - \int_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} u_n ( u, v ) \,{\rm d} s. \end{align}
\begin{align} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{\text{(i)}} &= \left( \frac{F_{x}}{\rho}, \frac{F_{y}}{\rho} \right)_{{\mathscr{D}}_f} + \left( \frac{F_{b x}}{\rho}, \frac{F_{by}}{\rho} \right)_{{\mathscr{C}}_\infty} \nonumber\\ &= \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} - \int_{{\mathscr{C}}_\infty - {\mathscr{C}}_+} u_n ( u, v ) \,{\rm d} s. \end{align}
Therefore, we can see that ![]() $( F_{b x} / \rho, F_{b y} / \rho )_{\text {(i)}} = ( F_{bx} / \rho, F_{b y} / \rho )_{{\mathscr {C}}_+}$, since in the case of the present study of the circular cylinder, that is, because of
$( F_{b x} / \rho, F_{b y} / \rho )_{\text {(i)}} = ( F_{bx} / \rho, F_{b y} / \rho )_{{\mathscr {C}}_+}$, since in the case of the present study of the circular cylinder, that is, because of ![]() $u_n = u_r^i = O ( \epsilon )$ as shown in § 3.3.2, the last term of (3.156) is found to be of the order of
$u_n = u_r^i = O ( \epsilon )$ as shown in § 3.3.2, the last term of (3.156) is found to be of the order of ![]() $\epsilon$. It is therefore found that the asymptotic behaviour of
$\epsilon$. It is therefore found that the asymptotic behaviour of ![]() $F_{b x}$ for
$F_{b x}$ for ![]() $\lambda _o \gg 1$ and
$\lambda _o \gg 1$ and ![]() $T \ll 1$ is the same as
$T \ll 1$ is the same as ![]() $F_x$ obtained in § 3.4. For approach (ii) in the case of
$F_x$ obtained in § 3.4. For approach (ii) in the case of ![]() $u_n = 0$ on
$u_n = 0$ on ![]() ${\mathscr {C}}_-$, we have from (3.159)
${\mathscr {C}}_-$, we have from (3.159)
 \begin{align} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{\text{(ii)}} & = \left( \frac{F_{b x}}{\rho}, \frac{F_{by}}{\rho} \right)_{{\mathscr{C}}_-} + \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_s}\nonumber\\ & = \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} + \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_s} + \int_{\mathscr{C}} \left( \frac{\Delta p}{\rho} \,{\rm d} y, - \frac{\Delta p}{\rho} \,{\rm d}\kern0.06em x \right). \end{align}
\begin{align} \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{\text{(ii)}} & = \left( \frac{F_{b x}}{\rho}, \frac{F_{by}}{\rho} \right)_{{\mathscr{C}}_-} + \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_s}\nonumber\\ & = \left( \frac{F_{b x}}{\rho}, \frac{F_{b y}}{\rho} \right)_{{\mathscr{C}}_+} + \left( \frac{F_x}{\rho}, \frac{F_y}{\rho} \right)_{{\mathscr{D}}_s} + \int_{\mathscr{C}} \left( \frac{\Delta p}{\rho} \,{\rm d} y, - \frac{\Delta p}{\rho} \,{\rm d}\kern0.06em x \right). \end{align}
We see that even when the velocity inside the cylinder is zero, there is the difference in the third term of the right-hand side of (3.162) between approach (i) and (ii) by the pressure jump. Since the present analysis takes the relative coordinate system fixed with the centre of the cylinder, the first term on the right-hand side of (3.160) becomes zero. It can then be found that the calculation of the hydrodynamic force by the integration of the penalization layer (i.e. (2.3)) is formulated, assuming that the pressure difference ![]() $\Delta p$ and the force on the cylinder surface exerted by the momentum due to the fluid flow are zero. In this assumption,
$\Delta p$ and the force on the cylinder surface exerted by the momentum due to the fluid flow are zero. In this assumption, ![]() $u_n = 0$,
$u_n = 0$, ![]() $\Delta p = 0$ and
$\Delta p = 0$ and ![]() $(F_x /\rho, F_y /\rho)_{\mathscr{D}_s} = 0$. Therefore, we have
$(F_x /\rho, F_y /\rho)_{\mathscr{D}_s} = 0$. Therefore, we have ![]() $(F_x /\rho, F_y /\rho)_{\rm i} = (F_x /\rho, F_y /\rho)_{\rm ii}$. Here, the pressure difference,
$(F_x /\rho, F_y /\rho)_{\rm i} = (F_x /\rho, F_y /\rho)_{\rm ii}$. Here, the pressure difference, ![]() $\Delta p$, between the inside and the outside of the cylinder surface is given from (3.81) and (3.110).
$\Delta p$, between the inside and the outside of the cylinder surface is given from (3.81) and (3.110).
 \begin{align} \frac{\Delta p}{\rho} & = \frac{1}{\rho} \left(\kern0.7pt p|_{r \to 1 + 0} - p|_{r \to 1 - 0} \right)\nonumber\\ & = 2 \frac{{\rm d} A}{{\rm d} T} \cos{\theta} - 2 \sin^2{\theta} + \frac{1}{2} ( 1 - \varOmega^2 ) - C\nonumber\\ &\quad + \epsilon \left\{ \frac{\partial}{\partial T} \int_0^\infty [ u_{r 1}^i - 2 ( A + R ) \cos{\theta} ] \,{\rm d} R - \int_0^\infty ( u_{\theta 0}^{i 2} - 4 \sin^2{\theta} ) \,{\rm d} R + \nu_o\left. \frac{\partial u_{r 1}^i}{\partial R} \right|_{R =+ 0}\right.\nonumber\\ &\quad \left.-\, 2 \nu_o \cos{\theta} - \frac{{\rm d}}{{\rm d} T} ( a_1^c \cos{\theta} + a_1^s \sin{\theta} + a_2^c \cos{2 \theta} ) + 4 A \sin^2{\theta} \right\}. \end{align}
\begin{align} \frac{\Delta p}{\rho} & = \frac{1}{\rho} \left(\kern0.7pt p|_{r \to 1 + 0} - p|_{r \to 1 - 0} \right)\nonumber\\ & = 2 \frac{{\rm d} A}{{\rm d} T} \cos{\theta} - 2 \sin^2{\theta} + \frac{1}{2} ( 1 - \varOmega^2 ) - C\nonumber\\ &\quad + \epsilon \left\{ \frac{\partial}{\partial T} \int_0^\infty [ u_{r 1}^i - 2 ( A + R ) \cos{\theta} ] \,{\rm d} R - \int_0^\infty ( u_{\theta 0}^{i 2} - 4 \sin^2{\theta} ) \,{\rm d} R + \nu_o\left. \frac{\partial u_{r 1}^i}{\partial R} \right|_{R =+ 0}\right.\nonumber\\ &\quad \left.-\, 2 \nu_o \cos{\theta} - \frac{{\rm d}}{{\rm d} T} ( a_1^c \cos{\theta} + a_1^s \sin{\theta} + a_2^c \cos{2 \theta} ) + 4 A \sin^2{\theta} \right\}. \end{align} For ![]() $\lambda _o \gg 1$, (3.96a)–(3.96c) and (D9a)–(D9d) are written as
$\lambda _o \gg 1$, (3.96a)–(3.96c) and (D9a)–(D9d) are written as
where ![]() $\eta = r / ( 2 \sqrt {\nu _oT} )$. Then, the following integral involved in (3.163) is calculated as
$\eta = r / ( 2 \sqrt {\nu _oT} )$. Then, the following integral involved in (3.163) is calculated as
 \begin{align} \int_0^\infty ( u_{\theta 0}^{i 2} - 4 \sin^2{\theta} ) \,{\rm d} R & \sim 2 \sqrt{\nu_o T} \int_0^\infty ( \varOmega + 2 \sin{\theta} ) \, \text{erfc} ( \eta )\nonumber\\ &\quad \times \left[ - 4 \sin{\theta} + ( \varOmega + 2 \sin{\theta} ) \, \text{erfc} ( \eta ) \right] {\rm d} \eta\nonumber\\ & =2 \sqrt{\frac{\nu_o T}{\rm \pi}}[ - 4 \sin{\theta} ( \varOmega + 2 \sin{\theta} ) + ( \varOmega + 2 \sin{\theta} )^2 ( 2 - \sqrt{2} )]. \end{align}
\begin{align} \int_0^\infty ( u_{\theta 0}^{i 2} - 4 \sin^2{\theta} ) \,{\rm d} R & \sim 2 \sqrt{\nu_o T} \int_0^\infty ( \varOmega + 2 \sin{\theta} ) \, \text{erfc} ( \eta )\nonumber\\ &\quad \times \left[ - 4 \sin{\theta} + ( \varOmega + 2 \sin{\theta} ) \, \text{erfc} ( \eta ) \right] {\rm d} \eta\nonumber\\ & =2 \sqrt{\frac{\nu_o T}{\rm \pi}}[ - 4 \sin{\theta} ( \varOmega + 2 \sin{\theta} ) + ( \varOmega + 2 \sin{\theta} )^2 ( 2 - \sqrt{2} )]. \end{align}Here, the following relations are used for the calculation of (3.165):
Taking into account ![]() $A \sim 2 \sqrt {\nu _o T / {\rm \pi}}$ and using (3.164a)–(3.164f) together with (3.165), (3.163) can be written as
$A \sim 2 \sqrt {\nu _o T / {\rm \pi}}$ and using (3.164a)–(3.164f) together with (3.165), (3.163) can be written as
 \begin{align} \frac{\Delta p}{\rho} & \sim 2 \sqrt{\frac{\nu_o}{{\rm \pi} T}} \cos{\theta} - 2 \sin^2{\theta} + \frac{1}{2} ( 1 - \varOmega^2 ) + \epsilon \left\{ 8 \sqrt{\frac{\nu_o T}{\rm \pi}} \sin^2{\theta} - \nu_o \cos{\theta}\right.\nonumber\\ &\quad - 2 \sqrt{\frac{\nu_o T}{\rm \pi}} \left[ - 4 \varOmega \sin{\theta} - 8 \sin^2{\theta} + ( 2 - \sqrt{2} ) ( \varOmega^2 + 4 \varOmega \sin{\theta} + 4 \sin^2{\theta} ) \right]\nonumber\\ &\quad + {\mathcal{L}}^{- 1} \left( \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R - \int_0^\infty F^c \,{\rm d} R \right) \sin{\theta}\nonumber\\ & \quad \left.+\,{\mathcal{L}}^{- 1} \left( \int_0^\infty F^{cs} {\rm e}^{- a R} \,{\rm d} R - \int_0^\infty F^{c s} \,{\rm d} R \right) \cos{2 \theta} \vphantom{\sqrt{\frac{\nu_o T}{\rm \pi}}}\right\} + O ( \epsilon^2, 1 / \sqrt{\lambda_o} ). \end{align}
\begin{align} \frac{\Delta p}{\rho} & \sim 2 \sqrt{\frac{\nu_o}{{\rm \pi} T}} \cos{\theta} - 2 \sin^2{\theta} + \frac{1}{2} ( 1 - \varOmega^2 ) + \epsilon \left\{ 8 \sqrt{\frac{\nu_o T}{\rm \pi}} \sin^2{\theta} - \nu_o \cos{\theta}\right.\nonumber\\ &\quad - 2 \sqrt{\frac{\nu_o T}{\rm \pi}} \left[ - 4 \varOmega \sin{\theta} - 8 \sin^2{\theta} + ( 2 - \sqrt{2} ) ( \varOmega^2 + 4 \varOmega \sin{\theta} + 4 \sin^2{\theta} ) \right]\nonumber\\ &\quad + {\mathcal{L}}^{- 1} \left( \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R - \int_0^\infty F^c \,{\rm d} R \right) \sin{\theta}\nonumber\\ & \quad \left.+\,{\mathcal{L}}^{- 1} \left( \int_0^\infty F^{cs} {\rm e}^{- a R} \,{\rm d} R - \int_0^\infty F^{c s} \,{\rm d} R \right) \cos{2 \theta} \vphantom{\sqrt{\frac{\nu_o T}{\rm \pi}}}\right\} + O ( \epsilon^2, 1 / \sqrt{\lambda_o} ). \end{align}
Integrating the ![]() $x$ and
$x$ and ![]() $y$ components of (3.155) acting on the cylinder surface, we have
$y$ components of (3.155) acting on the cylinder surface, we have
Therefore, the hydrodynamic forces can be found to behave like, for ![]() $\lambda _o \gg 1$,
$\lambda _o \gg 1$,
Note that (3.169a) is derived as follows:
Equation (3.169a) is the same result as Badr & Dennis (Reference Badr and Dennis1985) and our previous study (Ueda & Kida Reference Ueda and Kida2021). Using the value of ![]() $s_o$ which is calculated in (3.148), (3.169b) is obtained as
$s_o$ which is calculated in (3.148), (3.169b) is obtained as
 \begin{align} F_{b y}& \sim 2 \rho {\rm \pi}
\epsilon \Biggl[ - 4 \varOmega \sqrt{\frac{\nu_o T}{\rm \pi}} (
\sqrt{2} - 1 ) - 4 \varOmega \sqrt{\frac{\nu T}{\rm \pi}} s_o
\Biggr] + 8 \rho \varOmega \sqrt{{\rm \pi} \nu t} ( 1 - \sqrt{2}
)\nonumber\\ & \sim- 16 \rho \varOmega \sqrt{{\rm \pi} \nu t} (
\sqrt{2} - 1 ) - 8 \rho \varOmega \sqrt{{\rm \pi} \nu t} s_o.
\end{align}
\begin{align} F_{b y}& \sim 2 \rho {\rm \pi}
\epsilon \Biggl[ - 4 \varOmega \sqrt{\frac{\nu_o T}{\rm \pi}} (
\sqrt{2} - 1 ) - 4 \varOmega \sqrt{\frac{\nu T}{\rm \pi}} s_o
\Biggr] + 8 \rho \varOmega \sqrt{{\rm \pi} \nu t} ( 1 - \sqrt{2}
)\nonumber\\ & \sim- 16 \rho \varOmega \sqrt{{\rm \pi} \nu t} (
\sqrt{2} - 1 ) - 8 \rho \varOmega \sqrt{{\rm \pi} \nu t} s_o.
\end{align}The value of (3.171), which is the present result, is calculated as
whereas the value of the asymptotic solution obtained by Badr & Dennis (Reference Badr and Dennis1985) is given by
It can therefore be found that the variance on the values of the lift force calculated by the two approaches (see § 3.4) results from the pressure jump on the body (cylinder) surface. The inner expansion of the pressure in the outer domain of the fluid cannot continuously connect to the inner expansion of the pressure in the outer domain of the solid body (circular cylinder). Therefore, the pressure jump is found to be caused by the matching procedure of the outer solution in the fluid domain.
4. Concluding remarks
This study aims to elucidate the variance of the drag force calculated by the integration of the penalization layer against the asymptotic solution for ![]() $t\ll 1$, which is demonstrated in our previous paper (see Ueda & Kida Reference Ueda and Kida2021). We first consider the problem that a circular cylinder impulsively rotates from a quiescent state. In this first problem, it is verified that the results of the moment calculated by the different two approaches (approaches (I) and (II) in § 3.2) are the same as the result calculated by the integration of the penalization layer. Note that the pressure on the cylinder surface is independent of the moment and, therefore, it can be deduced that the pressure plays a key role to the drag force on the cylinder.
$t\ll 1$, which is demonstrated in our previous paper (see Ueda & Kida Reference Ueda and Kida2021). We first consider the problem that a circular cylinder impulsively rotates from a quiescent state. In this first problem, it is verified that the results of the moment calculated by the different two approaches (approaches (I) and (II) in § 3.2) are the same as the result calculated by the integration of the penalization layer. Note that the pressure on the cylinder surface is independent of the moment and, therefore, it can be deduced that the pressure plays a key role to the drag force on the cylinder.
We therefore consider the second problem in § 3.3 that a circular cylinder impulsively starts with rotating and translating velocities from a quiescent state. The drag and lift forces are calculated by two approaches: (i) based on the time derivative of the momentum of an entire fluid domain and the pressure on the control surface of which radius is sufficiently large, and (ii) based on the integration of the penalization layer. For ![]() $t \ll 1$ and
$t \ll 1$ and ![]() $\lambda _o \gg 1$, the drag force calculated by approach (ii) gives a half-value of that calculated by approach (i) that yields the same result as the classical asymptotic solution of Bar-Lev & Yang (Reference Bar-Lev and Yang1975). This finding is the same as our previous study (Ueda & Kida Reference Ueda and Kida2021) for an impulsively started translating circular cylinder without rotation. Furthermore, the calculated lift force is completely different between the two approaches, as shown in figure 7(a). To resolve the variance, this study successfully derives an alternative formula to calculate the hydrodynamic force, assuming that there is a pressure jump between the outside and inside of the cylinder surface. It can be found that the variance is caused by the pressure jump on the cylinder surface. Furthermore, the comparison of the drag force with the previous result is discussed in Appendix F. In the penalization method the no-slip boundary condition on the cylinder surface is not imposed, although it is imposed in the previous analysis. This condition generates the additional terms on the time derivative of the slip velocity, which is related to the pressure jump.
$\lambda _o \gg 1$, the drag force calculated by approach (ii) gives a half-value of that calculated by approach (i) that yields the same result as the classical asymptotic solution of Bar-Lev & Yang (Reference Bar-Lev and Yang1975). This finding is the same as our previous study (Ueda & Kida Reference Ueda and Kida2021) for an impulsively started translating circular cylinder without rotation. Furthermore, the calculated lift force is completely different between the two approaches, as shown in figure 7(a). To resolve the variance, this study successfully derives an alternative formula to calculate the hydrodynamic force, assuming that there is a pressure jump between the outside and inside of the cylinder surface. It can be found that the variance is caused by the pressure jump on the cylinder surface. Furthermore, the comparison of the drag force with the previous result is discussed in Appendix F. In the penalization method the no-slip boundary condition on the cylinder surface is not imposed, although it is imposed in the previous analysis. This condition generates the additional terms on the time derivative of the slip velocity, which is related to the pressure jump.
Acknowledgements
The authors express their warm thanks to anonymous referees who kindly gave valuable comments for the description of the additional terms to Ueda & Kida (Reference Ueda and Kida2021).
Funding
Y.U. gratefully acknowledges the financial support provided by the Japan Society for Promotion of Science (JSPS) under its Grant-in-Aid for Scientific Research (C) number 21K04757.
Declaration of interests
The authors report no conflict of interest.
Appendix A
Using the formulae of Abramowitz & Stegun (Reference Abramowitz and Stegun1954), the following relations of the inverse Laplace transform are obtained;
 $$\begin{gather} {\mathcal{L}}^{- 1} \Bigg( \sqrt{\frac{s + 2 a}{s}} - 1 \Bigg) = a {\rm e}^{- a T} \left[ {\rm I}_1 ( a T ) + {\rm I}_0 ( a T ) \right], \end{gather}$$
$$\begin{gather} {\mathcal{L}}^{- 1} \Bigg( \sqrt{\frac{s + 2 a}{s}} - 1 \Bigg) = a {\rm e}^{- a T} \left[ {\rm I}_1 ( a T ) + {\rm I}_0 ( a T ) \right], \end{gather}$$Appendix B
We look at the following differential equation, in which ![]() $U$ is a function of
$U$ is a function of ![]() $R$ and
$R$ and ![]() $\theta$:
$\theta$:
Setting ![]() $U$ as
$U$ as ![]() $U = A ( R, \theta ) {\rm e}^{- a R}$, (B1) is rewritten as, by the differential equation with respect to the function
$U = A ( R, \theta ) {\rm e}^{- a R}$, (B1) is rewritten as, by the differential equation with respect to the function ![]() $A$,
$A$,
The solution to (B2) is readily obtained as
where ![]() $C_0$ and
$C_0$ and ![]() $C_1$ are the integral constants. Therefore, we obtain the function
$C_1$ are the integral constants. Therefore, we obtain the function ![]() $U$ that is the solution to (B1):
$U$ that is the solution to (B1):
When ![]() $U \to 0$ as
$U \to 0$ as ![]() $R \to \infty$, the integral constant
$R \to \infty$, the integral constant ![]() $C_0$ is determined as
$C_0$ is determined as ![]() $C_0 = 0$ and, therefore, the solution to (B1) is obtained as
$C_0 = 0$ and, therefore, the solution to (B1) is obtained as
Appendix C
Using the Laplace transform, (3.84a) is written as, for ![]() $R \geq 0$,
$R \geq 0$,
where ![]() $U_{\theta 1}^0 = {\mathcal {L}} ( \hat {u}_{\theta 1}^0)$ and
$U_{\theta 1}^0 = {\mathcal {L}} ( \hat {u}_{\theta 1}^0)$ and ![]() $U_{\theta 0}^0 = {\mathcal {L}} ( \hat {u}_{\theta 0}^0 )$. From (3.61), we find that
$U_{\theta 0}^0 = {\mathcal {L}} ( \hat {u}_{\theta 0}^0 )$. From (3.61), we find that ![]() $U_{\theta 0}^0 = \{ \bar {a} / [ s ( a + \bar {a} ) ] \} \varOmega {\rm e}^{- a R}$. Based on the boundary condition of (3.85a–d), the solution to (C1) is obtained as, using Appendix B,
$U_{\theta 0}^0 = \{ \bar {a} / [ s ( a + \bar {a} ) ] \} \varOmega {\rm e}^{- a R}$. Based on the boundary condition of (3.85a–d), the solution to (C1) is obtained as, using Appendix B,
where ![]() $D$ is an integral constant that is a function of
$D$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$.
$\theta$.
For ![]() $R < 0$, by virtue of (3.61) and (3.85a–d), the function
$R < 0$, by virtue of (3.61) and (3.85a–d), the function ![]() $\hat {u}_{\theta 1}^0$ is found to be written as the form of
$\hat {u}_{\theta 1}^0$ is found to be written as the form of ![]() $\hat {u}_{\theta 1}^0 = R \varOmega H ( T ) + \bar {u}_{\theta 1}^0$. Then, (3.84a) reduces to
$\hat {u}_{\theta 1}^0 = R \varOmega H ( T ) + \bar {u}_{\theta 1}^0$. Then, (3.84a) reduces to
where ![]() $\bar {U}_{\theta 1}^0 = {\mathcal {L}} ( \bar {u}_{\theta 1}^0 )$. The solution to (C3) is obtained as, using Appendix B,
$\bar {U}_{\theta 1}^0 = {\mathcal {L}} ( \bar {u}_{\theta 1}^0 )$. The solution to (C3) is obtained as, using Appendix B,
where ![]() $E$ is an integral constant that is a function of
$E$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$. These integral constants
$\theta$. These integral constants ![]() $D$ and
$D$ and ![]() $E$ can be determined as, from the enforcements of the continuity of the velocity and its radial derivative at
$E$ can be determined as, from the enforcements of the continuity of the velocity and its radial derivative at ![]() $R = 0$,
$R = 0$,
The velocity ![]() $\hat {u}_{\theta 1}^0$ can be found to be the same as the solution of the pure rotation problem obtained in (3.32).
$\hat {u}_{\theta 1}^0$ can be found to be the same as the solution of the pure rotation problem obtained in (3.32).
The Laplace transform to (3.84c) is written as, for ![]() $R \geq 0$,
$R \geq 0$,
where ![]() $U_{\theta 1}^s = {\mathcal {L}} ( \hat {u}_{\theta 1}^s )$. Here, we introduce
$U_{\theta 1}^s = {\mathcal {L}} ( \hat {u}_{\theta 1}^s )$. Here, we introduce ![]() $\bar {U}_{\theta 1}^s$ as
$\bar {U}_{\theta 1}^s$ as ![]() $U_{\theta 1}^s = 2 ( R / s ) + 2 [ ( a - \bar {a} ) / ( s a \bar {a} ) ] + \bar {U}_{\theta 1}^s$. Then, (C6) reduces to
$U_{\theta 1}^s = 2 ( R / s ) + 2 [ ( a - \bar {a} ) / ( s a \bar {a} ) ] + \bar {U}_{\theta 1}^s$. Then, (C6) reduces to
By virtue of the boundary condition (3.85a–d), ![]() $\bar {U}_{\theta 1}^s$ is found to be not divergent as
$\bar {U}_{\theta 1}^s$ is found to be not divergent as ![]() $R \to \infty$. Hence, we set
$R \to \infty$. Hence, we set ![]() $\bar {U}_{\theta 1}^s$ as
$\bar {U}_{\theta 1}^s$ as
where ![]() $D_s$ is an integral constant that is a function of
$D_s$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$.
$\theta$.
For ![]() $R < 0$, the Laplace transform to (3.84c) is written as, taking into account
$R < 0$, the Laplace transform to (3.84c) is written as, taking into account ![]() ${\mathcal {L}} ( \partial \hat {u}_{\theta 0}^s / \partial R ) = - 2 a \bar {a} / [ s ( a + \bar {a} ) ] {\rm e}^{\bar {a} R}$ from (3.61) and
${\mathcal {L}} ( \partial \hat {u}_{\theta 0}^s / \partial R ) = - 2 a \bar {a} / [ s ( a + \bar {a} ) ] {\rm e}^{\bar {a} R}$ from (3.61) and ![]() $\hat {u}_{\theta 1} \to 0$ as
$\hat {u}_{\theta 1} \to 0$ as ![]() $R \to - \infty$ from (3.86a–d),
$R \to - \infty$ from (3.86a–d),
The solution to (C9) is therefore obtained as
where ![]() $E_s$ is an integral constant that is a function of
$E_s$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$. These indeterminate constants can be determined as, by the enforcements of the continuity of the velocity and its radial derivative at
$\theta$. These indeterminate constants can be determined as, by the enforcements of the continuity of the velocity and its radial derivative at ![]() $R = 0$,
$R = 0$,
Thus, we obtain (3.88).
In contrast, ![]() $\hat {u}_{\theta 1}^c$ can be obtained for
$\hat {u}_{\theta 1}^c$ can be obtained for ![]() $R \geq 0$ by the Laplace transform to (3.84b),
$R \geq 0$ by the Laplace transform to (3.84b),
 \begin{equation} s U_{\theta 1}^c - \nu_o \frac{\partial^2 U_{\theta 1}^c}{\partial R^2} =- F^c, \quad F^c = {\mathcal{L}} \Bigg( \hat{u}_{r 1} \frac{\partial \hat{u}_{\theta 0}^0}{\partial R} + \hat{u}_{\theta 0}^0 \hat{u}_{\theta 0}^s \Bigg), \end{equation}
\begin{equation} s U_{\theta 1}^c - \nu_o \frac{\partial^2 U_{\theta 1}^c}{\partial R^2} =- F^c, \quad F^c = {\mathcal{L}} \Bigg( \hat{u}_{r 1} \frac{\partial \hat{u}_{\theta 0}^0}{\partial R} + \hat{u}_{\theta 0}^0 \hat{u}_{\theta 0}^s \Bigg), \end{equation}
where ![]() $U_{\theta 1}^c = {\mathcal {L}} ( \hat {u}_{\theta 1}^c )$. The solution to (C12a,b) is readily obtained as, based on the boundary condition of (3.85a–d) (i.e.
$U_{\theta 1}^c = {\mathcal {L}} ( \hat {u}_{\theta 1}^c )$. The solution to (C12a,b) is readily obtained as, based on the boundary condition of (3.85a–d) (i.e. ![]() $U_{\theta 1}^c \to 0$ as
$U_{\theta 1}^c \to 0$ as ![]() $R \to \infty$),
$R \to \infty$),
 \begin{equation} U_{\theta 1}^c =- \frac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^c {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^c {\rm e}^{a R} \,{\rm d} R \right) + D_c {\rm e}^{- a R}, \end{equation}
\begin{equation} U_{\theta 1}^c =- \frac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^c {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^c {\rm e}^{a R} \,{\rm d} R \right) + D_c {\rm e}^{- a R}, \end{equation}
where ![]() $D_c$ is an integral constant that is a function of
$D_c$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$.
$\theta$.
Similarly, the governing equation for ![]() $R < 0$ is written as, taking the Laplace transform to (3.84b),
$R < 0$ is written as, taking the Laplace transform to (3.84b),
The solution to (C14) is obtained as, based on the boundary condition of (3.86a–d) (i.e. ![]() $U_{\theta 1}^c \to 0$ as
$U_{\theta 1}^c \to 0$ as ![]() $R \to - \infty$),
$R \to - \infty$),
 \begin{equation} U_{\theta 1}^c =- \frac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^c {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^c {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_c {\rm e}^{\bar{a} R}, \end{equation}
\begin{equation} U_{\theta 1}^c =- \frac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^c {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^c {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_c {\rm e}^{\bar{a} R}, \end{equation}
where ![]() $E_c$ is an integral constant that is a function of
$E_c$ is an integral constant that is a function of ![]() $s$ and
$s$ and ![]() $\theta$. These indeterminate constants,
$\theta$. These indeterminate constants, ![]() $D_c$ and
$D_c$ and ![]() $E_c$, can be determined as, by the enforcements of the continuity of the velocity and its derivative with respect to
$E_c$, can be determined as, by the enforcements of the continuity of the velocity and its derivative with respect to ![]() $R$ at
$R$ at ![]() $R = 0$,
$R = 0$,
Similar to the above, the Laplace transform to (3.84d) is also written as
 \begin{align} s U_{\theta 1}^{c s} - \nu_o \frac{\partial^2 U_{\theta 1}^{c s}}{\partial R^2} + \lambda_o \chi U_{\theta 1}^{c s} =- F^{c s}, \quad F^{c s} = {\mathcal{L}} \left( \hat{u}_{r1} \frac{\partial \hat{u}_{\theta 0}^s}{\partial R} + \left\{ \begin{array}{@{}ll} \displaystyle \hat{u}_{\theta 0}^{s 2} - 4 & \text{for} \ R \geq 0\\ \displaystyle \hat{u}_{\theta 0}^{s 2} & \text{for}\ R < 0 \end{array} \right\}\right), \end{align}
\begin{align} s U_{\theta 1}^{c s} - \nu_o \frac{\partial^2 U_{\theta 1}^{c s}}{\partial R^2} + \lambda_o \chi U_{\theta 1}^{c s} =- F^{c s}, \quad F^{c s} = {\mathcal{L}} \left( \hat{u}_{r1} \frac{\partial \hat{u}_{\theta 0}^s}{\partial R} + \left\{ \begin{array}{@{}ll} \displaystyle \hat{u}_{\theta 0}^{s 2} - 4 & \text{for} \ R \geq 0\\ \displaystyle \hat{u}_{\theta 0}^{s 2} & \text{for}\ R < 0 \end{array} \right\}\right), \end{align}
where ![]() $U_{\theta 1}^{c s} = {\mathcal {L}} ( \hat {u}_{\theta 1}^{c s})$. The solution to (C17a,b) is obtained as, based on the boundary condition of (3.85a–d) and (3.86a–d) (i.e.
$U_{\theta 1}^{c s} = {\mathcal {L}} ( \hat {u}_{\theta 1}^{c s})$. The solution to (C17a,b) is obtained as, based on the boundary condition of (3.85a–d) and (3.86a–d) (i.e. ![]() $U_{\theta 1}^{c s} \to 0$ as
$U_{\theta 1}^{c s} \to 0$ as ![]() $R \to \pm \infty$),
$R \to \pm \infty$),
 \begin{equation} U_{\theta 1}^{c s} = \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^{c s} {\rm e}^{a R} \,{\rm d} R \right) + D_{c s} {\rm e}^{- a R} & \text{for} \ R \geq 0,\\[10pt] \displaystyle - \dfrac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^{c s} {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_{c s} {\rm e}^{\bar{a} R} & \text{for} \ R < 0, \end{array} \right. \end{equation}
\begin{equation} U_{\theta 1}^{c s} = \left\{ \begin{array}{@{}ll} \displaystyle - \dfrac{1}{2 \nu_o a} \left( {\rm e}^{a R} \int_R^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + {\rm e}^{- a R} \int_0^R F^{c s} {\rm e}^{a R} \,{\rm d} R \right) + D_{c s} {\rm e}^{- a R} & \text{for} \ R \geq 0,\\[10pt] \displaystyle - \dfrac{1}{2 \nu_o \bar{a}} \left( {\rm e}^{- \bar{a} R} \int_{- \infty}^R F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R - {\rm e}^{\bar{a} R} \int_0^R F^{c s} {\rm e}^{- \bar{a} R} \,{\rm d} R \right) + E_{c s} {\rm e}^{\bar{a} R} & \text{for} \ R < 0, \end{array} \right. \end{equation}
in which the indeterminate constants ![]() $D_{c s}$ and
$D_{c s}$ and ![]() $E_{c s}$ are determined by
$E_{c s}$ are determined by
Appendix D
In order to obtain the pressure ![]() $p_1^o$ of the outer flow, it is necessary to obtain the outer flow of the order of
$p_1^o$ of the outer flow, it is necessary to obtain the outer flow of the order of ![]() $\epsilon ^2$, because
$\epsilon ^2$, because ![]() ${p_1^o}/{\rho }\sim -{\partial \phi _2^o}/{\partial T}$, where
${p_1^o}/{\rho }\sim -{\partial \phi _2^o}/{\partial T}$, where ![]() $\phi _2^o$ is the velocity potential of the order of
$\phi _2^o$ is the velocity potential of the order of ![]() $\epsilon ^2$. Therefore, let us attempt to derive the solution of the order of
$\epsilon ^2$. Therefore, let us attempt to derive the solution of the order of ![]() $\epsilon ^2$ in the outer fluid domain where the solution exhibits the inviscid one (i.e. potential flow). To do so, we need to obtain
$\epsilon ^2$ in the outer fluid domain where the solution exhibits the inviscid one (i.e. potential flow). To do so, we need to obtain ![]() $u_{r2}^i$ in the inner fluid domain that is governed by the continuity equation (3.10c):
$u_{r2}^i$ in the inner fluid domain that is governed by the continuity equation (3.10c):
Since the matching procedure yields ![]() $u_{r 2}^i \to 0$ as
$u_{r 2}^i \to 0$ as ![]() $R \to -\infty$, (D1) is rewritten as
$R \to -\infty$, (D1) is rewritten as
Taking the Laplace transform to (D2) and using (3.62), (3.67) and (3.83), we have, for ![]() $R \geq 0$,
$R \geq 0$,
in which the coefficients are defined by
 \begin{equation} \left.\begin{gathered} {\rm I}_r^o = \int_{- \infty}^0 U_{r 1} {\rm d} R + \int_0^R U_{r 1} \,{\rm d} R, \quad {\rm I}_{\theta 1}^c = \int_{- \infty}^0 U_{\theta 1}^s \,{\rm d} R + \int_0^R U_{\theta 1}^s \,{\rm d} R,\\ {\rm I}_{\theta 1}^s =- \int_{- \infty}^0 U_{\theta 1}^c \,{\rm d} R - \int_0^R U_{\theta 1}^c \,{\rm d} R, \quad {\rm I}_{\theta 0}^c =- \int_{- \infty}^0 R U_{\theta 0}^s \,{\rm d} R - \int_0^R R U_{\theta 0}^s \,{\rm d} R,\\ {\rm I}_{\theta 1}^{c s} = \int_{- \infty}^0 U_{\theta 1}^{c s} \,{\rm d} R + \int_0^R U_{\theta 1}^{c s} \,{\rm d} R. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} {\rm I}_r^o = \int_{- \infty}^0 U_{r 1} {\rm d} R + \int_0^R U_{r 1} \,{\rm d} R, \quad {\rm I}_{\theta 1}^c = \int_{- \infty}^0 U_{\theta 1}^s \,{\rm d} R + \int_0^R U_{\theta 1}^s \,{\rm d} R,\\ {\rm I}_{\theta 1}^s =- \int_{- \infty}^0 U_{\theta 1}^c \,{\rm d} R - \int_0^R U_{\theta 1}^c \,{\rm d} R, \quad {\rm I}_{\theta 0}^c =- \int_{- \infty}^0 R U_{\theta 0}^s \,{\rm d} R - \int_0^R R U_{\theta 0}^s \,{\rm d} R,\\ {\rm I}_{\theta 1}^{c s} = \int_{- \infty}^0 U_{\theta 1}^{c s} \,{\rm d} R + \int_0^R U_{\theta 1}^{c s} \,{\rm d} R. \end{gathered}\right\} \end{equation}
Here, ![]() $U_{\theta 0}^s = {\mathcal {L}} ( \hat {u}_{\theta 0}^s )$,
$U_{\theta 0}^s = {\mathcal {L}} ( \hat {u}_{\theta 0}^s )$, ![]() $U_{r 1} = {\mathcal {L}} ( \hat {u}_{r 1} )$,
$U_{r 1} = {\mathcal {L}} ( \hat {u}_{r 1} )$, ![]() $U_{\theta 1}^s = {\mathcal {L}} ( \hat {u}_{\theta 1}^s )$,
$U_{\theta 1}^s = {\mathcal {L}} ( \hat {u}_{\theta 1}^s )$, ![]() $U_{\theta 1}^c = {\mathcal {L}} ( \hat {u}_{\theta 1}^c )$ and
$U_{\theta 1}^c = {\mathcal {L}} ( \hat {u}_{\theta 1}^c )$ and ![]() $U_{\theta 1}^{c s} = {\mathcal {L}} ( \hat {u}_{\theta 1}^{c s} )$. These coefficients can be calculated as, using the asymptotic solutions that are obtained above,
$U_{\theta 1}^{c s} = {\mathcal {L}} ( \hat {u}_{\theta 1}^{c s} )$. These coefficients can be calculated as, using the asymptotic solutions that are obtained above,
 \begin{align} {\rm I}_{\theta 1}^c & =- \frac{a}{s \bar{a}^2 ( a + \bar{a} )} + \frac{E_s}{\bar{a}} + \frac{D_s}{a} ( 1 - {\rm e}^{- a R} ) + \frac{R^2}{s} + 2 \frac{a - \bar{a}}{s a \bar{a}} R + \frac{\bar{a}}{s a ( a + \bar{a} )} R {\rm e}^{- a R}\nonumber\\ &\quad - \frac{\bar{a}}{s a^2 ( a + \bar{a} )} ( 1 - {\rm e}^{- a R} ), \end{align}
\begin{align} {\rm I}_{\theta 1}^c & =- \frac{a}{s \bar{a}^2 ( a + \bar{a} )} + \frac{E_s}{\bar{a}} + \frac{D_s}{a} ( 1 - {\rm e}^{- a R} ) + \frac{R^2}{s} + 2 \frac{a - \bar{a}}{s a \bar{a}} R + \frac{\bar{a}}{s a ( a + \bar{a} )} R {\rm e}^{- a R}\nonumber\\ &\quad - \frac{\bar{a}}{s a^2 ( a + \bar{a} )} ( 1 - {\rm e}^{- a R} ), \end{align} \begin{align} {\rm I}_{\theta 1}^s & =- \frac{E_c}{\bar{a}} - \frac{D_c}{a} ( 1 - {\rm e}^{- a R} ) - \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^c \,{\rm d} R\nonumber\\ &\quad + \frac{{\rm e}^{a R}}{2 \nu_o a^2} \int_R^\infty F^c {\rm e}^{- a R} \,{\rm d} R - \frac{{\rm e}^{- a R}}{2 \nu_o a^2} \int_0^R F^c {\rm e}^{a R} \,{\rm d} R - \frac{1}{2 \nu_o a^2} \int_{0}^\infty F^c {\rm e}^{- a R} \,{\rm d} R\nonumber\\ &\quad + \frac{1}{\nu_o a^2} \int_0^R F^c \,{\rm d} R, \end{align}
\begin{align} {\rm I}_{\theta 1}^s & =- \frac{E_c}{\bar{a}} - \frac{D_c}{a} ( 1 - {\rm e}^{- a R} ) - \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^c \,{\rm d} R\nonumber\\ &\quad + \frac{{\rm e}^{a R}}{2 \nu_o a^2} \int_R^\infty F^c {\rm e}^{- a R} \,{\rm d} R - \frac{{\rm e}^{- a R}}{2 \nu_o a^2} \int_0^R F^c {\rm e}^{a R} \,{\rm d} R - \frac{1}{2 \nu_o a^2} \int_{0}^\infty F^c {\rm e}^{- a R} \,{\rm d} R\nonumber\\ &\quad + \frac{1}{\nu_o a^2} \int_0^R F^c \,{\rm d} R, \end{align} \begin{align} {\rm I}_{\theta 1}^{c s} & = \frac{E_{c s}}{\bar{a}} + \frac{D_{c s}}{a} ( 1 - {\rm e}^{- a R} ) + \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R - \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} \,{\rm d} R\nonumber\\ &\quad - \frac{{\rm e}^{a R}}{2 \nu_o a^2} \int_R^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + \frac{{\rm e}^{- a R}}{2 \nu_o a^2} \int_0^R F^{c s} {\rm e}^{a R} \,{\rm d} R\nonumber\\ &\quad + \frac{1}{2 \nu_o a^2} \int_0^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R - \frac{1}{\nu_o a^2} \int_0^R F^{c s} \,{\rm d} R. \end{align}
\begin{align} {\rm I}_{\theta 1}^{c s} & = \frac{E_{c s}}{\bar{a}} + \frac{D_{c s}}{a} ( 1 - {\rm e}^{- a R} ) + \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R - \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} \,{\rm d} R\nonumber\\ &\quad - \frac{{\rm e}^{a R}}{2 \nu_o a^2} \int_R^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + \frac{{\rm e}^{- a R}}{2 \nu_o a^2} \int_0^R F^{c s} {\rm e}^{a R} \,{\rm d} R\nonumber\\ &\quad + \frac{1}{2 \nu_o a^2} \int_0^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R - \frac{1}{\nu_o a^2} \int_0^R F^{c s} \,{\rm d} R. \end{align}
The outer expansion of ![]() $U_{r 2}$ (i.e.
$U_{r 2}$ (i.e. ![]() $U_{r 2}^{i o}$) is written as, using (D3) with (D5a)–(D5e),
$U_{r 2}^{i o}$) is written as, using (D3) with (D5a)–(D5e),
 \begin{align} U_{r 2}^{i o}&=-
\cos{\theta} \left[ 4 \frac{a - \bar{a}}{s a \bar{a}} R +
\frac{3}{s} R^2 + \frac{E_s}{\bar{a}} + \frac{D_s}{a} -
\frac{\bar{a}}{s a^2 ( a + \bar{a} )} - \frac{a}{s
\bar{a}^2 ( a + \bar{a} )} \right] \nonumber\\ &\quad -
\sin{\theta} \Bigg[ - \frac{E_c}{\bar{a}} - \frac{D_c}{a} -
\frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^c {\rm
e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2}
\int_{- \infty}^0 F^c \,{\rm d} R
\nonumber\\ &\quad -\, \frac{1}{2 \nu_o a^2}
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R +
\frac{1}{\nu_o a^2} \int_0^\infty F^c \,{\rm d} R
\Bigg]\nonumber\\ &\quad - \cos{2 \theta} \Bigg[ -
\frac{E_{c s}}{\bar{a}} - \frac{D_{c s}}{a} - \frac{1}{2
\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} {\rm e}^{\bar{a}
R} \,{\rm d} R\nonumber\\ &\quad + \,\frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} \,{\rm
d} R - \frac{1}{2 \nu_o a^2} \int_0^\infty F^{c s} {\rm
e}^{- a R} \,{\rm d} R + \frac{1}{\nu_o a^2} \int_0^\infty
F^{c s} \,{\rm d} R \Bigg].
\end{align}
\begin{align} U_{r 2}^{i o}&=-
\cos{\theta} \left[ 4 \frac{a - \bar{a}}{s a \bar{a}} R +
\frac{3}{s} R^2 + \frac{E_s}{\bar{a}} + \frac{D_s}{a} -
\frac{\bar{a}}{s a^2 ( a + \bar{a} )} - \frac{a}{s
\bar{a}^2 ( a + \bar{a} )} \right] \nonumber\\ &\quad -
\sin{\theta} \Bigg[ - \frac{E_c}{\bar{a}} - \frac{D_c}{a} -
\frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^c {\rm
e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2}
\int_{- \infty}^0 F^c \,{\rm d} R
\nonumber\\ &\quad -\, \frac{1}{2 \nu_o a^2}
\int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R +
\frac{1}{\nu_o a^2} \int_0^\infty F^c \,{\rm d} R
\Bigg]\nonumber\\ &\quad - \cos{2 \theta} \Bigg[ -
\frac{E_{c s}}{\bar{a}} - \frac{D_{c s}}{a} - \frac{1}{2
\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} {\rm e}^{\bar{a}
R} \,{\rm d} R\nonumber\\ &\quad + \,\frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} \,{\rm
d} R - \frac{1}{2 \nu_o a^2} \int_0^\infty F^{c s} {\rm
e}^{- a R} \,{\rm d} R + \frac{1}{\nu_o a^2} \int_0^\infty
F^{c s} \,{\rm d} R \Bigg].
\end{align}
On the other hand, since the outer solution in the fluid domain becomes potential, the velocity potential ![]() $\phi ^o$ of the outer solution in the fluid domain can be expressed as
$\phi ^o$ of the outer solution in the fluid domain can be expressed as
The inner expansion of ![]() $\phi ^o$ is then written as
$\phi ^o$ is then written as
 \begin{align} u_{r}^{o i} & = ( 2 \epsilon R - 3 \epsilon^2 R^2 ) \cos{\theta} H ( T ) + 2 A \epsilon ( 1 - 2 \epsilon R ) \cos{\theta}\nonumber\\ &\quad - \epsilon^2 \sum_{n = 1} n ( a_n^c \cos{n \theta} + a_n^s \sin{n \theta} ) + O ( \epsilon^3 ). \end{align}
\begin{align} u_{r}^{o i} & = ( 2 \epsilon R - 3 \epsilon^2 R^2 ) \cos{\theta} H ( T ) + 2 A \epsilon ( 1 - 2 \epsilon R ) \cos{\theta}\nonumber\\ &\quad - \epsilon^2 \sum_{n = 1} n ( a_n^c \cos{n \theta} + a_n^s \sin{n \theta} ) + O ( \epsilon^3 ). \end{align}
The matching procedure to the inner solution in the fluid domain (i.e. ![]() ${\mathcal {L}} ( u_{r}^{o i} ) = U_r^{i o}$) yields
${\mathcal {L}} ( u_{r}^{o i} ) = U_r^{i o}$) yields
 \begin{align} {\mathcal{L}} ( a_1^s ) & =- \frac{E_c}{\bar{a}} - \frac{D_c}{a} - \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^c \,{\rm d} R\nonumber\\ &\quad - \frac{1}{2 \nu_o a^2} \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R + \frac{1}{\nu_o a^2} \int_0^\infty F^c \,{\rm d} R, \end{align}
\begin{align} {\mathcal{L}} ( a_1^s ) & =- \frac{E_c}{\bar{a}} - \frac{D_c}{a} - \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^c {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^c \,{\rm d} R\nonumber\\ &\quad - \frac{1}{2 \nu_o a^2} \int_0^\infty F^c {\rm e}^{- a R} \,{\rm d} R + \frac{1}{\nu_o a^2} \int_0^\infty F^c \,{\rm d} R, \end{align} \begin{align} {\mathcal{L}} ( a_2^c ) & =- \frac{E_{c s}}{\bar{a}} - \frac{D_{c s}}{a} - \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} \,{\rm d} R\nonumber\\ &\quad - \frac{1}{2 \nu_o a^2} \int_0^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + \frac{1}{\nu_o a^2} \int_0^\infty F^{c s} \,{\rm d} R, \end{align}
\begin{align} {\mathcal{L}} ( a_2^c ) & =- \frac{E_{c s}}{\bar{a}} - \frac{D_{c s}}{a} - \frac{1}{2 \nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} {\rm e}^{\bar{a} R} \,{\rm d} R + \frac{1}{\nu_o \bar{a}^2} \int_{- \infty}^0 F^{c s} \,{\rm d} R\nonumber\\ &\quad - \frac{1}{2 \nu_o a^2} \int_0^\infty F^{c s} {\rm e}^{- a R} \,{\rm d} R + \frac{1}{\nu_o a^2} \int_0^\infty F^{c s} \,{\rm d} R, \end{align}
The velocity potential ![]() $\phi ^o$ in the outer fluid domain is therefore written as
$\phi ^o$ in the outer fluid domain is therefore written as
which also gives
Differentiating (D10) with respect to either ![]() $r$ or
$r$ or ![]() $\theta$, the velocities,
$\theta$, the velocities, ![]() $u_r^o$ and
$u_r^o$ and ![]() $u_\theta ^o$, in the outer fluid domain are calculated as, for
$u_\theta ^o$, in the outer fluid domain are calculated as, for ![]() $r > 1$,
$r > 1$,
 \begin{align} u_r^o& = \left( 1 - \frac{1}{r^2} \right) \cos{\theta} + 2 \epsilon A \frac{1}{r^2} \cos{\theta} - \epsilon^2 ( a_1^c \cos{\theta} + a_1^s \sin{\theta} ) \frac{1}{r^2}\nonumber\\ &\quad - \epsilon^2 \frac{2}{r^3} a_2^c \cos{2 \theta} + O ( \epsilon^3 ), \end{align}
\begin{align} u_r^o& = \left( 1 - \frac{1}{r^2} \right) \cos{\theta} + 2 \epsilon A \frac{1}{r^2} \cos{\theta} - \epsilon^2 ( a_1^c \cos{\theta} + a_1^s \sin{\theta} ) \frac{1}{r^2}\nonumber\\ &\quad - \epsilon^2 \frac{2}{r^3} a_2^c \cos{2 \theta} + O ( \epsilon^3 ), \end{align} \begin{align} u_\theta^o & =-\left( 1 + \frac{1}{r^2} \right) \sin{\theta} + 2 \epsilon A \frac{1}{r^2} \sin{\theta} - \epsilon^2 ( a_1^c \sin{\theta} - a_1^s \cos{\theta} ) \frac{1}{r^2}\nonumber\\ &\quad- \epsilon^2 \frac{2}{r^3} a_2^c \sin{2 \theta} + O ( \epsilon^3 ). \end{align}
\begin{align} u_\theta^o & =-\left( 1 + \frac{1}{r^2} \right) \sin{\theta} + 2 \epsilon A \frac{1}{r^2} \sin{\theta} - \epsilon^2 ( a_1^c \sin{\theta} - a_1^s \cos{\theta} ) \frac{1}{r^2}\nonumber\\ &\quad- \epsilon^2 \frac{2}{r^3} a_2^c \sin{2 \theta} + O ( \epsilon^3 ). \end{align}
The inner expansion of ![]() $u_r^o$ and
$u_r^o$ and ![]() $u_\theta ^o$ are then written as, respectively,
$u_\theta ^o$ are then written as, respectively,
The inner expansion of the pressure in the outer fluid domain, ![]() $p^{o i}$, is then obtained as, using the unsteady Bernoulli's equation,
$p^{o i}$, is then obtained as, using the unsteady Bernoulli's equation,
 \begin{align} \frac{p^{o i}}{\rho} & = 2 \frac{{\rm d} A}{{\rm d} T} \cos{\theta} - 2 \sin^2{\theta} + \frac{1}{2} - \epsilon \left[ 2 R \frac{{\rm d} A}{{\rm d} T} \cos{\theta}\right.\nonumber\\ &\quad - \left. 4 A \sin^2{\theta} + \frac{{\rm d}}{{\rm d} T} ( a_1^c \cos{\theta} + a_1^s \sin{\theta} ) + \frac{{\rm d}}{{\rm d} T} ( a_2^c \cos{2 \theta} ) \right] + O ( \epsilon^2 ). \end{align}
\begin{align} \frac{p^{o i}}{\rho} & = 2 \frac{{\rm d} A}{{\rm d} T} \cos{\theta} - 2 \sin^2{\theta} + \frac{1}{2} - \epsilon \left[ 2 R \frac{{\rm d} A}{{\rm d} T} \cos{\theta}\right.\nonumber\\ &\quad - \left. 4 A \sin^2{\theta} + \frac{{\rm d}}{{\rm d} T} ( a_1^c \cos{\theta} + a_1^s \sin{\theta} ) + \frac{{\rm d}}{{\rm d} T} ( a_2^c \cos{2 \theta} ) \right] + O ( \epsilon^2 ). \end{align}
From the matching condition ![]() $p^{io}=p^{o1}$, we can obtain (3.109).
$p^{io}=p^{o1}$, we can obtain (3.109).
Appendix E
Let us estimate the order of the following integral for ![]() $\lambda _o \gg 1$:
$\lambda _o \gg 1$:
 \begin{align} I& = {\mathcal{L}}^{-1} \left( \int_{- \infty}^0 F^c \exp({\bar{a} R}) \,{\rm d} R \right)\nonumber\\ & = \int_{- \infty}^0 {\rm d} R \int_0^T f^c ( T - \xi, R ) \frac{| R |}{2 \sqrt{{\rm \pi} \nu_o \xi^3}} \exp\left({- \lambda_o \xi - \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} \xi. \end{align}
\begin{align} I& = {\mathcal{L}}^{-1} \left( \int_{- \infty}^0 F^c \exp({\bar{a} R}) \,{\rm d} R \right)\nonumber\\ & = \int_{- \infty}^0 {\rm d} R \int_0^T f^c ( T - \xi, R ) \frac{| R |}{2 \sqrt{{\rm \pi} \nu_o \xi^3}} \exp\left({- \lambda_o \xi - \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} \xi. \end{align}
Assuming that ![]() $f^c$ is continuous in the integral domain,
$f^c$ is continuous in the integral domain, ![]() $f^c$ has a finite maximum value
$f^c$ has a finite maximum value ![]() $|\,f^c |_{{max}}$ in the domain. Therefore, we have
$|\,f^c |_{{max}}$ in the domain. Therefore, we have
 \begin{align} | I | & \leq |\, f^c
|_{{max}} \int_{- \infty}^0 {\rm d} R \,\int_0^T
\frac{| R |}{2 \sqrt{{\rm \pi} \nu_o \xi^3}} \exp\left({-
\lambda_o \xi - \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} \xi\nonumber\\ & \leq |\, f^c |_{{max}}
\sqrt{\frac{\nu_o}{\rm \pi}} \int_0^T \frac{\exp({- \lambda_o
\xi})}{\sqrt{\xi}} \,{\rm d} \xi =|\, f^c |_{{max}}
\sqrt{\frac{\nu_o}{\rm \pi}} \frac{2}{\sqrt{\lambda_o}} \,
\text{Erf} ( \sqrt{\lambda_o T} ) \sim O ( 1 /
\sqrt{\lambda_o} ),
\end{align}
\begin{align} | I | & \leq |\, f^c
|_{{max}} \int_{- \infty}^0 {\rm d} R \,\int_0^T
\frac{| R |}{2 \sqrt{{\rm \pi} \nu_o \xi^3}} \exp\left({-
\lambda_o \xi - \frac{R^2}{4 \nu_o \xi}}\right) {\rm d} \xi\nonumber\\ & \leq |\, f^c |_{{max}}
\sqrt{\frac{\nu_o}{\rm \pi}} \int_0^T \frac{\exp({- \lambda_o
\xi})}{\sqrt{\xi}} \,{\rm d} \xi =|\, f^c |_{{max}}
\sqrt{\frac{\nu_o}{\rm \pi}} \frac{2}{\sqrt{\lambda_o}} \,
\text{Erf} ( \sqrt{\lambda_o T} ) \sim O ( 1 /
\sqrt{\lambda_o} ),
\end{align}
where ![]() $\text {Erf}(x)=\int _0^x {\rm e}^{-x^2} \,{\rm d}\kern0.06em x$.
$\text {Erf}(x)=\int _0^x {\rm e}^{-x^2} \,{\rm d}\kern0.06em x$.
Appendix F
The hydrodynamic forces ![]() $( F_{b x}, F_{b y} )$ are given by (3.153a) and (3.153b). Therefore, we have, for a circular cylinder,
$( F_{b x}, F_{b y} )$ are given by (3.153a) and (3.153b). Therefore, we have, for a circular cylinder,
 \begin{equation} \left[\begin{array}{@{}c@{}}
F_{b x} / \rho\\ F_{b y} / \rho \end{array}\right] =
\int_0^{2 {\rm \pi}} \left[ \begin{array}{@{}c@{}} \dfrac{\partial}{\partial \theta} \left( \dfrac{p}{\rho} \right)
\sin{\theta} - \nu \omega \sin{\theta} - u_r u\\[10pt] -
\dfrac{\partial}{\partial \theta} \left( \dfrac{p}{\rho}
\right) \cos{\theta} + \nu \omega \cos{\theta} - u_r v
\end{array} \right]_{r = 1} \,{\rm d} \theta.
\end{equation}
\begin{equation} \left[\begin{array}{@{}c@{}}
F_{b x} / \rho\\ F_{b y} / \rho \end{array}\right] =
\int_0^{2 {\rm \pi}} \left[ \begin{array}{@{}c@{}} \dfrac{\partial}{\partial \theta} \left( \dfrac{p}{\rho} \right)
\sin{\theta} - \nu \omega \sin{\theta} - u_r u\\[10pt] -
\dfrac{\partial}{\partial \theta} \left( \dfrac{p}{\rho}
\right) \cos{\theta} + \nu \omega \cos{\theta} - u_r v
\end{array} \right]_{r = 1} \,{\rm d} \theta.
\end{equation}
Since ![]() $\chi = 0$ in the fluid domain, the governing equation of the motion becomes, with respect to
$\chi = 0$ in the fluid domain, the governing equation of the motion becomes, with respect to ![]() $\theta$,
$\theta$,
Therefore, we have
 \begin{align} \left[ \begin{array}{@{}c@{}}
F_{b x} / \rho \\ F_{b y} / \rho \end{array} \right] & =
\left.\nu \int_0^{2 {\rm \pi}} \left( \frac{\partial
\omega}{\partial r} - \omega \right) \right|_{r = 1}
\left[\begin{array}{@{}c@{}} \sin{\theta}\\ - \cos{\theta}
\end{array} \right]{\rm d} \theta - \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} u_\theta |_{r = 1}
\left[ \begin{array}{@{}c@{}} \sin{\theta}\\ - \cos{\theta}
\end{array} \right]{\rm d} \theta\nonumber\\ &\quad
- \int_0^{2 {\rm \pi}} u_r |_{r = 1} \left[ \begin{array}{@{}c@{}} u\\
v \end{array} \right]_{r = 1} \,{\rm d} \theta.
\end{align}
\begin{align} \left[ \begin{array}{@{}c@{}}
F_{b x} / \rho \\ F_{b y} / \rho \end{array} \right] & =
\left.\nu \int_0^{2 {\rm \pi}} \left( \frac{\partial
\omega}{\partial r} - \omega \right) \right|_{r = 1}
\left[\begin{array}{@{}c@{}} \sin{\theta}\\ - \cos{\theta}
\end{array} \right]{\rm d} \theta - \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} u_\theta |_{r = 1}
\left[ \begin{array}{@{}c@{}} \sin{\theta}\\ - \cos{\theta}
\end{array} \right]{\rm d} \theta\nonumber\\ &\quad
- \int_0^{2 {\rm \pi}} u_r |_{r = 1} \left[ \begin{array}{@{}c@{}} u\\
v \end{array} \right]_{r = 1} \,{\rm d} \theta.
\end{align}
An alternative expression of the force imposed by the no-slip condition on the cylinder surface is defined as ![]() $F_{\omega x}$ and
$F_{\omega x}$ and ![]() $F_{\omega y}$ and, then,
$F_{\omega y}$ and, then,
Applying Green's theorem and the definition of vorticity ![]() $\omega$, we easily have
$\omega$, we easily have
where ![]() ${\mathscr {C}}_\infty$ and
${\mathscr {C}}_\infty$ and ![]() ${\mathscr {C}}_o$ denote the contours of the control surfaces in the far field and on the cylinder surface, respectively. The tangential velocity is then described by
${\mathscr {C}}_o$ denote the contours of the control surfaces in the far field and on the cylinder surface, respectively. The tangential velocity is then described by ![]() $u_s$ on
$u_s$ on ![]() ${\mathscr {C}}_\infty$ or
${\mathscr {C}}_\infty$ or ![]() ${\mathscr {C}}_o$. In addition,
${\mathscr {C}}_o$. In addition, ![]() ${\rm d} v$ and
${\rm d} v$ and ![]() ${\rm d} s$ indicate the small elements of
${\rm d} s$ indicate the small elements of ![]() ${\mathscr {F}}$ and the contour
${\mathscr {F}}$ and the contour ![]() ${\mathscr {C}}_\infty$ or
${\mathscr {C}}_\infty$ or ![]() ${\mathscr {C}}_o$. From the equations of motion, we have
${\mathscr {C}}_o$. From the equations of motion, we have
 \begin{equation} \frac{{\rm d}}{{\rm d} t} \int_{\mathscr{F}} \left[ \begin{array}{@{}c@{}} u \\ v \end{array} \right] {\rm d} v = \int_{\mathscr{F}} \left[ \begin{array}{@{}c@{}} - \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} + \nu \Delta u\\[10pt] - \dfrac{1}{\rho} \dfrac{\partial p}{\partial y} + \nu \Delta v \end{array} \right] {\rm d} v. \end{equation}
\begin{equation} \frac{{\rm d}}{{\rm d} t} \int_{\mathscr{F}} \left[ \begin{array}{@{}c@{}} u \\ v \end{array} \right] {\rm d} v = \int_{\mathscr{F}} \left[ \begin{array}{@{}c@{}} - \dfrac{1}{\rho} \dfrac{\partial p}{\partial x} + \nu \Delta u\\[10pt] - \dfrac{1}{\rho} \dfrac{\partial p}{\partial y} + \nu \Delta v \end{array} \right] {\rm d} v. \end{equation}
Since ![]() $\Delta u = - \partial \omega / \partial y$ and
$\Delta u = - \partial \omega / \partial y$ and ![]() $\Delta v = \partial \omega / \partial x$, we have
$\Delta v = \partial \omega / \partial x$, we have
Here, the conditions that ![]() $p$ is constant and
$p$ is constant and ![]() $\omega = 0$ on
$\omega = 0$ on ![]() ${\mathscr {C}}_\infty$ has been used. Therefore, we finally arrive at
${\mathscr {C}}_\infty$ has been used. Therefore, we finally arrive at
where ![]() $u_n$ is the normal component of the velocity from the cylinder to the fluid flow domain at
$u_n$ is the normal component of the velocity from the cylinder to the fluid flow domain at ![]() ${\mathscr {C}}_o$. Therefore, in the penalization method the two terms are needed in addition to the formula that is derived from the no-slip boundary condition.
${\mathscr {C}}_o$. Therefore, in the penalization method the two terms are needed in addition to the formula that is derived from the no-slip boundary condition.
Using the present results, we have, at ![]() $R = 0$,
$R = 0$,
 \begin{align} \frac{{\text{D}} u_\theta}{{\text{D}} t} & = \frac{1}{\epsilon} {\mathcal{L}}^{-1} \left( \frac{\bar{a}}{a + \bar{a}} \varOmega \right) + \frac{3}{2} {\mathcal{L}}^{-1} \left( \frac{\varOmega}{a + \bar{a}} \right) - \frac{2}{\epsilon} {\mathcal{L}}^{-1} \left( \frac{a}{a + \bar{a}} \right) \sin{\theta} \nonumber\\ &\quad + \hat{u}_{r 1} \left( \frac{\partial \hat{u}_{\theta0}^o}{\partial \theta} \cos{\theta} + \frac{\hat{u}_{\theta 0}^s}{\partial \theta} \sin{\theta} \cos{\theta} \right) + \hat{u}_{\theta 0}^o \hat{u}_{\theta 0}^s \cos{\theta} + \hat{u}_{\theta 0}^{s 2} \sin{\theta} \cos{\theta} + O ( \epsilon ). \end{align}
\begin{align} \frac{{\text{D}} u_\theta}{{\text{D}} t} & = \frac{1}{\epsilon} {\mathcal{L}}^{-1} \left( \frac{\bar{a}}{a + \bar{a}} \varOmega \right) + \frac{3}{2} {\mathcal{L}}^{-1} \left( \frac{\varOmega}{a + \bar{a}} \right) - \frac{2}{\epsilon} {\mathcal{L}}^{-1} \left( \frac{a}{a + \bar{a}} \right) \sin{\theta} \nonumber\\ &\quad + \hat{u}_{r 1} \left( \frac{\partial \hat{u}_{\theta0}^o}{\partial \theta} \cos{\theta} + \frac{\hat{u}_{\theta 0}^s}{\partial \theta} \sin{\theta} \cos{\theta} \right) + \hat{u}_{\theta 0}^o \hat{u}_{\theta 0}^s \cos{\theta} + \hat{u}_{\theta 0}^{s 2} \sin{\theta} \cos{\theta} + O ( \epsilon ). \end{align}Hence, we have
 \begin{align} \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} u_\theta \sin{\theta} \,{\rm d} \theta & =- \frac{2 {\rm \pi}}{\epsilon} {\mathcal{L}}^{-1} \left( \frac{a}{a + \bar{a}} \right) + O ( \epsilon )\nonumber\\ & =- \frac{\rm \pi}{\epsilon} \frac{{\rm d}}{{\rm d} T} \left[ {\rm e}^{- \lambda_o T / 2} \left( {\rm I}_0 ( \lambda_o T / 2 ) + {\rm I}_1 ( \lambda_o T / 2 ) \right) \right] + O ( \epsilon )\nonumber\\ & =\frac{\rm \pi}{4} \frac{\lambda_o}{\epsilon}{\rm e}^{- \lambda_o T / 2} \left[ {\rm I}_0 ( \lambda_o T / 2 ) - {\rm I}_2 ( \lambda_o T / 2 ) \right] + O ( \epsilon ). \end{align}
\begin{align} \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} u_\theta \sin{\theta} \,{\rm d} \theta & =- \frac{2 {\rm \pi}}{\epsilon} {\mathcal{L}}^{-1} \left( \frac{a}{a + \bar{a}} \right) + O ( \epsilon )\nonumber\\ & =- \frac{\rm \pi}{\epsilon} \frac{{\rm d}}{{\rm d} T} \left[ {\rm e}^{- \lambda_o T / 2} \left( {\rm I}_0 ( \lambda_o T / 2 ) + {\rm I}_1 ( \lambda_o T / 2 ) \right) \right] + O ( \epsilon )\nonumber\\ & =\frac{\rm \pi}{4} \frac{\lambda_o}{\epsilon}{\rm e}^{- \lambda_o T / 2} \left[ {\rm I}_0 ( \lambda_o T / 2 ) - {\rm I}_2 ( \lambda_o T / 2 ) \right] + O ( \epsilon ). \end{align}It can therefore be found that the present result of the drag force is the same as our previous result (see Ueda & Kida Reference Ueda and Kida2021) by adding the above result to the previous one. For the lift force, the additional term is written as
 \begin{align} \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} u_\theta \cos{\theta} \,{\rm d} \theta & = {\rm \pi}\left( \hat{u}_{r 1} \frac{\partial \hat{u}_{\theta 0}^o}{\partial \theta} + \hat{u}_{\theta 0}^o \hat{u}_{\theta 0}^s \right) + O ( \epsilon )\nonumber\\ & \approx O ( 1 / \sqrt{\lambda_o} ) + O ( \epsilon ). \end{align}
\begin{align} \frac{{\rm d}}{{\rm d} t} \int_0^{2 {\rm \pi}} u_\theta \cos{\theta} \,{\rm d} \theta & = {\rm \pi}\left( \hat{u}_{r 1} \frac{\partial \hat{u}_{\theta 0}^o}{\partial \theta} + \hat{u}_{\theta 0}^o \hat{u}_{\theta 0}^s \right) + O ( \epsilon )\nonumber\\ & \approx O ( 1 / \sqrt{\lambda_o} ) + O ( \epsilon ). \end{align}