Algebras A and coalgebras C over a commutative ring R are defined by properties of the (endo)functors A ⊗R – and C ⊗R – on the category of R-modules R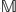 . Generalising these notions, monads and comonads were introduced on arbitrary categories, and it turned out that some of their basic relations do not depend on the specific properties of the tensor product. In particular, the adjoint of any comonad is a monad (and vice versa), and hence, for any coalgebra C, HomR(C, –), the right adjoint of C ⊗R –, is a monad on R
. Generalising these notions, monads and comonads were introduced on arbitrary categories, and it turned out that some of their basic relations do not depend on the specific properties of the tensor product. In particular, the adjoint of any comonad is a monad (and vice versa), and hence, for any coalgebra C, HomR(C, –), the right adjoint of C ⊗R –, is a monad on R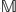 . The modules for the monad HomR(C, –) were called contramodules by Eilenberg–Moore and the purpose of this talk is to outline the related constructions and explain the relationship between C-comodules and C-contramodules. The results presented grew out from cooperation with G. Böhm, T. Brzeziński and B. Mesablishvili.
. The modules for the monad HomR(C, –) were called contramodules by Eilenberg–Moore and the purpose of this talk is to outline the related constructions and explain the relationship between C-comodules and C-contramodules. The results presented grew out from cooperation with G. Böhm, T. Brzeziński and B. Mesablishvili.