Introduction
Adaptive beamforming is a crucial and indispensable technique where the received beam can be adaptively formed to maintain the desired signal while suppressing the interference. It has been extensively employed in wireless communication, radar, and navigation [Reference Zhou, Chen, Zhang, Wang and Guo1–Reference Ma, Miao and Wu3]. The standard Capon beamforming is a popular and essential adaptive beamforming algorithm, and it is denoted as the minimum variance distortionless response (MVDR) beamformer [Reference Liu, Du, Wu, Zhou, Zhang and Cheng4, Reference Yang, Wang and Ye5], which can suppress interferences well and output the desired signal without distortion when the direction of arrival (DOA) of the desired signal is accurate [Reference Ge, Fan, Wang and Huang6, Reference Zheng, Yang, Wang and Zhang7].
However, adaptive beamforming is widely acknowledged to be susceptive to mismatch errors such as the DOA estimation error, incoherent local scattering error and sensor position error. Mismatch errors will severely deteriorate the capability of traditional adaptive approaches, such as the sidelobe rising and signal cancelation [Reference Yang, Tu, Lu and Yang8, Reference Wax and Anu9]. Therefore, several approaches have been developed to enhance the efficacy of the MVDR beamforming approach. A diagonal loading factor can be automatically computed via a parameter-free approach [Reference Du, Li and Stoica10]. This approach has demonstrated satisfactory performance in instances where there are minor mismatch errors. However, an extent of performance deterioration will be observed at the high input signal-to-noise ratio (SNR) levels. To achieve superior performance of the robustness, a novel algorithm utilizing eigenspace-based (ESB) methodology is devised. The beamforming weight vector is determined through the projection of the nominal steering vector (SV) onto the signal-plus-interference subspace of the signal covariance matrix [Reference Jia, Jin, Zhou and Yao11]. Nevertheless, it has a higher sidelobe level with the lower SNR. To achieve greater of suppressing interferences, a beamforming solution is presented that relies on worst-case performance optimization (WCP) principles [Reference Vorobyov, Gershman and Luo12]. The desired signal SV is obtain by imposing an uncertainty constraint. The proposed approach involves the resolution of a second-order cone programming problem, which is computationally intensive. The performance of the aforementioned algorithms would be limited in situations where the desired signal is strong [Reference Zheng, Yang, Wang and So13]. A robust adaptive beamforming (RAB) solution is introduced in response to the challenges with the strong desired signal. The proposed approach employs reconstructing the interference-plus-noise covariance matrix and estimating the desired signal SV for suppressing the desired signal in the sample covariance matrix [Reference Gu and Leshem14]. It is evident that the method enjoys the outstanding output signal-to-interference-plus-noise-ratio (SINR) compared with the aforementioned beamformers. However, the presented approach has unsatisfactory computation time because it needs to solve a quadratically constrained quadratic programming problem to obtain the desired signal SV. Additionally, the interference-plus-noise covariance matrix is redesigned by estimating all interference SVs and corresponding powers [Reference Zheng, Zheng, Wang and Zhang15]. The quadratic convex optimization problem serves to estimate the desired signal SV. The aforementioned algorithms show the excellent performance, but it is inevitable to solve the convex optimization that brings a lot of computation.
Recently, deep learning has received significant attention in addressing beamforming problems [Reference Liu, Zhang and Yu16–Reference Hao, X and Y19]. These researches indicate that neural networks have the capability to effectively identify and extract the most important characteristics of the desired signal, even in noisy and interference scenarios. This ability renders neural networks a useful tool in tackling beamforming challenges. For example, a deep neural network (DNN) framework is devised with an autoencoder and several classifiers as a solution to address the issue of the DOA estimation [Reference Liu, Zhang and Yu16]. The proposed approach exhibits exceptional adaptability to different array-related imperfections, including but not limited to gain and phase inconsistency, sensor position error, and mutual coupling error. In order to improve the beamforming performance of suppressing interferences, a novel beamformer is employed based on a convolutional neural network (CNN) to predict nearly-optimal beamforming weight vector [Reference Ramezanpour and Mosavi17], which has less computation time than the MVDR approach. To further enhance the precision of predictions for realizing the predictive beamforming, a convolutional long-short term memory recurrent neural network is designed for angle prediction based on the historical estimated angles, and then performs the predictive beamforming [Reference Liu, Liu, Li, Yuan and Ng18]. To suppress jamming during the transmission of information, a novel preprocessing deep reinforcement learning algorithm is proposed using a CNN to obtain the optimal decision of beamforming [Reference Hao, X and Y19]. Simulations demonstrate that the presented approach has greater performance in estimating the desired signal in comparison with conventional algorithms. However, the aforementioned algorithms are proposed based on deep learning in an ideal scenario. When there are mismatch errors, including DOA estimation error, incoherent local scattering error, sensor position error, and so on [Reference Yang, Tu, Lu and Yang8, Reference Wax and Anu9], the beamforming performance will deteriorate, such as sidelobe rising and signal cancelation. Therefore, it is still a crucial problem to present an effective RAB approach against mismatch errors and high complexity.
A RAB residual CNN (RAB-RCNN) method is presented in this paper to reduce the computation time for beamforming. The presented approach formulates the computation of the beamforming weight vector as a regression prediction problem of the neural network. The proposed RAB-RCNN framework is designed to tackle the challenge of mapping the signal sample covariance matrix to the relevant beamforming weight vector. In the proposed approach, the beamforming weight vector as the training label is derived from an excellent interference-plus-noise covariance matrix reconstruction and desired signal SV estimation approach. Then, invoking a deep residual block unit, the proposed RAB-RCNN structure can learn deeper spatial features of the signal sample covariance matrix during the training. In the end, the trained RAB-RCNN can rapidly and precisely predict the beamforming weight vector without complex matrix operations, including the inverse of the signal covariance matrix. Simulations indicate that the presented approach has the promising capability of the robustness compared with other approaches. The contributions are summarized as follows.
(1) In the proposed RAB-RCNN model, a residual block unit is utilized to extract the deeper features from the signal sample covariance matrix and excavate the spatial correlation information about the received signal, so that it can improve the prediction performance of the proposed RAB-RCNN.
(2) The training label utilized for the proposed RAB-RCNN is an outstanding beamformer that achieves a high output SINR. The proposed model is trained by the aforementioned label, which can output the predicted beamforming weight vector with avoiding complex matrix operations, so that the computation time is reduced.
This paper is organized as follows. The signal model is introduced detailedly in “Signal model” section. Section “Presented RAB-RCNN algorithm” describes the presented approach. Section “Simulations” presents the simulation results. Finally, section “Conclusion” concludes the whole paper.
Signal model
Consider a uniform linear array which consists of M sensors with L + 1 received narrowband signals. The sensor spacing d is half of the wavelength λ. The array received vector ![]() $\mathbf{x}(k)\in\mathbb{C}^{{M}\times 1}$ at time k can be given by:
$\mathbf{x}(k)\in\mathbb{C}^{{M}\times 1}$ at time k can be given by:
where ![]() $\mathbf{x}_{s}(k)$ denotes the statistically independent components of the desired signal.
$\mathbf{x}_{s}(k)$ denotes the statistically independent components of the desired signal. ![]() $\mathbf{x}_{in}(k)$ stands for interferences and
$\mathbf{x}_{in}(k)$ stands for interferences and ![]() $\mathbf{x}_{n}(k)$ represents the noise.
$\mathbf{x}_{n}(k)$ represents the noise.
The adaptive beamformer output is represented as:
where ![]() $\mathbf{w}=[w_{1},\cdots, w_{M}]^{\rm T}$ denotes the beamforming weight vector.
$\mathbf{w}=[w_{1},\cdots, w_{M}]^{\rm T}$ denotes the beamforming weight vector. ![]() $(\cdot)^{\rm H}$ represents conjugate transpose.
$(\cdot)^{\rm H}$ represents conjugate transpose.
According to [Reference Liu, Sun, Wang and Du20], γ denotes the SINR of the array output, so γ can be defined as:
 \begin{equation}
{\gamma}=\frac{\sigma_{s}^{2}\left|\mathbf{w}^{\rm H}\mathbf{a}\right|^{2}}{\mathbf{w}^{\rm H}\mathbf{R}_{\mathbf{in}+\mathbf{n}}\mathbf{w}},
\end{equation}
\begin{equation}
{\gamma}=\frac{\sigma_{s}^{2}\left|\mathbf{w}^{\rm H}\mathbf{a}\right|^{2}}{\mathbf{w}^{\rm H}\mathbf{R}_{\mathbf{in}+\mathbf{n}}\mathbf{w}},
\end{equation} where ![]() $\sigma_{s}^{2}$ denotes the desired signal power.
$\sigma_{s}^{2}$ denotes the desired signal power. ![]() $\mathbf{R}_{\mathbf{in}+\mathbf{n}}$ represents the theoretical interference-plus-noise covariance matrix, so it can be given by:
$\mathbf{R}_{\mathbf{in}+\mathbf{n}}$ represents the theoretical interference-plus-noise covariance matrix, so it can be given by:
where ![]() $\sigma_{n}^{2}$ represents the noise power.
$\sigma_{n}^{2}$ represents the noise power. ![]() $\mathbf{R}_{in}$ denotes the theoretical interference covariance matrix.
$\mathbf{R}_{in}$ denotes the theoretical interference covariance matrix. ![]() $\mathbf{I}\in\mathbb{C}^{{M}\times {M}}$ stands for an identity matrix.
$\mathbf{I}\in\mathbb{C}^{{M}\times {M}}$ stands for an identity matrix.
It is intractable to maximize (3) directly. To tackle this issue, it is rendered equivalent to the subsequent constrained minimization issue:
 \begin{equation}
\begin{split}
&\mathop{\min}\limits_{\mathbf{w}}\mathbf{w}^{\rm H}\mathbf{R}_{\mathbf{in}+\mathbf{n}}\mathbf{w}\\
&\textrm{subject to}\quad\mathbf{w}^{\rm H}\mathbf{a}=1,
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\mathop{\min}\limits_{\mathbf{w}}\mathbf{w}^{\rm H}\mathbf{R}_{\mathbf{in}+\mathbf{n}}\mathbf{w}\\
&\textrm{subject to}\quad\mathbf{w}^{\rm H}\mathbf{a}=1,
\end{split}
\end{equation} where the constraint ![]() $\mathbf{w}^{\rm H}\mathbf{a}=1$ serves to prevent the reduction in gain along the direction of the desired signal.
$\mathbf{w}^{\rm H}\mathbf{a}=1$ serves to prevent the reduction in gain along the direction of the desired signal.
However, the precise interference-plus-noise covariance matrix ![]() $\mathbf{R}_{\mathbf{in}+\mathbf{n}}$ is unavailable in practical scenarios. It can be replaced by the signal sample covariance matrix
$\mathbf{R}_{\mathbf{in}+\mathbf{n}}$ is unavailable in practical scenarios. It can be replaced by the signal sample covariance matrix ![]() ${\hat{\mathbf{R}}}$ which can be expressed by:
${\hat{\mathbf{R}}}$ which can be expressed by:
 \begin{equation}
{\hat{\mathbf{R}}}= \frac{1}{K}\sum_{k=1}^{K}\mathbf{x}(k)\mathbf{x}(k)^{\rm H}, \\[4pt]
\end{equation}
\begin{equation}
{\hat{\mathbf{R}}}= \frac{1}{K}\sum_{k=1}^{K}\mathbf{x}(k)\mathbf{x}(k)^{\rm H}, \\[4pt]
\end{equation}where K represents the number of snapshots.
The solution of the problem (5) is beamforming weight vector ![]() $\mathbf{w}_{mvdr}$, which can be expressed as [Reference Capon21]:
$\mathbf{w}_{mvdr}$, which can be expressed as [Reference Capon21]:
 \begin{equation}
{\mathbf{w}_{mvdr}}=\frac{\hat{\mathbf{R}}^{-1}\mathbf{a}}{\mathbf{a}^{\rm H}\hat{\mathbf{R}}^{-1}\mathbf{a}}, \\[4pt]
\end{equation}
\begin{equation}
{\mathbf{w}_{mvdr}}=\frac{\hat{\mathbf{R}}^{-1}\mathbf{a}}{\mathbf{a}^{\rm H}\hat{\mathbf{R}}^{-1}\mathbf{a}}, \\[4pt]
\end{equation} where ![]() $(\cdot)^{-1}$ stands for the matrix inverse operation.
$(\cdot)^{-1}$ stands for the matrix inverse operation.
The aforementioned solution is called as the MVDR method. The MVDR beamformer provides excellent interferences suppression performance when the desired signal SV is known precisely and the interference-plus-noise covariance matrix is available. However, when there are SV mismatch errors, the approach will be susceptible to substantial performance degradation.
Presented RAB-RCNN algorithm
In this section, the RAB-RCNN architecture is introduced detailedly. Firstly, the nearly-optimal beamforming weight vector is calculated by an excellent RAB algorithm, and it is used as the training label of the proposed RAB-RCNN model. Then, the adaptive beamforming weight vector problem is transformed into a regression problem based on neural network. Subsequently, the trained RAB-RCNN model can rapidly and precisely output the predicted beamforming weight vector.
Structure of proposed RAB-RCNN
The architecture of the presented RAB-RCNN is designed as shown in Figure 1, which comprises an input layer, two convolutional layers, two maxpooling layers, a residual block unit, a fully connected layer, and an output layer. The functions and hyperparameters are described as follows.

Figure 1. The presented RAB-RCNN framework.
The input layer
The first layer is the input layer. It has been studied that real-valued neural networks can achieve superior performance. So the signal sample covariance matrix ![]() ${\hat{\mathbf{R}}}$ as a complex-valued data should be converted into a real-valued input vector.
${\hat{\mathbf{R}}}$ as a complex-valued data should be converted into a real-valued input vector.
The convolutional layer
A series of convolutional layers are designed to learn the abundant information about the spatial correlation in the received signals. In the proposed RAB-RCNN framework, it consists of two convolutional layers. The first convolutional layer includes 64 kernels of size ![]() $1\times3$ and the other includes 256 kernels of size
$1\times3$ and the other includes 256 kernels of size ![]() $1\times3$. The activation function utilized within the convolutional layers is the exponential linear unit (ELU), which is defined as follows:
$1\times3$. The activation function utilized within the convolutional layers is the exponential linear unit (ELU), which is defined as follows:
 \begin{equation}
{\rm ELU}(l)=
\begin{cases}
l,\quad &l \geq 0 \\
\beta (e^l-1),\quad &l \lt 0,
\end{cases}
\end{equation}
\begin{equation}
{\rm ELU}(l)=
\begin{cases}
l,\quad &l \geq 0 \\
\beta (e^l-1),\quad &l \lt 0,
\end{cases}
\end{equation}where l denotes the output of a linear unit of the RAB-RCNN. β represents an adjustable parameter.
The maxpooling layer
The maxpooling layers are used to further learn deeper spatial features of received signals, and remove some unimportant features, which are detrimental to the beamforming weight vector estimation. Each convolutional layer is preceded by a maxpooling layer which comprises kernel of size 1 × 3.
The residual block unit
As the number of the network layers increases, the beamforming weight vector estimation accuracy gets saturated and then degrades rapidly [Reference He, X, S and J22]. In order to improve estimation performance, a residual block unit is introduced into CNN. The unit consists of four residual blocks with the same structure. The first two residual blocks have 64 kernels of size ![]() $1\times3$ and the last two have 128 kernels of size
$1\times3$ and the last two have 128 kernels of size ![]() $1\times3$. Each residual block structure is shown in Figure 2, which consists of two convolutional layers and is given by:
$1\times3$. Each residual block structure is shown in Figure 2, which consists of two convolutional layers and is given by:
where x stands for the input vectors of the residual unit designed and y denotes the output. The function ![]() $\mathbf{F}(\mathbf{x},{\mathbf{W}})=\mathbf{W}_{2}\delta(\mathbf{W}_{1}\mathbf{x})$ denotes a residual mapping function, in which δ stands for ELU activation function, W1 and W2 represent weight matrices.
$\mathbf{F}(\mathbf{x},{\mathbf{W}})=\mathbf{W}_{2}\delta(\mathbf{W}_{1}\mathbf{x})$ denotes a residual mapping function, in which δ stands for ELU activation function, W1 and W2 represent weight matrices.
Compared with the previous works based on the classical neural networks such as DNN and CNN, the residual block provides several advantages, such as: (a) the residual block only learns the residual ![]() $\mathbf{F}(\mathbf{x},\mathbf{W})=\mathbf{y}-\mathbf{x}$ , which is easier to learn essential features of the signal sample covariance matrix during the training phase than conventional CNN. Therefore, a sequence of residual blocks is utilized to learn more features, so that the beamforming weight vector estimation performance is improved; (b) the residual block utilizes a shortcut to connect the input and output information, which can solve the beamforming weight vector estimation performance degradation problem caused by deficient information. Furthermore, the shortcut in the residual block introduces neither extra parameters nor computation complexity.
$\mathbf{F}(\mathbf{x},\mathbf{W})=\mathbf{y}-\mathbf{x}$ , which is easier to learn essential features of the signal sample covariance matrix during the training phase than conventional CNN. Therefore, a sequence of residual blocks is utilized to learn more features, so that the beamforming weight vector estimation performance is improved; (b) the residual block utilizes a shortcut to connect the input and output information, which can solve the beamforming weight vector estimation performance degradation problem caused by deficient information. Furthermore, the shortcut in the residual block introduces neither extra parameters nor computation complexity.
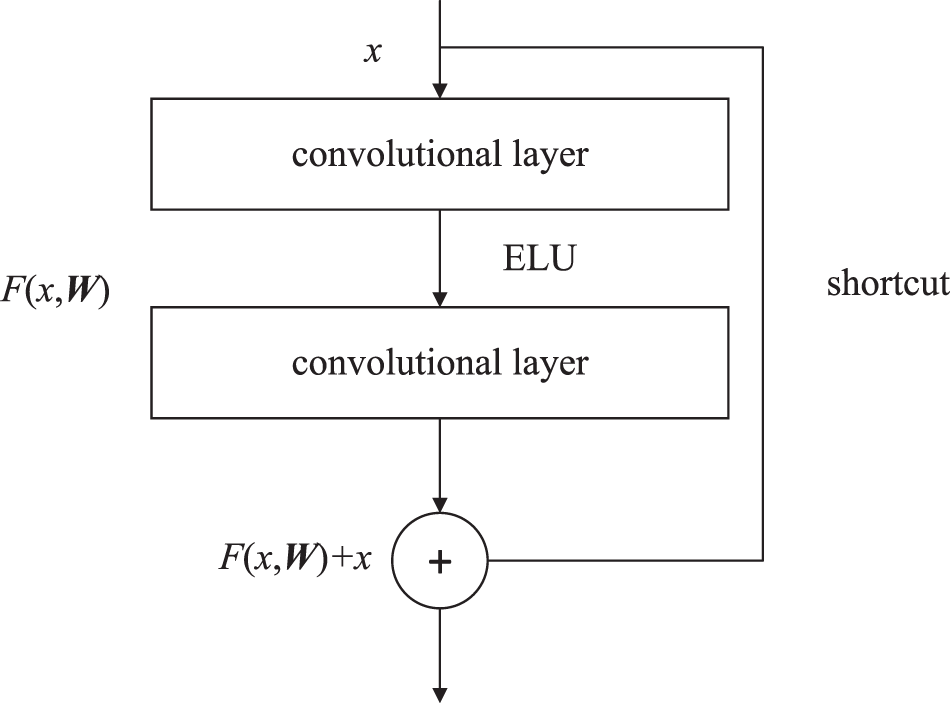
Figure 2. A residual block.
The fully connected layer
Similar to most related works [Reference Liu, Zhang and Yu16–Reference Hao, X and Y19], a fully connected layer is added prior to the output layer, which can put all the features together. Then the output layer can rapidly and precisely output the predicted beamforming weight vector ![]() $\mathbf{w}^{pred}$ with avoiding complex matrix operations.
$\mathbf{w}^{pred}$ with avoiding complex matrix operations.
Generation label
The weight vector label is utilized to train the proposed RAB-RCNN. The process for generating the beamforming weight vector label through SV estimation and interference-plus-noise covariance matrix reconstruction can be detailed as follows.
Steering vector estimation
It is challenging to obtain the precise SV in practical scenarios, to solve this problem, the solution is usually to replace ![]() $\mathbf{a}(\theta)$ by a nominal SV
$\mathbf{a}(\theta)$ by a nominal SV ![]() $\overline{\mathbf{a}}(\theta)$. To obtain precise estimation of the SV for the desired signal, the desired signal covariance matrix
$\overline{\mathbf{a}}(\theta)$. To obtain precise estimation of the SV for the desired signal, the desired signal covariance matrix ![]() $\hat{\mathbf{R}}_{\mathbf{s}}$ is redesigned as [Reference Wan, Xu, Xu and Zhang23]:
$\hat{\mathbf{R}}_{\mathbf{s}}$ is redesigned as [Reference Wan, Xu, Xu and Zhang23]:
 \begin{align}
\hat{\mathbf{R}}_{\mathbf{s}}
& =\int_{\Theta_{s}}(\hat{P}(\theta)-\overline{\sigma}_{n}^{2})\overline{\mathbf{a}}(\theta)\overline{\mathbf{a}}^{\rm H}(\theta)\,d\theta\nonumber \\
& =\int_{\Theta_{s}}(\frac{1}{\overline{\mathbf{a}}^{\rm H}(\theta)\hat{\mathbf{R}}^{-1}\overline{\mathbf{a}}(\theta)}-\overline{\sigma}_{n}^{2})\overline{\mathbf{a}}(\theta)\overline{\mathbf{a}}^{\rm H}(\theta)\,d\theta,
\end{align}
\begin{align}
\hat{\mathbf{R}}_{\mathbf{s}}
& =\int_{\Theta_{s}}(\hat{P}(\theta)-\overline{\sigma}_{n}^{2})\overline{\mathbf{a}}(\theta)\overline{\mathbf{a}}^{\rm H}(\theta)\,d\theta\nonumber \\
& =\int_{\Theta_{s}}(\frac{1}{\overline{\mathbf{a}}^{\rm H}(\theta)\hat{\mathbf{R}}^{-1}\overline{\mathbf{a}}(\theta)}-\overline{\sigma}_{n}^{2})\overline{\mathbf{a}}(\theta)\overline{\mathbf{a}}^{\rm H}(\theta)\,d\theta,
\end{align} where ![]() $\Theta_{s}$ stands for an area where the desired signal angle is located.
$\Theta_{s}$ stands for an area where the desired signal angle is located. ![]() $\hat{P}(\theta)$ denotes the Capon spatial power spectrum.
$\hat{P}(\theta)$ denotes the Capon spatial power spectrum. ![]() $\overline{\sigma}_{n}^{2}$ represents the estimated residual noise power.
$\overline{\sigma}_{n}^{2}$ represents the estimated residual noise power.
The eigenvector corresponding to the largest eigenvalue contains the most information on desired signal covariance matrix ![]() $\hat{\mathbf{R}}_{\mathbf{s}}$ in (10). Hence, the eigendecomposition of the desired signal covariance matrix
$\hat{\mathbf{R}}_{\mathbf{s}}$ in (10). Hence, the eigendecomposition of the desired signal covariance matrix ![]() $\hat{\mathbf{R}}_{\mathbf{s}}$ is given by:
$\hat{\mathbf{R}}_{\mathbf{s}}$ is given by:
 \begin{equation}
\hat{\mathbf{R}}_{\mathbf{s}}=\sum_{m=1}^{M}\alpha_{m}\mathbf{c}_{m}\mathbf{c}_{m}^{\rm H}, \\[3pt]
\end{equation}
\begin{equation}
\hat{\mathbf{R}}_{\mathbf{s}}=\sum_{m=1}^{M}\alpha_{m}\mathbf{c}_{m}\mathbf{c}_{m}^{\rm H}, \\[3pt]
\end{equation} where αm represents the eigenvalue of desired signal covariance matrix ![]() $\hat{\mathbf{R}}_{\mathbf{s}}$. cm denotes the eigenvectors corresponding to αm.
$\hat{\mathbf{R}}_{\mathbf{s}}$. cm denotes the eigenvectors corresponding to αm.
Therefore, the corrected desired signal SV ![]() $\hat{\mathbf{a}}_{s}$ is defined as follows [Reference Zhu, Xu and Ye24]:
$\hat{\mathbf{a}}_{s}$ is defined as follows [Reference Zhu, Xu and Ye24]:
where c1 denotes the eigenvector of the largest eigenvalue.
Interference-plus-noise covariance matrix reconstruction
To remove the negative effects of the desired signal, its components ![]() $\tilde{\mathbf{x}}(k)$ are eliminated from the received snapshots through the projection, and it is expressed as [Reference Zhu, Ye, Xu and Zheng25]:
$\tilde{\mathbf{x}}(k)$ are eliminated from the received snapshots through the projection, and it is expressed as [Reference Zhu, Ye, Xu and Zheng25]:
where ![]() $\mathbf{\varPhi}=\mathbf{\varPhi}^{\rm H}=\mathbf{I}-\mathbf{C}_{1}\mathbf{C}_{1}^{\rm H}$ denotes the projection matrix. C1 comprises N eigenvectors associated with N largest eigenvalues of the desired covariance matrix
$\mathbf{\varPhi}=\mathbf{\varPhi}^{\rm H}=\mathbf{I}-\mathbf{C}_{1}\mathbf{C}_{1}^{\rm H}$ denotes the projection matrix. C1 comprises N eigenvectors associated with N largest eigenvalues of the desired covariance matrix ![]() $\hat{\mathbf{R}}_{\mathbf{s}}$.
$\hat{\mathbf{R}}_{\mathbf{s}}$.
Substituting (13) into (6), the sample covariance matrix ![]() $\tilde{\mathbf{R}}$ absent of the desired signal components can be expressed as:
$\tilde{\mathbf{R}}$ absent of the desired signal components can be expressed as:
 \begin{equation}
\begin{split}
\tilde{\mathbf{R}}
&=\frac{1}{K}\sum_{k=1}^{K}\tilde{\mathbf{x}}(k)\tilde{\mathbf{x}}^{\rm H}(k)\\
&=\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}\mathbf{\varPhi},
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\tilde{\mathbf{R}}
&=\frac{1}{K}\sum_{k=1}^{K}\tilde{\mathbf{x}}(k)\tilde{\mathbf{x}}^{\rm H}(k)\\
&=\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}\mathbf{\varPhi},
\end{split}
\end{equation} where ![]() $\tilde{\mathbf{R}}$ is obtained from the signal sample covariance matrix
$\tilde{\mathbf{R}}$ is obtained from the signal sample covariance matrix ![]() $\hat{\mathbf{R}}$ by projecting.
$\hat{\mathbf{R}}$ by projecting.
Substituting (13) into (14), it follows that:
 \begin{equation}
\begin{split}
\tilde{\mathbf{R}}
=&\frac{1}{K}\sum_{k=1}^{K}\tilde{\mathbf{x}}(k)\tilde{\mathbf{x}}^{\rm H}(k)\\
\widetilde{=}&\mathbf{\varPhi}^{\rm H}(\hat{\mathbf{R}}_{in}+\hat{\sigma}_{n}^{2}\mathbf{I})\mathbf{\varPhi}\\
\widetilde{=}&\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}_{in}\mathbf{\varPhi}+\hat{\sigma}_{n}^{2}\mathbf{\varPhi}^{\rm H}\mathbf{\varPhi},
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\tilde{\mathbf{R}}
=&\frac{1}{K}\sum_{k=1}^{K}\tilde{\mathbf{x}}(k)\tilde{\mathbf{x}}^{\rm H}(k)\\
\widetilde{=}&\mathbf{\varPhi}^{\rm H}(\hat{\mathbf{R}}_{in}+\hat{\sigma}_{n}^{2}\mathbf{I})\mathbf{\varPhi}\\
\widetilde{=}&\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}_{in}\mathbf{\varPhi}+\hat{\sigma}_{n}^{2}\mathbf{\varPhi}^{\rm H}\mathbf{\varPhi},
\end{split}
\end{equation} where ![]() $\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}_{in}\mathbf{\varPhi}$ and
$\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}_{in}\mathbf{\varPhi}$ and ![]() $\hat{\sigma}_{n}^{2}\mathbf{\varPhi}^{\rm H}\mathbf{\varPhi}$ denote interference and noise components, respectively.
$\hat{\sigma}_{n}^{2}\mathbf{\varPhi}^{\rm H}\mathbf{\varPhi}$ denote interference and noise components, respectively. ![]() $\hat{\sigma}_{n}^{2}$ represents the actual noise power, which is estimated by
$\hat{\sigma}_{n}^{2}$ represents the actual noise power, which is estimated by ![]() $M-L-1$ smallest eigenvalues of the signal sample covariance matrix
$M-L-1$ smallest eigenvalues of the signal sample covariance matrix ![]() $\hat{\mathbf{R}}$.
$\hat{\mathbf{R}}$.
According to [Reference Wan, Xu, Xu and Zhang23], ![]() $\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}_{in}\mathbf{\varPhi}\widetilde{=}\hat{\mathbf{R}}_{in}$ can be drawn. Then,
$\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}_{in}\mathbf{\varPhi}\widetilde{=}\hat{\mathbf{R}}_{in}$ can be drawn. Then, ![]() $\hat{\mathbf{R}}_{in}$ can be defined as
$\hat{\mathbf{R}}_{in}$ can be defined as ![]() $\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}\mathbf{\varPhi}-\hat{\sigma}_{n}^{2}\mathbf{\varPhi}^{\rm H}\mathbf{\varPhi}\widetilde{=} \hat{\mathbf{R}}_{in}$ by combining (13) and (14). However, the interference covariance matrix
$\mathbf{\varPhi}^{\rm H}\hat{\mathbf{R}}\mathbf{\varPhi}-\hat{\sigma}_{n}^{2}\mathbf{\varPhi}^{\rm H}\mathbf{\varPhi}\widetilde{=} \hat{\mathbf{R}}_{in}$ by combining (13) and (14). However, the interference covariance matrix ![]() $\hat{\mathbf{R}}_{in}$ is unprecise because the projection operation brings a high potential for inducing numerous errors. Therefore, the inaccurate interference covariance matrix
$\hat{\mathbf{R}}_{in}$ is unprecise because the projection operation brings a high potential for inducing numerous errors. Therefore, the inaccurate interference covariance matrix ![]() $\hat{\mathbf{R}}_{in}$ is aimed to estimate the powers of the individual interference. Therefore, the estimated interferences power
$\hat{\mathbf{R}}_{in}$ is aimed to estimate the powers of the individual interference. Therefore, the estimated interferences power ![]() $ \tilde{\mathbf{P}}_{in}$ are expressed as [Reference Zhu, Ye, Xu and Zheng25]:
$ \tilde{\mathbf{P}}_{in}$ are expressed as [Reference Zhu, Ye, Xu and Zheng25]:
where the diagonal elements of the estimated interferences power ![]() $\tilde{\mathbf{P}}_{in}$ stand for the corresponding interferences powers.
$\tilde{\mathbf{P}}_{in}$ stand for the corresponding interferences powers. ![]() $\tilde{\mathbf{A}}_{i}=\{\hat{\mathbf{a}}_{1},\hat{\mathbf{a}}_{2},\cdots, \hat{\mathbf{a}}_{L}\}$ denotes the estimated SVs of interferences obtained via the same method as desired signal SV estimation.
$\tilde{\mathbf{A}}_{i}=\{\hat{\mathbf{a}}_{1},\hat{\mathbf{a}}_{2},\cdots, \hat{\mathbf{a}}_{L}\}$ denotes the estimated SVs of interferences obtained via the same method as desired signal SV estimation. ![]() $\hat{{\alpha}}_{t}$ represents the interference SV.
$\hat{{\alpha}}_{t}$ represents the interference SV.
Based on the interferences power ![]() $\tilde{\mathbf{P}}_{in}$ and corresponding SVs
$\tilde{\mathbf{P}}_{in}$ and corresponding SVs ![]() $\tilde{\mathbf{A}}_{i}$, the precise interference-plus-noise covariance matrix
$\tilde{\mathbf{A}}_{i}$, the precise interference-plus-noise covariance matrix  $\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}$ is expressed as:
$\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}$ is expressed as:
 \begin{equation}
\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}=\tilde{\mathbf{A}}_{i}\text{diag}(\tilde{\mathbf{P}}_{in})\tilde{\mathbf{A}}_{i}^{\rm H}+ \hat{\sigma}_{n}^{2}\mathbf{I}.
\end{equation}
\begin{equation}
\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}=\tilde{\mathbf{A}}_{i}\text{diag}(\tilde{\mathbf{P}}_{in})\tilde{\mathbf{A}}_{i}^{\rm H}+ \hat{\sigma}_{n}^{2}\mathbf{I}.
\end{equation} Consequently, the beamforming weight vector as the label of the presented approach ![]() $\mathbf{w}^{label}$ is obtained by:
$\mathbf{w}^{label}$ is obtained by:
 \begin{equation}
\mathbf{w}^{label}=\frac{\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}^{-1}\hat{\mathbf{a}}_{s}}{\hat{\mathbf{a}}_{s}^{H}\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}^{-1}\hat{\mathbf{a}}_{s}}.
\end{equation}
\begin{equation}
\mathbf{w}^{label}=\frac{\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}^{-1}\hat{\mathbf{a}}_{s}}{\hat{\mathbf{a}}_{s}^{H}\tilde{\mathbf{R}}_{\mathbf{in}+\mathbf{n}}^{-1}\hat{\mathbf{a}}_{s}}.
\end{equation}Training and testing of proposed RAB-RCNN
Generation of training data
Apparent, the signal sample covariance matrix ![]() $\hat{\mathbf{R}}$ is a conjugate symmetric matrix, so the upper or lower triangular part of the signal sample covariance matrix
$\hat{\mathbf{R}}$ is a conjugate symmetric matrix, so the upper or lower triangular part of the signal sample covariance matrix ![]() ${\hat{\mathbf{R}}}$ is rearranged into a vector r:
${\hat{\mathbf{R}}}$ is rearranged into a vector r:
 \begin{equation}
\begin{split}
\mathbf{r}=[&\hat{\mathbf{R}}_{12},\cdots,\hat{\mathbf{R}}_{1M},\hat{\mathbf{R}}_{23},\cdots,\\
&\hat{\mathbf{R}}_{2M},\cdots,\hat{\mathbf{R}}_{(M-1)M}]
\end{split},
\end{equation}
\begin{equation}
\begin{split}
\mathbf{r}=[&\hat{\mathbf{R}}_{12},\cdots,\hat{\mathbf{R}}_{1M},\hat{\mathbf{R}}_{23},\cdots,\\
&\hat{\mathbf{R}}_{2M},\cdots,\hat{\mathbf{R}}_{(M-1)M}]
\end{split},
\end{equation} where ![]() $\hat{{R}}_{i,j}$ denotes the (i, j)th element of the signal sample covariance matrix
$\hat{{R}}_{i,j}$ denotes the (i, j)th element of the signal sample covariance matrix ![]() ${\hat{\mathbf{R}}}$. r
${\hat{\mathbf{R}}}$. r ![]() $\in\mathbb{C}^ {M(M-1)/2\times1}$ stands for a complex-valued vector.
$\in\mathbb{C}^ {M(M-1)/2\times1}$ stands for a complex-valued vector.
Afterward, to enhance the convergence, the (19) is normalized by norm definition:
 \begin{equation}
\mathbf{r}_{n}=\frac{\mathbf{r}}{\Vert\mathbf{r}\Vert_2}.
\end{equation}
\begin{equation}
\mathbf{r}_{n}=\frac{\mathbf{r}}{\Vert\mathbf{r}\Vert_2}.
\end{equation} By taking the real and imaginary part of ![]() $\mathbf{r}_{n},$ as the input to the network the input
$\mathbf{r}_{n},$ as the input to the network the input ![]() $\mathbf{z}\in\mathbb{C}^{M(M-1)\times 1}$ of the RAB-RCNN is given by:
$\mathbf{z}\in\mathbb{C}^{M(M-1)\times 1}$ of the RAB-RCNN is given by:
 \begin{equation}
\begin{split}
\mathbf{z}=[&\text{Re}\{r_{1}^{n}\},\text{Im}\{r_{1}^{n}\},\cdots,\\ &\text{Re}\{r_{M(M-1)/2}^{n}\},\text{Im}\{r_{M(M-1)/2}^{n}\}],
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\mathbf{z}=[&\text{Re}\{r_{1}^{n}\},\text{Im}\{r_{1}^{n}\},\cdots,\\ &\text{Re}\{r_{M(M-1)/2}^{n}\},\text{Im}\{r_{M(M-1)/2}^{n}\}],
\end{split}
\end{equation} where ![]() $r_{p}^{n}, p=1,\cdots,M(M-1)/2$ represents the pth element of
$r_{p}^{n}, p=1,\cdots,M(M-1)/2$ represents the pth element of ![]() $\mathbf{r}_{n}.$ Re
$\mathbf{r}_{n}.$ Re![]() $\{\cdot\}$ denotes the real part. Im
$\{\cdot\}$ denotes the real part. Im![]() $\{\cdot\}$ stands for the imaginary part.
$\{\cdot\}$ stands for the imaginary part.
The beamforming weight vector ![]() $\mathbf{w}^{label}$
$\mathbf{w}^{label}$ ![]() $\in\mathbb{C}^ {2M\times1}$ which is the label of the RAB-RCNN is formed as follows:
$\in\mathbb{C}^ {2M\times1}$ which is the label of the RAB-RCNN is formed as follows:
 \begin{equation}
\begin{split}
\mathbf{w}^{label}=[&\text{Re}\{w_{1}^{label}\},\text{Im}\{w_{1}^{label}\},\cdots,\\
&\text{Re}\{w_{M}^{label}\}, \text{Im}\{w_{M}^{label}\}].
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\mathbf{w}^{label}=[&\text{Re}\{w_{1}^{label}\},\text{Im}\{w_{1}^{label}\},\cdots,\\
&\text{Re}\{w_{M}^{label}\}, \text{Im}\{w_{M}^{label}\}].
\end{split}
\end{equation} Via collecting signal samples located at different DOAs and SNRs, the training data are given, that is,  $\{(\mathbf{z}_{q},\mathbf{w}_{q}^{label}), q=1,2,\ldots,Q\}$, in which Q is the number of training samples.
$\{(\mathbf{z}_{q},\mathbf{w}_{q}^{label}), q=1,2,\ldots,Q\}$, in which Q is the number of training samples.
Phase of training and testing
During the training phase, the proposed RAB-RCNN approach is trained to learn a nearly optimal beamforming weight vector from the vectorized covariance matrix z of the received signals. The loss function of the proposed RAB-RCNN approach ![]() $\mathbf{L}_{RAB-RCNN}(\mathbf{w}^{pred},\mathbf{w}^{label})$ is calculated as:
$\mathbf{L}_{RAB-RCNN}(\mathbf{w}^{pred},\mathbf{w}^{label})$ is calculated as:
 \begin{equation}
\mathbf{L}_{RAB-RCNN}(\mathbf{w}^{pred},\mathbf{w}^{label})=\frac{1}{2M}\Vert\mathbf{w}^{pred}-\mathbf{w}^{label}\Vert_{2}^{2},
\end{equation}
\begin{equation}
\mathbf{L}_{RAB-RCNN}(\mathbf{w}^{pred},\mathbf{w}^{label})=\frac{1}{2M}\Vert\mathbf{w}^{pred}-\mathbf{w}^{label}\Vert_{2}^{2},
\end{equation} where ![]() $\mathbf{w}^{label}$ represents the training label of the proposed RAB-RCNN model.
$\mathbf{w}^{label}$ represents the training label of the proposed RAB-RCNN model. ![]() $\mathbf{w}^{pred}$ denotes the predicted value.
$\mathbf{w}^{pred}$ denotes the predicted value.
Summary
The proposed approach is succinctly outlined as follows:
1) Design the presented RAB-RCNN model.
2) Obtain received signal samples
 $\{\mathbf{x}_{q}, q=1,2,\ldots,Q\}$ with varying SNRs and DOAs.
$\{\mathbf{x}_{q}, q=1,2,\ldots,Q\}$ with varying SNRs and DOAs.3) Compute the covariance matrices of the signal samples
 $\{\hat{\mathbf{R}}_{q}, q=1,2,\ldots,Q\}$.
$\{\hat{\mathbf{R}}_{q}, q=1,2,\ldots,Q\}$.4) Derive samples of the weight vector for beamforming
 $\{\mathbf{w}_{q}^{label}, q=1,2,\ldots,Q\}$ by (18).
$\{\mathbf{w}_{q}^{label}, q=1,2,\ldots,Q\}$ by (18).5) Carry out pre-processing of the samples using equations (19)–(22), thereby generating the training data.
6) Introduce the training data to facilitate the training of the presented RAB-RCNN through the use of the loss function (23).
7) Employ the trained RAB-RCNN to predict the beamforming weight vector
 $\mathbf{w}^{pred}$ that are nearly optimal.
$\mathbf{w}^{pred}$ that are nearly optimal.
Simulations
To assess the effectiveness of the RAB-RCNN approach, the uniform linear array under consideration consists of M = 10 omnidirectional sensors. The distance between two adjacent antennas is ![]() $\lambda/2$, where λ denotes the wavelength. There are three signals impinging from the directions
$\lambda/2$, where λ denotes the wavelength. There are three signals impinging from the directions ![]() $\theta_{0}= 1^{\circ}$,
$\theta_{0}= 1^{\circ}$, ![]() $\theta_{1}= 55^{\circ}$ and
$\theta_{1}= 55^{\circ}$ and ![]() $\theta_{2}= -69^{\circ}$. One is postulated to serve as the desired signal, and others are postulated to act as interferences, possessing an interference-to-noise ratio equivalent to 30 dB.
$\theta_{2}= -69^{\circ}$. One is postulated to serve as the desired signal, and others are postulated to act as interferences, possessing an interference-to-noise ratio equivalent to 30 dB.
The 100 times Monte Carlo approach is utilized to ensure the generality of the simulations. Unless otherwise stated, all simulations use the parameters above. For convenience, the existing methods in [Reference Jia, Jin, Zhou and Yao11], [Reference Vorobyov, Gershman and Luo12], [Reference Zheng, Zheng, Wang and Zhang15], and [Reference Ramezanpour and Mosavi17] are named as ESB, WCP, CIP, and CNN, respectively.
Mismatch caused by DOA estimation error
In the experiment, a scenario is considered with DOA estimation error. The random errors of both the desired signal and two interferences are uniformly distributed in ![]() $[-4^{\circ},4^{\circ}]$ for each simulation. The number of snapshots is fixed at K = 30.
$[-4^{\circ},4^{\circ}]$ for each simulation. The number of snapshots is fixed at K = 30.
Figure 3 demonstrates the beampatterns of the aforementioned approaches. From this figure, the WCP method exhibits an unacceptable directional pattern due to its mainlobe shifting and sidelobe rising. The reason is that the algorithm does not consider the impact of the desired signal. Fortunately, the presented approach, the CIP algorithm, and the CNN method suppress interferences while preserving the desired signal. Additionally, the presented algorithm has lower nulls than the other algorithms and it also has lower sidelobes than other approaches.
Figure 4 indicates the SINR curves of the aforementioned approaches versus the SNR in a range from −5 to 30 dB. It shows that the presented approach, the CNN approach, and the CIP approach achieve better capability than the ESB method and the WCP algorithm. It is also clear that the ESB method occurs significant performance degradation at the high SNR. It is evident that the presented RAB-RCNN approach has the higher output SINR than the same approach based on the CNN method. The reason why the proposed RAB-RCNN approach outperforms other methods is fully leveraging the residual block unit to extract the critical feature information. When the SNR ≥10 dB, the output SNR of the ESB algorithm begins to decline, because the signal sample covariance matrix with the high input SNR contains a strong desired signal, which leads to the existence of covariance matrix errors so that the output beamforming performance deteriorates.
The output SINR of the aforementioned approaches is considered versus the number of snapshots and the simulation result is shown in Figure 5. The presented approach gets the greater output SINR compared with the other methods and verifies the RAB-RCNN is not sensitive to the DOA estimation error. The performance of the ESB approach and the WCP approach is easily affected by snapshots, so the performance is not satisfactory.

Figure 3. The beampatterns of different approaches under DOA estimation errors.

Figure 4. SINR versus SNR under the DOA estimation error.

Figure 5. SINR versus the number of snapshots under the DOA estimation error.
Mismatch caused by sensor position error
In the experiment, the impact of the sensor position error on the capability of the approaches is researched. The positioning errors of the sensors are evenly distributed within a specific interval ![]() $[-0.025\lambda, 0.025\lambda]$.
$[-0.025\lambda, 0.025\lambda]$.
Figure 6 indicates the beampatterns of the aforementioned approaches. Evidently, a smaller sensor position error can incur a higher sidelobe level for the ESB method. The presented algorithm, the CNN algorithm, and the CIP algorithm can be capable of suppressing interferences, while simultaneously retaining an undistorted response toward the target signal. Especially, the proposed algorithm has lower nulls than the others. This is because that the presented approach has an outstanding beamforming weight vector label (18) and the residual block unit can help the proposed approach to improve the output SINR.
Figure 7 shows the SINR curves of the aforementioned approaches with the SNR ranging from −5 to 30 dB. The output SINR curves of the proposed RAB-RCNN algorithm, CNN algorithm, and CIP algorithm gradually increase. It is not difficult to see that the difference between the output SINR curves of the proposed RAB-RCNN algorithm and the optimal output SNR wireless is the smallest. The presented figure illustrates that the SINR of the ESB approach experiences a sharp decline as the input SNR increases, when the SNR ≥5 dB. The CIP algorithm has the worst performance in the low SNR, and it would not correct the mismatched desired signal SV well, and its output SNR needs to be further improved.
Figure 8 indicates the SINR of the aforementioned methods versus the number of snapshots at the SNR = 15 dB. Compared with aforementioned algorithms, the proposed RAB-RCNN has the highest output SINR with the snapshot changes. This is due to the deep feature extraction capability of the residual unit in the presented algorithm.
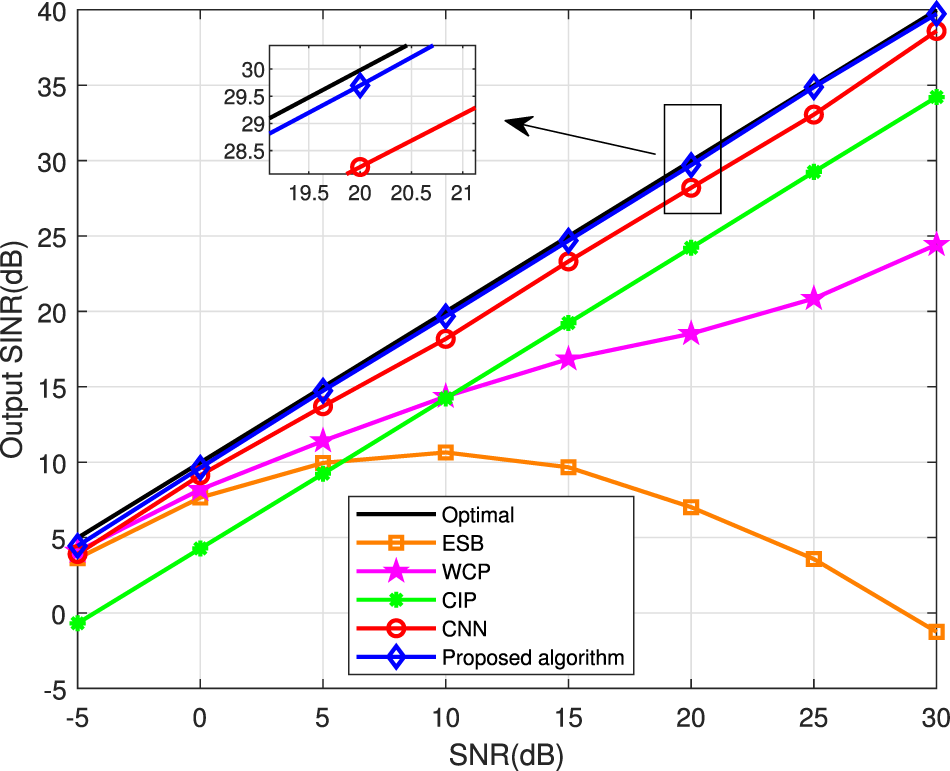
Figure 6. The beampatterns of different approaches under the circumstance of sensor position error.
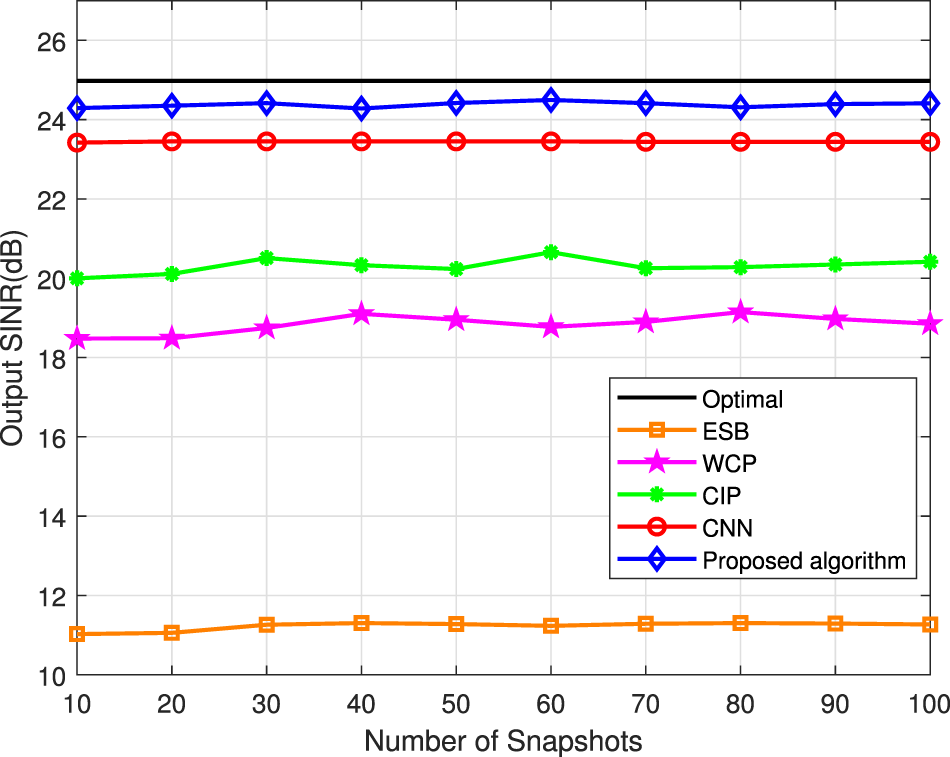
Figure 7. SINR versus SNR under the sensor position error.

Figure 8. SINR versus the number of snapshots under the sensor position error.
Computation time and prediction accuracy analysis
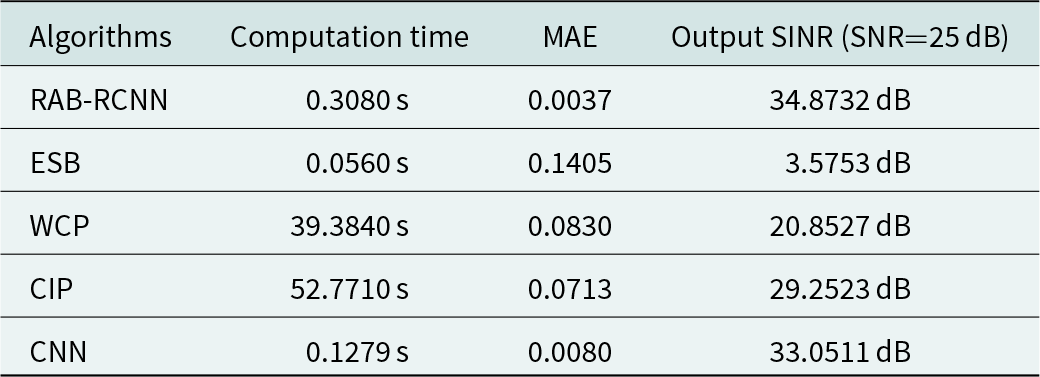
Table 1 demonstrates the computation time and prediction accuracy of the presented RAB-RCNN approach and several previous methods. The computation time is the time spent generating the beamforming weight vectors via feeding 100 covariance matrices into different approaches. It can be found the computation time of the presented algorithm is less than the CIP method and WCP algorithm in Table 1. The proposed approach outperforms the aforementioned approaches because of its ability to avoid the complex eigenvalue decomposition and matrix inversion processes, so it can be applied to practical engineering. Additionally, compared with the ESB method and the CNN method, the proposed approach exhibits a slightly longer computation time, but the performance of the proposed approach is better than them. Meanwhile, the mean absolute error (MAE) is used as an evaluation index of prediction accuracy [Reference Saeed, Vítor, Rodrigo and Noushin26], which represents the average of the absolute error between the predicted beamforming weight vector and the label. It can clearly be seen that the well-trained network (RAB-RCNN and CNN) can achieve lower mean absolute error than other traditional algorithms (ESB, WCP, and CIP), thus they can perform excellent beamforming prediction ability. However, because of the residual unit, the proposed RAB-RCNN approach is superior to the CNN in terms of the output SINR.
Table 1. Comparing the computation time and prediction accuracy of various beamforming algorithms
Conclusion
When the covariance matrix includes the desired signal and the desired signal SV mismatches, the beamforming performance will be degraded. In response to this problem, this paper presents a RAB-RCNN approach for beamforming. Firstly, the beamforming {weight vector is obtained by an excellent interference-plus-noise covariance matrix reconstruction and SV estimation methods. Then by using it as the beamforming weight vector label of the proposed approach, the beamforming prediction problem is reformulated as the neural network regression problem. The presented RAB-RCNN framework automatically learns to reduce the loss between the nearly-optimal beamforming weight vector label and predicts the beamforming weight vector. Eventually, because of the depth extraction ability of the residual unit, the well-trained RAB-RCNN can rapidly and precisely predict the beamforming weight vector without complex matrix operations. Simulations shows that the presented approach exhibits superior capability compared to conventional robust beamforming algorithms.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61971117), by the Natural Science Foundation of Hebei Province (Grant No. F2020501007), and by the S&T Program of Hebei (No. 22377717D).
Author contributions
Fulai Liu and Xubin Li have contributed equally to this work.
Competing interests
The authors report no conflict of interest.

Fulai Liu received the M.S. degree and Ph.D. degree from Northeastern University, Shenyang, China, in 2002 and in 2005, respectively. Since 2010, he is a professor in Northeastern University, Qinhuangdao, China. His research interests include array signal processing and its applications, cognitive radio, millimeter wave MIMO system, deep learning, etc.

Dongbao Qin received the B.S. degree from Shenyang Institute of Engineering, Shenyang, China, in 2019 and the M.S. degree from Shenyang Institute of Engineering, Shenyang, China, in 2022. He is currently a researcher at Huawei.

Xubin Li received the B.S. degree from Hebei Normal University, Shijiazhuang, China, in 2022. He is currently pursuing the M.S. degree at Northeastern University. His research interests include deep learning, beamforming, and reconfigurable intelligent surface.

Yufeng Du received the M.S. degree from Xidian University, Xian, China, in 2012. Since 2019, he is senior engineer in Hebei Key Laboratory of Electromagnetic Spectrum Cognition and Control, Shijiazhuang, China. His research interests include digital signal processing, cognitive radio, etc.

Xiuquan Dou received the M.S degree from The Institute of Communication Measurement and Control Technology, Shijiazhuang, China, in 2007. Since 2019, he has been an associate professor at Hebei Key Laboratory of Electromagnetic Spectrum Cognition and Control, Shijiazhuang, China. His research interests include array signal processing and applications, passive positioning and tracking, space-based electronic reconnaissance, etc.

Ruiyan Du received her B.S. degree from Hebei Normal University, Shijiazhuang, China, in 1999, the M.S. degree from Yanshan University, Qinhuangdao, China, in 2006, and the Ph.D. degree from Northeastern University, Shenyang, China, in 2012. Since 2012, she is an associate professor in Northeastern University, Qinhuangdao, China. Her research interests include wireless communications, signal processing, and deep learning.














