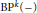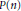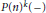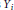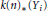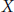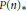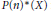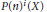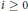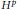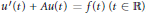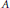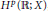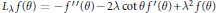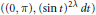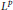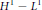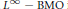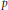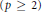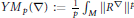Research Article
Meromorphic Continuation of Spherical Cuspidal Data Eisenstein Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1121-1134
-
- Article
-
- You have access
- Export citation
Sobolev Extensions of Hölder Continuous and Characteristic Functions on Metric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1135-1153
-
- Article
-
- You have access
- Export citation
k(n)-Torsion-Free H-Spaces and P(n)-Cohomology
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1154-1206
-
- Article
-
- You have access
- Export citation
Hp-Maximal Regularity and Operator Valued Multipliers on Hardy Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1207-1222
-
- Article
-
- You have access
- Export citation
Calderón–Zygmund Operators Associated to Ultraspherical Expansions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1223-1244
-
- Article
-
- You have access
- Export citation
On Gap Properties and Instabilities of p-Yang–Mills Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1245-1259
-
- Article
-
- You have access
- Export citation
Generic Extensions and Canonical Bases for Cyclic Quivers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1260-1283
-
- Article
-
- You have access
- Export citation
On Effective Witt Decomposition and the Cartan–Dieudonné Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1284-1300
-
- Article
-
- You have access
- Export citation
Strichartz Inequalities for the Wave Equation with the Full Laplacian on the Heisenberg Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1301-1322
-
- Article
-
- You have access
- Export citation
On a Conjecture of Jacquet, Lai, and Rallis: Some Exceptional Cases
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1323-1340
-
- Article
-
- You have access
- Export citation
Other
Index of Volume 59
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1341-1344
-
- Article
-
- You have access
- Export citation