hex-programs are an extension of answer set programs (ASP) with external sources. To this end, external atoms provide a bidirectional interface between the program and an external source. The traditional evaluation algorithm for hex-programs is based on guessing truth values of external atoms and verifying them by explicit calls of the external source. The approach was optimized by techniques that reduce the number of necessary verification calls or speed them up, but the remaining external calls are still expensive. In this paper, we present an alternative evaluation approach based on inlining of external atoms, motivated by existing but less general approaches for specialized formalisms such as DL-programs. External atoms are then compiled away such that no verification calls are necessary. The approach is implemented in the dlvhex reasoner. Experiments show a significant performance gain. Besides performance improvements, we further exploit inlining for extending previous (semantic) characterizations of program equivalence from ASP to hex-programs, including those of strong equivalence, uniform equivalence, and 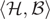$\langle\mathcal{H},\mathcal{B}\rangle$- equivalence. Finally, based on these equivalence criteria, we characterize also inconsistency of programs w.r.t. extensions. Since well-known ASP extensions (such as constraint ASP) are special cases of hex, the results are interesting beyond the particular formalism.

Logic programming with tabling and constraints (TCLP, tabled constraint logic programming) has been shown to be more expressive and in some cases more efficient than LP, CLP, or LP + tabling. Previous designs of TCLP systems did not fully use entailment to determine call/answer subsumption and did not provide a simple and well-documented interface to facilitate the integration of constraint solvers in existing tabling systems. We study the role of projection and entailment in the termination, soundness, and completeness of TCLP systems and present the design and an experimental evaluation of Mod TCLP, a framework that eases the integration of additional constraint solvers. Mod TCLP views constraint solvers as clients of the tabling system, which is generic w.r.t. the solver and only requires a clear interface from the latter. 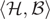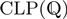We validate our design by integrating four constraint solvers: a previously existing constraint solver for difference constraints, written in C; the standard versions of Holzbaur’s and 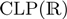, written in Prolog; and a new constraint solver for equations over finite lattices. We evaluate the performance of our framework in several benchmarks using the aforementioned solvers. Mod TCLP is developed in Ciao Prolog, a robust, mature, next-generation Prolog system.

When modeling real-world domains, we have to deal with information that is incomplete or that comes from sources with different trust levels. This motivates the need for managing uncertainty in the Semantic Web. To this purpose, we introduced a probabilistic semantics, named DISPONTE, in order to combine description logics (DLs) with probability theory. The probability of a query can be then computed from the set of its explanations by building a Binary Decision Diagram (BDD). The set of explanations can be found using the tableau algorithm, which has to handle non-determinism. Prolog, with its efficient handling of non-determinism, is suitable for implementing the tableau algorithm. TRILL and TRILLP are systems offering a Prolog implementation of the tableau algorithm. TRILLP builds a pinpointing formula that compactly represents the set of explanations and can be directly translated into a BDD. Both reasoners were shown to outperform state-of-the-art DL reasoners. In this paper, we present an improvement of TRILLP, named TORNADO, in which the BDD is directly built during the construction of the tableau, further speeding up the overall inference process. An experimental comparison shows the effectiveness of TORNADO. All systems can be tried online in the TRILL on SWISH web application at http://trill.ml.unife.it/.

We describe the new version of the Planning Domain Definition Language (PDDL)-to-Answer Set Programming (ASP) translator plasp. First, it widens the range of accepted PDDL features. Second, it contains novel planning encodings, some inspired by Satisfiability Testing (SAT) planning and others exploiting ASP features such as well-foundedness. All of them are designed for handling multivalued fluents in order to capture both PDDL as well as SAS planning formats. Third, enabled by multishot ASP solving, it offers advanced planning algorithms also borrowed from SAT planning. As a result, plasp provides us with an ASP-based framework for studying a variety of planning techniques in a uniform setting. Finally, we demonstrate in an empirical analysis that these techniques have a significant impact on the performance of ASP planning.