In this paper, we propose a condition that can guarantee the lower bound property of the discrete eigenvalue produced by the finite element method for the Stokes operator. We check and prove this condition for four nonconforming methods and one conforming method. Hence they produce eigenvalues which are smaller than their exact counterparts.

In this work, two-level stabilized finite volume formulations for the 2D steady Navier-Stokes equations are considered. These methods are based on the local Gauss integration technique and the lowest equal-order finite element pair. 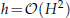Moreover, the two-level stabilized finite volume methods involve solving one small Navier-Stokes problem on a coarse mesh with mesh size H, a large general Stokes problem for the Simple and Oseen two-level stabilized finite volume methods on the fine mesh with mesh size or a large general Stokes equations for the Newton two-level stabilized finite volume method on a fine mesh with mesh size 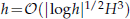. These methods we studied provide an approximate solution 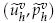with the convergence rate of same order as the standard stabilized finite volume method, which involve solving one large nonlinear problem on a fine mesh with mesh size h. Hence, our methods can save a large amount of computational time.

This paper deals with the two-level Newton iteration method based on the pressure projection stabilized finite element approximation to solve the numerical solution of the Navier-Stokes type variational inequality problem. We solve a small Navier-Stokes problem on the coarse mesh with mesh size H and solve a large linearized Navier-Stokes problem on the fine mesh with mesh size h. The error estimates derived show that if we choose h = O (|logh|1/2H3), then the two-level method we provide has the same H1 and L2 convergence orders of the velocity and the pressure as the one-level stabilized method. However, the L2 convergence order of the velocity is not consistent with that of one-level stabilized method. Finally, we give the numerical results to support the theoretical analysis.

A fully higher-order compact (HOC) finite difference scheme on the 9-point two-dimensional (2D) stencil is formulated for solving the steady-state laminar mixed convection flow in a lid-driven inclined square enclosure filled with water-Al2O3 nanofluid. Two cases are considered depending on the direction of temperature gradient imposed (Case I, top and bottom; Case II, left and right). The developed equations are given in terms of the stream function-vorticity formulation and are non-dimensionalized and then solved numerically by a fourth-order accurate compact finite difference method. Unlike other compact solution procedure in literature for this physical configuration, the present method is fully compact and fully higher-order accurate. The fluid flow, heat transfer and heat transport characteristics were illustrated by streamlines, isotherms and averaged Nusselt number. Comparisons with previously published work are performed and found to be in excellent agreement. A parametric study is conducted and a set of graphical results is presented and discussed to elucidate that significant heat transfer enhancement can be obtained due to the presence of nanoparticles and that this is accentuated by inclination of the enclosure at moderate and large Richardson numbers.

This paper deals with the solvability and the convergence of a class of unsymmetric Meshless Local Petrov-Galerkin (MLPG) method with radial basis function (RBF) kernels generated trial spaces. Local weak-form testings are done with step-functions. It is proved that subject to sufficiently many appropriate testings, solvability of the unsymmetric RBF-MLPG resultant systems can be guaranteed. Moreover, an error analysis shows that this numerical approximation converges at the same rate as found in RBF interpolation. Numerical results (in double precision) give good agreement with the provided theory.

Based on the Mindlin’s first-order shear deformation plate theory this paper focuses on the free vibration behavior of functionally graded nanocomposite plates reinforced by aligned and straight single-walled carbon nanotubes (SWCNTs). The material properties of simply supported functionally graded carbon nanotube-reinforced (FGCNTR) plates are assumed to be graded in the thickness direction. The effective material properties at a point are estimated by either the Eshelby-Mori-Tanaka approach or the extended rule of mixture. Two types of symmetric carbon nanotubes (CNTs) volume fraction profiles are presented in this paper. The equations of motion and related boundary conditions are derived using the Hamilton’s principle. A semi-analytical solution composed of generalized differential quadrature (GDQ) method, as an efficient and accurate numerical method, and series solution is adopted to solve the equations of motions. The primary contribution of the present work is to provide a comparative study of the natural frequencies obtained by extended rule of mixture and Eshelby-Mori-Tanaka method. The detailed parametric studies are carried out to study the influences various types of the CNTs volume fraction profiles, geometrical parameters and CNTs volume fraction on the free vibration characteristics of FGCNTR plates. The results reveal that the prediction methods of effective material properties have an insignificant influence of the variation of the frequency parameters with the plate aspect ratio and the CNTs volume fraction.

Poisson-Nernst-Planck equations are a coupled system of nonlinear partial differential equations consisting of the Nernst-Planck equation and the electrostatic Poisson equation with delta distribution sources, which describe the electrodiffusion of ions in a solvated biomolecular system. In this paper, some error bounds for a piecewise finite element approximation to this problem are derived. Several numerical examples including biomolecular problems are shown to support our analysis.