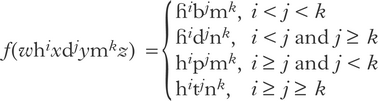1 Introduction
Non-cyclic rule-based models such as the word-level phonology of Chomsky & Halle (Reference Chomsky and Halle1968) are computationally regular (Johnson Reference Johnson1972, Kaplan & Kay Reference Kaplan and Kay1994); in other words, their computation does not require unbounded counting. Insofar as these models are empirically adequate, phonology also appears to be regular (see Heinz Reference Heinz, Hyman and Plank2018 for an overview). Optimality Theory (OT; Prince & Smolensky Reference Prince and Smolensky1993) is known to implement functions whose computations do involve counting (Eisner Reference Eisner1997, Frank & Satta Reference Frank and Satta1998, Karttunen Reference Karttunen, Karttunen and Oflazer1998), meaning it overgenerates. However, the total generative capacity of OT with familiar phonological constraints has not yet been characterised. This squib contributes to that characterisation by implementing a function in OT whose computation requires not only counting, but also maintaining multiple unbounded counts. In and of itself, this result is not novel: Lamont (Reference Lamont2021) constructs OT grammars that are at least as complex. However, whereas those constructions use markedness constraints whose loci are subsequences, this squib uses substring constraints. Subsequences are subsets of strings whose elements are not necessarily contiguous at any level of representation. Constraints over subsequences and substrings are the simplest kind of constraints (McNaughton & Papert Reference McNaughton and Papert1971, Rogers et al. Reference Rogers, Heinz, Bailey, Edlefsen, Visscher, Wellcome, Wibel, Ebert, Jäger and Michaelis2010, Heinz Reference Heinz, Hyman and Plank2018), and represent a large proportion of the markedness constraints familiar to phonologists. Together, these results indicate that Con is not the source of OT's generative capacity, and imply that, whenever constraints evaluate candidates by counting an unbounded number of violations, it is possible to construct very complex OT grammars. Further, because this squib uses familiar constraints like Agree, Max and Ident, it may be the case that a large proportion of OT grammars are more powerful than necessary as a model of phonology.
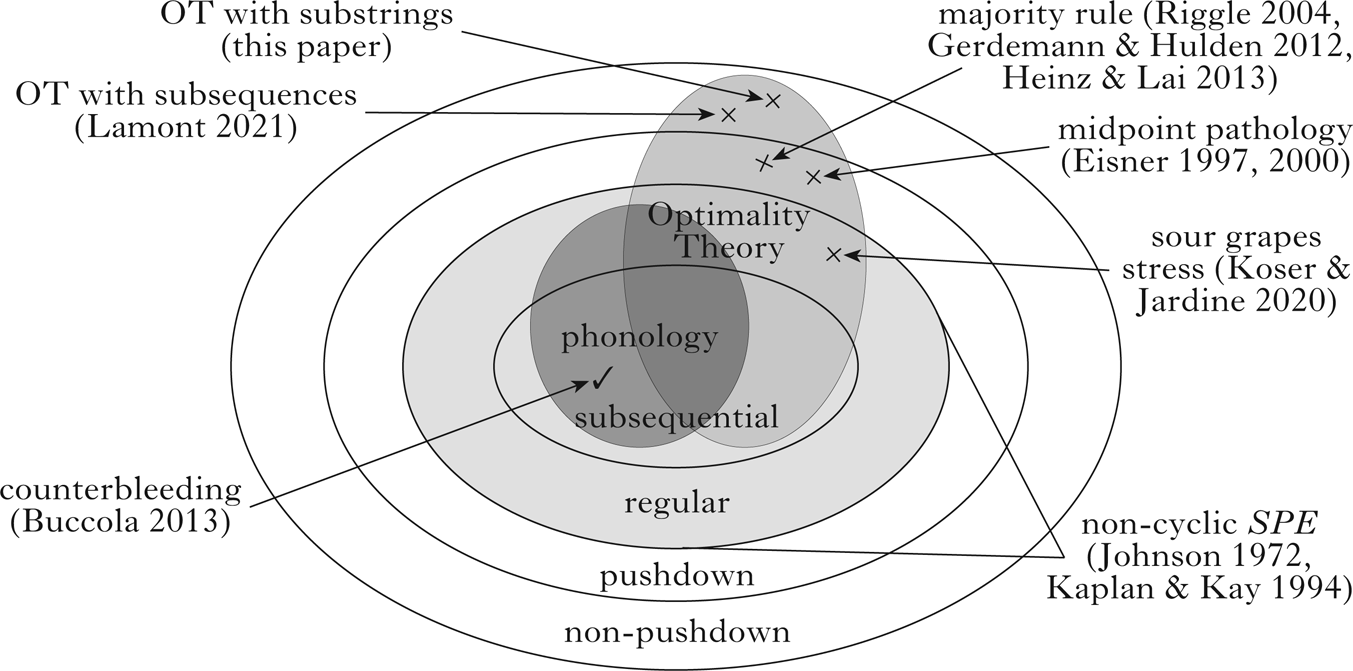
Figure 1 illustrates OT's expressivity on a partial hierarchy of functions. While it successfully models phonological patterns, it also implements non-regular functions, which, by hypothesis, should not be phonological. Note that this does not imply that OT can implement all regular functions. For example, Buccola (Reference Buccola2013) proves that certain OT grammars cannot implement counterbleeding-on-focus mappings.

Figure 1 A partial hierarchy of functions illustrating that attested phonological mappings are regular, and that Optimality Theory implements both non-regular and non-pushdown functions.
Regular functions divide inputs into finitely many equivalence classes. For example, ‘sour grapes stress’ assigns feet only to even-parity words (Koser & Jardine Reference Koser and Jardine2020), thus differentiating between inputs with an even or odd number of syllables. Non-regular functions cannot be characterised by a finite number of equivalence classes. For example, consider majority rule, an unattested pattern in which disharmonic inputs are mapped onto outputs that preserve the feature value associated with the greater number of input segments (Lombardi Reference Lombardi1999, Baković Reference Baković2000). Majority rule [place] assimilation maps /tttmm/ onto [tttnn] and /ttmmm/ onto [ppmmm]. Every input /timj/ defines its own equivalence class, and is mapped onto [tinj] when i > j, and onto [pimj] when i < j. To compute majority rule, it is necessary to compare the number of coronals to the number of labials in the input, which can be modelled by a finite-state machine with unbounded pushdown memory (see Meduna Reference Meduna2000: ch. 9 for an overview). As it reads input strings, such a machine (a pushdown automaton) can push a symbol onto the top of its memory or pop the top symbol from its memory. To model majority rule, a machine starts by pushing the first segment it reads to its memory. Then, if it reads a matching segment or if the memory is empty, it pushes that segment, or, if it reads a mismatched segment, it pops the top segment. At every step in the computation, the memory contains n segments of one type, meaning that the machine has seen n more of that segment type so far. At the end of the input, if the memory is empty, then there were an equal number of segment types; otherwise, whichever segment type is stored represents the majority.
Non-pushdown functions, such as the topic of this squib, involve comparing at least three arbitrarily large numbers simultaneously, and cannot be modelled by pushdown automata with only one stack (note that unrestricted pushdown automata with two stacks are equivalent to Turing machines). The intuition is that in order to compare two arbitrarily large numbers, pushdown automata must empty their memory. For example, after reading an input /timj/, the machine's memory will contain i−j coronals or j−i labials, which is sufficient to determine whether i or j is larger. However, pushdown automata cannot identify the majority [place] feature for inputs like /timjgk/: by comparing the coronals to the labials, the machine forgets how many coronals and labials there were, and has nothing to compare to the dorsals.
This squib implements a non-pushdown function in OT that simultaneously models majority rule [place] and [voice] assimilation. Like the example above, because this function must compare more than two unbounded counts, it is non-pushdown. §2 defines the function of interest and constructs an OT grammar that implements it, proving the main result of the squib. §3 discusses the implications of this result and concludes.
2 A non-pushdown function in Optimality Theory
This section proves the main result of the paper by constructing an OT grammar that implements a non-pushdown function. The function of interest is defined in (1) for all inputs /whixdjymkz/, where w, x, y, z ∈ {p, b, ɦ}﹡; the segment inventory is limited to the consonants {p, t, b, d, h, ɦ, m, n}. In part, the function implements both majority rule [place] and [voice] assimilation; it voices the string of obstruents when there are more voiced obstruents underlyingly (i < j) and devoices them otherwise (i ≥ j), and maps the string of supralaryngeals onto labials when there are more labials than coronals underlyingly (j < k) and onto coronals otherwise (j ≥ k). The range of this function is not a context-free language: i < j < k for all outputs of the form [ɦibjmk] (for a formal proof that this is not a context-free language, see Sipser Reference Sipser2013: 128). Note that the restriction to strings ɦ﹡b﹡m﹡ does not increase the complexity of this language. Context-free languages are closed under intersection with regular languages (Bar-Hillel et al. Reference Bar-Hillel, Perles and Shamir1961), so if the range of the function were context-free, then its intersection with ɦ﹡b﹡m﹡ would be too. Because the range of pushdown functions are context-free languages (Evey Reference Evey1963), it follows that (1) is not a pushdown function.
-
(1)

In addition to implementing majority rule [place] and [voice] assimilation, the grammar deletes underlying /p b ɦ/. Because [p b ɦ] can surface as the result of [place] or [voice] assimilation, this yields a monostratal chain shift, e.g. /t/→[p] and /p/→[ɛ], where [ɛ] represents the empty string. This is neither beyond the capacity of standard OT (see Baković Reference Baković2007, Łubowicz Reference Łubowicz, van Oostendorp, Ewen, Hume and Rice2011 for discussion) nor responsible for the complexity of the function. A variant without deletion can be shown to be non-pushdown, using the pumping lemma for pushdown relations (Gurari Reference Gurari1989: ch. 3). The purpose of the chain shift is to translate function complexity into language complexity, which is often more familiar.
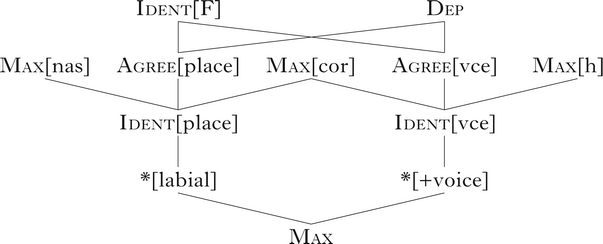
The Hasse diagram in (2) summarises the grammar's constraint ranking; constraints are defined in the text. The rest of this section presents the grammar. §2.1 illustrates the deletion of underlying /p b ɦ/, §2.2 presents majority rule [place] and [voice] assimilation and §2.3 demonstrates that i < j < k for all output strings [ɦibjmk].
-
(2)

2.1 Underlying /p b ɦ/ delete
Deletion of underlying /p b ɦ/ is motivated by the constraints *[labial] and *[+voice], which penalise labial supralaryngeals ([p b m]) and voiced obstruents ([b d ɦ]) respectively. Deletion violates Max, which requires segments in the input to have correspondents in the output. Specific Max constraints prevent other segments from deleting: Max[nas] and Max[cor] respectively require input nasals (/m n/) and input coronals (/t d n/) to have output correspondents. In isolation, Ident[place] and Ident[vce] respectively prevent underlying labials from surfacing as coronals and underlying voiced segments from devoicing. Ident[place] penalises pairs of correspondent supralaryngeals ({p, t, b, d, m, n}) with different specifications of [place]. Ident[vce] penalises pairs of correspondent obstruents ({p, t, b, d, h, ɦ}) with different specifications of [voice].
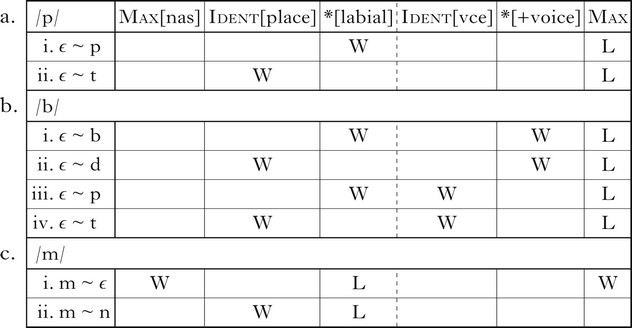
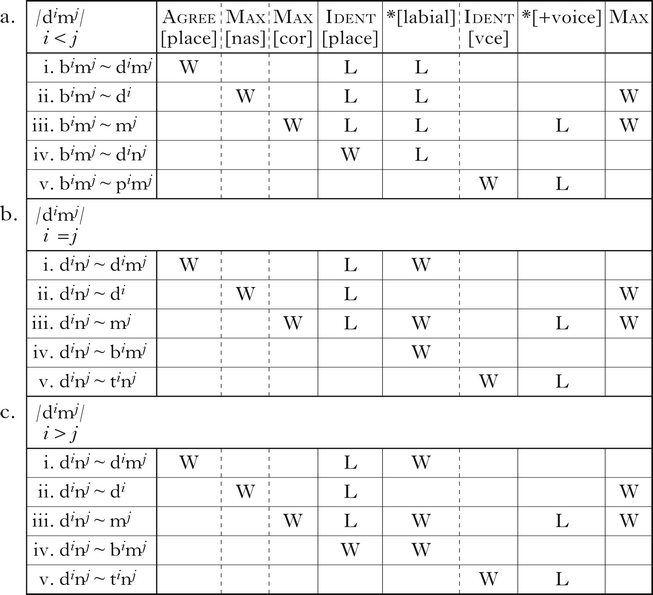
The tableaux in (3) illustrate the deletion of underlying /p, b/, but not /m/. For each input, a set of winner ~ loser pairs and their evaluation by the relevant constraints are shown. The faithful realisation of /p/ and /b/ violates *[labial], and is dispreferred to deletion (3a.i, b.i). Mapping /p/ onto [t] and /b/ onto [d] also satisfies *[labial], but fatally violates Ident[place] (3a.ii, b.ii). Deleting underlying /b/ is also preferred by *[+voice] (3b.i, ii). Devoicing would also satisfy *[+voice], but fatally violates Ident[vce] (3b.iii, iv). Underlying /m/ surfaces faithfully (3c), because deleting underlying nasals fatally violates Max[nas] (3c.i) and mapping /m/ onto [n] fatally violates Ident[place] (3c.ii).
-
(3)

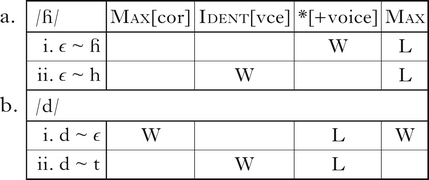
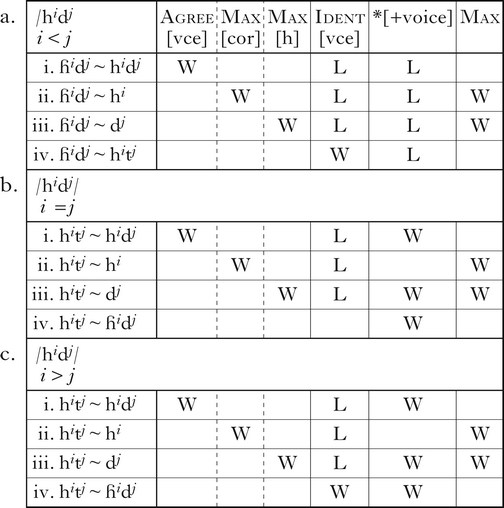
Along similar lines, *[+voice] motivates the deletion of underlying /ɦ/, but not /d/ (4). Devoicing either segment fatally violates Ident[vce] (4a.ii, b.ii), and Max[cor] prevents underlying /d/ from deleting (4b.i). Because *[+voice] does not penalise nasals, another option would be to map /d/ onto [n]. Though not shown in the tableau, this is ruled out by the cover constraint Ident[F], which penalises pairs of correspondent segments with different specifications of any feature other than [place] or [voice].
-
(4)

Because underlying /p b ɦ/ delete, no segments in the output correspond to /p b ɦ/ segments in the input. The set of possible input correspondents is tightened further by Ident[F] and Dep, which require segments in the output to have correspondents in the input. Ranking Dep above the grammar's markedness constraints means that epenthesis cannot be optimal. Thus, because no segments in the output are epenthetic, they must all correspond to underlying /t d h m n/. Ident[F] also dominates all markedness constraints, preventing any featural change except to [place] or [voice]. Together, these limitations on input–output correspondents mean that [p t b d] in the output must correspond to /t d/ in the input, [h ɦ] in the output must correspond to /h/ in the input and [m n] in the output must correspond to /m n/ in the input.
2.2 Majority rule controls [place] and [voice] assimilation
While *[labial] and *[+voice] motivate the deletion of underlying /p b ɦ/, they do not prevent [p b ɦ] from surfacing via [place] and [voice] assimilation (hence the chain shift). Assimilation is motivated by the constraints Agree[place] and Agree[vce], which respectively penalise adjacent supralaryngeals ([p t b d m n]) with different specifications of [place] and adjacent obstruents ([p t b d h ɦ]) with different specifications of [voice].
The tableaux in (5) illustrate [place] assimilation targeting underlying /dimj/ strings of various lengths. The faithful candidates violate Agree[place], and are dispreferred to candidates that map /di/ onto [bi] (5a.i) or /mj/ onto [nj] (5b.i, c.i). Deleting either underlying /mj/ strings (5a.ii, b.ii, c.ii) or /di/ strings (5a.iii, b.iii, c.iii) also satisfies Agree[place], but fatally violates Max[nas] or Max[cor]. Likewise, inserting a laryngeal ([diɦmj]; not shown), satisfies Agree[place], but is ruled out by Dep. Whether it is optimal to map /di/ onto [bi] or /mj/ onto [nj] is determined by the relative magnitudes of i and j. When there are fewer coronals than labials (i < j), /di/ is mapped onto [bi] (5a.iv), because Ident[place] prefers making as few changes as possible. When there are fewer labials than coronals (i > j), /mj/ is mapped onto [nj] (5c.iv). With equal numbers of labials and coronals (i = j), Ident[place] does not prefer either mapping, and the decision falls to *[labial], which prefers mapping /mj/ onto [nj] (5b.iv). As in previous tableaux, devoicing the underlying /di/ satisfies *[+voice], but fatally violates Ident[vce] (5a.v, b.v, c.v).
-
(5)

Along similar lines, Agree[vce] motivates majority rule assimilation within strings of obstruents ({p, t, b, d, h, ɦ}). The tableaux in (6) illustrate this with /hidj/ strings of various lengths. As above, Max[cor] prevents underlying /dj/ from deleting (6a.ii, b.ii, c.ii), and Max[h], which requires /h/ in the input to have a correspondent in the output, prevents underlying /hi/ from deleting (6a.iii, b.iii, c.iii). Dep prevents the insertion of a nasal ([hindj]; not shown). When there are fewer underlying voiceless laryngeals (i < j), they are voiced (6a), and when there are at least as many voiceless laryngeals as voiced coronals (i ≥ j), the coronals devoice (6b, c), with *[+voice] breaking any ties in favour of devoicing (6b.iv). Mapping /dj/ onto [nj] (not shown) would satisfy Agree[vce] and *[+voice], but is ruled out by Ident[F].
-
(6)

As argued in the previous section, surface [p b] must derive from underlying /t d/, and surface [ɦ] must derive from underlying /h/. The only mechanism that motivates these mappings is majority rule [place] or [voice] assimilation. Thus, for [p b ɦ] to surface, their input correspondents must have had the minority specification of [place] or [voice]. It follows that, for example, i < j for all strings [bimj] in the output, and k < l for all strings [ɦkdi] in the output. In isolation, these string-sets are context-free, but their intersection is not (Scheinberg Reference Scheinberg1960). In other words, string-sets produced by this grammar are not context-free languages.
2.3 Simultaneous majority rule is non-pushdown
To complete the argument, consider output strings of the form [ɦibjmk]. According to the discussion in the previous sections, these strings must derive from underlying /… hi … {t, d} j … {m, n} k …/, which may also contain arbitrarily many /p b ɦ/ segments. It must be true that i < j < k. Let h, t, d, m, n denote the number of /h t d m n/ in the input, respectively. Observe that h = i, t + d = j, and m + n = k. Majority rule [voice] assimilation produces voiced obstruents, and so the input must contain more voiced obstruents than voiceless: h + t < d. Majority rule [place] assimilation produced labial supralaryngeals, and so the input must have contained more labials than coronals: t + d + n < m. These inequalities combine to h ≤ h + t < d ≤ t + d ≤ t + d + n < m ≤ m + n, which implies h < t + d < m + n, or, equivalently, i < j < k. Therefore, because the range of the function implemented by this grammar is not a context-free language, the function is non-pushdown.
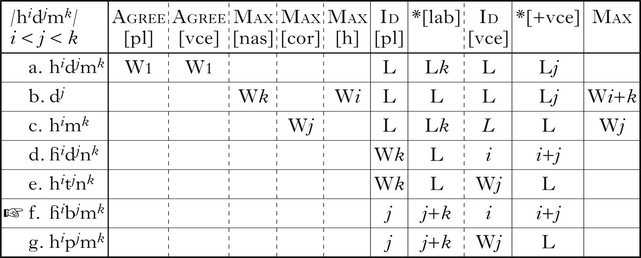
The tableau in (7) illustrates /hidjmk/ mapping onto [ɦibjmk], with i < j < k. The faithful candidate (7a) violates both Agree constraints, and is dispreferred to the candidate that maps /hi/ onto [ɦi] and /dj/ onto [bj] (7f). Deleting both /hi/ and /mk/ also satisfies the Agree constraints (7b), as does deleting /dj/ (7c), but fatally violates the input-specific Max constraints. Because there are more labial supralaryngeals than coronal underlyingly, Ident[place] prefers mapping /di/ onto [bj] or [pj] (7f, g) to mapping /mk/ onto [nk] (7d, e). Likewise, because there are more voiced obstruents than voiceless underlyingly, Ident[vce] prefers mapping /hi/ onto [ɦi] (7d, f) to mapping /di/ onto [tj] or [pj] (7e, g). Per (1), candidates (7d, e, g) are optima for other relative values of i, j, k: the supralaryngeals surface as coronals when j ≥ k (7d, e), and the obstruents surface as voiceless when i ≥ j (7e, g). Though not shown in (7), Ident[F] and Dep prevent other mappings from being optimal.
-
(7)

3 Discussion
The OT grammar constructed in this squib implements a function that deletes underlying /p b ɦ/ and subjects supralaryngeals ({p, t, b, d, m, n}) to majority rule [place] assimilation and obstruents ({p, t, b, d, h, ɦ}) to majority rule [voice] assimilation. This function was shown to be non-pushdown by demonstrating that its range is not a context-free language. Assuming that phonology is regular, OT significantly overgenerates, even with simple constraints. Further, it is possible to generalise this construction to model majority rule over arbitrarily many features, implying that OT is beyond the generative capacity of tree-adjoining grammars (Joshi Reference Joshi, Dowty, Karttunen and Zwicky1985). While this construction assumes a finite feature inventory, it may be possible to accommodate an unbounded feature set and thereby model functions whose ranges are even more complex (Radzinski Reference Radzinski1991, Michaelis & Kracht Reference Michaelis, Kracht and Retoré1997).
Computational analysis of OT has often focused on constraints on subsequences, because their loci of violation grow quadratically in the length of candidates (Eisner Reference Eisner1997, Reference Eisner2000, Bíró Reference Bíró2003, Heinz Reference Heinz2005, Lamont Reference Lamont2021), which in and of itself is not a regular relation. However, as this squib has demonstrated, quadratic growth is not necessary for OT to implement complex functions, as substrings grow linearly in the length of candidates. Notably, if the Ident constraints employed in the construction could not distinguish between arbitrarily large violation sets, the grammar would be much less expressive, mapping all inputs onto a set of least marked outputs similar to Chomsky's (Reference Chomsky2015: 350) [ba] problem. This reaffirms the result that unbounded counting is the source of OT's complexity (Eisner Reference Eisner1997, Frank & Satta Reference Frank and Satta1998, Karttunen Reference Karttunen, Karttunen and Oflazer1998): by freely combining constraints that count unboundedly, OT grammars can be very complex. Further, as Hao (Reference Hao2019) demonstrates, switching from parallel to serial evaluation does not address the problem; constraints on substrings also motivate non-regular mappings in Harmonic Serialism.
Studying the generative capacity of OT characterises it as a computational framework, while abstracting away from particular theories of Con. Comparison to the expressivity of attested phenomena is informative, because it provides a coarse view of under- and overgeneration. As discussed in the introduction, non-cyclic rule-based models are known to be regular, and are consistent with the hypothesis that phonology is regular. Because OT implements non-regular functions, it appears to overgenerate, from our current empirical perspective. This approach is distinct from evaluating other instances of overgeneration, such as the too-many-repairs problem (Wilson Reference Wilson2000, Blumenfeld Reference Blumenfeld2006, Steriade Reference Steriade, Hanson and Inkelas2009). In particular, the grammar in this squib was constructed specifically to implement a complex function, and not to propose that, for example, Max[h] is an empirically desirable or undesirable constraint. Banning particular constraints may accidentally rein in OT's expressivity, but such an approach fails to address the problem of unbounded violation counting, which is a core component of OT. It would therefore be a quixotic exercise to manipulate Con without solving this underlying issue. Results like this squib's contribute to our understanding of OT, and point to alternative approaches to optimisation, such as bounded evaluation (Frank & Satta Reference Frank and Satta1998) or directional evaluation (Eisner Reference Eisner2000, Reference Eisner2002), whose computational restrictiveness explains why majority rule and other complex mappings should be impossible.