Pilot simulation study using meat inspection data for syndromic surveillance: use of whole carcass condemnation of adult cattle to assess the performance of several algorithms for outbreak detection

Summary

The objective of this study was to assess the performance of several algorithms for outbreak detection based on weekly proportions of whole carcass condemnations. Data from one French slaughterhouse over the 2005–2009 period were used (177 098 slaughtered cattle, 0.97% of whole carcass condemnations). The method involved three steps: (i) preparation of an outbreak-free historical baseline over 5 years, (ii) simulation of over 100 years of baseline time series with injection of artificial outbreak signals with several shapes, durations and magnitudes, and (iii) assessment of the performance (sensitivity, specificity, outbreak detection precocity) of several algorithms to detect these artificial outbreak signals. The algorithms tested included the Shewart p chart, confidence interval of the negative binomial model, the exponentially weighted moving average (EWMA); and cumulative sum (CUSUM). The highest sensitivity was obtained using a negative binomial algorithm and the highest specificity with CUSUM or EWMA. EWMA sensitivity was too low to select this algorithm for efficient outbreak detection. CUSUM's performance was complementary to the negative binomial algorithm. The use of both algorithms on real data for a prospective investigation of the whole carcass condemnation rate as a syndromic surveillance indicator could be relevant. Shewart could also be a good option considering its high sensitivity and simplicity of implementation.

INTRODUCTION

Slaughterhouses are central processing points for cattle where each animal undergoes an ante-mortem and post-mortem inspection. During this inspection, veterinary inspectors aim to detect any lesions that could have an impact on meat consumption without necessarily performing a diagnosis of each case. Consequently, meat inspection data (condemned portions and reasons for condemnation) are generally non-diagnostic, except in cases of regulated diseases such as tuberculosis. These data cover a large population and are complementary to other sources such as mortality records or on-farm information, and present information that are not available through any other type of animal records. All these characteristics make meat inspection data a good candidate for syndromic surveillance [1]. Syndromic surveillance can be defined as the monitoring of non-specific health indicators including clinical signs, symptoms and proxy measures, to enable early identification of the impact (or absence of impact) of potential human or veterinary public health threats [2].

Meat inspection data availability was scarce at worldwide level until recently. In France, a pilot project called ‘Nergal-Abattoir’ was implemented from 2005 to 2010 to collect data in real time in ten cattle slaughterhouses. Based on these meat inspection data, several health indicators could be used for early detection of outbreaks (of known or emerging diseases) through syndromic surveillance [3]. Using such indicators could raise alarms that should be investigated to identify the cause (animal health hazards, public health hazards, slaughtering process issues). We started investigating whole carcass condemnation as an indicator because it is often linked to acute conditions. It therefore reduces the dilution bias due to the variable period of time between cattle infection and the detection of lesions at the slaughterhouse. Little information is available to enable the interpretation of an abnormal increase in the proportion of whole carcass condemnations retrospectively. So a simulation approach already used in previous studies [4, 5] was applied to investigate the potential of monitoring whole carcass condemnation rates for syndromic surveillance. This objective work was to assess the performance of several algorithms for outbreak detection based on weekly proportions of whole carcass condemnations in one French slaughterhouse.

MATERIALS AND METHODS

Materials

The Nergal-Abattoir project made it possible to collect data in real time during the slaughtering process. Data were collected using touch screens on the slaughter lines and transmitted through a constant data flow to the database of the French Ministry of Agriculture.

Of the ten slaughterhouses involved in the Nergal-Abattoir project, one in the Manche département (French administrative area) provided adequate representativeness of the slaughtered cattle of the département and was therefore selected for this pilot study. Veal calves (cattle aged <8 months) were excluded because the farming practices and commercial network for this animal category are very specific and because they were not well represented in the dataset [6].

Condemnation data from this slaughterhouse from the years 2005–2009 were used. For each animal included, the database contained the identification number, dates of birth and slaughter, département of last farm location, sex, breed and reasons for condemnation. This last information was not used because this study focused on a generic surveillance indicator. The age of cattle was classified according to European Regulations [7] and zootechnical considerations into three age groups: 8–24 months, 2–5 years, and >5 years. Cattle breeds were grouped according to production type as defined by the French national organization of agriculture products, into three categories ‘dairy’, ‘beef’ and ‘mixed’ cattle [8].

Methods

The method used comprised three steps. First was the preparation of an outbreak-free historical baseline, representing weekly condemnation proportions over 5 years. The second step was the use of these historical data to simulate over 100 years of baseline time series, and the injection of artificial outbreak signals with several shapes, durations and magnitudes. The last step was the assessment of the performance of several algorithms to detect these artificial outbreak signals.

Retrospective time-series analysis: definition of an outbreak-free historical baseline

A descriptive analysis of the weekly proportion of cattle with whole carcass condemnation was performed using summary statistics by week, month and year as well as moving average charts. Autocorrelation and partial autocorrelation were investigated.

To define an outbreak-free historical baseline, regression models were fit to the time series of the weekly number of cattle with whole carcass condemnation (227 weeks available from 6 June 2005 to 9 October 2009). Poisson and negative binomial models were investigated. For each model tested, an offset with the weekly number of slaughtered cattle was used.

The following covariates were investigated: age, sex, production type, seasonality through a sinusoidal trend (annual, bi-annual, quarterly, monthly) and all possible combinations of these seasonalities. Age and sex were taken into account as a combined age-sex variable because of the correlation between these two variables [6]. It was systematically included in each model tested because of its known impact on whole carcass condemnation [6]. Interactions between all variables were also investigated. For each model, fit was assessed using the analysis of residuals and Pearson goodness-of-fit test. Comparisons between models were performed using Akaike's Information Criteria (AIC); the model with the lowest AIC was selected.

Because no information was available regarding outbreaks during the period of data available for this study, it was not possible to remove aberrations based on biological reasons. To remove temporal aberrations, the procedure elaborated by Tsui et al. [9] and tested by Dórea et al. on veterinary laboratory data [10] was used. The procedure consisted in fitting the previously selected model on the entire dataset and replacing each data point above the one-sided 95% confidence interval (CI) (Fig. 1) by the value of this CI. This value was obtained using the 95th percentile of the Poisson or negative binomial distribution (depending on the nature of the model previously selected) with the mean defined as the value estimated by the model for each time point (week). The assumption was made that these time points above the one-sided 95% CI represented aberrations in the time series (indicative or not of outbreak signals) or excessive random noise. The new dataset could then be considered as an outbreak-free historical baseline (Fig. 1).

Fig. 1. Description of steps in the method for outbreak-free baseline construction and simulation of 40 outbreak scenarios.

Simulated data with outbreak signals

The model including all significant covariates previously selected was fitted to this outbreak-free historical dataset. It was then used to predict weekly values on the following 5048 weeks, using the method presented by Dórea et al. [4]: the predicted value for each week was used to define the mean of a Poisson or negative binomial distribution (depending on the model selected). A value was randomly sampled for each week using the distribution defined for that week. The dataset created was the simulated baseline (Fig. 1).

Artificial outbreak signals were introduced in the simulated baseline. An initial period of 208 weeks with no outbreaks was set, and a buffer period (fixed number of weeks between two outbreaks) of 12 weeks was defined using baseline values. Due to the lack of information regarding outbreak shapes based on the analysis of the impact of real outbreaks on condemnation data, we decided to use several outbreaks shapes previously proposed in the literature [5, 11].

Different combinations of outbreak shape (spike, flat, linear, exponential), magnitude (1–4) and duration (2, 4, 8 weeks) made it possible to create 40 scenarios (Fig. 1):

• • Four scenarios with introduction of outbreaks with a spike shape (magnitudes 1, 2, 3 and 4).

• • Twelve scenarios with introduction of outbreaks with respectively flat, linear and exponential shapes, combining the four outbreak magnitudes with the three durations.

To implement the four outbreak magnitudes, the weekly Poisson or negative binomial distributions, previously used to create the simulated baseline, were used to sample four values (number of cattle with whole carcass condemnation) for each week. For an outbreak of magnitude 1, one value was added to the baseline value for the dedicated week, for an outbreak of magnitude 2, two values were added to the baseline value, and so forth. This value was called the ‘intensified value’. To obtain the four shapes and three durations, a coefficient was applied to the intensified value. For spike and flat shapes, the intensified value was kept without modification. For linear and exponential shapes, the coefficients increased from 0 to 1 linearly and exponentially respectively during the outbreak duration to obtain the right shape. For example, for a linear outbreak with a duration of 4 weeks, the value of the first week was multiplied by 0.25, the second by 0.5, the third by 0.75 and the fourth by 1 to obtain a linear increasing shape. The same process was applied for the exponential shape, e.g. for 4 weeks: 0.46 for the first week, 0.59 for the second, 0.77 for the third and 1 for the last week.

Outbreak detection and performance assessment

Detection algorithms. Four algorithms were investigated for outbreak detection: the Shewart p chart, one-sided confidence interval of the previously selected model (Poisson or negative binomial model), exponentially weighted moving average (EWMA) and cumulative sum (CUSUM). These algorithms are commonly used for outbreak detection [12-14]. For each method, several detection parameters were evaluated (Table 1).

Table 1. Description of algorithms tested for outbreak detection

EWMA, Exponentially weighted moving average; CUSUM, cumulative sum; CI, confidence interval; k, number of standard deviations; λ, smoothing parameter of the EWMA; L, number of standard deviations; H, value of the upper control limit.

Shewart p chart is an attribute control chart, based on the binomial distribution that enables the detection of outbreaks through proportions [15]. For each week j, the mean proportion of whole carcass condemnation ${\bar p}$ and an upper control limit [UCL( ${\bar p}$ )] were computed as follows:

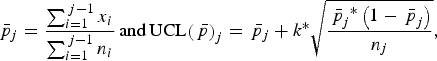$${{\bar p}_j} = \displaystyle{{\mathop \sum \nolimits_{i = 1}^{\,j - 1} {x_i}} \over {\mathop \sum \nolimits_{i = 1}^{\,j - 1} {n_i}}}\,{\rm and}\,{\rm UCL}{\left( {\,{\bar p}} \right)_j} = {\,{\bar p}_j} + k^{\ast}\sqrt {\displaystyle{{{{\,{\bar p}}_j}^{\ast}\left( {1 - {{\,{\bar p}}_j}} \right)} \over {{n_j}}}},$$

where x_i is the number of cattle with whole carcass condemnation in week i; n_i and n_j are the number of cattle slaughtered during weeks i and j, respectively; and k is a constant that determines how sensitive the control chart will be.

An alarm was raised for week j if the observed proportion of whole carcass condemnation was higher than UCL( ${\bar p}_j$ ).

Poisson or negative binomial models were also used for outbreak detection. The number of cattle with whole carcass condemnation for week j was predicted by the model selected to build the outbreak-free historical baseline on data of the j – 1 previous weeks. A baseline of 208 weeks was used, meaning that prediction only started at week 209. The one-sided CI defined the UCL for week j [UCL(M) _j ]. If the observed value for week j was higher than the UCL(M) _j , an alarm was raised. The observed value for week j was replaced by UCL(M) _j for the next step (i.e. fitting the model on the j previous weeks and predicting the number of whole condemnations for week j + 1).

EWMA was applied on residuals of the model previously selected. The EWMA statistic Z and the upper control limit UCL(Z) for each week j were computed as [16]:

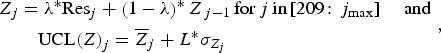$$\eqalign{{Z_j} &= \lambda^{\ast}{\rm Re}{{\rm s}_j} + \left( {1 - \lambda} \right)^{\ast}{Z_{\,j - 1}}\,{\rm for}\,j\,{\rm in}{\rm} \left[ {209\!:{\,j_{{\rm max}}}} \right]\; \; \; \; {\rm and}\,\cr&\quad{\rm UCL}{\left( Z \right)_j} = {{\overline Z}_j} + L^{\ast}{\sigma _{{Z_j}}}},$$

where λ is the smoothing parameter, Res _j is the residual for week j, L is the magnitude above the expected value, ${\overline Z}_j$ is the mean value of Z _j from week₁ to week _j−1,

$${\sigma _{{Z_j}}}^2 = {\rm var}\left( {{\rm Re}{{\rm s}_{\,j \in \left[ {1;\ j - 1} \right]}}} \right)^{\ast}\left( {\displaystyle{\lambda \over {2 - \lambda}}} \right)^{\!\ast}\left[ {1 - {{\left( {1 - \lambda} \right)}^{2j}}} \right].$$

The first value Z ₀ was defined as the mean of residuals from week₁ to week₂₀₈ (baseline).

An alarm was raised for week j if Z _j was higher than UCL(Z) _j .

CUSUM was performed on residuals of the model previously selected. CUSUM for each week j was calculated as follows [16]:

$${\rm CUSUM}_{j} = \max \left\{ 0,\left( \hbox{res}_{j} - {\overline res}_{\lt {j}} \right) + \hbox{CUSUM}_{{j} - 1} \right\}$$

If CUSUM _j was above H (an a priori fixed upper control limit), an alarm was raised and the CUSUM value was reset to zero.

Performance indicators

Three performance indicators were calculated for each outbreak detection algorithm, i.e. sensitivity, specificity and outbreak detection precocity.

Sensitivity was defined as the number of real outbreaks detected (injected outbreak signal for which an alarm was raised) divided by the total number of outbreak signals injected in the dataset. An outbreak was considered as detected if the outbreak was detected for at least 1 week.

Specificity was defined as the proportion of weeks for which no alarm was raised in weeks without an injected outbreak (i.e. weeks between the injected outbreaks).

Outbreak detection precocity was defined as the mean week of detection for a given simulated outbreak signal shape, when this outbreak signal lasts more than 1 week. This indicator is therefore not relevant for the spike shape, simulated to last only 1 week.

Performance indicators were computed for each outbreak detection algorithm applied to each of the 40 scenarios and for each age-sex category. For each algorithm and parameter evaluated, the median, minimum and maximum values of each performance indicator were calculated for the 16 values for the spike shape (four age-sex categories, four scenarios) and 48 values for the other shapes (four age-sex categories, 12 scenarios). These ‘summary statistics’ were also computed separately for each age-sex category.

For each algorithm, the selection of what could be considered as the best parameter of those investigated was made through examination of the four combinations of median sensitivity and specificity (one for each shape). We set a minimum median sensitivity of 0.95; if this condition was fulfilled, we chose the parameter that gave the best median sensitivity while maintaining an acceptable median specificity of at least 0.97. If the sensitivity and specificity values were similar, then detection precocity was compared. For each algorithm, we then had one best parameter for each shape. If it was not the same for each shape, we chose the one that had the highest occurrence out of the four. Only results with these selected parameters are presented and discussed.

All methods were implemented using the R environment [17].

RESULTS

Studied population

The 177 098 cattle slaughtered in the slaughterhouse of the Manche département from 6 June 2005 to 9 October 2009 (227 weeks) were included in the study. Females aged 8–24 months (n = 465) and males aged >5 years (n = 423) were excluded (too few animals). During the study period, the proportion of cattle within the studied population ranged from 16.2% to 33.7% according to age-sex categories (Table 2). The proportions of cattle with whole carcass condemnation were similar in the female age groups (1.34% and 1.38% for age groups 2-5 and >5 years, respectively), and lower in males (0.49% and 0.42% for age groups 8-24 months and 2-5 years, respectively) (Table 2).

Table 2. Number of cattle slaughtered and proportion of cattle with whole carcass condemnation in the studied population according to age-sex and production type

Retrospective time-series analysis and simulated data

The descriptive analysis highlighted that the weekly proportions of cattle with whole carcass condemnation presented low autocorrelations and a week number effect.

A model selection process was conducted to select the following negative binomial model:

(1) $$\eqalign{&Y \sim {\rm age} - {\rm sex} ^{\ast} \left(\cos\left(2^{\ast} pi^{\ast}t/52) \right) + \sin\left(2^{\ast} pi^{\ast}t/52 \right)\right) \cr & \quad\quad + {\rm offset}\left(\log (N) \right),} $$

where Y is the weekly number of cattle with whole carcass condemnation, age-sex is the combined age and sex categorical variable, t is the week number (from 1 to 227), and N is the weekly number of cattle slaughtered.

The production type was not kept in the final model. The age-sex variable led to the construction of four time series, one for each category.

The outlier removal procedure enabled the removal of 1–5 time points (out of the 227) depending on the age-sex category considered (Fig. 1). We obtained 227 weeks of data that could be considered as the outbreak-free historical baseline for each age-sex category. After the simulation of 5675 weeks of data for each age-sex category, outbreak signals were injected based on the 40 possible scenarios (Fig. 1). Depending on the scenario, the number of outbreaks injected ranged from 274 to 421.

Outbreak detection algorithm performance

Parameter selection for each algorithm

Based on the summary statistics values of the performance indicators, the best parameter values were:

• • A value of 1.3 for K for the Shewart chart.

• • The one-sided 80% confidence interval (CI) for the negative binomial model.

• • An UCL of 2 for CUSUM.

• • A value of 1.3 for L and of 0.4 for λ for EWMA.

Performance indicators

For each algorithm, the sensitivity and specificity were higher for detection of outbreaks with a flat shape than for those with a spike shape, with the linear and exponential shapes falling between the two (Table 3). Detection precocity was higher for the detection of outbreaks with an exponential shape than for those with a linear shape. For each algorithm, the sensitivity increased with the outbreak magnitude, especially from magnitudes 1 to 3. Specificity increased with the outbreak magnitude for the Shewart and CUSUM algorithms but was not impacted by magnitude for EWMA and the negative binomial algorithm (Table 4). This effect of the magnitude on sensitivity and specificity decreased with outbreak duration. For each algorithm, the sensitivity and specificity increased with outbreak duration except for EWMA, for which sensitivity decreased between the durations of 2 and 4 weeks (Table 5).

Table 3. Summary statistical values of performance indicators for all age-sex categories. For each indicator the median (minimum-maximum) values for each age-sex category, each outbreak duration and magnitude are presented by outbreak shape and outbreak detection algorithm

CUSUM, Cumulative sum; EWMA, exponentially weighted moving average.

Parameters for each algorithm were: Shewart, K = 1·3; CUSUM, H = 2; EWMA, lambda = 0·4 and L = 1·3; negative binomial, CI 80%.

Table 4. Summary statistical values of performance indicators for all age-sex categories. For each indicator the median (minimum-maximum) values for each age-sex category and outbreak duration are presented by outbreak shape and outbreak detection algorithm

Se, Sensitivity; Sp, specificity; CUSUM, cumulative sum; EWMA, exponentially weighted moving average.

Parameters for each algorithm were: Shewart, K = 1·3; CUSUM, H = 2; EWMA, lambda = 0·4 and L = 1·3; negative binomial, CI 80%.

Table 5. Summary statistical values of performance indicators for all age-sex categories. For each indicator the median (minimum-maximum) values for each age-sex category and outbreak magnitude are presented by outbreak shape and outbreak detection algorithm

Se, Sensitivity; Sp, specificity; CUSUM, cumulative sum; EWMA, exponentially weighted moving average.

Parameters for each algorithm were: Shewart, K = 1·3; CUSUM, H = 2; EWMA, lambda = 0·4 and L = 1·3; negative binomial, CI 80%.

For the CUSUM and EWMA algorithms, specificity was similar for each age-sex category. For the Shewart control chart, specificity was lower for males aged 2–5 years than for all other age-sex categories. For the negative binomial algorithm, males aged 8–24 months and 2–5 years had lower specificities than females aged 2–5 years and >5 years (Supplementary Tables S1–S4). For each algorithm, the sensitivity decreased according to age-sex categories in the following order: females aged >5 years; females aged 2–5 years; males aged 8–24 months; males aged 2–5 years (Supplementary Tables S1–S4).

For each outbreak shape, sensitivity was higher for the negative binomial algorithm than for the EWMA algorithm, with the CUSUM and Shewart chart falling between the two. Specificity was higher for EWMA and CUSUM than for the negative binomial algorithm with the Shewart chart falling between the two (Table 3).

DISCUSSION

The objective of this study was to assess the performance of several outbreak detection algorithms applied to the weekly proportion of whole carcass condemnations through a simulation strategy. More than 4 years of historical data were used to simulate more than 100 years of data and then evaluate the performance of the Shewart p control chart, EWMA, CUSUM and negative binomial algorithms.

Algorithm performance

The number of weeks of simulated data (n = 5675 weeks) was chosen in order to be able to include enough outbreaks signals, at least 200 as recommended by Dórea et al., to obtain relevant performance indicator estimations [4].

The sensitivity definition was based on an outbreak scale whereas the specificity definition was based on a weekly scale. This was necessary to enable comparisons between outbreaks of different durations.

The simulated data into which outbreak signals were injected were meant to represent the raw, unprocessed data that a fully operational syndromic surveillance system would have to analyse daily. These data will have some expected noise, which the simulation process aimed to reproduce (that is, a cut-off value for removal of outbreaks was not applied). However, the aberration detection algorithms were trained with data that were pre-processed in order to remove excessive noise (using a cut-off value of 95% for outlier removal). This removed not only possible outbreak signals in historical data, but also normal variation and noise. This causes the aberration detection algorithms to have increased sensitivity, which is a desired feature of the system, at a cost of decreased specificity.

For each outbreak detection algorithm, several parameters were investigated. The best parameters were those that induced the best sensitivity while striving at the same time to maintain an acceptable specificity. A specificity of at least 0.97, meaning that less than 3% of false alarms are generated, is commonly used in biosurveillance [18]. In this study we stressed sensitivity, setting a minimum level of 0.95 before considering specificity, because we thought that in the context of meat inspection higher sensitivity was worth a higher number of false alarms. Hence the negative binomial algorithm had a median specificity of only 0.94 for linear and exponential shapes. This was also the case for the spike shape for which all the algorithms investigated gave a median specificity of between 0.9 and 0.96. A specificity of 0.94 means a 6% false alarm rate, corresponding to three false alarms per year in the absence of aberrations. Even if the number of false alarms must be low in order to maintain trust in the system and an appropriate communication strategy between all surveillance stakeholders, this number seems reasonable and compatible with appropriate investigations at the département level.

The same tendency was observed for all the algorithms with regard to outbreak shape: sensitivity and specificity were higher for detection of outbreaks with a flat shape than for those with a spike shape, with the linear and exponential shapes falling between the two. This is surprising because each algorithm is commonly known to have dedicated performances: Shewart charts for detection of single spikes, CUSUM for detection of shifts in the process mean and EWMA for detection of gradual increases in the mean. Their performance was found to be similar regarding outbreak shape when applied to the weekly proportion of whole carcass condemnations. For the spike shape, none of the algorithms investigated were able to obtain high sensitivity (median sensitivity between 0.56 and 0.89) or high specificity (median specificity between 0.90 and 0.96). The best sensitivity/specificity pair was obtained for the negative binomial algorithm (median sensitivity = 0.89, median specificity = 0.90) but no algorithm provided satisfactory detection of this type of outbreak. However, this lack of detection compared to the other outbreak shapes could be an artefact due to the short duration of these outbreaks compared to other shapes. It was also logical that the highest sensitivity values were obtained for the flat shape, and not for the linear or exponential shapes, because these latter had the highest number of days with high proportions for each scenario.

The difference observed in terms of detection performances between females and males could be linked to the fact that the proportion of cattle with whole carcass condemnation was higher for females than for males in our dataset. This had a direct effect on sensitivity and specificity.

This study showed that the highest sensitivity was obtained using the negative binomial algorithm and the highest specificity using CUSUM or EWMA. EWMA sensitivity was too low to select this algorithm for efficient outbreak detection. CUSUM showed performance that was complementary to the negative binomial algorithm. The use of both algorithms on real data for a prospective investigation of the whole carcass condemnation rate as a syndromic surveillance indicator could be relevant. The Shewart control chart could also be a good option considering its high sensitivity and simplicity of implementation.

Combining several algorithms could be a way of improving syndromic surveillance system performance. For instance, to obtain maximum sensitivity, an investigation could be performed if at least one algorithm generates an alert. To obtain maximum specificity, an investigation could be performed only if an alert is generated by all algorithms. A balance between sensitivity and specificity should be found in order to define the threshold of the number of alerts above which investigations must be conducted. This will depend on the objective of the system and the financial resources allocated to investigations.

Factors to take into account when using meat inspection data for syndromic surveillance

Due to the complexity of the culling decision process, there is a necessity to evaluate the representativeness of meat inspection data available before instigating syndromic surveillance. The result is a restriction of the dataset and possibly the conclusion that not enough data are available. In this study we had to discard veal calves as the dataset was too small. A similar study should therefore be conducted on this animal category when data become available.

Considering the previous studies, the number of cattle slaughtered should be taken into account as well as age and sex. Statistical analyses are then more complex than just monitoring a raw number of cattle with whole carcass condemnation. Control charts must be applied under the assumption of independent and identically distributed observations [12]. In this study we have accounted for explainable patterns, including the denominator data (total number of slaughtered animals) using regression models, and then applied outbreak signal detection with well-known algorithms using model residuals [19]. This made it possible to process proportions and not just numbers, which could be a better indicator for surveillance.

Perspectives

This study, based on a simulation approach, showed that the proportion of whole carcass condemnations could be a useful indicator for syndromic surveillance since it enables good detection performance especially for flat, linear and exponential outbreak shapes. The recent implementation of a national meat inspection database in France will make it possible to investigate this indicator on real data in a prospective way. The Shewart control chart could be used as a first step and then CUSUM and the negative binomial algorithm when historical data becomes available. Other indicators based on meat inspection data could be further investigated using the same approach.