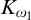 $ K_{\omega _1}$
AND
$ K_{\omega _1}$
AND
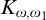 $K_{\omega ,\omega _1}$
$K_{\omega ,\omega _1}$