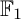 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
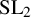 $\operatorname {SL}_2$-web bases
$\operatorname {SL}_2$-web bases
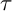 $\tau $
-)TILTING INFINITE ALGEBRAS
$\tau $
-)TILTING INFINITE ALGEBRAS