We study higher uniformity properties of the Möbius function  $\mu $, the von Mangoldt function
$\mu $, the von Mangoldt function 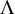 $\Lambda $, and the divisor functions
$\Lambda $, and the divisor functions 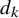 $d_k$ on short intervals
$d_k$ on short intervals 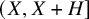 $(X,X+H]$ with
$(X,X+H]$ with 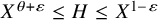 $X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$ for a fixed constant
$X^{\theta +\varepsilon } \leq H \leq X^{1-\varepsilon }$ for a fixed constant 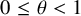 $0 \leq \theta < 1$ and any
$0 \leq \theta < 1$ and any 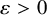 $\varepsilon>0$.
$\varepsilon>0$.
More precisely, letting 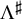 $\Lambda ^\sharp $ and
$\Lambda ^\sharp $ and 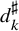 $d_k^\sharp $ be suitable approximants of
$d_k^\sharp $ be suitable approximants of 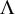 $\Lambda $ and
$\Lambda $ and 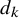 $d_k$ and
$d_k$ and 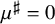 $\mu ^\sharp = 0$, we show for instance that, for any nilsequence
$\mu ^\sharp = 0$, we show for instance that, for any nilsequence 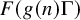 $F(g(n)\Gamma )$, we have
$F(g(n)\Gamma )$, we have 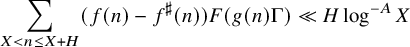 $$\begin{align*}\sum_{X < n \leq X+H} (f(n)-f^\sharp(n)) F(g(n) \Gamma) \ll H \log^{-A} X \end{align*}$$
$$\begin{align*}\sum_{X < n \leq X+H} (f(n)-f^\sharp(n)) F(g(n) \Gamma) \ll H \log^{-A} X \end{align*}$$
when 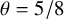 $\theta = 5/8$ and
$\theta = 5/8$ and 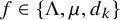 $f \in \{\Lambda , \mu , d_k\}$ or
$f \in \{\Lambda , \mu , d_k\}$ or 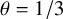 $\theta = 1/3$ and
$\theta = 1/3$ and 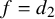 $f = d_2$.
$f = d_2$.
As a consequence, we show that the short interval Gowers norms 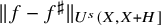 $\|f-f^\sharp \|_{U^s(X,X+H]}$ are also asymptotically small for any fixed s for these choices of
$\|f-f^\sharp \|_{U^s(X,X+H]}$ are also asymptotically small for any fixed s for these choices of 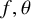 $f,\theta $. As applications, we prove an asymptotic formula for the number of solutions to linear equations in primes in short intervals and show that multiple ergodic averages along primes in short intervals converge in
$f,\theta $. As applications, we prove an asymptotic formula for the number of solutions to linear equations in primes in short intervals and show that multiple ergodic averages along primes in short intervals converge in 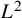 $L^2$.
$L^2$.
Our innovations include the use of multiparameter nilsequence equidistribution theorems to control type 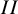 $II$ sums and an elementary decomposition of the neighborhood of a hyperbola into arithmetic progressions to control type
$II$ sums and an elementary decomposition of the neighborhood of a hyperbola into arithmetic progressions to control type 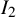 $I_2$ sums.
$I_2$ sums.
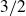 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 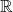 $\mathbb R$
$\mathbb R$
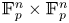 $\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
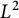 $L^2$ autoconvolution inequality
$L^2$ autoconvolution inequality