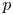 $p$-adic families and
$p$-adic families and 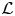 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
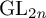 $\mathrm {GL}_{2n}$
OF UNITARY TYPE
$\mathrm {GL}_{2n}$
OF UNITARY TYPE
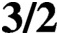 $\textbf{3/2}$
ETA-PRODUCTS
$\textbf{3/2}$
ETA-PRODUCTS
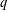 $q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
$q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE