Let  $p$ be a prime number ≥ 5 and
$p$ be a prime number ≥ 5 and  $a,\,b,\,c$ be non zero natural numbers. Using the works of K. Ribet and A. Wiles on the modular representations, we get new results about the description of the primitive solutions of the diophantine equation
$a,\,b,\,c$ be non zero natural numbers. Using the works of K. Ribet and A. Wiles on the modular representations, we get new results about the description of the primitive solutions of the diophantine equation  $a{{x}^{p}}\,+\,b{{y}^{p}}\,=\,c{{z}^{2}}$, in case the product of the prime divisors of
$a{{x}^{p}}\,+\,b{{y}^{p}}\,=\,c{{z}^{2}}$, in case the product of the prime divisors of 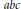 $abc$ divides
$abc$ divides  $2\ell $, with
$2\ell $, with  $\ell $ an odd prime number. For instance, under some conditions on
$\ell $ an odd prime number. For instance, under some conditions on  $a,\,b,\,c$, we provide a constant
$a,\,b,\,c$, we provide a constant  $f(a,\,b,\,c)$ such that there are no such solutions if
$f(a,\,b,\,c)$ such that there are no such solutions if  $p\,>\,f(a,\,b,\,c)$. In application, we obtain information concerning the
$p\,>\,f(a,\,b,\,c)$. In application, we obtain information concerning the  $\mathbb{Q}$-rational points of hyperelliptic curves given by the equation
$\mathbb{Q}$-rational points of hyperelliptic curves given by the equation  ${{y}^{2}}\,=\,{{x}^{p}}\,+\,d$ with
${{y}^{2}}\,=\,{{x}^{p}}\,+\,d$ with  $d\,\in \,\mathbb{Z}$.
$d\,\in \,\mathbb{Z}$.
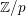 $\mathbb{Z}/p$ metabelian birational
$\mathbb{Z}/p$ metabelian birational 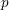 $p$-adic section conjecture for varieties
$p$-adic section conjecture for varieties
 $a{{x}^{p}}\,+\,b{{y}^{p}}\,=\,c{{z}^{2}}$
$a{{x}^{p}}\,+\,b{{y}^{p}}\,=\,c{{z}^{2}}$