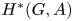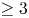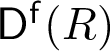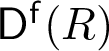14 results
Equivalences of stable categories of Gorenstein local rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 338-348
- Print publication:
- March 2025
-
- Article
- Export citation
Derived functors and Hilbert polynomials over regular local rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1137-1147
-
- Article
-
- You have access
- HTML
- Export citation
Duality pairs, phantom maps, and definability in triangulated categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Annihilators and decompositions of singularity categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 23 April 2024, pp. 699-713
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TILTING COMPLEXES AND CODIMENSION FUNCTIONS OVER COMMUTATIVE NOETHERIAN RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 618-693
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
The Balmer spectrum of certain Deligne–Mumford stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1314-1346
- Print publication:
- June 2023
-
- Article
- Export citation
ANNIHILATORS AND DIMENSIONS OF THE SINGULARITY CATEGORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 533-548
- Print publication:
- June 2023
-
- Article
- Export citation
New examples of non-Fourier–Mukai functors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 12 August 2022, pp. 1254-1267
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRUCTING NONPROXY SMALL TEST MODULES FOR THE COMPLETE INTERSECTION PROPERTY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 21 June 2021, pp. 412-429
- Print publication:
- June 2022
-
- Article
- Export citation
DEGENERATING 0 IN TRIANGULATED CATEGORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 08 June 2020, pp. 158-167
- Print publication:
- December 2021
-
- Article
- Export citation
Perfect complexes on algebraic stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 2318-2367
- Print publication:
- November 2017
-
- Article
- Export citation
REFLEXIVITY AND CONNECTEDNESS
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 231-240
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
A note on thick subcategories of stable derived categories
-
- Journal:
- Nagoya Mathematical Journal / Volume 212 / December 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 87-96
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Hopfological algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 07 October 2013, pp. 1-45
- Print publication:
- January 2014
-
- Article
- Export citation