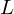5 results
Computing
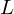 $L$-series of geometrically hyperelliptic curves of genus three
$L$-series of geometrically hyperelliptic curves of genus three
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 220-234
-
- Article
-
- You have access
- Export citation
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
ON A CONJECTURE OF IGUSA
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 399-425
- Print publication:
- July 2013
-
- Article
- Export citation
On the parity of ranks of Selmer groups IV. With an appendix by Jean-Pierre Wintenberger
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 03 December 2009, pp. 1351-1359
- Print publication:
- November 2009
-
- Article
-
- You have access
- Export citation
The Weil-étale topology on schemes over finite fields
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 21 April 2005, pp. 689-702
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation