Refine search
Actions for selected content:
6 results
 $K$ -theory of Furstenberg Transformation Group
$K$ -theory of Furstenberg Transformation Group  ${{\text{C}}^{\text{*}}}$ -algebras
${{\text{C}}^{\text{*}}}$ -algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 6 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1287-1319
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC BEHAVIOR OF EIGENVALUES OF RECIPROCAL POWER LCM MATRICES
-
- Journal:
- Glasgow Mathematical Journal / Volume 50 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 163-174
- Print publication:
- January 2008
-
- Article
-
- You have access
- Export citation
CLUSTER ALGEBRAS OF FINITE TYPE AND POSITIVE SYMMETRIZABLE MATRICES
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 16 June 2006, pp. 545-564
- Print publication:
- June 2006
-
- Article
- Export citation
ASYMPTOTIC BEHAVIOR OF EIGENVALUES OF GREATEST COMMON DIVISOR MATRICES
-
- Journal:
- Glasgow Mathematical Journal / Volume 46 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 11 October 2004, pp. 551-569
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation
The Equation Xk + Yk = Zk In Commuting Rational Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 4 / 01 December 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 406-409
- Print publication:
- 01 December 1983
-
- Article
-
- You have access
- Export citation
On the structure and existence of some amicable orthogonal designs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 1 / February 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 118-128
- Print publication:
- February 1978
-
- Article
-
- You have access
- Export citation










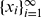 be an arbitrary strictly increasing infinite sequence of positive integers. For an integer
be an arbitrary strictly increasing infinite sequence of positive integers. For an integer  . Let
. Let 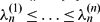 be the eigenvalues of the reciprocal power LCM matrix
be the eigenvalues of the reciprocal power LCM matrix 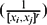 having the reciprocal power
having the reciprocal power 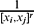 of the least common multiple of
of the least common multiple of 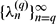 converges and
converges and 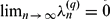 . We show that the sequence
. We show that the sequence 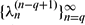 converges if
converges if 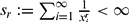 and
and 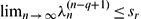 . We show also that if
. We show also that if 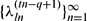 converges and
converges and 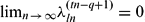 , where
, where 