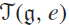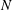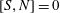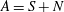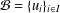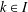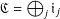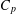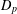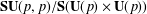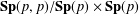10 results
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND  $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 July 2024, pp. 157-201
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
Centers and Azumaya loci for finite W-algebras in positive characteristic
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 35-66
- Print publication:
- July 2022
-
- Article
- Export citation
CLOSED IDEALS AND LIE IDEALS OF MINIMAL TENSOR PRODUCT OF CERTAIN C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 03 July 2020, pp. 414-425
- Print publication:
- May 2021
-
- Article
- Export citation
ON REPRESENTATIONS OF SYMMETRIC LEIBNIZ ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 23 May 2019, pp. S99-S107
- Print publication:
- December 2020
-
- Article
- Export citation
Jordan–Chevalley Decomposition in Lie Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 28 February 2019, pp. 349-354
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
(ANTI)COMMUTATIVE ALGEBRAS WITH A MULTIPLICATIVE BASIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 15 December 2014, pp. 211-218
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
CONVOLUTION OF ORBITAL MEASURES ON SYMMETRIC SPACES OF TYPE
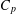 $C_{p}$ AND
$C_{p}$ AND 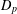 $D_{p}$
$D_{p}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 232-256
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
The Kostrikin Radical and the Invariance of the Core of Reduced Extended Affine Lie Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 2 / 01 June 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 298-309
- Print publication:
- 01 June 2008
-
- Article
-
- You have access
- Export citation
The General Structure of G-Graded Contractions of Lie Algebras I. The Classification
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 6 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1291-1340
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation
Some Factorizations in Universal Enveloping Algebras of Three Dimensional Lie Algebras and Generalizations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 4 / 01 December 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-536
- Print publication:
- 01 December 2002
-
- Article
-
- You have access
- Export citation