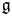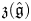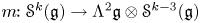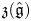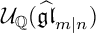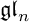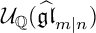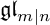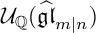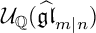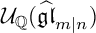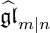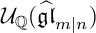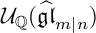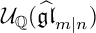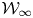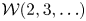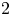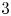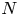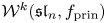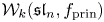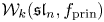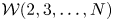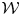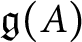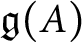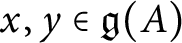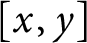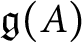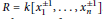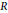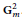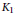38 results
Singularities of nilpotent Slodowy slices and collapsing levels of W-algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 November 2024, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 29 August 2023, pp. 2191-2259
- Print publication:
- October 2023
-
- Article
- Export citation
Cohomology in singular blocks of parabolic category \mathcal{O}
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 555-568
- Print publication:
- September 2023
-
- Article
- Export citation
Symmetrisation and the Feigin–Frenkel centre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 19 May 2022, pp. 585-622
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Defining relations of quantum symmetric pair coideal subalgebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 05 October 2021, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A REALIZATION OF THE ENVELOPING SUPERALGEBRA {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 516-551
- Print publication:
- September 2022
-
- Article
- Export citation
Beilinson–Drinfeld Schubert varieties and global Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 25 May 2021, e42
-
- Article
-
- You have access
- Open access
- Export citation
Universal two-parameter 𝒲∞-algebra and vertex algebras of type 𝒲(2, 3, …, N)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 10 February 2021, pp. 12-82
- Print publication:
- January 2021
-
- Article
- Export citation
On the structure of Kac–Moody algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 1124-1152
- Print publication:
- August 2021
-
- Article
- Export citation
Quantum Langlands duality of representations of {\mathcal{W}}-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2235-2262
- Print publication:
- December 2019
-
- Article
- Export citation
ROUQUIER’S CONJECTURE AND DIAGRAMMATIC ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 16 November 2017, e27
-
- Article
-
- You have access
- Open access
- Export citation
On the Notion of Conductor in the Local Geometric Langlands Correspondence
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 1 / 01 February 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 107-129
- Print publication:
- 01 February 2017
-
- Article
-
- You have access
- Export citation
JOSEPH IDEALS AND LISSE MINIMAL W-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 07 March 2016, pp. 397-417
- Print publication:
- April 2018
-
- Article
- Export citation
Non-stable K1-functors of Multiloop Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 1 / 01 February 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 150-178
- Print publication:
- 01 February 2016
-
- Article
-
- You have access
- Export citation
BGG reciprocity for current algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 09 February 2015, pp. 1265-1287
- Print publication:
- July 2015
-
- Article
- Export citation
Classification of irreducible Harish-Chandra modules over generalized Virasoro algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 697-709
-
- Article
-
- You have access
- Export citation
Semicanonical bases and preprojective algebras II: A multiplication formula
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 5 / September 2007
- Published online by Cambridge University Press:
- 20 September 2007, pp. 1313-1334
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Elliptic determinant evaluations and the Macdonald identities for affine root systems
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 14 July 2006, pp. 937-961
- Print publication:
- July 2006
-
- Article
-
- You have access
- Export citation
Verma Modules and Preprojective Algebras
-
- Journal:
- Nagoya Mathematical Journal / Volume 182 / June 2006
- Published online by Cambridge University Press:
- 11 January 2016, pp. 241-258
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
SIGNED QUIVERS, SYMMETRIC QUIVERS AND ROOT SYSTEMS
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 16 June 2006, pp. 586-606
- Print publication:
- June 2006
-
- Article
- Export citation