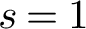 $s=1$
$s=1$
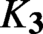 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
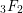 $_{3}F_{2}$
$_{3}F_{2}$
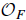
 $K$-Theory Galois Module Structure Invariants
$K$-Theory Galois Module Structure Invariants