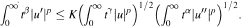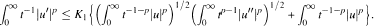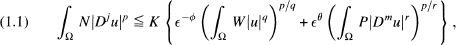4 results
The Brascamp–Lieb Polyhedron
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 870-888
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation
Symmetrization Inequalities for Composition Operators of Carathéodory type
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 2 / September 2003
- Published online by Cambridge University Press:
- 26 September 2003, pp. 396-418
- Print publication:
- September 2003
-
- Article
- Export citation
A Remark on a Weighted Landau Inequality of Kwong and Zettl
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 1 / 01 March 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 34-41
- Print publication:
- 01 March 1995
-
- Article
-
- You have access
- Export citation
Weighted Interpolation Inequalities and Embeddings in Rn
-
- Journal:
- Canadian Journal of Mathematics / Volume 42 / Issue 6 / 01 December 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 959-980
- Print publication:
- 01 December 1990
-
- Article
-
- You have access
- Export citation