A subset ${\mathcal D}$ of a domain $\Omega \subset {\mathbb C}^d$ is determining for an analytic function $f:\Omega \to \overline {{\mathbb D}}$ if whenever an analytic function $g:\Omega \rightarrow \overline {{\mathbb D}}$ coincides with f on ${\mathcal D}$, equals to f on whole $\Omega $. This note finds several sufficient conditions for a subset of the symmetrized bidisk to be determining. For any $N\geq 1$, a set consisting of $N^2-N+1$ many points is constructed which is determining for any rational inner function with a degree constraint. We also investigate when the intersection of the symmetrized bidisk intersected with some special algebraic varieties can be determining for rational inner functions.

In 1955, Lehto showed that, for every measurable function $\psi $ on the unit circle ${\mathbb T}$ , there is a function f holomorphic in the unit disc ${{\mathbb D}}$ , having $\psi $ as radial limit a.e. on ${\mathbb T}$ . We consider an analogous boundary value problem, where the unit disc is replaced by a Stein domain on a complex manifold and radial approach to a boundary point p is replaced by (asymptotically) total approach to p.

In this paper we study holomorphic Legendrian curves in the standard holomorphic contact structure on $\mathbb{C}^{2n+1}$ for any $n\in \mathbb{N}$. We provide several approximation and desingularization results which enable us to prove general existence theorems, settling some of the open problems in the subject. In particular, we show that every open Riemann surface $M$ admits a proper holomorphic Legendrian embedding $M{\hookrightarrow}\mathbb{C}^{2n+1}$, and we prove that for every compact bordered Riemann surface $M={M\unicode[STIX]{x0030A}}\,\cup \,bM$ there exists a topological embedding $M{\hookrightarrow}\mathbb{C}^{2n+1}$ whose restriction to the interior is a complete holomorphic Legendrian embedding ${M\unicode[STIX]{x0030A}}{\hookrightarrow}\mathbb{C}^{2n+1}$. As a consequence, we infer that every complex contact manifold $W$ carries relatively compact holomorphic Legendrian curves, normalized by any given bordered Riemann surface, which are complete with respect to any Riemannian metric on $W$.

We establish the existence of power series in ${{\mathbb{C}}^{N}}$ with the property that the subsequences of the sequence of partial sums uniformly approach any holomorphic function on any well chosen compact subset outside the set of convergence of the series. We also show that, in a certain sense, most series enjoy this property.

We study complex commutative Banach algebras (and, more generally, continuous inverse algebras) in which the holomorphic functions of a fixed $n$-tuple of elements are dense. In particular, we characterize the compact subsets of ${{\mathbb{C}}^{n}}$ which appear as joint spectra of such $n$ -tuples. The characterization is compared with several established notions of holomorphic convexity by means of approximation conditions.

Considering a mapping $g$ holomorphic on a neighbourhood of a rationally convex set $K\subset {{\mathbb{C}}^{n}}$, and range into the complex projective space $\mathbb{C}{{\mathbb{P}}^{m}}$, the main objective of this paper is to show that we can uniformly approximate $g$ on $K$ by rational mappings defined from ${{\mathbb{C}}^{n}}$ into $\mathbb{C}{{\mathbb{P}}^{m}}$. We only need to ask that the second Čech cohomology group ${{\overset{\scriptscriptstyle\smile}{H}}^{2}}\left( K,\mathbb{Z} \right)$ vanishes.

We characterize composition operators on spaces of real analytic functions which at the same time have closed image and are open onto their images. Under some mild assumptions, we also characterize composition operators with closed range and composition operators open onto their images.

Continuous mappings defined from compact subsets $K$ of complex Euclidean space ${{\mathbb{C}}^{n}}$ into complex projective space ${{\mathbb{P}}^{m}}$ are approximated by rational mappings. The fundamental tool employed is homotopy theory.

On a locally rectifiable arc going to infinity, each continuous function can be approximated by entire functions.

In this paper we obtain the asymptotic expansions of the Carathéodory and Kobayashi metrics of strictly pseudoconvex domains with C∞ smooth boundaries in ℂn. The main result of this paper can be stated as following:

Main Theorem. Let Ω be a strictly pseudoconvex domain with C∞ smooth boundary. Let FΩ(z,X) be either the Carathéodory or the Kobayashi metric of Ω. Let δ(z) be the signed distance from z to ∂Ω with δ(z) < 0 for z ∊ Ω and δ(z) ≥ 0 for z ∉ Ω. Then there exist a neighborhood U of ∂Ω, a constant C > 0, and a continuous function C(z,X):(U ∩ Ω) × ℂn -> ℝ such that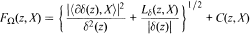

and|C(z,X)| ≤ C|X| for z ∊ U ∩ Ω and X ∊ ℂn

Let L1, L2 ⊂ Cn be two totally real subspaces of real dimension n, and such that L1 ∩ L2 = {0}. We show that continuous functions on L1 ∪L2 allow Carleman approximation by entire functions if and only if L1 ∪L2 is polynomially convex. If the latter condition is satisfied, then a function f:L1 ∪L2 —> C such that f|LiCk(Li), i = 1,2, allows Carleman approximation of order k by entire functions if and only if f satisfies the Cauchy-Riemann equations up to order k at the origin.