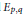5 results
ERRATUM/CORRIGENDUM, OCTOBER 2020, FOR ’A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION’ (J. INST. MATH. JUSSIEU 19 (2018), 1509–1519)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 16 April 2021, pp. 275-277
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
A BOGOMOLOV UNOBSTRUCTEDNESS THEOREM FOR LOG-SYMPLECTIC MANIFOLDS IN GENERAL POSITION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 09 November 2018, pp. 1509-1519
- Print publication:
- September 2020
-
- Article
- Export citation
Dynamical construction of Kähler-Einstein metrics
-
- Journal:
- Nagoya Mathematical Journal / Volume 199 / September 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 107-122
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Embeddability of Some Three-Dimensional Weakly Pseudoconvex
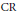 $\text{CR}$ Structures
$\text{CR}$ Structures
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 1 / 01 March 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 133-143
- Print publication:
- 01 March 2004
-
- Article
-
- You have access
- Export citation
A Note on the Analogue of the Bogomolov Type Theorem on Deformations of CR-Structures
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 8-12
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation

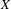
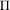
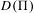
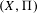
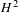
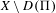
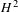
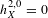
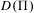
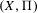
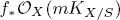 with semipositive curvature in the sense of Nakano.
with semipositive curvature in the sense of Nakano.