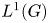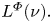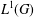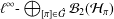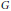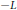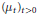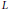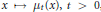6 results
Convolution structures for an Orlicz space with respect to vector measures on a compact group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 87-98
-
- Article
- Export citation
CHARACTERISATION OF THE FOURIER TRANSFORM ON COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 13 November 2015, pp. 467-472
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Hypoelliptic Bi-Invariant Laplacians on Infinite Dimensional Compact Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 4 / 01 August 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 691-725
- Print publication:
- 01 August 2006
-
- Article
-
- You have access
- Export citation
Second Order Operators on a Compact Lie Group
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 1 / 01 February 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 99-113
- Print publication:
- 01 February 2005
-
- Article
-
- You have access
- Export citation
Vector-valued Hausdorff–Young inequality on compact groups
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 88 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 14 April 2004, pp. 796-816
- Print publication:
- May 2004
-
- Article
- Export citation
Group Actions and Singular Martingales II, The Recognition Problem
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 2 / 01 April 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 431-448
- Print publication:
- 01 April 2004
-
- Article
-
- You have access
- Export citation