9 results
A Chebyshev-type alternation theorem for best approximation by a sum of two algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 971-978
-
- Article
- Export citation
Horseshoes and Lyapunov exponents for Banach cocycles over non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 674-704
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Compact and weakly compact Lipschitz operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 1002-1020
- Print publication:
- June 2023
-
- Article
- Export citation
COMPACT FACTORIZATION OF OPERATORS WITH λ-COMPACT ADJOINTS
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 20 March 2017, pp. 123-134
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
Compactness in quasi-Banach function spaces and applications to compact embeddings of Besov-type spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 905-927
- Print publication:
- October 2016
-
- Article
- Export citation
On the loss of compactness in the vectorial heteroclinic connection problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 595-608
- Print publication:
- June 2016
-
- Article
- Export citation
ON A QUESTION OF BOURAS CONCERNING WEAK COMPACTNESS OF ALMOST DUNFORD–PETTIS SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 111-114
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
AN OPERATOR SUMMABILITY OF SEQUENCES IN BANACH SPACES
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 13 August 2013, pp. 427-437
- Print publication:
- May 2014
-
- Article
-
- You have access
- Export citation
Application of Measure of Noncompactness to Infinite Systems of Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 388-394
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation

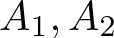
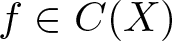
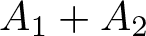
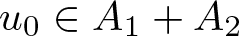
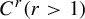
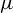
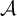
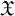
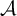
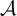
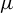
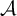
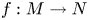
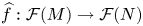
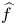
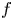
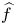
 , into Lorentz-type spaces.
, into Lorentz-type spaces.